Keywords

1 Introduction

Robotic systems designed for collaborative work with humans have been a focus of research for last decades. Especial interest has been placed on assistive and rehabilitation devices, such as exoskeletons. Such robots not only allow to improve the life quality for the patients, but also can be used to make the work of medical personnel easier, simplifying operations related to exercise, patients transportation and others [1,2,3,4].

Successful development of exoskeletons and similar technology depends on solving a number of control problems. These include guaranty of vertical stability of the device when it performs motion [4,5,6,7,8,9], planning footsteps that can be safely executed [10, 11], tuning controllers [12,13,14,15], designing algorithms for processing sensor information [16] and deriving methods for determining human intentions and integration of these to the control loop. Solutions for some of these problems have been proposed. However, the problem of introducing the human into the control loop of an exoskeleton remains open.

There are a number of works on using EMG in order connect human and the exoskeleton [17,18,19]. Alternative approaches can include use of pressure sensors [20]. In this paper we consider an alternative approach, based on use of elastic connector elements between the human operator and the exoskeleton links. The elastic properties of these connectors can be used to measure the relative motions between the human and the robot’s links. There are previous works that considered introducing elastic elements into the exoskeleton structure, focusing on minimizing the energy consumption [21,22,23,24,25]. However, the possibility of using the properties of these elements in the control loop have not been studied yet.

2 Description of the Sensory Connector

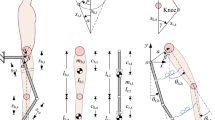
In this section, we introduce the model of the sensory connector device. The device can be installed at each link of an exoskeleton. Figure 1 illustrates the places where the sensory connector device can be installed.

Fig. 1.
figure 1

General view of ExoLite exoskeleton with a user with fixed using connector pads; 1 – pads for torso connectors, 2 and 3 – pads for hip connectors, 4 – pad for shin connector, 5 – pad for foot connector.

Full size image

The pads shown in Fig. 1 are typical for a range of exoskeleton devices, as they are used to fixate the patient on the device, to make wearing the exoskeleton for long durations of time more comfortable, and to minimize the risks of traumatic events related to human body coming into contact with moving mechanical parts. Therefore, installation of sensory connectors should be simple for a range of exoskeleton models and would not require significant changes in their designs.

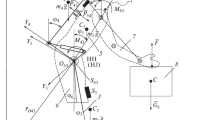
Connectors can be modelled as a system of rigid and elastic elements, equipped with pressure sensors. The scheme of the sensory connector is shown in Fig. 2.

Fig. 2.
figure 2

The scheme of the sensory connector device; 1 – the cross section of the human limb fixed in the connector, 2 – frame of the sensory connector, 3, 4 – spring and damper between the fixator and the connector frame, 5 – pressure sensors, 6 – the exoskeleton’s link to which the connector is attached.

Full size image

One of the features of this system is that it allows inferring the movements of the human body relative to the exoskeleton links, using the pressure sensor feedback. The positions and velocities of the exoskeleton links in turn are measured by its sensor system (including encoders and MEMS gyroscopes). This allows to estimate the absolute position and velocity of the human body, which can be used to organized the human-driven control.

3 Model Description

Let us consider the motion of the frame of the connector relative to the human body part (from here on we refer to it as “leg”) in a one-dimensional case. As it was shown in Fig. 2, the two are connected via elastic elements and dampers. The frame is actuated, where are the leg’s motion can be arbitrary. Figure 3 shows a simplified model of the integration between the leg and the frame.

Fig. 3.
figure 3

The diagram of the integration between the leg and the frame; 1 – leg, 2 – the connector frame.

Full size image

The Fig. 3 uses the following notation: \( x_{1} \) is the position of the leg, \( x_{2} \) is the position of the frame, \( F_{12} \) is the force generated by the elastic element between the leg and the connector frame, \( F_{a} \) is the actuator force and \( F_{p} \) is the perturbation force.

The equation of motion for the frame can be written as follows:

$$ \left\{ {\begin{array}{*{20}l} {m_{2} \ddot{x}_{2} = F_{12} + F_{a} + F_{p} } \hfill \\ {F_{12} = \mu_{e} (\dot{x}_{1} - \dot{x}_{2} ) + c_{e} (x_{1} - x_{2} )} \hfill \\ \end{array} } \right., $$
(1)

where \( m_{2} \) is the equivalent mass of the frame, \( \mu_{e} \) and \( c_{e} \) are the coefficients of the spring-damper system.

The perturbation force \( F_{p} \) is modelled as follows:

$$ F_{p} = - \mu_{p} \dot{x}_{2} - k_{p} {\text{sign}}(\dot{x}_{2} ), $$
(2)

where \( \mu_{p} \) and \( k_{p} \) are constant coefficients, which in the simulation are taken as random numbers with normal distribution, parametrized by the means \( \mu_{p,mean} \), \( k_{p,mean} \) and standard deviations \( \sigma_{p,\mu } \), \( \sigma_{p,k} \).

The actuator equation have the following form:

$$ \left\{ {\begin{array}{*{20}l} {L_{a} \frac{dI}{dt} + R_{a} I + C_{e} \eta \dot{x}_{2} = u} \hfill \\ {F_{a} = C_{\tau } \eta I} \hfill \\ \end{array} } \right., $$
(3)

where \( L_{a} \) is the inductance of the motor coils, \( R_{a} \) is the resistance, \( C_{e} \) and \( C_{\tau } \) are the motor constants, \( \eta \) is the actuator gear ration, \( I \) is the current and \( u \) is the voltage supplied to the motor.

4 Control System Design

In this work we consider a feedback control system that minimizes the difference between \( x_{1} \) and \( x_{2} \). This can be achieved with a proportional-derivative controller. There are examples of using this type of controller with exoskeletons described in [15, 26]. For the system described here this controller takes the following form:

where \( e = x_{1} - x_{2} \) is the control error,

$$ u = K_{d} \dot{e} + K_{p} e, $$
(4)

\( K_{d} \) and \( K_{p} \) are controller gains. Paper [14] describes tuning this type of controller for multi-input multi-output systems using Sobol sequences and work [27] compares global optimization methods for this task.

In order to compute the control error the value of \( x_{1} \) needs to be measured. This value can be calculated using the force sensor data, measuring the value of the force \( F_{12} \). Let us consider the case when the force \( F_{12} \) is measured by a sensor with additive white noise and a quantized output. The model for such sensor is shown below:

$$ F_{12}^{m} = \xi \bmod (F_{12} + \rho ,\;\;\xi ), $$
(5)

where \( \xi \) is the accuracy of the sensor, \( \rho \) is the additive noise and \( F_{12}^{m} \) is the measured value of the force \( F_{12} \).

There are two alternative approaches to using the feedback from the force sensor to compute \( x_{1} \). First approach requires an assumption that the value of \( \mu_{e} \) is sufficiently low. Then it is possible to produce the following estimate of \( x_{1} \):

$$ x_{1}^{m} = {{F_{12}^{m} } \mathord{\left/ {\vphantom {{F_{12}^{m} } {c_{e} + x_{2} }}} \right. \kern-0pt} {c_{e} + x_{2} }}, $$
(6)

where \( x_{1}^{m} \) is the estimation of \( x_{1} \).

The second approach does not require the assumption about the value of \( \mu_{e} \), but it requires the value of \( x_{1} \) measured on the previous iteration of the algorithm (denoted as \( x_{1}^{m} (t - \Delta t) \) to be known:

$$ \left[ {\begin{array}{*{20}c} {x_{1}^{m} (t)} \\ {\dot{x}_{1}^{m} (t)} \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {c_{e} } & {\mu_{e} } \\ 1 & { - \Delta t} \\ \end{array} } \right]^{ - 1} \left[ {\begin{array}{*{20}c} {F_{12}^{m} + c_{e} x_{2} + \mu_{e} \dot{x}_{2} } \\ {x_{1}^{m} (t - \Delta t)} \\ \end{array} } \right], $$
(7)

Unlike the first method, this approach requires information about velocity \( \dot{x}_{2} \) and its accuracy is affected by the error in the initial value estimation for \( x_{1} \).

5 Simulation Results

In this section, we present the simulation results for the system described previously. The simulation was carried out for the following parameters of the model: \( m_{2} = 1\,{\text{kg}} \), \( \mu_{e} = 1\,{\text{Ns/m}} \), \( c_{e} = 100\,{\text{N/m}} \), \( L_{a} = 0.1\,{\text{H}} \), \( R_{a} = 1\,{\text{Om}} \), \( C_{e} = 0.01\,{\text{Vs/m}} \), \( C_{\tau } = 0.01\,{\text{N/A}} \), \( \eta = 50 \), \( K_{d} = 100 \), \( K_{p} = 1000 \), \( \xi = 1\,{\text{N}} \), \( \rho \in [\begin{array}{*{20}c} { - 0.5} & {0.5} \\ \end{array} ]\,{\text{N}} \). Motion of the leg is modeled as \( x_{1} (t) = 0.05\sin (10t) \).

Figure 4 shows the time functions for \( x_{1} (t) \) and \( x_{2} (t) \) obtained for the case, when formula (6) was used to calculate \( x_{1}^{m} \). The first derivative of that value was obtained through finite differences.

Fig. 4.
figure 4

Time functions of the positions x1(t) and x2(t).

Full size image

Figure 4 shows that the estimation \( x_{1}^{m} \) becomes slightly more accurate after the transient process is over, however it does not converge to the actual value \( x_{1} (t) \) and remains noisy. The value of \( x_{2} (t) \) demonstrates phase lag and lesser amplitude compared to \( x_{1} (t) \).

Figure 5 shows the work of the force sensor, the feedback from which is used to calculate \( x_{1}^{m} \).

Fig. 5.
figure 5

Time functions of the measured and real values of F12(t).

Full size image

We can see that the sensor introduces noticeable measurement errors, which in turn affects the quality of estimation for \( x_{1}^{m} (t) \).

Figure 6 shows time functions for \( x_{1} (t) \) and \( x_{2} (t) \) from the same experiment done with the estimation function (7). For this and following experiments we introduce initial estimation error for \( x_{1}^{m} (t) \): \( x_{1} (0) - x_{1}^{m} (0) = 0.02\,{\text{M}} \).

Fig. 6.
figure 6

Time functions of the positions x1(t) and x2(t) for the case when estimation (7) is used.

Full size image

Comparing these results with what was shown in Fig. 4 we can see that the jitter of the estimated value \( x_{1}^{m} (t) \) has lessened significantly. The alterations in the behavior of \( x_{2} (t) \) are minimal.

To analyze the influence the parameters of the control input and the controller settings have on the behavior of the control system we can look at its frequency response. Figure 7 shows how the amplitude ratio of the input and the output signals change with the frequency of the control input. The graph was plotted for different values of proportional gain of the controller: \( K_{p} = 100,\;200 \) and 500.

Fig. 7.
figure 7

Amplitude ratio of the input and the output signals for the control system plotted versus the frequency of the control input.

Full size image

As we can see, there is a weak maximum in the amplitude ratio achieved at the control input frequencies at 33–35 rad/s. Change in the proportional controller gain scales the graphs without shifting this peak.

Figure 8 shows how the phase difference between the input and the output signals changes with the frequency of the control input. The phase was calculated using the algorithm [28]. The graph was plotted for the same three values of the proportional controller gain.

Fig. 8.
figure 8

Phase difference between the input and the output signals for the control system plotted versus the frequency of the control input.

Full size image

We can notice that the phase lag (in absolute values) increases with the frequency and shows a minimum at 2–3 rad/s. The increase in the phase difference might be significant for the user of the device, as it affects the responsiveness of the system. The effect of both lag and amplitude errors on the perceived comfort of using exoskeletons needs to be investigated further.

6 Conslusions

In this paper, the problem controlling a human-robot system have been considered. The design of the connector element outfitted with pressure sensors have been presented. It was proposed to use the pressure sensor in order to estimate the relative position of the human body part and the robot link. This information can then be used in the feedback control loop. The simulations were conducted with a nonlinear pressure sensor module which included additive white noise and quantization of the output signal. PD controller was used for stabilization and tracking.

Two methods for retrieving the positional information from the pressure sensor data has been proposed, their comparison was shown in simulation. The result suggested that both methods are viable, however they require different assumptions. It was shown that the proposed control system design can demonstrate lag and magnitude errors when tracking periodic signal.

The future work includes integrating the proposed sensor data processing methods into the full scale control system of the robot and combining it with other sensor processing algorithms.