Overview of High-Energy X-Ray Diffraction Microscopy (HEDM) for Mesoscale Material Characterization in Three-Dimensions

Abstract

Over the past two decades, several non-destructive techniques have been developed at various light sources for characterizing polycrystalline materials microstructure in three-dimensions (3D) and under various in-situ thermo-mechanical conditions. High-energy X-ray diffraction microscopy (HEDM) is one of the non-destructive techniques that facilitates 3D microstructure measurements at the mesoscale. Mainly, two variations of HEDM techniques are widely used: (1) Near-field (nf) and (2) far-field (ff) which are employed for non-destructive measurements of spatially resolved orientation ($\sim$1.5 $\upmu$m and 0.01$^\circ$), grain resolved orientation, and elastic strain tensor ($\sim$10$^{-3}$–10$^{-4}$) from representative volume elements (RVE) with hundreds of bulk grains in the measured microstructure (mm$^{3}$). To date HEDM has been utilized to study variety of material systems under quasi-static conditions, while tracking microstructure evolution. This has revealed new physical mechanisms that were previously not observed through destructive testing and characterization. Furthermore, measured 3D microstructural evolution data obtained from HEDM are valuable for informing, developing, and validating microstructure aware models for accurate material property predictions. A path forward entails utilizing HEDM for initial material characterization for enabling microstructure evolution measurements under dynamic conditions.

7.1 Introduction

The understanding of materials at the mesoscale (1–100 $\upmu$m) is of extreme importance to basic energy science because the properties of materials, critical to large-scale behavior, are impacted by local-scale heterogeneities such as grain boundaries, interfaces, and defects [1]. One challenge of mesoscale science is capturing a 3D view inside of bulk materials, at sub-grain resolution ($\sim$1 $\upmu$m), while undergoing dynamic change. Techniques, such as electron microscopy, neutron scattering, or micro-computed tomography ($\mu$-CT) are limited in being either destructive, providing only average data, or providing only density data, respectively. High energy X-ray diffraction microscopy (HEDM) is a novel, non-destructive method for capturing 3D mesoscale structure and evolution inside of material samples of $\sim$1 mm size, with $\sim$1 $\upmu$m spatial and $\sim$0.1$^{\circ }$ grain orientation resolution. In this chapter, we give a brief overview of existing diffraction and imaging techniques for material characterization. In particular, HEDM datasets are discussed and a few examples of microstructure evolution under quasi-static conditions are presented to demonstrate the unique advantages provided by HEDM. However, this chapter will not attempt to summarize all the ongoing work on the subject. Additionally, future prospects of utilizing HEDM for enabling dynamic measurements are briefly discussed.

7.1.1 The Mesoscale

Multi-scale materials modeling is extremely challenging because it must cover many orders of magnitude of length scales ranging from the atomistic 10$^{-10}$ m to the continuum >10$^{-3}$ m [1, 2]. Because of the difficulty of this task, there is a knowledge gap in terms of our ability to accurately pass insight from atomistic calculations/simulations to continuum scale predictions of engineering performance. At the lowest length scales, completely general and extremely accurate atomistic and molecular dynamics models exist that can simulate the behavior of many material systems based on fundamental physics simulations. Unfortunately, such models are extremely computationally intensive and limited to systems of hundreds to thousands of atoms even when using state of the art super computers. Therefore, while they can realistically predict the behavior of groups of atoms, it is impossible to scale them to sizes useful for manufacturing. At the other end of the spectrum, continuum mechanics models are mainly empirical and can reasonably predict bulk behaviors for a large family of materials. Extensive empirical tests have been carried out over many years to build databases on material properties such as ductility, elastic modulus, Poisson’s ratio, shear modulus, yield strength for variety of material systems. The measured information are then incorporated into finite element models for predicting materials properties as well as engineering performance. However, such extensive experimental testing is inefficient, expensive, and time consuming.

Between these two extreme ends lies the mesoscale, a length scale at which current models are the least predictive and various model predictions exhibit extremely large variance. Structural materials are polycrystalline in nature with each individual grain experiencing constraints from its local neighborhood inducing heterogeneities and incompatibilities in adjacent grains. Complex properties and behaviors arise due to interaction between large population of heterogeneities such as defects, grain boundaries, phase boundaries, and dislocations. For instance, the relationship between “hot spots” in micro-mechanical fields and microstructural features such as grain boundaries and interfaces can be connected to material failure [3]. Therefore, the local variation in orientation and strain during plastic deformation are important in understanding damage nucleation in polycrystalline materials.

While constitutive relationships employed in most crystal plasticity simulations show some reasonable agreement with observation in terms of average properties, they are unable to reproduce local variations in orientation or strain [4]. This lack of agreement at the local scale is a direct evidence of our lack of physical understanding of the mesoscale regime. This missing link prevents material scientists from designing new, exotic materials with desired properties such as stronger, more durable, and lighter engineering components utilizing advanced manufacturing or accident tolerant nuclear fuels with higher thermal conductivity. As our understanding of a material’s micro-mechanical properties relies heavily on the accurate knowledge of the underlying microstructure, spatially resolved information on evolution of microstructural parameters is imperative for understanding a material’s internal response to accommodating imposed external loads. Therefore, a major goal of mesoscale science is capturing a 3D view inside of bulk materials, at sub-grain resolution ($\sim$1 $\upmu$m), while undergoing dynamic change.

7.1.2 Imaging Techniques

Various material characterization techniques exist, of which one of the most popular is electron backscatter diffraction (EBSD), a standard technique for crystallographic orientation mapping and is heavily utilized by the materials community for surface characterization [5]. EBSD in concert with serial sectioning using focused ion beam (FIB) provides three-dimensional microstructure data; however, this route is destructive and mostly limited to post-mortem characterizations. Because this method is destructive, a single sample can only be fully characterized in 3D in one single state.

Non-destructive crystal structure determination techniques utilizing X-ray diffraction from a single crystal or powder diffraction for a large ensemble of crystals were first demonstrated over a century ago. However, most samples of interest are polycrystalline in nature, and therefore cannot be studied with a single crystal diffraction technique. In addition, powder diffraction is limited as it applies only to bulk samples with extremely large numbers of grains and provides only averaged measurements.

Nearly two decades ago, an alternate approach, multi-grain crystallography was successfully demonstrated [6], utilizing which 57 grains were mapped, for the first time, in an $\alpha$-Al$_2$O$_3$ material [7, 8]. Since then, utilizing the third and fourth generation light sources, high-energy X-rays (in the energy range of 20–90 keV) based experimental techniques have enabled non-destructive measurements of a range of polycrystalline materials. These techniques have been transformational in advancing material microstructure characterization capability providing high-dimensional experimental data for microstructures in three-dimensions (3D) and their evolution under various in-situ conditions. Moreover, these datasets provide previously inaccessible information at the length scales (i.e. the mesoscale, 1–100 $\upmu$m) relevant for informing and validating microstructure-aware models [2, 9,10,11,12] for linking materials processing-structure/property/performance (PSPP) relationships for advanced engineering applications [1, 13].

Since the first demonstration of 3D measurements, high-energy X-ray-based experimental techniques have advanced considerably, and 3D microstructure measurements are becoming routine. The multi-grain crystallography technique is now commonly referred to as high-energy X-ray diffraction microscopy (HEDM) or 3D X-ray diffraction (3DXRD) [14]. Various suites of HEDM techniques have been developed over the years for probing material microstructure and micro-mechanical field in polycrystals. Typically, the HEDM technique can probe 1 mm diameter samples and provide information on crystallographic orientation and elastic strain tensor averaged over a volume, commonly a grain. For example, near-field HEDM has been employed to study spatially resolved microstructures (orientation field, grains structure and morphology, sub-structure) and their evolution under thermo-mechanical conditions [15,16,17,18,19,20,21,22]. Far-field HEDM has been employed to study grain resolved micro-mechanics and variation in inter- and intra-granular stress states [6, 7, 23,24,25,26,27,28,29,30,31,32]. Utilizing both spatially resolved orientation and grain resolved elastic strains, stress evolution in Ti alloys have been studied [33,34,35]. Recently the HEDM technique has been extended to study deformation in shape memory alloys [36] and microstructure characterization of nuclear fuel materials [37, 38].

Apart from HEDM, other microstructure characterization techniques have been developed in parallel, utilizing either high-energy X-rays or neutrons for diffraction and imaging. Diffraction contrast tomography (DCT) is one such complementary non-destructive method that combines diffraction and tomographic techniques for mapping crystallographic orientation and grain morphology, in near pristine samples [39,40,41]. Micro-tomography provides additional density evolution information, ideal for imaging density contrast resulting from materials with high contrast in atomic number (Z) or contrast due to the presence of pores and cracks in the materials. Differential-aperture X-ray microscopy (DAXM) is another X-ray based technique for near-surface measurement, which enables in-situ material microstructure evolution measurements under various thermo-mechanical conditions [42]. Similarly, neutron diffraction and imaging based techniques can also provide non-destructive bulk measurements of structure and mechanical strains under in-situ conditions [43]. In this chapter, we will mainly focus on the HEDM technique and its application.

The remainder of the chapter is organized as follows. A brief background on physics of diffraction is presented in Sect. 7.2. In Sect. 7.3, the basic principle of HEDM technique and experimental geometry are presented. In addition, information on various tools that have been developed in the past decade for analyzing HEDM data are also provided. In Sect. 7.4, application of HEDM is presented where examples from literature on various experiments and material systems are presented and results are discussed. In Sect. 7.5, the current state is summarized and perspectives for future applications of HEDM and its relevance for future light sources are discussed.

7.2 Brief Background on Scattering Physics

In this section, basic concepts of the physics of elastic scattering are presented to establish a relationship between diffracted light and crystal structure, our approach is based on [44]. Diffraction is a result of constructive interference of the scattered wave after incident X-rays are scattered by electrons. Elastic scattering assumes that the incident and scattered X-ray photons have the same energy, that no energy is absorbed by the material during the scattering process. Consider an incident beam of X-rays as an electromagnetic plane wave:

$$\begin{aligned} E(t)=E_0 \cos (2 \pi \nu t ), \end{aligned}$$

(7.1)

with amplitude $\mathrm {E_0}$ and frequency $\nu$. The interaction between the X-ray beam and an isolated electron can be approximated by forced simple harmonic motion of the form:

$$\begin{aligned} \ddot{x} = -\omega ^2_0x - b\dot{x} + \frac{q_{e}}{m_{e}}E(t), \end{aligned}$$

(7.2)

where $\mathrm {x}$ is the displacement of the electron from equilibrium, $\omega _0$ is the natural frequency of the system, $q_{e}$ and $m_{e}$ are the mass and charge of the electron, b is a damping term, and the third term on RHS is the force exerted on the electron by the electric field. According to the approximation (7.2), the electron oscillates according with the trajectory:

$$\begin{aligned} x(t) = A\cos (2 \pi \nu t + \phi ) + e^{-\frac{bt}{2}}f(t). \end{aligned}$$

(7.3)

The term $e^{-\frac{bt}{2}}f(t)$ quickly decays and we are left with oscillations of the form

$$\begin{aligned} x(t) = A\cos (2 \pi \nu t + \phi ), \end{aligned}$$

(7.4)

where both the amplitude $A=A(\nu )$ and the phase $\phi =\phi (\nu )$ depend on $\nu$. The most important feature of (7.4) is that the electron oscillates at the same frequency as the driving force, and thereby emits light which has the same wavelength as the incident beam.

When a group of electrons $(e_1, \ldots , e_n)$ within an atom are illuminated by a plane wave of coherent light of the form (7.1), an observer at some location O will see, from each electron, a phase shifted electric field of the form:

$$\begin{aligned} \epsilon _j(t)= & {} A_j\cos \left( 2\pi \nu t - \frac{2\pi l_j}{\lambda } \right) \nonumber \\= & {} A_j \cos (2\pi \nu t) \cos \left( \frac{2\pi l_j}{\lambda } \right) + A_j \sin (2\pi \nu t) \sin \left( \frac{2\pi l_j}{\lambda } \right) , \end{aligned}$$

(7.5)

with $\lambda$ being the light’s wavelength and the amplitudes $A_j$ and phase shifts $\frac{2\pi l_j}{\lambda }$ depend on the path lengths from the wave front to the observers, $l_j$. The total electric field observed at O is the sum of all of the individual electron contributions:

$$\begin{aligned} \epsilon (t)= & {} \sum _j \epsilon _j (t) \nonumber \\= & {} \sum _j A_j \cos (2\pi \nu t) \cos \left( \frac{2\pi l_j}{\lambda } \right) + \sum _j A_j \sin (2\pi \nu t) \sin \left( \frac{2\pi l_j}{\lambda } \right) \nonumber \\= & {} \cos (2\pi \nu t)\underbrace{\sum _j A_j \cos \left( \frac{2\pi l_j}{\lambda } \right) }_{A\cos (\phi )} + \sin (2\pi \nu t) \underbrace{\sum _j A_j\sin \left( \frac{2\pi l_j}{\lambda } \right) }_{A\sin (\phi )} \nonumber \\= & {} A\cos (2\pi \nu t) \cos (\phi ) + A\sin (2\pi \nu t) \sin (\phi ) \nonumber \\= & {} A \cos (2 \pi \nu t - \phi ). \end{aligned}$$

(7.6)

The actual detected quantity is not the instantaneous diffracted electric field (7.6), but rather the intensity $I = \frac{cE^2}{8\pi }$, where

$$\begin{aligned} E^2 = \left( \sum _n E_n \cos \left( \frac{2 \pi l_n}{\lambda } \right) \right) ^2 + \left( \sum _n E_n \sin \left( \frac{2 \pi l_n}{\lambda } \right) \right) ^2. \end{aligned}$$

(7.7)

Or, using complex notation,

$$\begin{aligned} \epsilon _j = A_j e^{i (2\pi \nu t - 2\pi l_j / \lambda )} \end{aligned}$$

(7.8)

we can simply write $\epsilon \epsilon ^\star = A^2$.

7.2.1 Scattering by an Atom

When considering scattering by a group of electrons in an atom the convention is to consider the center of the atom as the origin, O, the electrons located at positions $\mathbf {r}_n$, and an observer at position $\mathbf {P}$. We consider a plane wave of light incident on the plane passing through the origin, from which there is a distance $l_1$ to an electron at position $\mathbf {r}_n$, as shown on the left side of Fig. 7.1. Relative to the wavefront at O, the field acting on electron n is then given by

$$\begin{aligned} \epsilon _n = A_n \cos \left( 2\pi \nu t - \frac{2\pi l_1}{\lambda } \right) \end{aligned}$$

(7.9)

and for an observer at position P, the field is

$$\begin{aligned} \epsilon _n = \frac{A_n e^2}{mc^2 l_2} \cos \left( 2\pi \nu t - \frac{2\pi }{\lambda } \left( l_1 + l_2 \right) \right) . \end{aligned}$$

(7.10)

Assuming that both the source and observation distances are much larger than $|r_n|$, we make the simplifying assumptions

$$\begin{aligned} l_2 \rightarrow R, \quad l_1 + l_2 \rightarrow r_n \cdot s_0 + R - r_n \cdot s = R - (s-s_0) \cdot r_n. \end{aligned}$$

(7.11)

Summing over all instantaneous fields at P we are left with

$$\begin{aligned} \epsilon = \frac{Ae^2}{mc^2R}e^{2\pi i \left( \nu t - R/\lambda \right) } \sum _n e^{(2\pi i /\lambda )(s-s_0)\cdot r_n}. \end{aligned}$$

(7.12)

Fig. 7.1

Diffraction from the electrons in an atom with the approximation that $R \gg |\mathbf {r}_n|$

Rather than considering each electron individually the quantum mechanics inspired approach is to consider a charge density $\rho$, such that $\rho dV$ is the ratio of charge in the volume dV relative to the charge of one electron. The sum (7.12) is then replaced with the integral

$$\begin{aligned} \epsilon _e = \frac{A e^2}{mc^2 R} e^{2\pi i \left( \nu t - R/\lambda \right) } \int e^{(2\pi i /\lambda )(s-s_0)\cdot r_n}\rho dV, \end{aligned}$$

(7.13)

where

$$\begin{aligned} f_e = \int e^{(2\pi i /\lambda )(s-s_0)\cdot r_n}\rho dV \end{aligned}$$

(7.14)

is typically referred to as the scattering factor per electron. The equation for $f_e$ is simplified by assuming spherical symmetry for the charge distribution $\rho = \rho (r)$. Then, considering right side of Fig. 7.1, $(s-s_0) \cdot r = 2\sin \theta \cos \varphi$, and after performing integration with respect to $\varphi$ we get

$$\begin{aligned} f_e = \int 4\pi r^2 \rho (r) \frac{\sin kr}{kr}dr, \end{aligned}$$

(7.15)

where $k=\frac{4\pi \sin \theta }{\lambda }$.

For a collection of electrons in an atom we simply sum all of the contributions:

$$\begin{aligned} f = \sum _{n}f_{e,n} = \sum _{n}\int \limits _{0}^{\infty }4\pi r^2 \rho _n(r)\frac{\sin (kr)}{kr}dr, \end{aligned}$$

(7.16)

this sum is known as the atomic scattering factor and gives the amplitude of scattered radiation per atom. The scattering factor given by (7.16) is only accurate when the X-ray wavelength is much smaller than any of the absorption edge wavelengths in the atom and when the electron distribution has spherical symmetry. For wavelengths comparable to absorption edge wavelengths, dispersion correction factors are necessary.

Fig. 7.2

Definition of the hkl planes relative to the crystal axes $a_j$

7.2.2 Crystallographic Planes

We consider a crystal with crystal axes $\left\{ \mathbf {a}_1, \mathbf {a}_2, \mathbf {a}_3 \right\}$, such that the position of an atom of type n in a unit cell $m_1m_2m_3$ is given by the vector $\mathbf {R}_m^n = m_1\mathbf {a}_1 + m_2\mathbf {a}_2 + m_3+\mathbf {a}_3 + \mathbf {r}_n$. In order to derive the Bragg’s law for such a crystal, we must consider the crystallographic planes hkl as shown in Fig. 7.2, where the first plane passes through the origin, O, and the next intercepts the crystal axes at locations $a_1/h$, $a_2/k$, $a_3/l$. The Bragg law depends on the orientation and spacing of these hkl, both properties are conveniently represented by the vector $\mathbf {H}_{hkl}$ which is normal to the planes and whose magnitude is reciprocal to the spacing, where the values (h, k, l) are commonly referred to as the Miller indices. In order to represent the $\mathbf {H}_{hkl}$ vectors for a given crystal, we introduce a reciprocal basis, $\left\{ \mathbf {b}_1, \mathbf {b}_2, \mathbf {b}_3 \right\}$, which is defined based on the crystal axes, given by:

$$\begin{aligned} \mathbf {b}_1 = \frac{\mathbf {a}_2 \times \mathbf {a}_3}{\mathbf {a}_1 \cdot \mathbf {a}_2 \times \mathbf {a}_3}, \qquad \mathbf {b}_2 = \frac{\mathbf {a}_3 \times \mathbf {a}_1}{\mathbf {a}_1 \cdot \mathbf {a}_2 \times \mathbf {a}_3}, \qquad \mathbf {b}_3 = \frac{\mathbf {a}_1 \times \mathbf {a}_2}{\mathbf {a}_1 \cdot \mathbf {a}_2 \times \mathbf {a}_3}. \end{aligned}$$

(7.17)

These vectors are defined such that each reciprocal vector $\mathbf {b}_i$ is perpendicular to the plane defined by the two crystal axes of the other indices, $\mathbf {a}_{j \ne i}$. Furthermore, the $\mathbf {a}_i$ and $\mathbf {b}_j$ vectors satisfy the following scalar products:

$$\begin{aligned} \mathbf {a}_i \cdot \mathbf {b}_i = 1, \qquad \mathbf {a}_i \cdot \mathbf {b}_j = 0, \qquad \Longrightarrow \qquad \mathbf {a}_i \cdot \mathbf {b}_j = \left\{ \begin{array}{cc}1 &{} i=j \\ 0 &{} i \ne j .\end{array}\right. \end{aligned}$$

(7.18)

Any $\mathbf {H}_{hkl}$ vector can then be written as the linear combination

$$\begin{aligned} \mathbf {H}_{hkl} = h\mathbf {b}_1 + k\mathbf {b}_2 + l\mathbf {b}_3, \end{aligned}$$

(7.19)

and it can be easily calculated that if the perpendicular spacing between hkl planes is $d_{hkl}$, then

$$\begin{aligned} d_{hkl} = \frac{1}{|\mathbf {H}_{hkl}|}. \end{aligned}$$

(7.20)

The usefulness of the $\mathbf {H}_{hkl}$ vector is that the Bragg condition can be concisely stated as:

$$\begin{aligned} \frac{\mathbf {s}- \mathbf {s}_0}{\lambda } = \mathbf {H}_{hkl}, \end{aligned}$$

(7.21)

where $\mathbf {s}$ and $\mathbf {s}_0$ are unit vectors in the direction of the incident and diffracted light, as shown in Fig. 7.3. Equation 7.21 simultaneously guarantees that the incident and diffracted beam make equal angles with the diffracting planes and taking the magnitude of either side gives us:

$$\begin{aligned} \left| \frac{\mathbf {s}- \mathbf {s}_0}{\lambda } \right| = \frac{2\sin ( \theta )}{\lambda } = \left| \mathbf {H}_{hkl} \right| = \frac{1}{d_{hkl}}, \end{aligned}$$

(7.22)

which is equivalent to the usual form of the Bragg law $\lambda = 2d_{hkl}\sin (\theta )$.

Fig. 7.3

Bragg law in terms of $\mathbf {H}_{hkl}$

7.2.3 Diffraction by a Small Crystal

Consider a monochromatic beam of wavelength $\lambda$ with direction of propagation $\mathbf {s}_0$ incident on an atom at position $\mathbf {R}^n_m = m_1\mathbf {a}_1 + m_2\mathbf {a}_2 + m_3\mathbf {a}_3 + \mathbf {r}_n$. The diffracted light observed at point $\mathbf {P}$, as shown in Fig. 7.4, is given by

$$\begin{aligned} \epsilon _p = \frac{E_0 e^2}{mc^2R} f_n \cos \left[ 2\pi \nu t - \frac{2 \pi }{\lambda } (x_1 + x_2) \right] , \end{aligned}$$

(7.23)

where $f_n$ is the atomic scattering factor. We assume the crystal to be so small relative to all distances involved that the scattered wave is also treated as a plane-wave and approximate $x_2 \sim x'_2$. The instantaneous field at position $\mathbf {P}$ due to atom (m, n) is then given by

$$\begin{aligned} \epsilon _p = \frac{E_0e^2}{mc^2R}f_n \exp \left\{ i \left[ 2\pi \nu t - (2\pi /\lambda ) \left( R - (\mathbf {s}- \mathbf {s}_0) \cdot (m_1\mathbf {a}_1 + m_2\mathbf {a}_2 + m_3\mathbf {a}_3 + \mathbf {r}_n) \right) \right] \right\} . \end{aligned}$$

(7.24)

If we sum (7.24) over all atoms in the crystal, we then get the total field at $\mathbf {P}$. Assuming a crystal with edges $N_1\mathbf {a}_1$, $N_2\mathbf {a}_2$, $N_3\mathbf {a}_3$, and carrying out the sum, we can represent the observable quantity $\epsilon _p \epsilon ^*_p$ which is proportional to the light intensity, as

$$\begin{aligned} \epsilon _p\epsilon ^*_p = I_e F^2 \frac{\sin ^2(\pi /\lambda )(\mathbf {s}-\mathbf {s}_0) \cdot N_1\mathbf {a}_1}{\sin ^2(\pi /\lambda )(\mathbf {s}-\mathbf {s}_0)\cdot \mathbf {a}_1} \frac{\sin ^2(\pi /\lambda )(\mathbf {s}-\mathbf {s}_0) \cdot N_2\mathbf {a}_2}{\sin ^2(\pi /\lambda ) (\mathbf {s}-\mathbf {s}_0)\cdot \mathbf {a}_2} \frac{\sin ^2(\pi /\lambda )(\mathbf {s}-\mathbf {s}_0) \cdot N_3\mathbf {a}_3}{\sin ^2(\pi /\lambda )(\mathbf {s}-\mathbf {s}_0)\cdot \mathbf {a}_3}, \end{aligned}$$

(7.25)

where

$$\begin{aligned} F = \sum _n f_n e^{ \left( 2\pi i / \lambda \right) (\mathbf {s}- \mathbf {s}_0) \cdot \mathbf {r}_n } \end{aligned}$$

(7.26)

is the structure factor which depends on the atomic positions $\mathbf {r}_n$ and

$$\begin{aligned} I_e = I_0 \frac{e^4}{m^2c^4 R^2} \left( \frac{1+\cos ^2(2\theta )}{2} \right) , \end{aligned}$$

(7.27)

where $I_0$ is the intensity of the primary beam and $(1+\cos ^2(2\theta ))/2$ is a polarization factor.

Fig. 7.4

Diffraction from the electrons in an atom with the approximation that $R \gg |\mathbf {r}_n|$

On the right hand side of (7.25) are terms of the form

$$\begin{aligned} \frac{\sin ^2(Nx)}{\sin ^2(x)}, \end{aligned}$$

(7.28)

where $x_i = (\pi /\lambda )(\mathbf {s}- \mathbf {s}_0)\cdot \mathbf {a}_i$. Such functions have large peaks $\sim N^2$ at positions $x = n\pi$ and quickly fall to zero elsewhere. Therefore, the observed intensity will be zero almost everywhere except at those places satisfying the simultaneous Laue equations:

$$\begin{aligned} (\mathbf {s}- \mathbf {s}_0) \cdot \mathbf {a}_1 = h' \lambda , \qquad (\mathbf {s}- \mathbf {s}_0) \cdot \mathbf {a}_2 = k' \lambda , \qquad (\mathbf {s}- \mathbf {s}_0) \cdot \mathbf {a}_3 = l' \lambda , \end{aligned}$$

(7.29)

where $h'$, $k'$, and $l'$ are integers, a condition which is equivalent to the Bragg law.

Representing atomic positions relative to the crystal axes, we can write $\mathbf {r}_n = x_n \mathbf {a}_1 + y_n \mathbf {a}_2 + z_n \mathbf {a}_3$ and consider the value of the structure factor when the Bragg law is satisfied for a set of hkl planes, that is, when $\mathbf {s}- \mathbf {s}_0 = \lambda \mathbf {H}_{hkl}$. We then get

$$\begin{aligned} F_{hkl}&= \sum _n f_n \exp \left[ 2\pi i \left( h \mathbf {b}_1 + k \mathbf {b}_2 + l \mathbf {b}_3 \right) \cdot \left( x_n \mathbf {a}_1 + y_n \mathbf {a}_2 + z_n \mathbf {a}_3 \right) \right] \\ \nonumber&= \sum _n f_n \exp \left[ 2\pi i \left( h x_n + k y_n + l z_n \right) \right] , \end{aligned}$$

(7.30)

and if the structure factor for reflection hkl is zero, then so is the reflected intensity.

7.2.4 Electron Density

If we consider a small crystal relative with sides of length a, b, and c, we can represent the 3D electron density by its 3D Fourier transform

$$\begin{aligned} \rho (x,y,z) = \sum _{p}\sum _{q}\sum _{r}C_{pqr}\exp \left[ -2\pi i \left( p\frac{x}{a} + q\frac{y}{b} + r\frac{z}{c} \right) \right] , \end{aligned}$$

(7.31)

where the Fourier coefficients $C_{pqr}$ can be found by integrating

$$\begin{aligned} \int \limits _{0}^{a}\int \limits _{0}^{b}\int \limits _{0}^{c}\rho (x,y,z)\exp \left[ 2\pi i \left( h\frac{x}{a} + k\frac{y}{b} + l\frac{z}{c} \right) \right] = abc C_{hkl}. \end{aligned}$$

(7.32)

If we now replace the coordinates $x_n$, $y_n$, and $z_n$ in (7.30) by $x_n/a$, $y_n/b$, and $z_n/c$, we can rewrite the discrete structure factor as

$$\begin{aligned} F_{hkl} = \sum _n f_n \exp \left[ 2\pi i \left( h \frac{x_n}{a} + k \frac{y_n}{b} + l \frac{z_n}{c} \right) \right] , \end{aligned}$$

(7.33)

which we can then rewrite in terms of a continuous electron density:

$$\begin{aligned} F_{hkl} = \int \limits _{0}^{a}\int \limits _{0}^{b}\int \limits _{0}^{c} \rho (x,y,z) \exp \left[ 2\pi i \left( h \frac{x}{a} + k \frac{y}{b} + l \frac{z}{c} \right) \right] dV, \end{aligned}$$

(7.34)

and so the electron density in electrons per unit volume is given by the Fourier coefficients of the structure factors $F_{hkl}$ according to

$$\begin{aligned} \rho (x,y,z) = \frac{1}{V} \sum _h \sum _k \sum _l F_{hkl} \exp \left[ -2\pi i \left( h \frac{x}{a} + k \frac{y}{b} + l \frac{z}{c} \right) \right] . \end{aligned}$$

(7.35)

Therefore, according to (7.35), the observed hkl reflections from a crystal correspond to the Fourier series of the crystal’s electron density and therefore X-ray diffraction of a crystal can be thought of as a Fourier transform of the crystal’s electron density. Each coefficient in the series for $\rho (x,y,z)$ corresponds to a point hkl in the reciprocal lattice. Unfortunately, rather than observing the $F_{hkl}$ values directly, which would allow for the direct 3D calculation of the electron density according to (7.35), the quantities that are actually observed are 2D projections of the intensities $F_{hkl}F^*_{hkl} = \left| F_{hkl} \right| ^2$, in which all phase information is lost and must be recovered via iterative phase retrieval techniques provided that additional boundary condition and support information about the crystal structure are available.

7.3 High-Energy X-Ray Diffraction Microscopy (HEDM)

7.3.1 Experimental Setup

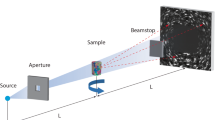
There are mainly two experimental setups utilized for performing HEDM measurements: (1) Near-field (nf-) HEDM and (2) far-field (ff-) HEDM, where the main difference between the two setups is the sample to detector distance. In the case of nf-HEDM, the sample to detector distance range from 3 to 10 mm while the ff-HEDM setup can range anywhere from 500 to 2500 mm. The schematic of the experimental setup is shown in Fig. 7.5. A planar focused monochromatic beam of X-rays is incident on a sample mounted on the rotation stage, where crystallites that satisfy the Bragg condition give rise to diffracted beams that are imaged on a charge coupled detector (CCD).

Fig. 7.5

HEDM setup at APS beamline 1-ID E. a Far-field detector setup, b specimen mounted on a rotation stage, and c near-field detector setup [33]

HEDM employs a scanning geometry, where the sample is rotated about the axis perpendicular to the planar X-ray beam and diffraction images are acquired over integration intervals $\delta \omega =1^\circ$ and 180 diffraction images are collected. Note that the integration interval can be decreased if the sample consist of small grains and large orientation mosaicity. During sample rotation, it is important to ensure that the sample is not precessing in and out of the beam, as some fraction of the Bragg scattering would be lost from that portion that passes out of the beam. Mapping the full sample requires rotating the sample about the vertical axis ($\omega$-axis) aligned perpendicular to the incident beam. Depending on the dimensions of the parallel beam, translation of the sample along the z-direction might be required to map the full 3D volume.

The near-field detector at APS 1ID-E and CHESS comprise of an interline CCD camera, which is optically coupled through 5$\times$ (or 10$\times$) magnifying optics to image fluorescent light from a 10 $\upmu$m thick, single crystal, Lutecium aluminum garnet scintillator. This results in a final pixel size that is approximately 1.5 $\upmu$m (${\sim }3 \times 3$ mm$^2$ field of view). The far-field data is also recorded on an area detector with an active area of ${\sim }410 \times 410$ mm$^2$ (2K $\times$ 2K pixel array). The flat panel detector has a layer of cesium iodide and a-silicon scintillator materials for converting X-ray photons to visible light. The final pixel pitch of the detector is 200 $\upmu$m. Research is underway for developing in-situ and ex-situ environments as well as area detectors with improved efficiency and data collection rates [45].

To obtain spatially resolved information on local orientation field, near-field geometry is utilized where the diffraction image is collected at more than one sample to detector distances per rotation angle, to aid in high-fidelity orientation reconstructions. Ff-HEDM provides center of mass position of individual grains, average orientations, relative grain sizes, and grain resolved elastic strain tensors. The ff- detector can be translated farther back along the beam path (i.e. very far-field geometry), if higher strain resolution is desirable and if permitted by the beam/beamline specifications. Therefore, HEDM measurements can be tailored to fit individual experimental needs and as necessitated by the science case by tuning parameters such as beam dimensions, setups, and data collection rates.

7.3.2 Data Analysis

In the case of nf-HEDM, the diffraction spots seen on the detector are randomly positioned and the spot size and shape correlates directly with the grain size and morphology. Since the grain shape is projected on the detector, spatially resolved orientation field reconstruction is possible using the near-field geometry. In contrast, the diffraction spots in the far-field geometry sit on the Debye-Scherrer ring, similar to what is observed during the powder diffraction measurements. The difference is that in ff-HEDM measurements, the ring is discontinuous and individual spots are more or less isolated, which is important for obtaining high-fidelity data reconstructions.

The diffraction images obtained in the HEDM measurements need to be pre-processed in order to extract diffraction signals from the sample. First, as a clean-up step, background and stray scattering are removed from the raw detector images and hot pixels can be removed using median filtering, if required. One of the most critical steps in the reconstruction process is identifying the instrument parameters. A calibration sample is used for this purpose. Critical parameters include calibrated beam energy, sample to detector distance, rotation axis and detector tilts with respect to the incident beam plane.

Several orientation and strain indexing tools have been developed for analyzing HEDM data. Fully automated beam line experiment (FABLE) software was initially developed for analyzing far-field data. Recently, grain indexing tool has been added that enables near-field data reduction for a box-beam geometry, where the incoming beam is incident on the middle of the detector, allowing Friedel pairs detection. Hexrd software [46] was developed in parallel at Cornell University for reconstructing grain orientations and strain tensors from ff-HEDM data. This software is currently maintained and updated by Lawrence Livermore National Laboratory. Integrating nf-HEDM data reconstruction capability in Hexrd in collaboration with CHESS is underway.

IceNine software developed at Carnegie Mellon University [47] operates mainly on the nf-HEDM data collected using a planar focused beam. Therefore, both the data collection and reconstruction take longer compared to the other two methods. However, forward model method utilized by the IceNine software enables high resolution spatially resolved orientation field reconstructions and provides unique capability to characterize heavily deformed materials.

Fig. 7.6

Reconstruction yields 2D orientation maps, which are stacked to obtain a 3D volume [48]

Figure 7.6 shows a schematic demonstrating the nf-HEDM measurements using planar beam and 3D orientation field reconstruction. The raw diffraction data is background subtracted and the peaks are segmented. The image is then utilized by the reconstruction software for 2D microstructure reconstructions. These steps are repeated for all the 2D layers measured by translating the sample along the z-direction. Finally, 3D microstructure map is obtained by stacking the 2D layers on top of each other. Since the sample is not touched during the full volume mapping, the stacking procedure does not require registration, which are otherwise needed in EBSD+FIB type measurements.

Recently, Midas software [49] was developed at APS for simultaneous reconstruction of nf-HEDM and ff-HEDM data. In this case, the average grain orientation information from the ff-HEDM reconstruction is given as guess orientations for spatially resolved orientation reconstructions in nf-HEDM. Such seeding significantly reduces the search space for both spatial and orientation reconstruction and significantly speeds up the reconstruction process. However, the seeding results in overestimating some grain sizes, while missing grains that were not indexed in the far-field. Another drawback is that the technique does not work well for highly deformed materials, as far-field accuracy drops with increasing peaks smearing and overlap that occurs with increasing deformation level.

Continued improvement and development are underway.

7.4 Microstructure Representation

Figure 7.7 schematically demonstrate the orientation and misorientation representations used in crystallography.

Fig. 7.7

Conventions used for microstructure representation

Crystallographic orientation or rotation required to bring a crystal in coincidence with another (termed as misorientation) can be represented as a proper rotation matrix R in basis $B_{x,y,z}$, which can be written in terms of the basic rotations matrices as:

$$\begin{aligned} R = R_{x}(\alpha ) R_{y}(\beta ) R_{z}(\gamma ), \end{aligned}$$

(7.36)

where $R_{x}$, $R_{y}$, and $R_{z}$ are 3D rotations about x, y, and z axes, respectively. It is convenient to represent the final rotation matrix R as an axis/angle pair, where axis is a rotation axis in some other basis $B_{u,v,w}$ at some angle $\theta$. Additionally, for any proper rotation matrix, there exists Eigen value $\lambda = 1$, such that

$$\begin{aligned} Ru = \lambda u = u. \end{aligned}$$

(7.37)

The vector u is the rotation axis of the rotation matrix R. We also want to find $\theta$, the rotation angle. We know that if we start with u and choose two other orthonormal vectors v and w, then the rotation matrix can be written in the u, v, w basis, $B_{u,v,w}$, as

$$\begin{aligned} M_{u}(\theta ) = \left( \begin{array}{ccc} 1 &{} 0 &{} 0 \\ 0 &{} \cos (\theta ) &{}-\sin (\theta ) \\ 0 &{} \sin (\theta ) &{} \cos (\theta ) \end{array}\right) \end{aligned}$$

(7.38)

Since the trace of a matrix is invariant to change of basis, we know

$$\begin{aligned} tr(R)=tr(M)=1+2\cos (\theta ). \end{aligned}$$

(7.39)

This allows us to calculate the rotation angle, $\theta$, without ever expressing $M_u$ in the form (7.38), we simply use the given form, R, and calculate

$$\begin{aligned} \theta = \arccos \left( \frac{tr(R)-1}{2} \right) , \end{aligned}$$

(7.40)

which is known as misorientation angle in crystallography.

Figure 7.8 illustrates the type of microstructure data that HEDM technique provides. Figure 7.8a represents the grain average information that ff-HEDM provides, where the colors correspond to either orientation or components of elastic strain tensor. Figure 7.8b shows a spatially resolved 3D orientation field that could be obtained from nf-HEDM measurements. From the spatially resolved microstructure map, individual 3D grains are segmented as a post-processing step by clustering points belonging to similar orientations within some specified threshold misorientation angle.

Fig. 7.8

Synthetic microstructure resembling microstructure maps obtained from HEDM data. a Ff-HEDM and b nf-HEDM [10]

7.5 Example Applications

7.5.1 Tracking Plastic Deformation in Polycrystalline Copper Using Nf-HEDM

Nf-HEDM is mainly suitable for structure determination of individual crystallites as well as their local neighborhood in a polycrystalline material. Utilizing nf-HEDM, Pokharel et al. [4, 17] demonstrated characterization of 3D microstructure evolution due to plastic deformation in a single specimen of polycrystalline material. A 99.995% pure oxygen free electrical (OFE) Cu was used for this study, where a tensile specimen with a gage length of 1 mm and a cylindrical cross section of 1 mm diameter was prepared. The tensile axis was parallel to the cylindrical axis of the sample. The Cu specimen was deformed in-situ under tensile loading and nf-HEDM data were collected at various strain levels. Figure 7.9 [17] shows the stress-strain curve along with the example 2D orientation field maps and corresponding confidence maps for strain levels up to 21% tensile strain. Figure 7.10 [17] shows the corresponding 3D volumetric microstructure maps for 3 out of 5 measured strain states, where $\sim$5000 3D grains were tracked through initial, 6, and 12% tensile deformation. The measured microstructure evolution information was used to study spatially resolved orientation change and grain fragmentation due to intra-granular misorientation development during tensile deformation.

Fig. 7.9

Experimental stress-strain curve along with one of the 2D slices of orientation and confidence maps from each of the five measured strain states. Nf-HEDM measurements were taken at various strain levels ranging from 0 to 21% tensile strain. IceNine software was used for data reconstruction. The 2D maps plotted outside the stress-strain curve represent the orientation fields from each of the corresponding strain levels obtained using forward modeling method analysis software. The 2D maps plotted inside the stress-strain curve are the confidence, C, maps for the reconstructed orientation fields at different strain levels. Confidence values of the five plots range from 0.4 to 1, where C = 1 means all the simulated scatterings coincide with the experimental diffraction data and C = 0.4 corresponds to 40% overlap with the experimental diffraction peaks. For each strain level a 3D volume was measured, where each strain state consists on average 100 layers [17]

Fig. 7.10

Three 3D volumes of the measured microstructures a initial, b 6% strain, and c 12% strain. Colors correspond to an RGB mapping of Rodrigues vector components specifying the local crystal orientation [17]

Fig. 7.11

Tracking deformation in individual grains through deformation [4, 17]

Figure 7.11 [4, 17] shows the ability to track individual 3D grains at different strain levels. Figure 7.11a shows the kernel average misorientation (KAM) map indicating local orientation change development due to plastic deformation. The higher KAM value indicates that the intra-granular misorientation between adjacent crystallite orientation is high. Figure 7.11b shows the inverse pole figure (left) where average grain reorientation of 100 largest grains in the material was tracked. The tail of the arrow corresponds to the average orientation in the initial state and the arrow head represents average orientation after subjecting the sample to 14% tensile strain. Inverse pole figure (right) shows the trajectory of individual voxels in a grain tracked at 4 different strain levels. The insets show the grain rotations for two grains near <111>- and <001>-corners of the stereographic triangle. The black arrow shows the grain averaged rotation from the initial to the final strain. It is observed that the two grains, $\#$2 and $\#$15, show very different intra-granular orientation change, where grain fragmentation is observed for grain $\#$15. It is evident that spatially resolved information is needed to capture the local details within a grain. These plots further indicate that only grain averaged orientation information was insufficient to capture the local heterogeneities that develop in individual grains due to plastic deformation. Variation in the combinations of slip systems activated during plastic deformation can lead to such heterogeneous internal structure development in a polycrystalline material. In addition, a strong dependence was observed between orientation change and grain size, where larger grains developed higher average local orientation change in comparison to smaller grains. This suggests that the type of deformation structures formation is also dependent on the initial orientation and grain size. Moreover, decrease in average grain size was observed with deformation due to grain fragmentation and sub-grain formation.

7.5.2 Combined nf- and ff-HEDM for Tracking Inter-granular Stress in Titanium Alloy

A proof-of-principle combined nf- and ff-HEDM measurements were reported by Schuren et al. [33], where microstructure and micro-mechanical field evolution were measured in a single sample undergoing creep deformation. In-situ measurements of titanium alloy (Ti-7Al) were performed, where HEDM data were collected during quasi-static loading. Experimental setup employed for this multi-modal diffraction and tomography measurements is shown in Fig. 7.5. Nf- and ff- data were reconstructed using IceNine and Hexrd software, respectively. Spatially resolved grain maps and corresponding grain cross-section averaged stress field were used for studying local neighborhood effect on observed anisotropic elastic and plastic properties.

Fig. 7.12

Combined nf- and ff-HEDM measurements of Ti microstructure. a ff-COM overlaid on nf-orientation map. b Hydrostatic and deviatoric stress evolution pre- and post-creep. c Hydrostatic and deviatoric stresses versus coaxiality angle [33]

Figure 7.12 shows the microstructure and micro-mechanical properties obtained from the HEDM measurements. Figure 7.12a shows the spatially resolved orientation field map from nf-HEDM with corresponding COM positions for individual grains obtained from ff-HEDM. Figure 7.12b shows the spatial maps colored by hydrostatic and the effective stresses. Figure 7.12c plots the hydrostatic and effective stresses versus the coaxiality angle defined as the angle between the grain scale stress vector and applied macroscopic stress direction. In pre-creep state clear evidence of higher hydrostatic stress was observed for grains with stress states aligned with the applied macroscopic stress. In post-creep state, bifurcation of hydrostatic stress was observed where grain scale stress deviated away from the applied macroscopic stress.

The same experimental setup was utilized by Turner et al. [50] to perform in-situ ff-HDEM measurements during tensile deformation of the Ti-7Al sample, previously measured during the creep deformation [33]. 69 bulk grains in the initial state of the nf-HEDM volume (200 $\upmu$m $\times$ 1 mm $\times$ 1 mm) were matched with the ff-HEDM data at various stages of tensile loading. Nf-HEDM data were not collected at the loaded states as the measurements are highly time intensive (24 h/volume). Due to the complexity of the experimental setup, the tensile specimen was subjected to axial load of 23 MPa during mounting the sample in the load frame. Therefore, the initial state of the material was not in a fully unloaded state. The grain averaged elastic strain tensor were tracked through deformation and distinct inter-granular heterogeneity was observed, which seems to have resulted directly from the strain heterogeneity in the unloaded state (23 MPa). This indicated that the initial residual stresses present in the material influenced the strain and corresponding stress evolution during deformation.

Combined nf- and ff-HEDM in-situ data enabled polycrystal model instantiation and validation, where crystal plasticity simulation of tensile deformation of Ti-7Al was performed using the Ti-7Al data [34]. Predicted strain and stress evolution showed good qualitative agreement with measurements; however, grain scale stress heterogeneity was not well captured by the crystal plasticity simulations. The comparison could be improved by incorporating initial residual stresses present in the material along with measured 3D microstructure as input to simulation.

7.5.3 Tracking Lattice Rotation Change in Interstitial-Free (IF) Steel Using HEDM

Lattice rotation in polycrystalline material is a complex phenomenon influenced by factors such as microstructure, grain orientation, interaction between neighboring grains, which result in grain level heterogeneity. 3D X-ray diffraction microscopy (3DXRD) was employed by Oddershede et al. and Winther et al. [29, 30] to study lattice rotation evolution in 3D bulk grains of IF steel. Monochromatic X-ray beam energy, E $=$ 69.51 keV, and beam height of 10 $\upmu$m were used for microstructure measurements. Initial microstructure of a tensile specimen with dimensions $0.7\,\times \,0.7\,\times \,30$ mm$^3$ were mapped via HEDM, then the sample was re-measured after subjecting it to 9% tensile deformation. FABLE software was used for 3D microstructure reconstruction.

Fig. 7.13

Tracking deformation in individual grains through deformation [29, 30]

Three bulk grains with similar initial orientations, close to <522> orientation located between [001]–[-111] line in a stereographic triangle, were identified for detailed study of intra-granular variation in lattice rotation. It was observed that the tensile axes of all three deformed grains rotated towards the [001] direction, which was also the macroscopic loading direction. To investigate the intra-granular variation in rotation, raw diffraction spots were tracked before and after deformation. Three different reflections for each grain orientation were considered, where the observed change in location and morphology of the diffraction spots were linked to intra-granular orientation change in individual grains.

Crystal plasticity simulations were performed to identify slip systems activity that led to orientation spread. The peak broadening effect was quantified by integrating the diffraction spots along the $\omega$ (rotation about the tensile loading direction) and $\eta$ (along the Debye-Scherrer ring) directions. Figure 7.13 shows the measured and predicted reflections for one of the three grains after deformation. Predicted orientation spread were in good agreement with measurements, where large spread in diffraction spots were observed along both $\omega$ and $\eta$ directions. Four slip systems were predicted to be active based on both Schmid and Taylor models. However, large intra-granular variation in the spread was attributed mostly to the activity of (0-1-1)[11-1] and‘ (-101)[11-1] slip systems, which also had the highest Schmid factors. Moreover, the results indicated that the initial grain orientation played a key role in the development of intra-granular orientation variation in individual grains.

7.5.4 Grain-Scale Residual Strain (Stress) Determination in Ti-7Al Using HEDM

HEDM technique was employed by Chatterjee et al. [35] to study deformation induced inter-granular variation in orientation and micro-mechanical field in Ti-7Al material. Tensile specimen of Ti-7Al material consisting of fully recrystallized grains with 100 $\upmu$m average grain size were prepared for grain scale orientation and residual stress characterization. Planar-focused high-energy X-ray beam of 1.7 $\upmu$m height and 65.351 keV energy were used for probing 2D cross-section (layer) of the 3D sample. 3D data were collected by translating the material along the vertical axis of the tensile specimen, mapping volumetric region of $1.5\,\times \,1.5\,\times \,0.54$ mm$^3$. Total of 15 layers around the gage volume were measured with 40 $\upmu$m vertical spacing between layers. Diffraction data were collected at various load steps as well as during loading and unloading of the material. FABLE software was used for diffraction data analysis for grain center of mass and grain cross-section averaged strain determination.

Fig. 7.14

Stress jacks to demonstrate complex grain scale stress states development for three neighboring grains in a sample subjected to uniaxial macroscopic load [35]

Figure 7.14 shows the grain scale stress states developed in three neighboring grains in the sample. Upon unloading, grain scale residual stresses were observed in the material. Although uniaxial load was applied to the tensile specimen, complex multi-axial stress-states resembling combined ‘bending’ and tension were observed in individual grains. Co-axiality angle was calculated as an angle between the macroscopic loading direction and the grain scale loading state. Spatial variation in the co-axiality angle indicated variation in inter-granular stress states, which was mainly attributed to the local interactions between neighboring grains irrespective of the macroscopic loading conditions. Such local heterogeneity that develop at the grain scale influences macroscopic behavior and failure mechanisms in polycrystalline material.

7.5.5 In-Situ ff-HEDM Characterization of Stress-Induced Phase Transformation in Nickel-Titanium Shape Memory Alloys (SMA)

Paranjape et al. [36] studied the variation in super-elastic transformation strain in shape memory alloys (SMA) materials utilizing ff-HEDM technique with 2 mm wide by 0.15 mm tall beam of energy 71.676 keV. In-situ diffraction data were collected during cyclic loading in tension (11 cycles of loading and unloading) of Ti-50.9at.%Ni samples, exhibiting super-elasticity property at room temperature. Two phases were present in the material: austenite and martensite, upon loading and unloading, where 3D microstructure and micro-mechanical field were analyzed only for the austenite phase. Martensitic grains were not resolved by the ff-HEDM technique due to their large number resulting in a uniform powder pattern on the detector. The ff-HEDM analyses were performed using MIDAS software and powder diffraction patterns were analyzed using GSAS-II software.

Fig. 7.15

Inverse pole figure and a 3D view of the grain center of mass is shown at three key stages: 0 load (0), peak load (4) showing fewer B2 grains remaining due to phase transformation, and full unload (8) showing near-complete reverse transformation to B2. The grains are colored according to an inverse pole figure colormap [36]

HEDM data enabled capturing phase transformation during cyclic loading. Initial state data were collected prior to loading and 10 more cycles were performed to stabilize the macroscopic stress-strain response. Figure 7.15 shows the macro stress-strain curve and the corresponding grains from ff HEDM measurements from the 11th cycle. In the 11th cycle, ff-HEDM data were collected at nine different strain levels (five during loading and four during unloading). At peak load of 311 MPa (state 4), a fraction of the austenite grains was found to have transformed to martensitic phase. After full unload, near complete reverse transformation was observed with some hysteresis in the stress-strain response. Cyclic loading resulted in location dependent axial strains in the material, where the interior grains were mostly in tension while the surface grains exhibited combined tension and compression loading states.

Elasticity simulations were instantiated using the measured microstructure to quantify grain scale deformation heterogeneity with respect to relative location in the sample (surface versus interior). The origin of the heterogeneities was attributed to the neighboring grain interaction, which also led to intra-granular variation in stress states in similarly oriented grains. In addition, large grains with higher number of neighbors exhibited large intra-granular stress variation. Difference in the family of slip systems activated in the interior versus the surface grains were also suspected to play a role in variation in intra-granular stress states. Resulting stress heterogeneity influenced the strain induced phase transformation in SMA materials.

7.5.6 HEDM Application to Nuclear Fuels

Properties of nuclear fuels strongly depend on microstructural parameters, where residual porosity reduces thermal conductivity of the fuel and grain size and morphology dictates fission gas release rates as well as dimensional change during operation. Both of these factors can greatly limit the performance and life-time of nuclear fuel. HEDM technique is well-suited for characterizing microstructures of ceramics and metallic nuclear fuels due to minimal amount of plastic deformation exhibited by these materials. In addition, nuclear fuel sample preparation for conventional metallography and microstructure characterization are both costly and hazardous. In contrast, HEDM requires little to no sample preparation where a small parallelepiped can be cut from the fuel pellet for 3D characterization. Recently, conventional, UO$_{2}$, and candidate accident tolerant fuels (ATF), UN-U$_{3}$Si$_{5}$, materials have been characterized utilizing nf-HEDM technique. Brown et al. [37] employed the nf-HEDM technique, for the first time, to non-destructively probe 3D microstructure of nuclear fuel materials. High-energy X-ray beam of 1.3 mm wide by 3 $\upmu$m tall and 85.53 keV energy were used to measure 3D microstructure of ceramic UO$_{2}$. Similarly, the nf-HEDM technique was also utilized to characterized 3D microstructure of ATF fuels [43]. The 3D microstructures were reconstructed using IceNine software.

Figure 7.16a shows of 3D characterization of a UO$_{2}$ materials, where 2D maps from different region on the samples are plotted. Similarly, Fig. 7.16b shows the orientation field maps of the two-phase ATF fuel, where the 3D microstructure of the major phase, UN, is shown on the left and the 2D projection of 10 layers of the U$_{3}$Si$_{5}$ phase is shown on the right. Note that in both case no intra-granular orientation gradient were present in the grains, which suggest that minimal dislocation density or plastic deformation is present in these materials.

Fig. 7.16

Grain orientation maps for a UO$_{2}$ at 25 $\upmu$m intervals from near the top (left) of the sample. Arrows indicate grains that span several layers are indicated [37], and b UN-USi ATF fuel, where 3D microstructure is shown for the major phase (UN) and 2D projection of 10 layers are shown for the minor phase (USi) [43]

Figure 7.17 shows the orientation maps for UO$_2$ material before and after heat treatment. Visual inspection indicates significant grain growth after heat treatment, where the initial residual porosity disappeared resulting in a near fully dense material. The measured microstructures were utilized for instantiating grain growth models for nuclear fuels [51].

Fig. 7.17

Microstructure evolution in UO$_2$. a As-sintered and b after heat-treatment to 2200 $^{\circ }$C for 2.5 h [51]

7.5.7 Utilizing HEDM to Characterize Additively Manufactured 316L Stainless Steel

Additive manufacturing (AM) is a process of building 3D materials in a layer by layer manner. Variety of AM processing techniques and AM process parameters are employed for material fabrication, which lead to AM materials with large variation in materials properties and performance. AM materials could greatly benefit from HEDM technique, where in-situ or ex-situ measurements of microstructure and residual stress could improve the current understanding of SPP relationships in AM materials.

Fig. 7.18

Near-field detector image for AM 304L SS steel for a as-built and b after heat treatment to 1060 $^{\circ }$C for 1 h. Before and after detector images show sharpening of diffraction signals after annealing. Nf-HEDM orientation maps are shown for c as-built and d annealed material. Small austenite and ferrite grains were not resolved in the reconstruction. After annealing the residual ferrite phase in the initial state completely phase transformed to austenite phase, resulting in a fully dense material

As a feasibility test, nf-HEDM measurements were performed on AM 316L stainless steel (SS) materials before and after heat treatment. Figure 7.18a, b show the detector images for as-built and annealed 316L SS sample, respectively. In the case of as-built material, the detector image is complex, resembling either diffraction from a powder sample with large number of small grains or diffraction from highly deformed material. On the other hand, annealed material exhibited sharp isolated peaks common of recrystallized materials. IceNine software was employed for microstructure reconstruction. Complimentary powder diffraction measurements revealed the presence of austenite and ferrite phase in the initial microstructure.

In the as-built state, the secondary ferrite phase with fine grain size was not resolved by nf-HEDM measurements; therefore, only austenite phase was reconstructed. Figure 7.18c shows the first attempt at reconstructing the austenite phase in the as-built microstructure. As the sample was >99.5% dense, the white spaces shown in the microstructure map corresponds to either small/deformed austenite grains or small ferrite grains. Upon annealing, complete ferrite to austenite phase transformation was observed along with recovery of austenite grains. Figure 7.18d shows the austenite phase orientation maps resulting in equiaxed and recrystallized austenite grains.

7.6 Conclusions and Perspectives

The following are some of the conclusions that can be drawn from the literature employing the HEDM technique for microstructure and micro-mechanical field measurements:

• HEDM provides previously inaccessible mesoscale data on a microstructure and its evolution under operating conditions. Such data is unprecedented and provides valuable insight for microstructure sensitive model development for predicting material properties and performance.

• HEDM provides the flexibility to probe a range of material systems, from low-Z to high-Z. One of the major limitations of HEDM technique in terms of probing high-Z material is that the signal to noise ratio drastically decreases due to high absorption cross-section of high-Z materials. In addition, the quantum efficiency of the scintillator deteriorates with increasing energy (>80 keV used for nuclear materials). As a result, longer integration times per detector image are required for high-quality data acquisition. This means that the data collection time can easily increase by factor of 3–4 for uranium in comparison to low-Z materials such as titanium and copper.

• Nf-HEDM is ideal for probing spatially resolved 3D microstructure and provides information on sub-structure formation within a grain as well as evolution of its local neighborhood under in-situ conditions. As defect accumulation and damage nucleation are local phenomena, spatially resolved microstructure and internal structure evolution information from experiments are valuable for providing insight into physical phenomena that affect materials properties and behavior.

• Ff-HEDM data provides center of mass of a grain and grain resolved elastic strain for thousands of grains in a polycrystalline material. Employing a box beam geometry, statistically significant numbers of grains can be mapped in a limited beam time. In addition, due to faster data collection rates of ff-HEDM in comparison to nf-HEDM, a large number of material states can be measured while the sample is subjected to external loading conditions. This enables detailed view of microstructure and micro-mechanical field evolution in a single sample.

• Various HEDM studies elucidated development of mesoscale heterogeneities in polycrystalline materials subjected to macroscopic loading conditions. Variations in intra-granular stress states were observed in various material systems. This variation was mainly attributed to the local interaction between neighboring grains with minor effects from initial grain orientations and loading conditions.

• In the case of deformed materials or AM materials with large deformation and complex grain size and morphology, the diffracted peaks smeared out and the high order diffraction intensities dropped. Development of a robust method for background subtraction and diffraction peak segmentation will be crucial for high-fidelity microstructure reconstructions for highly deformed samples..

The main insight from various applications utilizing the HEDM techniques was that macroscopic responses of polycrystalline materials were affected by the heterogeneities in microstructure and micro-mechanical fields at the local scale. All the examples presented here demonstrated in-situ uniaxial loading of the polycrystalline materials; however, experimental setups for more complex loading conditions such as bi-axial loading are currently being explored [52]. Furthermore, major challenges remain in terms of characterization of more complex materials such as additively manufactured materials where large variations in initial grain orientation as well as grain morphology are observed. The technique is still highly limited to polycrystals with relatively large grains (>10 $\upmu$m as pixel pitch of the near-field detector is $\sim$1.5 $\upmu$m) and with low deformation level (e.g. <20% tensile strain). Advancement in detector technology as well as data reduction tools will be required to apply HEDM techniques for materials with small grains and large deformation. Note that in the current data analysis framework uncertainty quantification is one of the areas that is not fully explored. Therefore, how errors propagate from measurements to data reconstruction and when the experimental data is used for model instantiation how that affects predicted material properties and behaviors are not yet understood.

7.6.1 Establishing Processing-Structure-Property-Performance Relationships

The advent of 3rd and 4th generation light sources has enabled the development of advanced non-destructive microstructure characterization techniques such as HEDM. As a result, high-resolution and high-dimensional data acquisition have been made possible. The goal is to utilize these techniques to obtain high-fidelity information for establishing processing-structure-property-performance (PSPP) relationships in materials. However, the ability to design material microstructures with desired properties and performance is still limited. Any advancement in material design requires the development of multi-mechanism and multi-physics predictive models, which can rely heavily on experimental testing and measurements. Because HEDM type data collection is expensive, only a limited number of sample states can be experimentally tested and the resulting data sets are extremely sparse in the vast PSPP material space.

Currently, lengthy measurements (hours) severely limit the time scales at which mesoscale 3D microstructure evolution data can be collected with high spatial ($\sim$1 $\upmu$m) and orientation, ($\sim$0.01$^{\circ }$) resolution. Furthermore, extremely long reconstruction times (days) prevent sample evolution-based feedback during an experiment. The reconstruction techniques currently used are brute force and the turnaround time from data collection to reconstruction is very long. For example, the 2D spatially resolved orientation field reconstruction shown in Fig. 7.9 took $\sim$20 mins per sample cross-section on 512 processors, requiring $\sim$650 K core-seconds/layer on a system rated at 9.2 Gflops/core. Typically, there are 50–100 such cross-sections in a full 3D volume, which would require several minutes of reconstruction on a $\sim$6.5 Pflop machine. In addition, the first step of reconstruction requires lengthy, manual calibration to find appropriate instrument parameters for a given experiment.

The Advanced Photon Source (APS), Linac Coherent Light Source (LCLS) and Cornell High Energy Synchrotron Source (CHESS) are upgrading their X-ray sources and detector technologies over the next few years to obtain better temporal resolution in imaging and diffraction, which means faster data collection rates. Therefore, it is important that more focus is placed on meeting the data reduction and reconstruction demands created by these increasing data collection rates. This will not only improve the information extraction capability from high dimensional data but also provide faster feedback to drive experiments.

For instance, the current Edisonian approach in materials measurement and testing needs to be replaced with more strategic approach to maximize information extraction capability from sparse datasets. Furthermore, the current norm in HEDM type measurements is to collect large amounts of data (several hundred GBs to TBs) for a given sample state, only to later discard or never analyze most of the acquired data. The main reason for such an inefficient measurement protocol is due to the lack of real-time analyses tools that can guide measurements during the limited available beam time. Investment in the development of efficient, fast, and user-friendly data reduction and reconstruction software has the potential to change how experiments (analysis, throughput) are performed. This could improve the data quality as well as enable multiple sample state measurements, lending to high-temporal resolution.

For dynamic conditions, both spatially and temporally resolved ($\sim$1 $\upmu$m and $\sim$1 ps) microstructure information is desired to understand materials properties and performance for engineering applications. Current literature demonstrates that non-destructive techniques can be successfully utilized for studying 3D microstructure evolution under quasi-static conditions. However, extending such studies to dynamic loading conditions is still a challenge. Currently, the most common approach to mapping 3D microstructures is by rotating the sample and collecting multiple views. However, to capture the dynamics during shock loading or during high strain-rate loading conditions, data needs to be acquired at the same temporal scale as the dynamic process. Waiting for a sample to be rotated and imaged from multiple angles during such in-situ measurements is just too slow. In order to speed up the HEDM measurement process, we must consider more sophisticated approaches to measurement and reconstruction, including iterative techniques which utilize past sample state data and dynamic models for subsequent reconstructions.

Fig. 7.19

Schematic to illustrate data analysis pipeline for physics based model development

Figure 7.19 demonstrates a possible work flow for enabling dynamic measurements. HEDM and various other 3D characterization techniques discussed earlier can be utilized to fully characterize the initial state of the material before dynamic loading. This would provide information such as chemistry, composition, microstructure, phase, and defect structures of the material of interest. Note that Fig. 7.19 is a vastly simplified vision, where this prior information about the sample would help develop a data analysis framework in concert with available microstructure based models and the forward modeling method for direct simulation of diffraction. The measured initial 3D structure will be used as input to an existing model. The model will then evolve the structure based on some governing equations and proper boundary conditions. The forward modeling method can then be used to simulate diffraction from the evolved structure. The simulated diffraction can then be compared with experiments. Given the physics in the model is adequate, iteratively changing associated model parameters could give us a reasonable match between the observation and simulation, at least for the initial time steps. A feedback loop would be created for iterating and updating each step. Note that there are uncertainties in the measured data (detector images in our case) that will propagate in the predicted features (reconstructed microstructural properties), which are then used for predicting the corresponding material properties. Therefore, measurement uncertainty needs to be accounted for when adaptively tweaking the model parameters. Such an approach could provide new insight into and understanding of the mechanisms driving dynamic processes in polycrystalline materials. However, it is highly unlikely that the existing models have adequate physics to accurately capture the complex micro-mechanical field development throughout the whole dynamic process. Given the possibility of acquiring data with high temporal resolution, albeit sparse spatial views, an assumption can be made that the material change from one state to the next is relatively small. Therefore, utilizing the initial characterization and linking the dynamic measurements, diffraction simulations, data mining tools, and existing models could enable extraction of 3D information from limited views and highly incomplete datasets.