Experimental Validation of Angular Viscoelastic Dynamic Neutralizers Designed for Flexural Vibration Control in Rotating Machines

Abstract

The installation of micro hydroelectric power plants has recently been growing in Brazil, where small hydraulic generators are combined with hydraulic turbines. Some technical solutions require different runaway factors, from 1.2 up to 3.0 times the synchronous speed of the generator, so that the mechanical design of them must be reinforced or changed to support this critical dynamic condition, affecting costs and reducing competitiveness. An effective technique to control vibration is the use of simple devices called ‘dynamic vibration neutralizers’. These devices can contain viscoelastic material to introduce high mechanical impedance onto the system to reduce its vibration levels. There is a special kind of neutralizer, called ‘angular viscoelastic dynamic neutralizer’ (angular VDN), which acts indirectly in slope degree of freedom controlling flexural vibration. They have the predicted ability to control more than one single mode once the device is assembled where the maximum slope happens. The aim of the current work is to present a methodology to design angular VDNs and validate it by using a simplified experimental rotor exploring two different geometries. The results show that, if well-tuned, this kind of control is effective not only for the frequency band of interest, but also over higher modes.

1 Introduction

In order to make the most of the Brazilian hydraulic power capacity, the installation of micro hydroelectric power plants (MHPs) has been growing year after year. In Brazil, the plants with power capacity up to 5 MW are considered MHPs, using small hydraulic generators combined with hydraulic turbines to generate this amount of energy, where the turbine set depends on the fall height.

The design of the hydraulic generator is intimately related to the type of turbine, since it influences the generator runaway factor. Therefore, in applications concerning Pelton and Francis turbines, it is a common practice to use a runaway factor up to 2.0 times the nominal speed of the generator. However, for Kaplan turbines, this runaway factor usually grows from 2.3 up to 3.0, so that the mechanical design of the generator must be reinforced to support this critical dynamic condition.

These generators should be small and low-priced, so their construction employs roller bearings to support the rotor and turbine loads. So, if a generator is mechanically designed to operate at a runaway factor 2.0, and then one wishes to use it in an application with a higher runaway factor, it is necessary to modify the mechanical project by increasing the diameters of the shaft, the bearings, or even changing the roller bearings to hydrodynamic bearings, in order to comply with the API 541 vibration requirements. All these modifications impact the generator costs, reducing competitiveness.

When it comes to flexural vibration control, there are some techniques consolidated by the literature [1,2,3,4,5,6,7], most of them based on the addition of damping to the vibration control system. Another effective technique consists of using simple and relatively low-cost devices called ‘dynamic vibration neutralizers’ [8,9,10,11,12,13]. These devices can contain viscoelastic material - instead of spring and dashpot - introducing high mechanical impedance into the primary system (dynamic structures to be controlled), to reduce vibration levels in a frequency band of interest. That is, the neutralizers add not only damping, but they also introduce reaction forces into the primary system.

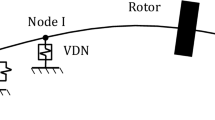
There is a special kind of neutralizer, called ‘angular viscoelastic dynamic neutralizer’ (angular VDN), which acts indirectly on slope degree-of-freedom (DOF) - as shown in Fig. 1 - controlling flexural vibration. It is attached near the bearings, where one finds the maximum angular displacement for the shaft regarding its neutral axis. Furthermore, the angular VDN has the predicted ability to control more than one single mode, since, for a simply supported beam, regardless of the mode shape, the DOF slope is never null close to the supports.

Fig. 1.

Slope degree-of-freedom in rotating systems.

The aim of current study is to present a methodology to design angular VDNs – and validate it using a simplified experimental rotor – by exploring two different geometries. The studies and the results show that the auxiliary support has to be carefully designed in order to ensure the angular degree of freedom control, since the neutralizer motion could be exposed, through this support, to the displacement and angular motion in all directions due to shaft whirling. The results show that, if well-tuned, this kind of control is effective not only for the frequency band of interest, but also over higher modes.

2 Viscoelastic Material Model

Viscoelastic materials are widely used in vibration and noise control applications due to their relative low cost and attractive physical properties: the dynamic behavior depends on their complex elasticity moduli, which are frequency and temperature dependent. The properties of a typical and thermorheologically simple viscoelastic material are detailed in [14, 15].

The four-parameter fractional derivative model for viscoelastic solid materials was introduced by [10, 15]. This simple model may numerically characterize a wide range of viscoelastic materials in engineering. So, in the frequency domain, the complex shear modulus $(\bar{G}(\varOmega ,T))$ is represented by:

$$ \bar{G}\left( {\varOmega ,T} \right) = \frac{{G_{0} + G_{\infty } b_{1} \left( {i\varOmega \alpha \left( T \right)} \right)^{\beta } }}{{1 + b_{1} \left( {i\varOmega \alpha \left( T \right)} \right)^{\beta } }} = G_{r} \left( {\varOmega ,T} \right)\left( {1 + i\eta \left( {\varOmega ,T} \right)} \right) $$

(1)

where $G_{r} (\varOmega ,T) = {Re} (\bar{G}(\varOmega ,T))$ is the dynamic shear modulus or storage modulus and $\eta (\varOmega ,T) = {Im} (\bar{G}(\varOmega ,T)) /{Re} (\bar{G}(\varOmega ,T))$ is the loss factor; parameters $G_{0}$ and $G_{\infty }$ represent the asymptotic values of the dynamic shear modulus at low and high frequencies, respectively; $b_{1} = b^{\beta }$ is an experimental constant, where b is the relaxation time [10] and β is the fractional derivative power; Ω is the excitation frequency and i is the imaginary unit $(i = \sqrt { - 1} )$. Parameter α(T) is actually a function called ‘shift factor’ and represents the temperature influence in the dynamic behavior of viscoelastic materials. This factor was experimentally proposed by Willian–Landel–Ferry (WLF) and empirically equated by [16]:

$$ log \alpha \left( T \right) = - \theta_{1} \frac{{T - T_{0} }}{{\theta_{2} + T - T_{0} }} $$

(2)

where constants $\theta_{1}$ and $\theta_{2}$ may be experimentally determined, parameter $T_{0}$ is an arbitrary reference temperature, and T is the working temperature, both in Kelvin. For the sake of simplicity, parameter T will be suppressed from now on, since the present paper will fix a constant temperature for the system modelling.

3 Viscoelastic Dynamic Neutralizer Applied to Slope Degree of Freedom

The approach of the present paper is related to the angular VDN, i.e., the neutralizer works in slope DOF instead of the transversal displacement. Based on the methodology showed on [11], the generalized equivalent parameters model for slope degree-of-freedom of a simple neutralizer is propose in order to replace the classical one, as shown in Fig. 2. Then, the simple neutralizer attached on the primary system can be represented by an equivalent model compound just by an equivalent mass, $m_{es} \left(\Omega \right)$, and an equivalent damping, $c_{es} \left(\Omega \right)$. These equivalent dynamic parameters are found equating the dynamic stiffness on the base of the neutralizer of the both models presented in Fig. 2.

Fig. 2.

Generalized equivalent model for a system with VDN – slope DOF.

The dynamic stiffness at the base of angular VDN $(\bar{K}_{bs} (\varOmega ))$ is calculated through the relation between the external moment applied to the base $(M_{b} (\varOmega ))$ and the slope displacement at base $(\theta_{b} (\varOmega ))$, as shown in Fig. 3. This figure shows a lateral view of a simplified model for the VDN, where is represented the shaft, as indicated, the arm of the neutralizer, with an inertia $I_{b}$, the viscoelastic blanket in blue, and the mass of neutralizer above the viscoelastic.

$$ \bar{K}_{bs} \left( \varOmega \right) = \frac{{M_{ext} (\varOmega )}}{{\theta_{b} (\varOmega )}} $$

(3)

Fig. 3.

Simplified physical model for angular VDN.

The lateral action force $\left( {F_{R} \left( \varOmega \right)} \right)$ of the viscoelastic element is obtained in the frequency domain, as shown by [13], as a relation between the dynamic stiffness and the displacements at base $X_{b} \left( \varOmega \right)$ and at mass X(Ω). The free body diagram and Newton’s second law are also applied to the bodies, and, by handling these equations, it is possible to obtain the dynamic stiffness for the angular VDN, as shown below. The relations are obtained as follows:

$$ \bar{K}_{bs} \left( \varOmega \right) = \frac{{M_{ext} (\varOmega )}}{{\theta_{b} (\varOmega )}} = \frac{{\bar{K}\left( \varOmega \right)R^{2} ( - \varOmega^{2} I)}}{{ - \varOmega^{2} I + \bar{K}\left( \varOmega \right)R^{2} }} - \varOmega^{2} I_{b} $$

(4)

where variables I and I_b are the mass inertias of the neutralizer mass and its base, respectively.

As shown in [17], handling Eq. (4) and comparing with the stiffness on the base of the simple neutralizer shown in Fig. 2b given by $\bar{K}_{bs} \left( \varOmega \right) = -\Omega ^{2} m_{es} \left(\Omega \right) + i\Omega c_{es} \left(\Omega \right)$, the generalized equivalent mass and damping can be obtained taking the real and imaginary part of the Eq. (4) and dividing by $-\Omega ^{2}$ and $\Omega$, respectively. Then, these generalized equivalent parameters are defined as:

$$ m_{es} \left( \varOmega \right) = \frac{{r\left( \varOmega \right)R^{2} \left( {I + I_{b} } \right)\left[ { - \varepsilon \left( \varOmega \right)^{2} + r\left( \varOmega \right)R^{2} \left( {1 + \eta \left( \varOmega \right)^{2} } \right)} \right] - \varepsilon \left( \varOmega \right)^{2} I_{b} \left[ { - \varepsilon \left( \varOmega \right)^{2} + r\left( \varOmega \right)R^{2} } \right]}}{{\left[ { - \varepsilon \left( \varOmega \right)^{2} + r\left( \varOmega \right)R^{2} } \right]^{2} + r\left( \varOmega \right)^{2} \eta \left( \varOmega \right)^{2} R^{4} }} $$

(5)

$$ c_{es} \left( \varOmega \right) = \frac{{\varOmega r\left( \varOmega \right)R^{2} \eta \left( \varOmega \right)\varepsilon \left( \varOmega \right)^{2} I}}{{\left[ { - \varepsilon \left( \varOmega \right)^{2} + r\left( \varOmega \right)R^{2} } \right]^{2} + r\left( \varOmega \right)^{2} \eta \left( \varOmega \right)^{2} R^{4} }} $$

(6)

where $r\left( \varOmega \right) = LG_{r} (\varOmega ) /LG_{r} (\varOmega_{n} )$, $\varOmega_{n}$ is the natural frequency of the system given by $\varOmega_{n}^{2} = LG_{r} (\varOmega_{n} ) /m$ and $\varepsilon \left( \varOmega \right) = \varOmega /\varOmega_{n}$.

To find the control frequency $\varOmega_{\theta }$, it is necessary to equal the denominator of Eq. (4) to zero, as follows:

$$ \varOmega_{\theta } = \sqrt {\frac{{LG_{r} \left( {\varOmega_{n} } \right)R^{2} }}{{m\rho^{2} }}} $$

(7)

The mass inertia of the neutralizer mass is defined by $I = m\rho^{2}$, where ρ is the distance between the center of the neutralizer mass and the centerline of the shaft (Fig. 3). So, the relation between the natural frequency of the system and the control frequency is given by:

$$ \varOmega_{\theta } = \varOmega_{n} \frac{R}{\rho } $$

(8)

Based on Eq. (8) and Fig. 3, given that R < ρ, the relation between the frequencies will be $\varOmega_{\theta } < \varOmega_{n}$. So, it is possible to obtain a control frequency as low as necessary.

4 The Rotating System: Primary and Compound Systems

The rotating primary system may be discretized through the finite element method by using the beam finite element with three nodes and four degrees of freedom each, as shown in Fig. 4.

Fig. 4.

Finite element method: discretization of a beam element.

The equation of motion [18, 19] for a simple rotating system with multiple DOF, in the frequency domain, is expressed by:

$$ \left[ { - \varOmega^{2} \left[ M \right] + i\varOmega \left( {\left[ C \right] + \left[ {G\left( {\varOmega_{r} } \right)} \right]} \right) + \left[ K \right]} \right]\left\{ {Q\left( \varOmega \right)} \right\} = \left\{ {F\left( \varOmega \right)} \right\} $$

(9)

where [M] is the global mass matrix defined by the kinetic energy of the system; [C] is the global damping matrix; [G(Ω_r)] is the global gyroscopic effect matrix obtained by the kinetic energy as well; [K] is the global stiffness matrix defined by the potential deformation; {Q(Ω)} is the generalized coordinate vector and {F(Ω)} is the generalized excitation vector. For the sake of simplification, the effects of rotating damping and stiffness were disregarded in Eq. (9).

The motion equation, in the state space, can be rewritten as follows:

$$ \left( {i\varOmega \left[ {\begin{array}{*{20}c} {\left( {\left[ C \right] + \left[ {G\left( {\varOmega_{r} } \right)} \right]} \right)} & {\left[ M \right]} \\ {\left[ M \right]} & 0 \\ \end{array} } \right] + \left[ {\begin{array}{*{20}c} {\left[ K \right]} & 0 \\ 0 & {\left[ { - M} \right]} \\ \end{array} } \right]} \right)\left\{ {Y\left( \varOmega \right)} \right\} = \left\{ {\begin{array}{*{20}c} {F\left( \varOmega \right)} \\ 0 \\ \end{array} } \right\} = \left\{ {N\left( \varOmega \right)} \right\} $$

(10)

For the compound system (primary system plus angular VDV), the generalized equivalent parameters must be added to the primary system. These parameters are expressed in matrix terms by:

$$ \left[ {C_{e} \left( \varOmega \right)} \right] = \left[ {\begin{array}{*{20}c} 0 & 0 & \cdots & 0 & 0 \\ 0 & {c_{{es_{1} }} \left( \varOmega \right)} & \cdots & 0 & 0 \\ \vdots & \vdots & \ddots & \vdots & \vdots \\ 0 & 0 & \cdots & {c_{{es_{p} }} \left( \varOmega \right)} & 0 \\ 0 & 0 & \cdots & 0 & 0 \\ \end{array} } \right]\begin{array}{*{20}c} \vdots \\ { \leftarrow \theta_{j1} } \\ \vdots \\ { \leftarrow \theta_{jp} } \\ \vdots \\ \end{array} $$

(11)

$$ \left[ {M_{e} \left( \varOmega \right)} \right] = \left[ {\begin{array}{*{20}c} 0 & 0 & \cdots & 0 & 0 \\ 0 & {m_{{es_{1} }} \left( \varOmega \right)} & \cdots & 0 & 0 \\ \vdots & \vdots & \ddots & \vdots & \vdots \\ 0 & 0 & \cdots & {m_{{es_{p} }} \left( \varOmega \right)} & 0 \\ 0 & 0 & \cdots & 0 & 0 \\ \end{array} } \right]\begin{array}{*{20}c} \vdots \\ { \leftarrow \theta_{j1} } \\ \vdots \\ { \leftarrow \theta_{jp} } \\ \vdots \\ \end{array} $$

(12)

where parameters $c_{{es_{j} }}$ and $m_{{es_{j} }}$ are the j^th term, with j = 1 to p with p being the number of angular VDNs used.

Then, the motion equation for the compound system is given by:

$$ \left[ { - \varOmega^{2} \left( {\left[ M \right] + \left[ {M_{e} \left( \varOmega \right)} \right]} \right) + i\varOmega \left( {\left[ C \right] + \left[ {C_{e} \left( \varOmega \right)} \right] + \left[ {G\left( {\varOmega_{r} } \right)} \right]} \right) + \left[ K \right]} \right]\left\{ {Q\left( \varOmega \right)} \right\} = \left\{ {F\left( \varOmega \right)} \right\} $$

(13)

In the state space, Eq. (13) can be rewritten as

$$ i\varOmega \left[ {\tilde{A}\left( {\varOmega ,\varOmega_{r} } \right)} \right]\left\{ {Y\left( \varOmega \right)} \right\} + \left[ {\tilde{B}\left( \varOmega \right)} \right]\left\{ {Y(\varOmega )} \right\} = \left\{ {\begin{array}{*{20}c} { F\left( \varOmega \right)} \\ \cdots \\ 0 \\ \end{array} } \right\} = \left\{ {N\left( \varOmega \right)} \right\} $$

(14)

where:

$$ \left[ {\tilde{A}\left( {\varOmega ,\varOmega_{r} } \right)} \right] = \left[ {A\left( {\varOmega_{r} } \right)} \right] + \left[ {A_{e} \left( \varOmega \right)} \right] $$

(15)

$$ \left[ {\tilde{B}\left( \varOmega \right)} \right] = \left[ B \right] + \left[ {B_{e} \left( \varOmega \right)} \right] $$

(16)

the matrices $\left[ {A\left( {\varOmega_{r} } \right)} \right]$ and $\left[ B \right]$ represent the primary system behavior and $\left[ {A_{e} \left( \varOmega \right)} \right]$ and $\left[ {B_{e} \left( \varOmega \right)} \right]$ represent the influence of the dynamic neutralizers attached to the primary system. These matrices are given by:

$$ \left[ {A\left( {\varOmega_{r} } \right)} \right] = \left[ {\begin{array}{*{20}c} {\left( {\left[ C \right] + \left[ {G\left( {\varOmega_{r} } \right)} \right]} \right)} & {\left[ M \right]} \\ {\left[ M \right]} & 0 \\ \end{array} } \right] $$

(17)

$$ \left[ {A_{e} \left( \varOmega \right)} \right] = \left[ {\begin{array}{*{20}c} {\left[ {C_{e} \left( \varOmega \right)} \right]} & {\left[ {M_{e} \left( \varOmega \right)} \right]} \\ {\left[ {M_{e} \left( \varOmega \right)} \right]} & {\left[ 0 \right]} \\ \end{array} } \right] $$

(18)

and

$$ \left[ B \right] = \left[ {\begin{array}{*{20}c} {\left[ K \right]} & 0 \\ 0 & {\left[ { - M} \right]} \\ \end{array} } \right] $$

(19)

$$ \left[ {B_{e} \left( \varOmega \right)} \right] = \left[ {\begin{array}{*{20}c} {\left[ 0 \right]} & {\left[ 0 \right]} \\ {\left[ 0 \right]} & {\left[ { - M_{e} \left( \varOmega \right)} \right]} \\ \end{array} } \right] $$

(20)

To solve the motion equation, it is necessary to transform Eq. (14), in the configuration system, into the modal or sub-modal space of the state space by using the right eigenvector matrix of the primary system [Θ](λ[A(Ω_r)][Θ]) = [B][Θ].

$$ \left\{ {Y\left( \varOmega \right)} \right\} = \left[ \varTheta \right]\left\{ {P\left( \varOmega \right)} \right\} $$

(21)

and, then, pre-multiplying Eq. (14) by the transpose left eigenvectors [Ψ]^T(λ[A(Ω_r)]^T[Ψ]) = [B]^T[Ψ], its adjoint problem, the motion equation can be solved as:

$$ \left[ {i\varOmega \left[ \varPsi \right]^{T} \left[ {\tilde{A}\left( {\varOmega ,\varOmega_{r} } \right)} \right]\left[ \varTheta \right] + \left[ \varPsi \right]^{T} \left[ {\tilde{B}\left( \varOmega \right)} \right]\left[ \varTheta \right]} \right]\left\{ {P\left( \varOmega \right)} \right\} = \left[ \varPsi \right]^{T} \left\{ {N\left( \varOmega \right)} \right\} $$

(22)

or, simplified as:

$$ \left\{ {\bar{Y}\left( \varOmega \right)} \right\} = \left[ \varTheta \right]\left[ {D\left( \varOmega \right)} \right]\left[ \varPsi \right]^{T} \left\{ {N\left( \varOmega \right)} \right\} $$

(23)

with

$$ \left[ {D\left( \varOmega \right)} \right] = \left[ {i\varOmega \left( {\left[ I \right] + \left[ \varPsi \right]^{T} \left[ {A_{e} \left( \varOmega \right)} \right]\left[ \varTheta \right]} \right) + \left( {\left[ \varLambda \right] + \left[ \varPsi \right]^{T} \left[ {B_{e} \left( \varOmega \right)} \right]\left[ \varTheta \right]} \right)} \right]^{ - 1} $$

(24)

For the angular VDN design, the subspace can be obtained by limiting the size of eigenvectors matrices [Θ] and [Ψ] to the first 2$\hat{n}$ modes, with $\hat{n} \ll n$, since the contribution of the higher order modes is insignificant and can be ignored. This significantly reduces the computational time, which is proportional in n³.

5 Optimization Problem

In the present work, the optimization problem consists of reducing the flexural vibration level for the primary system as much as possible. This control is made by the indirect reduction of the slope degree of freedom of the primary system obtained by using angular VDNs. For that, the angular VDN must be optimally designed, in other words, its natural frequency must be determined in an optimization environment.

To this end, it is suggested a non-linear optimization method, and the objective function f_obj is defined by:

$$ f_{obj} \left( x \right) = \left\| {\mathop {max}\nolimits_{{\varOmega_{1} < \varOmega < \varOmega_{2} }} \left| {P\left( {\varOmega ,x} \right)} \right|} \right\| $$

(25)

where x is the design vector containing the natural frequencies of the p neutralizers $\left( {x^{T} = \left[ {\varOmega_{a1} ,\,\varOmega_{a2} ,\, \ldots ,\,\varOmega_{ap} } \right]} \right)$; parameters Ω₁ and Ω₂ constitute the frequency band control related to the operation of the machine and its flexural modes; “max” is the maximum value for each component of vector P(Ω,x) and ║║indicates the use of the Euclidian Norm.

When it comes to ensure the convergence of an optimization problem, it is advisable to use barrier functions, which are inequality functions defined by $\varOmega_{ai}^{L} < \varOmega_{ai} < \varOmega_{ai}^{U}$ with i = 1 to p, and L and U are the lower and upper constrains, respectively.

The aim of this optimization problem is to find a vector with the frequencies for the angular VDNs that minimize function P(Ω, x).

The complete methodology used in the present paper is based on the following instructions:

• 1. the generalized equivalent parameters for the slope DOF are calculated (Eqs. (5) and (6)) based on the viscoelastic material selected and the rotor geometry studied;

• 2. matrix [D(Ω)] from Eq. (24) is assembled and equated;

• 3. the unbalance excitation and the matrix [D(Ω)] are solved to obtain vector {P(Ω,x)};

• 4. the absolute values of vector {P(Ω,x)} are evaluated for the optimization algorithm, and its maximum values are chosen;

• 5. the objective function is solved, and a new project vector is assembled;

• 6. steps 1 to 5 are repeated until the minimal value for vector {P(Ω, x)} is found; then, the optimal natural frequencies are finally obtained.

After having found the natural frequencies of the angular VDN, the other parameters can be found out to physically design the neutralizer. The mass inertia of the neutralizer was defined by [13] for the mode-to-mode control and is adapted for this application as follow:

$$ \mu_{j} = \frac{{I_{a} \mathop \sum \nolimits_{s = 1}^{p} \left| {\phi_{{k_{s} j}} } \right|^{2} }}{{I_{j} }} $$

(26)

where $\phi_{{k_{s} j}}$ are the k_s,j elements of the right modal matrix on state space; I_a is the neutralizer mass inertia considering it in modal space; p is the number of neutralizers; k_s is the position where the i^th neutralizer is fixed on the primary system with s = 1 to j, where j is the j^th mode to be controlled. Finally, μ_j is the relation between the mass moment of inertia of the neutralizer, considered in the modal space of the primary system, and the modal mass moment of inertia of the primary system and can typically go up 10% to 25%.

6 Numerical-Experimental Development and Results

The current work presents three different geometries performed to experimentally validate the methodology presented above. They are the compact angular VDN using E-A-R Isodamp C-1002 rubber (item 6.1), the same design by using butyl rubber (item 6.2), and the center of percussion of the angular VDN design (item 6.3).

The three types of angular VDN were designed for the same rotor geometry, as detailed in Fig. 5, and the same unbalance mass was used: 0.0002 kg m applied to the central disk, or 458 mm from the driven side of the shaft.

Fig. 5.

Rotor geometry used for all types of angular VDN tested.

The neutralizers were assembled in the same position, as close as possible to the rear bearing, 50 mm away from the bearing in the shaft end direction, as presented in Figs. 7 and 14.

6.1 Compact Angular VDN – C-1002

The first geometry proposed was designed by using the E-A-R Isodamp C-1002, and the parameters of the four-parameter fractional derivative model are preset in Table 1.

Table 1. Rubber parameters.

The design starts by modelling the rotor, as shown previously, and applying it to the optimization environment. So, for this case, the optimal natural frequency found was 24.9 Hz, as presented in Fig. 6. For other neutralizer geometries, the same unbalance frequency response shown in Fig. 6 is used, since the primary system is the same.

Fig. 6.

Unbalance frequency response with and without compact angular VDN C-1002.

Based on that geometry, the modal inertia is obtained and, considering a μ_j equal to 10%, the neutralizer inertia is I_a = 0.0077496 kg m². This inertia was divided into four identical devices, consisting of an aluminum base with three pieces of rubber glued to a steel sleeve; fixed on it by threading bars are two steel cylinders serving as the mass of the device, as presented on Fig. 7. The device is attached to a fake bearing by using a threading bar. This bearing consists of an aluminum sleeve mounted above the rolling bearing and anchored on the structure by steel wires.

Fig. 7.

Rotor assembled with compact angular VDN compound with C-1002.

The experimental validation of the VDN natural frequency is presented in Fig. 8 and shows the inertance curve measured. The curve was obtained by fixing the accelerometer to the cylinder mass of the neutralizer (measuring point) and by applying an impact force near this point (exciting point). This curve presents a damped behavior due the physical properties of the material. The natural frequency presented was approximately 25 Hz, as expected.

Fig. 8.

Inertance to C-1002 VDN.

Two of the angular VDNs were positioned parallel to the faces of the disks, as shown in Fig. 7. Due to the size of the mass, the other two devices were assembled slightly misaligned in relation the other ones. From now on, this configuration will be called ‘standard position’. The rundown test was conducted, and the unbalance frequency response (UFR) for ‘X’ direction, according Fig. 4, is shown in Fig. 9.

Fig. 9.

UFR for standard position – angular VDN C-1002.

Based on Fig. 9, it is possible to note that the angular VDNs do not insert the necessary impedance to effectively control the vibration level of the primary system for the first mode, and barely had any effect on the second one. This behavior was initially associated to clearance in ball bearings. The hypothesis was rebutted after assembling a new hub using roller bearings, without a significant change in the results. Other tests were conducted by altering the angular position of neutralizers, as showed on Fig. 11, resulting in distinct dynamic behaviors, increasing or reducing control capacity, as presented in Fig. 10.

Fig. 10.

UFR for variation of angular positioning – angular VDN C-1002.

When comparing the curves in Figs. 9 and 11, there is a reduction in the amplitude of vibration for both modes, which is stronger for the case with variation of the angular positioning in relation to the standard position, showing the sensitivity of the device to this design variable. This behavior seems to be due to the combined displacement presented in operation, that is, the rotor whirling combines translational (X and Z directions) and slope (δ and γ) displacements.

Fig. 11.

Variation of angular positioning – angular VDVN C-1002.

6.2 Compact Angular VDN – Butyl Rubber

The second geometry of angular VDN proposes to change only the viscoelastic material from C-1002 to a butyl rubber available in the laboratory where the tests were conducted. The parameters of the four-parameter fractional derivative model for this material are present in Table 1.

For the present case, the optimal natural frequency obtained was 28.8 Hz. The μ_j used to calculate the neutralizer inertia was changed to 25%, resulting in I_a = 0.019374 kg m². The same geometry concept of the previous case was used, just changing the rubber blanks. Just to clarify: the device on the top of the figure is the C-1002 neutralizer, and the other four, at the bottom of the figure, are the butyl rubber ones. The device was positioned at the same point the C-1002 one was.

The inertance of this angular VDN was measured, and the curve is shown in Fig. 12. This curve can be compared the one shown in Fig. 8, presenting the difference in the dynamic behavior of the butyl rubber and compared to E-A-R Isodamp C-1002. The inspection of the inertance shows that the natural frequency of VDN with butyl rubber was not in accordance with the design (25 Hz × 28.8 Hz). When this occurs, the temperature used in the project must have been different from that experienced in the laboratory during the tests. This shows the vulnerability of the project related to the use of some kinds of viscoelastic material, which are more susceptible to the influence of temperature in their dynamic behaviors.

Fig. 12.

Inertance curve to compact angular VDN butyl rubber.

Subsequently, the unbalance frequency response curves of the rotor, with and without neutralizer, were obtained by the rundown test. In a more detailed analysis of the rotor response curves, it was found that there was a region being controlled, below the first critical rotation. The hypothesis associated to this behavior was that the rotor was not exciting the design frequency of the neutralizer, in other words, the neutralizers were vibrating in a different way from that expected. To test this hypothesis, the natural frequency of the neutralizer was increased to coincide with the first critical rotation of the primary system. For this, the masses were approximated in increments of 10 mm of the neutralizer center until achieving a satisfactory control of the primary system. Figure 13 shows the unbalance frequency response curves with and without neutralizer, in the X direction.

Fig. 13.

UFR for Angular VDN butyl rubber.

Although rotor vibration was significantly controlled for the first mode, great difficulty was encountered in predicting the behavior of the neutralizer, that is, how the rotor will excite the neutralizer. This hinders the design and the correct tuning, the same problem faced on the C-1002 device.

6.3 Center of Percussion Angular VDN

The third angular VDN design used a butyl rubber material, the parameters of which are presented in Table 1. The primary system is the same as shown in Fig. 5.

In this case, the neutralizer was designed to control the second rotor vibration mode, since the higher the frequency of the neutralizer, the easier its physical construction due to the viscoelastic material form factor. Based on this, an optimum frequency of 62.2 Hz and a mass inertia of I_a = 0.019374 kg m² were obtained for a μ_j = 25%.

This inertia was divided into four identical pieces with a different geometry, here called ‘center of percussion’. This geometry has been arranged in order to operate in shear as much as possible, and to obtain the minimal distance R possible and, then, minimize the influence of the other neutralizer modes.

However, this geometry proved to be very fragile, due to its form of assembly, with the viscoelastic material segments attached between the base of the mass and the hub of the fake bearing. In an attempt to measure the unbalance frequency response to runway/rundown, the viscoelastic segments came loose, making it impossible to operate and take measurements. In addition, this geometry shown a tendency to move in the direction of traction/compression of the material, further altering the frequency of the device in operation. Figure 14 shows the neutralizer assembled on the rotor.

Fig. 14.

Center of percussion angular VDN – experimental set.

Since the natural frequency of the device was lower than the one designed, the thickness of the viscoelastic material was reduced until the frequency coincided with the calculated one. The inertance of the system without neutralizer - with a designed neutralizer for the 1^st mode and for the 2^nd mode - was measured, as shown in Fig. 15.

Fig. 15.

Inertance for the center of percussion angular VDN.

Evaluating Fig. 15, one observes that there was an expressive control for the mode corresponding to the designed mode of the VDN. This behavior presents potential regarding the control of the primary system, once the previously listed problems are eliminated.

7 Conclusions

The current paper presents a revision of the methodology on optimal design of angular viscoelastic dynamic neutralizers, as well as the experimental application of three different concepts in a controlled laboratory environment.

The results obtained were promising: the reduction of the response to the rotor unbalance frequency response of the primary system - by using angular VDNs - achieved 20 dB for the last geometry, for example.

However, several questions concerning the analytical design of the devices were identified in relation to the non-analytical prediction of the excitation behavior of the neutralizer by the rotor. Due to the rotor whirling, the angular VDN vibrates in different planes and not preferably in the one it was designed for, thus decreasing its effectiveness. These questions are being reviewed, and other geometries are under study for the neutralizer support.