Computational Analysis of Nonlinear Dynamics of a Multi-disk Rotor-Bearing-Brush Seal System

Abstract

The seal force and oil-film force are two of the main factors which would cause the instability of rotor system, so it is important to further study the nonlinear dynamic characteristics of the multi-disk rotor-bearing-seal system. In order to establish the multi-disk rotor-bearing-brush seal system model of a gas turbine, the seal force model of brush seal and the nonlinear oil-film force model based on short bearing theory were adopted considering the lateral deflection of the disks. The equation of motion was solved by time simulation using the fourth order Runge-Kutta method. The influences of key parameters including rotor speed and eccentricity phase-difference on the vibration response and dynamic behavior of multi-disk rotor-bearing-brush seal system were discussed. The result showed that the system became more stable when the eccentricity phase-difference decreased.

1 Introduction

Brush seals have superior sealing performance, which could enhance the thrust force and working efficiency of gas turbine [1, 2]. When the gas turbine is working under high temperature, high pressure, and high velocity condition, there would be some complex dynamic behavior fault arising, which could seriously affect the security and reliability of the system [3,4,5].

Currently the dynamic behaviors of multi-disk rotor-brush seal system are mostly studied by numerical simulation or test results for a specific structure. Chu and Lu [6] proposed a dynamic stiffness-based method to detect the rubbing position effectively in a multi-disk rotor system. The authors found that the dynamic stiffness at the position with rotor-to-stator rub increased as the rubbing developed, but the variation of stiffness at other positions was not obvious. Wan et al. [7] theoretically and experimentally studied the dynamic response of an unbalanced multi-disk rotor system with flexible coupling misalignment, and the governing equations of the system was deduced by the lumped mass model considering the nonlinear oil film force. But these researches are still not perfect, so the effects of coupling of the contact of bristle pack and rotor surface, and the fluid flow in the bristle pack to the dynamic behavior of the system need further study.

In this paper, the authors adopted the seal force model of brush seal and the nonlinear oil-film force model based on short bearing theory considering the lateral deflection of the disks, in order to build the nonlinear dynamic model of a multi-disk rotor-bearing-brush seal system. The effects of the rotor speed and eccentricity phase difference on the vibration response and dynamic behavior of a multi-disk rotor-bearing-seal system were discussed under different operating conditions by axis orbit, Poincaré map, and spectrum cascade.

2 Nonlinear Dynamic Model of a Multi-disk Rotor-Bearing-Brush Seal System

2.1 Nonlinear Dynamic Model of the Multi-disk Rotor-Bearing-Seal System

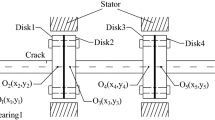
Figure 1 shows the rotor-bearing-seal system of a gas turbine. The finite element model is obtained by discretization based on the structural features of the system, as shown in Fig. 1a. In this paper, the compressor and turbine are simplified as disk m8 and disk m9, which located at joint 8 and joint 9, respectively. Similarly, the supporting bearings are simplified as disk m4 and disk m12, which located at joint 4 and joint 12, respectively.

Fig. 1.

Rotor-bearing-seal system of a gas turbine.

Considering the lateral deflection of the disks, the nonlinear dynamic equation of the system can be obtained by the simplified model as below:

$$ M\ddot{q} + C\dot{q} + Kq = - F_{\text{g}} + F_{\text{b}} + F_{\text{s}} + F_{\text{e}} $$

(1)

With

$$ \Gamma = Kq = \left[ {\begin{array}{*{20}l} { - 6EI\left[ {\frac{1}{{l_{48}^{3} }}\left( { - 2x_{8} + 2x_{4} + \theta_{y8} l_{48} + \theta_{y4} l_{48} } \right)} \right]} \hfill \\ { - 6EI\left[ {\frac{1}{{l_{48}^{3} }}\left( { - 2y_{8} + 2y_{4} + \theta_{x8} l_{48} + \theta_{x4} l_{48} } \right)} \right]} \hfill \\ {6EI\left[ {\frac{1}{{l_{48}^{3} }}\left( { - 2x_{8} + 2x_{4} + \theta_{y8} l_{48} + \theta_{y4} l_{48} } \right) + \frac{1}{{l_{89}^{3} }}\left( { - 2x_{9} + 2x_{8} + \theta_{y9} l_{89} + \theta_{y8} l_{89} } \right)} \right]} \hfill \\ {6EI\left[ {\frac{1}{{l_{48}^{3} }}\left( { - 2y_{8} + 2y_{4} + \theta_{x8} l_{48} + \theta_{x4} l_{48} } \right) + \frac{1}{{l_{89}^{3} }}\left( { - 2y_{9} + 2y_{8} + \theta_{x9} l_{89} + \theta_{x8} l_{89} } \right)} \right]} \hfill \\ { - 2EI\left[ {\frac{1}{{l_{89}^{2} }}\left( {3y_{9} - 3y_{8} - \theta_{x9} l_{89} - 2\theta_{x8} l_{89} } \right) - \frac{1}{{l_{48}^{2} }}\left( {3y_{8} - 3y_{4} - \theta_{x8} l_{48} - 2\theta_{x4} l_{48} } \right)} \right]} \hfill \\ { - 2EI\left[ {\frac{1}{{l_{89}^{2} }}\left( {3x_{9} - 3x_{8} - \theta_{y9} l_{89} - 2\theta_{y8} l_{89} } \right) - \frac{1}{{l_{48}^{2} }}\left( {3x_{8} - 3x_{4} - \theta_{y8} l_{48} - 2\theta_{y4} l_{48} } \right)} \right]} \hfill \\ {6EI\left[ {\frac{1}{{l_{89}^{3} }}\left( { - 2x_{9} + 2x_{8} + \theta_{y9} l_{89} + \theta_{y8} l_{89} } \right) + \frac{1}{{l_{912}^{3} }}\left( { - 2x_{12} + 2x_{9} + \theta_{y12} l_{912} + \theta_{y9} l_{912} } \right)} \right]} \hfill \\ {6EI\left[ {\frac{1}{{l_{89}^{3} }}\left( { - 2y_{9} + 2y_{8} + \theta_{x9} l_{89} + \theta_{x8} l_{89} } \right) + \frac{1}{{l_{912}^{3} }}\left( { - 2y_{12} + 2y_{9} + \theta_{x12} l_{912} + \theta_{x9} l_{912} } \right)} \right]} \hfill \\ { - 2EI\left[ {\frac{1}{{l_{912}^{2} }}\left( {3y_{12} - 3y_{9} - \theta_{x12} l_{912} - 2\theta_{x9} l_{912} } \right) - \frac{1}{{l_{89}^{2} }}\left( {3y_{9} - 3y_{8} - \theta_{x9} l_{89} - 2\theta_{x8} l_{89} } \right)} \right]} \hfill \\ { - 2EI\left[ {\frac{1}{{l_{912}^{2} }}\left( {3x_{12} - 3x_{9} - \theta_{y12} l_{912} - 2\theta_{y9} l_{912} } \right) - \frac{1}{{l_{89}^{2} }}\left( {3x_{9} - 3x_{8} - \theta_{y9} l_{89} - 2\theta_{y8} l_{89} } \right)} \right]} \hfill \\ {6EI\left[ {\frac{1}{{l_{912}^{3} }}\left( { - 2x_{12} + 2x_{9} + \theta_{y12} l_{912} + \theta_{y9} l_{912} } \right)} \right]} \hfill \\ {6EI\left[ {\frac{1}{{l_{912}^{3} }}\left( { - 2y_{12} + 2y_{9} + \theta_{x12} l_{912} + \theta_{x9} l_{912} } \right)} \right]} \hfill \\ \end{array} } \right] $$

where M is the mass matrix of the system, $M = \left( {\begin{array}{*{20}c} {M_{x} } & 0 \\ 0 & {M_{y} } \\ \end{array} } \right)$, $M_{x} = M_{y} = {\text{diag}}[m_{4} ,m_{8} ,J_{d8} ,m_{9} ,J_{d9} ,m_{12} ]$, C is the damping matrix of the system, $C = \left( {\begin{array}{*{20}c} {C_{x} } & 0 \\ 0 & {C_{y} } \\ \end{array} } \right)$, $C_{x} = C_{y} = {\text{diag}}[c_{4} ,c_{8} ,c_{\theta 8} ,c_{9} ,c_{\theta 9} ,c_{12} ]$, K is the stiffness matrix of the system, q is the displacement of geometry center O_i in the X and Y direction, respectively, $q = [x_{4} ,y_{4} ,x_{8} ,y_{8} ,\theta_{x8} ,\theta_{y8} ,x_{9} ,y_{9} ,\theta_{x9} ,\theta_{y9} ,x_{12} ,y_{12} ]^{T}$, F_g is the gravity vector of the system, $F_{\text{g}} = [0,m_{4} g,0,m_{8} g,0,0,0,m_{9} g,0,0,0,m_{12} g]^{T}$, F_b is the nonlinear oil-film force vector [8, 9], $F_{\text{b}} = [F_{{{\text{b}}x4}} ,F_{{{\text{b}}y4}} ,0,0,0,0,0,0,0,0,F_{{{\text{b}}x12}} ,F_{{{\text{b}}y 1 2}} ]^{T}$, $\left[ \begin{aligned} F_{{{\text{b}}xi}} \hfill \\ F_{{{\text{b}}yi}} \hfill \\ \end{aligned} \right] = S_{0} \left[ \begin{aligned} f_{{{\text{b}}xi}} \hfill \\ f_{{{\text{b}}yi}} \hfill \\ \end{aligned} \right]$, $i = 4,12$, F_s is the seal force vector [10], $F_{\text{s}} = [0,0,F_{{{\text{s}}x8}} ,F_{{{\text{s}}y8}} ,0,0,F_{{{\text{s}}x9}} ,F_{{{\text{s}}y9}} ,0,0,0,0]^{T}$, $\left[ \begin{aligned} F_{{{\text{s}}xi}} \hfill \\ F_{{{\text{s}}yi}} \hfill \\ \end{aligned} \right] = \left[ \begin{aligned} F_{{{\text{b}}i}} \cos (\alpha + \theta - \mu - \phi ) \hfill \\ F_{{{\text{b}}i}} \sin (\alpha + \theta - \mu - \phi ) \hfill \\ \end{aligned} \right]$, $i = 8,9$, F_e is the unbalanced force vector,

$$ \begin{aligned} & F_{e} = [0,0,m_{8} e_{u8} \omega^{2} \cos (\omega t),m_{8} e_{u8} \omega^{2} \sin (\omega t),0,0,m_{9} e_{u9} \omega^{2} \cos (\omega t + \sigma ), \\ & \quad \quad m_{8} e_{u8} \omega^{2} \sin (\omega t + \sigma ),0,0,0,0]^{T} . \\ \end{aligned} $$

For the facility of calculation, dimensionless transformations are introduced into the Eq. (1):

$$ \omega t = \tau ,\;X_{i} = \frac{{x_{i} }}{\delta },\;Y_{i} = \frac{{y_{i} }}{\delta },\;\frac{\text{d}}{{{\text{d}}\tau }} = \frac{\text{d}}{{\omega {\text{d}}t}},\;\frac{{{\text{d}}^{2} }}{{{\text{d}}^{2} \tau }} = \frac{{{\text{d}}^{2} }}{{\omega^{2} {\text{d}}t^{2} }} $$

where $\dot{X}_{i} = \frac{{\dot{x}_{i} }}{\omega \delta }$, $\dot{Y}_{i} = \frac{{\dot{y}_{i} }}{\omega \delta }$, $\ddot{X}_{i} = \frac{{\ddot{x}_{i} }}{{\omega^{2} \delta }}$, $\ddot{Y}_{i} = \frac{{\ddot{y}_{i} }}{{\omega^{2} \delta }}$, ${\dot{\varTheta }}_{i} = \frac{{\dot{\theta }_{i} }}{\omega }$, ${\ddot{\varTheta }}_{i} = \frac{{\ddot{\theta }_{i} }}{{\omega^{ 2} }}$, $E_{ui} = \frac{{e_{ui} }}{\delta }$, $G = \frac{g}{{\omega^{2} \delta }}$, $M_{i} = \frac{{m_{i} \omega \psi^{3} }}{{\mu l_{412} }}$, $k_{i} = \frac{{6EI_{i} }}{{l_{i}^{3} }}$, $K_{i} = k_{i} \cdot \frac{{\psi^{3} }}{{\omega \mu l_{412} }}$, $C_{i} = c_{i} \cdot \frac{{\psi^{3} }}{{\omega \mu l_{412} }}$, $C_{\theta i} = c_{\theta i} \cdot \frac{{\omega \psi^{3} }}{{\mu l_{412} c^{2} }}$, $L_{i} = \frac{{l_{i} }}{{l_{412} }}$, $J_{di}^{*} = \frac{{J_{di}^{{}} \omega \psi^{3} }}{{\mu l_{412} \delta^{2} }}$, $J_{pi}^{*} = \frac{{J_{pi}^{{}} \omega \psi^{3} }}{{\mu l_{412} \delta^{2} }}$, $f_{{{\text{s}}i}} = \frac{{F_{{{\text{s}}i}} \psi^{3} }}{{\mu l_{412} \omega \delta }}$, $f_{{{\text{b}}i}} = \frac{{S_{0} F_{{{\text{b}}i}} \psi^{2} }}{{\mu l_{412} \omega r}}$, $S_{0} = \mu_{0} \omega rl(\frac{r}{\delta })^{2} (\frac{l}{2r})^{2}$, $\mu_{0}$ is the absolute viscosity of lubricate, $\delta$ is the clearance of radius, $\omega$ is the rotor speed.

Then $\Gamma$ can be rewritten as below:

$$ \Gamma ^{{\prime }} = \left[ {\begin{array}{*{20}l} {\frac{{K_{48} }}{{M_{4} }}\left( { - 2X_{8} + 2X_{4} +\Theta _{y8} L_{48} +\Theta _{y4} L_{48} } \right)} \hfill \\ {\frac{{K_{48} }}{{M_{4} }}\left( { - 2Y_{8} + 2Y_{4} +\Theta _{x8} L_{48} +\Theta _{x4} L_{48} } \right)} \hfill \\ { - \frac{{K_{48} }}{{M_{8} }}\left( { - 2X_{8} + 2X_{4} +\Theta _{y8} L_{48} +\Theta _{y4} L_{48} } \right) + \frac{{K_{89} }}{{M_{8} }}\left( { - 2X_{9} + 2X_{8} +\Theta _{y9} L_{89} +\Theta _{y8} L_{89} } \right)} \hfill \\ { - \frac{{K_{48} }}{{M_{8} }}\left( { - 2Y_{8} + 2Y_{4} +\Theta _{x8} L_{48} +\Theta _{x4} L_{48} } \right) + \frac{{K_{89} }}{{M_{8} }}\left( { - 2Y_{9} + 2Y_{8} +\Theta _{x9} L_{89} +\Theta _{x8} L_{89} } \right)} \hfill \\ {\frac{{K_{89} L_{89} }}{{3J_{d8}^{*} }}\left( {3Y_{9} - 3Y_{8} -\Theta _{x9} L_{89} - 2\Theta _{x8} L_{89} } \right) - \frac{{K_{48} L_{48} }}{{3J_{d4}^{*} }}\left( {3Y_{8} - 3Y_{4} -\Theta _{x8} L_{48} - 2\Theta _{x4} L_{48} } \right)} \hfill \\ {\frac{{K_{89} L_{89} }}{{3J_{d8}^{*} }}\left( {3X_{9} - 3X_{8} -\Theta _{y9} L_{89} - 2\Theta _{y8} L_{89} } \right) - \frac{{K_{48} L_{48} }}{{3J_{d4}^{*} }}\left( {3X_{8} - 3X_{4} -\Theta _{y8} L_{48} - 2\Theta _{y4} L_{48} } \right)} \hfill \\ { - \frac{{K_{89} }}{{M_{9} }}\left( { - 2X_{9} + 2X_{8} +\Theta _{y9} L_{89} +\Theta _{y8} L_{89} } \right) + \frac{{K_{912} }}{{M_{9} }}\left( { - 2X_{12} + 2X_{9} +\Theta _{y12} L_{912} +\Theta _{y9} L_{912} } \right)} \hfill \\ { - \frac{{K_{89} }}{{M_{9} }}\left( { - 2Y_{9} + 2Y_{8} +\Theta _{x9} L_{89} +\Theta _{x8} L_{89} } \right) + \frac{{K_{912} }}{{M_{9} }}\left( { - 2Y_{12} + 2Y_{9} +\Theta _{x12} L_{912} +\Theta _{x9} L_{912} } \right)} \hfill \\ {\frac{{K_{912} L_{912} }}{{3J_{d12}^{*} }}\left( {3Y_{12} - 3Y_{9} -\Theta _{x12} L_{912} - 2\Theta _{x12} L_{912} } \right) - \frac{{K_{89} L_{89} }}{{3J_{d8}^{*} }}\left( {3Y_{9} - 3Y_{8} -\Theta _{x9} L_{89} - 2\Theta _{x8} L_{89} } \right)} \hfill \\ {\frac{{K_{912} L_{912} }}{{3J_{d12}^{*} }}\left( {3X_{12} - 3X_{9} -\Theta _{y12} L_{912} - 2\Theta _{y12} L_{912} } \right) - \frac{{K_{89} L_{89} }}{{3J_{d8}^{*} }}\left( {3X_{9} - 3X_{8} -\Theta _{y9} L_{89} - 2\Theta _{y8} L_{89} } \right)} \hfill \\ { - \frac{{K_{912} }}{{M_{12} }}\left( { - 2X_{12} + 2X_{9} +\Theta _{y12} L_{912} +\Theta _{y9} L_{912} } \right)} \hfill \\ { - \frac{{K_{912} }}{{M_{12} }}\left( { - 2Y_{12} + 2Y_{9} +\Theta _{x12} L_{912} +\Theta _{x9} L_{912} } \right)} \hfill \\ \end{array} } \right] $$

where m_i and M_i are the mass of disk and dimensionless mass of disk, respectively, k_i and K_i are the stiffness of shaft and dimensionless stiffness of shaft, respectively, c_i and C_i are the damping of disk and dimensionless damping of disk, respectively, c_θi and C_θi are the deflection damping of disk and dimensionless deflection damping of disk, respectively, $J_{di}$ and $J_{di}^{*}$ are the moment of inertia of disc diameter and dimensionless moment of inertia of disc diameter, respectively, $J_{pi}$ and $J_{pi}^{*}$ are polar moment of inertia of disc and dimensionless polar moment of inertia of disc, respectively, e_ui and E_ui are the eccentricity of disk mass and dimensionless eccentricity of disk mass, respectively, f_si and F_si are the dimensionless seal force and seal force, respectively, f_bi and F_bi are the dimensionless oil-film force and oil-film force, respectively, $\sigma$ is the phase-difference of disk 8 and disk 9, r is the radius of bearing, $\psi$ is the clearance ratio, $\psi = {c \mathord{\left/ {\vphantom {c r}} \right. \kern-0pt} r}$, l_i and L_i are the span between disk and dimensionless span between disk, respectively, g and G are the acceleration of gravity and dimensionless acceleration of gravity, respectively, E is the elastic modulus, and I_i is the moment of inertia of cross-section of shaft.

As the moment of inertia of discs M₄ and M₁₂ can be negligible, the rotation angle of disc 4 and disc 12 $\theta_{x4} ,\theta_{y4} ,\theta_{x12} ,\theta_{y12}$ can be obtained through the bending moment equation and shear equation in the bending deformation formula of the beam. Assuming the left side and right side bending moment of disk 4 and disk 12 are equal, that is $M_{4}^{R} = M_{48} \left( 0 \right)$ and $M_{12}^{L} = M_{912} \left( l \right)$, then the expression of the rotation angle can be derived as follows:

$$ \left\{ {\begin{array}{*{20}l} {\theta_{x4} = (3y_{8} - 3y_{4} - \theta_{x8} l_{48} )/(2l_{48} )} \hfill \\ {\theta_{y4} = (3x_{8} - 3x_{4} - \theta_{y8} l_{48} )/(2l_{48} )} \hfill \\ \end{array} } \right. $$

(2)

$$ \left\{ {\begin{array}{*{20}l} {\theta_{x12} = (3y_{12} - 3y_{9} - 2\theta_{x9} l_{912} )/l_{912} } \hfill \\ {\theta_{y12} = (3x_{12} - 3x_{9} - 2\theta_{y9} l_{912} )/l_{912} } \hfill \\ \end{array} } \right. $$

(3)

Suppose

$$ \begin{aligned} \lambda & = \left[ {\lambda_{1} ,\lambda_{2} , \ldots ,\lambda_{i} , \ldots ,\lambda_{24} } \right]^{T} \\ & = \left[ {x_{4} ,\dot{x}_{4} ,{\kern 1pt} y_{4} ,\dot{y}_{4} ,x_{8} ,\dot{x}_{8} ,y_{8} ,\dot{y}_{8} ,\theta_{x8} ,\dot{\theta }_{x8} ,\theta_{y8} ,\dot{\theta }_{y8} ,x_{9} ,\dot{x}_{9} ,y_{9} ,\dot{y}_{9} ,\theta_{x9} ,\dot{\theta }_{x9} ,\theta_{y9} ,\dot{\theta }_{y9} ,x_{12} ,\dot{x}_{12} ,y_{12} ,\dot{y}_{12} } \right]^{T} \\ \end{aligned} $$

then

$$ \begin{aligned} \dot{\lambda } & = \left[ {\dot{\lambda }_{1} {\kern 1pt} ,\dot{\lambda }_{2} , \ldots ,\dot{\lambda }_{i} , \ldots {\kern 1pt} ,\dot{\lambda }_{24} {\kern 1pt} } \right]^{T} \\ & = \left[ {\dot{x}_{4} ,\ddot{x}_{4} ,\dot{y}_{4} ,\ddot{y}_{4} ,\dot{x}_{8} ,\ddot{x}_{8} ,\dot{y}_{8} ,\ddot{y}_{8} ,{\kern 1pt} \dot{\theta }_{x8} ,\ddot{\theta }_{x8} ,\dot{\theta }_{y8} ,\ddot{\theta }_{y8} ,\dot{x}_{9} ,\ddot{x}_{9} ,\dot{y}_{9} ,\ddot{y}_{9} ,\dot{\theta }_{x9} ,\ddot{\theta }_{x9} ,\dot{\theta }_{y9} ,\ddot{\theta }_{y9} ,\dot{x}_{12} ,\ddot{x}_{12} ,\dot{y}_{12} ,\ddot{y}_{12} } \right]^{T} \\ \end{aligned} $$

Thus, the Eq. (1) can be converted to a first-order equation.

2.2 Numerical Results and Discussion

The fourth order Runge-Kutta method is adopted to solve the dimensionless equation of Eq. (1). And then the vibration response of the system under a certain parameter condition can be obtained and the response results can be analyzed. In order to make the selected parameters close to the actual structure of the gas turbine, the geometry parameters of the rotor-bearing-brush seal system are given as follows: $m_{8} = 10000$ kg, $m_{9} = 3200$ kg, $m_{ 4} = m_{12} = 400$ kg, $k_{ 4 8} = 3.19 \times 10^{8}$ N/m, $k_{ 8 9} = 3.02 \times 10^{8}$ N/m, $k_{ 9 1 2} = 3.13 \times 10^{8}$ N/m, $l_{ 4 8} = 1.5$ m, $l_{89} = 2$ m, $l_{912} = 1.5$ m, $\mu = 0.02$.

The influence of the rotor speed on the response of the rotor-bearing-brush seal system usually is more obvious. Figures 2, 3, 4 and 5 show the axis orbit and Poincaré map of joint 4, joint 8, joint 9, and joint 12 with different rotor rotational speed, respectively. As observed in Figs. 2 and 5, the variation of amplitude versus rotor speed at the position of bearing is not obvious, and all of the axis orbits are regular ellipse. When the rotor speed is 960 rad/s, the Poincaré map of joint 4 and joint 12 presents a closed circle, which shows the system are in quasi-periodic motion. But when the rotor speed is 760 rad/s, the Poincaré map of joint 4 and joint 12 are discrete scattered points, which shows the system are in chaos motion and the system is unstable.

Fig. 2.

Axis orbit and Poincaré map of joint 4 with different rotor rotational speed.

Fig. 3.

Axis orbit and Poincaré map of joint 8 with different rotor rotational speed.

Fig. 4.

Axis orbit and Poincaré map of joint 9 with different rotor rotational speed.

Fig. 5.

Axis orbit and Poincaré map of joint 12 with different rotor rotational speed.

As observed in Figs. 3 and 4, the amplitude at the position of disk increase with the rotor speed at first, and then decrease with the increase of rotor speed. The axis orbit of joint 8 and joint 9 is a circular ring, when the rotor speed is 360, 560, and 960 rad/s. And the Poincaré map of joint 8 and joint 9 is a closed ring when the rotor speed is 960 rad/s, which indicates the system are in quasi-periodic motion. But when the rotor speed is 760 rad/s, the axis orbit of joint 9 is irregular, which shows the system is in chaos motion.

The eccentricity phase-difference between the discs of joint 8 and joint 9 would affect the unbalanced force and the dynamic characteristics of the rotor system. Figure 6 shows the axis orbit and Poincaré map with different eccentricity phase-difference when rotor rotational speed is 900 rad/s. As observed in Fig. 6a, with different phase-difference, the axis orbits are circular ring, and the amplitude increases with the increase of the phase difference. As observed in Fig. 6b, when the phase-difference is π/6 and π/2, the Poincaré map is a closed ring, which indicates the system is in quasi-periodic motion. But when the phase-difference is 5π/6, some scattered points are appeared around the closed circle in the Poincaré map, and the axis orbit tends to be unstable. Therefore, decrease the eccentricity phase-difference between two disks during installation is beneficial to the stability of the system.

Fig. 6.

Axis orbit and Poincaré map with different eccentricity phase-difference when rotor rotational speed ω = 900 rad/s.

Figure 7 shows the spectrum cascade as a function of the eccentricity phase-difference. As observed in Fig. 7a, when the rotor speed is 30 rad/s, the power spectrum at the position of fundamental frequency is much greater than other position. The frequency division gradually decreases from the initial position to the 1 times fundamental frequency, and some small frequency division appear at the position of 2 times and 3 times fundamental frequency. As observed in Fig. 7b, when the rotor speed is 900 rad/s, there is a larger frequency division at the position of 1/3 times fundamental frequency, but power spectrum is very small at the position of 1 times fundamental frequency.

Fig. 7.

Spectrum cascade with different eccentricity phase-difference.

3 Conclusions

In order to build the nonlinear dynamic model of a multi-disk rotor-bearing-brush seal system, the seal force model of brush seal and the nonlinear oil-film force model based on short bearing theory were adopted considering the lateral deflection of the disks. The influences of the rotor speed and eccentricity phase-difference on the dynamic response of a multi-disk rotor-bearing-brush seal system were discussed. The conclusions were drawn below:

• 1. The variation of amplitude versus rotor speed at the position of bearing is not obvious.

• 2. The amplitude at the position of disk increase with the rotor speed at first, and then decrease with the increase of rotor speed.

• 3. Decrease the eccentricity phase-difference of the rotor system between two disks during the installation is beneficial to the stability of the system.