A Rotordynamics Model for Rotary Drillstring with Nonlinear Interactions in a 3D Well

Abstract

Rotating drilling for oil or geothermic applications uses a very slenderness structure hanging from to a derrick and made of a drill-string inside the drill well and linked to the bottom hole assembly (BHA). Vibrations provided by the nonlinear dynamics is due to the distributed unbalance masses, to well-assembly interactions, pulsating mud flow, bit-bouncing, stick-slip phenomena, etc. Understanding and controlling the vibration level of the rotating assembly in the well becomes an important key to avoid the fatigue failures and improve the reliability of the drilling operations. The paper focuses on the finite element modelling of the drilling assembly non-linear dynamics. The drill string-well bore contacts are modeled by a set of elastic stops. First, the static position of drilling assembly in the 3D-geometry well is calculated. Therefore, contact points and pre-stresses are predicted. The effect of the speed of rotation on the eigenvalues is then studied by plotting the Campbell diagram.

1 Introduction

Rotating drilling for oil or geothermic applications uses a very slenderness structure hanging from to a derrick and made of a drill-string inside the drill well and linked to the bottom hole assembly (BHA). The drill-string is composed with a great amount of screwed steel nine-meter pipes. The BHA is equipped with drill-collars, stabilizers and with a drill-bit. The BHA made of extra-heavy pipes insures the Weight-On-Bit (WOB). The stabilizers act as bearings to make easier the drilling direction and faster the penetration speed. The drilling assembly rotates in a well bore which is several hundred meters long and whose top part is equipped of steel tube casings. The downward mud flow is pumped in the interior of drill-pipes and the mud flow rides up in the well-pipe annular space to clear out the cut rock debris, the calories and to insure a lubrication.

Vibrations [1] provided by the nonlinear dynamics is due to the distributed unbalance masses, to the well-assembly interactions, pulsating mud flow, bit-bouncing, stick-slip phenomena [2,3,4], etc. Multiple vibrations induce premature wear and damage of equipment, mainly due to fatigue failures [5]. Understanding and controlling the vibration level of the rotating assembly in the 3D well becomes an important key to improve the reliability of the drilling operations.

One of the existing controlling techniques is the determination of the natural frequencies of the axial, the torsional and lateral vibrations. The analytical investigation of axial vibrations has been conducted since the 1960s [6]. The torsional behavior was modeled by using the wave equation [7], a single degree of freedom approach [8] or the continuous system approach [9]. Lateral vibrations have been the focus of several publications by two modeling techniques involving the finite-element discretization [10,11,12]. However, the dependence of natural frequencies of drilling assembly on the rotating velocity has not been thoroughly investigated. This analysis is well known in rotordynamics [19] as the Campbell diagrams to identify the speeds of rotation which may induce the system instabilities and the critical speeds which may yield the response resonances. The drilling assembly can be considered as a long rotor which has a more complicated dynamics due to the fluids effects and the multiple contacts with the well. The Campbell diagrams of simple rotors in fluid have been studied in a few works [14,15,16,17] involving both theoretical and experimental approaches.

This paper focuses on the finite element modelling of the drilling assembly to plot the Campbell diagram by using Timoshenko beams. Section 2 represents the beam element formulation and summarizes the modelling of well-bore-assembly contacts and the fluid forces and interactions with the drill strings. Section 3 shows the algorithm of the Campbell computation. First, the static position of the drilling assembly in the 3D-geometry well is calculated. Contact points and pre-stresses are then predicted. The following step consists in analyzing the effect of the speed of rotation on the eigenvalues by plotting the Campbell diagram. Finally in Sect. 4, the results are discussed to identify the instability ranges of speeds of rotation and the critical speeds of rotation. The modal coupling is also illustrated by some mode shapes.

2 Modeling of the System Dynamics by Beam Elements

2.1 Drilling Assembly

All components of the drilling assembly are modeled by using beam elements. Each element contains two nodes and six degrees of freedom (dofs) per node. The energy of one beam element is characterized by its kinetic and strain energies.

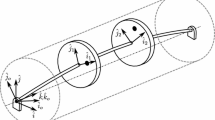
The kinetic energy of a rotating element is given by

$$\begin{aligned} \begin{aligned} E^e_{ca}=&\int _0^l \frac{\rho S}{2}\dot{w^e}^2 dz+\int _0^l\frac{\rho I_p}{2}\dot{\theta _z^e}^2dz+\int _0^l\left[ \frac{\rho S}{2}\left( \dot{u^e}^2+\dot{v^e}^2\right) +\frac{\rho I_p}{2}\left( \dot{\theta _x^e}^2+\dot{\theta _y^e}^2\right) \right] dz \\&+\int _0^l\rho I\varOmega \dot{\theta _x^e}\theta _y^e dz \end{aligned} \end{aligned}$$

(1)

where $u^e(z)$, $v^e(z)$, $w^e(z)$, $\theta _x^e(z)$, $\theta _y^e(z)$, $\theta _z^e(z)$ are the displacements and rotations in the element frame of reference (see Fig. 1a), $\rho$ is the mass density, l is the element length. The beam elements considered in this work have circular cross-sections with the inner and outer radii $R_e$ and $R_i$, the cross-sectional area S is $\pi (R_e^2-R_i^2)$. The cross-sectional moment of inertia I is $\pi (R_e^4-R_i^4)/4$ and the polar moment of inertia around the z-axis $I_p=2I$. The first two terms represents the kinetic energies due to the axial and torsional movements respectively. The next two terms correspond to the lateral displacements. The last term shows the Coriolis effect due to the rotating velocity $\varOmega$.

The strain energy is defined by

$$\begin{aligned}&E^e_{da} = \frac{1}{2}\int _0^l ES\left( \frac{dw^e}{dz}\right) ^2dz+\frac{1}{2}\int _0^l G (2I)\left( \frac{d\theta ^e_z}{dz}\right) ^2dz\nonumber \\&\quad +\frac{1}{2}\int _0^l EI\left[ \left( \frac{d^2u^e}{dz^2}\right) ^2+\left( \frac{d^2v^e}{dz^2}\right) ^2\right] dz \end{aligned}$$

(2)

where E and G are the Young and shear modulus.

Fig. 1.

(a) Element frame, (b) element (blue) and nodal (red) frames of reference.

For each node of an element, six displacements can be interpolated by the nodal displacements as

$$\begin{aligned} \begin{aligned}&u^e = N_1u^e_1+N_2\theta ^e_{y1}+N_3u^e_2+N_4\theta _{y2}^e,~v^e = N_1v^e_1-N_2\theta ^e_{x1}+N_3v_2^e-N_4\theta ^e_{x2},\\&\theta ^e_x = -\frac{dN_1}{dz}v^e_1+\frac{dN_2}{dz}\theta ^e_{x1}-\frac{dN_3}{dz}v^e_2+\frac{dN_4}{dz}\theta ^e_{x2},~\theta _y^e = \frac{dN_1}{dz}u^e_1+\frac{dN_2}{dz}\theta ^e_{y1}\\&\quad +\frac{dN_3}{dz}u^e_2+\frac{dN_4}{dz}\theta ^e_{y2},\\&w^e = N_5w^e_1+N_6w^e_2,~\theta ^e_z = N_5\theta ^e_{z1}+N_6\theta ^e_{z2} \end{aligned} \end{aligned}$$

(3)

where the interpolating functions are defined by :

$$\begin{aligned} \begin{aligned} N_1&= 1-\frac{3z^2}{l^2}+\frac{2z^3}{l^3},N_2 = z-\frac{2z^2}{l}+\frac{z^3}{l^2}, N_3 =\frac{3z^2}{l^2}-\frac{2z^3}{l^3},\\ N_4&= -\frac{z^2}{l}+\frac{z^3}{l^2},N_5 =1-\frac{z}{l}, N_6 = \frac{z}{l}. \end{aligned} \end{aligned}$$

(4)

Considering the nodal displacement vector $\varvec{\delta }^e=[u_i^e, v_i^e, w_i^e, \theta _{xi}^e, \theta _{yi}^e, \theta _{zi}^e]^T_{i=1,2}$, the elementary kinetic and strain energies are then rewritten as

$$\begin{aligned} E^e_{ca}=\frac{1}{2}\dot{\varvec{\delta }}^{eT}{} \mathbf M ^e_a\dot{\varvec{\delta }}^e+\varvec{\delta }^{eT}(\varOmega \mathbf C ^e_{ac})\dot{\varvec{\delta }^e} \end{aligned}$$

(5)

and

$$\begin{aligned} E^e_{da}=\frac{1}{2}\varvec{\delta }^{eT}{} \mathbf K _a^e\varvec{\delta }^e. \end{aligned}$$

(6)

Assembling all element gives the total kinetic and strain energies of the structure $E_{ca}=\frac{1}{2}\dot{\varvec{\delta }}^T\mathbf M _a\dot{\varvec{\delta }}+\varvec{\delta }^T(\varOmega \mathbf C _{ac})\dot{\varvec{\delta }}$ and $E_{da}=\frac{1}{2}\varvec{\delta }^T\mathbf K _a\varvec{\delta }$ where $\varvec{\delta }$ contains dofs of all nodes defined in the nodal frame. As shown in Fig. 1b, the frame of one node is the frame of its left element. The shear effect is introduced by a coefficient $12EI/(GS\beta l^2)$ which slightly modifies the terms of stiffness matrix. $S\beta$ is the reduced cross-sectional with $\beta =0.9$.

The axial force $F_0^e$ and torque $T_0^e$ modify also the structure stiffness. The axial force gives a supplementary strain energy while the non conservative axial torque is modelled by using the virtual work:

$$\begin{aligned} E_{GF}^e = \frac{F_0^e}{2}\int _0^l \left[ \frac{du^e}{dz}^2+\frac{dv^e}{dz}^2\right] dz, \delta \mathcal {T}_{GT}^e = T_0^e\int _0^l\left[ \frac{dv^e}{dz}\delta \left( \frac{d^2u^e}{dz^2}\right) -\frac{du^e}{dz}\delta \left( \frac{d^2v^e}{dz^2}\right) \right] dz \end{aligned}$$

(7)

These energies yields the geometric stiffness matrices $\mathbf K _{GF}^e$, $\mathbf K _{GT}^e$ of each element and the total matrices $\mathbf K _{GF}$, $\mathbf K _{GT}$.

2.2 Well-Assembly Interactions

When the structure deforms laterally, the contact between the rotating drillstring and the well may occur and gives rise to friction and shock effects. The contact between one node of structure and the well is modeled by a radial elastic stop of nominal stiffness $k_c$ and damping $c_c$. As shown in Fig. 2, the normal contact force is defined in the frame of reference of the contact node as:

$$\begin{aligned} \overrightarrow{F}_{cn} = -\left( K_c(G)G+C_c(G)\dot{G}\right) [u/r,v/r,0]^T \end{aligned}$$

(8)

with $G=\sqrt{u^2+v^2}-j_0$ the contact gap, $j_0$ the radial clearance and $\dot{G}=(\dot{u}u+\dot{v}v)/r$ the penetration velocity. The contact law is regularized by using the $\arctan$ function for the stiffness and damping, see [13]:

$$\begin{aligned} K_c(G) = \frac{k_c}{2}\left[ \frac{2}{\pi }\arctan (\pi \lambda G)+1\right] , C_c(G) = \frac{c_c}{2}\left[ \frac{2}{\pi }\arctan (\pi \lambda G)+1\right] \end{aligned}$$

(9)

where $\lambda$ is the regularization parameter.

The tangent friction force is related to the sliding velocity $v_g$ [13]. Both the tangential force and torque are modeled by the smoothed Coulomb law, so that the force is given by

$$\begin{aligned} \overrightarrow{F}_{ct} = -\mu (v_g)\left( K_c(G)G+C_c(G)\dot{G}\right) [-v/r,u/r,0]^T \end{aligned}$$

(10)

and the friction torque is described by

$$\begin{aligned} \overrightarrow{T}_{ct} = -\mu (v_g)\left( K_c(G)G+C_c(G)\dot{G}\right) R_e\overrightarrow{z}. \end{aligned}$$

(11)

The friction function $\mu (v_g)$ is defined by the dynamic and static friction coefficients and is regularized as in [13].

Fig. 2.

Contact between one node of drillstring and the well casing represented in the local frame of this node.

2.3 Fluid Effects

The fluid inside the drill-pipes and in the well-pipe annular space induces the elastic forces on the structure. In this work, the effects of inner fluid are characterized by the inertial force while the effects of the outer fluid are based on the model developed in  [14,15,16,17]. The authors considered the influence of fluid elastic forces induced by co-rotating flow surrounding the shaft with a relatively slow speeds of rotation. This model does not take into account the axial fluid flow can be applied for fluids with the small compressibility and the cylindrical beams of a large length-radius ratio.

The viscosity effects are defined in the modal basis [15, 16] and are detailed in Sect. 3.2. The inertial force of outer fluid in the $x-y$ plane of the element frame is taken from [16] and reads as:

$$\begin{aligned} -\left[ \begin{array}{l} m_a\left( \ddot{u^e}+\varOmega \dot{v^e}-\frac{\varOmega ^2}{4}u^e\right) \\ m_a\left( \ddot{v^e}-\varOmega \dot{u^e}-\frac{\varOmega ^2}{4}v^e\right) \end{array} \right] \end{aligned}$$

(12)

with $m_a=\rho _{f}\pi R^2_{fi}(R^2_{fi}+R^2_{fe})/(R^2_{fe}-R^2_{fi})$ the added mass, $R_{fe}$ and $R_{fi}$ the outer and inner radii of the annular space, $\rho _f$ the mass density of fluid.

Dissipation in the steady state rotating outer fluid is taken into account by the friction force [16]:

$$\begin{aligned} -m_a\gamma \varOmega \left[ \begin{array}{l} \dot{u^e}+\frac{\varOmega }{2}v^e\\ \dot{v^e}-\frac{\varOmega }{2}u^e \end{array} \right] ,~~\gamma =f_f\frac{R_{fe}+R_{fi}}{2h},~~h=R_{fe}-R_{fi} \end{aligned}$$

(13)

where $f_f$ is the friction coefficient.

By using Eq. (3), the inertial and friction forces from the outer fluid are rewritten as $\mathbf M ^e_{fe}\ddot{\varvec{\delta }^e}+\varOmega \mathbf C ^e_{fe}\dot{\varvec{\delta }^e}+\varOmega ^2\mathbf K ^e_{fe}\varvec{\delta }^e$ and the element inertial force of the inner fluid corresponds to $\mathbf M ^e_{fi}\ddot{\varvec{\delta }^e}$. The assembly of all elements yields the total matrices $\mathbf M _{fe}$, $\mathbf C _{fe}$, $\mathbf K _{fe}$ and $\mathbf M _{fi}$.

3 Computation of the Campbell Diagram

In this section, the algorithm for the Campbell diagram computation is presented (see Fig. 3). First, the static position of the drilling assembly in the well is calculated by taking into account the well-pipe contacts and all static external forces. The internal axial force and torque of each beam element are then computed and give the geometric stiffness matrices $\mathbf K _{GF}$ and $\mathbf K _{GT}$ by using Eq. (7). The prestressed state of the drilling assembly is applied by adding these matrices to the structure stiffness. The contact nodes from the static position are identified and presumed to be in the permanent contact with the well for the modal analysis. Their lateral displacements are limited by adding the contact stiffness matrix $\mathbf K _b$. Finally, the Campbell diagram is computed by implementing the modal reduction technique. These two steps are shown in details in the following subsections.

Fig. 3.

Principle for computing the Campbell diagram.

3.1 Static Computation

The static equilibrium equation is given by

$$\begin{aligned} \mathbf K _a\varvec{\delta }=\mathbf F _s+\mathbf F _c(\varvec{\delta }) \end{aligned}$$

(14)

where $\mathbf F _s$ is the static force vector due to the gravity, to the Archimède force, to the external static forces and torques. $\mathbf F _c$ denotes the contact forces and torques. $\mathbf F _c$ contains the normal contact force $\mathbf F _{cn}$. In the case where the drill-pipe is rotated and stuck on the well casing, $\mathbf F _c$ includes also the static tangential friction forces and torques $\mathbf F _{cts}$. The static friction force and torque applied at each contact node can be obtained from Sect. 2.2:

$$\begin{aligned} \overrightarrow{F}_{cts} = -\mu _s K_c(G)G[-v/r,u/r,0]^T,~\overrightarrow{T}_{cts} = -\mu _s K_c(G)GR_e\mathbf z \end{aligned}$$

(15)

In this case, Eq. (14) describes the “quasi"-static equilibrium. Otherwise, no friction terms are considered and Eq. (14) shows the real static equilibrium. This equation is solved by applying the Newton-Raphson method with four steps:

• 1. Initial guess $\varvec{\delta }_0$ is chosen as $\mathbf K _a^{-1}{} \mathbf F _s$.

• 2. Assuming that $\varvec{\delta }_i$ is known at the i-th iteration, the correction term is defined by :

  $$\begin{aligned} d\varvec{\delta }_i=-\left( \mathbf K _a-\frac{\partial \mathbf F _c}{\partial \varvec{\delta }}(\varvec{\delta }_i)\right) ^{-1}\left( \mathbf K _a\varvec{\delta }_i-\mathbf F _s-\mathbf F _c(\varvec{\delta }_i)\right) \end{aligned}$$

  (16)

  where $\dfrac{\partial \mathbf F _c}{\partial \varvec{\delta }}$ denotes the total Jacobian matrix $\mathbf F _c$ with respect to $\varvec{\delta }$.

• 3. Applying the correction : $\varvec{\delta }_{i+1}=\varvec{\delta }_i+d\varvec{\delta }_i$.

• 4. If $\displaystyle \frac{\Vert d\varvec{\delta }_i\Vert _2}{\Vert \varvec{\delta }_{i+1}\Vert _2}<\varepsilon _0$, $\varepsilon _0$ being the criterion error, the convergence is obtained. Otherwise, the process returns to step 2.

3.2 Reduction in the Modal Basis

Since the drilling assembly is a large system with a potential length of several kilometers, the pseudo-modal method is applied to reduce the dof number. This method is based on the modal basis which is the solution of the following eigenproblem:

$$\begin{aligned} \tilde{\mathbf{K }}_1\varvec{\phi }_m=\omega _m^2\mathbf M \varvec{\phi }_m \end{aligned}$$

(17)

where $(\omega _m,\varvec{\phi }_m)$ denotes the set of eigenvalue and eigenvector of each mode, $\tilde{\mathbf{K }}_1=(\mathbf K _1+\mathbf K _1^T)/2$ with $\mathbf M =\mathbf M _a+\mathbf M _{fi}+\mathbf M _{fe}$ and $\mathbf K _1=\mathbf K _a+\mathbf K _{GF}+\mathbf K _{GT}+\mathbf K _b$.

The eigenmodes of a rotating system, $\varvec{\delta }_k=\mathbf X _ke^{r_k t}$, is the solution of quadratic eigenproblem:

$$\begin{aligned} (r_k^2\mathbf M +r_k\mathbf C +\mathbf K )\mathbf X _k=\mathbf 0 \end{aligned}$$

(18)

where $\mathbf C =\mathbf C _{ad}+(\mathbf C _{ac}+\mathbf C _{fe})\varOmega$ and $\mathbf K =\mathbf K _1+\mathbf K _{fe}\varOmega ^2$. $\mathbf C _{ad}$ denotes the structural damping matrix defined by $c_M\mathbf M _a+c_K(\mathbf K _a+\mathbf K _{GF}+\mathbf K _{GT})$ with $c_M,c_K$ the two Rayleigh coefficients.

By using the modal reduction matrix $\varvec{\varPhi }$ whose each column corresponds to the eigenvector $\varvec{\phi }_m$ of the modal basis, Eq. (18) is transformed as :

$$\begin{aligned} (r_k^2\mathbf m +r_k\mathbf c +\mathbf k )\mathbf q _k=\mathbf 0 \end{aligned}$$

(19)

with $\mathbf X =\varvec{\varPhi }{} \mathbf q$, $\mathbf m =\varvec{\varPhi }^T\mathbf M \varvec{\varPhi }$, $\mathbf k =\varvec{\varPhi }^T\mathbf K \varvec{\varPhi }$, $\mathbf c =\varvec{\varPhi }^T\mathbf C \varvec{\varPhi }+\mathbf c _\eta$. $\mathbf c _\eta$ is a diagonal matrix representing the viscous damping [15, 16] in which $\eta$ is the kinematic viscosity coefficient.

Since $\mathbf k$ and $\mathbf c$ are not symmetric, the eigenvalue $r_k$ is a complex with the form $2\pi (\alpha \pm jf)$ where f is the eigen-frequency. The system is stable if $\alpha \le 0$ and becomes unstable if $\alpha >0$. The dependence of f on the speed of rotation gives the Campbell diagram. The rotating modes are classified by three categories: (F) like-flexural modes, (T) like-torsional modes and (L) like-longitudinal modes. The classification criterion is based on three coefficients defined by the ratios of energies:

$$\begin{aligned} N_i=\frac{\sum \limits _{e}E_{ci}^e}{E_{ca}}+\frac{\sum \limits _{e}E_{di}^e}{E_{da}},~~i=\{F,T,L\} \end{aligned}$$

(20)

where $E_{ci}^e=\frac{1}{2}\left| (r\mathbf X _i)^*\mathbf M _a(r\mathbf X _i)\right|$, $E_{di}^e=\frac{1}{2}\left| \mathbf X _i^*\mathbf K _a\mathbf X _i\right|$. $*$ denotes the transposed conjugately operator. One mode is qualified (F) if $N_F>N_T,~N_L$ ; (T) if $N_T>N_F,~N_L$ ; (L) if $N_L>N_F,~N_T$.

4 Results

4.1 Test Cases

Let a 2000 m drilling assembly be presented in Fig. 4. It consists of a polycrystalline diamond compact (PDC) drill-bit, drill-collars, stabilizers-gauges and a chain of drill-pipes. The drilling assembly are made of steel and characterized by $\rho =7860$ kg.m$^{-3}$, $E=2.1~10^{11}$ Pa, $\nu =0.3$. The two Rayleigh damping coefficients are: $c_M=0.03$ s$^{-1}$ and $c_K=0$ s. The geometric properties of each component are shown in Table 1. A drill-pipe consists of two tooljoints of 0.3 m length and a body of 8.9 m length (see Fig. 4). The outer and inner diameters of the tooljoint are 0.162 m and 0.095 m. Two geometries of the well neutral lines are plotted by Fig. 5. As shown in Table 2, the well consists of three parts (casing 1, casing 2, openhole) of decreasing diameter from the surface. The static friction coefficients of the contact between the structure and the casings, openhole are respectively 0.2 and 0.3. The inner and outer fluids have the rheological properties: $\rho _f=1200$ kg.m$^{-3}$, $f_f=0.013$, $\eta =10^{-6}$ m$^2$.s$^{-1}$.

Fig. 4.

Components of drilling assembly and geometry of drill-pipe.

Table 1. Geometric properties of the components of drilling assembly

The mesh contains 1811 beam elements and 1812 nodes. The drill-bit and a tooljoint are modeled by one element. The pipe body contains 5 elements. Each drill collar and stabilizer are discretized by 20 and 5 elements respectively. The lateral displacements of gauge nodes, of last bit node and six dofs of the surface node are blocked. An axial torque of −4905 N.m and a axial force of −49050 N are applied at the bit to model the Torque on Bit (TOB) and the Weight on Bit (WOB).

Fig. 5.

(a) 2D-S well, (b) 3D well represented in the Cartesian coordinates.

Table 2. Geometric properties of the well

The elastic stops modelling the contacts have the nominal stiffness $k_c=10^7$ N/m with the regularized parameter $\lambda =7~10^7$ m$^{-1}$. Different clearances $j_0$ between the undeformed drilling components and the well are: 0.163 m (pipe-body - casing 1), 0.048 m (pipe-body - casing 2), 0.045 m (pipe-body - openhole), 0.029 m (stabilizer - openhole and drill-collar - openhole), 0.145 m (tooljoint - casing 1), 0.030 m (tooljoint - casing 2), 0.0270 m (tooljoint - openhole). Supplementary clearances are considered to take into account the change of the structure and well cross-section: 0.031 m, 0.145 m.

4.2 Static Computation

The quasi-static equilibrium position of the structure is computed for the two wells of Fig. 5 by taking into account the friction contacts. The difference between the quasi-static and static positions are then highlighted.

Figure 6 shows three displacements of the quasi-static positions of the structure as a function of the curvilinear position. One can observe that the lateral displacements u and v are limited by the structure-well contacts. Since the geometry of the S well is steeper than the 3D well (see Fig. 5), the structure weight induces a larger axial displacement w of the structure in the S well than in the 3D well. Figure 7 represents the normal and tangential friction forces, the tangential friction torque applied to the structure. For the S well, the contact forces are the largest for a depth Z from 400 m to 1200 m, especially for the curved zones of the well. For the 3D well, the most important contact forces are observed at $Z\simeq 50$ m close to the surface and $Z\simeq 800$ m close to the bit.

Figure 8 compares the quasi-static/static positions of one cross section at the curvilinear position 113 m from the surface, computed with/without friction. The friction effects modify slightly the contact direction. Figure 9 represents the axial force and torque for each finite element. The continuous and dash lines denote the results computed with/without friction. The axial force and torque of one element are proportional to the difference between two nodal axial displacements and two nodal torsion angles respectively. The axial force and torque of the last element are equal to the ones imposed at the bit. The friction effects have no influence on the element axial forces. However, the element axial torque is strongly modified by the tangential friction torque. Moreover, the element axial torque curve shows more oscillations with the friction effect. Indeed, the friction torque applied to one contact node yields the jump of the axial torque curve between two adjacent beam elements associated with this node.

Fig. 6.

Node displacements for the static equilibrium position of the drilling assembly in the cases: (a) 2D-S well, (b) 3D well as a function of the curvilinear position by taking into account the friction forces.

Fig. 7.

Normal contact force (red), tangential friction force (blue) and torque (green) applied to the drilling assembly for the (a) 2D-S well and for the (b) 3D well.

Fig. 8.

Cross-section of the drilling structure at the curvilinear abscissa s = 113 m for the (a) 2D-S well and in the (b) 3D well. Black: no friction, blue: with friction

Fig. 9.

Element axial force and torque obtained from the equilibrium positions. Continuous lines: with friction, dash lines: no friction.

The results computed with the friction effects are used for plotting the Campbell diagrams in the next section. The geometric stiffness obtained from the static equilibrium computation represents the pre-loaded state of the structure due to the curve well geometry, the structure-well contacts, the fluid effects and the static forces such as the gravity, the constant TOB and WOB. The system stiffness is modified by adding this geometric stiffness to compute the Campbell diagram. Analyzing the Campbell diagram with constant TOB and WOB is a first approach which permits understanding roughly the modal contribution of the drilling structure.

4.3 Campbell Diagram

In this section, the natural frequencies are computed as a function of the speed of rotation to determine the Campbell diagram. The speed range which may induce the system instability is then identified. Some mode shapes are studied to show the phenomenon of the modal coupling.

The pseudo-modal method with the first 10 modes is applied to reduce the computational system size. Figure 10 represents the Campbell diagrams of the drilling structure from 0 rpm to 600 rpm. The drilling assembly has low-frequency modes due to its long structure. The dotted lines denote the (L), (T), (F) modes. The cyan color shows the (F) modes which make the system unstable. The system becomes unstable from the rotating speed of 250 rpm for the S well and 200 rpm for the 3D well. The gray continuous curves linking the points represents the mode shape tracking, based on the NC$^2$O criterion [18]. The intersection between the mode curves and the dashed line gives the frequencies equal to the speeds of rotation. They are considered as the critical speeds which may yield to the dangerous resonances when the system is excited by the external forces (the mass-unbalanced and asynchronous forces) [19].

Fig. 10.

Campbell diagram of the drilling structure for (a) 2D-S well and for (b) 3D well. Blue : (F) modes, red : (T) modes, black: (L) modes, cyan : instable (F) modes, dashed line : critical line, gray continuous curves : the mode shape tracking.

Fig. 11.

Normalized lateral displacement of some (F) modes of the drilling structure in the (a, b) 2D-S well and in the (c, d) 3D well. Blue : orbit, green : the mode shape at $t=0$.

Fig. 12.

Normalized lateral displacement orbits of one (F) modes and one (T) modes of the drilling structure in the 3D well.

For the case of S well, the Campbell diagram represented by Fig. 10a shows that two curves of each (F) mode are strongly deviated at the low speeds of rotation due to the outer fluid effects and then converge at the high speeds of rotation. The gap between these curves at high speeds of rotation is due to the damping effects such as the structural damping, the fluid viscosity and friction. As shown in [16], the outer fluid friction has more important effects than the viscous and structural damping. The horizontal curves of (L) and (T) modes show the negligible dependence on the rotating speed. On the contrary to the S well, the Campbell diagram for 3D well in Fig. 10b shows two horizontal curves which do not have a pure flexural, torsional or longitudinal nature. Since the geometry of this well is more complicated than the 2D well, the modal coupling mechanism occurs stronger and will be illustrated by Fig. 12.

Figure 11 shows the orbits of some (F) modes as a function of the curvilinear position. Their most important displacements can be observed in the vicinity of the surface ($s=0$ m) and of the drill-bit ($s\simeq 1800$ m).

Figure 12 shows two modes representing the coupling between the flexural and torsional motions for the case of 3D well. These modes are on the horizontal curve of Fig. 10b with the blue and red colors. The orbits of flexural motions can be observed only in the vicinity of the surface. The lower part of the structure have both torsional and flexural motions. The mode in Fig. 12a shows more energy related to flexural motions than to torsional ones. Hence, the classification criterion given by Eq. (20) consider it as a (F) mode. On the contrary, this mode in Fig. 12b shows that the torsional motions has more important energy than the flexural ones, which suggest to consider it as a (T) mode.

5 Conclusion

In this work, the static position is computed by taking into account the structure-well contact. The influence of the static friction effects on the equilibrium position is studied. The Campbell diagram is then computed over an operating range of the drilling speeds of rotation by considering the prestressed structure with a constant TOB and WOB and by assuming that the contact nodes remains in the permanent contact with the well. The unstable speeds of rotation and the critical speeds are observed. The rotating fluids show a strong influence on the (F) modes, contrary to the (L) and (T) modes. The modal coupling mechanisms are more remarkable for the structure in a 3D well than in a 2D well. In the future works, the model can be extended to take into account the speed dependent TOB and WOB for the Campbell diagram computation.