Identification of Coupling Parameters in Flexibly Coupled Jeffcott Rotor Systems with Angular Misalignment and Integrated Through Active Magnetic Bearing

Abstract

In the present work, a rotor train system is connected by a flexible coupling and integrated with an auxiliary active magnetic bearing. Due to angular misalignment that exists between the shafts, coupling stiffness varies with shaft rotation. A mathematical function that is time-dependent and which can yield integer harmonics has been chosen to numerically model coupling additive stiffness. The equations of motion have been obtained from Lagrange’s equation. The amplitude and phase of peaks of rotor vibration and AMB current signatures have been obtained in time and frequency domains using least-squares regression technique and full spectrum technique, respectively. They are eventually utilized to identify the intact and additive stiffness of coupling, viscous damping, unbalance magnitude and phase, and the AMB displacement and current stiffness. A SIMULINK^TM has been built to generate time domain responses of discs and AMB current. From the EOM of rotors regression equations have been formed in frequency domain to create an inverse problem. The identification algorithm has been found to be robust against noise levels up to 5%.

1 Introduction

Among the faults that are encountered in field operation of rotating system, misalignment is the one of the predominant faults. It arises due to of loss of co-axiality between rotors and bearings, which is caused due to improper assembly and deformation caused due to thermal effects. It leads to decrease in transmission efficiency, bearing wear, noise and reduction of life in bearings.

Gibbons [1] made study on parallel misalignment and gave expressions for forces and moments generated in the coupling. Sekhar and Prabhu [2] and Rao and Sekhar[3] considered both parallel and angular misalignment in flexible coupling and set up formulae for reaction forces and moments. Prabhu [4] studied the influence of misalignment on various harmonics of vibration response in rotor system with multiple disks supported on journal bearings. It was concluded that with increase in misalignment the amplitude of 2^nd harmonic initially decreased and then increased. Rao et al. [5] studied parallel misalignment in a coupled Jeffcott rotor test rig. Higher vibrations and loopy orbits were noticed at one-half and one-third of the first critical speed. Numerical studies done in [6] on rigidly coupled rotors indicated that parallel misalignment could produce both translational and angular excitations.

In [7] rigid coupling stiffness is considered to be a sum of static and fluctuating components. The effect of parallel offset in a rotor system is considered in the presence of torsional excitation. In [8], the parallel and angular misalignments were introduced in a test set up, fluctuating forces and moments were then measured at the bearing location with a 6-axis load cell and input as force terms in the finite element model. The FFT of the vibration responses yielded all the integer harmonics. Jalan and Mohanty [9] identified unbalance and misalignment by comparing the equivalent forces generated due to faults obtained from both experiment and theoretical fault model. Avendano and Childs [10] used Cosmos^TM solid modeling tool to create three types of disc-pack couplings. The forces and moments obtained from FE analysis for various misalignment conditions were fit into Fourier series expansion. Verma et al. [11] used both vibration and motor current signals for misalignment detection in machinery fault simulator. In [12], it was reported that the spectral characteristics of torque sensor measurements for the parallel and angular misalignments differ from each other. Moreover, wavelets are found to be more sensitive than FFT to the presence of misalignment. Lal and Tiwari [13, 14] studied the numerical and experimental identification of coupling parameters in rigid and flexible rotor systems from run-down data.

Works on misalignments broadly deal with the following methods (i) numerical and experimental identification of static forces and moments, (ii) experimental identification/diagnosis using techniques such as orbits, spectral plots, thermal imaging [15], stator current analysis [11]. For more information on diagnostics of misalignment, apart from the numerous papers, the readers are referred to the books by [16, 17, 18, 19, 20] For information on applications of AMB in condition monitoring and vibration suppression, readers are requested to refer to [21].

This work aims to study the static and more importantly time dependent coupling misalignment forces in coupled rotor systems using an AMB. AMB current has been used for suppressing vibration and identification of unbalance magnitude and phase, coupling stiffness parameters, displacement and current constants of AMB. The mathematical formulation of coupled rotor-AMB system has been developed. The development of Simulink^TM model is then described. The equations used for the identification of harmonics of displacement of the two rotors and the AMB current using time domain regression technique have been developed. The application of full spectrum to the present problem has been explained. Finally, the equations used for the identification of system parameters have been developed and tested numerically.

2 System Configuration

2.1 Introduction

Coupled rotor systems are widely used in industrial gas turbines, compressors, and turbo generators. Power is transmitted from driving unit to driven unit across multiple stages of rotors through couplings. The coupling used can be of rigid or flexible type, the choice depending upon the rpm, power transmitted and application. Rigid couplings offer better power transmission with not much allowance for misalignment, while flexible couplings allow significant misalignment between the bearing centers of rotating units.

Coupled Rotor-Bearing-AMB System.

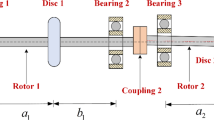
A motor drives a coupled rotor bearing system through a drive coupling. The drive is transmitted from rotor-1 to rotor-2 by an intermediate flexible coupling (see Fig. 1). The behavior of intermediate coupling alone is considered in this work. The unbalance force is defined by a residual mass located at an angle from the reference x axis (see Fig. 2).

Fig. 1.

Coupled rotor bearing system supported on auxiliary AMB

Fig. 2.

Angular position of unbalance

3 Assumptions

• 1. Coupling is modeled as a torsion spring since only angular misalignment is considered in the present study (see Fig. 3). The cross-coupled stiffness of coupling is less than direct stiffness.

  Fig. 3.

  

  Flexible coupling replaced by helical torsion spring

• 2. Since the formulation uses Jeffcott rotors, the slopes at coupling and support are assumed to be equal. Putting it differently, it is assumed that coupling is near to support axially.

• 3. Coupling is assumed to be flexible and disc is assumed to be heavy. These are the crucial assumptions in the development of mathematical model for the present problem.

• 4. The previous assumptions lead to a linear mathematical relation between the deflection of central disc and coupling slope. This is on account of the fact that the slope of shaft at coupling location is due to the central heavy disc.

• 5. In other words, the linear and angular deflections of rotors produced by coupling forces and moments are less than that due to their self-weight, i.e. weight dominance is assumed. Similar assumption has been made by [4].

• 6. Since the coupling is flexible, reaction moments and the corresponding slopes due to misalignment are small compared to that caused by the heavy disc at the shaft center. This assumption does not hold good for the rigid coupling model.

4 Mathematical Modeling

Translational displacements at 2 disc locations, i.e. $x_{1} ,y_{1} ,x_{2} ,y_{2}$, are the generalized coordinates of the coupled rotor system. The slopes at coupling locations for shafts are given by $\varphi_{{x_{1} }} ,\varphi_{{y_{1} }} ,\varphi_{{x_{2} }} ,\varphi_{{y_{2} }}$. With heavy central disc assumption, there is a linear relation between disc deflections and shaft slopes at coupling locations. From the relations for deflection and slope of a simply supported shaft with point load at center, the following relation applies

$$ \varphi_{{x_{1} }} = \frac{{3y_{1} }}{l};\quad \varphi_{{x_{2} }} = \frac{{3y_{2} }}{l};\quad \varphi_{{y_{1} }} = \frac{{3x_{1} }}{l};\quad \varphi_{{y_{2} }} = \frac{{3x_{2} }}{l} $$

(1)

The expressions for kinetic energy and potential energy are given by

$$ KE = \frac{1}{2}m_{1} \dot{x}_{1}^{2} + \frac{1}{2}m_{1} \dot{y}_{1}^{2} + \frac{1}{2}m_{2} \dot{x}_{2}^{2} + \frac{1}{2}m_{2} \dot{y}_{2}^{2} $$

(2)

$$ PE = \frac{1}{2}k_{1} x_{1}^{2} + \frac{1}{2}k_{1} y_{1}^{2} + \frac{1}{2}k_{1} x_{2}^{2} + \frac{1}{2}k_{1} y_{2}^{2} + \frac{1}{2}k_{{\varphi_{x} }} (\varphi_{{y_{1} }} + \varphi_{{y_{2} }} ) + \frac{1}{2}k_{{\varphi_{y} }} (\varphi_{{x_{1} }} + \varphi_{{x_{2} }} ) $$

(3)

Since there is no slope at the central span disc the rotational kinetic energy term about transverse axes is zero. The equations of motion for rotor-1 and rotor-2 are obtained by applying Lagrange’s equation. Since AMB acts as auxiliary support for rotor-2, the corresponding terms appear on the RHS of Eq. 2. To reduce computational complexity the equations are written in complex form by introducing, $r = x + iy$. The FFT of the complex form also helps in the extraction of harmonics, which shall be discussed in later sections

$$ m_{1} \ddot{r}_{1} + c_{1} \dot{r}_{1} + (k_{1} + k_{{t_{o} }} )r_{1} - k_{{t_{o} }} r_{2} \, = f_{{unb_{1} }} + f_{{mis_{1} }} - F_{{const_{1} }} $$

(4)

$$ m_{2} \ddot{r}_{2} + c_{2} \dot{r}_{2} + (k_{2} + k_{{t_{o} }} - k_{s} )r_{2} - k_{{t_{o} }} r_{1} \, = f_{{unb_{2} }} + f_{{mis_{2} }} - f_{cur} - F_{{const_{2} }} $$

(5)

where

$$ k_{{t_{x} }} = \left( {{3 \mathord{\left/ {\vphantom {3 l}} \right. \kern-0pt} l}} \right)^{2} k_{{\varphi_{x} }} \quad {\text{and}}\quad k_{{t_{y} }} = \left( {{3 \mathord{\left/ {\vphantom {3 l}} \right. \kern-0pt} l}} \right)^{2} k_{{\varphi_{y} }} $$

(6)

Complex unbalance forces for rotors are given by

$$ f_{{unb_{i} }} = m_{i} e_{i} \omega^{2} e^{{j(\omega t + \beta_{i} )}} $$

(7)

Complex coupling misalignment forces for rotors are given by

$$ f_{{mis_{1} }} = f_{{mis_{2} }} = \left( {{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}} \right)s(t)\Delta k\left( {\delta x_{1} + \delta x_{2} } \right)\left( {1 + e^{2j\omega t} } \right) $$

(8)

Constant coupling force is given by

$$ F_{{const_{1} }} = F_{{const_{2} }} = k_{{t_{0} }} \left( {\delta x_{1} + \delta x_{2} } \right) $$

(9)

Complex AMB current force is given by

$$ f_{cur} = k_{I} \sum\limits_{i = - n}^{ + n} {I_{i} } e^{ij\omega t} $$

(10)

4.1 Coupling Excitation Function

Experimental data on the misalignment published by [8] have shown the presence of all integer harmonics on either side of full-spectrum. Hence, it is essential that a suitable coupling stiffness function, which generates integer harmonics in the response, is chosen as a steering function in the mathematical model.

40% duty cycle pulse waveform with (see Fig. 4) is used to represent coupling misalignment. The Fourier expansion is shown below

Fig. 4.

Time domain signal of 40% duty cycle square wave

$$ \begin{aligned} s(t) & = 0.5 + 0.6055\cos (\omega t) + 0.1871\cos (2\omega t) - 0.1247\cos (3\omega t) \\ & \quad - 0.1514\cos (4\omega t) + 0.1009\cos (6\omega t) + 0.0535\cos (7\omega t) \\ \end{aligned} $$

(11)

The expanded form of complex coupling misalignment forces is then given by

$$ \begin{aligned} f_{{mis_{1} }} & = f_{{mis_{2} }} = \Delta k\left( {\delta x_{1} + \delta x_{2} } \right)\left\{ {0.25 + 0.3027e^{j\omega t} + 0.1201e^{ - j\omega t} } \right. \\ & \quad + 0.2967e^{2j\omega t} + 0.0089e^{ - 2j\omega t} { + 0} . 1 2 0 2e^{3j\omega t} - 0.0312e^{ - 3j\omega t} \\ & \quad + 0.0089e^{4j\omega t} \left. { - 0.0037e^{ - 4j\omega t} - 0.0312e^{5j\omega t} - 0.0133e^{ - 5j\omega t} + \ldots } \right\} \\ \end{aligned} $$

(12)

The above Fourier expansion from [22] shall be used in the derivation of time dependent coupling excitation force caused by bearing misalignment.

Numerical Experiment with Simulink ^TM Model.

The simplified model of the Simulink^TM block that has been built from Eqs. (4) and (5) (see Fig. 5). Assumed values used for the generation of responses in time domain are shown in Table 1. The model generates complex displacement of rotor-1, rotor-2, complex AMB current and a multi-harmonic reference signal in time domain. The role and necessity of reference signal shall be discussed in Sect. 5.

Fig. 5.

Simulink model of coupled rotor – AMB system

Table 1. Assumed parameters of rotor system

5 Estimation of Coefficients of Harmonics in Time Domain: Least Squares Regression Method

Complex vibration responses of rotor-1 which are caused by misalignment at various instants of time and obtained from Simulink^TM model are multi-harmonic in nature and are given by

$$ \left( {{\mathbf{A}}_{1} } \right)_{n \times i} \left( {{\mathbf{X}}_{{R_{1} }} } \right)_{i \times 1} = \left( {{\mathbf{b}}_{{r_{1} }} } \right)_{n \times 1} $$

(13)

with

$$ \left( {{\mathbf{A}}_{1} } \right)_{n \times i} = \left[ {\begin{array}{*{20}c} 1 & {e^{{j\omega t_{1} }} } & \cdots & {e^{{j(5\omega )t_{1} }} } & \cdots & {e^{{j( - \omega )t_{1} }} } & \cdots & {e^{{j( - 5\omega )t_{1} }} } \\ 1 & {e^{{j\omega t_{2} }} } & \cdots & {e^{{j(5\omega )t_{2} }} } & \cdots & {e^{{j( - \omega )t_{2} }} } & \cdots & {e^{{j( - 5\omega )t_{2} }} } \\ \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots \\ \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots \\ 1 & {e^{{j\omega t_{n} }} } & \cdots & {e^{{j(5\omega )t_{n} }} } & \cdots & {e^{{j( - \omega )t_{n} }} } & \cdots & {e^{{j( - 5\omega )t_{n} }} } \\ \end{array} \begin{array}{*{20}c} \cdots \\ \cdots \\ \vdots \\ \vdots \\ \cdots \\ \end{array} } \right] $$

(14)

$$ \left( {{\mathbf{b}}_{{r_{1} }} } \right)_{n \times 1} = \left\{ {\begin{array}{*{20}c} {r_{{1_{c} }} (t_{1} )} & {r_{{1_{c} }} (t_{2} )} & {r_{{1_{c} }} (t_{3} )} & \ldots & \ldots & \ldots & {r_{{1_{c} }} (t_{2} )} \\ \end{array} } \right\}^{T} $$

(15)

And the vectors of unknowns are given by

$$ \left( {{\mathbf{X}}_{{R_{1} }} } \right)_{i \times 1} = \left\{ {\begin{array}{*{20}c} {R_{10} (\omega )} & {R_{11} (\omega )} & \ldots & {R_{15} (\omega )} & \ldots & {R_{ - 11} (\omega )} & \ldots & {R_{ - 15} (\omega )} & \ldots \\ \end{array} } \right\}^{T} $$

(16)

Analogous matrix relations exist for rotor-2 vibration response and AMB current. All three relations are combined in to a single matrix equation. The complex harmonics of vibration and current are obtained by solving this equation

$$ \left[ {\begin{array}{*{20}c} {{\mathbf{X}}_{{R_{1} }} } & {{\mathbf{X}}_{{R_{2} }} } & {{\mathbf{X}}_{I} } \\ \end{array} } \right] = \left( {{\mathbf{A}}_{1}^{T} {\mathbf{A}}_{1} } \right)^{ - 1} {\mathbf{A}}_{1}^{T} \left[ {\begin{array}{*{20}c} {{\mathbf{b}}_{{r_{1} }} } & {{\mathbf{b}}_{{r_{2} }} } & {{\mathbf{b}}_{i} } \\ \end{array} } \right] $$

(17)

where A is the regression matrix, X is the vector of unknowns (complex harmonics, in this case) to be determined and b is the vector of known quantities.

6 Estimation of Coefficients of Harmonics in Frequency Domain: Full Spectrum FFT

The frequencies contained in the time domain current and displacement signals can be extracted using Fast Fourier Transform (FFT) algorithm. Since both positive and negative frequencies are contained in the signal, a full spectrum plot needs to be used to understand the qualitative nature of fault the time domain signal represents. A comprehensive treatment of the mathematical procedure to obtain full spectrum and its application to rotating machinery diagnostics has been given in [23]. Coefficients of harmonics from −5 to +5 can be seen in the full spectrum amplitude plot of rotor-1 complex displacement (see Fig. 6). The phase plot shows the phase angle of each harmonic with reference to the timing marker on the shaft.

Fig. 6.

Full spectrum of amplitude and phase of rotor-1 complex displacement

6.1 Phase Correction and Its Necessity

It has been noticed that as the time instants of signal acquisition change, a variation in phase information takes place. The amplitude information of harmonics, on the other hand, remains unaffected by this time shift. To account for this phase variation, a complex multi-harmonic reference signal has been envisaged by Singh and Tiwari [24], who were the first to utilize this technique for the identification of phase of the harmonics of current and displacement of a cracked Laval rotor (see Fig. 7). Table 2 shows the comparison of amplitudes and phases of harmonics obtained from time domain and full spectrum with phase compensation. It can be seen that the full spectrum shows good similarity to the values obtained from time domain inverse problem. Using full spectrum technique with “peak finding algorithm”, the coefficients of harmonics of interest can be obtained quicker than it can be done with time domain analysis.

Fig. 7.

Flow chart of phase compensation procedure

Table 2. Comparison of harmonics obtained from time domain and full spectrum with phase compensation

7 Identification of Rotor, Coupling and AMB Parameters in Frequency Domain by Least Squares Regression Method

The expressions for complex displacement, velocity, acceleration and complex current are substituted in Eqs. (4) and (5). After writing the equations of rotor-1 and rotor-2 for $i = 0,i = 1,i \ne 1$, real and imaginary parts are separated from equations. The equations are later grouped into identifiable parameters and known parameters and grouped in regression matrix form as shown below.

$$ {\mathbf{A}}_{2} {\mathbf{X}}_{2} = {\mathbf{b}}_{2} $$

(18)

The system parameters or identifiable parameters are grouped in the column vector ${\mathbf{X}}_{2}$. They can be obtained by solving

$$ {\mathbf{X}}_{2} = \left[ {\left( {{\mathbf{A}}_{2} } \right)^{T} \left( {{\mathbf{A}}_{2} } \right)^{ - 1} } \right]^{ - 1} \left( {{\mathbf{A}}_{2} } \right)^{T} {\mathbf{b}}_{2} $$

(19)

The values of X₂ and b₂ can be obtained from n number of spin speeds, which improves the condition number of regression matrix, thereby yielding closer estimates.

$$ \left\{ {\begin{array}{*{20}c} {{\mathbf{A}}_{{\mathbf{2}}} {\mathbf{(}}\omega_{{\mathbf{1}}} {\mathbf{)}}} \\ {{\mathbf{A}}_{{\mathbf{2}}} {\mathbf{(}}\omega_{{\mathbf{2}}} {\mathbf{)}}} \\ \vdots \\ {{\mathbf{A}}_{{\mathbf{2}}} {\mathbf{(}}\omega_{{\mathbf{n}}} {\mathbf{)}}} \\ \end{array} } \right\}{\mathbf{X}}_{{\mathbf{2}}} = \left\{ {\begin{array}{*{20}c} {{\mathbf{b}}_{{\mathbf{2}}} {\mathbf{(}}\omega_{{\mathbf{1}}} {\mathbf{)}}} \\ {{\mathbf{b}}_{{\mathbf{2}}} {\mathbf{(}}\omega_{{\mathbf{2}}} {\mathbf{)}}} \\ \vdots \\ {{\mathbf{b}}_{{\mathbf{2}}} {\mathbf{(}}\omega_{{\mathbf{n}}} {\mathbf{)}}} \\ \end{array} } \right\} $$

(20)

The sequence of steps followed right from mathematical modeling till parameter identification is shown in the flow chart (see Fig. 8).

Fig. 8.

Sequence of steps in rotor-coupling-AMB parameter identification

8 Results and Discussion

Table 3 shows the estimates of rotor-coupling-AMB parameters obtained from the inverse problem (17) at 18 Hz spin speed. The estimates obtained from clean signal are almost identical to the assumed values with error % less than −1%.

Table 3. Error percentage in identified parameters at various levels of noise at 18 Hz

Rotor-2’s equivalent viscous damping, AMB constants undergo comparatively higher deviations compared to other estimates. Gaussian noise at various levels (1, 2, and 5%) has been added to the clean signal and estimation was carried out. Rotor-2 damping and AMB current stiffness have been underestimated by as much as 2.56 and 3.98%, respectively, at 5% noise level. The variation in static and additive coupling stiffness values stands at a reasonable 0.7%. Next the error percentages in the estimation of system parameters for a range of speeds are performed. The rotor system is ramped up with an angular acceleration of $20\pi \,{\text{rad/s}}^{ 2}$ to identify the critical speed. The Hilbert envelope of vibration response of rotor-1 in x direction reveals the peaks in response, which correspond to critical speeds (see Fig. 9). The speeds on the either side of half power points can be taken for estimation (20 to 30 Hz). Here AMB displacement stiffness has displayed considerable variation from the assumed value by as much as 59.96%, while AMB current stiffness displayed a variation of about 10% (see Fig. 10). Even though the speed range is sufficiently away from half power points, a large variance is observed at 24 and 25 Hz. This can be explained by the fact that the aforesaid speeds are half the 1st critical speed, which is 316 rad/s. This can be resolved by considering the accumulated data from many speeds and feeding them to Eq. (18). When collective data from the same speed range (20 to 30 Hz) is considered, the estimates show very good closeness to the assumed values (see Table 4). This exercise adequately justifies the usefulness of including multiple speeds in the identification algorithm.

Fig. 9.

Hilbert envelope of Rotor-1 X displacement during ramp –up $(\alpha = 20\pi {\text{ rad/s}}^{ 2} )$

Fig. 10.

Error percentage in identified parameters at various individual spin speeds (20–30 Hz)

Table 4. Parameters estimated after considering collective data from 20 to 30 Hz in the identification algorithm

9 Conclusions

A mathematical model of coupled rotor system has been developed from Jeffcott rotor formulation. A Simulink^TM model has been constructed from complex equations of motion. The model has been used to perform numerical experiments to generate vibration and current data in time domain. A reference signal which is multi-harmonic in nature has been used to correct the anomaly of phase variation that happens to the coefficients of vibration and current when signals are picked at different instants of time which would adversely affect the parameter identification if left uncorrected. A modal based identification algorithm has been developed that utilizes the coefficients of amplitude and phase harmonics of rotor vibration and AMB current, obtained either from inverse problem in time domain or from full spectrum, to estimate the flexible coupling, rotor and AMB parameters. The algorithm has been found to be robust to noise levels up to as much as 5%. The algorithm can be tested with data obtained from experimental data. The mathematical model can be extended to the case of Jeffcott rotor with offset disc to incorporate gyroscopic effects also.