Modelling Ion Channels

Abstract

Plant adaption and survival relies on signalling, much of which is achieved through concentration changes in ions. Furthermore, plants can influence their growth and shape via changes in hydraulic pressure which in turn can be modulated by changes in ionic concentrations that drive osmosis. We present an introduction to mathematical modelling of ionic currents and transmembrane voltages, both intracellular and intercellular. We introduce the modelling techniques used to describe the physical processes involved in ion channel dynamics and illustrate their application using generic examples. We begin by discussing modelling of individual ion channels. Next, we present computational algorithms most commonly employed in simulating ionic currents passing via a single as well as an ensemble of the same ion channel type. We then discuss modelling of ionic current flow across cellular membrane that could involve different ion channel species. We end with an overview of modelling action potentials and their propagation resulting from interactions between different ion channels within as well as between cells. We illustrate this using a simplified example of plant action potential.

3.1 Introduction

One of the most interesting aspects of ion channel dynamics is that local opening and closing events can be organised into complex spatio-temporal patterns such as action potentials that can propagate from cell to cell. Not only are these phenomena physiologically important, they are also mathematically interesting, and challenging to grasp. Like in all living systems, ion channels in plants are involved in signal transduction and are vital for normal plant function, being associated with rapid responses to environmental stimuli [9, 26]. Reviews of the experimental literature on ion channels in plants are given by Tester [24], Gradmann [11], and Hedrich [14]. The mathematics behind ion channel modelling has a lot in common with the study of action potential propagation in excitable models such as the Hodgkin-Huxley or FitzHugh-Nagumo models [7, 18, 19]. However, useful insights into the mechanisms of plants signal propagation would require the use of more than simple generic excitable models. Therefore, the biophysical framework described in this chapter could be used a starting point for construction of models that are tailor-made to the particular type of cell or electrical activity under consideration.

3.2 Modelling Single Ion Channel Dynamics

Single ion channels are proteins that make a (intra)cellular membrane permeable to specific ions by allowing them to pass through a transmembrane pore. By changing conformation, or other mechanisms, the pore is able to ‘open' or ‘close' in each case permitting, or not, the passage of ions [17]. Under voltage-clamp conditions, when permeable ions are present in solution surrounding the channel, steps in current amplitude can be seen as the channel opens or closes [17]. In this section, we introduce the modelling steps involved in mathematically describing single ion channel currents.

3.2.1 Diffusion of Ionic Species

The movement of charged ionic particles down a concentration gradient creates an electric current. The cellular membrane provides a barrier to the movement of charged ionic particles and thus induces a charge separation and establishes a transmembrane potential difference. Along the cellular membrane, there exist ion channels that facilitate the diffusion of ionic species across the membrane. In addition to these channels are pumps that actively move ionic species against the concentration gradient to maintain a transmembrane concentration difference.

We can model the average movement across the cellular membranes through passive diffusion. The general form describing the passive diffusion of a particular ionic species, Y , obeys the Fickian flux rules:

$$\displaystyle \begin{aligned} \frac{\partial Y}{\partial t} = -D \frac{\partial Y}{\partial x}, {} \end{aligned} $$

(3.1)

where $x\in \mathbb {R}$ represents the distance across the membrane and D > 0 is the diffusion coefficient, which describes how easily the particles move across the membrane. If we assume that the cellular membranes are thin compared to the cell and its surroundings, we can replace (3.1) with

$$\displaystyle \begin{aligned} \frac{\mathrm{d} Y_{\mathrm{i}}}{\mathrm{d} t} = -D [ Y_{\mathrm{i}} - Y_{\mathrm{o}} ], \end{aligned} $$

(3.2)

where Y _i and Y _o, respectively, represent the ionic concentrations on the inside and outside of the membrane. The diffusion coefficient is dependent on the permeability of the membrane to that particular ionic species, the surface area of the cell, the density of channels, and the thickness of the cellular membranes. The membrane permeability is then controlled in a dynamic fashion through the opening and closing of ion channels, which we refer to as the gating. It is the aim of this chapter to mathematically describe this gating and its impact on the transmembrane potential difference.

3.2.2 Channel Dynamics

Ion channels are transmembrane proteins that connect the intracellular as well as intercellular compartments. These proteins can exist in conformations which either allow or prevent the diffusion of particles across cellular membranes. Conformational changes that switch between these states depend on a variety of factors, including the transmembrane potential difference, hereby referred to as the voltage, the binding to specific ligands, temperature or mechanical force. We will first describe the scenario in which transitions between states are purely random, that is, they depend on no external factors. We note that the modelling paradigm we describe is applicable to all types of channels, but that care must be taken to ensure that the correct dependencies on extrinsic factors are included when modelling specific ion channels.

Consider a generic ion channel that can exist in one of two states: an open state (O) in which ions are free to pass through; and a closed state (C) in which they are not. Transitions between these states are random in nature, though the probabilities of moving from open to closed states and vice versa do not have to be the same. Stable conformations of proteins representing the closed and open states are achieved by minimising the Gibb’s free energy. The open and closed states thus correspond to minima of the free energy landscape. Conformational changes are then represented as transitions between these minima induced by noise caused by thermal fluctuations.

Given the considerations above, our two state channel can be represented by the stochastic differential equation:

$$\displaystyle \begin{aligned} \frac{\mathrm{d} x}{\mathrm{d} t} = - U_x(x) + \xi(t), \quad x\in\mathbb{R}, {} \end{aligned} $$

(3.3)

where x is a coordinate that represents the conformational state of the channel, ξ is a Gaussian noise process with mean 〈ξ(t)〉 = 0 and autocorrelation 〈ξ(t)ξ(t′)〉 = 2k _B T δ(t − t′), where k _B is the Boltzmann constant and T is the temperature in Kelvin. The function U(x) represents the energy landscape, and for exposition, we will here choose this to be a quartic of the form

$$\displaystyle \begin{aligned} U(x) = \frac{1}{4}x^4 -\frac{\mu}{2} x^2 - \eta x. {} \end{aligned} $$

(3.4)

This energy landscape has two minima, located at x _±, separated by a maximum at x ₀. Associated with the two minima are ‘wells’, which are separated by the ‘barrier’ at x ₀. When x(t) is in the well corresponding to x ₋, we say that the channel is in the closed conformation, and when it is in the well associated with x ₊, it is in the open conformation. The parameters μ > 0 and $\eta \in \mathbb {R}$, respectively, control the height of the barrier at x ₀ and the difference between the depths of the two wells. Thus, increasing μ makes transitions between states harder, whilst varying η alters the relative probabilities of transition.

If the barrier separating the two minima is sufficiently high compared to the thermal fluctuations, transitions between states will be rare, and we here consider the expected transition times between them. The magnitude of the energy barrier relative to the closed (open) state is equal to ΔU _± = U(x ₀) − U(x _±). Writing σ = (k _B T)⁻¹, the expected transition time, τ _±, from the closed (open) state is then

$$\displaystyle \begin{aligned} \tau_\pm = \frac{{\mathrm{e}}^{\sigma \varDelta U_\pm}}{\nu_\pm}. {} \end{aligned} $$

(3.5)

We note that the functional form of the transition rate, (3.5) was derived first by Arrhenius [1], who left ν _± as undetermined parameters. The specific forms for ν _± was later derived using a number of different methods; our presentation here is based on the exposition by Eyring [4, 5].

As a representative example, we show in Fig. 3.1 the double-well potential system according to (3.3)–(3.4). The energy landscape is depicted in Fig. 3.1a, with an example trajectory shown in Fig. 3.1b. Superimposed on this trajectory is an indicator showing the state of the channel at time t.

Fig. 3.1

(a) Double well potential landscape given by (3.4) with μ = 10 and η = −2. (b) A sample path of (3.3)–(3.4) with σ = 0.05. Superimposed on this sample path is a bold line indicating which state the channel is in

3.2.3 Markov Processes

Whilst the potential well system defined by (3.3) is a good descriptor of channel dynamics, it is impractical for large scale channel modelling, since it requires computation of sample paths. Instead of considering the full system, considerable simplification can be made by noting that trajectories will spend most of the time near the minima of the system, making infrequent excursions over the barrier and transitioning into the well associated with the other minima. This leads us to think of simplifying the system to only consider these transition times, which are formally known as passage times or escape times.

We can take the reciprocal of the transition times given in (3.5) to provide rate constants that describe the probability per unit time of transitioning to the other state. In what follows, we shall denote the probability per unit time of transitioning from the closed state to the open state by α = 1∕τ ₋, and the probability per unit time of making the opposite transition as β = 1∕τ ₊. Schematically, the system can now be represented as

(3.6)

This system is Markovian in nature, meaning that the evolution of the state is dependent only on the current state of the system and not on previous states. This system can then be easily simulated as follows. Initialise the system with the channel being either in the closed or the open state and pick a time discretisation dt ≪ 1. At each time point, draw a random number ξ from the standard uniform distribution. If the channel is closed, transition to the open state if ξ < α dt, else remain closed. If the channel is open, transition to the closed state if ξ < βdt, else remain open. After completing this step, advance time by dt and repeat as much as necessary.

3.3 Modelling the Dynamics of an Ensemble of Ion Channels

For a single channel, the method described in the previous section is a simple and convenient way to simulate its gating dynamics. However, cells may have many channels of the same type. Using this method to describe a cell with N channels thus requires drawing N samples per time step. Furthermore, many of these samplings will ultimately result in no transition being made, particularly if α and β are small. An alternative way to simulate the system is offered by the Gillespie algorithm [10], which exactly simulates a network of Markov processes under the assumption that all channels act independently of one another and are identical in nature.

3.3.1 Gillespie Algorithm

Instead of assessing at each step whether each channel in the system has transitioned, the Gillespie algorithm estimates a time over which an event has occurred, then computes which event has occurred and updates the system as appropriate. Thus, the Gillespie algorithm only requires drawing two random numbers per time step and only considers times at which events have occurred. In our network of N channels, let us assume that N _c(t) of these are closed and that N _o(t) are open at time t, so that N _c(t) + N _o(t) = N.

Each step of the Gillespie algorithm then involves drawing ξ _1,2. The probability density function describing the time to the next transition, τ, is given by

$$\displaystyle \begin{aligned} P(\tau = t) = \lambda {\mathrm{e}}^{-\lambda t}, \end{aligned} $$

(3.7)

where λ = N _c α + N _o β is the average rate of the next transition. The time to the next transition is then sampled as

$$\displaystyle \begin{aligned} \tau = \frac{-\ln{\xi_1}}{\lambda}. \end{aligned} $$

(3.8)

Between times t and t + τ, we then know that a transition must have occurred. If λξ ₂ < N _c(t)α, we say that one of the channels has opened, and we thus set N _c(t + τ) = N _c(t) − 1 and N _o(t + τ) = N _o(t) + 1. Otherwise, if λξ ₂ > N _c(t)α, then one of the channels has closed and we thus set N _c(t + τ) = N _c(t) + 1 and N _o(t + τ) = N _o(t) − 1. Time is then updated by setting t = t + τ and the process is continued. We can see the rationale behind these choices by noting that N _c(t)α∕λ is the probability that a channel opening has occurred and N _o(t)β∕λ is the probability that a channel closing has occurred, conditioned on the fact that one of these events has happened. Note that during the simulation of the system, the Gillespie algorithm automatically selects the timestep τ over which to evolve the system. Whilst this is an advantage in terms of computational efficiency, since the system is only sampled at event times, one must take care that any extrinsic factors that affect the transition probabilities α and β are approximately constant over the interval [t, t + τ).

3.3.2 Transition Probabilities

Thus far, we have considered the case where transition probabilities are constant. In general, however, the gating of ion channels may be dependent on a variety of factors, including the transmembrane voltage, see, e.g., [14] in plants; ligands such as intracellular Ca²⁺ and nucleotides, see, e.g., [3, 13, 15] in plants. We can capture this dependence by making the transition probabilities depend on one or more of these factors. For example, for voltage-gated ion channels, we can write α = α(V ), β = β(V ), where

$$\displaystyle \begin{aligned} \alpha(V) = A {\mathrm{e}}^{k_\alpha(V-V_{\alpha})},\quad \beta(V) = B {\mathrm{e}}^{k_\beta(V-V_\beta)}, {} \end{aligned} $$

(3.9)

is an often used functional form.

A simple way to incorporate Ca²⁺ dependence is via the following schematic

(3.10)

so that the transition rate from the closed to the open state has a linear dependence on the intracellular Ca²⁺ concentration. Modelling the dependence on other factors, such as ligands and nucleotides, follows in a similar fashion, with functional forms chosen to either match the physiology of the channel, or more commonly, fitted to empirical data.

Making transition probabilities depend explicitly on factors such as voltage does not significantly alter the approach to simulating channel dynamics; the transition probabilities α and β are simply altered to reflect this dependence. However, as we shall later see, the movement of ions across cellular membranes impacts upon the transmembrane voltage. In addition, this can induce further downstream effects, for example by opening Ca²⁺ channels so that intracellular Ca²⁺ concentrations vary. As such, channel gating dynamics are tightly coupled to such factors and the approximation in the Gillespie algorithm that these are unaltered in the interval [t, t + τ) may not hold. In this case, however, a simple fix is to impose a maximum timestep that can be taken by the algorithm.

3.3.3 Many Gates

We have thus far considered channels with only one (activating) gate. However, many ion channels have a multitude of these gates and the channel will only be permeable to ions if all gates are in the open state. In this case, there exist a number of closed states that correspond to the case where at least one of the gates is closed. In addition to the so-called ‘activating gates’ that we have thus far discussed, ion channels may also possess ‘inactivating gates’. Inactivating gates can close ion channels through mechanisms independent of the closing of activating gates and thus a channel will only allow particles to pass through when the activating gates are open and the channel is not inactivated. This gives rise to the four mechanisms that govern channel gating: activation, inactivation, deactivation and reactivation.

Activation describes the process whereby channels move from closed to open states; inactivation occurs when the inactivating gates close; deactivation arises when activating gates close; and reactivation (or recovery from inactivation) describes the process by which inactivating gates open. Consider the simplified model of Cl⁻ channel in the plasmalemma of cells of C. corallina., which has three activating gates and one inactivating gate [21]. The schematic for this channel can be represented as where m _i, i = 0, 1, 2, 3, is the number of channels with i open activating gates and h _j, j = 0, 1 is the number of channels with j closed inactivated gates. Recall that the only state in which the channel is permeable is the one in which the inactivating gate and all three activating gates are open, which is indicated by the asterisk. Also note the transitions between the different closed and open states are now scaled by a factor that captures how many gates must be open/closed in that state and that this factor assumes that the opening and closing of gates are independent of the state of the other gates.

The inclusion of multiple activating and inactivating gates does not affect the method of simulation, as long as the assumption that the opening and closing of channels are independent events. In cases where channels have ‘memory’, that is, that transition probabilities are dependent on the history of the channel, or the length of time the channel has been in a certain state, this does not hold. In the latter case, where transition probabilities are dependent on the ‘dwell times’ in specific states, a modified Markov chain description that respects this behaviour can be constructed, so that the Gillespie algorithm can be used [20].

3.3.4 Master Equation

Since the processes that we are describing are Markovian, we can instead represent the dynamics of the system through evolution of the probability, P(S, t) of being in state S at time t. For the simple two state system represented by (3.6), the evolution of P is given by:

$$\displaystyle \begin{aligned} \frac{\mathrm{d} }{\mathrm{d} t}P(C,t) &= -\alpha P(C,t) + \beta P(O,t) \end{aligned} $$

(3.11)

$$\displaystyle \begin{aligned} \frac{\mathrm{d} }{\mathrm{d} t}P(O,t) &= \alpha P(C,t) - \beta P(O,t). {} \end{aligned} $$

(3.12)

The linear equation (3.12) is known as the master equation, and is often the starting point for many considerations of biochemical reactions. General schema describing the states of channels with M states can be written in the form

(3.13)

where S _i and S _j, (i, j = 1, …, M), are two distinct states of the system and q _ij represents the probability (which may be zero) of entering state S _j from S _i. The master equation for system (3.13) can then be written as

$$\displaystyle \begin{aligned} \frac{\mathrm{d} }{\mathrm{d} t} P(S_i,t) = \sum_{j=1}^M P(S_j,t) q_{ji} - \sum_{j=1}^M P(S_i,t) q_{ij}, \quad i=1,\dots M. {} \end{aligned} $$

(3.14)

The term on the left represents a source term describing all the routes to state S _i, whilst the right-hand sink term captures all the transition away from state S _i. Since (3.14) is linear, we can write it in matrix form as

$$\displaystyle \begin{aligned} \frac{\mathrm{d} }{\mathrm{d} t} \mathbf{P} = \mathbf{P} Q, \quad \mathbf{P}\in[0,1]^M, \end{aligned} $$

(3.15)

where the M × M matrix Q contains all of the transition probabilities between the distinct states.

Whilst the master equation is a succinct way to describe the probability density function of the system, it is often impractical when simulating a system since it captures dynamics in a distributional sense, and does not provide a stochastic representation of a specific realisation of the process. However, when the number of channels becomes large, we can use a similar density based representation to describe the average behaviour across the whole cell.

3.3.5 Averaging

When the number of channels is large, instead of considering the probability of the system being in state S _i at time t, we can instead construct an equation to describe the fraction of channels in state S _i, which we shall denote s _i. Under this approximation, we replace (3.14) with

$$\displaystyle \begin{aligned} \frac{\mathrm{d} s_i}{\mathrm{d} t} = \sum_{j=1}^M s_j r_{ji} - \sum_{j=1}^M s_i r_{ij}, \quad i = 1,\dots M, {} \end{aligned} $$

(3.16)

where r _ij now represents the rate at which channels transition from state S _i to state S _j. Since channels are only permeable when the channel is open, we can simplify (3.16) by only considering the fraction of channels that are in the open state. Letting m represent the fraction of open channels, we replace (3.16) with

$$\displaystyle \begin{aligned} \frac{\mathrm{d} m}{\mathrm{d} t} = \alpha_m (1-m) - \beta_m m, \quad m\in[0,1], {} \end{aligned} $$

(3.17)

where α _m is the rate of channels entering the open state and β _m is the rate of channels exiting the open state. Note that these rates are the same as the probabilities of transitioning to the open state that we considered earlier. Thus, in the limit of infinitely many channels, transition probabilities are replaced with transition rates. Of course, cells do not have infinitely many channels and since (3.17) is deterministic, one may wonder how we are supposed to reflect the fluctuations arising from having finitely many channels. One way to incorporate these fluctuations, for example in a system with N _m channels, is to add an additive noise term to (3.17) [8]

$$\displaystyle \begin{aligned} \frac{\mathrm{d} m}{\mathrm{d} t} = \alpha_m (1-m) - \beta_m m + \xi_m(t), \end{aligned} $$

(3.18)

where ξ(t) is a Gaussian noise term with moments given by 〈ξ _m(t)〉 = 0 and

$$\displaystyle \begin{aligned} \big\langle \xi_m(t) \xi_m(t') \big\rangle = \frac{\alpha_m(1-m)+\beta_m m}{N_m} \,\delta(t-t'). \end{aligned}$$

When incorporating this noise term in, care must be taken to ensure that m remains in the interval [0, 1]. For practical reasons, these finite size fluctuations are very often ignored in most ion channel based models of cell electrophysiology.

It is very common to see (3.17) written in the form

$$\displaystyle \begin{aligned} \tau_m \frac{\mathrm{d} m}{\mathrm{d} t} = m_\infty - m, {} \end{aligned} $$

(3.19)

where

$$\displaystyle \begin{aligned} \tau_m = \frac{1}{\alpha_m+\beta_m}, \quad m_\infty = \frac{\alpha_m}{\alpha_m+\beta_m}. {} \end{aligned} $$

(3.20)

If α and β are given as in (3.9), with A = B, then we can write

$$\displaystyle \begin{aligned} m_\infty(V) = \frac{1}{1+{\mathrm{e}}^{-(V-V_0)/S_0}}, {} \end{aligned} $$

(3.21)

where

$$\displaystyle \begin{aligned} S_0 = \frac{1}{k_\beta - k_\alpha}, \quad V_0 = \frac{k_\beta d_\beta - k_\alpha d_\alpha}{k_\beta - k_\alpha}. \end{aligned} $$

(3.22)

Thus, according to (3.19), m evolves towards m _∞ at a rate determined by τ _m. The form of m _∞ given by (3.21) suggests that as the cell depolarises, the fraction of open channels increases or decreases in a sigmoidal fashion, which is often observed in experiments. In particular, the form given in (3.19) is often preferred over (3.17) since the parameters V ₀ and S ₀ in (3.21) can be fit directly to electrophysiological recordings.

3.4 Modelling Cellular Membrane Excitability

Now that we have arrived at a deterministic description for the channel dynamics, we are ready to start describing the currents that flow into and out of the cellular compartments as a result of channel opening.

3.4.1 Nernst Potential

In order to understand the current flow induced by the movement of ions across a cellular membrane, we need to first provide an equation that describes the electrochemical gradient across it. This can be done by equating the chemical potentials across the membrane. For space reasons, we here omit the derivation and simply state that, at equilibrium, the voltage across the cell membrane for ionic species X independent of all other species is given by the Nernst potential:

$$\displaystyle \begin{aligned} V_X = \frac{RT}{z_X F} \ln \left( \frac{[X]_{\mathrm{o}}}{[X]_{\mathrm{i}}} \right), \end{aligned} $$

(3.23)

where R is the ideal gas constant, T is the temperature in Kelvin, z _X is the valence of species X, F is the Faraday constant and [X]_i,o are the concentrations of species X on the inside and outside of the membrane, respectively. Similar calculations can be used to find the voltage across cellular compartments at equilibrium accounting for all ionic species of interest.

3.4.2 Membrane Currents

We are now in a position to describe current flow across the cellular membranes, such as plasma, vacuolar or nuclear envelope membranes. Under the assumption that the concentrations of ions in the outside and inside of the membrane remain constant, the opening of channels permeable to ionic species X will push the transmembrane voltage towards the Nernst potential V _X. The current I _X induced by the flow of this species across cellular membranes is then given by Ohm’s law, which can be written as

$$\displaystyle \begin{aligned} I_X = g_X (V-V_X), {} \end{aligned} $$

(3.24)

where g _X is the summed channel conductance over the whole cell.

This conductance is proportional to the fraction of open channels, and thus we can rewrite (3.24) as

$$\displaystyle \begin{aligned} I_X = \overline{g}_X m^a h^b (V-V_X), {} \end{aligned} $$

(3.25)

in which there are a activating gates and b inactivating gates per channel, m and h, respectively, represent the fraction of open activating gates and inactivating gates and $\overline {g}_X$ is the total conductance when all channels are open. The dynamics of m and h obey the equation given by (3.19), though we note that the sigmoid for h _∞ is reversed compared to m _∞.

In Fig. 3.2, we demonstrate how the number of channels in the cell impacts the variability of the cell response. Figure 3.2a illustrates how the fraction of open activating channels varies as the transition rates are instantaneously changed from α ₀ = 0.1, β ₀ = 0.5 to α ₁ = 0.2, β ₁ = 0.4 at t = 50. In this subfigure, we also vary the total number of channels, N, in the cell and observe a reduction in the variability around the steady states, which are at $\overline {m}_i = \alpha _i/(\alpha _i+\beta _i),\,i=0,1$. The lowermost plot shows the system in the thermodynamic limit as N →∞, and we observe that as N is increased, the sample paths approach this deterministic limit.

Fig. 3.2

(a) Sample paths representing the fraction of open channels for different values of the total channel number N. At t = 50, the transition rates for the channels are instantaneously changed as per the text. (b) Prototypical steady state currents under variation of voltage. The bold line represents the deterministic I − V curve in the limit as N →∞. The shaded regions represent the mean ± standard error corresponding to the indicated number of channels. For further details, please refer to the text

To assess the variability of channel opening and closing on current flow, we illustrate in Fig. 3.2b a prototypical I − V curve, relating the steady-state current to the transmembrane voltage, assuming that the channels exhibit voltage dependence. The bold line indicates the current flow in the limit as N →∞, and we clearly see that as N increases, the variability around the deterministic profile decreases. In this example, we assume that the current is modelled according to (3.25), with $\overline {g}_X = 10$, a = 3, b = 1, V _x = 50 using steady state representations for m and h in the form given by (3.20) with α and β in the form (3.9). Specific parameters used are A = B = 1, $k_\alpha ^m = 0.1$, $V_\alpha ^m = -30$, $k_\beta ^m = -0.4$, $V_\beta ^m = -25$, $k_\alpha ^h = 0.1$, $V_\alpha ^h = -40$, $k_\beta ^h = 0.3$ and $V_\beta ^h = -40$.

In the following, we assume that the number of channels in plant cells is always high, so that we can use the deterministic limit to describe the ionic currents flowing through the channels.

3.4.3 Action Potentials

Equation (3.24) reflects the notion that we can represent the electrophysiology of the cell by making comparisons to electrical circuits. The Nernst potential provides an electromotive force similar to that produced by an electrical battery (cell), whilst the ion channels collectively behave as a variable conductance obeying nonlinear dynamics. By extending the equivalence of the biological system with an electrical circuit, and considering the evolution of currents associated with all ionic species to which a cellular membrane is permeable, we can now describe the evolution of the voltage across such a cell membrane.

By providing a barrier to the movement of ions across it, the cell membrane effectively separates charge between the inside and outside of the cell and thus acts as a capacitor. This capacitor is in parallel with all the ion channels on the membrane. Upon applying Kirchoff’s second law, we can thus describe the evolution of the transmembrane voltage via

$$\displaystyle \begin{aligned} C \dot{V} = -\sum_{X} I_X, {} \end{aligned} $$

(3.26)

where C = 2 × 10⁻² F/cm² is the capacitance of the cell and $C \dot {V}$ is the current flowing through the capacitance. This equation, together with the equations that describe how the gating variables of each channel type vary with V and time (3.17), constitutes the Hodgkin-Huxley formalism for modelling action potentials [18].

As an example, we present a simple model of action potential in guard cells [11, 12]. This model incorporates three types of ion channels: one chloride channel that provides a fast activating and slowly inactivating inward current driving the action potential $I_{\mathrm {Cl}} = \overline {g}_{\mathrm {Cl}} m_{\mathrm {Cl}} h_{\mathrm {Cl}} (V-V_{Cl})$ with a Nernst potential at V _Cl = 100 mV, one slowly activity outward rectifier potassium channel that provides an outward current that helps terminate action potentials $I_{\mathrm {Ko}} = \overline {g}_{\mathrm {Ko}} m_{\mathrm {Ko}} (V-V_{\mathrm {K}})$, and one inward rectifier potassium channel responsible for potassium influx into the cytoplasm at negative resting membrane potential $I_{\mathrm {Ki}} = \overline {g}_{\mathrm {Ki}} h_{\mathrm {Ki}} (V-V_{\mathrm {K}})$. Both K⁺ currents have Nernst potentials at V _K = −100 mV. Two other ion transporters also create ionic currents. One is the proton pump, extruding H⁺ ions at negative membrane potentials and thus generating an outward current $I_{\mathrm {pu}} =\overline {g}_{\mathrm {pu}} h_{\mathrm {pu}} (V-V_{\mathrm {pu}})$ with Nernst potential V _pu = −400 mV, which is responsible for the resting membrane potential being more negative than V _K. The second one is a 2H⁺/Cl⁻ symporter that brings in chloride at negative membrane potentials and creates a net inward current $I_{\mathrm {sy}} = \overline {g}_{\mathrm {sy}} h_{\mathrm {sy}} (V-V_{\mathrm {sy}})$ that reverses at V _sy = 20 mV. Note that this model assumes there is no long-term change in ionic concentration that would be large enough to affect the Nernst potentials.

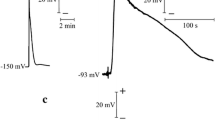
The steady state value of each current, i.e. the current observed at any given membrane potential V when the gating variables have reached their steady state values, is shown in Fig. 3.3a. The bottom panel shows the sum of all the currents, revealing three membrane potential values for which the total steady state current is 0. The lowest (leftmost) and highest (rightmost) values are stable steady states of V . This bistability provides a simple explanation for the observation that steady state membrane potential of many plant cells can be either at a hyperpolarised level well below V _K or at a level above V _K. The middle value acts as a threshold, if V is above/below that value it will converge toward the high/low steady state.

Fig. 3.3

(a) Steady state current of each ionic current. Bottom panel shows the sum of all the currents. Values for each conductance are: $\overline {g}_{pu} = \overline {g}_{Ko} = \overline {g}_{Ki} = \overline {g}_{sy} = \overline {g}_{Cl} = 1$ S/m². Other parameter values are given in text or in [12]. (b) Action potential are generated in response to a stimulating current if the current is larger than a threshold value. All parameters as in A, except $\overline {g}_{Cl} = 0.9\,{\mathrm{S/m^2}}$. Stimulating current of 2.8, 2.9, 3 (subthreshold), 3.1, 3.2, 3.4 mA/m² is applied for one second (inset). (c) Propagation of an action potential wave. The Cl⁻ conductance is increased by 0.1 S/m² between 10 and 11 s in the top cell. This triggers an action potential in this cell, which triggers an action potential in the next cell, and so on. The conductance of each plasmodesma is g _p = 0.05 S/mˆ2

To simulate the variations of V with time, we numerically integrate the differential equations for V (3.26) together with the equation for each gating variable (3.17). Results of several simulations are displayed in Fig. 3.3b. For each simulation we inject a brief (one second) stimulating current to the model cell, which creates a rapid rise in membrane potential. This results in a rapid return of membrane potential towards its equilibrium value, or in a large amplitude action potential before going back to equilibrium. The action potential is triggered only if the depolarizing current is sufficiently large, illustrating the threshold behaviour. Once the current is above its threshold value, a full action potential occurs. The shape of the action potential varies little with further increases in stimulating current, but the latency between stimulus and action potential onset decreases. Thus, this simple model of plant action potential exhibits features also found in action potentials produced by animal cells.

Plant action potentials can also propagate from cell to cell, thanks to plasmodesmata that create electrical connections between cells and allow exchange of ions [6]. To illustrate this action potential propagation [16], we model the electrical connection, which is similar to gap junctions that electrically connect excitable cells in animals [2, 25]. Thus, the current I _{p ab} flowing through a plasmodesma from cell a with membrane potential V _a to cell b with membrane potential V _b is simply given by

$$\displaystyle \begin{aligned} I_{p\,ab} = g_p (V_a - V_b) {} \end{aligned} $$

(3.27)

where g _p is the conductance of the plasmodesma [22, 23]. In Fig. 3.3c, an action potential is initiated in the first cell by a brief increase in the Cl⁻ conductance. This sequentially triggers action potentials in the neighbouring cells, thus propagating a wave of electrical excitation.

3.5 Conclusions

Plants (and animals) very effectively use concentration differences of ions across membranes (inside vs outside the cell and between cellular compartments) to regulate numerous processes. Calcium ions, for instance, are key information carriers in plants that regulate responses to abiotic and biotic stresses from their environment. In this chapter, we have introduced the fundamental physical principles that underpin ionic changes via the function of ion channels and provided some useful mathematical and computational approaches for modelling such systems. Many exciting questions in plant biology converge on ion channels and transporters and we hope that the tools offered here will provide a foundation on which interested researchers can build to develop specific biophysical models to address specific questions.