From Numerical Weather Prediction Outputs to Accurate Local Surface Wind Speed: Statistical Modeling and Forecasts

Abstract

Downscaling a meteorological quantity at a specific location from outputs of Numerical Weather Prediction models is a vast field of research with continuous improvement. The need to provide accurate forecasts of the surface wind speed at specific locations of wind farms has become critical for wind energy application. While classical statistical methods like multiple linear regression have been often used in order to reconstruct wind speed from Numerical Weather Prediction model outputs, machine learning methods, like Random Forests, are not as widespread in this field of research. In this paper, we compare the performances of two downscaling statistical methods for reconstructing and forecasting wind speed at a specific location from the European Center of Medium-range Weather Forecasts (ECMWF) model outputs. The assessment of ECMWF shows for 10 m wind speed displays a systematic bias, while at 100 m, the wind speed is better represented. Our study shows that both classical and machine learning methods lead to comparable results. However, the time needed to pre-process and to calibrate the models is very different in both cases. The multiple linear model associated with a wise pre-processing and variable selection shows performances that are slightly better, compared to Random Forest models. Finally, we highlight the added value of using past observed local information for forecasting the wind speed on the short term.

1 Introduction

The wind energy sector has seen a very sharp growth in recent years. According to the Global Wind Energy Council (GWEC), 54 GW has been installed in 2016, corresponding to an increase of 12.6% of the total installed capacity [11]. Worldwide, the number of wind farms increases each year and feeds the electrical network with a larger amount of energy. For instance, in 2016, France has seen its highest capacity growth rate ever recorded. This sharp increase of connected wind power has for instance allowed the network to receive 8.6 GW from wind power plants, on November 20th, corresponding to 17.9% of the energy produced this day [19]. The need to have access to accurate wind forecasts on several timescales is thus becoming crucial for the wind energy producer and grid operator, in order to anticipate the energy production, to plan maintenance operations and to handle balance between energy production and consumption. Changing regulations of the energy market with the end of feeding-in tariffs make this anticipation vital for wind energy producers. Finally, a related but different topic consists in the estimation of the wind resource of its long-term (multi-year) variability and trends mainly for prospecting purposes.

The increasing need for accurate forecasts of the surface wind speed fortunately comes with the improvement of the Numerical Weather Prediction models (NWP) describing and forecasting atmospheric motions. Indeed, they constitute a key source of information for surface wind speed forecasts all the more so as their realism, accuracy and resolution have increased steadily over the years [2].

Nevertheless, these models are not necessarily performing uniformly well for all atmospheric variables. Their astonishing performances are evaluated on variables such as mid-tropospheric pressure which reflect the large-scale mass distribution, which is effectively well understood physically (see, e.g., [23]) and efficiently modeled numerically. Variables tied to phenomena occurring on smaller scales (such as cloud-cover or near-surface winds) depend much more directly on processes that are parameterized (e.g, not resolved). In contrast to large-scale motions (governed by the Navier–Stokes equations), parameterizations are generally partly rooted in physical arguments, but also in large part empirical. When comparing output from a numerical model to a local measurement, there will therefore always be several sources of error: representativity error (contrast between the value over a grid-box and the value at a specific point), numerical error (even if we were describing only processes governed by well-established physical laws, discretization is unavoidable), and error tied to the physics described (because processes, especially parameterized ones, are not well modeled). To reduce representativity error and to better represent small-scale processes, in particular those tied to topography and surface roughness, one strategy consists in downscaling with models that describe the atmospheric flow on finer scales (see, e.g., [24]). One disadvantage of this approach is the numerical cost, and one limitation is the need for finer observations to initialize the state of the atmosphere, if details of the flow other than those directly implied by the topography and surface condition are sought for.

Strategies to estimate surface winds, or other meteorological variables, from the output of Numerical Weather Prediction models (NWP) or climate models have been developed in several contexts, with different motivations, and leading to different methodologies and applications.

Model Output Statistics (MOS) has been developed in weather forecasting for several decades to estimate the weather related variability of a physical quantity, based on NWP model output [10]. NWP models perform now very well in predicting large-scale systems. Relations thus can be derived to link the latters to local variables at an observation site. Linear models are generally used, with the outcome now expanded over a wider area than only the location of stations where observations are available [27].

In the context of climate change, downscaling a meteorological quantity at a given location in order to produce time series which have plausible statistical characteristics under climate change has for long been investigated [26]. The challenge is here to capture appropriately the relation between large-scale flow (as it can be described by a model with a moderate or low resolution) and a variable at a specific location (e.g. wind, temperature, precipitation) and then use climate models to provide a description of the large-scale atmospheric state under climate change. Local time series with appropriate variability and consistent with this large-scale state of the atmosphere are then generated, e.g. [17, 20, 25].

Wind energy domain is nowadays a very active branch in downscaling techniques because of the need for accurate forecasts at specific location of a wind farm. For describing winds close to the surface, 10 m wind speed is often a convenient variable as it has been for decades a reference observed variable and also now a reference NWP model output. In the case of wind energy, the wind speed then needs to be extrapolated at the hub height to have access to wind power, leading to an increase of the error on the predicted power [13, 16, 18]. Wind speed at the hub height (typically 100 m) is a variable of interest as it allows to avoid vertical extrapolation errors [4], but it is rarely available in observations. Different outputs of NWP models can be used as explanatory variables of the near surface wind speed. It seems that there is no strong consensus on the predictors to use, mainly because relations between predictors and predictand should differ from one location to the other. However, different studies have shown the importance of a certain set of variables to predict surface wind speed. Amongst them, markers of large-scale systems (geopotential height, pressure fields) and boundary layer stability drivers (surface temperature, boundary layer height, wind and temperature gradient) can be cited [5, 6, 20]. In terms of methodology, several models have already been studied, including Linear regression, Support Vector Models (SVM) or Artificial Neural Network (ANN) [14, 21].

The model of the European Center for Medium-range Weather Forecasts (ECMWF) has reached a resolution of about 9 km in the horizontal. In addition, ECMWF analyses and forecasts now give access to 100 m wind speed output, developed mainly for wind energy applications. If we can be very confident in the ability of NWP models to represent several variables, some others may not be so reliable. This is especially the case for surface variables such as 10 and 100 m wind speed. Consequently, using the robust information given by some variables to correct surface wind speed is straightforward. We have access to surface wind speed observed at 10, 100 m over a long period of 5 years at SIRTA observation platform [12]. The aim of this project is, in particular, to explore how different statistical models perform in forecasting the 10 and 100 m wind speed using informations of ECMWF analyses and forecasts outputs at different horizons. We choose multiple linear regression because it is a widely used technique, and Random Forests which have not been, to our knowledge, deeply studied in the framework of downscaling surface wind speed. For multiple linear regression, variable selection is a very important step for calibrating the statistical models, whereas Random Forests handle variables automatically. Moreover, Random Forests can handle nonlinear relations very well. Therefore, the comparison of those very different statistical models, as well as the information used by each of them, should be very instructive.

The paper is organized in 5 parts. The next section describes together the data and the statistical models to be used. In Sect. 2.3, the training dataset is explored, and used to calibrate the statistical models. In Sect. 2.4, forecasts of 10 and 100 m wind speed are run to downscale wind speed at the observation site. In the last section, we discuss the results, conclude and give perspectives to this work.

2 Data and Methodology

2.1 Data

Observed Wind Speed

In this paper, we use observations of the wind speed at the SIRTA observation platform [12]. Surface wind speed at 10 m height from anemometer recording is available at the 5-min frequency. The wind speed at 100 m height from Lidar recording is available at 10-min frequency. Both data span for 5 years from 2011 to 2015. We filter observations by a sinusoidal function over a 6-h window centered at 00, 06, 12 and 18 h to obtain a 6-h observed wind speed to be compared to the NWP model outputs available at this time frequency. We found that the resulting time series are not sensitive to the filter function. We also try different filtering windows, concluding that 6-h is the best to compare to the NWP model outputs. Due to some missing data, two final time series of 5049 filtered observations are computed (over 7304 if all data were available).

Fig. 2.1

Map of the SIRTA observation platform and its surroundings

SIRTA observatory is based 20 Km in the South of Paris on the Saclay plateau ($48.7^{\circ } N$ and $2.2^{\circ } E$). Figure 2.1 shows the SIRTA observation platform location, marked by the red point on the map, and its close environment. Regarding the relief near SIRTA, observe that a forest is located at about 50 m north to the measurement devices. South, buildings can be found at about 300 m from the SIRTA observatory. In the East-West axis, no close obstacle are encountered. Further south, the edge of the Saclay plateau shows a vertical drop of about 70 m, from 160 m on top to 90 m at the bottom.

NWP Model Outputs - ECMWF Analyses

Variables are retrieved from ECMWF analyses at 4 points around the SIRTA platform. The spatial resolution of ECMWF analyses is of about 16 km (0.125$^{\circ }$ in latitude and longitude). Topography is thus smoothed compared to the real one. As the surface wind speed is very influenced by the terrain, the modeled surface wind speed is not necessarily close to the observed wind speed. The data spans from the 01/01/2011 to 31/12/2015 at the 6-h frequency. It is sampled at each date where a filtered sampled observation is available.

The near surface wind speed at a given location can be linked to different phenomena. The large-scale circulation brings the flow to the given location explaining the slowly varying wind speed. The wind speed in altitude, the geopotential height, the vorticity, the flow divergence, sometimes the temperature can be markers of large systems like depressions, fronts, storms, or high pressure systems explaining a large part of the low frequency variations of the surface wind speed (Table 2.2). At a finer scale, what is happening in the boundary layer is very important to explain the intra-day variations of the wind speed. The state and stability of the boundary layer can be derived from surface variables describing the exchanges inside the layer. Exchanges are driven mostly by temperature gradient and wind shear that develop turbulent flow (Table 2.3). Thermodynamical variables like surface, skin, and dew point temperatures and surface heat fluxes can also inform on the stability of the boundary layer, as well as its height and dissipation on its state (Table 2.1). In the end, 20 output variables are retrieved from ECMWF analyses at the 4 points around the SIRTA observatory and at different pressure levels. Note that we restrict the study to local variables (at the location of measurements or in the column above). It might also be possible to take advantage from larger scale information [5, 27]. The choice of taking 4 points around the SIRTA platform has the advantage of being simple and straightforward. Providing instead the explanatory variables by their interpolated value at SIRTA and the two components of their gradient does not lead to significantly different results.

Table 2.1 Surface variables

Table 2.2 Altitude variables

Table 2.3 Computed variables

ECMWF Deterministic Forecasts

The year 2015 of deterministic forecasts is retrieved from ECMWF model. A forecast is launched every day at 00:00:00 UTC. The time resolution retained is of 3 h and the maximum lead-time is 5 days. The same variables as for the analyses are retrieved at the same points around the SIRTA platform.

2.2 Methodology

Our aim is to model the real observed wind speed from outputs of NWP model described above. More specifically, we use ECMWF analyses i.e the best estimate of the atmospheric state at a given time using a model and observations [15]. In what follows, the observed wind speed is the target and the analysed variables are potential explanatory features. Because of the complexity of meteorological phenomena, statistical modeling provides an appropriate framework for corrections of representativity errors and the modeling of site dependent variability. In this context, two main directions may be as usual investigated, parametric and nonparametric models.

Parametric models assume that the underlying relation between the target variable and the explanatory variables has, relatively to a certain noise, a particular analytical shape depending on some parameters, which need to be estimated through the data. Among this family of models, the linear model with a Gaussian noise is widely used, mostly thanks to its simplicity [8]. Associated to an adequate variable selection, it may be very effective.

Nonparametric models do not suppose in advance a specific relation between the variables: instead, they try to learn this complex link directly from the data itself. As such, they are very flexible, but their performance usually strongly depends on regularization parameters. The family of nonparametric models is quite large: among others, one may cite the nearest neighbors rule, the kernel rule, neural networks, support vector machines, regression trees, random forests... Regression trees, which have the advantage of being easily interpretable, show to be particularly effective when associated to a procedure allowing to reduce their variance as for the Random Forest Algorithm.

Let us describe the linear model and random forests in our context with more details. The linear model supposes a relation between the target $Y_t$, observed wind speed at time t, and explanatory variables $X_t^1,\dots , X_t^d$, available from the ECMWF, at this time t. For lightening the notation, we omit the index t in the next equation. The linear model is given by

$$\begin{aligned} Y=\beta _0+\sum _{j=1}^{d}\beta _j X_j+\varepsilon , \end{aligned}$$

where the $\beta _j$’s are coefficients to be estimated using least-square criterion minimization method, and $\varepsilon \sim {\mathscr {N}}(0,\sigma ^2)$ represents the noise. Among the meteorological variables $X_1,\dots , X_d$, some of them provide more important information linked to the target than others, and some of them may be correlated. In this case, the stepwise variable selection method is useful to keep only the most important uncorrelated variables [8]. Denoting by ${\beta }_0, \dots , {\beta }_d$ the final coefficients obtained this way (some of them are zero), the estimated wind ${\hat{Y}}$ is then given by

$$\begin{aligned} {\hat{Y}}={\beta }_0+\sum _{j=1}^{d}{\beta }_j X_j. \end{aligned}$$

(2.1)

An alternative approach to perform variable selection and regularization is to use the Lasso method (see for instance [22]), relying on minimization of the least square criterion penalized by the $\ell ^1$ norm of the coefficients $\beta _1,\dots ,\beta _d$. More specifically, for this model, the predicted wind speed at time t is a linear combination of all the previous variables as in Eq. (2.1), the coefficients $\beta _1,\dots , \hat{\beta }_d$ being estimated using the least square procedure, under the constraint $\sum _{j=1}^d |\beta _j|\le \kappa$ for some constant $\kappa >0$.

Regression trees are binary trees built by choosing at each step the cut minimizing the intra-node variance, over all explanatory variables $X_1,\dots ,X_d$ and all possible thresholds (denoted by $S_j$ hereafter). More specifically, the intra-node variance, usually called deviance, is defined by

$$\begin{aligned} D(X_j,S_j)=\sum _{X_j<S_j}(Y_s-\overline{ Y}^-)^2+\sum _{X_j\ge S_j}(Y_s-\overline{ Y}^+)^2, \end{aligned}$$

where $\overline{ Y}^-$ (respectively $\overline{ Y}^+$) denotes the average of the observed wind speed in the area $\{X_j<S_j\}$ (respectively $\{X_j\ge S_j\}$). Then, the selected $j_0$ variable and associated threshold is given by $(X_{j_0}, S_{j_0})=\arg \min _{j,S_j}D(X_j,S_j)$. The prediction is provided by the value associated to the leaf in which the observation falls.

To reduce variance and avoid over-fitting, it may be interesting to generate several bootstrap samples, fitting then a tree on every sample and averaging the predictions, which leads to the so-called Bagging procedure [3]. More precisely, for B bootstrap samples, the predicted power is given by

$$\begin{aligned} {\hat{Y}}=\frac{1}{B}\sum _{b=1}^{B}{\hat{Y}}^b, \end{aligned}$$

(2.2)

where ${\hat{Y}}^b$ denotes the wind speed predicted by the regression tree associated with the bth bootstrap sample. To produce more diversity in the trees to be averaged, an additional random step may be introduced in the previous procedure, leading to Random Forests, where the best cut is chosen among a smaller subset of randomly chosen variables. The predicted value is the mean of the predictions of the trees, as in Eq. (2.2).

3 The Relationship Between Analysed and Observed Winds

3.1 10/100 m Wind Speed Variability Comparison

In this section we compare the observed wind speed at 10 and 100 m with the 10 and 100 m wind speed output of the ECMWF analyses at the closest grid point, respectively. No significant difference can be found when using other grid points, or the mean of the four surrounding locations.

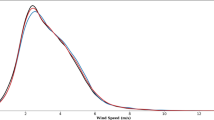
Figure 2.2 shows the Probability Density Function (PDF) of the wind speed coming from ECMWF analyses and observations, and also for illustration an example of a time series of corresponding wind speeds. It appears that the 10 m wind speed from ECMWF analyses displays a systematic bias by overestimating the 10 m observed wind speed (Fig. 2.2a, b). The wind at 100 m is comparatively well modeled in terms of variations in the time series, but also in terms of distribution (Fig. 2.2c, d). It seems that the errors mainly come from the overestimation of peaked wind speeds and the underestimation of low wind speeds (Fig. 2.2c, d). As 10 m wind speed is very influenced by even low topography and surrounding obstacles, which are smoothed or not represented in ECMWF analyses, some of its variations are not well described, and even a quite systematic bias is displayed. The effect of the topography and terrain specificity have less impact on the 100 m wind speed, so that it is much better represented in ECMWF analyses.

Fig. 2.2

10 m (top) and 100 m (bottom) wind speed time series in summer 2011 (panels a and c, respectively) and the respective probability density function estimated over the 5 years sample wind speed (panels b and d)

Table 2.4 MeanDeviation, RMSE, and correlation performed by ECMWF analyses for modeling the 10 and 100 m wind speed

The ability of the model to represent the observed wind speed is quantified in Table 2.4 by the deviation, the Root Mean Square Error (RMSE), and the Pearson correlation which formula are given by Eqs. (2.3), (2.5), and (6.8) respectively.

$$\begin{aligned} \text {Deviation for the }i\mathrm{th} \text { observation}&= (y_{i} - x_{i}) \end{aligned}$$

(2.3)

$$\begin{aligned} \text {RMSE}&= \sqrt{\frac{\sum _{i=1}^{n}{(x_{i} - y_{i})^{2}}}{n}} \end{aligned}$$

(2.4)

$$\begin{aligned} \text {Correlation}&= \frac{\sum _{i=1}^{n} (x_{i}-{\bar{x}})(y_{i}-{\bar{y}})}{{\sqrt{\sum _{i=1}^{n}(x_{i}-{\bar{x}})^{2}}}{\sqrt{\sum _{i=1}^{n}(y_{i}-{\bar{y}})^{2}}}}, \end{aligned}$$

(2.5)

where ${\displaystyle x_{i}}$ is the wind speed from the NWP model and ${\displaystyle y_{i}}$ the observed wind speed; ${\displaystyle n}$ is the number of samples ${\displaystyle (x_{i},y_{i})}$ and ${\displaystyle {\bar{x}}={\frac{1}{n}}\sum _{i=1}^{n}x_{i}}$ (the sample mean) and analogously for ${\displaystyle {\bar{y}}}$.

No clear improvement of the ECMWF analyses over the years from 2011 to 2015 can be detected in Table 2.4. The correlation stays quite constant over the years for both 10 and 100 m wind speeds. The Deviation and RMSE seem to decrease for the 10 m wind speed but it cannot be confirmed because of the good score performed in 2012. The variations of performance may only come from changes in the predictability of the weather over Europe [7]. Seasonal variations of the performance of ECMWF analyses can be seen, especially on the correlation between the observed and modeled wind speed. At both 10 and 100 m, the analysed wind speed is better correlated with the observations in winter and fall than in spring and summer. In all cases, the scores shown are better for the 100 m wind speed than for the 10 m wind speed.

Fig. 2.3

10 m wind speed from ECMWF analyses as function of the 10 m observed wind speed given cardinal directions. Panels correspond to a direction modeled by ECMWF analyses; the wind blows from a West, b Southwest, c South, d Southeast, e East, f Northeast, g North, h Northwest

Variations of the performance of the ECMWF analyses in representing the observed wind speed are evidenced by Fig. 2.3. The figure shows the 10 m wind speed from ECMWF analyses as a function of the 10 m observed wind speed for different directions of the analysed wind. It is obvious that the errors made by the numerical model differ regarding the direction of the wind. For instance, when the wind comes from the West (Fig. 2.3a), the correlation is very close to one, but for a wind coming from the North/Northeast (Fig. 2.3f, g), it is very low, and the model highly overestimates the 10 m wind speed. It can be easily linked to the specificity of the terrain. Indeed, when a northerly wind is recorded, it has been blocked by the forest north of the anemometer. The same happened for southerlies with the building situated further and which influence is thus not as substantial as the forest. Figure 2.4 displays the same as Fig. 2.3 but for the 100 m wind speed. It seems that there is no more dependence of the performance of the ECMWF analyses regarding the direction of the 100 m wind speed; it appears to be not significantly impacted by the surrounding forests and buildings.

Fig. 2.4

Same as Fig. 2.3 but for 100 m wind speed

3.2 Reconstruction of the 10/100 m Observed Wind Speed Using NWP Outputs

In the sequel, a k-fold cross validation is performed over 10 different periods taken within the 5-years of analyses and observation. Each time, statistical downscaling models are trained on a given period of about 4500 data points and applied over the remaining period of about 500 data points to reconstruct the 10 and 100 m wind speed, so that it results in 10 reconstructions that span the 5 years of data. Table 2.5 enumerates the statistical downscaling models assessed in this study. Models differ by their types (Linear Regression and Random Forests), the explanatory variable selection, and whether a model is conditionally fitted regarding the direction of the wind speed or not. We evaluate the different statistical models in terms of RMSE and Correlation with the observed wind speed on the reconstruction period.

Table 2.5 Statistical models used to downscale 10 and 100 m wind speed

10 m Wind Speed Reconstruction

Figure 2.5 shows results for the reconstruction of the 10 m wind speed. Each box contains the 10th reconstructed k-fold periods. First, by using only wind speed with a linear model $LR_F$, RMSE is reduced by about 40%, but the correlation stays constant. Adding other variables to linear model (i.e. $LR_{A}$, $LR_{SW}$ and $LR_{La}$) allows to reduce the RMSE by 60%, and to significantly improve correlation from 0.80 to 0.91 between reconstructed wind speed and observed one. Using stepwise selection of variables, the Lasso penalization or all variables does not change results in this case, showing that only a part of the information is useful. Using variable selection as stepwise or $\ell _1$ penalization (Lasso) avoids over-fitting. Random Forests models perform slightly better than linear models without defining one given model per cardinal wind directions. Variables selected stepwise are very diverse (wind speed, large scale variables, boundary layer state drivers), while Lasso technique mainly selects wind speed and wind component, thus using redundant information. Analyzing the main variables used by Random Forests shows that this methods seems to put much weight on wind component first, highlighting the dependence of the error on the 10 m wind speed regarding its direction.

Fig. 2.5

RMSE and correlation results when reconstructing 10 m wind speed with models described in Table 2.5. The first boxes stand for the ECMWF analyses 10 m wind speed

By fitting a linear model in each direction (noted with ‘dir’) we manually introduce a relevant information, especially for 10 m wind speed (Fig. 2.3). The model is however more exposed to under-fitting as the sample size of the training data in one direction can be low. Nevertheless, $LR_{SW}^{dir}$ performs better than all other models. Indeed, stepwise choice is made for each direction so that the model is deeply adapted to each direction. This method results in a significant improvement of the RMSE and correlation scores. As expected regarding Fig. 2.3g, the best improvement is retrieved for northerly wind speed and is of more than 0.1 m$\cdot$s$^{-1}$ compared to $LR_{SW}$. No improvement is found for easterlies, surely because the number of data is too small. Fitting a Random Forest in each direction does not improve results, maybe because the direction is already well handled by this model by using the zonal and meridional component of the wind. So one big advantage of Random Forests over linear regression is that it does not require to explore previously deeply the data for extracting appropriate and relevant features as inputs to the model. Figure 2.6 shows time series of 10 m observed wind speed, NWP model wind speed output over summer period of 2011 (panel a) and the probability density function corresponding to the entire period, 2011–2015 (panel b). Panels c and e show respectively time series of the reconstructed 10 m wind speed by $LR_{SW}^{dir}$ (red line) and $LR_{SW}$ (blue line), and by $RF_{A}^{dir}$ (magenta line) and $RF_A$ (cyan line). Panels d and f show the corresponding probability density functions. All statistical models allow for a good bias correction. All models underestimate the small quantiles of the distribution and give a distribution very peaked around the mean observed wind speed. High percentiles are however well reconstructed. This is encouraging because this part of the distribution is important in terms of energy production. We can nevertheless expect an overestimation of the wind energy production with those models because of the underestimation of small percentiles.

Fig. 2.6

Timeseries (left) and PDF (right) of the observed 10 m wind speed (straight black line), and 10 m wind speed from ECMWF (dotted black line) (a and b), Linear models ($LR_{SW}$ (blue) and $LR_{SW}^{dir}$ (red)) (c and d), Random Forest models ($RF_{A}$ (cyan) and $RF_{A}^{dir}$ (magenta)) (e and f)

100 m Wind Speed Reconstruction

Figure 2.7 shows results of the reconstruction of 100 m wind speed with statistical models described in Table 2.5. $LR_{F}$ allows a reduction of the RMSE of about 15% corresponding to 0.14 m$\cdot$s$^{-1}$ and the best model $LR_{SW}^{dir}$ reduces the RMSE by 23% corresponding to 0.23 m$\cdot$s$^{-1}$. The correlation is improved from 0.92 to 0.94. Adding the direction dependence to linear model with only 100 m wind speed (i.e. $LR_{F}^{dir}$) does not improve results regarding $LR_F$. Indeed, the error on the 100 m wind speed does not depend on the direction. Using all explanatory variables (i.e. $LR_{A}^{dir}$) leads to a strong over-fitting. Surprisingly, the linear model using stepwise selection of explanatory variables in each direction (i.e. $LR_{SW}^{dir}$) recovers an important information as it performs significantly better than the other. Again, its adaptability may be the cause of its good performance. In the case of 100 m wind speed, the best improvement is found for easterly wind speeds. The information on the direction in Random Forests does not improve the results like for 10 m wind speed reconstruction. The more important variables for Random forests and stepwise choice are mainly the 100 m wind speed, but also the wind shear in the boundary layer. Lasso technique selects mainly 100 m wind speed.

Fig. 2.7

Same as Fig. 2.7, for 100 m wind speed

Fig. 2.8

Same as Fig. 2.6, for 100 m wind speed

Figure 2.8 shows time series of 100 m observed wind speed, NWP model wind speed output over summer period of 2011 (panel a) and the probability density function corresponding to the entire period from 2011 to 2015 (panel b). panel c and e show respectively time series of the reconstructed 100 m wind speed by $LR_{SW}^{dir}$ (red line) and $LR_{SW}$ (blue line), and by $RF_{A}^{dir}$ (magenta line) and $RF_{A}$ (cyan line). Panels d and f show the corresponding probability density functions. Some peaked wind speeds are less overestimated after statistical downscaling. As for the 10 m wind speed, statistical models underestimate the small quantiles of the distribution and give a distribution peaked around the mean observed wind speed.

To conclude, we built different statistical models to improve the representation of the 10 and 100 m wind speed of the ECMWF analyses. It has been shown that the 100 m wind speed in ECMWF analyses is already well represented as it displays no systematic bias and a good correlation. Nevertheless the RMSE computed for the period 2011–2015 is still of 1.0 m$\cdot$s$^{-1}$. Statistical models reduces the RMSE on the 10 m wind speed between 40 and 65%, and between 15 and 23% for the 100 m wind speed. They improve at the same time the correlation between the observed wind speed and the reconstructed one. For linear models, the variables selection is of great importance to avoid over-fitting, and an exploration step allows to improves results significantly. Random Forests give quite comparable results as the best linear models, without needing variable selection and a preliminary exploration of the data.

4 Forecasts of Surface Winds

In this section we use the previous statistical models based on the knowledge of the observed wind speed and the outputs of ECMWF analyses to forecast wind speed at five days horizon with a frequency of 3 h. We have access to 1 year of forecasts in 2015. We train these statistical models on ECMWF analyses from 2011 to 2014, and apply the resulting model to the forecasts. Figures 2.9 and 2.10 show respectively the RMSE averaged over the 365 forecasts for the 10 and 100 m wind speed. A strong diurnal cycle of the performances of both ECMWF forecasts and downscaled statistical predictions of the 10 m wind speed is evidenced. This diurnal cycle seems to be observed also for 100 m wind speed forecasts, but with a less important amplitude. As the dataset is trained on the ECMWF analyses, we can affirm that diurnal cycle is better represented in the ECMWF analyses than in ECMWF forecasts. This could be indeed explained by the data assimilation system that may help to correct errors coming from NWP model parameterizations.

Fig. 2.9

RMSE, computed between the 10 m observed wind speed, and the 10 m forecast wind speed, averaged over the entire set of forecasts

Fig. 2.10

RMSE, computed between the 100 m observed wind speed, and the 100 m forecast wind speed, averaged over the entire set of forecasts

An interesting result shown in Fig. 2.9 is that performance of the $LR_F$ statistical model which is comparable to linear model $LR_{SW}$, showing that the added value of other explanatory variables is valuable mainly for small lead-times in this case. Adding the dependence with the direction (i.e. $LR_{SW}^{dir}$) allows for a significant reduction of the RMSE. Random Forests $RF_A$ shows the best performance. In addition to the simplicity to fit this model, its robustness seems to overcome linear regression models. For 100 m wind speed forecasts (Fig. 2.10), Linear models $LR_F$, $LR_{SW}$, and $LR_{SW}^{dir}$ and Random Forest $RF_A$ are comparable.

For both 10 and 100 m wind speed forecasts, statistical downscaling models allow for significant improvements regarding ECMWF predicted wind speed, at any lead-time from 3 h to 5 days. Training dataset on the analyses of ECMWF may not be optimal. Indeed, training a statistical model for each lead-time separately should deeply improve results. First, this could help to remove the displayed diurnal cycle, but may also let the increase in RMSE with the lead-time be less sharp.

5 Summary and Concluding Remarks

We have used statistical models to evaluate 10 and 100 m wind speed at a given location from output of a NWP model. Comparison of the observed wind speed and ECMWF wind speed output at 10 and 100 m within the 5 years of data show that ECMWF analyses well represent 100 m wind speed. The computed RMSE is of 1.0 m$\cdot$s$^{-1}$ (the mean wind speed being of 5.8 m$\cdot$s$^{-1}$) and no systematic bias is displayed. On the contrary, 10 m wind speed output from ECMWF analyses displays a systematic overestimation the observed wind speed. The computed RMSE is of 1.4 m$\cdot$s$^{-1}$ (the mean wind speed being of 2.4 m$\cdot$s$^{-1}$).

By applying linear regression between a certain amount of selected variables and observed wind speed, we reduce the RMSE for the 10 and 100 m reconstructed wind speed up to 65 and 23%, respectively. Those good results have been achieved by fitting a linear model in 8 directions and by automatic selection of valuable variables in those directions. Building such a model thus requires a special treatment and a good knowledge of the specific site so that it cannot be systematically applied to another site. Very interestingly, using Random Forests to reconstruct 10 and 100 m wind speed gives comparable results as the best linear models (about 57 and 20%, respectively), while their performance is not sensitive to any preparation of the data. Computing time is a bit longer than simple linear models, but it is quite similar when a linear model is fitted in each direction.

In a second step, we applied the statistical models to forecast up to 5 days. Note that statistical models are trained on past analyses. Applying it on forecasts will work ‘as well’ only if the relationship between NWP outputs and observed wind speed does not change with lead-time. This is not a-priori guaranteed as the analyses incorporate information from observation via data assimilation. Results are encouraging, because the RMSE between forecast wind speed and observed wind speed is significantly reduced compared to ECMWF forecasts whatever the lead-time, and for both 10 and 100 m wind speeds. Interestingly, Random Forests perform the same or better than linear models when applied to forecast 10 m or 100 m wind speed.

The results obtained for the forecasts are very encouraging: even though the training only involved analyses, the reduction in RMSE persisted for lead-times up to 5 days. Promisingly, there are evident changes to be tried which should lead to improvements of the performances. As a first, training statistical downscaling models directly on ECMWF forecasts makes sense as a transfer function adapted to each lead-time should take into account the reduced performance of ECMWF forecasts around 15 pm and thus correct systematic errors in the representation of the diurnal cycle. Moreover, training dataset for each lead-time separately should also help to reduce the increase of RMSE with lead-time by adapting the explanatory variables to forecasts performance. For instance, for short lead-time, statistical models may find out that surface wind speed in ECMWF forecasts gather valuable information so that this information would be used. It may nevertheless not be the case at longer timescales, so that statistical models would prefer using information from large-scale circulation (e.g. pressure) which is well modeled by ECMWF forecasts, even at lead-time up to 5 days. Secondly, the good performance of Random Forests together with linear regression models denotes that it is possible to reconstruct the wind speed with very different relations. Model aggregation may thus be a path to retrieve more information than when using a single statistical model. It also seems that using statistical downscaling techniques results in a more peaked distribution around the mean, whereas the ECMWF forecasted 100 m wind speed overestimates the extremes. As a consequence, a properly weighted mean of the two different forecasts could improve results as well.

In this study, we choose to use only local informations coming from NWP outputs. Additive valuable informations may be retrieved from larger-scale NWP outputs such as large-scale horizontal gradients of the pressure. However, the discussion on the added value of any other NWP outputs is site dependent, and is already part of research matters. For instance, it has been proved that large scale circulation patterns give valuable information at timescales up to months in some regions of France [1].

A wind farm is often equipped with many anemometers situated at 10 m and at the hub height, so that local intime observations are easily available as well as wind power output. Forecasting wind speed using only NWP outputs is a good way to improve forecasts, but local past observations may also be used as explanatory variable. Indeed, at very short lead-time (3-h), we can assume that the error the NWP model make at $t_{0h}$ (corresponding to the analyses) may be correlated to the future error at time $t_{3h}$. We could also imagine to create a direct link between NWP outputs and wind energy production as in [9], using in addition the information on the close past wind energy production at the considered wind farm.

As a preliminary illustration of the benefit of such an approach, we train Random Forests and Linear Regression with stepwise selection of variables to forecast 10 and 100 m wind speed at time $t_{3h}$ only, and add the error on the wind speed at time $t_{0h}$ as an explanatory variable of the future wind speed at time $t_{3h}$. We perform a k-fold of 10 forecasts over the year 2015. Results are represented in Fig. 2.11. When forecasting 10 m wind speed at $t_{3h}$, using the error at time $t_{0h}$ allows for a reduction of the RMSE of 5% with Random Forests and of 10% with linear model compared to Random Forest without the observation at time $t_{0h}$. When forecasting 100 m wind speed at $t_{3h}$, using the information on the 10 m wind speed observed at $t_{0h}$ allows for an improvement of 2 – 6%. Adding the information on the 100 m wind speed at time $t_{0h}$ spectacularly improves results by 18% with linear regression model.

Fig. 2.11

RMSE computed over 10 k-fold forecasts of 10 m (a) and 100 m (b) wind speed at 3 h lead-time, using the error on the 10 and 100 m wind speed at time $t_{0h}$ (denoted by $\varDelta 10$ and $\varDelta 100$, respectively) as an explanatory variable. The dashed line represent the averaged RMSE of Random Forest without using observations at $t_{0h}$, and boxes represents the RMSE over 10 k-fold forecasts

In addition of the good results obtained when reconstructing 10 and 100 m wind speed, we also showed encouraging results when forecasting wind speed up to 5 days. By using very different statistical models, we highlight advantages of Random Forests over multiple linear regression, e.g. simplicity and robustness. Finally, very promising perspective for improving downscaling at short-term horizon is exposed; it involves a pseudo-assimilation of a local past observed information into the statistical downscaling model.