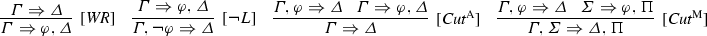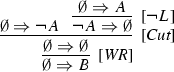Abstract
Paraconsistent logics are logical systems that reject the classical principle, usually dubbed Explosion, that a contradiction implies everything. However, the received view about paraconsistency focuses only the inferential version of Explosion, which is concerned with formulae, thereby overlooking other possible accounts. In this paper, we propose to focus, additionally, on a meta-inferential version of Explosion, i.e. which is concerned with inferences or sequents. In doing so, we will offer a new characterization of paraconsistency by means of which a logic is paraconsistent if it invalidates either the inferential or the meta-inferential notion of Explosion. We show the non-triviality of this criterion by discussing a number of logics. On the one hand, logics which validate and invalidate both versions of Explosion, such as classical logic and Asenjo–Priest’s 3-valued logic \(\mathbf {LP}\). On the other hand, logics which validate one version of Explosion but not the other, such as the substructural logics \(\mathbf {TS}\) and \(\mathbf {ST}\), introduced by Malinowski and Cobreros, Egré, Ripley and van Rooij, which are obtained via Malinowski’s and Frankowski’s q- and p-matrices, respectively.
Access provided by CONRICYT-eBooks. Download chapter PDF
Similar content being viewed by others
1 Introduction
Paraconsistent logics are logical systems that rebel against the classical principle, usually dubbed Explosion, that a contradiction implies everything, or that from a contradiction, everything follows.
As Priest, Tanaka and Weber say
The contemporary logical orthodoxy has it that, from contradictory premises, anything can be inferred (...) Inconsistency, according to received wisdom, cannot be coherently reasoned about (...) Paraconsistent logic challenges this orthodoxy. A logical consequence relation is said to be paraconsistent if it is not explosive. [24]
Similarly, in the recent book by Carnielli and Coniglio, it is said that
Paraconsistent logics are able to deal with contradictory scenarios, avoiding triviality by means of the rejection of the Principle of Explosion. [6, p. 3]
In a nutshell, as Ripley puts it
paraconsistency is a nonentailment claim. [28, p. 773]
The aim of this paper is to offer a new characterization of what paraconsistent logics are. Our main claim will be that a logic \(\mathbf {L}\) is paraconsistent if either the inferential or the meta-inferential formulation of Explosion is invalid in it. These two formulations of Explosion are, respectively, as follows

Where the inferential and the meta-inferential level coincide, roughly, with what are called (after Avron’s work in [2]), the internal and the external consequence of a given logic.Footnote 1 Let us clarify why we take our proposal to be a non-trivial contribution to the debate about paraconsistency.
First, the received view about paraconsistency has only focused on formulations of Explosion that concern formulae, i.e. a formula A and its negation \(\lnot A\). But surely this can be taken to be a restricted point of view. In what follows we will try to broaden this conception by putting forward the aforementioned two different formulations of Explosion: while the former (the traditional form, that is) is concerned with formulae, the latter is concerned with inferences or sequents. Thus, the traditional conception understands Explosion as an inference, whereas the supplementary conception that we are trying to bring to the table also suggest to understand Explosion as a meta-inference.
Secondly, this raises the question about the possibility of finding paraconsistent logics that are so for different inferential reasons. That this possibility is real implies that our proposed criterion does not collapse with previous characterizations. In other words, it does not make the (in)validity of Explosion at either of these levels to collapse into the (in)validity at the other level. To prove this, we will offer examples of logics which validate both versions of Explosion, logics that invalidate both, and of logics that invalidate only one of them but not the other.
To carry out our current investigation, this paper is structured as follows. In Sect. 2 we introduce the distinction between inferences and meta-inferences, along with the inferential and the meta-inferential formulations of Explosion, and our new criteria for paraconsistency. In Sect. 3 we present four study cases: one logic that is not paraconsistent, i.e. classical logic, and three logics that are paraconsistent: Asenjo–Priest’s \(\mathbf {LP}\), and two substructural logics \(\mathbf {TS}\) (a q-logic, as defined in [19], discussed by Cobreros, Ripley, Egré and van Rooij [8], Malinowski [21], and French [14]) and \(\mathbf {ST}\) (a p-logic, as defined in [12], discussed by Cobreros, Ripley, Egré and van Rooij [8]). These logics are shown to be paraconsistent in different inferential ways. While \(\mathbf {LP}\) invalidates both the inferential and the meta-inferential formulations of Explosion, \(\mathbf {TS}\) invalidates the former but not the latter, whereas \(\mathbf {ST}\) validates the former but not the latter. In Sect. 4 we provide some philosophical reflections drawn from our previous discussions, connecting our results with the debate on logical pluralism and the inferentialist stance towards the meaning of the logical connectives. Moreover, we consider three possible objections against our account and provide replies to all of them. Finally, in Sect. 5 we offer some concluding remarks, and point to some directions in which the present explorations can be further developed.
2 Different Inferential Ways of Being Paraconsistent
2.1 Inferences and Meta-Inferences
In order to understand and carry on our investigation, it will be important to have a more precise grasp of the received view about paraconsistent logics and Explosion. This view, traditionally takes paraconsistent logics as Tarskian logics and, so, we shall better understand what these are.
For the purpose of analyzing these matters, it will be useful to fix some terminology. Let \(\mathscr {L}\) be a propositional language, such that \(\mathbf {FOR}(\mathscr {L})\) is the absolutely free algebra of formulae of \(\mathscr {L}\), whose universe we denote by \(FOR(\mathscr {L})\).
Definition 1
A Tarskian consequence relation over a propositional language \(\mathscr {L}\) is a relation \(\vDash \ \subseteq \wp (FOR(\mathscr {L})) \times FOR(\mathscr {L})\) obeying the following conditions for all \(A \in FOR(\mathscr {L})\) and for all \(\varGamma , \varDelta \subseteq FOR(\mathscr {L})\):
-
1.
\(\varGamma \vDash A\) if \(A \in \varGamma \) (Reflexivity)
-
2.
If \(\varGamma \vDash A\) and \(\varGamma \subseteq \varGamma '\), then \(\varGamma ' \vDash A\) (Monotonicity)
-
3.
If \(\varDelta \vDash A\) and \(\varGamma \vDash B\) for every \(B \in \varDelta \), then \(\varGamma \vDash A\) (Cut)
Additionally, a (Tarskian) consequence relation \(\vDash \) is substitution-invariant whenever if \(\varGamma \vDash A\), and \(\sigma \) is a substitution on \(FOR(\mathscr {L})\), then \(\{ \sigma (B) \mid B \in \varGamma \} \vDash \sigma (A)\).
Definition 2
A Tarskian logic over a propositional language \(\mathscr {L}\) is an ordered pair \((FOR(\mathscr {L}), \vDash )\), where \(\vDash \) is a substitution-invariant Tarskian consequence relation.
Throughout the years many scholars have argued that the Tarskian conception of logic is quite narrow. For example, Shoesmith and Smiley [30], Avron [3] and Scott [29] claimed that the Tarskian account should be generalized to a logic having multiple consequences; and Avron [3] and Gabbay [15] have argued that the condition of Monotonicity should be relaxed; whereas it can be inferred that, derivatively, Malinowski [19] and Frankowski [12] argued for a generalization or liberalization which allows logics to drop Reflexivity and/or Cut.
These modifications, in turn, can be made sense of by noticing a shift in the nature of the collection of formulae featured in the consequence relation. Thus, for example, instead of treating logical consequence to hold between (sets of) formulae, it may hold between labelled formulae, sequences of formulae (where order matters), multisets of formulae (where repetition matters), etc. Interestingly, many of these approaches invalidate Explosion, regarded as an inference that relates collections (sets, sequences, multisets, etc.) of formulae. But none of the aforementioned alternatives proposed explicitly to move from logical consequence as a relation conceived between collections of formulae to a relation conceived between collections of some other entities. Therefore, none of these alternatives proposed explicitly to change from focusing on Explosion as an inference that relates formulae to an inference that relates other entities.
However, some other approaches did. That is the case of Avron in [2], first, and Blok and Jónsson in [5], second, which discuss a generalization of the Tarksian account that allows to move to logical consequence relations that do not hold only between collections of formulae, but between objects of other nature.
Definition 3
An inference or sequent on \(\mathscr {L}\) is an ordered pair \((\varGamma , A)\), where \(\varGamma \subseteq FOR(\mathscr {L})\) and \(A \in FOR(\mathscr {L})\) (written \(\varGamma \Rightarrow A\)). \(SEQ^{0}(\mathscr {L})\) is the set of all inferences or sequents on \(\mathscr {L}\).
Definition 4
([11]) A meta-inference or meta-sequent on \(\mathscr {L}\) is an ordered pair \((\varGamma , A)\), where \(\varGamma \subseteq SEQ^{0}(\mathscr {L})\) and \(A \in SEQ^{0}(\mathscr {L})\) (written \(\varGamma \Rightarrow ^{1} A\)). \(SEQ^{1}(\mathscr {L})\) is the set of all meta-inferences or meta-sequents on \(\mathscr {L}\).
We will say, accordingly, that from the following the one on the left is an inference, whereas the one on the right is a meta-inference

and, indeed, according to the following definitions adapted from Avron [2], both are valid in e.g. Gentzen’s sequent calculus \(\mathbf {LK}\) for classical logic—as we shall see next, when we define the corresponding notions of validity.
Now, going back to the proposed shifts from the ontology of the Tarskian account of logical consequence, Avron suggested in [2] that the idea that logical consequence can be said to hold of relata other than formulae is very reasonable to those used to sequent calculus—and, most prominently, with substructural sequent calculi.
For Avron there are two different notions of logical consequence for a given sequent calculus \(\mathbf {S}\): the internal and the external notion of logical consequence. In our work, however, instead of referring to these relations as internal and external, we will refer to these levels, respectively, as the inferential and the meta-inferential, characterized such that
-
A follows inferentially from \(\varGamma \) in \(\mathbf {S}\) (written \(\vdash _{\mathbf {S}} \varGamma \Rightarrow A\)) whenever \(\varGamma \Rightarrow A\) is a provable sequent of the calculus \(\mathbf {S}\). In such a case we will say that the inference from \(\varGamma \) to A is \(\mathbf {S}\)-valid.
This relation is concerned with which formulae follow from which (collection of) formulae, given the rules of the calculus—i.e. which sequents follow, given the axioms and rules of the calculus.
-
A follows meta-inferentially from \(\varGamma \) in \(\mathbf {S}\) (written \(\vdash _{\mathbf {S}} \varGamma \Rightarrow ^{1} A\)) whenever \({\Rightarrow }A\) is provable in the calculus that results from the addition to \(\mathbf {S}\) of all the sequents \({\Rightarrow }B\) (for B in \(\varGamma \)) as initial sequents or axioms.Footnote 2 In such a case we will say that the meta-inference from \(\varGamma \) to A is \(\mathbf {S}\)-valid.
This means that this relation is concerned with which sequents follow from which (set of) sequents, given the axioms and rules of the calculus.
That these relations are different can be easily exemplified by the fact, nicely noticed by Mares and Paoli in [22], that if a sequent calculus \(\mathbf {S}\) has no Weakening rules, then
Finally, notice also in passing that re-writing the meta-inference

with the aid of the previous notation, gives us as a result
which, for matters of readability, we will write as
reinforcing, thereby, the idea that we are dealing with nothing more than yet another formulation of Explosion. Something that we will argue for explicitly in the next section.
2.2 Explosion, Revisited
Explosion, so to speak, comes in different flavors. Many rules, meta-rules and principles are dubbed with that name. Nevertheless, there are what seems to be some central or essential features that every one of them share, and indeed it is that they embody the idea that contradiction equals triviality. This is traditionally understood, in terms of the received view about paraconsistency as saying that
An inference with an inconsistent premise set implies any conclusion
As is well-known, inconsistent premise sets for inferences are sets that include (some instance of) the (schematic) formulae A and \(\lnot A\). So, along these lines, Explosion is without any surprise taken to be the inference
The question is now, how to adapt this idea to the case of meta-inferences. For us, the most reasonable take is to say that
A meta-inference with an inconsistent premise set implies any conclusion
But, now, for meta-inferences, we must keep in mind that premise sets and conclusions are formed with sequents. Thus, we must define what an inconsistent premise set for meta-inferences is. We take these to be sets that include (some instance of) the (schematic) sequents \(\Rightarrow A\) and \(\Rightarrow \lnot A\). That this is, in fact, a right way to understand an inconsistent sequent set can be argued for by looking at e.g. the definition of an inconsistent belief set (cf. [17]). Along these lines, Explosion is without any surprise taken to be the meta-inference

Furthermore, we are in good company in claiming that these are in fact two versions or formulations of Explosion, one as an inference and the other as a meta-inference. For Lloyd Humberstone, in his reference book The Connectives says in [18, p. 118–119] that \(A, \lnot A \Rightarrow B\) is a sequent, i.e. an inferential form of Explosion, whereas the following is a rule, i.e. a meta-inferential form of Explosion.

By letting \(\varGamma \) and \(\varDelta \) be empty, Humberstone proposed form collapses with ours.Footnote 3
To conclude, let us rephrase in a more formal manner the main claim of this paper
Additionally, let us highlight that we are not claiming these two are the only dresses that Explosion can use. If a logic invalidates either of the previous formulations of Explosion, we will say that it is paraconsistent, although it need not invalidate either to be so, for it may invalidate some other formulation(s) of Explosion. For example, Explosion is sometimes formulated with the help of conjunction. Exploring ‘conjunctive’ versions of Explosion (both at the inferential and the meta-inferential level) is no doubt an interesting task, one which for matters of space we decided not to tackle here. In other words, we are not proposing a necessary, but a new sufficient condition for logics to be paraconsistent.
An additional caveat, which echoes the well-known reservations expressed by Igor Urbas in [34], should be mentioned concerning this characterization. In his work, Urbas points out that the traditional definition of paraconsistency in terms of invalidating the inferential form of Explosion counts as paraconsistent some logics “which satisfy the letter of [this criterion] while brazenly flouting its spirit” [34, p. 345]. For instance, Johansson’s Minimal Logic invalidates Explosion, while validating the scheme \(A, \lnot A \Rightarrow \lnot B\), for arbitrary formulae B. Furthermore, as highlighted by an anonymous referee, this logic will also invalidate the meta-inferential formulation of Explosion, while still validating the scheme \(A, \lnot A \Rightarrow ^{1} \lnot B\), for arbitrary formulae B. Thus, these considerations lead us to note that these pathological cases can—and probably should—be exempted from the definition.
In what follows we will compare different cases of different logics, showing that all of them take a distinctive stance with regard to the valid or invalid character of the above portrayed inferential and meta-inferential versions of Explosion.
3 Study Cases
To accomplish our task in this section, we will divide these systems in two groups. The first group will be composed of matrix logics and will include a logic that is not paraconsistent at any level, i.e. classical logic \(\mathbf {CL}\), and a logic that is paraconsistent both at the inferential and the meta-inferential level, i.e. Asenjo–Priest’s 3-valued logic \(\mathbf {LP}\) from [1, 23]. The second group will be composed of a q-matrix logic,Footnote 4 i.e. the logic \(\mathbf {TS}\), and a p-matrix logic,Footnote 5 i.e. the logic \(\mathbf {ST}\), both due to Cobreros, Ripley, Egré and van Rooij in [8], the former being also discussed by Malinowski in [21]. These logics will be shown to be, respectively, paraconsistent at the inferential but not the meta-inferential level, and paraconsistent at the meta-inferential but not the inferential level.
3.1 Matrix Logics
Definition 5
For \(\mathscr {L}\) a propositional language, an \(\mathscr {L}\)-matrix is a structure \(\mathscr {M} = \langle \mathscr {V}, \mathscr {D}, \mathscr {O} \rangle \), such that \(\langle \mathscr {V}, \mathscr {O} \rangle \) is an algebra of the same similarity type as \(\mathscr {L}\), with universe \(\mathscr {V}\) and a set of operations \(\mathscr {O}\), and \(\mathscr {D} \subseteq \mathscr {V}\).
Notice, in the first place, that the set \(\mathscr {O}\) includes for every n-ary connective \(\diamond \) in the language \(\mathscr {L}\), a corresponding n-ary truth-function \(f^{\diamond }_{\mathscr {M}}: \mathscr {V}^{n} \longrightarrow \mathscr {V}\). With regard to these, when context allows it, we will sometimes identify the connectives themselves (which are linguistic items), with their corresponding truth-functions in a given matrix. In the second place, notice that typically, when dealing with non-classical logics, the set \(\mathscr {V}\) is taken to be a superset of \(\{ {\mathbf {t}}, {\mathbf {f}}\}\).
Definition 6
For \(\mathscr {M}\) an \(\mathscr {L}\)-matrix (respectively, an \(\mathscr {L}\)-q-matrix or an \(\mathscr {L}\)-pmatrix), an \(\mathscr {M}\)-valuation v is an homomorphism from \(FOR(\mathscr {L})\) to \(\mathscr {V}\), for which we denote by \(v[\varGamma ]\) the set \(\{ v(B) \mid B \in \varGamma \}\), i.e. the image of v under \(\varGamma \).
Of interest are two-valued classical logic \(\mathbf {CL}\) (which we do not bother to present here due to the fact that it is perhaps the best known matrix logic), and the Asenjo–Priest’s 3-valued logic \(\mathbf {LP}\), which is defined based on the 3-element Kleene algebra.
Definition 7
The 3-element Kleene algebra is the structure
where the functions \(f^{\lnot }_{\mathbf {K}}, f^{\wedge }_{\mathbf {K}}, f^{\vee }_{\mathbf {K}}\) are as follows
Definition 8
([1, 23]) A 3-valued \(\mathbf {LP}\)-matrix is a structure
such that \(\langle \{ {\mathbf {t}}, {\mathbf {i}}, {\mathbf {f}}\}, \{ f^{\lnot }_{\mathbf {K}}, f^{\wedge }_{\mathbf {K}}, f^{\vee }_{\mathbf {K}} \} \rangle \) is the 3-element Kleene algebra.
With these definitions we are now in a position to ask which formulations of Explosion are valid, and which are invalid in classical logic and in \(\mathbf {LP}\). However, for this question to be meaningful, it is necessary to clarify how matrix logics validate or invalidate both inferences and meta-inferences. Notice that, below, \(\vDash _{\mathscr {M}}\) is a substitution-invariant Tarskian consequence relation over \(\mathscr {L}\), whence \((FOR(\mathscr {L}), \vDash _{\mathscr {M}})\) is a Tarskian logic. In addition to that, when some logic \(\mathbf {L}\) is induced by a matrix \(\mathscr {M}\), we may interchangeably refer to \(\vDash _{\mathscr {M}}\) as \(\vDash _{\mathscr {\mathbf {L}}}\).
Definition 9
For \(\mathscr {M}\) a matrix, an \(\mathscr {M}\)-valuation v satisfies a sequent or inference \(\varGamma \Rightarrow A\) (written \(v \vDash _{\mathscr {M}} \varGamma \Rightarrow A\)) iff if \(v[\varGamma ] \subseteq \mathscr {D}\), then \(v(A) \in \mathscr {D}\). A sequent or inference \(\varGamma \Rightarrow A\) is \(\mathscr {M}\)-valid (written \(\vDash _{\mathscr {M}} \varGamma \Rightarrow A\)) iff \(v \vDash _{\mathscr {M}} \varGamma \Rightarrow A\), for all \(\mathscr {M}\)-valuations v.
Definition 10
For \(\mathscr {M}\) a matrix, an \(\mathscr {M}\)-valuation v satisfies a meta-sequent or meta-inference \(\varGamma \Rightarrow ^{1} A\) (written \(v \vDash _{\mathscr {M}} \varGamma \Rightarrow ^{1} A\)) iff if \(v \vDash _{\mathscr {M}} B\), for all \(B \in \varGamma \), then \(v \vDash _{\mathscr {M}} A\). A meta-sequent or meta-inference \(\varGamma \Rightarrow ^{1} A\) is \(\mathscr {M}\)-valid (written \(\vDash _{\mathscr {M}} \varGamma \Rightarrow ^{1} A\)) iff if \(v \vDash _{\mathscr {M}} B\), for all \(B \in \varGamma \), then \(v \vDash _{\mathscr {M}} A\), for all \(\mathscr {M}\)-valuations v.
Recall that in the last definition e.g. B stands for a sequent, i.e. an object of the form \(\varSigma \Rightarrow C\), and therefore e.g. \(v \vDash _{\mathscr {M}} B\) should be read as \(v \vDash _{\mathscr {M}} \varSigma \Rightarrow C\). Accordingly, when \(\varSigma \) is empty, it should be read as \(\vDash _{\mathscr {M}} \emptyset \Rightarrow C\), which for matters of readability we write as \(\vDash _{\mathscr {M}} {\Rightarrow }C\).
Given these definitions it is easy to observe the following facts.
Fact 3.1
Classical logic \(\mathbf {CL}\) validates both the inferential and the meta-inferential formulation of Explosion, i.e. \(\vDash _{\mathbf {CL}} A, \lnot A \Rightarrow B\) and \(\vDash _{\mathbf {CL}} A, \lnot A \Rightarrow ^{1} B\).
Proof
These two facts are straightforwardly verified by noticing that there is no \(\mathbf {CL}\)-valuation v such that \(v(\{ A, \lnot A \}) \subseteq \{ {\mathbf {t}}\}\), i.e. that there is no \(\mathbf {CL}\)-valuation v such that \(v \vDash _{\mathbf {CL}} {\Rightarrow }A\) and \(v \vDash _{\mathbf {CL}} {\Rightarrow }\lnot A\). From this we infer, on the one hand, that there is no \(\mathbf {CL}\)-valuation v such that \(v(\{ A, \lnot A \}) \subseteq \{ {\mathbf {t}}\}\) and \(v(B) \notin \{ {\mathbf {t}}\}\), whence \(\vDash _{\mathbf {CL}} A, \lnot A \Rightarrow B\). And, on the other hand, that there is no \(\mathbf {CL}\)-valuation v such that \(v \vDash _{\mathbf {CL}} {\Rightarrow }A\) and \(v \vDash _{\mathbf {CL}} {\Rightarrow }\lnot A\) and \(v \nvDash _{\mathbf {CL}} {\Rightarrow }B\), whence \(\vDash _{\mathbf {CL}} A, \lnot A \Rightarrow ^{1} B\). \(\square \)
Fact 3.2
The logic \(\mathbf {LP}\) invalidates both the inferential and the meta-inferential formulation of Explosion, i.e. \(\nvDash _{\mathbf {LP}} A, \lnot A \Rightarrow B\) and \(\nvDash _{\mathbf {LP}} A, \lnot A \Rightarrow ^{1} B\).
Proof
To prove this facts, it is routine to construct an \(\mathbf {LP}\)-valuation v such that \(v(A) = v(\lnot A) = {\mathbf {i}}\), while \(v(B) = {\mathbf {f}}\). From this we infer, on the one hand, that v is a valuation such that \(v(\{ A, \lnot A \}) \subseteq \{ {\mathbf {t}}, {\mathbf {i}}\}\) and \(v(B) \notin \{ {\mathbf {t}}, {\mathbf {i}}\}\), whence \(\nvDash _{\mathbf {LP}} A, \lnot A \Rightarrow B\). On the other hand, we infer that v is a valuation such that \(v \vDash _{\mathbf {LP}} {\Rightarrow }A\) and \(v \vDash _{\mathbf {LP}} {\Rightarrow }\lnot A\), while \(v \nvDash _{\mathbf {LP}} {\Rightarrow }B\), whence we conclude that \(\nvDash _{\mathbf {LP}} A, \lnot A \Rightarrow ^{1} B\). \(\square \)
3.2 q-Matrix Logics and p-Matrix Logics
Two interesting generalizations of Tarskian consequence relations appeared in the last two decades, the notion of q-consequence relation, due to Malinowski [19] and the notion of p-consequence relation, due to Frankowski [12]. As Wansing and Shramko clearly explain in [31], the corresponding relation of q-logic is devised to qualify as valid derivations of true sentences from non-refuted premises (understood as hypotheses), whereas the notion of p-logic is devised to qualify as valid derivations of conclusions whose degree of strength (understood as the conviction in its truth) is smaller than that of the premises. We define these notions formally as follows.
Definition 11
([19]) A q-consequence relation over a propositional language \(\mathscr {L}\) is a relation \(\vDash \ \subseteq \wp (FOR(\mathscr {L})) \times FOR(\mathscr {L})\) obeying the following conditions for all \(A \in FOR(\mathscr {L})\) and for all \(\varGamma , \varDelta \subseteq FOR(\mathscr {L})\):
-
1.
If \(\varGamma \vDash A\) and \(\varGamma \subseteq \varGamma '\), then \(\varGamma ' \vDash A\) (Monotonicity)
-
2.
\(\varGamma \cup \{ B \mid \varGamma \vDash B \} \vDash A\) iff \(\varGamma \vDash A\) (Quasi-closure)
Definition 12
([19]) A q-logic over a propositional language \(\mathscr {L}\) is an ordered pair \((FOR(\mathscr {L}), \vDash )\), where \(\vDash \) is a substitution-invariant q-consequence relation.
Definition 13
([12]) A p-consequence relation over a propositional language \(\mathscr {L}\) is a relation \(\vDash \ \subseteq \wp (FOR(\mathscr {L})) \times FOR(\mathscr {L})\) obeying the following conditions for all \(A \in FOR(\mathscr {L})\) and for all \(\varGamma , \varDelta \subseteq FOR(\mathscr {L})\):
-
1.
\(\varGamma \vDash A\) if \(A \in \varGamma \) (Reflexivity)
-
2.
If \(\varGamma \vDash A\) and \(\varGamma \subseteq \varGamma '\), then \(\varGamma ' \vDash A\) (Monotonicity)
Definition 14
([12]) A p-logic over a propositional language \(\mathscr {L}\) is an ordered pair \((FOR(\mathscr {L}), \vDash )\), where \(\vDash \) is a substitution-invariant p-consequence relation.
Notice, moreover, that q-logics fail to validate Reflexivity, while p-logics fail to validate Cut and, thus, are both non-Tarskian or substructural logics.
Semantically speaking, q-logics and p-logics can be obtained from structures called, respectively, q-matrices and p-matrices, by similar means than Tarskian logics are obtained from regular matrices. Whence, we may refer to them as q-matrix logics and p-matrix logics.
Definition 15
([19]) For \(\mathscr {L}\) a propositional language, an \(\mathscr {L}\)-q-matrix is a structure \(\langle \mathscr {V}, \mathscr {D}^{+}, \mathscr {D}^{-}, \mathscr {O} \rangle \), such that \(\langle \mathscr {V}, \mathscr {O} \rangle \) is an algebra of the same similarity type as \(\mathscr {L}\), with universe \(\mathscr {V}\) and a set of operations \(\mathscr {O}\), where \(\mathscr {D}^{+}, \mathscr {D}^{-} \subseteq \mathscr {V}\) and \(\mathscr {D}^{+} \cap \mathscr {D}^{-} = \emptyset \).
Definition 16
([13]) For \(\mathscr {L}\) a propositional language, an \(\mathscr {L}\)-p-matrix is a structure \(\langle \mathscr {V}, \mathscr {D}^{+}, \mathscr {D}^{-}, \mathscr {O} \rangle \), such that \(\langle \mathscr {V}, \mathscr {O} \rangle \) is an algebra of the same similarity type as \(\mathscr {L}\), with universe \(\mathscr {V}\) and a set of operations \(\mathscr {O}\), where \(\mathscr {D}^{+}, \mathscr {D}^{-} \subseteq \mathscr {V}\) and \(\mathscr {D}^{+} \subseteq \mathscr {D}^{-}\).
A word on how q- and p-matrices generalize the usual notion of a logical matrix is in order. In a usual logical matrix \(\langle \mathscr {V}, \mathscr {D}, \mathscr {O} \rangle \) the truth-values of the matrix, i.e. the elements of \(\mathscr {V}\), are presented in a dichotomized way. By this we mean that they either belong to \(\mathscr {D}\)—and, hence, are designated—or they belong to \(\mathscr {V} \setminus \mathscr {D}\)—and, hence, are anti-designated.
Contrary to this, q- and p-matrices start from a non-dichotomized classification of the truth-values of the given matrix—i.e. the members of \(\mathscr {V}\)—letting them belong to two sets, which we here call \(\mathscr {D}^{+}\) and \(\mathscr {D}^{-}\).Footnote 6 We will, then, allow these sets to be jointly non-exhaustive and mutually non-exclusive. Paradigmatically, the first note of this generalization is associated with q-matrices, where it is allowed that \(\mathscr {D}^{+} \cup \mathscr {D}^{-} \ne \mathscr {V}\) (see e.g. [20, p. 12]). Analogously, the second note of this generalization is associated with p-matrices, where it is allowed that \(\mathscr {D}^{+} \cap \mathscr {D}^{-} \ne \emptyset \) (see e.g. [12, p. 45]).
From a purely abstract point of view, the sets \(\mathscr {D}^{+}\) and \(\mathscr {D}^{-}\) need not be attached any particular philosophical interpretation and, thus, the symbols \(+\) and − are taken by us to be arbitrary. Notwithstanding this, e.g. in the context of Malinowski’s discussion of q-matrices, they are usually taken to represent, respectively, the set of accepted and rejected elements (see [21]). Whereas, in the context of Frankowski’s discussion of p-matrices they are usually taken to represent, respectively, the set of values representing the degree of strength of the premises and the set of values representing the degree of strength of the conclusion (see [12]). Furthermore, in the context of Wansing and Shramko’s discussion of q-matrices, those truth-values belonging to \(\mathscr {D}^{+}\) are identified as representatives of a generalized notion of truth and those truth-values belonging to \(\mathscr {D}^{-}\) as representatives of a generalized notion of falsity (see [32, p. 195]).
There are two 3-valued q- and p-matrix logics associated to the 3-element Kleene algebra that are discussed in the literature, which we would like to present in connection to our ongoing investigation: the logic \(\mathbf {TS}\) and the logic \(\mathbf {ST}\).
Definition 17
([8, 21]) A 3-valued \(\mathbf {TS}\)-matrix is a q-matrix
such that \(\langle \{ {\mathbf {t}}, {\mathbf {i}}, {\mathbf {f}}\}, \{ f^{\lnot }_{\mathbf {K}}, f^{\wedge }_{\mathbf {K}}, f^{\vee }_{\mathbf {K}} \} \rangle \) is the 3-element Kleene algebra.
Definition 18
([8]) A 3-valued \(\mathbf {ST}\)-matrix is a p-matrix
such that \(\langle \{ {\mathbf {t}}, {\mathbf {i}}, {\mathbf {f}}\}, \{ f^{\lnot }_{\mathbf {K}}, f^{\wedge }_{\mathbf {K}}, f^{\vee }_{\mathbf {K}} \} \rangle \) is the 3-element Kleene algebra.
The former is discussed by e.g. Cobreros, Ripley, Egré and van Rooij in [8], and also by Chemla, Egré and Spector in [7] in the context of the more general discussion of what represents a ‘respectable’ consequence relation between formulae. Moreover, it was also discussed by Grzegorz Malinowski in [21] as a tool to model empirical inference with the aid of the 3-valued Kleene algebra, and more recently was also stressed by Rohan French in [14], in connection with the paradoxes of self-reference.
The latter is discussed by Cobreros, Ripley, Egré and van Rooij in several papers (among them [8, 9, 26, 27]), with the aim of solving the riddles raised by paradoxical phenomena, vagueness, and much more. It must be pointed out that it was also entertained by Girard in [16] as a 3-valued interpretation of the sequent calculus \(\mathbf {LK}\) for classical propositional logic, without the Cut rule.
Once more, equipped with these definitions we are now in a position to ask which formulations of Explosion are valid, and which are invalid in the q-matrix logic \(\mathbf {TS}\) and the p-matrix logic \(\mathbf {ST}\). Yet again, for this question to be meaningful, it is necessary to clarify how q- and p-matrix logics validate or invalidate both inferences and meta-inferences—following e.g. [12] and [32, p. 196]. Notice that, below, \(\vDash _{\mathscr {M}}\) is a substitution-invariant q-consequence (respectively, p-consequence) relation, whence \((FOR(\mathscr {L}), \vDash _{\mathscr {M}})\) is a q-logic (respectively, a p-logic). In addition to that, when some q- or p-logic \(\mathbf {L}\) is induced by, respectively, a q- or p- matrix \(\mathscr {M}\), we may interchangeably refer to \(\vDash _{\mathscr {M}}\) as \(\vDash _{\mathscr {\mathbf {L}}}\).
Definition 19
For \(\mathscr {M}\) a q-matrix, an \(\mathscr {M}\)-valuation v satisfies a sequent or inference \(\varGamma \Rightarrow A\) (written \(v \vDash _{\mathscr {M}} \varGamma \Rightarrow A\)) iff if \(v[\varGamma ] \cap \mathscr {D}^{-} = \emptyset \), then \(v(A) \in \mathscr {D}^{+}\). For \(\mathscr {M}\) a p-matrix, an \(\mathscr {M}\)-valuation v satisfies a sequent or inference \(\varGamma \Rightarrow A\) (written \(v \vDash _{\mathscr {M}} \varGamma \Rightarrow A\)) iff if \(v[\varGamma ] \subseteq \mathscr {D}^{+}\), then \(v(A) \in \mathscr {D}^{-}\).Footnote 7 For \(\mathscr {M}\) a q-matrix or p-matrix, a sequent or inference \(\varGamma \Rightarrow A\) is \(\mathscr {M}\)-valid (written \(\vDash _{\mathscr {M}} \varGamma \Rightarrow A\)) iff \(v \vDash _{\mathscr {M}} \varGamma \Rightarrow A\), for all \(\mathscr {M}\)-valuations v.
Definition 20
For \(\mathscr {M}\) a q-matrix or p-matrix, an \(\mathscr {M}\)-valuation v satisfies a meta-sequent or meta-inference \(\varGamma \Rightarrow ^{1} A\) (written \(v \vDash _{\mathscr {M}} \varGamma \Rightarrow ^{1} A\)) iff if \(v \vDash _{\mathscr {M}} B\), for all \(B \in \varGamma \), then \(v \vDash _{\mathscr {M}} A\). A meta-sequent or meta-inference \(\varGamma \Rightarrow ^{1} A\) is \(\mathscr {M}\)-valid (written \(\vDash _{\mathscr {M}} \varGamma \Rightarrow ^{1} A\)) iff if \(v \vDash _{\mathscr {M}} B\), for all \(B \in \varGamma \), then \(v \vDash _{\mathscr {M}} A\), for all \(\mathscr {M}\)-valuations v.
From these definitions the following facts follow.
Fact 3.3
([8]) \(\mathbf {TS}\) is a non-reflexive, and thus a substructural, logic.
Fact 3.4
([8]) \(\mathbf {ST}\) is a non-transitive, and thus a substructural, logic.
Fact 3.5
The logic \(\mathbf {TS}\) invalidates the inferential formulation of Explosion, i.e. \(\nvDash _{\mathbf {TS}} A, \lnot A \Rightarrow B\), but it validates the meta-inferential formulation of Explosion, i.e. \(\vDash _{\mathbf {TS}} A, \lnot A \Rightarrow ^{1} B\).
Proof
To prove that \(\nvDash _{\mathbf {TS}} A, \lnot A \Rightarrow B\) construct a \(\mathbf {TS}\)-valuation v such that \(v(A) = v(\lnot A) = {\mathbf {i}}\), i.e. \(v(\{ A, \lnot A \}) = \{ {\mathbf {i}}\}\), while \(v(B) = {\mathbf {f}}\). From this we infer that v is a valuation such that \(v(\{ A, \lnot A \}) \cap \{ {\mathbf {f}}\} = \emptyset \) and \(v(B) \notin \{ {\mathbf {t}}\}\), whence \(\nvDash _{\mathbf {TS}} A, \lnot A \Rightarrow B\).
To prove that \(\vDash _{\mathbf {TS}} A, \lnot A \Rightarrow ^{1} B\), suppose for reductio that \(\nvDash _{\mathbf {TS}} A, \lnot A \Rightarrow ^{1} B\). Then, there should be a \(\mathbf {TS}\)-valuation v, such that \(v \vDash _{\mathbf {TS}} {\Rightarrow }A\) and \(v \vDash _{\mathbf {TS}} {\Rightarrow }\lnot A\), while \(v \nvDash _{\mathbf {TS}} {\Rightarrow }B\). Such a valuation will require that \(v(A) = {\mathbf {t}}= v(\lnot A)\), which is impossible. Whence, we conclude \(\vDash _{\mathbf {TS}} A, \lnot A \Rightarrow ^{1} B\). \(\square \)
Fact 3.6
([4]) The logic \(\mathbf {ST}\) validates the inferential formulation of Explosion, i.e. \(\vDash _{\mathbf {ST}} A, \lnot A \Rightarrow B\), but it invalidates the meta-inferential formulation of Explosion, i.e. \(\nvDash _{\mathbf {ST}} A, \lnot A \Rightarrow ^{1} B\).
Proof
To prove that \(\vDash _{\mathbf {ST}} A, \lnot A \Rightarrow B\), suppose for reductio that \(\nvDash _{\mathbf {ST}} A, \lnot A \Rightarrow B\). Then, there should be an \(\mathbf {ST}\)-valuation v, such that \(v(\{ A, \lnot A \}) \subseteq \{ {\mathbf {t}}\}\), while \(v(B) \notin \{ {\mathbf {t}}, {\mathbf {i}}\}\). Such a valuation will require that \(v(A) = {\mathbf {t}}= v(\lnot A)\), which is impossible. Whence, we conclude \(\vDash _{\mathbf {ST}} A, \lnot A \Rightarrow B\).
To prove that \(\nvDash _{\mathbf {ST}} A, \lnot A \Rightarrow ^{1} B\) construct an \(\mathbf {ST}\)-valuation v such that \(v(A) = v(\lnot A) = {\mathbf {i}}\), i.e. \(v(\{ A, \lnot A \}) = \{ {\mathbf {i}}\}\), while \(v(B) = {\mathbf {f}}\). From this we infer that v is a valuation such that \(v \vDash _{\mathbf {ST}} {\Rightarrow }A\) and \(v \vDash _{\mathbf {ST}} {\Rightarrow }\lnot A\), while \(v \nvDash _{\mathbf {ST}} {\Rightarrow }B\), whence \(\nvDash _{\mathbf {ST}} A, \lnot A \Rightarrow ^{1} B\). \(\square \)
Before moving on, it might be worth noticing—as pointed out by an anonymous referee—that according to \(\mathbf {TS}\) and \(\mathbf {ST}\) the meta-inferential formulation of Explosion is closely related to a restricted form of Cut. To be more precise, given these systems validate e.g. the rule of right Weakening \([\textit{WR}]\) and also the left introduction rule for negation \([{\lnot }L]\), it is true that the meta-inferential formulation of Explosion is equivalent to a restricted form of Cut—indeed, of both the additive \([\textit{Cut}^{\mathrm {A}}]\) or the multiplicative \([\textit{Cut}^{\mathrm {M}}]\) version of CutFootnote 8—where the side formulae are empty.Footnote 9
We can, in fact, provide more general facts from which the previous can be seen as corollaries. We do think that, nevertheless, giving the proper counterexamples for the particular cases above is illustrative, as these logics are not so commonly mentioned in the literature about paraconsistent logics.
Fact 3.7
\(\mathbf {TS}\) has no valid inferences or sequents.
Proof
Consider an arbitrary inference or sequent \(\varGamma \Rightarrow A\), and consider a \(\mathbf {TS}\)-valuation v, such that v assigns the value \({\mathbf {i}}\) to every propositional variable of \(\mathscr {L}\). Given \(\mathbf {TS}\) is a q-matrix based on the 3-valued Kleene algebra, it is easy to see by looking at the operations of the algebra that if every propositional variable p is such that \(v(p) = {\mathbf {i}}\), then every formula C is such that \(v(C) = {\mathbf {i}}\), and in particular for every \(B \in \varGamma , v(B) = {\mathbf {i}}\). Now, it only remains to notice that v is a \(\mathbf {TS}\)-valuation such that \(v[\varGamma ] \cap \{ {\mathbf {f}}\} = \emptyset \), but \(v(A) \notin \{ {\mathbf {t}}\}\), whence \(\nvDash _{\mathbf {TS}} \varGamma \Rightarrow A\). Since \(\varGamma \Rightarrow A\) was arbitrary, we may conclude that \(\mathbf {TS}\) has no valid inferences or sequents. \(\square \)
Fact 3.8
([16, 26]) \(\mathbf {ST}\) and \(\mathbf {CL}\) have the same set of valid inferences or sequents.
About these logics we shall mention, in addition to the previous remarks, that in [4, 11, 25] it is shown that—through some suitable translation—the set of valid inferences in \(\mathbf {LP}\) coincides with the set of valid meta-inferences in \(\mathbf {ST}\), while in [14] it is conjectured that—again, through some suitable translation—the set of valid inferences in \(\mathbf {{K}_{3}}\), i.e. Strong Kleene logic,Footnote 10 coincides with the set of valid meta-inferences in \(\mathbf {TS}\). As Francesco Paoli pointed out to us, this conjecture was shown to be true, in light of the results proved in [33].
4 Philosophical Reflections
The previous discussion dealt with classical logic and three systems which, in light of the previously proposed criterion, might be legitimately called paraconsistent.
Certainly, that classical logic is not, but \(\mathbf {LP}\) is paraconsistent should not surprise anyone, since these are well-known facts. Nevertheless, given our proposal, the previous remarks allow to offer a new look at the these systems. In this regard, we will say that \(\mathbf {LP}\), as well as \(\mathbf {CL}\) adopt a uniform policy with regard to paraconsistency. We mean with this that, just like \(\mathbf {CL}\) is not paraconsistent at either the inferential or the meta-inferential level, \(\mathbf {LP}\) is both paraconsistent at the inferential and the meta-inferential level.
These remarks about uniformity suggest that it is reasonable to ask whether or not it is possible to have logics which have a non-uniform policy towards paraconsistency. A positive answer to this question has been offered in the previous sections. Two examples of the meaningfulness of this alternative are the substructural logics \(\mathbf {TS}\) and \(\mathbf {ST}\). The former is paraconsistent, although it is not uniformly so, for it is paraconsistent at the inferential level, but not at the meta-inferential level. The latter is paraconsistent, although it is also not uniformly so, for it is paraconsistent at the meta-inferential level, but not at the inferential level.
Let us now comment on two philosophically discussions where the above remarks can have some interesting repercussions. Claiming that there are some paraconsistent logics which give a uniform and other that have a non-uniform policy with regard to the validity of Explosion is relevant to the discussion of logical pluralism: different levels of logical consequence can give different answers about the validity of a certain inference, rule, or scheme—in the case that concerns us, about Explosion. But, of course, these remarks can be generalized. As Barrio, Rosenblatt and Tajer [4] have shown, meta-inferential validity in \(\mathbf {ST}\) coincides (through some suitable translation) with inferential validity in \(\mathbf {LP}\). If we also take into account that Cobreros, Ripley, Egré and van Rooij proved that \(\mathbf {ST}\) and \(\mathbf {CL}\) have the same set of valid inferences or sequents, this result can be interpreted conceptually as the admission that two rival logics are both right, i.e. \(\mathbf {CL}\) could be a correct response at the level of inferences and \(\mathbf {LP}\) could be a right answer at the level of meta-inferences.
Obviously, we are not claiming that cases in which the inferential and the meta-inferential notion of validity come apart are a proof of logic pluralism. It is also possible to support the view according to which meta-inferential validity imposes conditions on inferential validity, as e.g. Dicher and Paoli [11] seem to maintain. Or that meta-inferential validity has no weight, for the only thing that matters is inferential validity logic, as Ripley and the defenders of \(\mathbf {ST}\) seem to maintain. Instead, we affirm that logics like \(\mathbf {ST}\) and \(\mathbf {TS}\) open the possibility of adopting a pluralistic attitude about logic: depending on what level we are interested, different appropriate answers could be given.
Another important issue that the present discussion might have consequences for, is the question about the meaning of logical connectives, and—most importantly—the relation that their meanings have with their behavior in various inferential levels. For example, in \(\mathbf {ST}\) modus ponens is valid for the conditional at the inferential level, but it is not a valid rule at the meta-inferential level, as Zardini [35] points out. If the meaning of a logical connective is given by the valid inferences in which it is involved, logics as \(\mathbf {ST}\) seem to admit connectives with different meanings at different inferential levels.
Moreover, for inferentialists the question arises as to whether or not the meta-inferential properties of the logics (at least partly) determine the meaning of the connectives of the given system, as Dicher [10] seems to suggest. That is, if we compare the connectives of, for example, \(\mathbf {TS}\), \(\mathbf {ST}\) and \(\mathbf {CL}\) proof-theoreticallyFootnote 11—following the remarks of e.g. [14]—do they have the same meaning, given they are equipped with the same set of operational rules? All these questions are of deep philosophical import, and we hope to discuss them in future work.
4.1 Answers to Some Possible Objections
To conclude this section, let us evaluate a number of objections that might be raised against our approach. We consider, initially, two objections which question that \(\mathbf {TS}\) and \(\mathbf {ST}\) are genuine paraconsistent logics. After that, we consider an objection that questions the extent to which our proposed criterion of paraconsistency is reasonable.
The first objection aims at \(\mathbf {TS}\), and it concerns whether or not it is a paraconsistent logic in a trivial sense. Everyone would accept (even if they do not accept our proposed characterization of a paraconsistent logic) that an inferential consequence relation with no valid inferences is paraconsistent. For Explosion is a (schematic) inference, and if no (schematic) inference is valid, a fortiori Explosion will be invalid for that logical consequence relation. This is, in fact, the situation with inferential validity in \(\mathbf {TS}\).
Now, the objection goes: in which sense is a consequence relation with no valid inferences a genuine consequence relation? It seems that it is as meaningless as a consequence relation as the empty set itself, and—as Chemla, Egré and Spector suggest in [7]—it will be definitely non-standard to call the empty set a genuine consequence relation, let alone a logic. Furthermore, if a consequence relation with no valid inferences is not a genuine consequence relation, it hardly can represent a genuine paraconsistent consequence relation.
To this we reply by noticing, as is done in [7], that the fact that \(\mathbf {TS}\) has no valid inferences does not allow to identify its inferential consequence relation with the empty set. For, in a certain sense, the fact that \(\mathbf {TS}\) has no valid inferences is dependent on the language being employed. Were we to have a constant \(\top \) representing the value \({\mathbf {t}}\), and a constant \(\bot \) representing the value \({\mathbf {f}}\), then e.g. the following inferences will be valid in the referred extension of \(\mathbf {TS}\) (and, thus, of the 3-valued Kleene algebra)
More importantly, the addition of such constants to \(\mathbf {TS}\) will not imply the validity of Explosion at the inferential level. Therefore, \(\mathbf {TS}\) is a paraconsistent logic in a meaningful and non-trivial sense.
The second objection aims at \(\mathbf {ST}\), whose peculiarly non-uniform way of being paraconsistent has been called into question in some recent papers like [4, 11], causing an impasse regarding the qualification \(\mathbf {ST}\) deserves as a classical or non-classical logic.
On the one hand, some of its advocates (i.e. Cobreros, Ripley, Egré and van Rooij) seem to claim that, given \(\mathbf {ST}\) coincides with \(\mathbf {CL}\) at the inferential level, then \(\mathbf {ST}\) deserves to be referred nothing more than an alternative presentation of classical logic. This argumentative line appears to be supported by the fact that J.-Y. Girard employed in [16] the \(\mathbf {ST}\) 3-valued q-matrix to give a presentation of classical logic where Cut fails.
On the other hand, some of its critiques, like Barrio, Rosenblatt and Tajer in [4] and Dicher and Paoli in [11] appear to think that \(\mathbf {ST}\) should not be identified with classical logic, but with \(\mathbf {LP}\). This argumentative line appears to be supported also by the fact that e.g. Cobreros, Ripley, Egré and van Rooij usually present \(\mathbf {ST}\) as Gentzen’s sequent calculus \(\mathbf {LK}\) for classical logic, minus the structural Cut rule. But if they prefer to talk about \(\mathbf {ST}\) as a sequent calculus system, then they are prone to the following imputation due to Dicher and Paoli
Notice, however, that in a sequent calculus all of the action takes place at the level of sequent-to-sequent rules, whereby from one or more sequents (intuitively understood as ‘inferences’) we derive more sequents (i.e., more ‘inferences’). Which is to say, the action takes place at the level of metainferences. [11, p. 8, our emphasis]
The result of the previous dialectic is, then, that some say that \(\mathbf {ST}\) is not paraconsistent, but is classical, because the only thing that matters is inferential validity and at that level \(\mathbf {ST}\) coincides with \(\mathbf {CL}\), whereas some others say that \(\mathbf {ST}\) is paraconsistent, but is not classical, because the only thing that matters is meta-inferential validity and at that level \(\mathbf {ST}\) coincides with \(\mathbf {LP}\).
We stand in the middle: we take that both inferential and meta-inferential validity matter. Since both matter, then particularly meta-inferential validity matters and thus we think that \(\mathbf {ST}\) deserves to be taken as a genuine paraconsistent logic. But do we draw a symmetric conclusion and claim that \(\mathbf {ST}\) is classical? No. This might bother some objectors, and to the consideration of their potential objection we now turn.
Thus, the third objection concerns the extent to which our proposed criterion of paraconsistency is reasonable, and would run roughly as follows. It is unreasonable to say that a logic is paraconsistent if either its inferential or its meta-inferential consequence is, because this is an instance of a more general criterion that we would not accept, for it has instances that we would reject. Namely, the general criterion that
A logic is X if either its inferential or its meta-inferential consequence is X
Now, the objection may continue, if X is ‘classical’, then we have just said that it would not be reasonable to accept that a logic is classical if e.g. its inferential consequence is not classical, but its meta-inferential consequence is classical.
To this we reply as follows. First of all, by claiming that a logic is paraconsistent if either its inferential or its meta-inferential consequence is we are not necessarily committed to accept the general criterion that a logic is X if either its inferential or its meta-inferential consequence is X. This is so, just like accepting an instance of the Law of Excluded Middle (e.g. ‘Either Goldbach’s Conjecture is true, or Goldbach’s Conjecture is false’) does not necessarily commit oneself to the unrestricted acceptance of the Law of Excluded Middle, for one may think that there are cases in which it may fail to hold (e.g. future contingents, etc.).
Finally, we do in fact think that there is a reason to refrain from adopting the general criterion, i.e. that some of its instances are wrong, in particular, the instance where X is ‘classical’. We are of the opinion that a logic being classical at some inferential level does not propagate to a qualification of the entire logic, whereas a logic being non-classical—and, in particular, paraconsistent—does propagate to a qualification of the entire logic. The asymmetry resides, mainly, in the fact that being classical is a characteristic that requires the fulfillment of certain inferential features, while being non-classical and in particular paraconsistent is a characteristic that requires the non-fulfillment of certain inferential features. As is stressed by Ripley—in the quote of his that we mentioned in Sect. 1—paraconsistency is a nonentailment claim, whereas it appears that classicality is an entailment claim. For this reason, it is reasonable for us to say that there is a difference in being paraconsistent, which requires that at least at some level (either the inferential or the meta-inferential) this nonentailment claim holds, and being classical, which seems to require that at all levels the entailment claim holds.
5 Conclusion
In the present paper we presented a new criterion for a logic to be paraconsistent: if either the inferential or the meta-inferential formulation of Explosion is invalid in \(\mathbf {L}\), then it is paraconsistent. Interestingly, we showed that a logic may invalidate one but validate the other, contrary to what happens in logics that have a uniform policy towards these matters, such as classical logic and \(\mathbf {LP}\) which, respectively, validate both and validate neither of the formulations. The study cases that we focused on were two substructural logics, \(\mathbf {TS}\) and \(\mathbf {ST}\); the former invalidates the inferential, but invalidates the meta-inferential formulation of Explosion, and the latter validates the inferential, but invalidates the meta-inferential version of Explosion. This strongly suggests that the proposed criterion is non-trivial and that there are interesting cases of logics which deserve to be called paraconsistent and that have not been regarded as such by the received view about paraconsistency, which focused exclusively on the inferential formulation(s) of Explosion. By focusing on versions of Explosion which are not inferential, but meta-inferential, we argued that Explosion comes in very different flavors and that it should be explored with greater generality that it has been, until now.
Let us close these conclusions with one final comment. In this paper we dealt with logical consequence between formulae and between sequents, thereby considering and evaluating inferential and meta-inferential versions of Explosion. But nothing prevents us from taking the investigation one step further and considering consequence relations between e.g. meta-sequents. Yet, again, if this is plausible, why stop there? We can definitely consider consequence relations between meta-meta-sequents, and so on and so forth. It can be easily seen how this procedure can be further reproduced, giving us a whole hierarchy of inferences concerned with the logical relations between objects of the lower level(s). In doing so it is interesting to, thus, look at inferences as having, or being of, some level represented by some ordinal number. Common inferences relating formulae are, therefore, of level 0, whereas meta-inferences are of level 1, meta-meta-inferences are of level 2, and so on and so forth. In this vein, Explosion might be regarded as a meta-schematic inference \(A, \lnot A \Rightarrow ^{\alpha } B\), for \(\alpha \) an ordinal. In other words, as a meta-scheme or scheme of schemes, i.e. a scheme that gives, for each ordinal, a schematic inference, namely the formulation of Explosion for that inferential level.
These surely are interesting directions to explore. A full exposition of them will require defining how big the hierarchy is and if it has a fixed point or not, how inferences at some peculiar levels (e.g. at limit ordinals) look, how do the formulations of Explosion beyond the meta-inferential level look, and many other technical and conceptual matters. Settling this issues is no doubt an interesting task, but one which demands an amount of space beyond the one available for this paper. We hope to investigate them in further research.
Notes
- 1.
In this paper we will be focusing on the inferential and the meta-inferential level, but when making our closing remarks in Sect. 5 we will point towards a plausible (although not developed here) more general conception of paraconsistency, which will require looking at many more levels.
- 2.
We shall notice that in [2] Avron takes this definition to, additionally, require that Cut is taken as a primitive rule. Something that—for the sake of generality—we do not demand here.
- 3.
Let us notice, additionally, that Humberstone calls Ex Falso Quodlibet what we call Explosion, but this is just a terminological and non-substantial issue.
- 4.
q-consequence relations and q-matrices were introduced by Grzegorz Malinowski in [19].
- 5.
p-consequence relations and p-matrices were introduced by Szymon Frankowski in [12].
- 6.
Here we will adopt this terminology—i.e. talk of \(\mathscr {D}^{+}\) and \(\mathscr {D}^{-}\)—introduced by [32], emphasizing that we will take q- and p-logics to be induced by different type of structures, i.e. respectively q- and p-matrices. In this vein, what will be distinctive of these type of structures will be the properties of the sets \(\mathscr {D}^{+}\) and \(\mathscr {D}^{-}\), as detailed in Definitions 15 and 16, respectively.
- 7.
Notice that this definition takes a p-logic to be induced by a p-matrix \(\langle \mathscr {V}, \mathscr {D}^{+}, \mathscr {D}^{-}, \mathscr {O} \rangle \) where it is assumed that \(\mathscr {D}^{+} \subseteq \mathscr {D}^{-}\), whence this last clause reads: “if \(v[\varGamma ] \subseteq \mathscr {D}^{+}\), then \(v(A) \in \mathscr {D}^{-}\)”. Now, as remarked by an anonymous referee, if the same p-logic is taken to be induced by a q-matrix \(\langle \mathscr {V}, \mathscr {D}^{+}, \mathscr {D}^{-}, \mathscr {O} \rangle \) where it is assumed that \(\mathscr {D}^{+} \cap \mathscr {D}^{-} = \emptyset \)—as is done e.g. in [32, p. 210]—then this last clause should read: “if \(v[\varGamma ] \subseteq \mathscr {D}^{+}\), then \(v(A) \notin \mathscr {D}^{-}\)”.
These considerations highlight that if the sets \(\mathscr {D}^{+}\) and \(\mathscr {D}^{-}\) of a q-matrix are taken to, respectively, represent a generalized notion of truth and a generalized notion of falsity—as in [32]—then with regard to valuations on the 3-element Kleene algebra, \(\mathbf {TS}\) and \(\mathbf {ST}\) can be interpreted as follows. \(\mathbf {TS}\) consequence can be understood as requiring that for all valuations, if the premises are non-false, then the conclusion is true; whereas \(\mathbf {ST}\) consequence can be understood as requiring that for all valuations, if the premises are true, then the conclusion is non-false.
- 8.
By these rules we refer to the following, respectively.
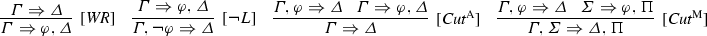
- 9.
Whence, the aforementioned equivalence is witnessed e.g. by the following derivation, where the application of \([\textit{Cut}]\) is a rightful instance of both \([\textit{Cut}^{\mathrm {A}}]\) and \([\textit{Cut}^{\mathrm {M}}]\).
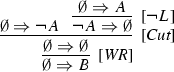
- 10.
That is, the matrix logic induced by the structure \(\mathscr {M}_{\mathbf {{K}_{3}}} = \langle \{ {\mathbf {t}}, {\mathbf {i}}, {\mathbf {f}}\}, \{ {\mathbf {t}}\}, \{ f^{\lnot }_{\mathbf {K}}, f^{\wedge }_{\mathbf {K}}, f^{\vee }_{\mathbf {K}} \} \rangle \), such that \(\langle \{ {\mathbf {t}}, {\mathbf {i}}, {\mathbf {f}}\}, \{ f^{\lnot }_{\mathbf {K}}, f^{\wedge }_{\mathbf {K}}, f^{\vee }_{\mathbf {K}} \} \rangle \) is the 3-element Kleene algebra.
- 11.
Along these lines, \(\mathbf {CL}\) can be proof-theoretically understood as Gentzen’s sequent calculi \(\mathbf {LK}\), \(\mathbf {TS}\) as \(\mathbf {LK}\) minus the structural rule of Reflexivity, and \(\mathbf {ST}\) as \(\mathbf {LK}\) minus the structural rule of Cut.
References
Asenjo, Florencio. 1966. A calculus of antinomies. Notre Dame Journal of Formal Logic 7 (1): 103–105.
Avron, Arnon. 1988. The semantics and proof theory of linear logic. Theoretical Computer Science 57 (2–3): 161–184.
Avron, Arnon. 1991. Simple consequence relations. Information and Computation 92 (1): 105–139.
Barrio, Eduardo, Lucas Rosenblatt, and Diego Tajer. 2015. The logics of strict-tolerant logic. Journal of Philosophical Logic 44 (5): 551–571.
Blok, Willem, and Bjarni Jónsson. 2006. Equivalence of consequence operations. Studia Logica 83 (1): 91–110.
Carnielli, Walter, and Marcelo Coniglio. 2016. Paraconsistent Logic: Consistency, Contradiction and Negation. Dordrecht: Springer.
Chemla, Emmanuel, Paul Egré, and Benjamin Spector. 2017. Characterizing logical consequence in many-valued logics. Journal of Logic and Computation 27 (7): 2193–2226.
Cobreros, Pablo, Paul Egré, David Ripley, and Robert van Rooij. 2012. Tolerant, classical, strict. Journal of Philosophical Logic 41 (2): 347–385.
Cobreros, Pablo, Paul Egré, David Ripley, and Robert van Rooij. 2014. Reaching transparent truth. Mind 122 (488): 841–866.
Dicher, Bogdan. 2016. A proof-theoretic defence of meaning-invariant logical pluralism. Mind 125 (499): 727–757.
Dicher, Bogdan, and Francesco Paoli. 2017. ST, LP, and Tolerant Metainferences. (Unpublished Manuscript).
Frankowski, Szymon. 2004. Formalization of a plausible inference. Bulletin of the Section of Logic 33 (1): 41–52.
Frankowski, Szymon. 2004. p-consequence versus q-consequence operations. Bulletin of the Section of Logic 33 (4): 197–207.
French, Rohan. 2016. Structural reflexivity and the paradoxes of self-reference. Ergo 3 (5): 113–131.
Gabbay, Dov. 1996. Labelled Deductive Systems. Oxford: Oxford University Press.
Girard, Jean-Yves. 1987. Proof Theory and Logical Complexity. Napoli: Bibliopolis.
Hansson, Sven Ove. 2016. Logic of belief revision. In The Stanford Encyclopedia of Philosophy, winter 2016 ed, ed. Edward N Zalta. Stanford University. http://plato.stanford.edu/archives/win2016/entries/logic-belief-revision/.
Humberstone, Lloyd. 2011. The Connectives. Cambridge: MIT Press.
Malinowski, Grzegorz. 1990. Q-consequence operation. Reports on Mathematical Logic 24 (1): 49–59.
Malinowski, Grzegorz. 2007. THAT p \(+\) q \(=\) c(onsequence). Bulletin of the Section of Logic 36 (1/2): 7–19.
Malinowski, Grzegorz. 2014. Kleene logic and inference. Bulletin of the Section of Logic 43 (1/2): 43–52.
Mares, Edwin, and Francesco Paoli. 2014. Logical consequence and the paradoxes. Journal of Philosophical Logic 43 (2–3): 439–469.
Priest, Graham. 1979. The logic of paradox. Journal of Philosophical logic 8 (1): 219–241.
Priest, Graham, Koji Tanaka, and Zach Weber. 2016. Paraconsistent logic. In The Stanford Encyclopedia of Philosophy, Winter 2016 ed, ed. Edward Zalta. Stanford University. http://plato.stanford.edu/archives/win2016/entries/logic-paraconsistent/.
Pynko, Alexej. 2010. Gentzens cut-free calculus versus the logic of paradox. Bulletin of the Section of Logic 39 (1/2): 35–42.
Ripley, David. 2012. Conservatively extending classical logic with transparent truth. The Review of Symbolic Logic 5 (02): 354–378.
Ripley, David. 2013. Paradoxes and failures of cut. Australasian Journal of Philosophy 91 (1): 139–164.
Ripley, David. 2015. Paraconsistent logic. Journal of Philosophical Logic 44 (6): 771–780.
Scott, Dana. 1971. On engendering an illusion of understanding. The Journal of Philosophy 68 (21): 787–807.
Shoesmith, David, and Timothy Smiley. 1978. Multiple-Conclusion Logic. Cambridge: Cambridge University Press.
Shramko, Yaroslav, and Heinrich Wansing. 2010. Truth values. In The Stanford Encyclopedia of Philosophy, Summer 2010 ed, ed. Edward Zalta. Stanford Uniersity. http://plato.stanford.edu/archives/sum2010/entries/truth-values/.
Shramko, Yaroslav, and Heinrich Wansing. 2011. Truth and Falsehood: An Inquiry into Generalized Logical Values. Dordrecht: Springer.
Stärk, Robert. 1991. A complete axiomatization of the three valued completion of logic programs. Journal of Logic and Computation 1 (6): 811–834.
Urbas, Igor. 1990. Paraconsistency. Studies in Soviet Thought 39 (3/4): 343–354.
Zardini, Elia. 2013. Naive modus ponens. Journal of Philosophical Logic 42 (4): 575–593.
Acknowledgements
The ideas contained in this paper were presented at the Work In Progress seminar of the Buenos Aires Logic Group, the XVI Trends in Logic conference, and the Kyoto Philosophical Logic Workshop II at Kyoto University. We are thankful to the members of those audiences for the discussion provided. We would also like to thank Rohan French, Andreas Fjellstad, Hitoshi Omori, Francesco Paoli, Graham Priest, Dave Ripley, Zach Weber and two anonymous reviewers for their helpful suggestions and comments on previous versions of this article. Finally, we are thankful to the editors of this volume, Walter Carnielli, and Jacek Malinowski, for their assistance through the editorial process.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2018 Springer Nature Switzerland AG
About this chapter
Cite this chapter
Barrio, E., Pailos, F., Szmuc, D. (2018). What is a Paraconsistent Logic?. In: Carnielli, W., Malinowski, J. (eds) Contradictions, from Consistency to Inconsistency. Trends in Logic, vol 47. Springer, Cham. https://doi.org/10.1007/978-3-319-98797-2_5
Download citation
DOI: https://doi.org/10.1007/978-3-319-98797-2_5
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-98796-5
Online ISBN: 978-3-319-98797-2
eBook Packages: Mathematics and StatisticsMathematics and Statistics (R0)