Abstract
We consider recent constructions of 1-out-of-N OT-extension from Kolesnikov and Kumaresan (CRYPTO 2013) and from Orrù et al. (CT-RSA 2017), based on binary error-correcting codes. We generalize their constructions such that q-ary codes can be used for any prime power q. This allows to reduce the number of base 1-out-of-2 OT’s that are needed to instantiate the construction for any value of N, at the cost of increasing the complexity of the remaining part of the protocol. We analyze these trade-offs in some concrete cases.
Access provided by CONRICYT-eBooks. Download conference paper PDF
Similar content being viewed by others
Keywords
These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.
1 Introduction
A K-out-of-N oblivious transfer, or \(\left( {\begin{array}{c}N\\ K\end{array}}\right) \)-OT, is a cryptographic primitive that allows a sender to input N messages and a receiver to learn exactly K of these with neither the receiver revealing which messages he has chosen to learn nor the sender revealing the other \(N-K\) input messages. This is a fundamental cryptographic primitive in the area of secure multiparty computation, and in fact [9] showed that any protocol for secure multiparty computation can be implemented if the OT functionality is available. However, the results in [6] indicate that OT is very likely to require a public key cryptosystem, and therefore implementing OT is relatively expensive. Unfortunately, well-known protocols such as Yao’s garbled circuits [13] and the GMW-compiler [5] rely on using a large number of independent instances of OT. It is therefore of interest to reduce the number of OT’s used in a protocol in an attempt to reduce the overall cost. This can be done using what is called OT-extensions, where a large number of OT’s are simulated by a much smaller number of base OT’s together with the use of cheaper symmetric crypto primitives, such as pseudorandom generators.
Beaver showed in [1] that OT-extension is indeed possible, but it was not before 2003 that an efficient \(\left( {\begin{array}{c}2\\ 1\end{array}}\right) \)-OT-extension protocol was presented by Ishai et al. in [7]. In addition, while this protocol had security against passive adversaries, subsequent has work showed that active security can be achieved at a small additional cost [8].
In [10], Kolesnikov and Kumaresan noticed that Ishai et al. were in essence relying on the fact that the receiver encodes its input as a codeword in a repetition code, and therefore one can generalize their idea by using other codes, such as the Walsh-Hadamard code, which not only obtains efficiency improvements for \(\left( {\begin{array}{c}2\\ 1\end{array}}\right) \)-OT-extension, but also allows to generalize the protocol into passively secure \(\left( {\begin{array}{c}N\\ 1\end{array}}\right) \)-OT-extension. In such an extension protocol the base OT’s are \(\left( {\begin{array}{c}2\\ 1\end{array}}\right) \)-OT’s, but the output consist of a number of \(\left( {\begin{array}{c}N\\ 1\end{array}}\right) \)-OT’s. In more recent work, Orrù et al. [12] transformed the protocol by [10] into an actively secure \(\left( {\begin{array}{c}N\\ 1\end{array}}\right) \)-OT-extension protocol by adding a “consistency check” which is basically a zero-knowledge proof that the receiver is indeed using codewords of the designated code to encode his selections. As shown in [12], 1-out-of-N oblivious transfer has a direct application to the problem of private set inclusion and, via this connection, to the problem of private set intersection. In fact this application requires only a randomized version of \(\left( {\begin{array}{c}N\\ 1\end{array}}\right) \)-OT, where the sender does not have input messages, but these are generated by the functionality and can be accessed on demand by the sender. The structure of the aforementioned OT extension protocols is especially well suited for this application, since such a randomized functionality is essentially implemented by the same protocol without the last step, where the sender would send its masked inputs to the receiver.
The aforementioned papers on \(\left( {\begin{array}{c}N\\ 1\end{array}}\right) \)-OT-extension relied on the use of binary linear codes, and the concrete parameters of the resulting construction, the number of OT’s and the value of N, are given respectively by the length and size of the binary linear code being used. Furthermore, the construction requires that the minimum distance of the code is at least the desired security parameter. Well-known bounds on linear codes, such as the Plotkin, Griesmer or Hamming bounds [11], provide lower bounds for the length of a code with certain size and minimum distance, and therefore these imply lower bounds on the number of base OT’s for the OT-extension protocol. In fact, even if we omit the requirement on the minimum distance, we can see that at least \(\log _2 N\) base OT’s are needed for those extension protocols.
In this paper, we discuss the use of q-ary linear codes, where q can be any power of a prime, as a way of reducing the number of required base OT’s in the 1-out-of-N OT-extension constructions mentioned above. We show that one can easily modify the protocol in [12] to work with q-ary codes, rather than just binary. Given that all parameters of the code still have the same significance for the construction and, in particular, N is still the size (the number of codewords) of the code, we obtain a reduction in the number of base OT’s required: indeed, for given fixed values N and d, the minimal length among all q-ary linear codes of size N and minimum distance d becomes smaller as q increases. In particular one can show cases where the lower bound of \(\log _2 N\) base OT’s can be improved even if we have relatively large minimum distance.
This improvement, however, comes at a cost: since we need to communicate elements of a larger field, the communication complexity of the OT-extension protocol (not counting the complexity of the base OT’s) increases. This increase is compensated to some extent by the fact that this communication complexity also depends on the number of base OT’s.
The concrete tradeoffs obtained by the use of q-ary codes depend of course on N and the security level. We show several examples comparing explicit results listed in [12] and the q-ary alternative achieving the same (or similar) N and security level. For example, for the largest value of N considered in [12] we show that by using a linear code over the finite field of 8 elements, we need less than half of the base OT’s, while the communication complexity increases only by \(33\%\).
When q is a power of two, we can show an improvement on the complexity of the consistency check that we use in the case of a general q. Namely, the consistency check in [12] works by asking the receiver, who has previously used the base OT’s to commit to both the codewords encoding his selections and some additional random codewords, to open sums of random subsets of these codewords. The natural way of generalizing this to a general prime power q is to ask the receiver to open random linear combinations over \({\mathbb {F}}_q\) of the codewords. However, in case q is a power of two, we show that it is enough to open random linear combinations over \({\mathbb {F}}_2\), i.e., sums, just as in [12] (naturally, this extends to the case where q is a power of p, where it would be enough to open combinations over \({\mathbb {F}}_p\)). The advantage of this generalization is of course that the verifier needs to send less information to describe the linear combinations that it requests to open, and in addition less computation is required from the committer to open these combinations.
We give a presentation of the protocol and its security proof that is inspired by a recent work on homomorphic universally composable secure commitments [2]. As noted in [12], there is a strong similarity between the OT-extension protocol constructions in the aforementioned works and several protocol constructions in a line of work on homomorphic UC commitments [2,3,4]. In the first part of the OT-extension protocol in [10], the base OT’s are used for the receiver to eventually create an additive 1-out-of-2 sharing of each coordinate in the codewords encoding his selection, so that the sender learns exactly one share of each. This is essentially the same as the committing phase of the passively secure homomorphic UC commitment proposed in [3] (one can say that the receiver from the OT-extension protocol has actually committed to his inputs at that point). In order to achieve active security, a consistency check was added in [4], which is basically the same as the one introduced in [12] in the context of OT-extension. Finally, [2] generalized this consistency check by proving that rather than requesting the opening of uniformly random linear combinations of codewords, these combinations can be determined by a hash function randomly selected from an almost universal family of hash functions. This leads to asymptotical complexity gains, both in terms of communication and computation (since one can use linear time encodable almost universal hash functions which can in addition be described by short seeds), but in our case it also allows us to give a unified proof of security in both the case where the linear combinations for the consistency check are taken over \({\mathbb {F}}_q\) and when they are taken over the subfield.
The work is structured as follows. After the preliminaries in Sect. 2, we present our OT-extension protocol and prove its security in Sect. 3. In Sect. 4, we show that the communication cost can be reduced by performing the consistency checks over a subfield, and finally Sect. 5 contains a comparison with previous protocols.
2 Preliminaries
This section contains the basic definitions needed to present and analyse the protocol for OT-extension.
2.1 Notation
Throughout this paper, q will denote a prime power and \({\mathbb {F}}_q\) a finite field of q elements. Every finite field has elements 0 and 1, and hence it will be natural to embed the set \(\{0,1\}\) in \({\mathbb {F}}_q\).Footnote 1 Bitstrings in \(\{0,1\}^n\) and vectors from \({\mathbb {F}}_q^n\) are denoted in boldface. The i-th coordinate of a vector or bitstring  is denoted \(b_i\).
is denoted \(b_i\).
For a bitstring  , we will use the notation
, we will use the notation  to denote the diagonal matrix in \({\mathbb {F}}_q^{n\times n}\) with entries from the vector
to denote the diagonal matrix in \({\mathbb {F}}_q^{n\times n}\) with entries from the vector  , i.e. the (i, i)-entry of
, i.e. the (i, i)-entry of  is \(b_i\). Note that for vectors
is \(b_i\). Note that for vectors  , the product
, the product  equals the componentwise product of
equals the componentwise product of  and
and  .
.
2.2 Linear Codes
Since our protocol depends heavily on linear codes, we recall here the basics of this concept. First, a (not necessarily linear) code of length n over an alphabet Q is a subset \({\mathcal {C}}\subseteq Q^n\). An \({\mathbb {F}}_q\)-linear code \({\mathcal {C}}\) is an \({\mathbb {F}}_q\)-linear subspace of \({\mathbb {F}}_q^n\). The dimension k of this subspace is called the dimension of the code, and therefore \({\mathcal {C}}\) is isomorphic to \({\mathbb {F}}_q^k\). A linear map \({\mathbb {F}}_q^k\rightarrow {\mathcal {C}}\) can be described by a matrix \(G\in {\mathbb {F}}_q^{k\times n}\), which is called a generator matrix for \({\mathcal {C}}\). Note that G acts on the right, so  is mapped to
is mapped to  by the aforementioned linear map.
by the aforementioned linear map.
For  we define the support of
we define the support of  to be the set indices where
to be the set indices where  is nonzero, and we denote this set by
is nonzero, and we denote this set by  . Using this definition we can turn \({\mathbb {F}}_q^n\) into a metric space. This is done by introducing the Hamming weight and distance. The Hamming weight of
. Using this definition we can turn \({\mathbb {F}}_q^n\) into a metric space. This is done by introducing the Hamming weight and distance. The Hamming weight of  is defined as
is defined as  , and this induces the Hamming distance
, and this induces the Hamming distance  , where
, where  as well. The minimum distance d of a linear code \({\mathcal {C}}\) is defined to be
as well. The minimum distance d of a linear code \({\mathcal {C}}\) is defined to be

and by the linearity of the code it can be shown that in fact

Since n, k, and d are fixed for a given linear code \({\mathcal {C}}\) over \({\mathbb {F}}_q\), we often refer to it as an \([n,k,d]_q\)-code.
It may be shown that if  is given by
is given by  for some codeword
for some codeword  and an error vector
and an error vector  with
with  , it is possible to recover
, it is possible to recover  from
from  and
and  . This process is called erasure decoding.
. This process is called erasure decoding.
Another way to see erasure decoding is by considering punctured codes. For a set of indices \(E\subseteq \{1,2,\ldots ,n\}\) we denote the projection of  onto the indices not in E by
onto the indices not in E by  . For a code \({\mathcal {C}}\) and a set of indices E, we call \(\pi _E({\mathcal {C}})\) a punctured code. Now consider the case where \(|E|<d\), which implies the existence of a bijection between \({\mathcal {C}}\) and \(\pi _E({\mathcal {C}})\). This is the fact exploited in erasure decoding, where E is the set of indices where the errors occur.
. For a code \({\mathcal {C}}\) and a set of indices E, we call \(\pi _E({\mathcal {C}})\) a punctured code. Now consider the case where \(|E|<d\), which implies the existence of a bijection between \({\mathcal {C}}\) and \(\pi _E({\mathcal {C}})\). This is the fact exploited in erasure decoding, where E is the set of indices where the errors occur.
As in [2], we will use interleaved codes. If \({\mathcal {C}}\subseteq {\mathbb {F}}_q^n\) is a linear code, \({\mathcal {C}}^{\odot s}\) denotes the set of \(s\times n\)-matrices with entries in \({\mathbb {F}}_q\) whose rows are codewords of \({\mathcal {C}}\). We can also see such an \(s\times n\)-matrix as a vector of length n with entries in the alphabet \({\mathbb {F}}_{q}^s\). Then we can see \({\mathcal {C}}^{\odot s}\) as a non-linearFootnote 2 code of length n over the alphabet \({\mathbb {F}}_q^s\).
Since the alphabet \({\mathbb {F}}_q^s\) contains a zero element (the all zero vector), we can define the notions of Hamming weight and Hamming distance in the space \(({\mathbb {F}}_q^s)^n\). We can then speak about the minimum distance of \({\mathcal {C}}^{\odot s}\) and even though \({\mathcal {C}}^{\odot s}\) is not a linear code, it is easy to see that the minimum distance of \({\mathcal {C}}^{\odot s}\) coincides with its minimum nonzero weight, and also with the minimum distance of \({\mathcal {C}}\).
2.3 Cryptographic Definitions
Consider a sender S and a receiver R participating in a cryptographic protocol. The sender holds  for \(j=1,2,\ldots ,N\) and \(i=1,2,\ldots ,m\). For each i the receiver holds a choice integer \(w_i\in [1,N]\). We let \({\mathcal {F}}_{N\text {-}{\mathsf {O}}{\mathsf {T}}}^{\kappa ,m}\) denote the ideal functionality that, on inputs
for \(j=1,2,\ldots ,N\) and \(i=1,2,\ldots ,m\). For each i the receiver holds a choice integer \(w_i\in [1,N]\). We let \({\mathcal {F}}_{N\text {-}{\mathsf {O}}{\mathsf {T}}}^{\kappa ,m}\) denote the ideal functionality that, on inputs  from S and \(w_i\) from R, outputs
from S and \(w_i\) from R, outputs  for \(i=1,2,\ldots ,m\) to the receiver R. For ease of notation, we will let the sender input N matrices of size \(\kappa \times m\) with entries in \(\{0,1\}\), and the receiver a vector of length m, with entries in [1, N]. Hence, for the i’th OT the sender’s inputs are the i’th column of each matrix, and the receiver’s input is the i’th entry of the vector.
for \(i=1,2,\ldots ,m\) to the receiver R. For ease of notation, we will let the sender input N matrices of size \(\kappa \times m\) with entries in \(\{0,1\}\), and the receiver a vector of length m, with entries in [1, N]. Hence, for the i’th OT the sender’s inputs are the i’th column of each matrix, and the receiver’s input is the i’th entry of the vector.
The protocol presented in Sect. 3 relies on two functions with certain security assumptions, the foundations of which we define in the following. For the first function let \({\mathcal {X}}\) be a probability distribution. The min-entropy of \({\mathcal {X}}\) is given by
where X is any random variable following the distribution \({\mathcal {X}}\). If \(H_\infty ({\mathcal {X}})=t\) we say that \({\mathcal {X}}\) is t-min-entropy. This is used in the following definition.
Definition 1
(t-Min-Entropy Strongly \({\mathcal {C}}\)-Correlation Robustness). Consider a linear code \({\mathcal {C}}\subseteq {\mathbb {F}}_q^n\), and let \({\mathcal {X}}\) be a distribution on \(\{0,1\}^n\) with min-entropy t. Fix  from some probability distribution and let \(\kappa \) be a positive integer. An efficiently computable function \(\mathsf {H}:{\mathbb {F}}_q^n \rightarrow \{0,1\}^\kappa \) is said to be t-min-entropy strongly \({\mathcal {C}}\)-correlation robust if
from some probability distribution and let \(\kappa \) be a positive integer. An efficiently computable function \(\mathsf {H}:{\mathbb {F}}_q^n \rightarrow \{0,1\}^\kappa \) is said to be t-min-entropy strongly \({\mathcal {C}}\)-correlation robust if

is computationally indistinguishable from the uniform distribution on \(\{0,1\}^{\kappa m|{\mathcal {C}}|}\) when  is sampled according to the distribution \({\mathcal {X}}\).
is sampled according to the distribution \({\mathcal {X}}\).
The second type of function we need is a pseudorandom generator.
Definition 2
A pseudorandom generator is a function \(\mathsf {PRG}:\{0,1\}^\kappa \rightarrow {\mathbb {F}}_q^m\) such that the output of \(\mathsf {PRG}\) is computationally indistinguishable from the uniform distribution on \({\mathbb {F}}_q^m\).
If  is a \(\kappa \times n\)-matrix with entries in \(\{0,1\}\) for some integer n, we use the notation
is a \(\kappa \times n\)-matrix with entries in \(\{0,1\}\) for some integer n, we use the notation  where we see
where we see  as columns of an \(m\times n\) matrix.
as columns of an \(m\times n\) matrix.
In addition to the usual concept of advantage, one can also consider the conditional advantage as it is done in [12]. Let A be an event such that there exist \(x_0\) and \(x_1\) in the sample space of the two random variables \(X_0\) and \(X_1\), respectively, where \(\Pr [X_i=x_i\mid A]>0\) for \(i=0,1\). Then we define the conditional advantage of a distinguisher \({\mathcal {D}}\) given A as
We end this section by presenting the following lemma, which allows us to bound the advantage by considering disjoint cases. The proof follows by the law of total probability and the triangle inequality.
Lemma 1
Let \(A_1,A_2,\ldots ,A_n\) be events as above. Additionally, assume that the events are disjoint. If \(\sum _{i=1}^n\Pr [A_i]=1\), then
for any distinguisher \({\mathcal {D}}\).
3 Actively Secure OT-Extension
In this section we describe and analyse a generalization of the protocol described in [12] which uses OT-extensions to implement the functionality \({\mathcal {F}}_{N\text {-}{\mathsf {O}}{\mathsf {T}}}^{\kappa ,m}\) by using only \(n\le m\) base OT’s, which are 1-out-of-2. Our OT-extension protocol is also using 1-out-of-2 base OT’s, but works with q-ary linear codes instead of binary. Our main result is summarized in the following theorem.
Theorem 1
Given security parameters \(\kappa \) and s, let \({\mathcal {C}} \) be an \([n,k,d]_q\) linear code with \(k=\log _q(N)\) and \(d\ge \max \{\kappa ,s\}\). Additionally, let \(\mathsf {PRG}:\mathbb \{0,1\}^{\kappa }\rightarrow {\mathbb {F}}_q^{m+2s}\) be a pseudorandom generator and let \(\mathsf {H}:{\mathbb {F}}_q^{n}\rightarrow \{0,1\}^{\kappa }\) be a t-min-entropy strongly \({\mathcal {C}}\)-correlation robust function for all \(t\in \{n-d+1,n-d+2,\ldots ,n\}\). If we have access to \({\mathcal {C}}\), the functions \(\mathsf {PRG}\) and \(\mathsf {H}\), and the functionality \({\mathcal {F}}_{2\text {-}{\mathsf {O}}{\mathsf {T}}}^{\kappa ,n}\), then the protocol in Fig. 1 on page 7 implements the functionality \({\mathcal {F}}_{N\text {-}{\mathsf {O}}{\mathsf {T}}}^{\kappa ,m}\).
The protocol is computationally secure against an actively corrupt adversary.Footnote 3
This protocol implements the functionality \({\mathcal {F}}_{N\text {-}{\mathsf {O}}{\mathsf {T}}}^{\kappa ,m}\) having access to \({\mathcal {F}}_{2\text {-}{\mathsf {O}}{\mathsf {T}}}^{\kappa ,n}\). The security of the protocol is controlled by the security parameters \(\kappa \) and s. The sender S and the receiver R have agreed on a linear code \({\mathcal {C}}\subseteq {\mathbb {F}}_q^n\) with generator matrix G of dimension \(k=\log _q(N)\) and minimum distance \(d\ge \max \{\kappa ,s\}\). The protocol uses a pseudorandom generator \(\mathsf {PRG}:\{0,1\}^\kappa \rightarrow {\mathbb {F}}_q^{m+2s}\) and a function \(\mathsf {H}:{\mathbb {F}}_q^n\rightarrow \{0,1\}^\kappa \), which is t-min-entropy strongly \({\mathcal {C}}\)-correlation robust for all \(t\in \{n-d+1,n-d+2,\ldots ,n\}\). R has m inputs  , which act as selection integers. S has inputs
, which act as selection integers. S has inputs  , indexed by \(i\in \{1,2,\ldots ,m\}\) and
, indexed by \(i\in \{1,2,\ldots ,m\}\) and  .
.
3.1 The Protocol
We start by noticing that in our protocol R has inputs  rather than choice integers \(w_i\in [1,N]\). However, the number of elements in \({\mathbb {F}}_q^k\) is \(q^k=N\), and hence
rather than choice integers \(w_i\in [1,N]\). However, the number of elements in \({\mathbb {F}}_q^k\) is \(q^k=N\), and hence  can for instance be the q-ary representation of \(w_i\). In this way we have a bijection between selection integers and input vectors.
can for instance be the q-ary representation of \(w_i\). In this way we have a bijection between selection integers and input vectors.
Our protocol is, like the protocol in [12], very similar to the original protocol in [7]. The idea in this protocol is that we first do OT’s with the roles of the participants interchanged such that the sender learns some randomness chosen by the receiver. Afterwards, R encodes his choice vectors using the linear code \({\mathcal {C}}\) and hides the value with a one-time pad. He sends these to S, who will combine this information with the outputs of the OT functionality to obtain a set of vectors, only m of which R can compute; namely the ones corresponding to his input vectors. When S applies a t-min-entropy strongly \({\mathcal {C}}\)-correlation robust function \(\mathsf {H}\) to the set of vectors, he can use the outputs as one-time pads of his input strings. Like in [12] the protocol contains a consistency check to ensure that R acts honestly, or otherwise he will get caught with overwhelming probability. The full protocol is presented in Fig. 1 on page 7.
In order to argue that the protocol is correct, we see that for each i, the sender S computes and sends the values  for all
for all  . Since \(k=\log _q(N)\), this yields N strings for each \(i\in \{1,2,\ldots ,m\}\). The receiver R obtains one of these because
. Since \(k=\log _q(N)\), this yields N strings for each \(i\in \{1,2,\ldots ,m\}\). The receiver R obtains one of these because

Furthermore, if both S and R act honestly, the consistency checks in phase 3 will always pass. This follows from the observation that

Hence, we note that if only passive security is needed in Protocol 1, we can omit phase 3 and set \(s=0\). The aforementioned steps are included to ensure that the receiver uses codewords in the matrix C. What a malicious receiver might gain by choosing rows which are not codewords is explained in [7, Sect. 4].
3.2 Proofs of Security
In this section we give formal proofs for security. The proof of security against a malicious sender works more or less the same as the proof in [12] but in a different notation. For completeness, we have included this proof. However, we present the proof against a malicious receiver in another way, where the structure, some strategies, and some arguments differ from the original proof.
Theorem 2
Protocol 1 is computationally secure against an actively corrupt sender.
Proof
To show this theorem we give a simulator, which simulates the view of the sender during the protocol. The view of S is \(\mathrm {View}_S=\{N,U,{\tilde{T}},{\tilde{W}}\}\). The simulator \(\mathrm {Sim}_S\) works as follows.
-
1.
\(\mathrm {Sim}_S\) receives
 from S and defines a uniformly random matrix N, sets \(T=\mathsf {PRG}(N)\), and passes N back to S.
from S and defines a uniformly random matrix N, sets \(T=\mathsf {PRG}(N)\), and passes N back to S. -
2.
Then \(\mathrm {Sim}_S\) samples U uniformly at random and sends this to S. Additionally, it computes Q as S should.
-
3.
In phase 3 the simulator receives \(M'\) from S, and constructs M. The matrix \({\tilde{W}}\) is sampled uniformly at random in \({\mathbb {F}}_q^{2s\times k}\), and using this, \(\mathrm {Sim}_S\) sets
 . It sends \({\tilde{T}}\) and \({\tilde{W}}\) to S.
. It sends \({\tilde{T}}\) and \({\tilde{W}}\) to S. -
4.
\(\mathrm {Sim}_S\) receives
 from S and since \(\mathrm {Sim}_S\) already knows Q and
from S and since \(\mathrm {Sim}_S\) already knows Q and  , it can recover
, it can recover  and pass these to the ideal functionality \({\mathcal {F}}_{N\text {-}{\mathsf {O}}{\mathsf {T}}}^{\kappa ,m}\).
and pass these to the ideal functionality \({\mathcal {F}}_{N\text {-}{\mathsf {O}}{\mathsf {T}}}^{\kappa ,m}\).
We now argue that the simulator produces values indistinguishable from \(\mathrm {View}_S\). The matrix N is distributed identically in the real and ideal world. Since both \(T_0\) and \(T_1\) are outputs of a pseudorandom generator, the matrix \(T_0-T_1\), and therefore also U, is computationally indistinguishable from a uniformly random matrix. In the real world, \({\tilde{W}}=M'(W')^T+(W'')^T\) is uniform since \(W''\) is chosen uniformly. The simulator \(\mathrm {Sim}_S\) constructs \({\tilde{T}}\) such that the consistency check will pass. This will always be the case in the real world, and hence S cannot distinguish between the real and ideal world. Additionally, we note that step 4 ensures that the receiver obtains the same output in both worlds. This shows security against an actively corrupt sender. \(\square \)
We now shift our attention to an actively corrupt receiver. This proof is not as straight forward as for the sender. The idea is to reduce the problem of breaking the security of the protocol to the problem of breaking the assumptions on \(\mathsf {H}\). Before delving into the proof itself, we will introduce some lemmata and notations that will aid in the proof. The focus of these will be the probability that certain events happen during the protocol. These events are based on situations that determine the simulator’s ability or inability to simulate the real world. Essentially, they are the event that R passes the consistency check, which we denote by \({\mathsf {P}}{\mathsf {C}}\); the event that R has introduced errors in too many positions, denoted by \({\mathsf {L}}{\mathsf {S}}\); and the event that the error positions from the consistency check line up with the errors in C, which we call \({\mathsf {E}}{\mathsf {S}}\). These will be defined more precisely below.
Inspired by the notation in the protocol, we define
A corrupt receiver may deviate from the protocol and may send an erroneous \({\tilde{W}}\), which we denote by \({\tilde{W}}_*\). Let
and let \(E=\mathrm {supp}({\bar{C}})\), where \({\bar{C}}\) is interpreted in \({\mathcal {C}}^{\odot 2s}\). When writing \({\tilde{C}}\), \({\bar{C}}\), and E later in this section these are the definitions we are implicitly referring to.
Lemma 2
Let \({\mathcal {C}}\), C, and M be as in Protocol 1. Further, let \({\mathsf {L}}{\mathsf {S}}\) be the event that \(|E|\ge s\), and let \({\mathsf {E}}{\mathsf {S}}\) be the event that for every \(C'\in {\mathcal {C}}^{\odot 2s}\) there exists a \({\hat{C}}\in {\mathcal {C}}^{\odot m+2s}\) such that \(\mathrm {supp}({\tilde{C}}-C')=\mathrm {supp}(C-{\hat{C}})\). Then the probability that neither \({\mathsf {E}}{\mathsf {S}}\) nor \({\mathsf {L}}{\mathsf {S}}\) happen is at most \(q^{-s}\).
Proof
The matrix \(M'\) in Protocol 1 is chosen uniformly at random, and hence M can be interpreted as a member of a universal family of linear hashes. Thus, this lemma is a special case of [2, Theorem 1] when letting \(m'=m+2s\), \(s'=s\), and \(t'=0\) where the primes denote the parameters in [2]. Additionally, note that our event \({\mathsf {L}}{\mathsf {S}}\) happens if MC has distance at least s from \({\mathcal {C}}^{\odot 2s}\).\(\square \)
We will now bound the probability that an adversary is able to pass the consistency check, even if C contains errors.
Lemma 3
Let \({\mathsf {P}}{\mathsf {C}}\) denote the event that the consistency check passes. Then
Proof
In order to compute \(\Pr [{\mathsf {P}}{\mathsf {C}}]\), we consider \({\bar{C}}\) and \({\bar{T}}={\tilde{T}}-{\tilde{T}}_*\), where the \(*\) indicates that the matrix may not be constructed as described in the protocol. The event \({\mathsf {P}}{\mathsf {C}}\) happens if  . However, from the definition of Q,
. However, from the definition of Q,  , implying that \({\mathsf {P}}{\mathsf {C}}\) happens if and only if
, implying that \({\mathsf {P}}{\mathsf {C}}\) happens if and only if

Now consider \({\bar{T}}\) and \({\bar{C}}\) in \( ({\mathbb {F}}_q^n)^{\odot 2s}\), meaning that the entries \({\bar{C}}_j\) and \({\bar{T}}_j\) are elements in \({\mathbb {F}}_q^{2s}\). If the adversary chooses \({\bar{C}}_j=0\) for some \(j\in \{1,2,\ldots ,n\}\), it must choose \({\bar{T}}_j=0\) as well since the check would fail otherwise. If it chooses \({\bar{C}}_j\ne 0\), it has two options. Either bet that \(b_j=0\) and set \({\bar{T}}_j=0\) or bet that \(b_j=1\) and set \({\bar{T}}_j=-{\bar{C}}_j\). This means that for each entry \(j\in E\) the adversary has probability \(\frac{1}{2}\) of guessing the correct value of \(b_j\). For every entry \(j\notin E\), each possible \(b_j\) gives a consistent value since \({\bar{C}}_j={\bar{T}}_j=0\). By this and the independence of the entries in  , it follows that the probability of the check passing is bounded by \(\Pr [{\mathsf {P}}{\mathsf {C}}]\le 2^{-|E|}\). \(\square \)
, it follows that the probability of the check passing is bounded by \(\Pr [{\mathsf {P}}{\mathsf {C}}]\le 2^{-|E|}\). \(\square \)
This immediately gives the following corollary.
Corollary 1
If \({\mathsf {L}}{\mathsf {S}}\) denotes the same event as in Lemma 2, then
We now have the required results to prove the security of Protocol 1 against an actively corrupt receiver. The events \({\mathsf {P}}{\mathsf {C}}\), \({\mathsf {L}}{\mathsf {S}}\), and \({\mathsf {E}}{\mathsf {S}}\) from the previous lemmata and corollaries will also be used in the proof of the following theorem.
Theorem 3
Protocol 1 is computationally secure against an actively corrupt receiver.
Proof
As in the proof of Theorem 2, we construct a simulator \(\mathrm {Sim}_R\) simulating the view of the receiver, which is  . The simulator works as follows.
. The simulator works as follows.
-
1.
\(\mathrm {Sim}_R\) receives \(N_{0}\) and \(N_{1}\) from R.
-
2.
The simulator receives U from R and combines these with \(T_0=\mathsf {PRG}(N_0)\) and \(T_1=\mathsf {PRG}(N_1)\) to reconstruct the matrix C. Additionally, it samples uniformly at random an internal value
 . Using this
. Using this  , the simulator \(\mathrm {Sim}_R\) computes
, the simulator \(\mathrm {Sim}_R\) computes 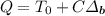 .
. -
3.
\(\mathrm {Sim}_R\) samples a random \(M'\) like the sender would have done in the protocol and sends this to R. In return, it receives \({\tilde{T}}_*\) and \({\tilde{W}}_*\), where the \(*\) indicates that the vectors may not be computed according to the protocol. The simulator runs the consistency check and aborts if it fails.
-
4.
Otherwise, it erasure decodes each row of C by letting E be the erasures to obtain \(W'\). If the decoding fails, it aborts. If the decoding succeeds, the simulator gives \(W'\) as inputs to the ideal functionality \({\mathcal {F}}_{N\text {-}{\mathsf {O}}{\mathsf {T}}}^{\kappa ,m}\), which returns the values
 to \(\mathrm {Sim}_R\). It can now compute
to \(\mathrm {Sim}_R\). It can now compute  , and chooses
, and chooses  uniformly at random in \({\mathbb {F}}_q^\kappa \) for all
uniformly at random in \({\mathbb {F}}_q^\kappa \) for all  .
.
The matrix \(M'\) is uniformly distributed both in the real and ideal world. Hence, we only need to show that the output  produced by the simulator is indistinguishable from the output of the protocol.
produced by the simulator is indistinguishable from the output of the protocol.
Let \({\mathcal {Z}}\) be a distinguisher for distinguishing between a real world execution of the protocol and an ideal execution using the simulator. By Lemma 1 its advantage is bounded by

where we have omitted some probability factors since they are all at most 1. Notice that  is constructed identically in both worlds. The remaining
is constructed identically in both worlds. The remaining  are uniformly distributed in the ideal world, but constructed as
are uniformly distributed in the ideal world, but constructed as

in the real world. Also notice that, if the consistency check fails, the simulator aborts before constructing the  . This is the same as in the real world, and the only information R has received before this is \(M'\), which is identically distributed in both worlds. Hence, the simulator is perfect in this case. This implies that the first term on the right-hand side in (2) is zero.
. This is the same as in the real world, and the only information R has received before this is \(M'\), which is identically distributed in both worlds. Hence, the simulator is perfect in this case. This implies that the first term on the right-hand side in (2) is zero.
Since the consistency check by the simulator is identical to the consistency check done by S, it follows that the probability for the consistency check to pass even if R might have sent inconsistent values is the same in both worlds. This means that \(\Pr [{\mathsf {P}}{\mathsf {C}}\mid {\mathsf {L}}{\mathsf {S}}]\le 2^{-s}\) by Corollary 1. In a similar fashion, Lemma 2 implies that the penultimate term in (2) can be bounded above by \(q^{-s}\). In summary, (2) can be rewritten as
To show that this is negligible in \(\kappa \) and s, assume the opposite; that is, \({\mathcal {Z}}\) has non-negligible advantage. We then construct a distinguisher \({\mathcal {D}}\) breaking the security assumptions on \(\mathsf {H}\).
The distinguisher \({\mathcal {D}}\) simulates the protocol with minor changes in order to produce its input to the challenger. After receiving the challenge it uses the output of \({\mathcal {Z}}\) to respond. There exist inputs and random choices for R and S, which maximize the advantage of \({\mathcal {Z}}\), and we can assume that \({\mathcal {D}}\) has fixed these in its simulation. This also means that \({\mathsf {P}}{\mathsf {C}}\), \(\overline{{\mathsf {L}}{\mathsf {S}}}\) and \({\mathsf {E}}{\mathsf {S}}\) happen in the simulation since otherwise, \(\mathrm {Adv}({\mathcal {Z}})\) is negligible.
Because \({\mathsf {E}}{\mathsf {S}}\) happens, puncturing C in the positions in E gives a codeword in \(\pi _E({\mathcal {C}}^{\odot m+2s})\). Further, the event \(\overline{{\mathsf {L}}{\mathsf {S}}}\) ensures that this corresponds to a unique codeword in \({\mathcal {C}}^{\odot m+2s}\). Hence, \({\mathcal {D}}\) is able to erasure decode and for \(i=1,2,\ldots ,m\,+\,2s\) obtain  , where
, where  is the i’th row of C,
is the i’th row of C,  , and
, and  .
.
The following arguments use that no matter which  the challenger chooses, the distinguisher \({\mathcal {D}}\) knows
the challenger chooses, the distinguisher \({\mathcal {D}}\) knows  . This follows from the fact that \({\mathsf {P}}{\mathsf {C}}\) has happened and therefore \(b_j\) for \(j\in E\) is known to the adversary, which is simulated by \({\mathcal {D}}\). Hence, the distinguisher is able to construct
. This follows from the fact that \({\mathsf {P}}{\mathsf {C}}\) has happened and therefore \(b_j\) for \(j\in E\) is known to the adversary, which is simulated by \({\mathcal {D}}\). Hence, the distinguisher is able to construct  , where the
, where the  is the vector eventually chosen by the challenger, and
is the vector eventually chosen by the challenger, and  the i’th row of \(T_0\). Letting \(t=n-|E|\), define the probability distribution \({\mathcal {X}}\) to be the uniform distribution on \({\mathbb {F}}_2^n\) under the condition that the indices in E are fixed to the corresponding entry of
the i’th row of \(T_0\). Letting \(t=n-|E|\), define the probability distribution \({\mathcal {X}}\) to be the uniform distribution on \({\mathbb {F}}_2^n\) under the condition that the indices in E are fixed to the corresponding entry of  . By uniformity this distribution has min-entropy t. The distinguisher passes \({\mathcal {X}}\) and the
. By uniformity this distribution has min-entropy t. The distinguisher passes \({\mathcal {X}}\) and the  to the challenger. It receives back
to the challenger. It receives back  for all \(i=1,2,\ldots ,n\) and
for all \(i=1,2,\ldots ,n\) and  and needs to distinguish them between being uniformly random and being constructed as
and needs to distinguish them between being uniformly random and being constructed as

As in the protocol, let  , where
, where  is again the vector chosen by the challenger. Therefore, if
is again the vector chosen by the challenger. Therefore, if  is constructed as in (5), we have that
is constructed as in (5), we have that

The distinguisher will now construct and input to \({\mathcal {Z}}\) the following

Since  , we have that
, we have that  is identical to the value computed in both the real and ideal worlds.
is identical to the value computed in both the real and ideal worlds.
For the remaining  we notice that if the challenger has chosen
we notice that if the challenger has chosen  uniformly at random, then the values
uniformly at random, then the values  are uniformly distributed as well. This is the same as the simulator will produce in the ideal world. On the other hand, if
are uniformly distributed as well. This is the same as the simulator will produce in the ideal world. On the other hand, if  , then we have
, then we have  . This is exactly the same as produced during the protocol in the real world. Hence, \({\mathcal {D}}\) can feed the values
. This is exactly the same as produced during the protocol in the real world. Hence, \({\mathcal {D}}\) can feed the values  to \({\mathcal {Z}}\), which can distinguish between the real and ideal world, and depending on the answer from \({\mathcal {Z}}\), \({\mathcal {D}}\) can distinguish whether the
to \({\mathcal {Z}}\), which can distinguish between the real and ideal world, and depending on the answer from \({\mathcal {Z}}\), \({\mathcal {D}}\) can distinguish whether the  are uniformly distributed or are constructed as
are uniformly distributed or are constructed as  . Hence, the advantage of \({\mathcal {D}}\) is the same as that of \({\mathcal {Z}}\) under the restriction that \({\mathsf {P}}{\mathsf {C}}\), \(\overline{{\mathsf {L}}{\mathsf {S}}}\), and \({\mathsf {E}}{\mathsf {S}}\) happen. This means that
. Hence, the advantage of \({\mathcal {D}}\) is the same as that of \({\mathcal {Z}}\) under the restriction that \({\mathsf {P}}{\mathsf {C}}\), \(\overline{{\mathsf {L}}{\mathsf {S}}}\), and \({\mathsf {E}}{\mathsf {S}}\) happen. This means that
where the inequality comes from (4). This contradicts that \(\mathsf {H}\) is t-min-entropy strongly \({\mathcal {C}}\)-correlation robust, and therefore \({\mathcal {Z}}\) must have negligible advantage in the security parameters \(\kappa \) and s.\(\square \)
4 Consistency Check in a Subfield
Assume that \(q=2^r\) and that \(r\mid s\). By restricting the matrix \(M'\) in Protocol 1 to have entries in \({\mathbb {F}}_2\), the set of possible matrices M form a \(2^{-2s}\)-almost universal family of hashes. The probability in Lemma 2 can then be replaced by \(2^{-s}\) by setting \(m'=m+2s\), \(s'=\frac{s}{r}\), and \(t'=2s(1-1/r)\). This modification will show itself in (4), but here only the term \(q^{-s}\) is replaced by \(2^{-s}\), and hence the advantage will still be negligible in \(\kappa \) and s. However, choosing \(M'\) in a subfield reduces the communication complexity, since the number of bits needed to transmit \(M'\) is lowered by a factor of r. Furthermore, the computation of \({\tilde{T}}\) and \({\tilde{W}}\) can be done using only sums in \({\mathbb {F}}_q\), instead of multiplication and sums.
This method of reducing the communication complexity can be done to an intermediate subfield, which will give a probability bound between \(q^{-s}\) and \(2^{-s}\). In a similar way, this procedure could also be applied to fields of other characteristics.
5 Comparison
We compare the parameters of our modified construction with those that can be achieved by the actively secure OT-extension construction from [12]. We will show that the ability to use larger finite fields in our modified construction induces a tradeoff between the number of base OT’s that are needed for a given N and given security parameters (and hence also the complexity of the set-up phase), and the complexity of the encoding and consistency check phases of the extension protocol.
We have shown that given an \([n,k,d]_q\)-code, with \(d\ge \max \{\kappa ,s\}\), one can build an OT-extension protocol that implements the functionality \({\mathcal {F}}_{N\text {-}{\mathsf {O}}{\mathsf {T}}}^{\kappa ,m}\) using the functionality \({\mathcal {F}}_{2\text {-}{\mathsf {O}}{\mathsf {T}}}^{\kappa ,n}\), where \(N=q^{k}\). The parameters achieved in [12] are the same as we obtain in the case \(q=2\).
We will limit our analysis to the case where \(q=2^r\), and \(r\mid s\). We fix the security parameters s and \(\kappa \), and fix N to be a power of q, \(N=q^k\). Note then that \(N=2^{k\cdot \log _2 q}\). Let \(n'\) and n be the smallest integers for which there exist an \([n',k\log _2 q,\ge d]_2\)-linear code and an \([n,k,\ge d]_q\)-linear code, respectively. As we discuss later, we can always assume that \(n\le n'\), and in most cases it is in fact strictly smaller. Therefore, by using q-ary codes one obtains a reduction on the number of base OT’s from \(n'\) to n, and therefore a more efficient initialization phase. Note for example that the binary construction always requires at least a minimum of \(\log _2 N\) base OT’s, while using q-ary codes allows to weaken this lower bound to \(n\ge \log _q N\).
On the other hand, however, this comes at the cost of an increase in the communication complexity of what we have called the encoding and consistency check phases of the protocol since we need to send a masking of codewords over a larger field. We compare these two phases separately since the consistency check is only needed for an actively secure version of the protocol and it has a smaller cost than the encoding phase anyway. In the encoding phase, [12] communicates a total of \((m+s)n'\) bits, while our construction communicates \((m+2s)n\log _2 q\) bits. However, typically \(m\gg s\), and therefore we only compare the terms \(mn'\) and \(mn\log _2 q\). Hence, the communication complexity of this phase gets multiplied by a factor \(\log _2 q\cdot n/n'\). During the consistency check phase, which is less communication intensive, [12] communicates a total of \(sm+sn'+sk\log _2 q\) bits while our construction communicates \(2sm\,+\,2sn\log _2 q\,+\,2sk\log _2 q\) bits when using the method from Sect. 4.
We now discuss in more detail the rates between n and \(n'\) that we can obtain for different values of q. In order to do that, having fixed d and k, let \(n'\) and n denote the minimum values for which \([n',k\log _2 q,\ge d]_2\)-linear codes and \([n,k,\ge d]_q\)-linear codes exist. Let \(k'\) denote \(k\log _2 q\). It is easy to see that \(n\le n'\) by considering a generator matrix for the binary code of length \(n'\) and considering the code spanned over \({\mathbb {F}}_q\) by that same matrix. In many situations, however, n is in fact considerably smaller than \(n'\). The extreme case is when \(q=N\), and therefore \(k=1\), in which case one can take the repetition code over \({\mathbb {F}}_q\) and set \(n=d\). It is difficult to give a general tight bound on the relation between n and \(n'\), although at least we can argue that \(n\le n'-k'+k\): indeed, given an \([n',k',\ge d]_2\)-code \({\mathcal {C}}_2\) then one can obtain an \([n',k',\ge d]_q\)-code \({\mathcal {C}}_q\) by simply considering the linear code spanned over the field \({\mathbb {F}}_q\) by the generator matrix of \({\mathcal {C}}_2\) and then shortenFootnote 4 \({\mathcal {C}}_q\) at \(k'-k\) positions, after which we obtain an \([n,\ge k,\ge d]_q\)-code \({\mathcal {C}}\), with \(n=n'-k'+k\). This bound is however by no means tight in general. We now consider concrete examples of codes, that will be summarized in Table 1.
Small Values of N
For relatively small values of N (\(N<1000\)), [10] suggests the use of Walsh-Hadamard codes, with parameters \([2^{k'},k',2^{k'-1}]_2\), while [12] improves on this by using punctured Walsh-Hadamard codes instead. Punctured Walsh-Hadamard codes (also known as first order Reed-Muller codes) are \([2^{k'-1},k',2^{k'-2}]_2\)-linear codes. These are the shortest possible binary linear codes for those values of N and d, as they attain the Griesmer bound. In terms of N, the parameters can be written as \([N/2,\log _2 N, N/4]_2\).
The natural generalization of these codes to \({\mathbb {F}}_q\) are first order q-ary Reed Muller codes, which have parameters \([q^{k-1},k,q^{k-1}-q^{k-2}]_q\). Moreover, there is a q-ary generalization of Walsh-Hadamard codes, known as simplex codes, which have parameters \([\frac{q^{k}-1}{q-1},k,q^{k-1}]_q\).
For example for \(q=4\), the parameters of the simplex code can be written in terms of N as \([(N-1)/3, \log _4 N, N/4]_4\), and hence, for the same values of d and N, the number of base OT’s is reduced by a factor 3/2 since \(n/n'<2/3\). On the other hand, the communication complexity of the encoding phase increases by a factor \(2n/n'<4/3\) compared to using binary punctured Walsh-Hadamard codes. We note, however, that this comparison is only valid if N is a power of 4.
Because of the fact that N needs to be a power of q, in Table 1 it will be convenient to use the juxtaposition of two copies of the same code. This means that given an \([n,k,d]_q\) code \({\mathcal {C}}'\), we can obtain a \([2n,k,2d]_q\) code by sending each symbol in a codeword twice. With respect to the examples listed in [12], we see that by choosing an adequate finite field and using juxtapositions of simplex codes, the number of OT’s gets divided by a factor slightly over 1.5, while the communication complexity increases by a somewhat smaller factor.
Larger Values of N
For larger values of N, [12] suggests using binary BCH codes. We use q-ary BCH codes instead. It is difficult to find BCH codes that match exactly the parameters (N, d) from [12] so in our comparison we have always used larger values of both N and d. This is actually not too advantageous for our construction since the codes in [12] were selected so that their length is of the form \(2^m-1\) (what is called primitive binary BCH codes, which usually yields the constructions with best parameters) and that results in a range of parameters where it is not adequate to choose primitive q-ary BCH codes. Nevertheless, in the case where the large value \(N'=2^{443}\) is considered in [12], we can reduce the number of base OT’s needed to less than half, while the communication complexity only increases by 4 / 3, and in addition to that we achieve a larger value \(N=2^{462}\). Observe that, for this value of N, with a binary code the number of base OT’s would be restricted by the naïve bound \(n'\ge \log _2 N=462\) in any case (i.e. even if \(d=1\)), while using a code over \({\mathbb {F}}_{8}\) we only need to use 455.
Notes
- 1.
Of course, the elements of \(\{0,1\}\) could be identified with the elements of the field of two elements, \({\mathbb {F}}_2\). But for the sake of clarity, we will prefer to use \(\{0,1\}\) where we refer to bits and bitstrings and no algebraic properties are needed.
- 2.
The code is linear over \({\mathbb {F}}_q\), but not the alphabet \({\mathbb {F}}_q^s\).
- 3.
In Sect. 4, we show that this is still true if the protocol relies on a code over \({\mathbb {F}}_{p^r}\), and the consistency check is changed such that \(M'\in {\mathbb {F}}_p^{2s\times m}\).
- 4.
Shortening a code at positions \(i_1,\dots ,i_t\) means first taking the subcode consisting of all codewords with \(0's\) at all those positions and then erasing those coordinates.
References
Beaver, D.: Correlated pseudorandomness and the complexity of private computations. In: Proceedings of the Twenty-eighth Annual ACM Symposium on Theory of Computing STOC 1996, pp. 479–488. ACM (1996). https://doi.org/10.1145/237814.237996
Cascudo, I., Damgård, I., David, B., Döttling, N., Nielsen, J.B.: Rate-1, linear time and additively homomorphic UC commitments. In: Robshaw, M., Katz, J. (eds.) CRYPTO 2016. LNCS, vol. 9816, pp. 179–207. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-53015-3_7
Cascudo, I., Damgård, I., David, B., Giacomelli, I., Nielsen, J.B., Trifiletti, R.: Additively homomorphic UC commitments with optimal amortized overhead. In: Katz, J. (ed.) PKC 2015. LNCS, vol. 9020, pp. 495–515. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-46447-2_22
Frederiksen, T.K., Jakobsen, T.P., Nielsen, J.B., Trifiletti, R.: On the complexity of additively homomorphic UC commitments. In: Kushilevitz, E., Malkin, T. (eds.) TCC 2016. LNCS, vol. 9562, pp. 542–565. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-49096-9_23
Goldreich, O., Micali, S., Wigderson, A.: How to play any mental game. In: Proceedings of the Nineteenth Annual ACM Symposium on Theory of Computing STOC 1987, pp. 218–229. ACM (1987). https://doi.org/10.1145/28395.28420
Impagliazzo, R., Rudich, S.: Limits on the provable consequences of one-way permutations. In: Proceedings of the Twenty-first Annual ACM Symposium on Theory of Computing STOC 1989, pp. 44–61. ACM (1989). https://doi.org/10.1145/73007.73012
Ishai, Y., Kilian, J., Nissim, K., Petrank, E.: Extending oblivious transfers efficiently. In: Boneh, D. (ed.) CRYPTO 2003. LNCS, vol. 2729, pp. 145–161. Springer, Heidelberg (2003). https://doi.org/10.1007/978-3-540-45146-4_9
Keller, M., Orsini, E., Scholl, P.: Actively secure OT extension with optimal overhead. In: Gennaro, R., Robshaw, M. (eds.) CRYPTO 2015. LNCS, vol. 9215, pp. 724–741. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-47989-6_35
Kilian, J.: Founding cryptography on oblivious transfer. In: Proceedings of the Twentieth Annual ACM Symposium on Theory of Computing STOC 1988, pp. 20–31. ACM (1988). https://doi.org/10.1145/62212.62215
Kolesnikov, V., Kumaresan, R.: Improved OT extension for transferring short secrets. In: Canetti, R., Garay, J.A. (eds.) CRYPTO 2013. LNCS, vol. 8043, pp. 54–70. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-40084-1_4
MacWilliams, F., Sloane, N.: The Theory of Error-Correcting Codes, 1st edn. North Holland Mathematical Library, Oxford (1983)
Orrù, M., Orsini, E., Scholl, P.: Actively secure 1-out-of-N OT extension with application to private set intersection. In: Handschuh, H. (ed.) CT-RSA 2017. LNCS, vol. 10159, pp. 381–396. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-52153-4_22
Yao, A.C.: Protocols for secure computations. In: Proceedings of the 23rd Annual Symposium on Foundations of Computer Science SFCS 1982, pp. 160–164. IEEE Computer Society, Washington, DC, USA (1982). https://doi.org/10.1109/SFCS.1982.88
Acknowledgements
The authors wish to thank Claudio Orlandi for providing helpful suggestions during the early stages of this work, and Peter Scholl for his valuable comments.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2018 Springer Nature Switzerland AG
About this paper
Cite this paper
Cascudo, I., Christensen, R.B., Gundersen, J.S. (2018). Actively Secure OT-Extension from q-ary Linear Codes. In: Catalano, D., De Prisco, R. (eds) Security and Cryptography for Networks. SCN 2018. Lecture Notes in Computer Science(), vol 11035. Springer, Cham. https://doi.org/10.1007/978-3-319-98113-0_18
Download citation
DOI: https://doi.org/10.1007/978-3-319-98113-0_18
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-98112-3
Online ISBN: 978-3-319-98113-0
eBook Packages: Computer ScienceComputer Science (R0)





 from S and defines a uniformly random matrix N, sets
from S and defines a uniformly random matrix N, sets  . It sends
. It sends  from S and since
from S and since  , it can recover
, it can recover  and pass these to the ideal functionality
and pass these to the ideal functionality  . Using this
. Using this  , the simulator
, the simulator 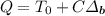 .
. to
to  , and chooses
, and chooses  uniformly at random in
uniformly at random in  .
.