Fourier Method for Approximating Eigenvalues of Indefinite Stekloff Operator

Abstract

We introduce an efficient method for computing the Stekloff eigenvalues associated with the indefinite Helmholtz equation. In general, this eigenvalue problem requires solving the Helmholtz equation with Dirichlet and/or Neumann boundary condition repeatedly. We propose solving the discretized problem with Fast Fourier Transform (FFT) based on carefully designed extensions and restrictions operators. The proposed Fourier method, combined with proper eigensolver, results in an efficient and easy approach for computing the Stekloff eigenvalues.

This work was supported in part by NSF DMS-1720114.

1 Introduction

We consider the problem of computing the Stekloff eigenvalues corresponding to the indefinite Helmholtz equation. The efficient computation of such eigenvalues is needed in several numerical models. For example, in inverse scattering, as discussed in Cakoni et al. (2016), these eigenvalues carry information of the refractive index of an obstacle. To begin with, we introduce the following boundary value problem:

$$\begin{aligned} \mathcal {L}(\alpha ,\lambda ;\eta )w\,\,{:}{=}\, {\left\{ \begin{array}{ll} -\varDelta w-\eta ^2 w =f\quad \text{ in } \quad \varOmega , \\ \alpha \frac{\partial w}{\partial n}+\lambda w=0 \quad \text{ on } \quad \varGamma =\partial \varOmega . \end{array}\right. } \end{aligned}$$

(1)

We call $\lambda$ a Stekloff eigenvalue when the homogenous problem ($f=0$ in (1)) has a non-trivial solution with $\alpha =1$. For details on existence and properties of such eigenvalue problems we refer to Cakoni et al. (2016) (Sects. 2 and 4 for real and complex $\eta$ respectively), Colton and Kress (2012).

As pointed out in Cakoni et al. (2016), the efficient computation of Stekloff eigenvalues is a challenging task. In addition, another important application of the techniques that we propose here is of interest in computing transmission eigenvalues where the aim is to find the kernel of the difference of two indefinite Stekloff operators, see Cakoni and Kress (2017). The efficient solution of such problems, whether direct or inverse, requires fast solution of the Dirichlet problem, corresponding to $\mathcal {L}(0,1;k(x))$, and the Neumann problem, corresponding to $\mathcal {L}(1,0;k(x))$, as defined in (1). Here, k(x) is the wave number and in case of non homogenous problem, the data f(x) is the external force.

The difficulties associated with solving the indefinite Helmholtz equation numerically, especially in high frequency regimes, are well known (see Brandt and Livshits (1997), Ernst and Gander (2012)). Traditional iterative methods, such as Krylov subspace methods or standard MultiGrid (MG) and Domain Decomposition (DD) methods, are inefficient as discussed in Ernst and Gander (2012).

Over the last two decades, different preconditioners and solvers for the Helmholtz equation have been proposed. We refer to the classical works by Brandt and Livshits (1997), and Elman et al. (2001) for MG solvers and also to the more recent developments in Helmholtz preconditioning presented in Gander et al. (2015), Osei-Kuffuor and Saad (2010), Lahaye and Vuik (2017) and Sheikh et al. (2016). More recently, Engquist and Ying (2011) introduced the so called sweeping preconditioners which were further extended by Eslaminia and Guddati (2016) to double-sweeping preconditioners. Stolk (2013) proposed a DD preconditioner based on special transmission conditions between subdomains. Other DD methods are found in Chen and Xiang (2013), Zepeda-Núnez and Demanet (2016).

In our focus are the computations of Stekloff eigenvalues and the techniques which we propose here lead to efficient algorithms in many cases of practical interest and provide preconditioners for the Helmholtz problem. More importantly, our techniques easily extend to the Maxwell’s system because they are based on the Fourier method.

The rest of the paper is organized as follows. We introduce the Fourier method for solving the constant coefficients boundary value problem in Sect. 2.1 (Dirichlet) and in Sect. 2.2 (Neumann). Further, in Sect. 3, we formulate the Stekloff eigenvalue problem and show how the FFT based Helmholtz solver can be applied. We conclude with several numerical tests on Stekloff eigenvalue computations as well as solution of the Helmholtz equation with variable wave number.

2 Periodic Extensions and Fourier Method

In this section, we focus on Fourier method for solving the Dirichlet problem and the Neumann problem with constant wave number $k(x)=k$. Non-constant case will also be considered in Sect. 4 as a numerical example.

2.1 Dirichlet Boundary Conditions

Dirichlet Problem in 1D. To explain the ideas, we consider the 1D version of (1) in the interval (0, 1) with constant wave number k:

$$\begin{aligned} {-}u'' - k^2 u = f, \quad u(0)=u(1) = 0. \end{aligned}$$

After discretization with central finite difference, we obtain the following linear system

$$\begin{aligned} A^D{\varvec{u}} = {\varvec{f}}, \quad A^D=T^D-k^2 h^2 I\in \mathbb {R}^{n\times n}, \end{aligned}$$

(2)

where $T^D=\mathrm{tridiag}(-1,2,-1)$ is a tri-diagonal matrix, ${\varvec{u}}=(u_1,\ldots ,u_n)^t$, $u_0=u_{n+1} = 0$, $h=1/(n+1)$, ${\varvec{f}}=h^2(f_1,\ldots ,f_n)^t$, and $f_j=f(jh)$, $u_j\approx u(jh)$, $j=1,\ldots n$. Here and in the following, the superscript t denotes transpose of a matrix or vector.

Let us now consider the same equation on a larger domain (0, 2) and with periodic boundary conditions:

$$\begin{aligned} -v''-k^2v = g, \quad v(0)=v(2),\quad v'(0)=v'(2). \end{aligned}$$

(3)

The finite difference discretization leads to a linear system for $\varvec{v} = (v_1,\ldots ,v_N)^t$, $N=2n+2$, which is as follows:

$$\begin{aligned} A^P\varvec{v} = \varvec{g}, \quad A^P = T^P- k^2h^2 I\in \mathbb {R}^{N\times N}. \end{aligned}$$

(4)

Here, $e_1=(1,0,\ldots ,0)^t$ and $e_N=(0,\ldots ,0,1)^t$ are the standard Euclidean basis vectors and $T^P=\mathrm{tridiag}(-1,2,-1) - e_1 e_N^t- e_N e_1^t$ is a circulant matrix. The right hand side $\varvec{g} = h^2(g_1,\ldots , g_N)^t$ is a given vector in $\mathbb {R}^{N}$ depending on ${\varvec{f}}$, which we specify later. The unknowns in this case are $v_j\approx v(2j/N)$, $j=1,\ldots ,N$. Notice that from the periodic boundary conditions, we have $v_N\approx v(0)=v(2)$ and $v_1\approx v(2/N)$ and this is reflected in the first and the last equation in the linear system (4).

The solution of systems with circulant matrices can be done efficiently using the Fast version (FFT) of the Discrete Fourier Transform (DFT) (see Cooley and Tukey (1965) for a description of FFT). The DFT is given by an operator $\mathcal {F}: \mathbb {C}^N\rightarrow \mathbb {C}^N$ represented by a matrix (denoted again with $\mathcal {F}$) defined as: $\mathcal {F}_{jm} = z^{(j-1)(m-1)}$, $z=\mathrm {e}^{-\frac{2\mathrm {i}\pi }{N}}$, with $j=1,\ldots ,N$ and $m=1,\ldots , N$. As is well known, we have the DFT inversion formula:

$$ \mathcal {F}^{-1} = \frac{1}{N}\mathcal {F}^* = \frac{1}{N}\overline{\mathcal {F}}. $$

Since $A^P$ here is a circulant matrix it is diagonalized by $\mathcal {F}$, see Cooley and Tukey (1965), Golub and Van Loan (2012), and

$$\begin{aligned} \mathcal {F} A^P\mathcal {F}^{-1} = D^P = \mathrm{diag}(d_l),\quad d_l = 4\sin ^2\frac{\pi (l-1)}{N}-k^2h^2, \quad l=1,\ldots N. \end{aligned}$$

(5)

As a consequence of this proposition, the solution $\varvec{v}$ to the problem (4) can be obtained by

$$\begin{aligned} {\varvec{v}} = \mathcal {F}^{-1} (D^P)^{-1}\mathcal {F} {\varvec{g}}. \end{aligned}$$

(6)

Let us now consider the special case when ${\varvec{g}}$ in (4) corresponds to an “odd” extension of ${\varvec{f}}$. That is ${\varvec{g}}\,{:}{=}\,E{\varvec{f}}$ defined as

$$\begin{aligned} \mathbb {C}^N \ni {\varvec{g}} = E{\varvec{f}},\quad g_j = {\left\{ \begin{array}{ll} f_{j},\quad j=1,\ldots ,n,\\ 0,\quad j=n+1,\\ -f_{N-j}, \quad j=n+2,\ldots ,2n+1,\\ 0,\quad j=N. \end{array}\right. } \end{aligned}$$

(7)

Here, $N=2n+2$. We have the following simple result.

Proposition 1

If $N=2n+2$ and ${\varvec{g}}$ satisfies $g_{j} = -g_{N-j}$, for $j=n+2, n+3,\ldots , 2n+1$ and $g_{n+1}=g_{2n+2}=0$, then the solution to (4) satisfies the relation:

$$\begin{aligned} v_{j} = -v_{N-j}, \quad j=n+2,\ldots ,2n+1. \end{aligned}$$

(8)

Proof

We note that by assumption, ${\varvec{g}}$ is an “odd” function with respect to the middle of the interval (0, 2). Since $A^D$ is an invertible matrix, let ${\varvec{u}}$ satisfy $[A^D{\varvec{u}}]_j={\varvec{g}}_j$, $j=1,\ldots ,n$. Next, we define ${\varvec{v}}=E{\varvec{u}}\in \mathbb {C}^{N}$ where E is defined in (7) and it is immediate to verify that $A^P{\varvec{v}}={\varvec{g}}$. Since $A^P$ is also invertible, ${\varvec{v}}$ must be the unique solution of $A^P{\varvec{v}}={\varvec{g}}$. From the definition of E, we conclude that $\varvec{v}$ satisfies (8).

Based on this observation, to solve the Dirichlet problem, we can define a linear operator B (which we will soon prove equals $(A^D)^{-1}$) as follows: we first define a restriction operator

$$\begin{aligned} \mathbb {C}^n \ni \varvec{w} = R \varvec{v}, \quad w_j =v_j, \quad j=1,\ldots n, \quad \varvec{v}\in \mathbb {R}^N. \end{aligned}$$

(9)

We then set

$$\begin{aligned} B\varvec{f} = R \mathcal {F}^{-1} (D^P)^{-1} \mathcal {F} E \varvec{f}. \end{aligned}$$

(10)

As the next proposition shows, B provides the exact solution to problem (2).

Proposition 2

With B defined in (10) we have

$$ B = (A^D)^{-1},\text{ and } \text{ hence, } \quad \varvec{u} = B \varvec{f}. $$

Proof

We notice that $R=(I_{n}, 0_{n,n+2})\in \mathbb {R}^{n\times N}$, and $E=(I_{n}, 0_{n\times 1},-\tilde{I}_{n}, 0_{n\times 1} )^t\in \mathbb {R}^{N\times n}$, where $I_n$ is the $n\times n$ identity matrix and $\tilde{I}_{n}=(\delta _{i,n+1-j})_{ij}$. Computing the product $A^DR(A^P)^{-1}E$ then shows that:

$$\begin{aligned} A^DR(A^P)^{-1}E=A^D(I, 0)(A^P)^{-1}E=(A^D, 0)(A^P)^{-1}E=(I, 0)E=I. \end{aligned}$$

(11)

Indeed, the identities in (11) are verified by direct calculation:

$$\begin{aligned}&((A^D, 0)(A^P)^{-1})_{ij}\nonumber \\&=-\frac{1}{N}(\mathcal {F}^{-1} (D^P)^{-1}\mathcal {F})_{i-1,j}+\frac{2}{N}(\mathcal {F}^{-1} (D^P)^{-1} \mathcal {F})_{i,j}-\frac{1}{N}(\mathcal {F}^{-1} (D^P)^{-1} \mathcal {F})_{i+1,j}\nonumber \\&=\frac{1}{N}\sum _{l=1}^N(-\bar{z}^{(i-2)(l-1)}+(2-k^2h^2){\varvec{\bar{z}}}^{(i-1)(l-1)}-\bar{z}^{i(l-1)})d_lz^{(k-1)(j-1)}\nonumber \\&=\frac{1}{N}\sum _{l=1}^N(2-k^{2} h^{2}-2\cos (\frac{2\pi (l-1)}{N}))d_lz^{(k-1)(j-i)}\nonumber \\&=\frac{1}{N}\sum _{l=1}^Nz^{(k-1)(j-i)}=\delta _{ij}. \end{aligned}$$

(12)

This completes the proof.

Generalization to Higher Dimensions (Dirichlet Problem). We now consider the Helmholtz problem $\mathcal {L}(0,1;k)$, defined in (1) in d-dimensions, i.e. we take $\varOmega =(0,1)^d$. With central finite difference discretization, we have the linear system:

$$\begin{aligned} A^D\varvec{u} = \varvec{f},\quad A^D = \sum _{j=1}^d \left( I^{\otimes (j-1)} \otimes T^D \otimes I^{\otimes (d-j)}\right) -k^2h^2 I^{\otimes d} \in {\mathbb R}^{n^d\times n^d}. \end{aligned}$$

(13)

Here $M^{\otimes p}\,{:}{=}\, \underbrace{M \otimes \ldots \otimes M}_{p\quad copies}$ for any matrix M and $T^D$ as in (2) is the tri-diagonal matrix.

The extension and restriction operators in higher dimensions can be written as $E^{\otimes d}$ and $R^{\otimes d}$. The “odd” extension of $\varvec{f}$ is then $\varvec{g}=E^{\otimes d} \varvec{f}$. As in the 1D case, the linear system for the extended Helmholtz equation is:

$$\begin{aligned} A^P\varvec{v} = \varvec{g},\quad A^P = \sum _{j=1}^d \left( I^{\otimes (j-1)} \otimes T^P \otimes I^{\otimes (d-j)}\right) -k^2h^2 I^{\otimes d} \in {\mathbb R}^{N^d\times N^d}, \end{aligned}$$

(14)

where $T^P$ has been defined in (4). As in the one dimensional case (5), the matrix $A^P$ is diagonalized by the multidimensional DFT $\mathcal {F}_d=\mathcal {F}^{\otimes d}$. The multidimensional version of (5) then is

$$ \mathcal {F}_d A^P\mathcal {F}_d^{-1} = D^P_d \, {:}{=} \, \sum _{j=1}^d \left( I^{\otimes (j-1)} \otimes D^P \otimes I^{\otimes (d-j)}\right) -k^2h^2 I^{\otimes d}. $$

As a consequence, we obtain inversion formula similar to the one presented in Proposition 2. To show such representation, we need the following result.

Lemma 1

Let E and R be extension and restriction operator defined in (7) and (9) respectively. Then the following identity holds

$$\begin{aligned} A^D = R^{\otimes d} A^P E^{\otimes d}. \end{aligned}$$

(15)

Proof

By using the standard properties of the tensor product, we have

$$\begin{aligned} R^{\otimes d} A^P E^{\otimes d}= & {} R^{\otimes d} \left( \sum _{j=1}^d \left( I^{\otimes (j-1)} \otimes T^P \otimes I^{\otimes (d-j)}\right) -k^2h^2 I^{\otimes d}\right) E^{\otimes d}\\= & {} R^{\otimes d}\left( \sum _{j=1}^d \left( E^{\otimes (j-1)} \otimes T^P E \otimes E^{\otimes (d-j)}\right) -k^2h^2 E^{\otimes d}\right) \\= & {} \sum _{j=1}^d \left( I^{\otimes (j-1)} \otimes RT^P E \otimes I^{\otimes (d-j)}\right) -k^2h^2 I^{\otimes d}. \end{aligned}$$

It is straightforward to check that $RT^PE=T^D$. Thus, $R^{\otimes d} A^P E^{\otimes d}=A^D$.

The following theorem gives the representation of the inverse of the discretized Dirichlet problem in the multidimensional case.

Theorem 1

The inverse of $A^D$ can be written as

$$\begin{aligned} (A^D)^{-1}=R^{\otimes d} (A^P)^{-1} E^{\otimes d},\quad \text{ and } \text{ hence, }\quad \varvec{u} = R^{\otimes d} (A^P)^{-1} E^{\otimes d} \varvec{f}. \end{aligned}$$

(16)

Proof

Clearly, it is straight forward to see the following

$$ A^DR^{\otimes d}(A^P)^{-1}E^{\otimes d}=R^{\otimes d}A^PE^{\otimes d}R^{\otimes d}(A^P)^{-1}E^{\otimes d}=I, $$

by the using properties of the matrix tensor product, Lemma 1 and identity $RE=I$.

Notice here, all the above results can be extended to rectangle (non-square) domain without too much difference. As a conclusion, we can solve the constant coefficient Helmholtz equation with Dirichlet boundary condition by FFT with complexity $O(n\log n)$, where n is the problem size.

2.2 Neumann Boundary Conditions

Neumann Problem in 1D. Let us consider the following 1D Helmholtz equation with one side Neumann boundary condition in (0, 1):

$$\begin{aligned} -u'' - k^2 u = f, \quad u(0)=0, \quad u'(0)=g. \end{aligned}$$

(17)

After discretization with central finite difference, we have the linear system

$$ A\varvec{u}= \varvec{f} $$

where

$$\begin{aligned} A=\mathrm{tridiag}(-1,2-k^2h^2,-1)-(1-\frac{1}{2}k^2h^2)e_{n+1}e_{n+1}^t\in \mathbb {R}^{(n+1)\times (n+1)}, \end{aligned}$$

(18)

and $\varvec{u}=(u_1,\ldots ,u_{n+1})^t$, $h=1/(n+1)$, $u_j\approx u(jh)$, $f_j= f(jh)$, for $j=1,\ldots , n+1$, and $\varvec{f}=(h^2f_1,\ldots ,h^2f_n,\frac{1}{2}h^2f_{n+1}+hg)^t$.

With Fourier method for the Dirichlet problem in mind, we do “even” extension of the system (18) to get a Toeplitz system similar to (2):

$$\begin{aligned} A^e\varvec{u}^e= \varvec{f}^e, \quad A^e=\mathrm{tridiag}(-1,2-k^2 h^2,-1) \in \mathbb {R}^{M\times M}, \end{aligned}$$

(19)

where $M=2n+1$, $\varvec{u}^e=(u_1,\ldots ,u_{M})^t$, and $\varvec{f}^e=(h^2f_1,\ldots , h^2f_n,h^2f_{n+1}+2hg,h^2f_{n},\ldots ,h^2f_1)^t$. By symmetry, the solution of system (19), when restricted on interval (0, 1), will be the same as solution of system (18). Even though the problem size has been doubled, the extended system is Toeplitz, thus can be solved by Fourier method from Sect. 2.

In summary, we have the following inverse of the Neumann operator, that is the solution of:

$$ A^{-1}\varvec{f} = R_n\mathcal {F}^{-1} (D^P)^{-1} \mathcal {F}E_{o}E_{e}\varvec{f}. $$

The operators involved in the definition above are (from right to left): even extension, odd extension followed by the inverse of the periodic problem and then restriction to Neumann problem. More precisely, for the even extension $E_e$ we have,

$$\begin{aligned} \mathbb {C}^M \ni \varvec{f}^e=[E_e\varvec{f}]_j = {\left\{ \begin{array}{ll} f_{j},\quad j=1,\ldots ,n,\\ 2f_{n+1}, \quad j=n+1, \\ f_{M+1-j}, \quad j=n+2,\ldots , M.\\ \end{array}\right. } \end{aligned}$$

(20)

Next, for the extension as to odd functions/vectors we have:

$$\begin{aligned} \mathbb {C}^{2M+2}\ni \varvec{f}^o= [E_o\varvec{f}^e]_j = {\left\{ \begin{array}{ll} f_{j}^e,\quad j=1,\ldots ,M,\\ 0,\quad j=M+1,\\ -f_{N-j}^e, \quad j=M+2,\ldots ,2M+1,\\ 0,\quad j=2M+2. \end{array}\right. } \end{aligned}$$

(21)

Finally, as in (5), we have the diagonal matrix $D^P=\mathrm{diag}(d_l)$ with $d_l = 4\sin ^2\frac{\pi (l-1)}{2M+2}-k^2h^2$ for $l=1,\ldots , 2M+2$, and the restriction $R_n$ operator (to Neumann problem (18)):

$$ \varvec{v}\in \mathbb {R}^{2M+2},\quad \mathbb {C}^{n+1} \ni \varvec{u} = R_n \varvec{v}, \quad u_j =v_{j}, \quad j=1,\ldots n+1. $$

Generalization to Higher Dimensions (Neumann problem). The Fourier method for Neumann problem can also be generalized to any dimension d in a fashion similar to the procedure given earlier for the Dirichlet problem. Just for illustration, we consider the following problem in 2D:

$$\begin{aligned} {\left\{ \begin{array}{ll} -\varDelta u-\eta ^2 u =f\quad \text{ in } \quad \varOmega =(0,1)^2, \\ \frac{\partial u}{\partial x}=g \quad \text{ on } \quad \varGamma _1=\{x=1\}\times (0,1), \\ u=0 \quad \text {on}\quad \partial \varOmega /\varGamma _1. \end{array}\right. } \end{aligned}$$

(22)

We first do an “even” extension of the linear system and arrive at

$$\begin{aligned} A^e\varvec{u}^e = \varvec{F}^e, \quad A^e=I_M\otimes T^d_n+T^d_M\otimes I_n-k^2 h^2I_{Mn} \in \mathbb {R}^{Mn\times Mn}, \end{aligned}$$

(23)

where $T^d_j=\mathrm{tridiag}(-1,2,-1) \in \mathbb {R}^{j\times j}$ for any j, $\varvec{u}^e=(\varvec{u}_1,\ldots ,\varvec{u}_{M})^t$, and $\varvec{F}^e=(h^2\varvec{f}_1,\ldots , h^2\varvec{f}_n,h^2\varvec{f}_{n+1}+2hg,h^2\varvec{f}_{n},\ldots ,h^2\varvec{f}_1)^t$. Clearly, the restriction of $\varvec{u}^e$ on $\varOmega \cup \varGamma _1$ is the same as the solution of the Neumann problem. Now, for the solution of (23) we can apply the method we have already described in Sect. 2.1.

3 Stekloff Eigenvalue Computation with Fourier Method

3.1 Variational Formulation

Multiplying the first equation in (1) with $\alpha =1$ by $v\in H^1(\varOmega )$ and integrating by parts, we get:

$$ \int _\varOmega \nabla w\nabla v-\eta ^2\int _\varOmega wv=-\lambda \int _\varGamma wv. $$

Define $A(\eta ):H^1(\varOmega )\rightarrow H^{-1}(\varOmega )$ as

$$\begin{aligned} \langle A(\eta )w,v\rangle \,{:}{=}\,(\nabla w, \nabla v)_\varOmega -\eta ^2(w,v)_\varOmega \quad \forall v\in H^1(\varOmega ), \end{aligned}$$

(24)

where $(\cdot , \cdot )_\varOmega$ is the $L^2$ inner product and $\langle \cdot , \cdot \rangle$ is duality pairing between $H^{-1}(\varOmega )$ and $H^1(\varOmega )$. The Stekloff operator, or Dirichlet-to-Neumann (DtN), $S(\eta )$ can be defined in two steps:

Firstly, for any $f\in H^{1/2}(\varGamma )$, define $f_0\in H_0^1(\varOmega )$ as the unique function satisfying:

$$ \langle A(\eta )f_0,v_0\rangle =-\langle A(\eta )(Ef),v_0\rangle , \quad \forall v_0\in H_0^1(\varOmega ), $$

where Ef is $H^1$-bounded extension of f, e.g. harmonic extension.

Secondly, define the action of $S(\eta ):H^{1/2}(\varGamma )\rightarrow H^{-1/2}(\varGamma )$ as

$$\begin{aligned} \langle S(\eta )f,g\rangle _{1/2}=\langle A(\eta )(f_0+Ef),Eg\rangle ,\quad \forall g\in H^{1/2}(\varGamma ), \end{aligned}$$

(25)

where $\langle \cdot ,\cdot \rangle _{1/2}$ is the duality pairing between $H^{1/2}(\varGamma )$ and $H^{-1/2}(\varGamma )$.

Lemma 2

The Eq. (1) with $\alpha =1$ has a non-trivial solution if and only if $-\lambda$ is an eigenvalue of the Stekloff operator $S(\eta )$.

Proof

We prove one side of this equivalence here since the other half is similar. Suppose u is solution to (1) with $\alpha =1$, then

$$ \langle A(\eta )u, v_0 \rangle =0,\quad \forall v_0 \in H^1_0(\varOmega ). $$

From the above equation, we have

$$ \langle A(\eta )(u-Eu_\varGamma ),v_0\rangle = -\langle A(\eta )Eu_\varGamma ,v_0 \rangle , \quad \forall v_0\in H^1_0(\varOmega ), $$

where $u_\varGamma \,{:}{=}\,u|_\varGamma$ is the trace of u on $\varGamma$. Denote $u_0\,{:}{=}\,u-Eu_\varGamma$. It is easy to see that $u_0\in H_0^1(\varOmega )$ and the following equation holds:

$$ \langle S(\eta )u_\varGamma , g\rangle _{1/2}=\langle A(\eta )(u_0+Eu_\varGamma ), Eg\rangle =\langle A(\eta )u,Eg\rangle =-(\lambda u_\varGamma , g). $$

This shows that $-\lambda$ must be the eigenvalue of $S(\eta )$.

This lemma implies that solving problem (1) is equivalent to finding the eigenvalue for $S(\eta )$ with given $\eta$. In the next section we describe an efficient method for this task, namely the Fourier method for Stekloff eigenvalues.

3.2 Neumann-to-Dirichlet and Dirichlet-to-Neumann Operators

We start with the definition of Neumann-to-Dirichlet operator $T: L^2(\varGamma )\rightarrow L^2(\varGamma )$. Let $\mu \in L^2(\varGamma )$ and define $w_\mu \in H^1(\varOmega )$ to be the solution of Neumann problem $\mathcal {L}(1,0;\eta )w=(0,\mu )^t$. Equivalently, $w_{\mu }\in H^1(\varOmega )$ satisfies

$$\begin{aligned} \langle A(\eta )w_\mu , v \rangle =\langle \mu , v \rangle _{1/2},\quad \text {for any} \quad v\in H^1(\varOmega ). \end{aligned}$$

(26)

Taking the trace of $w_\mu$, we can define Neumann-to-Dirichlet (NtD) operator T as $T\mu =w_\mu |_{\varGamma }$.

After discretization the Neumann problem $\mathcal {L}(1,0;\eta )w=(0,\mu )^t$ with finite differences¹, we have the following linear system:

$$\begin{aligned} \begin{bmatrix} A_{II}&A_{IB}\\ A_{BI}&A_{BB}\\ \end{bmatrix}\begin{bmatrix} \varvec{w}_I \\ \varvec{w}_B \end{bmatrix}=\begin{bmatrix} \varvec{0}\\ {\varvec{\mu }} \end{bmatrix}, \end{aligned}$$

(27)

where ${\varvec{\mu }}$ is discretized version of $\mu$, $\varvec{w}_I$ and $\varvec{w}_B$ are approximations to solution of (26) restricted inside $\varOmega$ and on boundary $\varGamma$ respectively. Notice here we order the grids by their positions in the domain for illustration purpose. As we discussed in Sect. 2.2, Eq. (27) can be solved efficiently with Fourier method.

The discretized NtD operator $T_h$ corresponding to the NtD operator T is

$$\begin{aligned} T_h{\varvec{\mu }}=\begin{bmatrix} \varvec{0}, I \end{bmatrix} \begin{bmatrix} A_{II}&A_{IB}\\ A_{BI}&A_{BB}\\ \end{bmatrix}^{-1}\begin{bmatrix} \varvec{0}\\ {\varvec{\mu }} \end{bmatrix}. \end{aligned}$$

(28)

To discretize the Dirichlet-to-Neumann operator, we consider the Dirichlet problem $\mathcal {L}(0,1;\eta )w=(0,g)^t$. With analogous discretization, we have the following linear system:

$$\begin{aligned} \begin{bmatrix} A_{II}&A_{IB}\\ \varvec{0}&I\\ \end{bmatrix}\begin{bmatrix} \varvec{w}_I \\ \varvec{w}_B \end{bmatrix}=\begin{bmatrix} \varvec{0}\\ \varvec{g} \end{bmatrix}. \end{aligned}$$

(29)

Here $\varvec{g}$ is discretization of g. Clearly, $\varvec{w}_B = \varvec{g}$ as expected and the discrete version of (25) gives the action of $S_h$ as

$$\begin{aligned} S_h\varvec{g}=(A_{BB}-A_{BI}A_{II}^{-1}A_{IB})\varvec{g}. \end{aligned}$$

(30)

We have the following Lemma, which shows that $T_h$ is the inverse of $S_h$.

Lemma 3

For the operators $T_h$ and $S_h$ defined in (28) and (30), respectively, we have $S_hT_h=I$.

Proof

We just need to show $S_hT_h{\varvec{\mu }}= {\varvec{\mu }}$ for any ${\varvec{\mu }}$. This can be easily proved by Block-LU factorization.

$$\begin{aligned} {\begin{matrix} S_hT_h{\varvec{\mu }} &{}=S_h\begin{bmatrix} {\varvec{0}}, I \end{bmatrix} \begin{bmatrix} A_{II} &{} A_{IB}\\ A_{BI} &{} A_{BB}\\ \end{bmatrix}^{-1}\begin{bmatrix} \varvec{0}\\ {\varvec{\mu }} \end{bmatrix}\\ &{}=S_h\begin{bmatrix} \varvec{0}, I \end{bmatrix} \bigg (\begin{bmatrix} I &{} \varvec{0}\\ A_{BI}A_{II}^{-1} &{} I\\ \end{bmatrix}\begin{bmatrix} A_{II} &{} A_{IB}\\ \varvec{0} &{} S_h\\ \end{bmatrix}\bigg )^{-1}\begin{bmatrix} \varvec{0}\\ {\varvec{\mu }} \end{bmatrix} ={\varvec{\mu }}. \end{matrix}} \end{aligned}$$

(31)

The results from the previous two sections show that we can efficiently compute the Stekloff eigenvalues of small magnitude as well as large magnitude. For example, the eigenvalues of small magnitude of $S_h$ can be approximated by the reciprocal of the eigenvalues of NtD operator $T_h$. The action of $T_h$, which is needed repeatedly in such a procedure, can be efficiently computed by the Fourier method applied to the solution of the Helmholtz-Neumann problem as we have discussed earlier. For eigenvalues of the largest magnitude the same applies, except that we need the action of $S_h$, which requires fast solution of the corresponding Dirichlet problems, which we also described earlier.

4 Numerical Examples

In this section, we present two applications of the Fourier method described in Sect. 2. In the first example, the Fourier method is utilized in computing the Stekloff eigenvalues as discussed in Sect. 3. For the second example, given the fact that we can compute the numerical solution of constant coefficient Helmholtz equation efficiently, we apply such solver as preconditioner for varying efficient problem. Both examples are implemented in MATLAB and all tests have been performed on the same computer with dual-core 2.5 GHz CPU.

4.1 Computing Stekloff Eigenvalues

In this numerical example, we calculate the Stekloff eigenvalues corresponding to the problem:

$$\begin{aligned} {\left\{ \begin{array}{ll} -\varDelta w-\eta ^2 w =0\quad \text{ in } \quad \varOmega =(0,1)^2, \\ \frac{\partial w}{\partial n}+\lambda w=0 \quad \text{ on } \quad \varGamma _1=\{x=1\}\times (0,1), \\ w=0 \quad \text {on}\quad \partial \varOmega /\varGamma _1. \end{array}\right. } \end{aligned}$$

(32)

As is discussed in Sect. 3, the Stekloff eigenvalues can be numerically approximated by the eigenvalues of discretized DtN operator $S_h$ in (30). To find the eigenvalues of $S_h$ with small magnitude, for example, we need an efficient algorithm to compute the action of $T_h=S_h^{-1}$ on a vector. As in (28), one Neumann problem needs to be solved for computing each action. Thus, we create a function handle that solves the Neumann boundary problem in (28) with FFT, which is then used in MATLAB eigensolver eigs. For different $\eta$ and grid size $n\times n$, the smallest six eigenvalues in magnitude are reported in Table 1.

Table 1. Smallest six Stekloff eigenvalues in magnitude for different $\eta$ on $n\times n$ grid with n = 50, 100.

4.2 Helmholtz Equation with Varying Wave Number

We consider the Helmholtz equation with homogeneous Dirichlet boundary condition and varying coefficient on domain $(0,1)^2$, i.e.

$$ \mathcal {L}(0,1;k(x,y))u=(f(x,y),0)^t. $$

The external force f(x, y) is set to be constant 1. The wave number fields are $k_i(x,y)=\omega /c_i(x,y)$ with constant angular frequency $\omega$ and varying velocity fields $c_i(x,y)$ for $i=1,2$ as follows:

• 1. $c_1(x,y)=\frac{4}{3}[1-0.5\exp (-0.5(x-0.5)^2]$,

• 2. $c_2(x,y)=\frac{4}{3}[1-0.5\exp (-0.5(x-0.5)^2+(y-0.5)^2)]$.

After discretizing the equation with central finite difference, we use GMRES as iterative solver for the linear system (relative residual tolerance $10^{-3}$). The preconditioner is implemented by solving the constant wave number problem with k equaling the average value of number field over the entire domain.

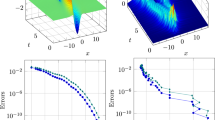
To study how the preconditioning performance is depending on the magnitude of $k_i(x,y)$, we gradually increase $\omega$ and grid size n (in each dimension), while keeping the ratio $\omega /n$ fixed. In fact, this is the most computationally challenging case, since the relative percentage of positive eigenvalues for the linear system is fixed. We record the number of iteration $N_i$ and CPU time $T_i$ for the preconditioned GMRES to converge in Table 2. As a special case, for $\omega =6.4\pi$, the wave number fields $k_i(x,y)$ and resulted wave fields $u_i(x,y)$ in each case have been shown in Fig. 1.

Table 2. Varying $\omega$ and n, GMRES iterations number and time.

Fig. 1.

Simulation results for different velocity fields.

5 Conclusions

In this paper, we proposed an efficient method for finding eigenvalues of indefinite Stekloff operators. The main tool that we developed is a fast Fourier method for solving constant coefficient Helmholtz equation with Dirichlet or Neumann boundary condition discretized on a uniform mesh. The resulting algorithm is efficient, transparent, and easy to implement. Our numerical experiments show that such algorithm works also as a solver for the Helmholtz problem with mildly varying coefficients (non-constant wave number). Another pool of important applications will be the computation of transmission eigenvalues, where our method has the potential to provide an efficient computational tool.