Reflectance and Transmittance of Cholesteric Liquid Crystal Sandwiched Between Polarizers

Abstract

In this paper we calculated reflection and transmission coefficients of the electromagnetic radiation (light) incident on the cholesteric liquid crystal sandwiched between two isotropic optical media and a pair of polarizers. To model optical phenomena (i.e. propagation and interference of the light waves) in liquid crystal, we applied the 4 × 4 matrix method. As a result of the performed computer simulation, we obtained some interesting reflection/transmission spectra and polar plots for different parameters of the considered system and arbitrary incident monochromatic light. The illustrated and discussed results can be useful for understanding different optical systems, especially liquid crystal displays. Moreover, the applied mathematical approach can be potentially used for modelling of more advances contemporary optical systems, i.e. photonic crystals.

1 Introduction

Liquid crystals (LCs) are an interesting fourth state of matter lying between the crystalline solid and amorphous liquid states. Therefore, in some temperature ranges, they exhibit both the properties of liquids and the properties of crystalline solid state. Most of them are organic compounds with elongated molecules that influence their interesting physical properties. The classification of LCs distinguishes three types of liquid crystalline phases, namely: nematic, smectic and cholesteric liquid crystals (CLCs). The above listed groups differ in physical properties, especially in optical ones. However, due to the strongly periodic helical structure, cholesteric liquid crystals exhibit unique optical properties. The first of these is the optical birefringence, i.e. two different refractive indices. In the birefringent medium, the propagating wave of the monochromatic radiation decomposes into two waves, which propagate with different velocities. In addition, CLCs are characterized by twisting of the plane of polarization and circular dichroism. However, the most popular engineering applications employ the selective reflection of incident radiation of the light. The colour of the reflected light depends on temperature, mechanical stress, external electric, magnetic fields, etc. Due to the abovementioned properties of LCs, they have been used in practical applications, especially in liquid crystal displays. Moreover, CLCs seems to be the promising candidates for numerous different photonic applications. Therefore, nowadays, a lot of attention is paid to the photonic crystals (PCs), whose optical properties are similar to the properties of liquid crystals due to their periodic dielectric structures. These substances contain a periodic distribution of both refractive indices in one, two, or three dimensions, and can be used to prohibit, confine, and control light propagation in a specific wavelength bandwidth. An interesting review of the fabrication of photonic band gap materials based on cholesteric liquid crystals is presented in the review paper [1]. In the present study, we tested the implemented computer algorithm of the 4 × 4 matrix method using CLC sandwiched within two isotropic media and optical polarizers. However, the used algorithm can be adopted to model optical phenomena in photonic crystals with a known distribution of the dielectric structure.

2 Methods—A Brief Literature Review

It should be noted that optical phenomena and the transmission of light through birefringent optical media (networks) have been treated by different methods. In the conventional Jones calculus, each optical element (wave plate, liquid crystal layer) is represented by a 2 × 2 matrix, and refraction and reflection of light at the plate surfaces (dielectric discontinuities) are neglected. This method is limited to normally incident light and does not explain the leakage of off-axis light through a pair of crossed ideal polarizers [2]. For treating the transmission of off-axis light in a general birefringent optical media, the extended Jones matrix method can be used, which takes into account the single reflection at the interfaces. This method is adequate for numerous practical applications, and has been widely used in the analysis of many optical systems [2,3,4,5,6,7]. In 2000, Li [8] applied the Jones matrix method to ellipsometry, i.e. for investigating the dielectric properties of a thin film. In turn, in 2010, Chen et al. [9] used a new 2 × 2 matrix method and discussed the polarization state of transmitted waves through the cholesteric liquid crystal.

On the contrary to the aforementioned methods dedicated to the birefringent networks, the exact solutions can be obtained by using the 4 × 4 matrix method, which takes into account both the effect of refraction and multiple reflections between plate interfaces [2]. This approach has been applied by many researches. For instance, Schwelb [10] analyzed lossy gyro electromagnetic layers in polar and longitudinal orientation. Chen et al. [11] applied the 4 × 4 matrix method to liquid crystal displays. Using this method, Ivanov and Sementsov [12] described the propagation of electromagnetic waves in stratified bianisotropic chiral structures. Most recently, the 4 × 4 matrix method was used by Ortega et al. [13] to study different kinds of cells of cholesteric liquid crystal lasers. Due to abovementioned anisotropic properties of CLCs and PCs, we used the exact 4 × 4 matrix method also in this paper, which is shortly presented in Sect. 3.

3 Model of the Considered Optical System

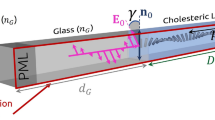
Figure 1a presents the model of the cholesteric liquid crystal placed in the Cartesian coordinate system xyz and sandwiched between two (i.e. lower and upper) isotropic media. The considered CLC with thickness $d$ is divided into N equal layers parallel to the xy plane. The incident light propagates in the lower medium (n = 0), and then partially propagates in the liquid crystal (n = 1, 2, …, N) and the upper isotropic medium (n = N + 1). The c-axis (optical axis) of the CLC lies in the xy plane and changes periodically along the z-direction. Periodical helical structure of the analyzed CLC is characterized by the pitch $p$. Both lower and upper isotropic media are quantified by a refractive index $n_{s}$. The liquid crystal has two refractive indices, $n_{o}$ and $n_{e}$, for the ordinary and extraordinary waves, respectively. Figure 1b presents orientation (described by angles $\theta$ and $\phi$) of the wave vector ${\mathbf{k}}$ of the incident non-polarized beam of monochromatic light with wavelength $\lambda$, in lower isotropic medium.

Fig. 1

Model of the investigated cholesteric liquid crystal sandwiched within two isotropic optical media (a) and the orientation of the wave vector ${\mathbf{k}}$ of the arbitrarily incident light (b)

The 4 × 4 matrix method used in the paper was developed on the basis of mathematical formalism presented in monograph [14]. Therefore, only the main stages of this method, which are needed in the further part of the paper dedicated to the modeling of CLCs sandwiched within optical polarizers, are presented below. In this method, the optical c-axes and the dielectric tensors ${\hat{\varvec{\upvarepsilon}}}(n)$ of the individual liquid crystal layers (n = 1,2, …, N) and bounded plates (n = 0 and n = N + 1) are determined first. In the second step, the wave vectors ${\mathbf{k}}_{\sigma } (n)$ of all four elementary waves ($\sigma = 1,2,3,4$) in all layers are calculated. The third stage is devoted to computing of the optical polarization vectors ${\mathbf{p}}_{\sigma } (n)$ of individual elementary waves representing the directions of the electric field and the corresponding vectors ${\mathbf{q}}_{\sigma } (n)$ representing the directions of the magnetic field. In the fourth stage of this method, transition matrices between individual layers are calculated based on the assumption of continuity of the tangential components of the vectors ${\mathbf{p}}_{\sigma } (n)$ and ${\mathbf{q}}_{\sigma } (n)$ at the dielectric interfaces. The product of the abovementioned individual matrices is the 4 × 4 transition matrix, which describes the relationships between amplitudes of the electric field of the incident waves $A_{s}$, $A_{p}$, reflected waves $B_{s}$, $B_{p}$, and transmitted waves $C_{s}$, $C_{p}$, both for s and p waves, respectively. Finally, in the last stage of this method, the coefficients of reflection $R$ and transmission $T$ of the incident light are computed.

Let us consider now two ideal optical polarizers bounding the optical system presented in Fig. 1a. In general, a polarizer is an optical filter that transmits light waves of a specific polarization and blocks light waves of other polarizations. It can also be used to analyze the polarized light, and then it is called an analyzer. The dependence of the intensity of the transmitted light on the angle $\varphi$ between polarization axes of the polarizer and analyzer is given by the Malus’s law

$$ I = I_{0} \cos^{2} \varphi , $$

(1)

where $I_{0}$ is the initial intensity of beam of light polarized by polarizer, whereas $I$ is the intensity of the light that passes through the analyzer. In general, the optical polarizer can be characterized by the axis of polarization. In our system, these axes (both for polarizer and analyzer) lie in the xy plane and can be oriented arbitrarily (angles $\phi_{po}$ and $\phi_{an}$) with respect to the x-axis, as it is shown in Fig. 2.

Fig. 2

Orientation of the polarization axes of the polarizer (a) and the analyzer (b)

The polarization axes can be characterized by the following unit vectors

$$ {\mathbf{po}} = [\cos \phi_{po} ,\sin \phi_{po} ,0]^{T} , $$

(2)

$$ {\mathbf{an}} = [\cos \phi_{an} ,\sin \phi_{an} ,0]^{T} . $$

(3)

The vector of the optical polarization of the light transmitted through the polarizer is normal to the wave vector ${\mathbf{k}}_{1} (0)$, which denotes the wave vector of the incident s wave in the lower isotropic medium. Therefore, the unit vector ${\mathbf{A}}$ of the optical polarization of the polarized incident light can be determined as follows

$$ {\mathbf{A}} = \frac{{{\mathbf{k}}_{1} (0) \times [{\mathbf{po}} \times {\mathbf{k}}_{1} (0)]}}{{\left| {{\mathbf{k}}_{1} (0) \times [{\mathbf{po}} \times {\mathbf{k}}_{1} (0)]} \right|}}. $$

(4)

The vector ${\mathbf{A}}$ can be decomposed into the components ${\mathbf{A}}_{s}$ and ${\mathbf{A}}_{p}$, with the amplitudes $A_{s}$ and $A_{p}$, respectively. These amplitudes can be determined as follow

$$ A_{s} = {\mathbf{A}} \cdot {\mathbf{p}}_{1} (0), $$

(5)

$$ A_{p} = {\mathbf{A}} \cdot {\mathbf{p}}_{3} (0), $$

(6)

where ${\mathbf{p}}_{1} (0)$ and ${\mathbf{p}}_{3} (0)$ are the optical polarization vectors of incident s and p waves, respectively, in lower isotropic optical medium.

Knowledge of the amplitudes $A_{s}$ and $A_{p}$ allows one to determine the values $B_{s}$, $B_{p}$ of the reflected s and p waves, and the values $C_{s}$ and $C_{p}$ of the transmitted s and p waves, respectively, using the 4 × 4 matrix method. As a result, the optical polarization vector ${\mathbf{B}}$ for the reflected wave and the vector ${\mathbf{C}}$ for the transmitted wave can be obtained as follow

$$ {\mathbf{B}} = B_{s} {\mathbf{p}}_{2} (0) + B_{p} {\mathbf{p}}_{4} (0), $$

(7)

$$ {\mathbf{C}} = C_{s} {\mathbf{p}}_{1} (N + 1) + C_{p} {\mathbf{p}}_{3} (N + 1), $$

(8)

where ${\mathbf{p}}_{2} (0)$ and ${\mathbf{p}}_{4} (0)$ denote optical polarization vectors of the reflected s and p waves, respectively. On the other hand, ${\mathbf{p}}_{1} (N + 1)$ and ${\mathbf{p}}_{3} (N + 1)$ stand for the optical polarization vectors of the transmitted to the upper isotropic medium s and p waves, respectively.

Let the vectors ${\mathbf{PO}}$ and ${\mathbf{AN}}$ be the unit vectors lying in the planes of the polarizer and the analyzer, which are normal to the wave vector ${\mathbf{k}}_{2} (0)$ of the reflected wave in the lower isotropic medium and the wave vector ${\mathbf{k}}_{1} (N + 1)$ of the transmitted wave to the upper isotropic medium, respectively. The unit vectors that have these properties have the following forms

$$ {\mathbf{PO}} = \frac{{{\mathbf{k}}_{2} (0) \times [{\mathbf{pol}} \times {\mathbf{k}}_{2} (0)]}}{{\left| {{\mathbf{k}}_{2} (0) \times [{\mathbf{pol}} \times {\mathbf{k}}_{2} (0)]} \right|}}, $$

(9)

$$ {\mathbf{AN}} = \frac{{{\mathbf{k}}_{1} (N + 1) \times [{\mathbf{pol}} \times {\mathbf{k}}_{1} (N + 1)]}}{{\left| {{\mathbf{k}}_{1} (N + 1) \times [{\mathbf{pol}} \times {\mathbf{k}}_{1} (N + 1)]} \right|}}. $$

(10)

The scalar product of the unit vectors is equal to the cosine of the angle between their directions. Therefore, both the reflection coefficient $R$ and the transmission coefficient $T$ can be determined from the formulas

$$ R = \frac{{B_{s}^{2} + B_{p}^{2} }}{{A_{s}^{2} + A_{p}^{2} }}\left( {\frac{{\mathbf{B}}}{{\left| {\mathbf{B}} \right|}} \cdot {\mathbf{PO}}} \right)^{2} , $$

(11)

$$ T = \frac{{C_{s}^{2} + C_{p}^{2} }}{{A_{s}^{2} + A_{p}^{2} }}\left( {\frac{{\mathbf{C}}}{{\left| {\mathbf{C}} \right|}} \cdot {\mathbf{AN}}} \right)^{2} . $$

(12)

4 Simulation Results

In what follows, we illustrated and discussed some calculations of the reflection and transmission coefficients $R$ and $T$ for different parameters of the considered optical system. In addition, we calculated values of these coefficients for different angles characterizing the orientation of the incident light in the form of colour polar plots.

To test the operation of the developed algorithm, at first, we considered the case when the non-polarized light propagated through the homogenous and lossless isotropic optical medium, i.e. we assumed that $n_{s} = n_{o} = n_{e}$. For this case, for arbitrary values of the parameters $d$, $\lambda$, $\theta$, $\phi$, $n_{s} = n_{o} = n_{e}$ and N, we obtained always $R = 0$ and $T = 1$. In such system, there are no dielectric discontinuities at the interfaces of the imaginary layers. Therefore there is a lack of reflection of the incident light, i.e. the incident light is completely transmitted through the analyzed optical medium.

In the next step of the performed tests, we took into account again a homogeneous isotropic medium sandwiched between two optical polarizers. Figure 3 shows the dependence of the transmission coefficient $T$ of the normally incident light as a function of the angle $\varphi$ (the angle between the axes of the polarizer and the analyzer). This dependence coincides with the theoretical dependence by means of Malus’s law defined by the formula (1). It should be noted that the presented relationships also coincide for other values of the analyzed lossless, homogenous, and isotropic optical medium as well as different values of the wavelength of the incident light.

Fig. 3

Transmission coefficient $T$ as a function of the angle $\varphi$ between polarization axes of the polarizer and the analyzer, obtained numerically and theoretically (based on Malus’s law)

Figure 4 shows the polar plots of the transmission coefficient $T$ as a function of the angles $\theta$ and $\phi$ of the incident non-polarized light for different orientations of the polarizer and the analyzer. It should be noted that in all polar plots presented in this paper, radial position corresponds to the angle $\theta$ (from 0 in the middle, to the 90° at the edges of the of the plotted polar distributions), whereas circumferential position corresponds to the angle $\phi$ (from 0 to 360°, as it is shown in plotted distributions). The presented results show that the values of the transmission coefficients depend both on the orientation of the wave vector of the incident light and relative orientations of the polarizer and analyzer.

Fig. 4

Polar plots of the transmission coefficient $T$ for different orientations of the polarizers

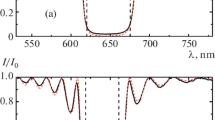
In the next step of the analysis, we presented some characteristics of the transmission coefficient $T$ for different parameters of the CLC sandwiched between two isotropic media. First, we investigated the system without polarizers. The parameters of the tested system are presented in Table 1. All calculations were carried out for N = 1000. Figure 5 shows the reflection $R$ and transmission $T$ spectra for normally incident non-polarized light.

Table 1 Parameters of the investigated CLC and the bounding isotropic media

Fig. 5

Reflection and transmission spectra of the normally incident non-polarized light. The colour scale below the plot corresponds to the colours of the light with wavelength presented on the x-axis. The sum of coefficients R + T equals 1 (for each value of the wavelength $\lambda$)

As can be seen, the presented curve is characterized by the reflection bandwidth, i.e. the range of the wavelength of the incident light where $R = 0.5$. The natural non-polarized incident light contains the same amount of both right- and left-circularly polarized light. Within the bandwidth, right-circularly polarized light is reflected by a right-handed helix, while left-circularly polarized light is transmitted by the cholesteric liquid crystal, and therefore values of both $R$ and $T$ coefficients are equal 0.5. Concluding, in our algorithm we confirmed the occurrence of the selective reflection of the incident radiation within the bandwidth and transmission of both polarization states outside the this bandwidth. Figure 6 presents reflection spectra for different parameters of the CLC.

Fig. 6

Reflection spectra of the normally incident non-polarized light for different values of the parameters $n_{o}$, $n_{e}$, $p$ and $d$. The colour scale below the picture corresponds to the colours of the light with wavelength presented on the x-axis

The obtained calculations showed that the bandwidth and its position in the wavelength spectrum strongly depend on the refractive indices $n_{o}$ and $n_{e}$ (see Fig. 6a and b). The bandwidth depends also strongly on the pitch $p$ of the helical structure of the CLC (see Fig. 6c), whereas the shape of the bandwidth is strongly dependent on the thickness $d$ of the investigated CLC (see Fig. 6d). The obtained results of computer simulations allowed us to analyze the basic properties of the optical polarizers as well as the optical properties of cholesteric liquid crystals.

For later comparative purposes, in Fig. 7a we presented the polar plot of the coefficient $T$ of the non-polarized light transmitted by the CLC, without polarizers. The calculations were performed for the parameters given in Table 1 and wavelength $\lambda = 507.5{\text{ nm}}$ (the middle of the selective reflection bandwidth presented in Fig. 5). As can be seen, the obtained plot does not depend on the angle $\phi$. However, we observed an interesting dependence on the angle $\theta$ presented in Fig. 7b, i.e. along the radius of the polar plot presented in Fig. 7a. For small values of angle $\theta$, we obtained $T = 0.5$ (selective reflection of the incident non-polarized light). For larger values of angle $\theta$, the transmission coefficient $T$ increases, because both right- and left-circularly polarized light can be transmitted. In turn, for large values of the angle $\theta$ (i.e. $\theta \approx 90^\circ$), the ray of the incident light slides on the surface and does not propagate within the investigated CLC.

Fig. 7

Polar plot (a) and the plot profile along the radius (b) of the non-polarized light transmitted through the CLC

Figure 8 presents polar plots of the transmission coefficient $T$ of the CLC sandwiched between differently oriented polarizers. All the presented distributions depend strongly on the angle $\phi$ and $\theta$ described orientation of the wave vector of the incident light. For instance, both for $\phi \approx \phi_{po}$ or $\phi \approx \phi_{an}$ we obtained $T \approx 0$. We also obtained a small value of the coefficient $T$ for $\theta \approx 90^\circ$ (as in Fig. 7). However, for other values of angle $\phi$, the value of the coefficient $T$ is characterized by large and frequent changes. The presented distribution is symmetrical only for small values of the angle $\theta$.

Fig. 8

Polar plots of the transmission coefficient $T$ of the investigated CLC sandwiched within differently oriented polarizer and analyzer

5 Conclusions

In the paper, an attempt to model optical phenomena in cholesteric liquid crystals sandwiched between two isotropic media and optical polarizers has been presented. The influence of the orientation of the applied polarizers on the intensity of the transmitted light in relation to the investigated cholesteric liquid crystal has been mathematically considered. Optical phenomena in the CLC have been modeled using the 4 × 4 matrix method, which takes into account the effect of refraction and multiple reflections between plate interferences, both ordinary and extraordinary waves.

The developed computer algorithm has been tested using lossless homogenous isotropic medium first, and the same medium sandwiched within two optical polarizers. Next, we have calculated reflection and transmission coefficient of the monochromatic light incident on the investigated CLC sandwiched within isotropic media, both without and with optical polarizers. Some interesting reflection and transmission spectra as well as polar plots of the reflection or transmission coefficient have been obtained, illustrated, and discussed. The implemented computer algorithm of the 4 × 4 matrix method has allowed us to understand optical properties of the considered optical system for different parameters. The gained experiences can be potentially used to model optical phenomena in photonic crystals, which have attracted a large amount of attention in recent years. They offer unique optical properties, including ability to control the propagation of light, and can be used in the future as a basic elements of all-optical integrated circuits [1].