Keywords

1 Introduction

A fall onto outstretched arms is one of the main reasons of the upper limb bone injuries. The resulting bone fractures are a serious medical and social problem due to long-term sick leave, absence from work, and sometimes a complicated rehabilitation process, especially among the elderly [1, 2]. The aforementioned upper extremity injuries may be the result of forward falls, backward falls or side falls. However, most cases of upper extremity injuries occur as a result of a forward fall with direct impact on the fully extended upper extremities [3, 4]. Due to the compromised bone quality/density and the increased risk of falling in the older part of population, distal radius fractures are especially common in elderly women with osteoporosis.

The so-called Colles’ fracture as an injury of distal radius is the most common type of fracture of the upper extremity resulting from a forward fall [5]. Colles’ fracture is a direct result of exceeding the maximum value of force allowable for the radius. Estimation of this value as a distal radius fracture threshold has been the research goal of many scientists. For instance, distal radius fractures at a mean force equal to 1640 N were observed by Spadaro and his co-workers [6]. In other paper, Kim and Ashton-Miller used the value equal to 2400 N as a distal radius fracture threshold in their investigations [7]. In turn, in one of the recent papers Burkhart and his co-investigators tested the real bones from cadavers and obtained value of the distal radius fracture threshold approximately equal to 2150 N [8].

The literature review indicates that recent decades have brought different models related to the impact of the upper extremities to the ground as a result of a fall in a forward direction. A model proposed by Chiu and Robinovitch [9] applies to the human forward fall from a low height on the outstretched and fully extended hand, and it is constructed as a two degrees-of-freedom (DoFs) lumped-parameter mechanical system with spring-damper elements imitating properties of human muscles. DeGoede and Ashton-Miller [10] applied Adams software in order to develop a half-body, symmetric human forward fall model consisting of five segments (lower limb, half torso with neck and head, upper arm, forearm, and hand). Using this model, the authors studied the probability of injury in older women. In other paper, Kim and Ashton-Miller [7] showed another planar model of a forward fall as a two DoFs system constructed based on a mechanical double pendulum (rotating freely around the pivot corresponding to the ankles of lower human extremities). Finally, the mechanical system was reduced to a linear system with 2-DoFs and spring-damper elements responsible for attenuation action of the human muscles.

To conclude, the considered falling process is usually modeled on the basis on planar and linear mechanical systems consisting of two rigid bodies with masses moved by transverse motion and connected by linear spring-damper elements. Simple models have been presented in the form of the second-order ordinary differential equations of motion [9], or the appropriate equations have been developed in the state space [7]. On the other hand, more complex mechanical models have been implemented only using commercial software, for instance see paper [10]. In this work, we proposed a novel mathematical model of the human forward fall on the outstretched arms. Mechanical, kinematical, and dynamical parameters of this model have been identified using experimental investigations of a real falling process of a faller. Moreover, we have investigated influence of different human speed just before a trip over an obstacle and starting the falling process, which affects the ground reaction force (GRF) acting on the upper extremity.

2 Biomechanical Model of a Human

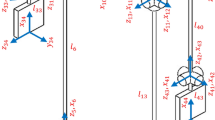
The human forward fall on outstretched arms is presented schematically in Fig. 1 as a planar 3-DoFs mechanical model. The xy plane corresponds to the sagittal plane of the human body.

Fig. 1
figure 1

The proposed forward fall biomechanical planar model with 3-DoFs embedded in the Cartesian coordinate system

Full size image

The bodies 1 (lower extremities), 2 (torso with neck and head) and 3 (upper extremities) have masses \( m_{1} \), \( m_{2} \), \( m_{3} \) and moments of inertia about centres of the masses \( I_{1} \), \( I_{2} \), \( I_{3} \), respectively. The angle \( \theta_{1} (t) \) is the angle between the \( x \) axis and the longitudinal axis of the body 1, \( \theta_{2} (t) \) is the angle measured from the axis of the body 1 to the axis of the body 2, while \( \theta_{3} (t) \) denotes the angle between the axes of the bodies 2 and 3. Parameters \( a_{1} \), \( a_{2} \), \( a_{3} \) denote distances between the centres of masses and rotation axes for bodies 1, 2 and 3, respectively, \( l_{1} \) is the distance between the ankle joint and the hip joint, \( l_{2} \) is the distance between the hip joint and the shoulder joint, whereas \( l_{3} \) denotes the length of the upper limbs. The equations of motion of the considered system have been obtained by the Newton-Euler method.

In our model, we take the vectors \( {\varvec{\uptheta}}_{1} (t) = \left[ {0,0,\theta_{1} (t)} \right]^{T} \), \( {\varvec{\uptheta}}_{2} (t) = \left[ {0,0,\theta_{2} (t)} \right]^{T} \), \( {\varvec{\uptheta}}_{3} (t) = \left[ {0,0,\theta_{3} (t)} \right]^{T} \) of the angles in the joints j1, j2, j3, and the following vectors:

$$ {\mathbf{r}}_{1} (t) = \left[ {x_{1} (t),y_{1} (t),0} \right]^{T} = \left[ {a_{1} \cos \theta_{1} (t),a_{1} \sin \theta_{1} (t),0} \right]^{T} , $$
(1)
$$ {\mathbf{r}}_{2} (t) = \left[ {x_{2} (t),y_{2} (t),0} \right]^{T} = \left[ {l_{1} \cos \theta_{1} (t) + a_{2} \cos \alpha (t),l_{1} \sin \theta_{1} (t) - a_{2} \sin \alpha (t),0} \right]^{T} , $$
(2)
$$ \begin{aligned} {\mathbf{r}}_{3} (t) & = \left[ {x_{3} (t),y_{3} (t),0} \right]^{T} \\ & = \left[ l_{1} \cos \theta_{1} (t) + l_{2} \cos \alpha (t) + a_{3} \cos \beta (t),l_{1} \sin \theta_{1} (t) \right. \\ &\left. - l_{2} \sin \alpha (t) - a_{3} \sin \beta (t),0 \right]^{T} , \\ \end{aligned} $$
(3)
$$ {\mathbf{l}}_{1} (t) = \left[ {l_{1} \cos \theta_{1} (t),l_{1} \sin \theta_{1} (t),0} \right]^{T} , $$
(4)
$$ {\mathbf{l}}_{2} (t) = \left[ {l_{1} \cos \theta_{1} (t) + l_{2} \cos \alpha (t),l_{1} \sin \theta_{1} (t) - l_{2} \sin \alpha (t),0} \right]^{T} , $$
(5)
$$ {\mathbf{l}}_{3} (t) = \left[ {l_{1} \cos \theta_{1} (t) + l_{2} \cos \alpha (t) + l_{3} \cos \beta (t),l_{1} \sin \theta_{1} (t) - l_{2} \sin \alpha (t) - l_{3} \sin \beta (t),0} \right]^{T} , $$
(6)

where \( \alpha (t) = \pi - \theta_{1} (t) - \theta_{2} (t) \) and \( \beta (t) = \pi + \alpha (t) - \theta_{3} (t) \). The forces \( {\mathbf{Q}}_{1} = \left[ {0, - m_{1} g,0} \right]^{T} \), \( {\mathbf{Q}}_{2} = \left[ {0, - m_{2} g,0} \right]^{T} \), and \( {\mathbf{Q}}_{3} = \left[ {0, - m_{3} g,0} \right]^{T} \) are the gravity forces acting on centres of gravity of bodies 1, 2 and 3, where \( g = 9.81{\text{ m/s}}^{ 2} \). The force \( {\mathbf{R}}(t) = \left[ {R_{x} (t),R_{y} (t),0} \right]^{T} \) is the reaction force in the joint j1. The unknown joint forces (resulting from presentation of the system as a free body diagram) are denoted as \( {\mathbf{P}}_{1} (t) = \left[ {P_{1x} (t),P_{1y} (t),0} \right]^{T} \) and \( {\mathbf{P}}_{2} (t) = \left[ {P_{2x} (t),P_{2y} (t),0} \right]^{T} \), respectively. The force \( {\mathbf{F}}(t) = \left[ {F_{x} (t),F_{y} (t),0} \right]^{T} \) is the ground reaction force acting on the body 3 at the moment of its impact to the ground. Let us assume further that torques \( {\mathbf{M}}_{1} (t) = \left[ {0,0,0} \right]^{T} \), \( {\mathbf{M}}_{2} (t) = \left[ {0,0,M_{2} (t)} \right]^{T} \), and \( {\mathbf{M}}_{3} (t) = \left[ {0,0,M_{3} (t)} \right]^{T} \) in joints j1, j2 and j3, correspond to the torques generated by human muscles in the ankle, hip and shoulder joints, respectively. Then, the analysed system can be described by the equations of motion in the following vector form:

$$ m_{1} {{\ddot{\bf r}}}_{1} (t) = {\mathbf{R}}(t) + {\mathbf{Q}}_{1} + {\mathbf{P}}_{1} (t), $$
(7)
$$ I_{1} {\ddot{\varvec{\uptheta }}}_{1} (t) = {\mathbf{M}}_{1} (t) - {\mathbf{M}}_{2} (t) + {\varvec{\uptau}}_{{\mathbf{R}}} (t) + {\varvec{\uptau}}_{{{\mathbf{P}}12}} (t), $$
(8)
$$ m_{2} {{\ddot{\bf r}}}_{2} (t) = - {\mathbf{P}}_{1} (t) + {\mathbf{Q}}_{2} + {\mathbf{P}}_{2} (t), $$
(9)
$$ I_{2} {\ddot{\varvec{\uptheta }}}_{2} (t) = {\mathbf{M}}_{2} (t) - {\mathbf{M}}_{3} (t) + {\varvec{\uptau}}_{{{\mathbf{P}}21}} (t) + {\varvec{\uptau}}_{{{\mathbf{P}}23}} (t), $$
(10)
$$ m_{3} {{\ddot{\bf r}}}_{3} (t) = - {\mathbf{P}}_{2} (t) + {\mathbf{Q}}_{3} + {\mathbf{F}}(t), $$
(11)
$$ I_{3} {\ddot{\varvec{\uptheta }}}_{3} (t) = {\mathbf{M}}_{3} (t) + {\varvec{\uptau}}_{{{\mathbf{P}}32}} (t) + {\varvec{\uptau}}_{{\mathbf{F}}} (t), $$
(12)

where

$$ {\varvec{\uptau}}_{{\mathbf{R}}} (t) = \left[ {0,0,\tau_{R} (t)} \right]^{T} = - {\mathbf{r}}_{1} (t) \times {\mathbf{R}}(t), $$
(13)
$$ {\varvec{\uptau}}_{{{\mathbf{P}}12}} (t) = \left[ {0,0,\tau_{P12} (t)} \right]^{T} = [{\mathbf{l}}_{1} (t) - {\mathbf{r}}_{1} (t)] \times {\mathbf{P}}_{1} (t), $$
(14)
$$ {\varvec{\uptau}}_{{{\mathbf{P}}21}} (t) = \left[ {0,0,\tau_{P21} (t)} \right]^{T} = [{\mathbf{l}}_{1} (t) - {\mathbf{r}}_{2} (t)] \times [ - {\mathbf{P}}_{1} (t)], $$
(15)
$$ {\varvec{\uptau}}_{{{\mathbf{P}}23}} (t) = \left[ {0,0,\tau_{P23} (t)} \right]^{T} = [{\mathbf{l}}_{2} (t) - {\mathbf{r}}_{2} (t)] \times {\mathbf{P}}_{2} (t), $$
(16)
$$ {\varvec{\uptau}}_{{{\mathbf{P}}32}} (t) = \left[ {0,0,\tau_{P32} (t)} \right]^{T} = [{\mathbf{l}}_{2} (t) - {\mathbf{r}}_{3} (t)] \times [ - {\mathbf{P}}_{2} (t)], $$
(17)
$$ {\varvec{\uptau}}_{{\mathbf{F}}} (t) = \left[ {0,0,\tau_{F} (t)} \right]^{T} = [{\mathbf{l}}_{3} (t) - {\mathbf{r}}_{3} (t)] \times {\mathbf{F}}(t), $$
(18)

are the torques generated by the forces \( {\mathbf{R}}(t) \), \( {\mathbf{P}}_{1} (t) \), \( {\mathbf{P}}_{2} (t) \) and \( {\mathbf{F}}(t) \), respectively, and

$$ P_{2x} (t) = F_{x} (t) - m_{3} \ddot{x}_{3} (t), $$
(19)
$$ P_{2y} (t) = F_{y} (t) - m_{3} \ddot{y}_{3} (t) - m_{3} g, $$
(20)
$$ P_{1x} (t) = P_{2x} (t) - m_{2} \ddot{x}_{2} (t), $$
(21)
$$ P_{1y} (t) = P_{2y} (t) - m_{2} \ddot{y}_{2} (t) - m_{2} g, $$
(22)
$$ R_{x} (t) = m_{1} \ddot{x}_{1} (t) - P_{1x} (t), $$
(23)
$$ R_{y} (t) = m_{1} \ddot{y}_{1} (t) + m_{1} g - P_{1y} (t). $$
(24)

In order to arrest and/or absorb the fall, the faller instinctively bends their body in the hip joints and pulls their upper extremities to the front. In the proposed fall model, these processes are described by functions \( \theta_{2} (t) \) and \( \theta_{3} (t) \), respectively. Taking into account the kinematic excitation as time histories of the angles \( \theta_{2} (t) \) and \( \theta_{3} (t) \), the considered system can be reduced to the 1-DoF model described by the following equation

$$ I_{1} \ddot{\theta }_{1} (t) + I_{2} \ddot{\theta }_{2} (t) + I_{3} \ddot{\theta }_{3} (t) = \tau_{R} (t) + \tau_{P12} (t) + \tau_{P21} (t) + \tau_{P23} (t) + \tau_{P32} (t) + \tau_{F} (t) $$
(25)

with the function \( \theta_{1} (t) \) as a solution of this equation of motion.

  • Ground reaction force

In order to predict the vertical component of the ground reaction force, we used a non-linear model of impact at the wrist-ground interface in the form [10,11,12]

$$ F_{y} (t) = k_{y} \left| {y(t)} \right|^{3} (1 - b_{y} \dot{y}(t)) \cdot J( - y(t)), $$
(26)

where \( k_{y} \) and \( b_{y} \) denote ground stiffness and damping coefficient in the vertical direction, respectively, \( y(t) = l_{1} \sin \theta_{1} (t) - l_{2} \sin \alpha (t) - l_{3} \sin \beta (t) \), and the function \( J( - y(t)) \) has the form

$$ J( - y(t)) = \left\{ {\begin{array}{*{20}l} 1 \hfill & {\text{for}} \hfill & {y(t) < 0,} \hfill \\ 0 \hfill & {\text{for}} \hfill & {y(t) \ge 0.} \hfill \\ \end{array} } \right. $$
(27)

  • Initial conditions

At the beginning of the trip, a human is usually in a standing position. Therefore, we take initial angular position \( \theta_{1} (0) = 90^\circ \). Initial angular velocity \( \dot{\theta }_{1} (0) \) is estimated based on the walking speed \( v_{0} \) of human gait, (which is referring to the whole body speed during walking) just before the moment of the trip, by using the principle of conservation of momentum according to the formula [12]

$$ \dot{\theta }_{1} (0) = - \frac{{(m_{1} + m_{2} + m_{3} )v_{0} r}}{I}, $$
(28)

where \( I \) is the moment of inertia of the human body about the axis of rotation placed in the ankle joint, and \( r \) is the distance between the human gravity centre and the ankle joint, in such position, when the upper extremities are adjusted along the body (it is a typical position of a human body during walking). As a result of the adopted assumptions, the proposed forward fall model allows for studying kinematic and dynamic parameters during the falling process for different walking speeds of the faller just before the moment of the trip over an obstacle.

  • Identification of the fall model parameters

To determine the appropriate lengths, masses, and moments of inertia of the faller’s body, we used the full 3D scanned human body model (see Fig. 2). Even though human body does not consist of a homogenous structure, the abovementioned values were calculated assuming the average density \( \rho = 1050{\text{ kg/m}}^{ 3} \). Parameters used in numerical simulations are presented in Table 1.

Fig. 2
figure 2

3D scanned human body model analysed in Inventor

Full size image
Table 1 Body segment lengths, masses, and moments of inertia
Full size table

3 Experimental Investigations

In our experimental investigations, kinematics of the faller from the moment of tripping over an obstacle to hitting their hands to the force plate were observed using the Optitrack system. This motion capture system has been successfully used before, for instance, to track the falling process [12] or gait [13] of a human. The location of 37 individual markers placed on the body of the faller (one of the authors of this work) is presented in Fig. 3. Figure 4 shows the pictures of the faller’s body configurations obtained at different times during the observation of the forward falling process. Time histories of angles \( \theta_{2} (t) \) and \( \theta_{3} (t) \), obtained from experiment and their analytical approximations by functions

Fig. 3
figure 3

Thirty seven passive reflective markers distributed on the faller’s body for observation of a forward falling process by using the Optitrack system

Full size image
Fig. 4
figure 4

Faller’s body configurations at different stages of the falling process obtained by the Optitrack system

Full size image
$$ \theta_{2} (t) = \left\{ {\begin{array}{*{20}l} {178^\circ - 58^\circ \sin^{2} (\lambda t^{3} )} \hfill & {\text{for}} \hfill & {t \le T,} \hfill \\ {120^\circ } \hfill & {\text{for}} \hfill & {t > T,} \hfill \\ \end{array} } \right. $$
(29)
$$ \theta_{3} (t) = \left\{ {\begin{array}{*{20}l} {15^\circ + 105^\circ \sin^{2} (\lambda t^{3} )} \hfill & {\text{for}} \hfill & {t \le T,} \hfill \\ {120^\circ } \hfill & {\text{for}} \hfill & {t > T,} \hfill \\ \end{array} } \right. $$
(30)

for \( \lambda = 1.59{\text{ 1/s}}^{ 3} \) and duration of the fall \( T = 1.00{\text{ s}} \) (the time between tripping and hitting the ground), are presented in Fig. 5.

Fig. 5
figure 5

Time histories of angles \( \theta_{2} (t) \) and \( \theta_{3} (t) \) obtained from the experiment and their approximations by analytical smooth functions

Full size image

Figure 6 shows the real time histories of the average impact force acting on the single hand of the faller, registered during the experiment using the force plate. During the experimental test the forearms of the faller were arranged in pronation positions. The impact force increases from zero to the maximum value of about 1510 N during the time about 0.05 s. Next, the force changes periodically and decreases to about 400 N during the time interval 0.8–1.0 s.

Fig. 6
figure 6

Time history of ground reaction force, obtained experimentally by using the force plate

Full size image

The forward fall model proposed in this paper is constructed based on the three rigid bodies connected by two rotary joints, which correspond to the human hip and shoulder joints, as well as immobile joint, which corresponds to the ankle joint. To carry out numerical simulations, we adopted parameters \( k_{y} = 3500{\text{ kN/m}}^{ 3} \) and \( b_{y} = 6.0{\text{ s/m}} \) based on the paper [10]. The human body is a complicated biomechanical system, which contains many different muscles that absorb the impact force during a fall. Therefore, in case of a real fall to the ground, a part of the impact energy is absorbed by the abovementioned muscles, which are not considered in the presented fall model. By comparing the real ground reaction force obtained from the force plate and the impact force generated by the proposed fall model, we estimated what a part of the impact energy (impact force) is transferred to the upper extremities, and what a part is dissipated in other parts of the human body. As a result, it is possible to estimate the real value of the impact force acting on the faller during the impact to the ground for different values of the walking speed \( v_{0} \) by extrapolating the proposed fall model.

4 Numerical Results

The proposed forward fall model has been implemented and visualised in Mathematica software. Figure 7 shows animation snapshots of the faller’s body, plotted at different stages of the fall from a standing position. The presented frames correspond to the fall tested experimentally and observed using the Optitrack system.

Fig. 7
figure 7

Animation snapshots of the faller’s body, plotted at different times of the fall from a standing position (obtained in Mathematica software)

Full size image

More detailed experimental observations with falls demonstrate that with an increase in the walking speed \( v_{0} \), the faller instinctively bends the body around the hip joint and pulls their arms in the forward direction. As a result, duration of the fall \( T \) is shorter, whereas the value of the parameter \( \lambda \) is greater. Therefore, in our further numerical analysis we used the time histories of the angles \( \theta_{2} (t) \) and \( \theta_{3} (t) \) governed by Eqs. (29) and (30) with different parameters \( T \) and \( \lambda \), depending on the speed \( v_{0} \) of the human walking just before the trip. The mentioned parameters are presented in Table 2.

Table 2 Values of parameters \( T \) and \( \lambda \) corresponding to different values of walking speed \( v_{0} \)
Full size table

Figure 8 presents the maximum values of GRF as a function of the velocity \( v_{0} \) and values of GRFs, which correspond to the distal radius fracture thresholds adopted by different authors [6,7,8]. As can be seen, the maximum value of GRF increases with the increasing speed \( v_{0} \). For the lowest presented value of \( v_{0} \) (equal to 0.5 m/s), the estimated maximum value of GRF is 1612 N. For the largest value of \( v_{0} \) (equal to 3.0 m/s), the maximum value of GRF is 2643 N. For small values of \( v_{0} \), the maximum value of GRF is less than the presented distal radius fracture thresholds. For large value of \( v_{0} \), the maximum of GRF exceeds all the presented distal radius fracture thresholds. Concluding, it can be stated that for a large walking speed of human gait before the falling process, the value of the distal radius fracture threshold is usually exceeded, eventually leading to injuries and/or fractures of the upper extremities. Both the presented results as well as further extrapolations of the proposed fall model can be used as a load conditions in the finite element analysis of the numerical model of the human upper extremity.

Fig. 8
figure 8

Distal radius fracture thresholds [6,7,8] and the maximum values of the ground reaction force as a function of velocity \( v_{0} \)

Full size image

5 Conclusions

The paper presents a 3-link mechanical model implemented in Mathematica, governing the forward fall on outstretched arms. The presented model is an extension of the fall models considered in papers [12, 14]. It enables to estimate the vertical ground reaction forces acting on the hands during the human falling process. Segments of the human body were modelled as three rigid bodies connected by rotary joints which correspond to the hip and shoulder human joints, as well as immobile joint, which corresponds to the ankle joint. In order to estimate parameters of the faller body we used three-dimensional scanned human body model, created and segmented in Inventor. Kinematics of the falling process was observed by the Optitrack system, while the real ground reaction force during impact to the ground was registered by the force plate. The proposed fall model allows one to estimate the value of the vertical ground reaction force acting on the hands of the faller during the impact to the ground for different speed just before a trip over an obstacle.

Concluding, it should be noted that the developed model has also some limitations. First, based on the scan of the human body, we are not able to determine accurately the distribution of human body mass density. Therefore, in our simulations we have adopted the average value resulting from the total weight and total body volume. Second, the movement of the shoulder with respect to the torso and stiffness/damping properties of the shoulder, hip and/or elbow joints were not implemented in the presented model. Eventually, only the vertical component of the ground reaction force was considered, whereas the horizontal component was omitted. In future studies, for instance, a two dimensional approach for modeling of human skeletal muscles, can also be considered [15, 16]. Nevertheless, the proposed forward fall model enables to obtain the results in the form of the time histories of the ground reaction force, which can be used as load conditions, for further finite element analysis of the human upper extremity.