Abstract
In this chapter, we define and analyze the four basic logical operations: the unary “not”, or complement, and the binary “and”, “inclusive or” and “exclusive or”. These are commonly known as bit-wise operations, as each one may be computed by performing a certain operation on each bit of its argument (in the unary case) or each pair of corresponding bits of its arguments (for binary operations). For example, the logical “and”  of two bit vectors may be specified in a bit-wise manner as the bit vector z such that for all \(k \in \mathbb {N}\), z[k] = 1 iff x[k] = y[k] = 1.
of two bit vectors may be specified in a bit-wise manner as the bit vector z such that for all \(k \in \mathbb {N}\), z[k] = 1 iff x[k] = y[k] = 1.
Access provided by Autonomous University of Puebla. Download chapter PDF
Keywords
These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.
In this chapter, we define and analyze the four basic logical operations: the unary “not”, or complement, and the binary “and”, “inclusive or” and “exclusive or”. These are commonly known as bit-wise operations, as each one may be computed by performing a certain operation on each bit of its argument (in the unary case) or each pair of corresponding bits of its arguments (for binary operations). For example, the logical “and”  of two bit vectors may be specified in a bit-wise manner as the bit vector z such that for all \(k \in \mathbb {N}\), z[k] = 1 iff x[k] = y[k] = 1.
of two bit vectors may be specified in a bit-wise manner as the bit vector z such that for all \(k \in \mathbb {N}\), z[k] = 1 iff x[k] = y[k] = 1.
In the context of our formalization, however, the logical operations are more naturally defined as arithmetic functions: the complement is constructed as an arithmetic difference and the binary operations are defined by recursive formulas, which facilitate inductive proofs of their relevant properties. Among these are the bit-wise characterizations, as represented by Lemmas 3.7 and 3.20.
1 Binary Operations
Following standard RTL syntax, we denote “and”, “inclusive or” and “exclusive or” with the infix symbols &, |, and ˆ, respectively.
Definition 3.1
For all \(x \in \mathbb {Z}\) and \(y \in \mathbb {Z}\),
-
(a)

-
(b)

-
(c)
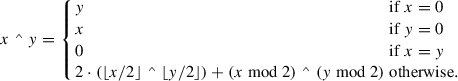
It is not obvious that these are admissible recursive definitions, i.e., that each of them is satisfied by a unique function. To establish this, it suffices to demonstrate the existence of a measure function \(\mu : \mathbb {Z} \times \mathbb {Z} \to \mathbb {N}\) that strictly decreases on each recursive call. Thus, we define
For the admissibility of each of the three definitions, we must show that μ satisfies the following two inequalities, corresponding to the two recursive calls, under the restrictions x ≠ 0, y ≠ 0, and x ≠ y:
-
(1)
μ(⌊x∕2⌋, ⌊y∕2⌋) < μ(x, y).
-
(2)
μ(x mod 2, y mod 2) < μ(x, y)..
Since the restrictions imply that at least one of x and y is neither 0 nor − 1, (1) follows from Lemma 1.3. To establish (2), note that either x mod 2 = 0, y mod 2 = 0, or x mod 2 = 1 = y mod 2. In any case,
The proof of the following is a typical inductive argument based on the recursion of Definition 3.1 (a).
Lemma 3.1
If \(x \in \mathbb {N}\) and \(y \in \mathbb {Z}\)
, then  .
.
Proof
We may assume that x ≠ 0, y ≠ 0, and x ≠ y. Thus,

and by induction,

□
Corollary 3.2
If x is an n-bit vector and
\(y \in \mathbb {Z}\)
, then
 is an n-bit vector.
is an n-bit vector.
Proof
By Lemma 3.1,  □
□
Lemma 3.3
If x and y and n-bit vectors, then so are  and
and  .
.
Proof
The same argument applies to both operations. The claim is trivial if n = 0, x = 0, y = 0, or x = y. In all other cases, ⌊x∕2⌋ and ⌊y∕2⌋ are (n − 1)-bit vectors and by induction, so is, for example,  . Thus,
. Thus,

□
Lemma 3.4
For all \(x \in \mathbb {Z}\) , \(y \in \mathbb {Z}\) , and \(n \in \mathbb {N}\) ,
-
(a)
 ;
;
-
(b)
 ;
;
-
(c)
 .
.
Proof
We present the proof for (a); (b) and (c) are similar.
We may assume that n > 0, x ≠ 0, y ≠ 0, and x ≠ y. By Definition 3.1 (a) and Lemma 1.22,

By induction and Lemmas 1.18, 2.3, and 2.13, the first addend may be written as

and by Lemmas 2.22 and 2.31, the second addend is

Thus, by Definition 3.1 (a) and Lemmas 3.2 and 2.3,

□
Lemma 3.5
For all \(x \in \mathbb {Z}\) , \(y \in \mathbb {Z}\) , and \(n \in \mathbb {N}\) ,
-
(a)
 ;
;
-
(b)
 ;
;
-
(c)
 .
.
Proof
We present the proof for (a); (b) and (c) are similar.
We may assume that n > 0, x ≠ 0, y ≠ 0, and x ≠ y. By Lemma 1.2, induction, and Definition 3.1 (a),

□
All three binary logical operators commute with the bit slice operator:
Lemma 3.6
For all \(x \in \mathbb {Z}\) , \(y \in \mathbb {Z}\) , \(i \in \mathbb {N}\) , and \(j \in \mathbb {N}\) ,
-
(a)
 ;
;
-
(b)
 ;
;
-
(c)
 .
.
Proof
We present the proof for (a); (b) and (c) are similar.
We may assume that n > 0, x ≠ 0, y ≠ 0, and x ≠ y. By Definition 2.2 and Lemmas 3.4 and 3.5,

□
Corollary 3.7
For all \(x \in \mathbb {Z}\) , \(y \in \mathbb {Z}\) , and \(k \in \mathbb {N}\) ,
-
(a)
 ;
;
-
(b)
 ;
;
-
(c)
 .
.
Lemma 3.8
For all \(x_1 \in \mathbb {Z}\) , \(y_1 \in \mathbb {Z}\) , \(x_2 \in \mathbb {Z}\) , \(y_2 \in \mathbb {Z}\) , \(m \in \mathbb {N}\) , and \(n \in \mathbb {N}\) ,
-
(a)
 ;
;
-
(b)
 ;
;
-
(c)
 .
.
Proof
We present the proof for (a); (b) and (c) are similar.

By Lemma 3.5,

where, by Definition 2.3 and the properties of the floor,
Thus,

Finally, by Definitions 1.3 and 2.3,

□
Lemma 3.9
For all \(x \in \mathbb {Z}\) , \(y \in \mathbb {Z}\) , and \(n \in \mathbb {N}\) ,
-
(a)
 ;
;
-
(b)
 ;
;
-
(c)
 .
.
Proof
We present the proof for (a); (b) and (c) are similar.
We may assume that n > 0, x ≠ 0, y ≠ 0, and x ≠ y. By induction and Definition 3.1 (a),

□
Lemma 3.10
For all \(x \in \mathbb {Z}\) , \(y \in \mathbb {Z}\) , and \(n \in \mathbb {N}\) ,
-
(a)
 ;
;
-
(b)
 ;
;
-
(c)
 .
.
Proof
-
(a)
The claim is trivial if x = 0, y = 0, or y = 2n x; otherwise, by Definition 3.1 (a), induction, and Lemma 1.2,

-
(b)
Similarly,

where, by Lemmas 2.3 and 2.12,
$$\displaystyle \begin{aligned} \begin{array}{rcl} 2(\lfloor y/2 \rfloor \bmod 2^{n-1}) + y \bmod 2 &\displaystyle = &\displaystyle 2\lfloor y/2 \rfloor[n-2:0] + y[0]\\ &\displaystyle = &\displaystyle 2y[n{-}1:1] + y[0] \\ &\displaystyle = &\displaystyle y[n{-}1:0] \\ &\displaystyle = &\displaystyle y \bmod 2^n. \end{array} \end{aligned} $$The proof of (c) is similar to that of (b). □
Corollary 3.11
Let \(x \in \mathbb {Z}\) and let y be an n-bit vector, where \(n \in \mathbb {N}\) . Then

Proof
By Lemmas 3.10 and 1.11 and Definition 3.1 (b),

□
Lemma 3.12
For all
\(x \in \mathbb {Z}\)
and
\(n \in \mathbb {N}\)
,

Proof
By Definition 2.2 and Lemmas 3.4, 3.8, and 2.32,

By Lemma 3.5,

The lemma follows from Definition 1.3. □
The logical “and” operator may be used to extract a bit slice:
Lemma 3.13
Let \(x \in \mathbb {Z}\) , \(n \in \mathbb {N}\) , and \(k \in \mathbb {N}\) . If k < n, then

Proof
The proof is by induction on n. If n = 1, then k = 0 and

If n > 1 and k = 0, then by induction and Lemmas 2.12 and 2.32,

In the remaining case, n > k > 1 and

□
Corollary 3.14
For all \(x \in \mathbb {Z}\) and \(n \in \mathbb {N}\)
,  .
.
Proof
By Lemma 3.13,

□
2 Complement
We have a simple arithmetic definition of the logical complement.
Definition 3.2
For all \(x \in \mathbb {Z}\),  .
.
Lemma 3.15
For all \(x \in \mathbb {Z}\)
,  .
.
Proof
By Definition 3.2,  . □
. □
Lemma 3.16
If \(x \in \mathbb {Z}\) and \(k\in \mathbb {N}\)
, then  .
.
Proof
By Definition 3.2,

□
Lemma 3.17
If \(x \in \mathbb {Z}\)
, \(n\in \mathbb {N}\)
, and n > 0, then  .
.
Proof
By Definition 3.2 and Lemma 1.5,

□
Lemma 3.18
If \(x \in \mathbb {Z}\) and \(n \in \mathbb {N}\) , then

Proof
First note that by Lemmas 1.10 and 1.11,
Therefore, by Lemmas 1.15, 1.23, and 1.11,

□
Notation
For the purpose of resolving ambiguous expressions, the complement has higher precedence than the bit slice operator, e.g.,  .
.
Lemma 3.19
If \(x \in \mathbb {Z}\) , \(i \in \mathbb {N}\) , \(j \in \mathbb {N}\) , and j ≤ i, then

Proof
By Definitions 3.2 and 2.2 and Lemmas 3.18, 1.1, and 1.5,

□
The usual bit-wise characterization of the complement is a special case of Lemma 3.19:
Corollary 3.20
If \(x \in \mathbb {Z}\) and \(n \in \mathbb {N}\)
, then  .
.
Proof
By Lemma 3.19,  . □
. □
The remaining results of this section are properties of complements of bit slices that have proved useful in manipulating expressions derived from RTL designs.
Lemma 3.21
Let \(x \in \mathbb {Z}\) , \(i \in \mathbb {N}\) , \(j \in \mathbb {N}\) , \(k \in \mathbb {N}\) , and \(\ell \in \mathbb {N}\) . If ℓ ≤ k ≤ i − j, then

Proof

□
Lemma 3.22
If \(x \in \mathbb {Z}\) and y in an n-bit vector, where \(n \in \mathbb {N}\) , then

Proof
By Lemma 3.21,  , and hence by Lemmas 3.2, 2.4, and 3.6
, and hence by Lemmas 3.2, 2.4, and 3.6

□
Lemma 3.23
Let \(x \in \mathbb {Z}\) , \(i \in \mathbb {N}\) , \(j \in \mathbb {N}\) , \(k \in \mathbb {N}\) , and \(\ell \in \mathbb {N}\) . If ℓ ≤ k ≤ i − j, then

Proof
By Lemmas 3.19, 2.19, and 3.15,

□
3 Algebraic Properties
We conclude this chapter with a set of identities pertaining to special cases and compositions of logical operations.
The first two lemmas are immediate consequences of the definitions.
Lemma 3.24
For all \(x \in \mathbb {Z}\) ,
-
(a)
 ;
;
-
(b)
 ;
;
-
(c)
 .
.
Lemma 3.25
For all \(x \in \mathbb {Z}\) and \(y \in \mathbb {Z}\) ,
-
(a)
 ;
;
-
(b)
 ;
;
-
(c)
 .
.
All of the remaining results of this section may be derived in a straightforward manner from Lemmas 3.20, 3.7, and 2.40.
Lemma 3.26
For all \(x \in \mathbb {Z}\) ,
-
(a)
 ;
;
-
(b)
 ;
;
-
(c)
 .
.
Lemma 3.27
For all \(x \in \mathbb {Z}\) and \(y \in \mathbb {Z}\) ,
-
(a)
 ;
;
-
(b)
 .
.
Proof
Suppose  . By Lemma 3.7, for all \(k \in \mathbb {N}\)
. By Lemma 3.7, for all \(k \in \mathbb {N}\)

and it is readily seen by exhaustive computation that this implies x[k] = y[k] = 0. It follows from Lemma 2.40 that x = y = 0. A similar argument applies to (b). □
The proofs of the remaining lemmas are sufficiently similar to that of Lemma 3.27 that they may be safely omitted.
Lemma 3.28
For all \(x \in \mathbb {Z}\) , \(y \in \mathbb {Z}\) , and \(n \in \mathbb {Z}\) ,
-
(a)
 ;
;
-
(b)
 ;
;
-
(c)
 .
.
Lemma 3.29
For all \(x \in \mathbb {N}\) , \(y \in \mathbb {N}\) , and \(z \in \mathbb {N}\) ,
-
(a)
 ;
;
-
(b)
 ;
;
-
(c)
 .
.
Lemma 3.30
For all \(x \in \mathbb {N}\) , \(y \in \mathbb {N}\) , and \(z \in \mathbb {N}\) ,
-
(a)
 ;
;
-
(b)
 ;
;
-
(c)
 .
.
Lemma 3.31
For all \(x \in \mathbb {N}\) and \(y \in \mathbb {N}\) ,
-
(a)
 ;
;
-
(b)
 .
.
Author information
Authors and Affiliations
Rights and permissions
Copyright information
© 2019 Springer Nature Switzerland AG
About this chapter
Cite this chapter
Russinoff, D.M. (2019). Logical Operations. In: Formal Verification of Floating-Point Hardware Design. Springer, Cham. https://doi.org/10.1007/978-3-319-95513-1_3
Download citation
DOI: https://doi.org/10.1007/978-3-319-95513-1_3
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-95512-4
Online ISBN: 978-3-319-95513-1
eBook Packages: EngineeringEngineering (R0)




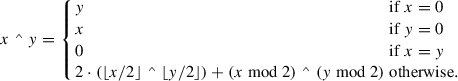
 ;
;
 ;
;
 .
. ;
;
 ;
;
 .
. ;
;
 ;
;
 .
. ;
;
 ;
;
 .
. ;
;
 ;
;
 .
. . By Lemmas
. By Lemmas  ;
;
 ;
;
 .
. ;
;
 ;
;
 .
.

 ;
;
 ;
;
 .
. ;
;
 ;
;
 .
. ;
;
 ;
;
 .
. ;
;
 .
. ;
;
 ;
;
 .
. ;
;
 ;
;
 .
. ;
;
 ;
;
 .
. ;
;
 .
.