Abstract
Isogeometric analysis (IGA) is a recent and successful extension of classical finite element analysis. IGA adopts smooth splines, NURBS and generalizations to approximate problem unknowns, in order to simplify the interaction with computer aided geometric design (CAGD). The same functions are used to parametrize the geometry of interest. Important features emerge from the use of smooth approximations of the unknown fields. When a careful implementation is adopted, which exploit its full potential, IGA is a powerful and efficient high-order discretization method for the numerical solution of PDEs. We present an overview of the mathematical properties of IGA, discuss computationally efficient isogeometric algorithms, and present some significant applications.
Access provided by CONRICYT-eBooks. Download chapter PDF
Similar content being viewed by others
4.1 Introduction
Isogeometric Analysis (IGA) was proposed in the seminal paper [70], with a fundamental motivation: to improve the interoperability between computer aided geometric design (CAGD) and the analysis, i.e., numerical simulation. In IGA, the functions that are used in CAGD geometry description (these are splines, NURBS, etcetera) are used also for the representation of the unknowns of Partial Differential Equations (PDEs) that model physical phenomena of interest.
In the last decade Isogeometric methods have been successfully used on a variety of engineering problems. The use of splines and NURBS in the representation of unknown fields yields important features, with respect to standard finite element methods. This is due to the spline smoothness which not only allows direct approximation of PDEs of order higher than two,Footnote 1 but also increases accuracy per degree of freedom (comparing to standard C 0 finite elements) and the spectral accuracy,Footnote 2 and moreover facilitates construction of spaces that can be used in schemes that preserve specific fundamental properties of the PDE of interest (for example, smooth divergence-free isogeometric spaces, see [37, 38, 57] and [58]). Spline smoothness is the key ingredient of isogeometric collocation methods, see [7] and [100].
The mathematics of isogeometric methods is based on the classical spline theory (see, e.g., [51, 102]), but also poses new challenges. The study of h-refinement of tensor-product isogeometric spaces is addressed in [15] and [22]. The study of k-refinement, that is, the use of splines and NURBS of high order and smoothness (C p−1 continuity for p-degree splines) is developed in [19, 40, 59, 115]. With a suitable code design, k-refinement boosts both accuracy and computational efficiency, see [97]. Stability of mixed isogeometric methods with a saddle-point form is the aim of the works [6, 21, 32, 33, 37, 56,57,58, 118].
Recent overview of IGA and its mathematical properties are [25] and [69].
We present in the following sections an introduction of the construction of isogeometric scalar and vector spaces, their approximation and spectral properties, of the computationally-efficient algorithms that can be used to construct and solve isogeometric linear systems, and finally report (from the literature) some significant isogeometric analyses of benchmark applications.
4.2 Splines and NURBS: Definition and Properties
This section contains a quick introduction to B-splines and NURBS and their use in geometric modeling and CAGD. Reference books on this topic are [25, 44, 51, 91, 93, 102].
4.2.1 Univariate Splines
Given two positive integers p and n, we say that Ξ := {ξ 1, …, ξ n+p+1} is a p-open knot vector if
where repeated knots are allowed, and ξ 1 = 0 and ξ n+p+1 = 1. The vector Z = {ζ 1, …, ζ N} contains the breakpoints, that is the knots without repetitions, where m j is the multiplicity of the breakpoint ζ j, such that
with \(\sum _{i=1}^{N}m_i = n+p+1\). We assume m j ≤ p + 1 for all internal knots. The points in Z form a mesh, and the local mesh size of the element I i = (ζ i, ζ i+1) is denoted h i = ζ i+1 − ζ i, for i = 1, …, N − 1.
B-spline functions of degree p are defined by the well-known Cox-DeBoor recursion:
and
where 0∕0 = 0. This gives a set of n B-splines that are non-negative, form a partition of unity, have local support, are linear independent.
The \( \{ \widehat B_{i,p} \} \) form a basis for the space of univariate splines, that is, piecewise polynomials of degree p with k j := p − m j continuous derivatives at the points ζ j, for j = 1, …, N:
Remark 1
The notation \( S^p_r \) will be adopted to refer to the space S p(Ξ) when the multiplicity m j of all internal knots is p − r. Then, \( S^p_r \) is a spline space with continuity C r.
The maximum multiplicity allowed, m j = p + 1, gives k j = −1, which represents a discontinuity at ζ j. The regularity vector k = {k 1, …, k N} will collect the regularity of the basis functions at the internal knots, with k 1 = k N = −1 for the boundary knots. An example of B-splines is given in Fig. 4.1. B-splines are interpolatory at knots ζ j if and only if the multiplicity m j ≥ p, that is where the B-spline is at most C 0.
Each B-spline \(\widehat B_{i,p}\) depends only on p + 2 knots, which are collected in the local knot vector
When needed, we will stress this fact by adopting the notation
The support of each basis function is exactly \(\mathrm {supp}(\widehat B_{i,p}) = [\xi _i , \xi _{i+p+1}]\).
A spline curve in \({\mathbb {R}}^d\), d = 2, 3 is a curve parametrized by a linear combination of B-splines and control points as follows:
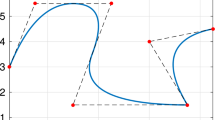
where \(\{ {\mathbf {c}}_i \}_{i=1}^n\) are called control points. Given a spline curve C(ζ), its control polygon C P(ζ) is the piecewise linear interpolant of the control points \(\{ {\mathbf {c}}_i \}_{i=1}^n\) (see Fig. 4.2).
In general, conic sections cannot be parametrized by polynomials but can be parametrized with rational polynomials, see [91, Sect. 1.4]. This has motivated the introduction of Non-Uniform Rational B-Splines (NURBS). In order to define NURBS, we set the weight function \(W(\zeta ) = \sum _{\ell =1}^n w_\ell \widehat B_{\ell ,p}(\zeta )\) where the positive coefficients w ℓ > 0 for ℓ = 1, …, n are called weights. We define the NURBS basis functions as
which are rational B-splines. NURBS (4.7) inherit the main properties of B-splines mentioned above, that is they are non-negative, form a partition of unity, and have local support. We denote the NURBS space they span by
Similarly to splines, a NURBS curve is defined by associating one control point to each basis function, in the form:
Actually, the NURBS curve is a projection into \({\mathbb {R}}^d\) of a non-rational B-spline curve in the space \({\mathbb {R}}^{d+1}\), which is defined by
where \({\mathbf {c}}^w_i = [{\mathbf {c}}_i, w_i] \in {\mathbb {R}}^{d+1}\) (see Fig. 4.3).
For splines and NURBS curves, refinement is performed by knot insertion and degree elevation. In IGA, these two algorithms generate two kinds of refinement (see [70]): h-refinement which corresponds to mesh refinement and is obtained by insertion of new knots, and p-refinement which corresponds to degree elevation while maintaining interelement regularity, that is, by increasing the multiplicity of all knots. Furthermore, in IGA literature k-refinement denotes degree elevation, with increasing interelement regularity. This is not refinement in the sense of nested spaces, since the sequence of spaces generated by k-refinement has increasing global smoothness.
Having defined the spline space S p(Ξ), the next step is to introduce suitable projectors onto it. We focus on so called quasi-interpolants A common way to define them is by giving a dual basis, i.e.,
where λ j,p are a set of dual functionals satisfying
δ jk being the Kronecker symbol. The quasi-interpolant Π p,Ξ preserves splines, that is
From now on we assume local quasi-uniformity of the knot vector ζ 1, ζ 2, …, ζ N, that is, there exists a constant θ ≥ 1 such that the mesh sizes h i = ζ i+1 − ζ i satisfy the relation θ −1 ≤ h i∕h i+1 ≤ θ, for i = 1, …, N − 2. Among possible choices for the dual basis {λ j,p}, j = 1, …, n, a classical one is given in [102, Sect. 4.6], yielding to the following stability property (see [15, 25, 102]).
Proposition 1
For any non-empty knot span I i = (ζ i, ζ i+1),
where the constant C depends only upon the degree p, and \(\widetilde {I}_i\) is the support extension, i.e., the interior of the union of the supports of basis functions whose support intersects I i
4.2.2 Multivariate Splines and NURBS
Multivariate B-splines are defined from univariate B-splines by tensorization. Let d be the space dimensions (in practical cases, d = 2, 3). Assume \(n_\ell \in {\mathbb {N}}\), the degree \(p_\ell \in {\mathbb {N}}\) and the p ℓ-open knot vector \(\varXi _\ell = \{\xi _{\ell ,1}, \ldots , \xi _{\ell ,n_\ell + p_\ell + 1} \}\) are given, for ℓ = 1, …, d. We define a polynomial degree vector p = (p 1, …, p d) and Ξ = Ξ 1 ×… × Ξ d. The corresponding knot values without repetitions are given for each direction ℓ by \(Z_\ell =\{\zeta _{\ell ,1},\ldots , \zeta _{\ell ,N_\ell } \}\). The knots Z ℓ form a Cartesian grid in the parametric domain \(\widehat \varOmega = (0,1)^d\), giving the Bézier mesh, which is denoted by \(\widehat {\mathscr {M}}\):
For a generic Bézier element \(Q_{\mathbf {j}} \in \widehat {\mathscr {M}}\), we also define its support extension \(\widetilde Q_{\mathbf {j}} = \widetilde I_{1,j_1} \times \ldots \times \widetilde I_{d,j_d}\), with \(\widetilde I_{\ell , j_\ell }\) the univariate support extension as defined in Proposition 1. We make use of the set of multi-indices I = {i = (i 1, …, i d) : 1 ≤ i ℓ ≤ n ℓ}, and for each multi-index i = (i 1, …, i d), we define the local knot vector \(\boldsymbol {\varXi }_{\mathbf {i},\mathbf {p}} = \varXi _{i_1,p_1} \times \ldots \times \varXi _{i_d,p_d} \). Then we introduce the set of multivariate B-splines
The spline space in the parametric domain \(\widehat {\varOmega }\) is then
which is the space of piecewise polynomials of degree p with the regularity across Bézier elements given by the knot multiplicities.
Multivariate NURBS are defined as rational tensor product B-splines. Given a set of weights {w i, i ∈I}, and the weight function \(W({\boldsymbol {\zeta }}) = \sum _{\mathbf {j} \in {\mathbf {I}}} w_{\mathbf {j}} \widehat B_{\mathbf {j},\mathbf {p}}({\boldsymbol {\zeta }})\), we define the NURBS basis functions
The NURBS space in the parametric domain \(\widehat {\varOmega }\) is then
As in the case of NURBS curves, the choice of the weights depends on the geometry to parametrize, and in IGA applications it is preserved by refinement.
Tensor-product B-splines and NURBS (4.7) are non-negative, form a partition of unity and have local support. As for curves, we define spline (NURBS, respectively) parametrizations of multivariate geometries in \({\mathbb {R}}^m\), m = 2, 3. A spline (NURBS, respectively) parametrization is then any linear combination of B-spline (NURBS, respectively) basis functions via control points \({\mathbf {c}}_{\mathbf {i}} \in {\mathbb {R}}^m\)
Depending on the values of d and m, the map (4.17) can define a planar surface in \({\mathbb {R}}^2\) (d = 2, m = 2), a manifold in \({\mathbb {R}}^3\) (d = 2, m = 3), or a volume in \({\mathbb {R}}^3\) (d = 3, m = 3).
The definition of the control polygon is generalized for multivariate splines and NURBS to a control mesh, the mesh connecting the control points c i. Since B-splines and NURBS are not interpolatory, the control mesh is not a mesh on the domain Ω. Instead, the image of the Bézier mesh in the parametric domain through F gives the physical Bézier mesh in Ω, simply denoted the Bézier mesh if there is no risk of confusion (see Fig. 4.4).
The interpolation and quasi-interpolation projectors can be also extended to the multi-dimensional case by a tensor product construction. Let, for i = 1, …, d, the notation \(\varPi ^i_{p_i}\) denote the univariate projector Π p,Ξ onto the space \(S^{p_i}(\varXi _i)\), then define
Analogously, the multivariate quasi-interpolant is also defined from a dual basis (see [51, Chapter XVII]). Indeed, we have
where each dual functional is defined from the univariate dual bases as \(\lambda _{\mathbf {i},\mathbf {p}} = \lambda _{i_1, p_1} \otimes \ldots \otimes \lambda _{i_d, p_d}.\)
4.2.3 Splines Spaces with Local Tensor-Product Structure
A well developed research area concerns extensions of splines spaces beyond the tensor product structure, and allow local mesh refinement: for example T-splines, Locally-refinable (LR) splines, and hierarchical splines. T-splines have been proposed in [107] and have been adopted for isogeometric methods since [16]. They have been applied to shell problems [68], fluid-structure interaction problems [17] and contact mechanics simulation [52]. The algorithm for local refinement has evolved since its introduction in [108] (see, e.g., [104]), in order to overcome some initial limitations (see, e.g.,[55]). Other possibilities are LR-splines [53] and hierarchical splines [36, 128].
We summarize here the definition of a T-spline and its main properties, following [25]. A T-mesh is a mesh that allows T-junctions. See Fig. 4.5 (left) for an example. A T-spline set
is a generalization of the tensor-product set of multivariate splines (4.15). Indeed the functions in (4.19) have the structure
where the set of indices, usually referred to as anchors, \(\mathscr {A}\) and the associated local knot vectors \(\varXi _{{\mathbf {A}}, \ell ,p_\ell }\), for all \({\mathbf {A}} \in \mathscr {A} \) are obtained from the T-mesh. If the polynomial degree is odd (in all directions) the anchors are associated with the vertices of the T-mesh, if the polynomial degree is even (in all directions) the anchors are associated with the elements. Different polynomial degrees in different directions are possible. The local knot vectors are obtained from the anchors by moving along one direction and recording the knots corresponding to the intersections with the mesh. See the example in Fig. 4.6.
Two bi-cubic T-spline anchors A ′ and A″ and related local knot vectors. In particular, the local knot vectors for A″ are \(\varXi _{{\mathbf {A}}'',d,3}= \{\xi ^{\prime \prime }_{1,d},\xi ^{\prime \prime }_{2,d},\xi ^{\prime \prime }_{3,d},\xi ^{\prime \prime }_{4,d},\xi ^{\prime \prime }_{5,d}, \}\), d = 1, 2. In this example, the two T-splines \(\widehat B _{{\mathbf {A}}', \mathbf {p}}\) and \(\widehat B _{{\mathbf {A}}'', \mathbf {p}}\) partially overlap (the overlapping holds in the horizontal direction)
On the parametric domain \(\widehat \varOmega \) we can define a Bézier mesh \(\widehat {\mathscr {M}}\) as the collection of the maximal open sets \(Q \subset \widehat \varOmega \) where the T-splines of (4.19) are polynomials in Q. We remark that the Bézier mesh and the T-mesh are different meshes.
The theory of T-splines focuses on the notion of Analysis-Suitable (AS) T-splines or, equivalently, Dual-Compatible (DC) T-splines: these are a subset of T-splines for which fundamental mathematical properties hold, of crucial importance for IGA.
We say that the two p-degree local knot vectors \(\varXi ' =\{ \xi ^{\prime }_1, \ldots \xi ^{\prime }_{p+2}\}\) and \(\varXi '' =\{ \xi ^{\prime \prime }_1, \ldots \xi ^{\prime \prime }_{p+2}\}\) overlap if they are sub-vectors of consecutive knots taken from the same knot vector. For example {ξ 1, ξ 2, ξ 3, ξ 5, ξ 7} and {ξ 3, ξ 5, ξ 7, ξ 8, ξ 9} overlap, while {ξ 1, ξ 2, ξ 3, ξ 5, ξ 7} and {ξ 3, ξ 4, ξ 5, ξ 6, ξ 8} do not overlap. Then we say that two T-splines \(\widehat B _{{\mathbf {A}}', \mathbf {p}}\) and \(\widehat B _{{\mathbf {A}}'', \mathbf {p}}\) in (4.19) partially overlap if, when A ′≠ A″, there exists a direction ℓ such that the local knot vectors \(\varXi _{{\mathbf {A}}',\ell ,p_\ell }\) and \(\varXi _{{\mathbf {A}}'',\ell ,p_\ell }\) are different and overlap. This is the case of Fig. 4.6. Finally, the set (4.19) is a Dual-Compatible (DC) set of T-splines if each pair of T-splines in it partially overlaps. Its span
is denoted a Dual-Compatible (DC) T-spline space. The definition of a DC set of T-splines simplifies in two dimension ([23]): when d = 2, a T-spline space is a DC set of splines if and only if each pair of T-splines in it have overlapping local knot vector in at least one direction.
A full tensor-product space (see Sect. 4.2.2) is a particular case of a DC spline space. In general, partial overlap is sufficient for the construction of a dual basis, as in the full tensor-product case. We only need, indeed, a univariate dual basis (e.g., the one in [102]), and denote by \(\lambda [\varXi _{{\mathbf {A}},\ell ,p_\ell }] \) the univariate functional as in (4.11), depending on the local knot vector \(\varXi _{{\mathbf {A}},\ell ,p_\ell }\) and dual to each univariate B-spline with overlapping knot vector.
Proposition 2
Assume that (4.19) is a DC set, and consider an associated set of functionals
Then (4.22) is a dual basis for (4.19).
Above, we assume that the local knot vectors in (4.23) are the same as in (4.19), (4.20). The proof of Proposition 2 can be found in [25]. The existence of dual functionals implies important properties for a DC set (4.19) and the related space \( S^{\mathbf {p}}(\mathscr {A})\) in (4.21), as stated in the following theorem.
Theorem 1
The T-splines in a DC set (4.19) are linearly independent. If the constant function belongs to \(S^{\mathbf {p}}(\mathscr {A})\) , they form a partition of unity. If the space of global polynomials of multi-degree p is contained in \(S^{\mathbf {p}}(\mathscr {A})\) , then the DC T-splines are locally linearly independent, that is, given \(Q \in \widehat {\mathscr {M}}\) , then the non-null T-splines restricted to the element Q are linearly independent.
An important consequence of Proposition 2 is that we can build a projection operator \(\varPi _{\mathbf {p}} : L^2(\widehat \varOmega ) \rightarrow S^{\mathbf {p}}(\mathscr {A})\) by
This is the main tool (as mentioned in Sect. 4.4.1) to prove optimal approximation properties of T-splines.
In general, for DC T-splines, and in particular for tensor-product B-splines, we can define so called Greville abscissae. Each Greville abscissa
is a point in the parametric domain \(\widehat \varOmega \) and its d-component \(\gamma [\varXi _{{\mathbf {A}},\ell ,p_\ell }]\)is the average of the p ℓ internal knots of \(\varXi _{{\mathbf {A}},\ell ,p_\ell }\). They are the coefficients of the identity function in the T-spline expansion. Indeed, assuming that linear polynomials belong to the space \(S^{\mathbf {p}}(\mathscr {A})\), we have that
Greville abscissae are used as interpolation points (see [51]) and therefore for collocation based IGA [7, 8, 100].
A useful result, proved in [20, 23], is that a T-spline set is DC if and only if (under minor technical assumptions) it comes from a T-mesh that is Analysis-Suitable. The latter is a topological condition for the T-mesh [16] and it refers to dimension d = 2. A horizontal T-junction extension is a horizontal line that extend the T-mesh from a T-junctions of kind ⊢ and ⊣ in the direction of the missing edge for a length of ⌈p 1∕2⌉ elements, and in the opposite direction for ⌊p 1∕2⌋ elements; analogously a vertical T-junction extension is a vertical line that extend the T-mesh from a T-junctions of kind ⊥ or ⊤ in the direction of the missing edge for a length of ⌈p 2∕2⌉ elements, and in the opposite direction for ⌊p 2∕2⌋ elements, see Fig. 4.6 (right). Then, a T-mesh is Analysis-Suitable (AS) if horizontal T-junction extensions do not intersect vertical T-junction extensions.
4.2.4 Beyond Tensor-Product Structure
Multivariate unstructured spline spaces are spanned by basis functions that are not, in general, tensor products. Non-tensor-product basis functions appear around so-called extraordinary points. Subdivision schemes, but also multipatch or T-splines spaces in the most general setting, are unstructured spaces. The construction and mathematical study of these spaces is important especially for IGA and is one of the most important recent research activities, see [35, 98]. We will further address this topic in Sects. 4.3.3 and 4.4.3.
4.3 Isogeometric Spaces: Definition
In this section, following [25], we give the definition of isogeometric spaces. We consider a single patch domain, i.e., the physical domain Ω is the image of the unit square, or the unit cube (the parametric domain \(\widehat \varOmega \)) by a single NURBS parametrization. Then, for a given degree vector p 0, knot vectors Ξ 0 and a weight function \(W \in {{S}}_{{\mathbf {p}}^0}(\boldsymbol {\varXi }^0)\), a map \(\mathbf {F} \in (N^{{\mathbf {p}}^0}(\boldsymbol {\varXi }^0,W))^d\) is given such that \(\varOmega = \mathbf {F}(\widehat \varOmega )\), as in Fig. 4.7.
After having introduced the parametric Bézier mesh \(\widehat {\mathscr {M}}\) in (4.14), as the mesh associated to the knot vectors Ξ, we now define the physical Bézier mesh (or simply Bézier mesh) as the image of the elements in \(\widehat {\mathscr {M}}\) through F:
see Fig. 4.7. The meshes for the coarsest knot vector Ξ 0 will be denoted by \(\widehat {\mathscr {M}}_0\) and \(\mathscr {M}_0\). For any element \(K = \mathbf {F}(Q) \in \mathscr {M}\), we define its support extension as \(\widetilde K = \mathbf {F}(\widetilde Q)\), with \(\widetilde Q\) the support extension of Q. We denote the element size of any element \(Q \in \widehat {\mathscr {M}}\) by h Q = diam(Q), and the global mesh size by \(h = \max \{h_Q : Q \in \widehat {\mathscr {M}}\}\). Analogously, we define the element sizes h K = diam(K) and \(h_{\widetilde K} = \text{diam}(\widetilde K)\).
For the sake of simplicity, we assume that the parametrization F is regular, that is, the inverse parametrization F −1 is well defined, and piecewise differentiable of any order with bounded derivatives. Assuming F is regular ensures that h Q ≃ h K. The case a of singular parametrization, that is, non-regular parametrization, will be discussed in Sect. 4.4.4.
4.3.1 Isoparametric Spaces
Isogeometric spaces are constructed as push-forward through F of (refined) splines or NURBS spaces. In detail, let \(\widehat V_h = N^{\mathbf {p}}(\boldsymbol {\varXi }, W)\) be a refinement of \(N^{{\mathbf {p}}^0}(\boldsymbol {\varXi }^0,W)\), we define the scalar isogeometric space as:
Analogously,
that is, the functions N i,p form a basis of the space V h. Isogeometric spaces with boundary conditions are defined straightforwardly.
Following [15], the construction of a projector on the NURBS isogeometric space V h (defined in (4.27)) is based on a pull-back on the parametric domain, on a decomposition of the function into a numerator and weight denominator, and finally a spline projection of the numerator. We have \(\varPi _{V_h}: \mathscr {V}(\varOmega ) \rightarrow V_h\)defined as
where Π p is the spline projector (4.18) and \(\mathscr { V}(\varOmega )\) is a suitable function space. The approximation properties of \(\varPi _{V_h}\) will be discussed in Sect. 4.4.
The isogeometric vector space, as introduced in [70], is just (V h)d, that is a space of vector-valued functions whose components are in V h. In parametric coordinates a spline isogeometric vector field of this kind reads
where u i are the degrees-of-freedom, also referred as control variables since they play the role of the control points of the geometry parametrization (4.17). This is an isoparametric construction.
4.3.2 De Rham Compatible Spaces
The following diagram

is the De Rham cochain complex. The Sobolev spaces involved are the two standard scalar-valued, H 1(Ω) and L 2(Ω) , and the two vector valued
Furthermore, as in general for complexes, the image of a differential operator in (4.31) is subset of the kernel of the next: for example, constants have null grad , gradients are curl-free fields, and so on. De Rham cochain complexes are related to the well-posedness of PDEs of key importance, for example in electromagnetic or fluid applications. This is why it is important to discretize (4.31) while preserving its structure. This is a well developed area of research for classical finite elements, called Finite Element Exterior Calculus (see the reviews [4, 5]) and likewise a successful development of IGA.
For the sake of simplicity, again, we restrict to a single patch domain and we do not include boundary conditions in the spaces. The dimension here is d = 3. The construction of isogeometric De Rham compatible spaces involves two stages.
The first stage is the definition of spaces on the parametric domain \(\widehat \varOmega \). These are tensor-product spline spaces, as (4.16), with a specific choice for the degree and regularity in each direction. For that, we use the expanded notation \(S^{p_1,p_2,p_3}(\varXi _1,\varXi _2,\varXi _3)\) for S p(Ξ). Given degrees p 1, p 2, p 3 and knot vectors Ξ 1, Ξ 2, Ξ 3 we then define on \(\widehat \varOmega \) the spaces:
where, given \(\varXi _\ell = \{\xi _{\ell ,1}, \ldots ,\xi _{\ell , n_\ell +p_\ell +1 }\}\), \(\varXi ^{\prime }_\ell \) is defined as the knot vector \(\{\xi _{\ell ,2}, \ldots ,\xi _{\ell , n_\ell +p_\ell }\}\), and we assume the knot multiplicities 1 ≤ m ℓ,i ≤ p ℓ, for i = 2, …, N ℓ − 1 and ℓ = 1, 2, 3. With this choice, the functions in \(\widehat {X}^0_h\) are at least continuous. Then,\(\widehat \,\mathbf {grad}\, (\widehat {X}^0_h) \subset \widehat {X}^1_h\), and analogously, from the definition of the curl and the divergence operators we get \(\widehat {\mathbf {curl}} (\widehat {X}^1_h) \subset \widehat {X}^2_h\), and \(\widehat \,\mathrm {div}\,(\widehat {X}^2_h) \subset \widehat {X}^3_h\). This follows easily from the action of the derivative operator on tensor-product splines, for example:
It is also proved in [38] that the kernel of each operator is exactly the image of the preceding one. In other words, these spaces form an exact sequence:

This is consistent with (4.31).
The second stage is the push forward of the isogeometric De Rham compatible spaces from the parametric domain \(\widehat \varOmega \) onto Ω. The classical isoparametric transformation on all spaces does not preserve the structure of the De Rham cochain complex. We need to use the transformations:
where D F is the Jacobian matrix of the mapping \(\mathbf {F}:\widehat \varOmega \rightarrow \varOmega \). The transformation above preserve the structure of the De Rham cochain complex, in the sense of the following commuting diagram (see [66, Sect. 2.2] and [86, Sect. 3.9]):

Note that the diagram above implicitly defines the isogeometric De Rham compatible spaces on Ω, that is \(X^0_h \), \(X^1_h \), \(X^2_h \) and \(X^3_h \); for example:
In this setting, the geometry parametrization F can be either a spline in \((\widehat {X}^0_h)^3\) or a NURBS.
In fact, thanks to the smoothness of splines, isogeometric De Rham compatible spaces enjoy a wider applicability than their finite element counterpart. For example, assuming m ℓ,i ≤ p ℓ − 1, for i = 2, …, N ℓ − 1 and ℓ = 1, 2, 3, then the space \( X^2_h \) is subset of (H 1(Ω))3. Furthermore there exists a subset \( K_h \subset X^2_h \) of divergence-free isogeometric vector fields, i.e.,
that can be characterized as
as well as
Both K h and \( X^2_h \) play an important role in the IGA of incompressible fluids, allowing exact point-wise divergence-free solutions that are difficult to achieve by finite element methods, or in linear small-deformation elasticity for incompressible materials, allowing point-wise preservation of the linearized volume under deformation. We refer to [37, 56,57,58, 123] and the numerical tests of Sect. 4.7. We should also mention that for large deformation elasticity the volume preservation constraint becomes \(\det \mathbf {f} =1\), f denoting the deformation gradient, and the construction of isogeometric spaces that allow its exact preservation is an open and very challenging problem.
4.3.3 Extensions
Isogeometric spaces can be constructed from non-tensor-product or unstructured spline spaces, as the ones listed in Sect. 4.2.3.
Unstructured multipatch isogeometric spaces may have C 0 continuity at patch interfaces, of higher continuity. The implementation of C 0-continuity over multipatch domains is well understood (see e.g. [81, 106] for strong and [34] for weak imposition of C 0 conditions). Some papers have tackled the problem of constructing isogeometric spaces of higher order smoothness, such as [35, 48, 76, 89, 98]. The difficulty is how to construct analysis-suitable unstructured isogeometric spaces with global C 1 or higher continuity. The main question concerns the approximation properties of these spaces, see Sect. 4.4.3.
An important operation, derived from CAGD, and applied to isogeometric spaces is trimming, see [85] Indeed trimming is very common in geometry representation, since it is the natural outcome of Boolean operations (union, intersection, subtraction of domains). One possibility is to approximate (up to some prescribed tolerance) the trimmed domain by an untrimmed multipatch or T-spline parametrized domain, see [109]. Another possibility is to use directly the trimmed geometry and deal with the two major difficulties that arise: efficient quadrature and imposition of boundary conditions, see [94, 95, 99].
4.4 Isogeometric Spaces: Approximation Properties
4.4.1 h-Refinement
The purpose of this section is to summarize the approximation properties of the isogeometric space V h defined in (4.27). We focus on the convergence analysis under h-refinement, presenting results first obtained in [15] and [22]. To express the error bounds, we will make use of Sobolev spaces on a domain D, that can be either Ω or \(\widehat \varOmega \) or subsets such as Q, \(\widetilde Q\), K or \(\widetilde K\). For example, H s(D), \(s\in {\mathbb {N}}\) is the space of square integrable functions f ∈ L 2(Ω) such that its derivatives up to order s are square integrable. However, conventional Sobolev spaces are not enough. Indeed, since the mapping F is not arbitrarily regular across mesh lines, even if a scalar function f in physical space satisfies f ∈ H s(Ω), its pull-back \(\widehat {f} = f \circ \mathbf {F}\) is not in general in \(H^s(\widehat {\varOmega })\). As a consequence, the natural function space in parametric space, in order to study the approximation properties of mapped NURBS, is not the standard Sobolev space H s but rather a “bent” version that allows for less regularity across mesh lines. In the following, as usual, C will denote a constant, possibly different at each occurrence, but independent of the mesh-size h. Note that, unless noted otherwise, C depends on the polynomial degree p and regularity.
Let d = 1 first. We recall that I i = (ζ i, ζ i+1) are the intervals of the partition of I = (0, 1) given by the knot vector. We define for any \(q\in {\mathbb {N}}\) the piecewise polynomial space
Given \(s \in {\mathbb {N}}\) and any sub-interval E ⊂ I, we indicate by H s(E) the usual Sobolev space endowed with norm \( \| \cdot \| _{H^s(E)}\) and semi-norm \( | \cdot |{ }_{H^s(E)}\). We define the bent Sobolev space (see [15]) on I as
where \(D^k_\pm \) denote the kth-order left and right derivative (or left and right limit for k = 0), and k i is the number of continuous derivatives at the break point ζ i. We endow the above space with the broken norm and semi-norms
where \( |\cdot |{ }_{H^0(I_i)} =\|\cdot \|{ }_{L^2(I_i)} \).
In higher dimensions, the tensor product bent Sobolev spaces are defined as follows. Let s = (s 1, s 2, …, s d) in \( {\mathbb N}^d\). By a tensor product construction starting from (4.40), we define the tensor product bent Sobolev spaces in the parametric domain \(\widehat {\varOmega }:=(0,1)^d\)
endowed with the tensor-product norm and seminorms. The above definition clearly extends immediately to the case of any hyper-rectangle \(E \subset \widehat {\varOmega }\) that is a union of elements in \(\widehat {\mathscr {M}}\).
We restrict, for simplicity of exposition, to the two-dimensional case. As in the one-dimensional case, we assume local quasi-uniformity of the mesh in each direction. Let \(\varPi _{p_{i},\varXi _{i}}: L^2(I) \rightarrow S^{p_i}(\varXi _i)\), for i = 1, 2, indicate the univariate quasi-interpolant associated to the knot vector Ξ i and polynomial degree p i. Let moreover \(\varPi _{\mathbf {p},\boldsymbol {\varXi }} = \varPi _{p_{1},\varXi _{1}} \otimes \varPi _{p_{2},\varXi _{2}}\) from L 2(Ω) to S p(Ξ) denote the tensor product quasi-interpolant built using the \(\varPi _{p_{i},\varXi _{i}}\) defined in (4.18) for d = 2. In what follows, given any sufficiently regular function \(f: \widehat \varOmega \rightarrow {\mathbb {R}}\), we will indicate the partial derivative operators with the symbol
Let \(E \subset \widehat {\varOmega }\) be any union of elements \(Q \in \widehat {\mathscr {M}}\) of the spline mesh. We will adopt the notation
The element size of a generic element \(Q_{\mathbf {i}} = I_{1,i_1} \times \ldots \times I_{d, i_d} \in \widehat {\mathscr {M}}\) will be denoted by \(h_{Q_{\mathbf {i}}} = \text{diam}(Q_{\mathbf {i}})\). We will indicate the length of the edges of Q i by \(h_{1,i_1}, h_{2,i_2},\). Because of the local quasi-uniformity of the mesh in each direction, the length of the two edges of the extended patch \(\widetilde {Q}_{\mathbf {i}}\) are bounded from above by \(h_{1,i_1}\) and \(h_{2,i_2}\), up to a multiplicative factor. The quasi-uniformity constant is denoted θ. We have the following result (see [22, 25] for its proof), that can be established for spaces with boundary conditions as well.
Proposition 3
Given integers 0 ≤ r 1 ≤ s 1 ≤ p 1 + 1 and 0 ≤ r 2 ≤ s 2 ≤ p 2 + 1, there exists a constant C depending only on p, θ such that for all elements \(Q_{\mathbf {i}} \in \widehat {\mathscr {M}}\) ,
for all f in \({\mathscr {H}}^{(s_1,{r_2})}(\widehat {\varOmega }) \cap {\mathscr {H}}^{({r_1},{s_2})}(\widehat {\varOmega })\).
We can state the approximation estimate for the projection operator on the isogeometric space V h, that is \( \varPi _{V_h} : L^2(\varOmega ) \rightarrow V_h \), defined in (4.29). In the physical domain \(\varOmega = \mathbf {F}(\widehat \varOmega )\), we introduce the coordinate system naturally induced by the geometrical map F, referred to as the F-coordinate system, that associates to a point x ∈ Ω the Cartesian coordinates in \(\widehat \varOmega \) of its counter-image F −1(x). At each \(\mathbf {x} \in K \in \mathscr {M}_0\) (more generally, at each x where F is differentiable) the tangent base vectors g 1 and g 2 of the F-coordinate system can be defined as
these are the images of the canonical base vectors \(\widehat {{\mathbf {e}}}_i\) in \(\widehat \varOmega \), and represent the axis directions of the F-coordinate system (see Fig. 4.8).
Analogously to the derivatives in the parametric domain (4.41), the derivatives of \( f: \varOmega \rightarrow {\mathbb {R}}\) in Cartesian coordinates are denoted by
We also consider the derivatives of \( f: \varOmega \rightarrow {\mathbb {R}}\) with respect to the F-coordinates. These are just the directional derivatives: for the first order we have
which is well defined for any x in the (open) elements of the coarse triangulation \(\mathscr {M}_0\), as already noted. Higher order derivatives are defined by recursion
more generally, we adopt the notation
Derivatives with respect to the F-coordinates are directly related to derivatives in the parametric domain, by
Let E be a union of elements \(K \in \mathscr {M}\). We introduce the broken norms and seminorms
where
We also introduce the following space
The following theorem from [22] states the main estimate for the approximation error of \(\varPi _{V_h} f\) and, making use of derivatives in the F-coordinate system, it is suitable for anisotropic meshes. For a generic element \(K_{\mathbf {i}} = \mathbf {F}(Q_{\mathbf {i}}) \in \mathscr {M}\), the notation \(\widetilde K_{\mathbf {i}} = \mathbf {F}(\widetilde Q_{\mathbf {i}})\) indicates its support extension (Fig. 4.9).
Theorem 2
Given integers r i, s i , such that 0 ≤ r i ≤ s i ≤ p i + 1, i = 1, 2, there exists a constant C depending only on p, θ, F, W such that for all elements \(K_{\mathbf {i}} = \mathbf {F}(Q_{\mathbf {i}}) \in \mathscr {M}\) ,
for all f in \(H_{\mathbf {F}}^{(s_1,r_2)}(\varOmega ) \cap H_{\mathbf {F}}^{(r_1,s_2)}(\varOmega )\).
We have the following corollary of Theorem 2, similar to [15, Theorem 3.1], or [25, Theorem 4.24] (the case with boundary conditions is handled similarly).
Corollary 1
Given integers r, s, such that \(0 \le r \le s \le \min {(p_1,\ldots ,p_d)}+1\) , there exists a constant C depending only on p, θ, F, W such that
for all f in H s(Ω).
The error bound above straightforwardly covers isogeometric/isoparametric vector fields. The error theory is possible also for isogeometric De Rham compatible vector fields. In this framework there exists commuting projectors, i.e., projectors that make the diagram

commutative. These projectors not only are important for stating approximation estimates, but also play a fundamental role in the stability of isogeometric schemes; see [4, 38].
4.4.2 p-Refinement and k-Refinement
Approximation estimates in Sobolev norms have the general form
where the optimal constant is therefore
where \(B^s(\varOmega ) = \{ f \in H^s(\varOmega ) \text{ such that } \| f \|{ }_{H^{s}(\varOmega )} \leq 1 \} \) is the unit ball in H s(Ω). The study in Sect. 4.4.1 covers the approximation under h-refinement, giving an asymptotic bound to (4.51) with respect to h which is sharp, for s ≤ p + 1,
This is the fundamental and most standard analysis, but it does not explain the benefits of k-refinement, a unique feature of IGA. High-degree, high-continuity splines and NURBS are superior to standard high-order finite elements when considering accuracy per degree-of-freedom. The study of k-refinement is still incomplete even though some important results are available in the literature. In particular, [19] contains h, p, k-explicit approximation bounds for spline spaces of degree 2q + 1 and up to C q global continuity, while the recent work [115] contains the error estimate
for univariate C p−1, p-degree splines, with 0 ≤ r ≤ q ≤ p + 1 on uniform knot vectors.
An innovative approach, and alternative to standard error analysis, is developed in [59]. There a theoretical/numerical investigation provides clear evidence of the importance of k-refinement. The space of smooth splines is shown to be very close to a best approximation space in the Sobolev metric. The approach is as follows: given the isogeometric space V h, with N = dimV h together with (4.51), we consider the Kolmogorov N-width:
Then the optimality ratio is defined as
In general, the quantity Λ(B s(Ω), V h, H r(Ω)) is hard to compute analytically but can be accurately approximated numerically, by solving suitable generalized eigenvalue problems (see [59]). In Fig. 4.10 we compare smooth C 3 quartic splines and standard quartic finite elements (that is, C 0 splines) under h-refinement. An interesting result is that smooth splines asymptotically achieve optimal approximation in the context considered, that is, they tend to be an optimal approximation space given the number of degrees-of-freedom, since \(\varLambda (B^5(0,1),S^4_{3} ,L^2 (0,1)) \rightarrow ~1\). This is not surprising as it is known that uniform periodic spline spaces are optimal in the periodic setting. On the contrary, C 0 finite elements are far from optimal. In Fig. 4.11 we plot the optimality ratios for the L 2 error for different Sobolev regularity s and for smooth splines with different degrees p. There is numerical evidence that \(\varLambda (B^s(0,1),S^p_{p-1} ,L^2 (0,1))\) is bounded and close to 1 for all p ≥ s − 1. It is a surprising result, but in fact confirms that high-degree smooth splines are accurate even when the solution to be approximated has low Sobolev regularity (see [59] for further considerations).
Optimality ratios: comparison between quartic C 3 splines (i.e., \(\varLambda (B^5(0,1), S^4_3, L^2(0,1)) \), blue line with circles) and C 0 finite elements (i.e., \(\varLambda (B^5(0,1), S^4_0, L^2(0,1)) \), red line with crosses) on the unit interval for different mesh-sizes h (the total number of degrees-of-freedom N is the abscissa)
Optimality ratios: for different Sobolev regularity s and for different spline degree p with maximal smoothness. The number of degrees-of-freedom is N = 30. The surface plot is capped at 10 for purposes of visualization. Note that if p ≥ s − 1 the optimality ratio is near 1. Even for low regularity (i.e., low s), smooth splines (i.e., high p) produce optimality ratios near 1. This supports the claim that “smooth splines are always good”
This issue has been further studied in [40], for the special case of solutions that are piecewise analytic with a localized singularity, which is typical of elliptic PDEs on domains with corners or sharp edges. The work [40] focus instead on the simplified one-dimensional problem, and consider a model singular solution f(ζ) = ζ α − ζ on the interval [0, 1], with 0 < α < 1. From the theory of hp-FEMs (i.e., hp finite elements; see [103]) it is known that exponential convergence is achieved, precisely
where C and b are positive constants, N is the total number of degrees-of-freedom, and f h is a suitable finite element approximation of f. The bound (4.55) holds if the mesh is geometrically refined towards the singularity point ζ = 0 and with a suitable selection of the polynomial degree, growing from left (the singularity) to the right of the interval [0, 1]. The seminal paper [10] gives the reference hp-FEM convergence rate which is reported in Fig. 4.12. Likewise, exponential convergence occurs with C p−1, p-degree spline approximation on a geometrically graded knot span, as reported in the same figure. Remarkably, convergence is faster (with the constant b in (4.55) that appears to be higher) for smooth splines, even though for splines the degree p is the same for all mesh elements, and grows proportionally with the total number of elements, whereas for hp-FEM a locally varying polynomial degree is utilized on an element-by-element basis.
Energy norm error versus the (square root of) number of degrees-of-freedom N for the approximation of the solution u(x) = x 0.7 − x of the problem − u″ = f with homogeneous Dirichlet boundary conditions. The mesh is geometrically graded (with ratio q = 0.35 for IGA) and the spline degree is proportional to the number of elements for IGA, and the smoothness is maximal, that is the spline space is C p−1 globally continuous. Mesh-size and degrees are optimally selected for hp-FEM, according to the criteria of [10]. Exponential convergence \( | u-u_h|{ }_{H^1} \leq C \exp {(-b \sqrt {N})}\) is evidenced in both cases, with larger b for IGA
Exponential convergence for splines is proved in the main theorem of [40], reported below.
Theorem 3
Assume that \(f\in H_0^1(0,1) \) and
for some 0 < β ≤ 1 and C u, d u > 0. Then there exist b > 0 and C > 0 such that for any q > 1, for any σ with 0 < σ < 1 and \(1 > \sigma > \left (1 + 2/d_u\right )^{-1} \) ,
where p = 2q + 1,
and N is the dimension of S p(Ξ).
Condition (4.56) expresses the piecewise analytic regularity of f. Theorem 3 is based on [19], and as such it covers approximation by 2q + 1 degree splines having C q global continuity. However, as is apparent from Fig. 4.12, exponential convergence is also observed for maximally smooth splines.
4.4.3 Multipatch
While C 0 isogeometric spaces with optimal approximation properties are easy to construct, when the mesh is conforming at the interfaces (see, e.g., [25]), the construction of smooth isogeometric spaces with optimal approximation properties on unstructured geometries is a challenging problem and still open in its full generality. The problem is related to one of accurate representation (fitting) of smooth surfaces having complex topology, which is a fundamental area of research in the community of CAGD.
There are mainly two strategies for constructing smooth multipatch geometries and corresponding isogeometric spaces. One strategy is to adopt a geometry parametrization which is globally smooth almost everywhere, with the exception of a neighborhood of the extraordinary points (or edges in 3D), see Fig. 4.13 (left). The other strategy is to use geometry parametrizations that are only C 0 at patch interfaces; see Fig. 4.13 (right). The first option includes subdivision surfaces [43] and the T-spline construction in [105] and, while possessing attractive features, typically lacks optimal approximation properties [76, 89]. One exception is the recent works [120], where a specific construction is shown to achieve optimal order in h-refinement. On the other hand, some optimal constructions have been recently obtained also following the second strategy, pictured in Fig. 4.13 (right) (see [27, 48, 77, 87]). We summarize here the main concepts and results from [48], referring to the paper itself for a complete presentation.
Consider a planar (d = 2) spline multipatch domain of interest
where the closed sets Ω (i) form a regular partition without hanging nodes. Assume each Ω (i) is a non-singular spline patch, with at least C 1 continuity within each patch, and that there exist parametrizations
where
Furthermore, assume global continuity of the patch parametrizations. This means the following. Let us fix Γ = Γ (i, j) = Ω (i) ∩ Ω (j). Let F (L), F (R) be given such that
where (F (L))−1 ∘F (i) and (F (R))−1 ∘F (j) are linear transformations. The set [−1, 1] × [0, 1] plays the role of a combined parametric domain. The coordinates in [−1, 1] × [0, 1] are denoted u and v. The global continuity condition states that the parametrizations agree at u = 0, i.e., there is an \({\mathbf {F}}_0:[0,1] \rightarrow {\mathbb R}^2\) with
For the sake of simplicity we assume that the knot vectors of all patches and in each direction coincide, are open and uniform. An example is depicted in Fig. 4.14.
The multipatch isogeometric space is given as
the space of continuous isogeometric functions is
and the space of C 1 isogeometric functions is
The graph \(\varSigma \subset \varOmega \times {\mathbb R}\) of an isogeometric function \(\phi :\varOmega \rightarrow \mathbb {R}\) splits into patches Σ i having the parametrization
where g (i) = ϕ ∘F (i). As in (4.62), we can select a patch interface Γ = Γ (i, j) = Ω (i) ∩ Ω (j), define g (L), g (R) such that
see Fig. 4.15. Continuity of ϕ is implied by the continuity of the graph parametrization, then we set
for all v ∈ [0, 1], analogous to (4.63).
Example of the general setting of (4.68)
Under suitable conditions, smoothness of a function is equivalent to the smoothness of the graph, considered as a geometric entity. In particular, for an isogeometric function that is C 1 within each patch and globally continuous, the global C 1 continuity is then equivalent to the geometric continuity of order 1 (in short G 1) of its graph parametrization. Geometric continuity of the graph parametrization means that, on each patch interface, with notation (4.68), the tangent vectors
are co-planar, i.e., linearly dependent. In the CAGD literature, G 1 continuity is commonly stated as below (see, e.g., [18, 82, 90]).
Definition 1 (G 1-Continuity at Σ (i) ∩ Σ (j))
Given the parametrizations F (L), F (R), g (L), g (R) as in (4.62), (4.68), fulfilling (4.61) and (4.69), we say that the graph parametrization is G 1 at the interface Σ (i) ∩ Σ (j) if there exist \(\alpha ^{(L)} : [0,1] \rightarrow {\mathbb R} \), \( \alpha ^{(R)} : [0,1] \rightarrow {\mathbb R} \) and \(\beta : [0,1] \rightarrow {\mathbb R} \) such that for all v ∈ [0, 1],
and
Since the first two equations of (4.71) are linearly independent, α (L), α (R) and β are uniquely determined, up to a common multiplicative factor, by F (L) and F (R), i.e. from the equation
We have indeed the following proposition (see [48] and [90]).
Proposition 4
Given any F (L) , F (R) then (4.72) holds if and only if \(\alpha ^{(S)} (v) = \gamma (v) \bar \alpha ^{(S)} (v) \) , for S ∈{L, R}, and \(\beta (v) = \gamma (v) \bar \beta (v) \) , where
and \(\gamma :[0,1]\rightarrow {\mathbb R} \) is any scalar function. In addition, γ(v) ≠ 0 if and only if (4.70) holds. Moreover, there exist functions β (S)(v), for S ∈{L, R}, such that
In the context of isogeometric methods we consider Ω and its parametrization given. Then for each interface α (L), α (R) and β are determined from (4.72) as stated in Proposition 4. It should be observed that for planar domains, there always exist α (L), α (R) and β fulfilling (4.72) (this is not the case for surfaces, see [48]). Then, the C 1 continuity of isogeometric functions is equivalent to the last equation in (4.71), that is
for all v ∈ [0, 1]. Optimal approximation properties of the isogeometric space on Ω holds under restrictions on α (L), α (R) and β, i.e. on the geometry parametrization. This leads to the definition below ([48]).
Definition 2 (Analysis-Suitable G 1-Continuity)
F (L) and F (R) are analysis-suitable G 1 -continuous at the interface Γ (in short, AS G 1) if there exist \(\alpha ^{(L)} , \alpha ^{(R)}, \beta ^{(L)}, \beta ^{(R)}\in \mathscr {P}^{1} ([0,1]) \) such that (4.72) and (4.75) hold.
The class of planar AS G 1 parametrizations contains all the bilinear ones and more, see Fig. 4.16.
In [48], the structure of C 1 isogeometric spaces over AS G 1 geometries is studied, providing an explanation of the optimal convergence of the space of p-degree isogeometric functions, having up to C p−2 continuity within the patches (and global C 1 continuity). On the other hand, no convergence under h-refinement occurs for C p−1 continuity within the patches. This phenomenon is referred to as C 1 locking. Moreover, it is shown that AS G 1 geometries are needed to guarantee optimal convergence, in general.
4.4.4 Singular Parametrizations
The theory of isogeometric spaces we have reviewed in previous sections assumes that the geometry parametrization is regular. However, singular parametrizations are used in IGA, as they allow more flexibility in the geometry representation. Figure 4.17 shows two examples of this kind, for a single-patch parametrization of the circle. Typically, a singularity appears when some of the control points near the boundary coincide or are collinear.
Isogeometric spaces with singular mapping have been studied in the papers [112,113,114,115]. The paper [113] addresses a class of singular geometries that includes the two circles of Fig. 4.17. It is shown that in these cases the standard isogeometric spaces, as they are constructed in the non-singular case, are not in H 1(Ω). However, [113] identifies the subspace of H 1 isogeometric functions, and constructs a basis. The study is generalized to H 2 smoothness in [114]. In [112], function spaces of higher-order smoothness C k are explicitly constructed on polar parametrizations that are obtained by linear transformation and degree elevation from a triangular Bézier patch. See also [119]. For general parametrizations, [116] gives a representation of the derivatives of isogeometric functions.
Singular parametrizations can be used to design smooth isogeometric spaces on unstructured multipatch domains. A different C 1 constructions is proposed in [88]. In both cases, the singular mapping is employed at the extraordinary vertices.
From the practical point of view, isogeometric methods are surprisingly robust with respect to singular parametrizations. Even if some of the integrals appearing in the linear system matrix are divergent, the use of Gaussian quadrature hides the trouble and the Galerkin variational formulation returns the correct approximation. However, it is advisable to use the correct subspace basis, given in [113] and [114], to avoid ill-conditioning of the isogeometric formulation.
In [12], the authors use isogeometric analysis on the sphere with a polar parametrization (the extension of Fig. 4.17a), and benchmark the h-convergence in H 2 and H 3 norms, for solution of 4th and 6th order differential equations, respectively. It is shown that enforcing C 0 continuity at the poles yields optimal convergence, that is, the higher-order smoothness of the isogeometric solution at the poles is naturally enforced by the variational formulation.
4.5 Isogeometric Spaces: Spectral Properties
We are interested in the Galerkin approximation of the eigenvalues and eigenfunction of the Laplacian differential operator, as a model problem. We will consider mainly the univariate case. As we will see in this section, the use of C p−1-continuous splines yields advantages when compared to standard C 0 FEM. The results shown here are taken from [71, 73]; we refer to that works for more details. Contrary to the previous Sect. 4.4, the error analysis considered here is not asymptotic, rather it may be characterized as a global analysis approach.
The asymptotic approach is more commonly found in the literature. Classical functional analysis results state that, given an eigenvalue of the differential operator, for a small enough mesh size this eigenvalue is well approximated in the discrete problem. However, for a given mesh size, this kind of analysis offers no information about which discrete modes are a good approximation of the exact modes, and which ones are not.
What happens in practice is that only the lowest discrete modes are accurate. In general, a large portion of the eigenvalue/eigenfunction spectrum, the so-called “higher modes,” are not approximations of their exact counterparts in any meaningful sense. It is well-known in the structural engineering discipline that the higher modes are grossly inaccurate, but the precise point in the spectrum where the eigenvalues and eigenfunctions cease to approximate their corresponding exact counterparts is never known in realistic engineering situations.
First, we focus on the approximations of eigenvalues from a global perspective, that is, we study the approximation errors of the full spectrum. This is done for the simplest possible case, that is the second derivative operator. Based on Fourier/von Neumann analysis, we show that, per degree-of-freedom and for the same polynomial degree p, C p−1 splines (i.e., k-method) are more accurate than C 0 splines (p-method), i.e., finite elements.
Then, we study the accuracy of k-method and p-method approximations to the eigenfunctions of the elliptic eigenvalue problem. The inaccuracy of p-method higher modal eigenvalues has been known for quite some time. We show that there are large error spikes in the L 2-norms of the eigenfunction errors centered about the transitions between branches of the p-method eigenvalue spectrum. The k-method errors are better behaved in every respect. The L 2-norms of the eigenfunction errors are indistinguishable from the L 2 best approximation errors of the eigenfunctions. As shown in [73], when solving an elliptic boundary-value problem, or a parabolic or an hyperbolic problem, the error can be expressed entirely in terms of the eigenfunction and eigenvalue errors. This is an important result but the situation is potentially very different for elliptic boundary-value problems and for parabolic and hyperbolic problems. In these cases, all modes may participate in the solution to some extent and inaccurate higher modes may not always be simply ignored. The different mathematical structures of these cases lead to different conclusions. The inaccuracy of the higher p-method modes becomes a significant concern primarily for the hyperbolic initial-value problem, while the k-method produces accurate results in the same circumstances.
4.5.1 Spectrum and Dispersion Analysis
We consider as a model problem for the eigenvalue study the one of free vibrations of a linear (∞-dimensional) structural system, without damping and force terms:
where \(\mathscr {M}\) and \(\mathscr {K}\) are, respectively, the mass and stiffness operators, and u = u(t, x) is the displacement. The nth normal mode ϕ n and its frequency ω n are obtained from the eigenvalue problem \(\mathscr {K}\boldsymbol {\phi }_n = \omega _n^2 \mathscr {M}\boldsymbol {\phi }_n\). Separating the variables as \( \mathbf {u}(t,\mathbf {x}) = \sum _n \widehat u _n(t) \boldsymbol {\phi }_n (\mathbf {x}), \) and, using Eq. (4.77), we obtain
Then \(\widehat u _n(t) = C_- e^{-\i \omega _n t} + C_+ e^{\i \omega _n t}\), that is each modal coefficient \( \widehat u _n\) oscillates at a frequency ω n. After discretization, the following discrete equations of motion are obtained
where M and K are, respectively, the finite-dimensional consistent mass and stiffness matrices, and u h = u h(t, x) is the discrete displacement vector. Analogously to the continuum case, the discrete normal modes \( \boldsymbol {\phi }^h_n\) and the frequencies \(\omega ^h_n\) are obtained from the eigenproblem
and separating the variables as \( {\mathbf {u}}^h(t,\mathbf {x}) = \sum _n \widehat u^h _n(t) \boldsymbol {\phi }^h_n (\mathbf {x}),\) we end up with \(\widehat u^h _n\) oscillating at a frequency \(\omega ^h_n\), that is: \(\widehat u^h _n = C_- e^{-\i \omega ^h_n t} + C_+ e^{\i \omega ^h_n t}.\) The nth discrete normal mode \( \boldsymbol {\phi }^h_n\) is in general different from the nth exact normal mode ϕ n (Fig. 4.18), for n = 1, …, N, N being the total number of degrees-of-freedom. The corresponding discrete and exact frequencies will be different The target of the frequency analysis is to evaluate how well the discrete spectrum approximates the exact spectrum.
We begin dealing with the eigenproblem (4.79) associated to a linear (p = 1) approximation on the one-dimensional domain (0, L). We employ a uniform mesh 0 = ζ 0 < ζ 1 < … < ζ A < … < ζ N+1 = L, where the number of elements is n el = N + 1 and the mesh-size is h = L∕n el. Considering homogeneous Dirichlet (fixed-fixed) boundary conditions, the eigenproblem (4.79) can be written as

where N is the total number of degrees-of-freedom, and ϕ A = ϕ h(ζ A) is the nodal value of the discrete normal mode at node ζ A. Equation (4.80) solutions are linear combinations of exponential functions ϕ A = (ρ 1)A and ϕ A = (ρ 2)A, where ρ 1 and ρ 2 are the distinct roots of the characteristic polynomial

Actually, (4.82) admits distinct roots when \(\omega ^h h \neq 0, \sqrt {12}\); for ω h h = 0, (4.82) admits the double root ρ = 1 (in this case, solutions of (4.80) are combinations of ϕ A ≡ 1 and ϕ A = A, that is, the affine functions), while for \(\omega ^h h = \sqrt {12}\) there is a double root ρ = −1 (and solutions of (4.80) are combinations of ϕ A = (−1)A and ϕ A = A(−1)A). Observe that, in general, \(\rho _2=\rho _1^{-1}\). For the purpose of spectrum analysis, we are interested in \(0 < \omega ^h h < \sqrt {12}\), which we assume for the remainder of this section. In this case, ρ 1,2 are complex conjugate (we assume Im(ρ 1) ≥ 0) and of unit modulus. Moreover, in order to compare the discrete spectrum to the exact spectrum, it is useful to represent the solutions of (4.80) as linear combinations of e ±iAωh (that is, ϕ A = C − e −iAωh + C + e iAωh), by introducing ω such that e iωh = ρ 1. With this hypothesis, ω is real and, because of periodicity, we restrict to 0 ≤ ωh ≤ π. Using this representation in (4.82) and using the identity \(2\cos {}(\alpha )=e^{\text{i}\alpha }+e^{-\text{i}\alpha }\), after simple computations the relation between ωh and ω h h is obtained:

Solving for ω h h ≥ 0, we get

Furthermore, taking into account the boundary conditions, (4.80)–(4.81) admit the non-null solution

for all ω = π∕L, 2π∕L, …, Nπ∕L. Precisely, (4.85) is the nth discrete normal mode, associated to the corresponding nth discrete natural frequency ω h, given by (4.84):

The nth discrete mode \( \phi _A= C \sin {}(A n \pi /(N+1))\) is the nodal interpolant of the nth exact mode \( \phi (x)= C \sin {}( n \pi x/L)\), whose natural frequency is ω = nπ∕L. The quantity  represents the relative error for the natural frequency. The plot of
represents the relative error for the natural frequency. The plot of

is shown in Fig. 4.19.
We now consider the quadratic p-method for the eigenproblem (4.79). Assuming to have the same mesh as in the linear case, there are N = 2n el − 1 degrees-of-freedom. If we consider the usual Lagrange nodal basis, the corresponding stencil equation is different for element-endpoint degrees-of-freedom and bubble (internal to element) degrees-of-freedom: one has

and

respectively. We also have the boundary conditions ϕ 0 = ϕ N+1 = 0. The bubble degrees-of-freedom can be calculated as
Eliminating them, we obtain a system of equations for the element-endpoints degrees of freedom:
for A = 1, …, N. The bubble elimination is not possible when the bubble equation (4.89) is singular for u A+1∕2, that happens for \(\omega ^h h=\sqrt {10}\).
Normal modes at the element-endpoints nodes can be written as
The boundary condition ϕ 0 = 0 determines C − = −C +, while \(\phi _{n_{el}}=0\) determines \(\frac {\omega L}{\pi } \in \mathbb Z\). Substituting (4.92) into (4.91), we obtain the relation between ω h h and ωh:
The natural frequencies are obtained solving (4.93) with respect to ω h h. Unlike the linear case, each real value of ωh is associated with two values of ω h h, on two different branches, termed acoustical and optical. It can be shown that a monotone ω h h versus ωh relation is obtained representing the two branches in the range ωh ∈ [0, π] and ωh ∈ [π, 2π] respectively (see Figs. 4.20 and 4.21). Therefore, we associate to
the smallest positive root of (4.93), obtaining the acoustical branch, and we associate to
the highest root of (4.93), obtaining the optical branch. These roots are the natural frequencies that can be obtained by bubble elimination. The frequency \(\omega ^h h = \sqrt {10}\), which gives bubble resonance is associated with the normal mode
Since \(\omega ^h h = \sqrt {10}\) is located between the two branches, this frequency is associated with mode number n = n el. Then, all normal modes at element endpoints are given by
n being the mode number. Therefore, (4.97) is an interpolate of the exact modes (at element endpoint nodes).
The numerical error in the calculation of natural frequencies is visualized by the graph of ω h∕ω versus ωh, shown in Fig. 4.21.
Finally, we discuss the quadratic k-method. A rigorous analysis of this case would be too technical; here we prefer to maintain the discussion informal and refer the reader to [71] for the technical details. The equations of (4.79) have different expression for the interior stencil points and for the stencil points close to the boundary (the first and last two equations). We also have for the boundary conditions ϕ 0 = ϕ N+1 = 0. In the interior stencil points, the equations read
A major difference from the cases considered previously is that (4.98) is a homogeneous recurrence relation of order 4. Because of its structure, its solutions can be written as linear combinations of the four solutions e ±ıωhA and \(e^{ \pm \i \widetilde {\omega } h A }\). Here ω h is real and positive while \(\widetilde {\omega }^h\) has a nonzero imaginary part. More precisely, the general solution of (4.98) has the form
for any constants C +, C −, \(\widetilde {C}_{+}\), \(\widetilde {C}_{-}\). Plugging this expression of ϕ A into the boundary equations and imposing the boundary conditions, one finds that \(\widetilde {C}_{+} = \widetilde {C}_{-} = 0\) and that C + = −C −. Similarly as before, substituting (4.99) into (4.98), we obtain the relation between ω h h and ωh (see Fig. 4.22):
The plot of ω h h vs. ωh is shown in Fig. 4.23.
The study above addresses a very simple case but can be generalized. The most interesting direction is to consider arbitrary degree. For degree higher than 2 “outlier frequencies” appear in the k-method: these are O(p) highest frequencies that are numerically spurious and, though they can be filtered out by a suitable geometric parametrization [71] or mesh refinement [45], their full understanding is an open problem. Most importantly, the higher-order p-elements give rise to so-called “optical branches” to spectra, which have no approximation properties, having relative errors that diverge with p; on the other hand there are no optical modes with the k-method and, excluding the possible outlier frequencies, the spectral errors converge with p. Based on the previous observations, we are able to confidently use numerics to calculate invariant analytical spectra for both p-method and k-method. This comparison is reported in Fig. 4.24 and registers a significant advantage for the latter. These results may at least partially explain why classical higher-order finite elements have not been widely adopted in problems for which the upper part of the discrete spectrum participates in a significant way, such as, for example, impact problems and turbulence.
The study can be extended to multidimensional problems as well, mainly confirming the previous findings. We refer again to [71] for the details.
Finally, we present a simple problem that shows how the spectrum properties presented above may affect a numerical solution. Consider the model equation
with boundary conditions
The solution to problem (4.101)–(4.102) can be written as

We numerically solve (4.101)–(4.102) for k = 71, selecting p = 3 and 31 degrees-of-freedom for the k- and p-method. The results are reported in Fig. 4.25. The k-method is able to reproduce correctly the oscillations of the exact solutions (phase and amplitude are approximately correct). There are no stopping bands for the k-method. On the contrary, since k = 71 is within the 2nd stopping band of the p-method, a spurious attenuation is observed. We refer to [71] for the complete study.
4.5.2 Eigenfunction Approximation
Let Ω be a bounded and connected domain in \(\mathbb {R}^d\), where \(d \in \mathbb {Z}^+\) is the number of space dimensions. We assume Ω has a Lipschitz boundary ∂Ω. We assume both are continuous and coercive in the following sense: For all \(v, w \in \mathscr {V}\),
where ∥⋅∥E is the energy-norm which is assumed equivalent to the (H m(Ω))n-norm on \(\mathscr {V}\) and ∥⋅∥ is the (L 2(Ω))n = (H 0(Ω))n norm. The elliptic eigenvalue problem is stated as follows: Find eigenvalues \(\lambda _l \in \mathbb {R}^+\) and eigenfunctions \(u_l \in \mathscr {V}\), for l = 1, 2, …, ∞, such that, for all \(w \in \mathscr {V}\),
It is well-known that 0 < λ 1 ≤ λ 2 ≤ λ 3 ≤…, and that the eigenfunctions are (L 2(Ω))n-orthonormal, that is, (u k, u l) = δ kl where δ kl is the Kronecker delta, for which δ kl = 1 if k = l and δ kl = 0 otherwise. The normalization of the eigenfunctions is actually arbitrary. We have assumed without loss of generality that ∥u l∥ = 1, for all l = 1, 2, …, ∞. It follows from (4.108) that
and a(u k, u l) = 0 for k ≠ l. Let \(\mathscr {V}^h\) be either a standard finite element space (p-method) or a space of maximally smooth B-splines (k-method). The discrete counterpart of (4.108) is: Find \(\lambda ^h_l \in \mathbb {R}^+\) and \(u^h_l \in \mathscr {V}^h\) such that for all \(w^h \in \mathscr {V}^h\),
The solution of (4.110) has similar properties to the solution of (4.108). Specifically, \(0 < \lambda ^h_1 \leq \lambda ^h_2 \leq \ldots \leq \lambda ^h_N\), where N is the dimension of \(\mathscr {V}^h\), \((u^h_k,u^h_l) = \delta _{kl}\), \(\| u^h_l \|{ }^2_E = a(u^h_l,u^h_l) = \lambda ^h_l\), and \(a(u^h_k,u^h_l) = 0\) if k ≠ l. The comparison of \(\left \{ \lambda ^h_l, u^h_l \right \}\) to \(\left \{ \lambda _l, u_l \right \}\) for all l = 1, 2, …, N is the key to gaining insight into the errors of the discrete approximations to the elliptic boundary-value problem and the parabolic and hyperbolic initial-value problems.
The fundamental global error analysis result for elliptic eigenvalue problems is the Pythagorean eigenvalue error theorem. It is simply derived and is done so on page 233 of Strang and Fix [111] The theorem is global in that it is applicable to each and every mode in the discrete approximation. Provided that \(\| u^h_l \| = \| u_l \|\),
Note that the relative error in the lth eigenvalue and the square of the relative (L 2(Ω))n-norm error in the lth eigenfunction sum to equal the square of the relative energy-norm error in the lth eigenfunction. Due to the normalization introduced earlier, (4.111) can also be written as
See Fig. 4.26. We note that the first term in (4.112) is always non-negative as \(\lambda ^h_l \geq \lambda _l\), a consequence of the “minimax” characterization of eigenvalues (see [111], p. 223). It also immediately follows from (4.112) that
We consider the elliptic eigenvalue problem for the second-order differential operator in one-dimension with homogeneous Dirichlet boundary conditions. The variational form of the problem is given by (4.108), in which
The eigenvalues are λ l = π 2 l 2 and the eigenfunctions are \(u_l = \sqrt {2} \sin \left (l \pi x \right )\), l = 1, 2, …, ∞. Now, we will present the eigenvalue errors, rather than the eigenfrequency errors, and, in addition, L 2(0, 1)- and energy-norm eigenfunction errors. We will plot the various errors in a format that represents the Pythagorean eigenvalue error theorem budget. We will restrict our study to quadratic, cubic, and quartic finite elements and B-splines. In all cases, we assume linear geometric parametrizations and uniform meshes. Strictly speaking, for the k-method the results are only true for sufficiently large N, due to the use of open knot vectors, but in this case “sufficiently large” is not very large at all, say N > 30. For smaller spaces, the results change slightly. The results that we present here were computed using N ≈ 1000 and, in [73], have been validated using a mesh convergence study and by comparing to analytical computations.
Let us begin with results for the quadratic k-method, i.e. C 1-continuous quadratic B-splines, presented in Fig. 4.27a. The results for the relative eigenvalue errors (red curve) follow the usual pattern that has been seen before. The squares of the eigenfunction errors in L 2(0, 1) are also well-behaved (blue curve) with virtually no discernible error until about l∕N = 0.6, and then monotonically increasing errors in the highest modes. The sums of the errors produce the squares of the relative energy-norm errors (black curve), as per the Pythagorean eigenvalue error theorem budget. There are no surprises here.
Pythagorean eigenvalue error theorem budget for quadratic elements. (a) C 1-continuous B-splines; (b) C 0-continuous finite elements. The blue curves are \(\| u^h_l - u_l \|{ }^2\), the red curves are \((\lambda ^h_l - \lambda _l)/\lambda _l\), and the black curves are \(\| u^h_l - u_l \|{ }^2_E/\lambda _l\). Note that \(\| u_l \| = \| u^h_l \| = 1\), \(\| u_l \|{ }^2_E = \lambda _l\), and \(\| u^h_l \|{ }^2_E = \lambda ^h_l\)
Next we compare with quadratic p-method, i.e., C 0-continuous quadratic finite elements in Fig. 4.27b. The pattern of eigenvalue errors (red curve), consisting of two branches, the acoustic branch for l∕N < 1∕2, and the optical branch for l∕N ≥ 1∕2, is the one known from Sect. 4.5.1. However, the eigenfunction error in L 2(0, 1) (blue curve) represents a surprise in that there is a large spike about l∕N = 1∕2, the transition point between the acoustic and optical branches. Again, the square of the energy-norm eigenfunction error term (black curve) is the sum, as per the budget. This is obviously not a happy result. It suggests that if modes in the neighborhood of l∕N = 1∕2 are participating in the solution of a boundary-value or initial-value problem, the results will be in significant error. The two unpleasant features of this result are (1) the large magnitude of the eigenfunction errors about l∕N = 1∕2 and (2) the fact that they occur at a relatively low mode number. That the highest modes are significantly in error is well-established for C 0-continuous finite elements, but that there are potential danger zones much earlier in the spectrum had not been recognized previously. The midpoint of the spectrum in one-dimension corresponds to the quarter point in two dimensions and the eighth point in three dimensions, and so one must be aware of the fact that the onset of inaccurate modes occurs much earlier in higher dimensions.
The spikes in the eigenfunction error spectrum for C 0-finite elements raise the question as to whether or not the eigenfunctions are representative of the best approximation to eigenfunctions in the vicinity of l∕N = 1∕2. To answer this question, we computed the L 2(0, 1) best approximations of some of the exact eigenfunctions and plotted them in Fig. 4.28b. (They are indicated by ×.) The case for C 1-continuous quadratic B-splines is presented in Fig. 4.28a for comparison. For this case there are almost no differences between the best approximation of the exact eigenfunctions and the computed eigenfunctions. However, for the C 0-continuous quadratic finite elements, the differences between the computed eigenfunctions and the L 2(0, 1) best approximations of the exact eigenfunctions are significant, as can be seen in Fig. 4.28b. The spike is nowhere to be seen in the best approximation results. We conclude that the Galerkin formulation of the eigenvalue problem is simply not producing good approximations to the exact eigenfunctions about l∕N = 1∕2 in the finite element case.
Comparisons of eigenfunctions computed by the Galerkin method with L 2(0, 1) best approximations of the exact eigenfunctions. (a) C 1-continuous quadratic B-splines; (b) C 0-continuous quadratic finite elements. The blue curves are \(\| u^h_l - u_l \|{ }^2\), where \(u^h_l\) is the Galerkin approximation of u l, and the ×’s are \(\| \widetilde {u}^h_l - u_l \|{ }^2\), where \(\widetilde {u}^h_l\) is the L 2(0, 1) best approximation of u l
For higher-order cases, in particular cubic and quartic, see [73] where it is shown that the essential observations made for the quadratic case persist. An investigation of the behavior of outlier frequencies and eigenfunctions is also presented in [73], along with discussion of the significance of eigenvalue and eigenfunction errors in the context of elliptic, parabolic and hyperbolic partial differential equations.
4.6 Computational Efficiency
High-degree high-regularity splines, and extensions, deliver higher accuracy per degree-of-freedom in comparison to C 0 finite elements but at a higher computational cost, when standard finite element implementation is adopted. In this section we present recent advances on the formation of the system matrix (Sects. 4.6.1 and 4.6.2), the solution of linear systems (Sect. 4.6.3) and the use a matrix-free approach (Sect. 4.6.4)
We consider, as a model case, the d-dimensional Poisson problem on a single-patch domain, and an isogeometric tensor-product space of degree p, continuity C p−1 and total dimension N, with N ≫ p. This is the typical setting for the k-method.
An algorithm for the formation of the matrix is said to be (computationally) efficient if the computational cost is proportional to the number of non-zero entries of the matrix that have to be calculated (storage cost). The stiffness matrix in our model case has about N(2p + 1)d ≈ CNp d non-zero entries.
An algorithm for the solution of the linear system matrix is efficient if the computational cost is proportional to the solution size, i.e., N.
A matrix-free approach aims at an overall computational cost and storage cost of CN.
4.6.1 Formation of Isogeometric Matrices
When a finite element code architecture is adopted, the simplest approach is to use element-wise Gaussian quadrature and element-by-element assembling. Each elemental stiffness matrix has dimension (p + 1)2d and each entry is calculated by quadrature on (p + 1)d Gauss points. The total cost is CN EL p 3d ≈ CNp 3d, where N EL is the number of elements and, for the k-method, N EL ≈ N.
A strategy to reduce the cost is to reduce the number of quadrature points. The paper [72] proposed to use generalized Gaussian rules for smooth spline integrands. These rules are not known analytically and need to be computed numerically (see also [9, 13, 14] and the recent paper [75] where the problem is effectively solved by a Newton method with continuation). Furthermore, reduced quadrature rules have been considered in [1, 101] and [65]. Another important step is to reduce the number of operations by arranging the computations in a way that exploits the tensor-product structure of multivariate splines: this is done by so-called sum factorization achieving a computational cost of CNp 2d+1, see [3].
Keeping the element-wise assembling loop is convenient, as it allows reusing available finite element routines. On the other hand, as the computation of each elemental stiffness matrix needs at least Cp 2d FLOPs (proportional to the elemental matrix size and assuming integration cost does not depend on p) the total cost is at least CN EL p 2d ≈ CNp 2d.
Further cost reduction is possible but only with a change of paradigm from element-wise assembling. This study has been recently initiated and two promising strategies have emerged.
One idea, in [84], is to use a low-rank expansion in order to approximate the stiffness matrix by a sum of R Kronecker type matrices that can be easily formed, thanks to their tensor-product structure. This approach has a computational cost of CNRp d FLOPs.
Another possibility, from [42], is based on two new concepts. The first is the use of a row loop instead of an element loop, and the second is the use of weighted quadrature. This will be discussed in the next section.
4.6.2 Weighted Quadrature
This idea has been proposed in [42]. Assume we want to compute integrals of the form:
where \(\{\widehat {B}_{i}\}_{i=1,\dots , n} \) are p-degree univariate B-spline basis functions. Consider for simplicity only the maximum regularity case, C p−1, and for the moment a periodic uniform knot vector. Being in the context of Galerkin method, \( \widehat {B}_{i} (\zeta )\) represents a test function and \(\widehat {B}_{j} (\zeta )\) represents a trial function.
We are interested in a fixed point quadrature rule. In the lowest degree case, p = 1, exact integration is performed by a composite Cavalieri-Simpson rule:
where \(x_q^{CS}\) are the quadrature points and \(w_q^{CS}\) the relative weights. In the above hypotheses the points \(x_q^{CS}\) are the knots and the midpoints of the knot-spans and \(w_q^{CS} = \frac {h}{3}\) on knots and \(w_q^{CS} = \frac {2h}{3}\) on midpoints.
Unbalancing the role of the test and the trial factors in (4.118), we can see it as a weighted quadrature:
where \(x_q^{CS}=x_{q,i}^{WQ}\) and \(w_{q,i}^{WQ}= \widehat {B}_{i} (x_{q,i}^{WQ}) w_q^{CS}\). Because of the local support of the function \(\widehat {B}_{i}\) only in three points the quadrature \(\mathbb {Q}_i^{WQ}\) is non-zero and the weights are equal to \(\frac {h}{3}\).
If we go to higher degree, we need more quadrature points in (4.118). For p-degree splines the integrand \(\widehat {B}_{i} \widehat {B}_{j}\) is a piecewise polynomial of degree 2p and an element-wise integration requires 2p + 1 equispaced points, or p + 1 Gauss points, or about p∕2 points with generalized Gaussian integration (see [9, 31, 41, 72]). On the other hand, we can generalize (4.119) to higher degree still using as quadrature points only the knots and midpoints of the knot spans. Indeed this choice ensures that, for each basis function \(\widehat {B}_{i}\), i = 1, …, n, there are 2p + 1 “active” quadrature points where \(\widehat {B}_{i}\) is nonzero. Therefore we can compute the 2p + 1 quadrature weights by imposing conditions for the 2p + 1 B-splines \(\widehat {B}_{j}\) that need to be exactly integrated. Clearly, the advantage of the weighted quadrature approach is that its computational complexity, i.e., the total number of quadrature points, is independent of p.
Given a weighted quadrature rule of the kind above, we are then interested in using it for the approximate calculation of integrals as:
For a non-constant function c(⋅), (4.120) is in general just an approximation.
We consider now the model reaction-diffusion problem
Its Galerkin approximation requires the stiffness matrix \(\mathbb {S}\) and mass matrix \(\mathbb {M}\). After change of variable we have \(\mathbb {M}= \{m_{{\boldsymbol {i}},\boldsymbol {j}} \} \in \mathbb {R}^{N \times N }\) with entries given by:
For notational convenience we write:
In more general cases, the factor c incorporates the coefficient of the equation and, for NURBS functions, the polynomial denominator. Similarly for the stiffness matrix \(\mathbb {S}= \{s_{{\boldsymbol {i}},\boldsymbol {j}} \}\in \mathbb {R}^{N \times N }\) we have:
which we write in compact form:
Here we have denoted by \( \bigl \{ c_{l,m} (\boldsymbol {\zeta }) \bigr \}_{ l,m=1,\dots ,d} \) the following matrix:
The number of non-zero elements N NZ of \(\mathbb {M}\) and \( \mathbb {S}\) depends on the polynomial degree p and the required regularity r. We introduce the following sets:
We have \( \# \mathscr {I}_{l,i} \le (2p+1) \) and N NZ = O(N p d). In particular, with maximal regularity in the case d = 1 one has N NZ = (2p + 1)N − p(p + 1).
Consider the calculation of the mass matrix. The first step is to write the integral in a nested way, as done in [3]:
The idea in is to isolate the test function \(\widehat {B}_{i_l}\) univariate factors in each univariate integral and to consider it as a weight for the construction of the weighted quadrature (WQ) rule. This leads to a quadrature rule for each i l that is:
Notice that we drop from now on the label WQ used in the introduction in order to simplify notation. The key ingredients for the construction of the quadrature rules that preserve the optimal approximation properties are the exactness requirements. Roughly speaking, exactness means that in (4.126) we have \(m_{{\boldsymbol {i}}, \boldsymbol {j}}= \widetilde m_{{\boldsymbol {i}}, \boldsymbol {j}} \) whenever c is a constant coefficient. When the stiffness term is considered, also terms with derivatives have to be considered.
We introduce the notation:
For each integral in (4.127) we define a quadrature rule: we look for
-
points \(\widetilde {\boldsymbol {x}}_{\boldsymbol {q}} = ( \widetilde {x}_{1,q_1} , \widetilde {x}_{2,q_2}, \dots , \widetilde {x}_{d,q_d} )\) with q l = 1, …n QP,l, with N QP is \( \# \left \{\widetilde {\boldsymbol {x}} \right \} =\prod _{l=1}^{d} n_{\mathsf {QP},l}\);
-
for each index i l = 1, …, n DOF,l;l = 1, …, d, four quadrature rules such that:
$$\displaystyle \begin{aligned} \begin{gathered} \mathbb{Q}^{(0,0)}_{i_l} (f) := \sum_{q_l = 1}^{n_{\mathsf{QP},l}} w^{(0,0)}_{l, i_l, q_l } f( \widetilde{x}_{l,q_l} ) \approx \int_0^1 f(\zeta_l) \widehat{B}_{i_l} (\zeta_l) d\zeta_l \,; \\ \mathbb{Q}^{(1,0)}_{i_l} (f) := \sum_{q_l = 1}^{n_{\mathsf{QP},l}} w^{(1,0)}_{l, i_l, q_l } f( \widetilde{x}_{l,q_l} ) \approx \int_0^1 f(\zeta_l) \widehat{B}_{i_l} (\zeta_l) d\zeta_l \,; \\ \mathbb{Q}^{(0,1)}_{i_l} (f) := \sum_{q_l = 1}^{n_{\mathsf{QP},l}} w^{(0,1)}_{l, i_l, q_l } f( \widetilde{x}_{l,q_l} ) \approx \int_0^1 f(\zeta_l) \widehat{B}^{\prime}_{i_l} (\zeta_l) d\zeta_l \,; \\ \mathbb{Q}^{(1,1)}_{i_l} (f) := \sum_{q_l = 1}^{n_{\mathsf{QP},l}} w^{(1,1)}_{l, i_l, q_l } f( \widetilde{x}_{l,q_l} ) \approx \int_0^1 f(\zeta_l) \widehat{B}^{\prime}_{i_l} (\zeta_l) d\zeta_l \, . \end{gathered} \end{aligned} $$(4.128)fulfilling the exactness requirement:
$$\displaystyle \begin{aligned} \displaystyle \begin{array}{l} \mathbb{Q}^{(0,0)}_{i_l} (\widehat{B}_{j_l} ) = \mathbb{I}^{(0,0)}_{l,i_l,j_l} \, \\ \mathbb{Q}^{(1,0)}_{i_l} (\widehat{B}^{\prime}_{j_l} ) = \mathbb{I}^{(1,0)}_{l,i_l,j_l} \, \\ \mathbb{Q}^{(0,1)}_{i_l} (\widehat{B}_{j_l} ) = \mathbb{I}^{(0,1)}_{l,i_l,j_l} \, \\ \mathbb{Q}^{(1,1)}_{i_l} (\widehat{B}^{\prime}_{j_l} ) = \mathbb{I}^{(1,1)}_{l,i_l,j_l} \, \end{array} \,,\ \forall j_l \in \mathscr{I}_{l,i_l} \, . \end{aligned} $$(4.129)
We also require that the quadrature rules \(\mathbb {Q}^{(\cdot ,\cdot )}_{i_l} \) have support included in the support of \(\widehat {B}_{i_l}\), that is
where \(\mathscr {Q}_{l,i_l}:= \left \{ q_l\in {1,\dots , n_{\mathsf {QP},l}} \text{ s.t. } \widetilde {x}_{l,q_l} \in \mbox{supp}\left (\widehat {B}_{i_l}\right ) \right \} \); recall that here the support of a function is considered an open set. Correspondingly, we introduce the set of multi-indexes \(\mathscr {Q}_{{\boldsymbol {i}} } := \prod _{l=1}^d \mathscr {Q}_{l,i_l} \).
Once the points \(\widetilde {\boldsymbol {x}}_{\boldsymbol {q}} \) are fixed, the quadrature rules have to be determined by the exactness requirements, that are a system of linear equations of the unknown weights (each of the (4.129)). For that we require
See[42] for a discussion on the well-posedness of the linear systems for the weights.
The construction of a global grid of quadrature points is done in order to save computations. For the case of maximum C p−1 regularity considered here, the choice for quadrature points of [42] is endpoints (knots) and midpoints of all internal knot-spans, while for the boundary knot-spans (i.e. those that are adjacent to the boundary of the parameter domain \(\widehat \varOmega \)) we take p + 1 equally spaced points. Globally N QP ≈ 2d N EL = O(N) considering only the dominant term.
When all the quadrature rules are available we can write the computation of the approximate mass matrix following (4.126), where the quadrature rules \(\mathbb {Q}^{(0,0)}_{i_1},\ldots ,\mathbb {Q}^{(0,0)}_{i_d}\) are used. Similar formulae and algorithms can be written for the stiffness matrix. In that case, all the integrals are approximated separately, and all the quadrature rules \(\mathbb {Q}^{(\cdot ,\cdot )}_{i_l}\) are necessary.
The mass matrix formation algorithm is mainly a loop over all rows i, for each i we consider the calculation of
where \( w^{(0,0)}_{{\boldsymbol {i}},\boldsymbol {q}} = w^{(0,0)}_{1,i_1,q_1} \ldots w^{(0,0)}_{d,i_d,q_d}\).
The computational cost of (4.132) is minimised by a sum factorization approach. Nota that (4.132) can be rearranged as in (4.126) to obtain the following sequence of nested summations:
To write (4.133) in a more compact form, we introduce the notion of matrix-tensor product. Let \(\mathscr {X} = \left \{x_{k_1, \ldots , k_d}\right \} \in \mathbb {R}^{n_{1} \times \ldots \times n_{d} }\) be a d −dimensional tensor, and let \(m \in \left \{1, \ldots , d\right \}\). The m −mode product of \(\mathscr {X}\) with a matrix \(A = \left \{a_{i,j}\right \} \in \mathbb {R}^{ t \times n_m}\), denoted with \(\mathscr {X} \times _{m} A \), is a tensor of dimension n 1 ×… × n m−1 × t × n m+1 ×… × n d, with components
For l = 1, …, d and i l = 1, …, n l we define the matrices
where diag(v) denotes the diagonal matrix obtained by the vector v. We also define, for each index i, the d −dimensional tensor
Using the above notations, we have
Since with this choice of the quadrature points \(\# \mathscr {Q}_{l,i_l}\) and \(\# \mathscr {I}_{l,i_l}\) are both O(p), the computational cost associated with (4.134) is O(p d+1) FLOPs. Note that \(\widetilde m_{{\boldsymbol {i}}, \mathscr {I}_{{\boldsymbol {i}}}}\) includes all the nonzeros entries of the i-th row of \(\widetilde {\mathbb {M}}\). Hence if we compute it for each i = 1, …, N the total cost amounts to O(N p d+1) FLOPs. This approach is summarized in Algorithm 1.
Algorithm 1: Construction of mass matrix by sum-factorization

From [42], we report CPU time results for the formation on a single patch domain of mass matrices. Comparison is made with GeoPDEs 3.0, the optimized but SGQ-based MATLAB isogeometric library developed by Rafael Vázquez, see[124]. In Fig. 4.29 we plot the time needed for the mass matrix formation up to degree p = 10 with N = 203. The tests confirm the superior performance of the proposed row-loop WQ-based algorithm vs SGQ. In the case p = 10 GeoPDEs takes more than 62 h to form the mass matrix while the proposed algorithm needs only 27 s, so the use high degrees is possible with WQ.
Time for mass matrix assembly in the framework of isogeometric-Galerkin method with maximal regularity on a single patch domain of 203 elements. The comparison is between the WQ approach and the SGQ as implemented in GeoPDEs 3.0 [125]
4.6.3 Linear Solvers and Preconditioners
The study of the computational efficiency of linear solvers for isogeometric discretizations has been initiated in the papers [46, 47], where it has been shown that the algorithms used with the finite element method suffer of performance degradation when used to solve isogeometric linear systems. Consider, for example, a Lagrangian finite element method with polynomial degree p and N degrees-of-freedom, in 3D, for a Poisson model problem:. As shown in [46], a multifrontal direct solver requires O(N 2) FLOPs (under the assumption N > p 9) to solve the resulting linear system. If, instead, we consider the isogeometric k-method with C p−1 p-degree splines and N degrees-of-freedom, the same direct solver requires O(N 2 p 3) FLOPs, i.e., p 3 times more than in the finite element case. The memory required is also higher for the k-method.
Iterative solvers have attracted more attention in the isogeometric community since they allow, though it is not trivial, optimal computational cost. The effort has been primarily on the development of preconditioners for the Poisson model problem, for arbitrary degree and continuity splines. As reported in [47], standard algebraic preconditioners (Jacobi, SSOR, incomplete factorization) commonly adopted for finite elements exhibit reduced performance when used in the context of the isogeometric k-method. Standard multilevel and multigrid approaches are studied respectively in [39] and [60], while advances in the theory of domain-decomposition based solvers are given in, e.g., [24, 28]. These papers also confirm the difficulty in achieving both robustness and computational efficiency for the high-degree k-method.
More sophisticated multigrid preconditioners have been proposed in the recent papers [54] and [67]. The latter, in particular, contains a proof of robustness, based on the theory of [115]. The two works are based on the following common ingredients: specific spectral properties of the discrete operator of the isogeometric k-method and the tensor-product structure of isogeometric spaces.
The tensor-product structure of multivariate spline space is exploited in [61, 96], based on approaches that have been developed for the so-called Sylvester equation. The tensor product structure of splines spaces yields to a Kronecker structure of isogeometric matrices.
We first recall the notation and basic properties of the Kronecker product of matrices. Let \(A \in \mathbb {R}^{n_a \times n_a}\), and \(B \in \mathbb {R}^{n_b \times n_b}\). The Kronecker product between A and B is defined as
where a ij, i, j = 1, …n a, denote the entries of A. The Kronecker product is an associative operation, and it is bilinear with respect to matrix sum and scalar multiplication. Some properties of the Kronecker product that will be useful in the following.
-
It holds
$$\displaystyle \begin{aligned} (A \otimes B)^T = A^T \otimes B^T. \end{aligned} $$(4.135) -
If C and D are matrices of conforming order, then
$$\displaystyle \begin{aligned} \left(A \otimes B\right) \left(C \otimes D\right) = (AC \otimes BD ). \end{aligned} $$(4.136) -
For any matrix \( X \in \mathbb {R}^{n_a\times n_b}\) we denote with εc(X) the vector of \(\mathbb {R}^{n_a n_b}\) obtained by “stacking” the columns of X. Then if A, B and X are matrices of conforming order, and x = εc(X), it holds
$$\displaystyle \begin{aligned} \left( A \otimes B\right)x = {\varepsilon}c( B X A ^T). \end{aligned} $$(4.137)
The last property can be used to cheaply compute matrix-vector products with a matrix having Kronecker structure. Indeed, it shows that computing a matrix-vector product with A ⊗ B is equivalent to computing n b matrix-vector products with A and n a matrix-vector products with B. Note in particular that A ⊗ B does not have to be formed.
Consider the Laplace operator with constant coefficients, on the square [0, 1]2, then the tensor-product spline Galerkin discretization leads to the system
where K ℓ and M ℓ denote the univariate stiffness and mass matrices in the ℓ direction, ℓ = 1, 2, and ⊗ is the Kronecker product. For simplicity, we assume that all the univariate matrices have the same order, which we denote with n. Note in particular that N = n 2.
Observe that in general, for variable coefficients, general elliptic problems, non-trivial and possibly multipatch geometry parametrization, the isogeometric system is not as in (4.138). In this case, a fast solver for (4.138) plays the role of a preconditioner. At each iterative step, the preconditioner takes the form
Using relation (4.137), we can rewrite this equation in matrix form
where εc(S) = s and εc(R) = r. Equation (4.140) takes the name of (generalized) Sylvester equation. Due to its many applications, the literature dealing with Sylvester equation (and its variants) is vast, and a number of methods have been proposed for its numerical solution. We refer to [110] for a recent survey on this subject.
Following [96], we consider the fast diagonalization (FD) method which is a direct solver, that is, \(s = { \mathscr {P} }^{-1}r\) is computed exactly. It was first presented in 1964 by Lynch, Rice and Thomas [83] as a method for solving elliptic partial differential equations discretized with finite differences. This approach was extended to a general Sylvester equation involving nonsymmetric matrices by Bartels and Stewart in 1972 [11], although this is not considered here.
We consider the generalized eigendecomposition of the matrix pencils (K 1, M 1) and (K 2, M 2), namely
where D 1 and D 2 are diagonal matrices whose entries are the eigenvalues of \({M}_1^{-1}K_1\) and \({M}_2^{-1}K_2\), respectively, while U 1 and U 2 satisfy
which implies in particular \(U_1^{-T} U_1^{-1} = {M}_1\) and \(U_2^{-T} U_2^{-1} = {M}_2\), and also, from (4.141), \(U_1^{-T} D_1 U_1^{-1} = K_1\) and \(U_2^{-T} D_2 U_2^{-1} = K_2\). Therefore we factorize \({ \mathscr {P} }\) in (4.139) as follows:
and adopt the following strategy:
Algorithm 2: FD direct method (2D)
-
Compute the generalized eigendecompositions (4.141)
-
Compute \(\widetilde {r} = (U_1 \otimes U_2) ^{ T} r \)
-
Compute \(\widetilde {s} = \left (D_1 \otimes I + I \otimes D_2 \right )^{-1} \widetilde {r} \)
-
Compute \(s = (U_1 \otimes U_2) \widetilde {s} \)
The exact cost of the eigendecompositions in line 1 depends on the algorithm employed. A simple approach is to first compute the Cholesky factorization M 1 = LL T and the symmetric matrix \(\widetilde {K_1} = L^{-1} K_1 L^{-T}\). Since M 1 and K 1 are banded, the cost of these computations is O(pn 2) FLOPs. The eigenvalues of \(\widetilde {K_1}\) are the same of (4.141), and once the matrix \(\widetilde {U_1}\) of orthonormal eigenvectors is computed then one can compute \(U_1 = L^{-T} \widetilde {U_1} \), again at the cost of O(pn 2) FLOPs. Being \(\widetilde {U_1}\) orthogonal, then \(U_1^T {M}_1 U_1 = I_n\). If the eigendecomposition of \(\widetilde {K_1}\) is computed using a divide-and-conquer method, the cost of this operation is roughly 4n 3 FLOPs. We remark that the divide-and-conquer approach is also very suited for parallelization. In conclusion, by this approach, line 1 requires roughly 8n 3 FLOPs.
Lines 2 and 4 each involve a matrix-vector product with a matrix having Kronecker structure, and each step is equivalent (see (4.137)) to 2 matrix products involving dense n × n matrices. The total computational cost of both steps is 8n 3 FLOPs. Line 3 is just a diagonal scaling, and its O(n 2) cost is negligible. We emphasize that the overall computational cost of Algorithm 2 is independent of p.
If we apply Algorithm 2 as a preconditioner, then Step 1 may be performed only once, since the matrices involved do not change throughout the CG iteration. In this case the main cost can be quantified in approximately 8n 3 FLOPs per CG iteration. The other main computational effort of each CG iteration is the residual computation, that is the product of the system matrix \(\mathscr {A} \) by a vector, whose cost in FLOPs is twice the number of nonzero entries of \(\mathscr {A} \), that is approximately 2(2p + 1)2 n 2. In conclusion, the cost ratio between the preconditioner application and the residual computation is O(n∕p 2).
When d = 3, Eq. (4.139) takes the form
where, as in the 2D case, we assume that all the univariate matrices have order n (and hence N = n 3).
The FD method above admits a straightforward generalization to the 3D case. We consider the generalized eigendecompositions
with D 1, D 2, D 3 diagonal matrices and
Then, (4.142) can be factorized as
which suggests the following algorithm.
Algorithm 3: FD direct method (3D)
-
Compute the generalized eigendecompositions (4.143)
-
Compute \(\widetilde {r} = (U_1 \otimes U_2 \otimes U_3) r \)
-
Compute \(\widetilde {s} = \left (D_1 \otimes I \otimes I + I \otimes D_2 \otimes I + I \otimes I \otimes D_3 \right )^{-1} \widetilde {r} \)
-
Compute \(s = (U_1 \otimes U_2 \otimes U_3)^T \widetilde {s} \)
Lines 1 and 3 require O(n 3) FLOPs. Lines 2 and 4, as can be seen by nested applications of formula (4.137), are equivalent to performing a total of 6 products between dense matrices of size n × n and n × n 2. Thus, neglecting lower order terms the overall computational cost of Algorithm 3 is 12n 4 FLOPs.
The FD method is even more appealing in the 3D case than it was in the 2D case, for at least two reasons. First, the computational cost associated with the preconditioner setup, that is the eigendecomposition, is negligible. This means that the main computational effort of the method consists in a few (dense) matrix-matrix products, which are level 3 BLAS operations and typically yield high efficiency thanks to a dedicated implementation on modern computers by optimized usage of the memory cache hierarchy Second, in a preconditioned CG iteration the cost for applying the preconditioner has to be compared with the cost of the residual computation (a matrix-vector product with \(\mathscr {A}\)) which can be quantified in approximately 2(2p + 1)3 n 3 for 3D problems, resulting in a FLOPs ratio of the preconditioner application to residual computation of O(n∕p 3). However in numerical tests we will see that, for all cases of practical interest in 3D, the computational time used by the preconditioner application is far lower that the residual computation itself. This is because the computational time depends not only on the FLOPs count but also on the memory usage and, as mentioned above, dense matrix-matrix multiplications greatly benefit of modern computer architecture.
We report some 3D single-patch numerical tests from [96]. We consider a two domains: the first one is a thick quarter of ring; note that this solid has a trivial geometry on the third direction. The second one is the solid of revolution obtained by the 2D quarter of ring. Specifically, we performed a π∕2 revolution around the axis having direction (0, 1, 0) and passing through (−1, −1, −1). We emphasize that here the geometry is nontrivial along all directions.
We consider a standard Incomplete Cholesky (IC) preconditioner (no reordering is used in this case, as the resulting performance is better than when using the standard reorderings available in Matlab).
In Table 4.1 we report the results for the thick quarter ring while in Table 4.2 we report the results for the revolved ring. The symbol “*” denotes the cases in which even assembling the system matrix \(\mathscr {A}\) was unfeasible due to memory limitations. From these results, we infer that most of the conclusions drawn for the 2D case still hold in 3D. In particular, both Sylvester-based preconditioners yield a better performance than the IC preconditioner, especially for small h.
Somewhat surprisingly, however, the CPU times show a stronger dependence on p than in the 2D case, and the performance gap between the ADI and the FD approach is not as large as for the cube domain. This is due to the cost of the residual computation in the CG iteration (a sparse matrix-vector product, costing O(p 3 n 3) FLOPs). This step represents now a significant computational effort in the overall CG performance. In fact, our numerical experience shows that the 3D FD method is so efficient that the time spent in the preconditioning step is often negligible w.r.t. the time required for the residual computation. This effect is clearly shown in Table 4.3, where we report the percentage of time spent in the application of the preconditioner when compared with the overall time of CG, in the case of the revolved ring domain. Interestingly, this percentage is almost constant w.r.t. h up to the finest discretization level, corresponding to about two million degrees-of-freedom.
For conforming multi-patch parametrization, we can easily combine the approaches discussed above with an overlapping Schwarz preconditioner. For details, see [96]. Extension of this approach to nonconforming discretizations would require the use of nonconforming DD preconditioners (e.g., [81]) instead of an overlapping Schwarz preconditioner.
4.6.4 Matrix-Free Computationally-Efficient k-Refinement
The techniques of Sects. 4.6.2 and 4.6.3 are still not enough to achieve the full potential of the k-method and motivate the k-refinement from the point of view of computational efficiency. Matrix operations are too slow and the matrix storage itself poses restrictions to degree elevation. Therefore in [97] the idea of forming and storing the needed matrices is abandoned and, still relying on weighted quadrature, a matrix-free approach is developed. In such a case, the system matrix is available only as a function that computes matrix-vector products. This is exactly what is needed by an iterative solver. Matrix-free approaches have been use in high-order methods based on a tensor construction like spectral elements (see [121]) and have been recently extended to hp-finite elements [2, 80]. They are commonly used in non-linear solvers, parallel implementations, typically for application that are computationally demanding, for example in computational-fluid-dynamics [74, 92].
The cost to initialize the matrix-free approach is only O(N) FLOPs, while the computation of matrix-vector products costs only O(Np) FLOPs. Moreover, the memory required by this approach is just O(N), i.e., it is proportional to the number of degrees of freedom. On the other hand, in 3D the memory required to store the matrix would be O(Np 3), and the cost to compute standard matrix-vector products would be O(Np 3) FLOPs. It is important to remark that, while in some cases the reduction in storage is the major motivation of the matrix-free approach, in this case framework both FLOPs and memory savings are fundamental in order to make the use of the high-degree k-method possible and advantageous. We emphasize that other matrix-free approaches which rely on more standard quadrature rules (e.g. Gaussian quadrature) require O(Np 4) FLOPs to compute matrix-vector products.
The innovative implementation described below is, in the case of the k-method (the isogeometric method based on splines or NURBS, etc., with maximum regularity), orders of magnitude faster than the standard implementation inherited by finite elements. The speedup on a mesh of 2563 elements is 13 times for degree p = 1, 44 times for degree p = 2, while higher degrees can not be handled in the standard framework. Indeed, in the standard implementation, higher degrees are beyond the memory constraints of nowadays workstations, while they are easily allowed in the new framework. This has the upshot: it gives, for the first time, clear evidence of the superiority of the high-degree k-method with respect to low-degree isogeometric discretizations in terms of computational efficiency.
This approach has been also studied, implemented and tested in an innovative environment and hardware for dataflow computing, in the thesis [122].
For brevity we only present here the weighted quadrature matrix-free algorithm for the mass matrix multiplication. Let \(\widetilde {\mathbb {M}}\) be the approximation of \(\mathbb {M}\) obtained with weighted quadrature, as described in Sect. 4.6.2. We use however indices instead of multi-indices, for the sake of simplicity. We want to compute the vector \(\widetilde {\mathbb {M}} v\), where \(v \in \mathbb {R}^N\) is a given vector.
For i = 1, …, N, we observe that
where we have used the definition of \(\widetilde {m}_{ij}\) from (4.133). If we define \( v_h= \sum _{j = 1}^N v_j \widehat {B}_j\), we have then the obvious relation
Above, we see that weighted-quadrature is well suited for a direct calculation of the i-th entry of \(\widetilde {\mathbb {M}} v\): this is just equivalent to approximating the integral of the function c v h using the i-th quadrature rule.
Then \(\widetilde {\mathbb {M}} v\) can be computed with the following steps:
-
1.
Compute \(\widetilde {v} \in \mathbb {R}^{N_{\mathsf {QP}} }\), with \(\widetilde {v}_{q} := v_h({\mathbf {x}}_{q})\), q = 1, …, N QP.
-
2.
Compute \(\widetilde {\widetilde {v}} \in \mathbb {R}^{N_{\mathsf {QP}} }\), with \( \widetilde {\widetilde {v}}_{q} := c({\mathbf {x}}_{q}) \cdot v_h({\mathbf {x}}_{q})\), q = 1, …, N QP.
-
3.
Compute \(\left (\widetilde {\mathbb {M}} v\right )_i = \sum _{q=1}^{N_{\mathsf {QP}} } w_{i,q} \, \widetilde {\widetilde {v}}_{q} \), i = 1, …, N.
This algorithm, and in particular steps 1 and 3, can be performed efficiently by exploiting the tensor structure of the basis functions and of the weights. In order to make this fact apparent, we now derive a matrix expression for the above algorithm. Consider the matrix of B-spline values \(\mathscr {B} \in \mathbb {R}^{N_{\mathsf {QP}} \times N}\), with \(\mathscr {B}_{q j} := \widehat {B}_{j}({\mathbf {x}}_{q})\), q = 1, …, N QP, j = 1, …, N, which can be written as
where
We also consider the matrix of weights \(\mathscr {W} \in \mathbb {R}^{N \times N_{\mathsf {QP}} }\), with \(\mathscr {W}_{iq} := w_{i,q}\), i = 1, …, N, q = 1, …, N QP. Thanks to the tensor structure of the weights, it holds
where
Finally we introduce the diagonal matrix of coefficient values
Then for every i, j = 1, …, N we infer that
Thus it holds
The factorization above of \(\widetilde {\mathbb {M}}\) justifies Algorithm 4, which computes efficiently the matrix-vector product.
Algorithm 4: Matrix-free product (mass)

We now analyze Algorithm 4 in terms of memory usage and of computational cost, where we distinguish between setup cost and application cost. The initialization of Algorithm 4 requires the computation and storage of the coefficient values c(x q), q = 1, …, N QP, and of the (sparse) matrices \( \mathrm {W} _l \in \mathbb {R}^{n\times n_q}\) and \(\mathrm {B}_l \in \mathbb {R}^{n_q\times n}\), for l = 1, …, d. The latter part, which involves only the computation and storage of univariate function values and weights, has negligible requirements both in terms of memory and arithmetic operations. The computational cost of the evaluation of the coefficients c(x q) is problem dependent. For example, when \(c\left (\boldsymbol {\xi }\right ) = \mbox{det}\left (J_{{FR}}(\boldsymbol {\xi })\right )\) and FR is a spline/NURBS parametrization of degree lower than the one of the isogeometric space, as it happens in the numerical benchmarks of the isogeometric k-method, one can assume this cost is O(N) FLOPs, i.e., independent of p. In general, the storage of such coefficients clearly requires N QP ≈ 2d N = O(N) memory.Footnote 3 We emphasize that this memory requirement is completely independent of p; this is a great improvement if we consider that storing the whole mass matrix would require roughly (2p + 1)d N = O(Np d) memory. As for the application cost, Step 2 only requires N FLOPs. Using the properties of Kronecker product and the fact that \(\mbox{nnz}\left (\mathrm {B}^{(l)}\right ) \approx 2pn\), l = 1, …, d, we find that the number of FLOPs required by Step 1 is
Approximately the same number of operations is required for Step 3. Hence we conclude that the total application cost of Algorithm is O(Np) FLOPs. This should be compared with the O(Np d) cost of the standard matrix-vector product.
Similar conclusions hold for the stiffness matrix, though it requires a different treatment of the different derivatives, in the spirit of the weighted quadrature.
Now we report some numerical tests of this approach, from [97], considering a Poisson problem on a mesh of 2563 elements, on a thick quarter of annulus as in Fig. 4.30 (left). For the sake of simplicity, a uniform mesh is considered but all the algorithms do not take any advantage of it and work on non-uniform meshes.
The problem solution is an oscillating manufactured solution, namely
In the tests we see that the k-refinement, whose use has always been discouraged by its prohibitive computational cost, becomes very appealing in the present setting.
For different values of h and p we report the total computation time (setup and solution of the system) and the error \(\left \|\mathrm {u} - \widetilde {\mathrm {u}}_h \right \|{ }_{H^1}\), where \(\widetilde {\mathrm {u}}_h \in V_h\) is the function associated with the approximate solution of the linear system (using BiCGStab and the preconditioner of Sect. 4.6.3). Results are shown in Table 4.4 and in Fig. 4.31.
Representation in the time-error plane of the results shown in Table 4.4
There is a minimal mesh resolution which is required to allow k-refinement convergence. This depends on the solution, which is in the example (4.150) a simple oscillating function with wavelength 1∕5 on a domain with diameter 3. Indeed, there is no approximation (i.e., the relative approximating error remains close to 1) for meshes of 163 elements or coarser, for any p. Convergence begin at a resolution of 323 elements.
The computation time of the proposed matrix-free method grows almost linearly with respect to \(N = \left ( \frac {1}{h} \right )^{3}\) (note that the growth is slower between the two coarser discretization level, where apparently we are still in the pre-asymptotic regime). Time dependence on p is also very mild: the computation time for p = 8 is 1∕3 the one for p = 2, keeping the same mesh resolution. The time growth with respect to N and p is due not only to the increased cost for system setup, matrix-vector product and application of the preconditioner, but also to the increased number of iterations. In turn, the number of iterations grows not because of a worsening of the preconditioner’s quality (according to the results in [96, 117]) but because of a smaller discretization error, which corresponds to a more stringent stopping criterion.
The higher the degree, the higher the computational efficiency of the k-method. This is clearly seen in Fig. 4.31 where the red dots (associated to p = 8, the highest degree in our experiments), are at the bottom of the error vs. computation time plot.
The k-refinement is superior to low-degree h-refinement given a target accuracy: for example, for a relative accuracy of order 10−3, we can select degree p = 8 on a mesh of 323 elements or p = 2 on a mesh of 2563 elements: the former approximation is obtained in 2.7 s while the latter takes about 690 s on our workstation, with speedup factor higher than 250.
4.7 Application Examples
In this section we present some numerical benchmarks of model problems. The first example, from [15], is the one of linear elasticity. The second one, from [57], is a fluid benchmark and utilizes the divergence-free isogeometric vector fields defined in Sect. 4.3.2.
4.7.1 Linear Elasticity
We start by considering the classical elliptic linear elastic problem. First we introduce some notation. The body occupies a two-dimensional domain \(\varOmega \subset {{\mathbb {R}}}^2\). We assume that the boundary ∂Ω is decomposed into a Dirichlet part Γ D and a Neumann part Γ N. Moreover, let \(\mathbf {f} : \varOmega \rightarrow {\mathbb {R}}^d\) be the given body force and \(\mathbf {g} : \varOmega : \varGamma _N \rightarrow {\mathbb {R}}^d\) the given traction on Γ N.
Then, the mixed boundary-value problem reads

where u is the body displacement and ε(u) its symmetric gradient, n is the unit outward normal at each point of the boundary and the fourth-order tensor \({\mathbb C}\) satisfies
for all second-order tensors w, where tr represents the trace operator and μ > 0, 0 ≤ ν < 1∕2 are, respectively, the shear modulus and Poisson’s ratio. The stress, σ, is given by Hooke’s law, \(\boldsymbol {\sigma } = {\mathbb C} {\boldsymbol {\varepsilon }}.\)
Assuming for simplicity a regular loading f ∈ [L 2(Ω)]2 and g ∈ [L 2(Γ N)]2, we introduce also
where ( , )Ω, \((\:, \:)_{\varGamma _N}\) indicate, as usual, the L 2 scalar products on Ω and Γ N, respectively. The variational form of problem (4.151) then reads: find \(\mathbf {u} \in [H_{\varGamma _D}^1(\varOmega )]^d\) such that
To solve (4.151), we introduce an isogeometric vector space V h as defined in Sect. 4.3.1 and look for the Galerkin isogeometric approximation u h ∈ V h such that
where
This is an elliptic problem, then a Galerkin method returns the best approximation in the energy norm. The order of convergence of the numerical error u −u h follows from the approximation properties of isogeometric spaces, see Sect. 4.4.
We will see this for the model of an infinite plate with a hole, modeled by a finite quarter plate. The exact solution [64, pp. 120–123], evaluated at the boundary of the finite quarter plate, is applied as a Neumann boundary condition. The setup is illustrated in Fig. 4.32. T x is the magnitude of the applied stress at infinity, R is the radius of the traction-free hole, L is the length of the finite quarter plate, E is Young’s modulus, and ν is Poisson’s ratio. The rational quadratic basis is the minimum order capable of exactly representing a circle.
The first six meshes used in the analysis are shown in Fig. 4.33. The cubic and quartic NURBS are obtained by order elevation of the quadratic NURBS on the coarsest mesh (for details of the geometry and mesh construction, see [70]). Continuity of the basis is C p−1 everywhere, except along the line which joins the center of the circular edge with the upper left-hand corner of the domain. There it is C 1 as is dictated by the coarsest mesh employing rational quadratic parametrization. In this example, the geometry parametrization is singular at the upper left-hand corner of the domain. Convergence results in the L 2-norm of stresses (which is equivalent to the H 1-seminorm of the displacements) are shown in Fig. 4.34. As can be seen, the L 2-convergence rates of stress for quadratic, cubic, and quartic NURBS are 2, 3, and 4, respectively, hence optimal in all cases, consistent with the approximation estimates described in Sect. 4.4.
4.7.2 Steady Navier-Stokes Problem
We consider now the steady Navier-Stokes Problem. The fluid occupies the domain \(\varOmega \subset {{\mathbb {R}}}^3\). We assume that the boundary ∂Ω = Γ D for simplicity and take \(\mathbf {f} : \varOmega \rightarrow {\mathbb {R}}^3\) as the external driving force. Then, the problem reads

where u is the fluid velocity, p is the pressure, ν is the kinematic viscosity and ε(u) is the symmetric gradient operator.
The variational form of (4.157) reads as follows: find \(\mathbf {u} \in [H_0^1(\varOmega )]^d\) and \( p \in L_0^2(\varOmega )\) such that
where \( L_0^2(\varOmega )\) is the subspace of L 2(Ω) functions having zero average on Ω. At the discrete level, we are going to adopt a divergence-free \((X^2_h,X^3_h)\) isogeometric discretization for the velocity-pressure pair, as defined in Sect. 4.3.2. In this case, only the Dirichlet boundary condition on the normal velocity component (i.e., no-penetration condition) can be imposed strongly (see [38]) while the other boundary conditions, including the Dirichlet boundary condition on the tangential velocity component, have to be imposed weakly, for example by Nitsche’s method, as studied in [57]. For that, we introduce the space \(\boldsymbol {H}_{\mathbf {n}}^1(\varOmega ) = \{{\mathbf {w}} \in [H^1(\varOmega )]^d \text{ such that } {\mathbf {w}} \cdot \mathbf {n} = 0 \text{ on } \partial \varOmega \}\), and the discrete variational formulation is: find \({\mathbf {u}}_h \in X^2_h \cap \boldsymbol {H}_{\mathbf {n}}^1(\varOmega ) \) and \( p_h \in X^3_h \cap L_0^2(\varOmega )\) such that
where F ⊂ ∂Ω denote the faces (in three dimensions) of the Bézier elements that are on the boundary of Ω and C pen > 0 is a suitable penalty constant.
We consider a simple configuration (see [57, Section 8.2]), with Ω = [0, 1]3 and select in (4.32) the polynomial degrees p 1 = p 2 = p 3 = 2 and p 1 = p 2 = p 3 = 3. Selecting knots with single multiplicity, the former choice \(X^2_h\) is formed by linear-quadratic splines and \(X^3_h\) is formed by trilinear splines, which is the minimum degree required to have \(X^2_h \in [H^1(\varOmega )]^d\). The right-hand side is set up in order to give the exact solution:
Streamlines associated with the exact solution are plotted in Fig. 4.35. The convergence rates are shown in Figs. 4.36 and 4.37 for Reynolds number Re = 1. Optimal convergence is obtained for both velocity and pressure. We remark that the discrete velocity is point-wise divergence-free, because of (4.38).
Vortex manufactured solution: Flow velocity streamlines colored by velocity magnitude (from [57])
Navier-Stokes: error measured in the H 1-norm of velocity vs. mesh-size h. The optimal convergence rates in red (from [57])
Navier-Stokes: error measured in the L 2-norm of pressure vs. mesh-size h. Optimal convergence rates in red (from [57])
Notes
- 1.
IGA of Cahn-Hilliard 4th-order model of phase separation is studied in [62, 63]; Kirchhoff-Love 4th-order model of plates and shells in [21, 26, 78, 79]; IGA of crack propagation is studied in [126], with 4th- and 6th-order gradient-enhanced theories of damage [127]; 4th-order phase-field fracture models are considered in [30] and [29], where higher-order convergence rates to sharp-interface limit solutions are numerically demonstrated.
- 2.
- 3.
It is possible to further reduce the memory requirements at the cost of increasing the number of computations. Indeed, note that it is not necessary to store the whole \(\mathscr {D} \), \( {\widetilde {v}} \) and \(\widetilde {\widetilde {v}} \) since w in Algorithm 4 can be computed component by component with on-the-fly calculation of the portion of \(\mathscr {D} \), \( {\widetilde {v}} \) and \(\widetilde {\widetilde {v}} \) that is needed).
References
C. Adam, T.J.R. Hughes, S. Bouabdallah, M. Zarroug, H. Maitournam, Selective and reduced numerical integrations for NURBS-based isogeometric analysis. Comput. Methods Appl. Mech. Eng. 284, 732–761 (2015)
M. Ainsworth, O. Davydov, L.L. Schumaker, Bernstein-Bézier finite elements on tetrahedral-hexahedral-pyramidal partitions. Comput. Methods Appl. Mech. Eng. 304, 140–170 (2016)
P. Antolin, A. Buffa, F. Calabrò, M. Martinelli, G. Sangalli, Efficient matrix computation for tensor-product isogeometric analysis: the use of sum factorization. Comput. Methods Appl. Mech. Eng. 285, 817–828 (2015)
D.N. Arnold, R.S. Falk, R. Winther, Finite element exterior calculus, homological techniques, and applications. Acta Numer. 15, 1–155 (2006)
D.N. Arnold, R.S. Falk, R. Winther, Finite element exterior calculus: from Hodge theory to numerical stability. Bull. Am. Math. Soc. 47, 281–354 (2010)
F. Auricchio, L. Beirão da Veiga, A. Buffa, C. Lovadina, A. Reali, G. Sangalli, A fully “locking-free” isogeometric approach for plane linear elasticity problems: a stream function formulation. Comput. Methods Appl. Mech. Eng. 197, 160–172 (2007)
F. Auricchio, L. Beirão da Veiga, T.J.R. Hughes, A. Reali, G. Sangalli, Isogeometric collocation methods. Math. Models Methods Appl. Sci. 20, 2075–2107 (2010)
F. Auricchio, L. Beirão da Veiga, T.J.R. Hughes, A. Reali, G. Sangalli, Isogeometric collocation for elastostatics and explicit dynamics. Comput. Methods Appl. Mech. Eng. 249–252, 2–14 (2012)
F. Auricchio, F. Calabrò, T.J.R. Hughes, A. Reali, G. Sangalli, A simple algorithm for obtaining nearly optimal quadrature rules for NURBS-based isogeometric analysis. Comput. Methods Appl. Mech. Eng. 249, 15–27 (2012)
I. Babuska, W. Gui, The h, p and h-p versions of the finite element method in 1 dimension. Part II. The error analysis of the h and h-p versions. Numer. Math. 49, 613–658 (1986)
R.H. Bartels, G.W. Stewart, Solution of the matrix equation AX + XB = C. Commun. ACM 15, 820–826 (1972)
A. Bartezzaghi, L. Dedè, A. Quarteroni, Isogeometric analysis of high order partial differential equations on surfaces. Comput. Methods Appl. Mech. Eng. 295, 446–469 (2015)
M. Bartoň, V.M. Calo, Gaussian quadrature for splines via homotopy continuation: rules for C 2 cubic splines. J. Comput. Appl. Math. 296, 709–723 (2016)
M. Bartoň, V.M. Calo, Optimal quadrature rules for odd-degree spline spaces and their application to tensor-product-based isogeometric analysis. Comput. Methods Appl. Mech. Eng. 305, 217–240 (2016)
Y. Bazilevs, L. Beirão da Veiga, J.A. Cottrell, T.J.R. Hughes, G. Sangalli, Isogeometric analysis: approximation, stability and error estimates for h-refined meshes. Math. Models Methods Appl. Sci. 16, 1031–1090 (2006)
Y. Bazilevs, V. Calo, J.A. Cottrell, J.A. Evans, T.J.R. Hughes, S. Lipton, M.A. Scott, T.W. Sederberg, Isogeometric analysis using T-splines. Comput. Methods Appl. Mech. Eng. 199, 229–263 (2010)
Y. Bazilevs, M.C. Hsu, M.A. Scott, Isogeometric fluid–structure interaction analysis with emphasis on non-matching discretizations, and with application to wind turbines. Comput. Methods Appl. Mech. Eng. 249, 28–41 (2012)
E. Beeker, Smoothing of shapes designed with free-form surfaces. Comput. Aided Des. 18, 224–232 (1986)
L. Beirão da Veiga, A. Buffa, J. Rivas, G. Sangalli, Some estimates for h-p-k-refinement in isogeometric analysis. Numer. Math. 118, 271–305 (2011)
L. Beirão da Veiga, A. Buffa, D. Cho, G. Sangalli, Analysis-suitable t-splines are dual-compatible. Comput. Methods Appl. Mech. Eng. 249–252, 42–51 (2012)
L. Beirão da Veiga, A. Buffa, C. Lovadina, M. Martinelli, G. Sangalli, An isogeometric method for the Reissner-Mindlin plate bending problem. Comput. Methods Appl. Mech. Eng. 209–212, 45–53 (2012)
L. Beirão da Veiga, D. Cho, G. Sangalli, Anisotropic NURBS approximation in isogeometric analysis. Comput. Methods Appl. Mech. Eng. 209–212, 1–11 (2012)
L. Beirão da Veiga, A. Buffa, G. Sangalli, R. Vázquez, Analysis-suitable T-splines of arbitrary degree: definition, linear independence and approximation properties. Math. Models Methods Appl. Sci. 23, 1979–2003 (2013)
L. Beirão da Veiga, D. Cho, L.F. Pavarino, S. Scacchi, BDDC preconditioners for isogeometric analysis. Math. Models Methods Appl. Sci. 23, 1099–1142 (2013)
L. Beirão da Veiga, A. Buffa, G. Sangalli, R. Vázquez, Mathematical analysis of variational isogeometric methods. Acta Numer. 23, 157–287 (2014)
Benson, D.J., Y. Bazilevs, M.C. Hsu, T.J.R. Hughes, A large deformation, rotation-free, isogeometric shell. Comput. Methods Appl. Mech. Eng. 200, 1367–1378 (2011)
M. Bercovier, T. Matskewich, Smooth Bezier surfaces over arbitrary quadrilateral meshes (2014, preprint). arXiv:1412.1125
M. Bercovier, I. Soloveichik, Overlapping non matching meshes domain decomposition method in isogeometric analysis (2015, preprint). arXiv:1502.03756
M.J. Borden, C.V. Verhoosel, M.A. Scott, T.J.R. Hughes, C.M. Landis, A phase-field description of dynamic brittle fracture. Comput. Methods Appl. Mech. Eng. 217–220, 77–95 (2012)
M.J. Borden, T.J.R. Hughes, C.M. Landis, C.V. Verhoosel, A higher-order phase-field model for brittle fracture: formulation and analysis within the isogeometric analysis framework. Comput. Methods Appl. Mech. Eng. 273, 100–118 (2014)
J. Bremer, Z. Gimbutas, V. Rokhlin, A nonlinear optimization procedure for generalized Gaussian quadratures. SIAM J. Sci. Comput. 32, 1761–1788 (2010)
A. Bressan, Isogeometric regular discretization for the Stokes problem. IMA J. Numer. Anal. 31, 1334–1356 (2011)
A. Bressan, G. Sangalli, Isogeometric discretizations of the Stokes problem: stability analysis by the macroelement technique. IMA J. Numer. Anal. 33, 629–651 (2013)
E. Brivadis, A. Buffa, B. Wohlmuth, L. Wunderlich, Isogeometric mortar methods. Comput. Methods Appl. Mech. Eng. 284, 292–319 (2015)
F. Buchegger, B. Jüttler, A. Mantzaflaris, Adaptively refined multi-patch B-splines with enhanced smoothness. Appl. Math. Comput. 272, 159–172 (2016)
A. Buffa, C. Giannelli, Adaptive isogeometric methods with hierarchical splines: optimality and convergence rates. Math. Models Methods Appl. Sci. 27, 2781 (2017)
A. Buffa, C. de Falco, G. Sangalli, Isogeometric analysis: stable elements for the 2D Stokes equation. Int. J. Numer. Methods Fluids 65, 1407–1422 (2011)
A. Buffa, J. Rivas, G. Sangalli, R. Vázquez, Isogeometric discrete differential forms in three dimensions. SIAM J. Numer. Anal. 49, 818–844 (2011)
A. Buffa, H. Harbrecht, A. Kunoth, G. Sangalli, BPX-preconditioning for isogeometric analysis. Comput. Methods Appl. Mech. Eng. 265, 63–70 (2013)
A. Buffa, G. Sangalli, C. Schwab, Exponential convergence of the hp version of isogeometric analysis in 1D, in Spectral and High Order Methods for Partial Differential Equations–ICOSAHOM 2012, ed. by M. Azaiez, H. El Fekih, J.S. Hesthaven. Lecture Notes in Computational Science and Engineering, vol. 95 (Springer, Berlin, 2014), pp. 191–203
F. Calabrò, C. Manni, F. Pitolli, Computation of quadrature rules for integration with respect to refinable functions on assigned nodes. Appl. Numer. Math. 90, 168–189 (2015)
F. Calabrò, G. Sangalli, M. Tani, Fast formation of isogeometric Galerkin matrices by weighted quadrature. Comput. Methods Appl. Mech. Eng. 316, 606–622 (2017)
F. Cirak, M.J. Scott, E.K. Antonsson, M. Ortiz, P. Schröder, Integrated modeling, finite-element analysis, and engineering design for thin-shell structures using subdivision. Comput. Aided Des. 34, 137–148 (2002)
E. Cohen, R. Riesenfeld, G. Elber, Geometric Modeling with Splines: An Introduction, vol. 1 (AK Peters, Wellesley, 2001)
E. Cohen, T. Martin, R.M. Kirby, T. Lyche, R.F. Riesenfeld, Analysis-aware modeling: understanding quality considerations in modeling for isogeometric analysis. Comput. Methods Appl. Mech. Eng. 199, 334–356 (2010)
N. Collier, D. Pardo, L. Dalcin, M. Paszynski, V.M. Calo, The cost of continuity: a study of the performance of isogeometric finite elements using direct solvers. Comput. Methods Appl. Mech. Eng. 213, 353–361 (2012)
N. Collier, L. Dalcin, D. Pardo, V.M. Calo, The cost of continuity: performance of iterative solvers on isogeometric finite elements. SIAM J. Sci. Comput. 35, A767–A784 (2013)
A. Collin, G. Sangalli, T. Takacs, Analysis-suitable G 1 multi-patch parametrizations for C 1 isogeometric spaces. Comput. Aided Geom. Des. 47, 93–113 (2016)
J.A. Cottrell, A. Reali, Y. Bazilevs, T.J.R. Hughes, Isogeometric analysis of structural vibrations. Comput. Methods Appl. Mech. Eng. 195, 5257–5296 (2006)
J.A. Cottrell, T.J.R. Hughes, Y. Bazilevs, Isogeometric Analysis: Toward Integration of CAD and FEA (Wiley, Hoboken, 2009)
C. de Boor, A Practical Guide to Splines, revised edn. (Springer, New York, 2001)
R. Dimitri, L. De Lorenzis, M. Scott, P. Wriggers, R. Taylor, G. Zavarise, Isogeometric large deformation frictionless contact using T-splines. Comput. Methods Appl. Mech. Eng. 269, 394–414 (2014)
T. Dokken, T. Lyche, K.F. Pettersen, Polynomial splines over locally refined box-partitions. Comput. Aided Geom. Des. 30, 331–356 (2013)
M. Donatelli, C. Garoni, C. Manni, S. Serra-Capizzano, H. Speleers, Robust and optimal multi-iterative techniques for IgA Galerkin linear systems. Comput. Methods Appl. Mech. Eng. 284, 230–264 (2015)
M. Dörfel, B. Jüttler, B. Simeon, Adaptive isogeometric analysis by local h-refinement with T-splines. Comput. Methods Appl. Mech. Eng. 199, 264–275 (2010)
J.A. Evans, T.J.R. Hughes, Isogeometric divergence-conforming B-splines for the Darcy-Stokes-Brinkman equations. Math. Models Methods Appl. Sci. 23, 671–741 (2013)
J.A. Evans, T.J.R. Hughes, Isogeometric divergence-conforming B-splines for the Steady Navier-Stokes Equations. Math. Models Methods Appl. Sci. 23, 1421–1478 (2013)
J.A. Evans, T.J.R. Hughes, Isogeometric divergence-conforming B-splines for the unsteady Navier-Stokes equations. J. Comput. Phys. 241, 141–167 (2013)
J.A. Evans, Y. Bazilevs, I. Babuška, T.J.R. Hughes, n-widths, sup-infs, and optimality ratios for the k-version of the isogeometic finite element method. Comput. Methods Appl. Mech. Eng. 198, 1726–1741 (2009)
K.P.S. Gahalaut, J.K. Kraus, S.K. Tomar, Multigrid methods for isogeometric discretization. Comput. Methods Appl. Mech. Eng. 253, 413–425 (2013)
L. Gao, Kronecker products on preconditioning, Ph.D. thesis, King Abdullah University of Science and Technology, 2013
H. Gómez, V. Calo, Y. Bazilevs, T.J.R. Hughes, Isogeometric analysis of the Cahn–Hilliard phase-field model. Comput. Methods Appl. Mech. Eng. 197, 4333–4352 (2008)
H. Gómez, T.J.R. Hughes, X. Nogueira, V.M. Calo, Isogeometric analysis of the isothermal Navier-Stokes-Korteweg equations. Comput. Methods Appl. Mech. Eng. 199, 1828–1840 (2010)
P.L. Gould, Introduction to Linear Elasticity (Springer, Berlin, 1994)
M. Hillman, J. Chen, Y. Bazilevs, Variationally consistent domain integration for isogeometric analysis. Comput. Methods Appl. Mech. Eng. 284, 521–540 (2015)
R. Hiptmair, Finite elements in computational electromagnetism. Acta Numer. 11, 237–339 (2002)
C. Hofreither, S. Takacs, W. Zulehner, A robust multigrid method for isogeometric analysis using boundary correction. Tech. Rep., NFN (2015)
S. Hosseini, J.J. Remmers, C.V. Verhoosel, R. Borst, An isogeometric solid-like shell element for nonlinear analysis. Int. J. Numer. Methods Eng. 95, 238–256 (2013)
T.J.R. Hughes, G. Sangalli, Mathematics of isogeometric analysis: a conspectus, in Encyclopedia of Computational Mechanics ed. by S. Erwin, R. de Borst, T.J.R. Hughes, 2nd edn. (Wiley, Hoboken, 2017)
T.J.R. Hughes, J.A. Cottrell, Y. Bazilevs, Isogeometric analysis: CAD, finite elements, NURBS, exact geometry and mesh refinement. Comput. Methods Appl. Mech. Eng. 194, 4135–4195 (2005)
T.J.R. Hughes, A. Reali, G. Sangalli, Duality and unified analysis of discrete approximations in structural dynamics and wave propagation: comparison of p-method finite elements with k-method NURBS. Comput. Methods Appl. Mech. Eng. 197, 4104–4124 (2008)
T.J.R. Hughes, A. Reali, G. Sangalli, Efficient quadrature for NURBS-based isogeometric analysis. Comput. Methods Appl. Mech. Eng. 199, 301–313 (2010)
T.J.R. Hughes, J.A. Evans, A. Reali, Finite element and NURBS approximations of eigenvalue, boundary-value, and initial-value problems. Comput. Methods Appl. Mech. Eng. 272, 290–320 (2014)
Z. Johan, T.J.R. Hughes, A globally convergent matrix-free algorithm for implicit time-marching schemes arising in finite element analysis in fluids. Comput. Methods Appl. Mech. Eng. 87, 281–304 (1991)
K.A. Johannessen, Optimal quadrature for univariate and tensor product splines. Comput. Methods Appl. Mech. Eng. 316, 84–99 (2017)
B. Jüttler, A. Mantzaflaris, R. Perl, M. Rumpf, On isogeometric subdivision methods for PDEs on surfaces. Technical Report (2015). arXiV:1503.03730
M. Kapl, V. Vitrih, B. Jüttler, K. Birner, Isogeometric analysis with geometrically continuous functions on two-patch geometries. Comput. Math. Appl. 70, 1518–1538 (2015)
J. Kiendl, K.U. Bletzinger, J. Linhard, R. Wuchner, Isogeometric shell analysis with Kirchhoff–Love elements. Comput. Methods Appl. Mech. Eng. 198, 3902–3914 (2009)
J. Kiendl, Y. Bazilevs, M.C. Hsu, R. Wüchner, K.U. Bletzinger, The bending strip method for isogeometric analysis of Kirchhoff–Love shell structures comprised of multiple patches. Comput. Methods Appl. Mech. Eng. 199, 2403–2416 (2010)
R.C. Kirby, Fast simplicial finite element algorithms using Bernstein polynomials. Numer. Math. 117, 631–652 (2011)
S.K. Kleiss, C. Pechstein, B. Jüttler, S. Tomar, IETI–isogeometric tearing and interconnecting. Comput. Methods Appl. Mech. Eng. 247–248, 201–215 (2012)
D. Liu, J. Hoschek, GC1 continuity conditions between adjacent rectangular and triangular Bézier surface patches. Comput. Aided Des. 21, 194–200 (1989)
R.E. Lynch, J.R. Rice, D.H. Thomas, Direct solution of partial difference equations by tensor product methods. Numer. Math. 6, 185–199 (1964)
A. Mantzaflaris, B. Jüttler, B. Khoromskij, U. Langer, Matrix generation in isogeometric analysis by low rank tensor approximation, in Curves and Surfaces: 8th International Conference, Paris, 2014
B. Marussig, T.J.R. Hughes, A review of trimming in isogeometric analysis: challenges, data exchange and simulation aspects. Arch. Comput. Methods Eng. 24, 1–69 (2017)
P. Monk, Finite Element Methods for Maxwell’s Equations (Oxford University Press, Oxford, 2003)
B. Mourrain, R. Vidunas, N. Villamizar, Dimension and bases for geometrically continuous splines on surfaces of arbitrary topology. Comput. Aided Geom. Des. 45, 108–133 (2016)
T. Nguyen, J. Peters, Refinable C 1 spline elements for irregular quad layout. Comput. Aided Geom. Des. 43, 123–130 (2016)
T. Nguyen, K. Karčiauskas, J. Peters, A comparative study of several classical, discrete differential and isogeometric methods for solving Poisson’s equation on the disk. Axioms 3, 280–299 (2014)
J. Peters, Smooth interpolation of a mesh of curves. Constr. Approx. 7, 221–246 (1991)
L. Piegl, W. Tiller, The NURBS Book (Springer, New York, 1997)
P. Rasetarinera, M.Y. Hussaini, An efficient implicit discontinuous spectral Galerkin method. J. Comput. Phys. 172, 718–738 (2001)
D.F. Rogers, An Introduction to NURBS: With Historical Perspective (Morgan Kaufmann, San Francisco, 2001)
T. Rüberg, F. Cirak, Subdivision-stabilised immersed B-spline finite elements for moving boundary flows. Comput. Methods Appl. Mech. Eng. 209–212, 266–283 (2012)
M. Ruess, D. Schillinger, Y. Bazilevs, V. Varduhn, E. Rank, Weakly enforced essential boundary conditions for NURBS-embedded and trimmed NURBS geometries on the basis of the finite cell method. Int. J. Numer. Methods Eng. 95, 811–846 (2013)
G. Sangalli, M. Tani, Isogeometric preconditioners based on fast solvers for the Sylvester equation. SIAM J. Sci. Comput. 38, A3644–A3671 (2016)
G. Sangalli, M. Tani, Matrix-free isogeometric analysis: the computationally efficient k-method (2017). ArXiv e-print 1712.08565
G. Sangalli, T. Takacs, R. Vázquez, Unstructured spline spaces for isogeometric analysis based on spline manifolds. Comput. Aided Geom. Des. 47, 61–82 (2016)
D. Schillinger, L. Dedè, M.A. Scott, J.A. Evans, M.J. Borden, E. Rank, T.R. Hughes, An isogeometric design-through-analysis methodology based on adaptive hierarchical refinement of NURBS, immersed boundary methods, and T-spline CAD surfaces. Comput. Methods Appl. Mech. Eng. 249–252, 116–150 (2012)
D. Schillinger, J.A. Evans, A. Reali, M.A. Scott, T.J.R. Hughes, Isogeometric collocation: cost comparison with Galerkin methods and extension to adaptive hierarchical NURBS discretizations. Comput. Methods Appl. Mech. Eng. 267, 170–232 (2013)
D. Schillinger, S.J. Hossain, T.J.R. Hughes, Reduced Bézier element quadrature rules for quadratic and cubic splines in isogeometric analysis. Comput. Methods Appl. Mech. Eng. 277, 1–45 (2014)
L.L. Schumaker, Spline Functions: Basic Theory, 3rd edn. (Cambridge University Press, Cambridge, 2007)
C. Schwab, p- and hp-Finite Element Methods (The Clarendon Press/Oxford University Press, New York, 1998)
M.A. Scott, X. Li, T.W. Sederberg, T.J.R. Hughes, Local refinement of analysis-suitable T-splines. Comput. Methods Appl. Mech. Eng. 213–216, 206–222 (2012)
M.A. Scott, R.N. Simpson, J.A. Evans, S. Lipton, S.P.A. Bordas, T.J.R. Hughes, T.W. Sederberg, Isogeometric boundary element analysis using unstructured T-splines. Comput. Methods Appl. Mech. Eng. 254, 197–221 (2013)
M.A. Scott, D.C. Thomas, E.J. Evans, Isogeometric spline forests. Comput. Methods Appl. Mech. Eng. 269, 222–264 (2014)
T. Sederberg, J. Zheng, A. Bakenov, A. Nasri, T-splines and T-NURCCSs. ACM Trans. Graph. 22, 477–484 (2003)
T. Sederberg, D. Cardon, G. Finnigan, N. North, J. Zheng, T. Lyche, T-spline simplification and local refinement. ACM Trans. Graph. 23, 276–283 (2004)
T.W. Sederberg, G.T. Finnigan, X. Li, H. Lin, H. Ipson, Watertight trimmed NURBS. ACM Trans. Graph. 27, 79 (2008)
V. Simoncini, Computational methods for linear matrix equations. SIAM Rev. 58(3), 377–441 (2013)
G. Strang, G.J. Fix, An Analysis of the Finite Element Method, vol. 212 (Prentice-Hall, Englewood Cliffs, 1973)
T. Takacs, Construction of smooth isogeometric function spaces on singularly parameterized domains, in Curves and Surfaces (Springer, Berlin, 2014), pp. 433–451
T. Takacs, B. Jüttler, Existence of stiffness matrix integrals for singularly parameterized domains in isogeometric analysis. Comput. Methods Appl. Mech. Eng. 200, 3568–3582 (2011)
T. Takacs, B. Jüttler, H 2 regularity properties of singular parameterizations in isogeometric analysis. Graph. Model. 74, 361–372 (2012)
S. Takacs, T. Takacs, Approximation error estimates and inverse inequalities for B-splines of maximum smoothness. Math. Models Methods Appl. Sci. 26, 1411–1445 (2016)
T. Takacs, B. Jüttler, O. Scherzer, Derivatives of isogeometric functions on n-dimensional rational patches in R d. Comput. Aided Geom. Des. 31, 567–581 (2014)
M. Tani, A preconditioning strategy for linear systems arising from nonsymmetric schemes in isogeometric analysis. Comput. Math. Appl. 74, 1690–1702 (2017)
R.L. Taylor, Isogeometric analysis of nearly incompressible solids. Int. J. Numer. Methods Eng. 87, 273–288 (2011)
D. Toshniwal, H. Speleers, R.R. Hiemstra, T.J.R. Hughes, Multi-degree smooth polar splines: a framework for geometric modeling and isogeometric analysis. Comput. Methods Appl. Mech. Eng. 316, 1005–1061 (2017)
D. Toshniwal, H. Speleers, T.J.R. Hughes, Smooth cubic spline spaces on unstructured quadrilateral meshes with particular emphasis on extraordinary points: geometric design and isogeometric analysis considerations. Comput. Methods Appl. Mech. Eng. 327, 411–458 (2017)
H.M. Tufo, P.F. Fischer, Terascale spectral element algorithms and implementations, in Proceedings of the 1999 ACM/IEEE Conference on Supercomputing (ACM, New York, 1999), p. 68
R. van Nieuwpoort, Solving Poisson’s equation with dataflow computing. Master’s thesis, Delft University of Technology, 2017
T.M. van Opstal, J. Yan, C. Coley, J.A. Evans, T. Kvamsdal, Y. Bazilevs, Isogeometric divergence-conforming variational multiscale formulation of incompressible turbulent flows. Comput. Methods Appl. Mech. Eng. 316, 859–879 (2017)
R. Vázquez, A new design for the implementation of isogeometric analysis in Octave and Matlab: GeoPDEs 3.0. Tech. Rep., IMATI Report Series (2016)
R. Vázquez, A new design for the implementation of isogeometric analysis in Octave and Matlab: GeoPDEs 3.0. Comput. Math. Appl. 72, 523–554 (2016)
C.V. Verhoosel, M.A. Scott, R. De Borst, T.J.R. Hughes, An isogeometric approach to cohesive zone modeling. Int. J. Numer. Methods Eng. 87, 336–360 (2011)
C.V. Verhoosel, M.A. Scott, T.J.R. Hughes, R. de Borst, An isogeometric analysis approach to gradient damage models. Int. J. Numer. Methods Eng. 86, 115–134 (2011)
A.V. Vuong, C. Giannelli, B. Jüttler, B. Simeon, A hierarchical approach to adaptive local refinement in isogeometric analysis. Comput. Methods Appl. Mech. Eng. 200, 3554–3567 (2011)
Acknowledgements
This chapter is a review of the mathematical results available on IGA. The presentation follows in particular [25, 48, 50, 57, 71, 73, 96]. We thank our colleagues and coauthors: Yuri Bazilevs, Lourenco Beirão da Veiga, Annalisa Buffa, Francesco Calabrò, Annabelle Collin, Austin Cottrell, John Evans, Alessandro Reali, Thomas Takacs, and Rafael Vázquez. Thomas J.R. Hughes was partially supported by the Office of Naval Research (Grant Nos. N00014-17-1-2119, N00014-17-1-2039, and N00014-13-1-0500), and by the Army Research Office (Grant No. W911NF-13-1-0220). Giancarlo Sangalli and Mattia Tani were partially supported by the European Research Council (ERC Consolidator Grant n.616563 HIGEOM). This support is gratefully acknowledged.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2018 Springer Nature Switzerland AG
About this chapter
Cite this chapter
Hughes, T.J.R., Sangalli, G., Tani, M. (2018). Isogeometric Analysis: Mathematical and Implementational Aspects, with Applications. In: Lyche, T., Manni, C., Speleers, H. (eds) Splines and PDEs: From Approximation Theory to Numerical Linear Algebra. Lecture Notes in Mathematics(), vol 2219. Springer, Cham. https://doi.org/10.1007/978-3-319-94911-6_4
Download citation
DOI: https://doi.org/10.1007/978-3-319-94911-6_4
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-94910-9
Online ISBN: 978-3-319-94911-6
eBook Packages: Mathematics and StatisticsMathematics and Statistics (R0)