Abstract
These notes are concerned with numerical analysis issues arising in the solution of certain systems involving stationary and instationary linear variational problems. Standard examples are second order elliptic boundary value problems, where particular emphasis is placed on the treatment of essential boundary conditions, and linear parabolic equations. These operator equations serve as a core ingredient for control problems where in addition to the state, the solution of the PDE, a control is to be determined which together with the state minimizes a certain tracking-type objective functional. Having assured that the variational problems are well-posed, we discuss numerical schemes based on B-splines and B-spline-type wavelets as a particular multiresolution discretization methodology. The guiding principle is to devise fast and efficient solution schemes which are optimal in the number of arithmetic unknowns. We discuss optimal conditioning of the system matrices, numerical stability of discrete formulations, and adaptive approximations.
Access provided by CONRICYT-eBooks. Download chapter PDF
Similar content being viewed by others
2.1 Introduction
Multilevel ingredients have for a variety of partial differential equations (PDEs) proved to achieve more efficient solution schemes than methods based on approximating the solution with respect to a fixed fine grid. The latter simple approach leads to the problem to solve a large ill-conditioned system of linear equations. The success of multilevel methods is due to the fact that solutions often exhibit a multiscale behaviour which one naturally wants to exploit. Among the first such schemes were multigrid methods. The basic idea of multigrid schemes is to successively solve smaller versions of the linear system which can be interpreted as discretizations with respect to coarser grids. Here ‘efficiency of the scheme’ means that one can solve the problem with respect to the finest grid with an amount of arithmetic operations which is proportional to the number of unknowns on this finest grid. Multigrid schemes provide an asymptotically optimal preconditioner for the original system on the finest grid. The search for such optimal preconditioners was one of the major topics in the solution of elliptic boundary value problems for many years. Another multiscale preconditioner which has this property is the BPX-preconditioner proposed first in [8]. It was proved to be asymptotically optimal with techniques from Approximation Theory in [27, 61]. In the context of isogeometric analysis, the BPX-preconditioner was further substantially optimized in [10]; this will be detailed in Sect. 2.2.
Wavelets as a particular example of a multiscale basis were constructed with compact support in the 1980s [36]. While mainly used for signal analysis and image compression, they were discovered to also provide optimal preconditioners in the above sense for elliptic boundary value problems [27, 47]. It was soon realized that biorthogonal spline-wavelets are better suited for the numerical solution of elliptic PDEs since they allow to work with piecewise polynomials instead of the only implicitly defined original wavelets [36], in addition to the fact that orthogonality of the Daubechies wavelets with respect to L2 cannot really be exploited for elliptic PDEs. The principal ingredient that allows to prove optimality of the preconditioner are norm equivalences between Sobolev norms and sequence norms of weighted wavelet expansion coefficients. Optimal conditioning of the resulting linear system of equations can be achieved by applying the Fast Wavelet Transform together with a weighting in terms of an appropriate diagonal matrix. The terminology ‘wavelets’ here and in the sequel is to mean that these are classes of multiscale bases with three main properties: (R) Riesz basis property for the underlying function spaces, (L) locality of the basis functions, (CP) cancellation properties, all of which are detailed in Sect. 2.4.1.
After these initial results, research on using wavelets for numerically solving elliptic PDEs has gone into different directions. The original constructions in [18, 36] and many others are based on using the Fourier transform. Thus, these constructions provide bases for function spaces only on all of \(\mathbb {R}\) or \(\mathbb {R}^n\). In order for these tools to be applicable for the solution of PDEs which naturally live on a bounded domain \({\varOmega }\subset \mathbb {R}^n\), there arose the need for having available constructions on bounded intervals without, of course, loosing the above mentioned properties (R), (L) and (CP). The first such systematic construction of biorthogonal spline-wavelets on [0, 1] (and, by tensor products, on [0, 1]n) was provided in [34].
Aside from the investigations to provide appropriate bases, the built-in potential of adaptivity for wavelets has played a prominent role when solving PDEs, on account of the fact that wavelets provide a locally supported Riesz basis for a whole range of function spaces. The key issue is to approximate the solution of the variational problem on an infinite-dimensional function space by the least amount of degrees of freedom up to a certain prescribed accuracy. Many approaches use wavelet coefficients in a heuristic way, i.e., judging approximation quality by the size of the wavelet coefficients together with thresholding. In contrast, convergence of wavelet-based adaptive methods for stationary variational problems was investigated systematically in [19,20,21]. These schemes are particularly designed to provide optimal complexity of the schemes: they provide the solution in a total amount of arithmetic operations which is comparable to the wavelet-best N-term approximation of the solution. This means that, given a prescribed tolerance, to find a sparse representation of the solution by extracting the N largest expansion coefficients of the solution during the solution process.
As soon as one aims at numerically solving a variational problem which can no longer be formulated in terms of a single elliptic operator equation such as a saddle point problem, one is faced with the problem of numerical stability. This means that finite approximations of the continuous well-posed problem may be ill-posed, obstructing its efficient numerical solution. This issue will also be addressed below.
In these notes, I also would like to discuss the potential proposed by wavelet methods for the following classes of problems. First, we will be concerned with second order elliptic PDEs with a particular emphasis placed on treating essential boundary conditions. Another interesting class that will be covered are linear parabolic PDEs which are formulated in full weak space-time from [66]. Then PDE-constrained control problems guided by elliptic boundary value problems are considered, leading to a system of elliptic PDEs. The starting point for designing efficient solution schemes are wavelet representations of continuous well-posed problems in their variational form. Viewing the numerical solution of such a discretized, yet still infinite-dimensional operator equation as an approximation helps to discover multilevel preconditioners for elliptic PDEs which yield uniformly bounded condition numbers. Stability issues like the LBB condition for saddle point problems are also discussed in this context. In addition, the compact support of the wavelets allows for sparse representations of the implicit information contained in systems of PDEs, the adaptive approximation of their solution.
More information and extensive literature on applying wavelets for more general PDEs addressing, among other things, the connection between adaptivity and nonlinear approximation and the evaluation of nonlinearities may be found in [16, 24, 25].
These notes are structured as follows. In Sect. 2.2, we begin with a simple elliptic PDE in variational form in the context of isogeometric analysis. For this problem, we address additive, BPX-type preconditioners and provide the main ingredients for showing optimality of the scheme with respect to the grid spacing. In Sect. 2.3, several well-posed variational problem classes are compiled to which later several aspects of the wavelet methodology are applied. The simplest example is a linear elliptic boundary value problem for which we derive two forms of an operator equation, the simplest one consisting just of one equation for homogeneous boundary conditions and a more complicated one in form of a saddle point problem where nonhomogeneous boundary conditions are treated by means of Lagrange multipliers. In Sect. 2.3.4, we consider a full weak space-time form of a linear parabolic PDE. These three formulations are then employed for the following classes of PDE-constrained control problems. In the distributed control problems in Sect. 2.3.5 the control is exerted through the right hand side of the PDE, while in Dirichlet boundary control problems in Sect. 2.3.6 the Dirichlet boundary condition serves this purpose. The most potential for adaptive methods to be discussed below are control problems constrained by parabolic PDEs as formulated in Sect. 2.3.7.
Section 2.4 is devoted to assembling necessary ingredients and basic properties of wavelets which are required in the sequel. In particular, Sect. 2.4.4 collects the essential construction principles for wavelets on bounded domains which do not rely on Fourier techniques, namely, multiresolution analyses of function spaces and the concept of stable completions. In Sect. 2.5 we formulate the problem classes introduced in Sect. 2.3 in wavelet coordinates and derive in particular for the control problems the resulting systems of linear equations arising from the optimality conditions. Section 2.6 is devoted to the iterative solution of these systems. We investigate fully iterative schemes on uniform grids and show that the resulting systems can be solved in the wavelet framework together with a nested iteration strategy with an amount of arithmetic operations which is proportional to the total number of unknowns on the finest grid. Finally, in Sect. 2.6.2 a wavelet-based adaptive scheme for the distributed control problem constrained by elliptic or parabolic PDEs as in [29, 44] will be derived together with convergence results and complexity estimates, relying on techniques from Nonlinear Approximation Theory.
Throughout these notes we will employ the following notational convention: the relation a ∼ b will always stand for  and
and  where the latter inequality means that b can be bounded by some constant times a uniformly in all parameters on which a and b may depend. Norms and inner products are always indexed by the corresponding function space. Lp(Ω) are for 1 ≤ p ≤∞ the usual Lebesgue spaces on a domain Ω, and \(W^k_p({\varOmega })\subset L_p({\varOmega })\) denote for \(k\in \mathbb {N}\) the Sobolev spaces of functions whose weak derivatives up to order k are bounded in Lp(Ω). For p = 2, we write as usual \(H^k({\varOmega })=W^k_2({\varOmega })\).
where the latter inequality means that b can be bounded by some constant times a uniformly in all parameters on which a and b may depend. Norms and inner products are always indexed by the corresponding function space. Lp(Ω) are for 1 ≤ p ≤∞ the usual Lebesgue spaces on a domain Ω, and \(W^k_p({\varOmega })\subset L_p({\varOmega })\) denote for \(k\in \mathbb {N}\) the Sobolev spaces of functions whose weak derivatives up to order k are bounded in Lp(Ω). For p = 2, we write as usual \(H^k({\varOmega })=W^k_2({\varOmega })\).
2.2 BPX Preconditioning for Isogeometric Analysis
For a start, we consider linear elliptic PDEs in the framework of isogeometric analysis, combining modern techniques from computer aided design with higher order approximations of the solution. In this context, one exploits that the solution exhibits a certain smoothness. We treat the physical domain by means of a regular B-spline mapping from the parametric domain \(\hat {\varOmega } = (0,1)^n\), n ≥ 2, to the physical domain Ω. The numerical solution of the PDE is computed by means of tensor product B-splines mapped onto the physical domain. We will construct additive BPX-type multilevel preconditioners and show that they are asymptotically optimal. This means that the spectral condition number of the resulting preconditioned stiffness matrix is independent of the grid spacing h. Together with a nested iteration scheme, this enables an iterative solution scheme of optimal linear complexity. The theoretical results are substantiated by numerical examples in two and three space dimensions. The results of this section are essentially contained in [10].
We consider linear elliptic partial differential operators of order 2r = 2, 4 on the domain Ω in variational form: for given f ∈ H−r(Ω), find \(u\in H^r_0({\varOmega })\) such that
holds. Here the energy space is \(H^r_0({\varOmega })\), a subset of the Sobolev space Hr(Ω), the space of square integrable functions with square integrable derivatives up to order r, containing homogeneous Dirichlet boundary conditions for r = 1 and homogeneous Dirichlet and Neumann derivatives for r = 2. The bilinear form a(⋅, ⋅) is derived from the linear elliptic PDE operator in a standard fashion, see, e.g., [7]. For example, the Laplacian is represented as a(v, w) =∫Ω∇v ⋅∇w dx. In order for the problem to be well-posed, we require the bilinear form \(a(\cdot ,\cdot ):H^r_0({\varOmega })\times H^r_0({\varOmega })\to \mathbb {R}\) to be symmetric, continuous and coercive on \(H^r_0({\varOmega })\). With 〈⋅, ⋅〉, we denote on the right hand side of (2.1) the dual form between H−r(Ω) and \(H^r_0({\varOmega })\). Our model problem (2.1) covers the second order Laplacian with homogeneous boundary conditions
as well as fourth order problems with corresponding homogeneous Dirichlet boundary conditions,
where ∂Ω denotes the boundary of Ω and n the outward normal derivative at ∂Ω. These PDEs serve as prototypes for more involved PDEs like Maxwell’s equation or PDEs for linear and nonlinear elasticity. The reason we formulate these model problems of order 2r involving the parameter r is that this exhibits more clearly the order of the operator and the scaling in the subsequently used characterization of Sobolev spaces Hr(Ω). Thus, for the remainder of this section, the parameter 2r denoting the order of the PDE operator is fixed.
The assumptions on the bilinear form a(⋅, ⋅) entail that there exist constants 0 < cA ≤ CA < ∞ such that the induced self-adjoint operator 〈Av, w〉 := a(v, w) satisfies the isomorphism relation
If the precise format of the constants in (2.4) does not matter, we abbreviate this relation as  , or shortly as
, or shortly as
Under these conditions, Lax-Milgram’s theorem guarantees that, for any given f ∈ H−r(Ω), the operator equation derived from (2.1)
has a unique solution \(u\in H^r_0({\varOmega })\), see, e.g., [7].
In order to approximate the solution of (2.1) or (2.6), we choose a finite-dimensional subspace of \(H^r_0({\varOmega })\). We will construct these approximation spaces by using tensor products of B-splines as specified next.
2.2.1 B-Spline Discretizations
Our construction of optimal multilevel preconditioners will rely on tensor products so that principally any space dimension \(n\in \mathbb {N}\) is permissible as long as storage permits; the examples cover the cases n = 2, 3. As discretization space, we choose in each spatial direction B-splines of the same degree p on uniform grids and with maximal smoothness. We begin with the univariate case and define B-splines on the interval [0, 1] recursively with respect to their degree p. Given this positive integer p and some \(m\in \mathbb {N}\), we call Ξ := {ξ1, …, ξm+p+1} a p-open knot vector if the knots are chosen such that
i.e., the boundary knots 0 and 1 have multiplicity p + 1 and the interior knots are single. For Ξ, B-spline functions of degree p are defined following the well-known Cox-de Boor recursive formula, see [38]. Starting point are the piecewise constants for p = 0 (or characteristic functions)
with the modification that the last B-spline Nm,0 is defined also for ζ = 1. For p ≥ 1 the B-splines are defined as
with the same modification for Nm,p. Alternatively, one can define the B-splines explicitly by applying divided differences to truncated powers [38]. This gives a set of m B-splines that form a basis for the space of splines, that is, piecewise polynomials of degree p with p − 1 continuous derivatives at the internal knots ξℓ for ℓ = p + 2, …, m. (Of course, one can also define B-splines on a knot sequence with multiple internal knots which entails that the spline space is not of maximal smoothness.) For p = 1, the B-splines are at least C0([0, 1]) which suffices for the discretization of elliptic PDEs of order 2, and for p = 2 they are C1([0, 1]) which suffices for r = 2. By construction, the B-spline Ni,p is supported in the interval [ξi, ξi+p+1].
These definitions are valid for an arbitrary spacing of knots in Ξ (2.7). Recall from standard error estimates in the context of finite elements, see, e.g., [7], that smooth solutions of elliptic PDEs can be approximated best with discretizations on a uniform grid. Therefore, in this section, we assume from now on that the grid is uniform, i.e., ξℓ+1 − ξℓ = h for all ℓ = p + 1, …, m.
For n space dimensions, we employ tensor products of the one-dimensional B-splines. We take in each space dimension a p-open knot vector Ξ and define on the closure of the parametric domain \(\hat {\varOmega } =(0,1)^n\) (which we also denote by \(\hat {\varOmega }\) for simplicity of presentation) the spline space
In the spirit of isogeometric analysis, we suppose that the computational domain Ω can also described in terms of B-splines. We assume that the computational domain Ω is the image of a mapping \(\mathbf {F}: \hat {\varOmega }\to {\varOmega }\) with F := (F1, …, Fn)T where each component Fi of F belongs to \(S_{\bar h}(\hat \varOmega ) \) for some given \(\bar h\). In many applications, the geometry can be described in terms of a very coarse mesh, namely, \(\bar h \gg h\). Moreover, we suppose that F is invertible and satisfies
This assumption on the geometry can be weakened in the sense that the mapping F can be a piecewise C∞ function on the mesh with respect to \(\bar h\), independent of h, or the domain Ω may have a multi-patch representation. This means that one can allow Ω also to be the union of domains Ωk where each one parametrized by a spline mapping of the parametric domain \(\hat {\varOmega }\).
We now define the approximation space for (2.6) as
We will formulate three important properties of this approximation space which will play a crucial role later for the construction of the BPX-type preconditioners. The first one is that we suppose from now on that the B-spline basis is normalized with respect to L2, i.e.,
Then one can derive the following facts [10].
Theorem 1
Let \(\{ B_i\} _{i \in {\mathscr {I}}}\) be the B-spline basis defined in (2.10) and normalized as in (2.13), \(N = \# {\mathscr {I}}\) and \( V_h^r\) as in (2.12). Then we have
-
(S)
Uniform stability with respect to L2(Ω) For any \(\mathbf {c} \in \ell _2({\mathscr {I}})\),
$$\displaystyle \begin{aligned} \left\|\sum_{i=1}^N c_i \, B_i\circ {\mathbf{F}}^{-1}\right\|{}^2_{L_2({\varOmega})} \sim ~ \sum_{i=1}^N |c_i|{}^2 =: \|\mathbf{c} \|{}_{\ell_2}^2, \qquad \mathbf{c}:= (c_i)_{i=1,\ldots,N}; \end{aligned} $$(2.14) -
(J)
Direct or Jackson estimates
 (2.15)
(2.15)where \(|\cdot |{ }_{H^s({\varOmega })}\) denotes the Sobolev seminorm of highest weak derivatives s;
-
(B)
Inverse or Bernstein estimates
 (2.16)
(2.16)
In all these estimates, the constants are independent of h but may depend on F , i.e., Ω, on the polynomial degree p and on the spatial dimension n.
In the next section, we construct BPX-type preconditioners for (2.6) in terms of approximations with (2.12) and show their optimality.
2.2.2 Additive Multilevel Preconditioners
The construction of optimal preconditioners are based on a multiresolution analysis of the underlying energy function space \(H^r_0({\varOmega })\). As before, 2r ∈{2, 4} stands for the order of the PDEs we are solving and is always kept fixed.
We first describe the necessary ingredients within an abstract basis-free framework, see, e.g., [24]. Afterwards, we specify the realization for the parametrized tensor product spaces in (2.12).
Let \({\mathscr {V}}\) be a sequence of strictly nested spaces Vj, starting with some fixed coarsest index j0 > 0, determined by the polynomial degree p which determines the support of the basis functions (which also depends on Ω), and terminating with a highest resolution level J,
The index j denotes the level of resolution defining approximations on a grid with dyadic grid spacing h = 2−j, i.e., we use from now on the notation Vj instead of Vh to indicate different grid spacings. Then, VJ will be the space relative to the finest grid 2−J. We associate with \({\mathscr {V}}\) a sequence of linear projectors \({\mathscr {P}}:=\{P_j\}_{j\ge j_0} \) with the following properties.
Properties 1
We assume that
-
(P1)
Pj maps \(H^r_0({\varOmega })\) onto Vj,
-
(P2)
PjPℓ = Pj for j ≤ ℓ,
-
(P3)
\({\mathscr {P}}\) is uniformly bounded on L2(Ω), i.e.,
 for any j ≥ j0 with a constant independent of j.
for any j ≥ j0 with a constant independent of j.
These conditions are satisfied, for example, for L2(Ω)-orthogonal projectors, or, in the case of splines, for the quasi-interpolant proposed and analyzed in [65, Chapter 4]. The second condition (P2) ensures that the differences Pj − Pj−1 are also projectors for any j > j0. We define next a sequence \({\mathscr {W}}:= \{ W_j\}_{j\ge j_0}\) of complement spaces
which then yields the direct (but not necessarily orthogonal) decomposition
Thus, for the finest level J, we can express VJ in its multilevel decomposition
upon setting \(W_{j_0-1} := V_{j_0}\). Setting also \(P_{j_0-1}:= 0\), the corresponding multilevel representation of any v ∈ VJ is then
We now have the following result which will be used later for the proof of the optimality of the multilevel preconditioners.
Theorem 2
Let \({\mathscr {P}},{\mathscr {V}}\) be as above where, in addition, we require that for each Vj, j0 ≤ j ≤ J, a Jackson and Bernstein estimate as in Theorem 1 (J) and (B) hold with h = 2−j. Then one has the function space characterization
Such a result holds for much larger classes of function spaces, Sobolev or even Besov spaces which are subsets of Lq(Ω) for general q, possibly different from 2 and for any function v ∈ Hr(Ω), then with an infinite sum on the right hand side, see, e.g., [24]. The proof of Theorem 2 for such cases heavily relies on tools from approximation theory and can be found in [27, 61].
Next we demonstrate how to exploit the norm equivalence (2.22) in the construction of an optimal multilevel preconditioner. Define for any v, w ∈ VJ the linear self-adjoint positive-definite operator CJ : VJ → VJ given by
which we call a multilevel BPX-type preconditioner. Let AJ : VJ → VJ be the finite-dimensional operator defined by \((A_J v,w)_{L_2({\varOmega })} := a(v,w)\) for all v, w ∈ VJ, the approximation of A in (2.6) with respect to VJ.
Theorem 3
With the same prerequisites as in Theorem 2 , C J is an asymptotically optimal symmetric preconditioner for A J , i.e., \(\kappa _2(C_J^{1/2} A_J C_J^{1/2}) \sim 1\) with constants independent of J.
Proof
For the parametric domain \(\hat {\varOmega }\), the result was proved independently in [27, 61] and is based on the combination of (2.22) together with the well-posedness of the continuous problem (2.6). The result on the physical domain follows then together with (2.11).\(\square \)
Realizations of the preconditioner defined in (2.23) based on B-splines lead to representations of the complement spaces Wj whose bases are called wavelets. For these, efficient implementations of optimal linear complexity involving the Fast Wavelet Transform can be derived explicitly, see Sect. 2.4.
However, since the order of the PDE operator r is positive, one can use here the argumentation from [8] which will allow to work with the same basis functions as for the spaces Vj. The first part of the argument relies on the assumption that the Pj are L2- orthogonal projectors. For a clear distinction, we shall use the notation Oj for L2-orthogonal projectors and reserve the notation Pj for the linear projectors with Properties 1. Then, the BPX-type preconditioner (2.23) (using the same symbol CJ for simplicity) reads as
which is by Theorem 3 a BPX-type preconditioner for the self-adjoint positive definite operator AJ. By the orthogonality of the projectors Oj, we can immediately derive from (2.24) that
Since r > 0, by rearranging the sum, the exponentially decaying scaling factors allow one to replace CJ by the spectrally equivalent operator
(for which we use the same notation CJ). Recall that two linear operators \(\mathscr {A}: V_J \to V_J\) and \(\mathscr {B}: V_J \rightarrow V_J \) are spectrally equivalent if they satisfy
with constants independent of J. Thus, the realization of the preconditioner is reduced to a computation in terms of the bases of the spaces Vj instead of Wj. The orthogonal projector Oj can, in turn, be replaced by a simpler local operator which is spectrally equivalent to Oj, see [50] and the derivation below.
Up to this point, the introduction to multilevel preconditioners has been basis-free. We now show how this framework can be used to construct a BPX-preconditioner for the linear system (2.6). Based on the definition (2.12), we construct a sequence of spaces satisfying (2.17) such that \(V_J= V_h^r\). In fact, we suppose that for each space dimension we have a sequence of p-open knot vectors \(\varXi _{j_0,\ell },\ldots , \varXi _{J,\ell }\), ℓ = 1, …, n, which provide a uniform partition of the interval [0, 1] such that Ξj,ℓ ⊂ Ξj+1,ℓ for j = j0, j0 + 1, …, J. In particular, we assume that Ξj+1,ℓ is obtained from Ξj,ℓ by dyadic refinement, i.e., the grid spacing for Ξj,ℓ is proportional to 2−j for each ℓ = 1, …, n. In view of the assumptions on the parametric mapping F, we assume that \(\bar h= 2^{-j_0}\), i.e., F can be represented in terms of B-splines on the coarsest level j0. By construction, we have now achieved that
Setting \(V_j^r := \{ v\in H^r_0({\varOmega }): ~ v \circ \mathbf {F}\in S_j(\hat {\varOmega }) \} \), we arrive at a sequence of nested spaces
Setting \({\mathscr {I}}_j:=\{1,\ldots ,\dim S_j(\hat \varOmega )\}\), we denote by \(B_{i}^j\), \(i\in {\mathscr {I}}_j\), the set of L2-normalized B-spline basis functions for the space \(S_j(\hat \varOmega )\). Define now the positive definite operator \(P_j:L_2(\varOmega ) \to V^r_j\) as
Corollary 1
For the basis
 , the operators P
j
and the L
2
-projectors O
j
are spectrally equivalent for any j.
, the operators P
j
and the L
2
-projectors O
j
are spectrally equivalent for any j.
Proof
The assertion follows by combining (2.11), (2.14), with Remark 3.7.1 from [50], see [8] for the main ingredients. \(\square \)
Finally, we obtain an explicit representation of the preconditioner CJ in terms of the mapped spline bases for \(V_j^r\), j = j0, …, J,
(denoted again by CJ). Note that this preconditioner involves all B-splines from all levels j with an appropriate scaling, i.e., a properly scaled generating system for \(V^r_J\).
Remark 1
The hierarchical basis (HB) preconditioner introduced for n = 2 in [71] for piecewise linear B-splines fits into this framework by choosing Lagrangian interpolants in place of the projectors Pj in (2.23). However, since these operators do not satisfy (P3) in Properties 1, they do not yield an asymptotically optimal preconditioner for n ≥ 2. For n = 3, this preconditioner does not have an effect at all.
So far we have not explicitly addressed the dependence of the preconditioned system on p. Since all estimates in Theorem 1 which enter the proof of optimality depend on p, it is to be expected that the absolute values of the condition numbers, i.e., the values of the constants, depend on and increase with p. Indeed, in the next section, we show some numerical results which also aim at studying this dependence.
2.2.3 Realization of the BPX Preconditioner
Now we are in the position to describe the concrete implementation of the BPX preconditioner. Its main ingredient are linear intergrid operators which map vectors and matrices between different grids. Specifically, we need to define prolongation and restriction operators.
Since \(V_j^r\subset V_{j+1}^r\), each B-spline \(B_i^j\) on level j can be represented by a linear combination of B-splines \(B_k^{j+1}\) on level j + 1. Arranging the B-splines in the set \(\{ B^j_i, i\in {\mathscr {I}}_j\}\) into a vector Bj in a fixed order, this relation denoted as refinement relation can be written as
with prolongation operator \({\mathbf {I}}_j^{j+1}\) from the trial space \(V_j^r\) to the trial space \(V_{j+1}^r\). The restriction \(\mathbf { I}_{j+1}^j\) is then simply defined as the transposed operator, i.e., \({\mathbf {I}}_{j+1}^j = ({\mathbf {I}}_j^{j+1})^T\). In case of piecewise linear B-splines, this definition coincides with the well known prolongation and restriction operators from finite element textbooks obtained by interpolation, see, e.g., [7].
We will exemplify the construction in case of quadratic and cubic B-splines on the interval, see, e.g., [38], as follows. We equidistantly subdivide the interval [0, 1] into 2j subintervals and obtain 2j and 2j + 1, respectively, B-splines for p = 2, 3 and the corresponding quadratic and cubic spline space \(V_j^r\) which is given on this partition, respectively, see Fig. 2.1 for an illustration. Note that the two boundary functions which do not vanish at the boundary were removed in order to guarantee that \(V_j^r \subset H^r_0(\varOmega )\). Moreover, recall that the B-splines are L2 normalized according to (2.13) which means that \(B^j_i\) is of the form \(B^j_i(\zeta ) = 2^{j/2} B(2^j \zeta -i)\) if \(B^j_i\) is an interior function, and correspondingly for the boundary functions.
Quadratic (p = 2) (left) and cubic (p = 3) (right) L2-normalized B-splines (see (2.13)) on level j = 3 on the interval [0, 1], yielding basis functions for \(V_j^r\subset H^r_0({\varOmega })\)
In case of quadratic B-splines (p = 2), the restriction operator \({\mathbf {I}}_{j+1}^j\) reads

For cubic B-splines (p = 3), it has the form

The normalization factor 2−1∕2 stems from the L2-normalization (2.13). The matrix entries are scaled in the usual fashion such that their rows sum to two. From these restriction operators for one dimensions, one obtains the related restriction operators on arbitrary unit cubes [0, 1]n via tensor products. Finally, we set \({\mathbf {I}}_{J}^{j} := {\mathbf {I}}_{J-1}^J{\mathbf {I}}_{J-2}^{J-1}\cdots {\mathbf {I}}_j^{j+1}\) and \({\mathbf {I}}_{J}^{j} := {\mathbf {I}}_j^{j+1}{\mathbf {I}}_{j+1}^{j+2}\cdots {\mathbf {I}}_{J-1}^J\) to define prolongations and restrictions between arbitrary levels j and J.
In order to derive the explicit form of the discretized BPX-preconditioner, for given functions uJ, vJ ∈ VJ with expansion coefficients uJ,k and vJ,ℓ, respectively, we conclude from (2.29) that
Next, one can introduce the mass matrix \({\mathbf {M}}_J =[(B_k^{J}\circ {\mathbf {F}}^{-1}, B_{\ell }^{J} \circ {\mathbf {F}}^{-1})_{L_2({\varOmega })}] _{k,\ell }\) and obtains by the use of restrictions and prolongations
The mass matrices which appear in this expression can be further suppressed since MJ is spectrally equivalent to the identity matrix. Finally, the discretized BPX-preconditioner to be implemented is of the simple form
involving only restrictions and prolongations. A further simple improvement can be obtained by replacing the scaling factor 2−2jr by \(\operatorname {diag}({\mathbf {A}}_j)^{-1}\), where \(\operatorname {diag}({\mathbf {A}}_j)\) denotes the diagonal matrix built from the diagonal entries of the stiffness matrix Aj. This diagonal scaling has the same effect as the levelwise scaling by 2−2jr but improves the condition numbers considerably, particularly if parametric mappings are involved. Thus, the discretized BPX-preconditioner takes on the form
which we will use in the subsequent computations presented in Tables 2.1 and 2.2. If the condition number \(\kappa ({\mathbf {A}}_{j_0})\) is already high in absolute numbers on the coarsest level j0, it is worth to use its exact inverse on the coarse grid, i.e., to apply instead of (2.32) the operator
see [11, 62]. Another substantial improvement of the BPX-preconditioner can be achieved by replacing the diagonal scaling on each level by, e.g., a SSOR preconditioning as follows. We decompose the system matrix as \({\mathbf {A}}_j = {\mathbf {L}}_j+{\mathbf {D}}_j +{\mathbf {L}}_{j}^{T}\) with the diagonal matrix Dj, the lower triangular part Lj, and the upper triangular part \({\mathbf {L}}_{j}^{T}\). Then we replace the diagonal scaling on each level of the BPX-preconditioner (2.32) by the SSOR preconditioner, i.e., instead of (2.32) we apply the preconditioner
In doing so, the condition numbers can be improved impressively. In Table 2.3, we list the ℓ2-condition numbers for the BPX-preconditioned Laplacian in case of cubic B-splines in two spatial dimensions. By comparing the numbers with those found in Tables 2.1 and 2.2 one can infer that the related condition numbers are all reduced by a factor about five. Note that the setup, storage and application of the operator defined in (2.33) is still of optimal linear complexity.
Finally, we provide numerical results in order to demonstrate the preconditioning and to specify the dependence on the spatial dimension n and the spline degree p. We consider an approximation of the homogeneous Dirichlet problem for the Poisson equation on the n-dimensional unit cube \(\hat {\varOmega }=(0,1)^n\) for n = 1, 2, 3. The mesh on level j is obtained by subdividing the cube j-times dyadically into 2n subcubes of mesh size hj = 2−j. On this subdivision, we consider the B-splines of degree p = 1, 2, 3, 4 as defined in Sect. 2.2.1. The ℓ2-condition numbers of the related stiffness matrices, preconditioned by the BPX-preconditioner (2.32), are shown in Table 2.1. The condition numbers seem to be independent of the level j, but they depend on the spline degree p and the space dimension n for n > 1. For fourth order problems on the sphere, corresponding results for the bi-Laplacian with and without BPX preconditioning were presented in [60].
We study next the dependence of the condition numbers on the parametric mapping F. We consider the case n = 2 in case of a smooth mapping (see the plot on the right hand side of Table 2.2 for an illustration of the mapping). As one can see from Table 2.2, the condition numbers are at most about a factor of five higher than the related values in Table 2.1. Nearly the same observation holds if we replace the parametric mapping by a \({\mathscr {C}}^0\)-parametrization which maps the unit square onto an L-shaped domain, see [10].
If we consider a singular map F, that is, a mapping that does not satisfy (2.11), the condition numbers grow considerably as expected, see [10]. But even in this case, the BPX-preconditioner with SSOR acceleration (2.33) is able to drastically reduce the condition numbers of the system matrix in all examples, see Table 2.3.
For further remarks concerning multiplicative multilevel preconditioners as the so-called multigrid methods in the context of isogeometric analysis together with references, one may consult [55].
2.3 Problem Classes
The variational problems to be investigated further will first be formulated in the following abstract form.
2.3.1 An Abstract Operator Equation
Let \({\mathscr {H}}\) be a Hilbert space with norm \(\|\cdot \|{ }_{{\mathscr {H}}}\) and let \({\mathscr {H}}'\) be the normed dual of \({\mathscr {H}}\) endowed with the norm
where 〈⋅, ⋅〉 denotes the dual pairing between \({\mathscr {H}}\) and \({\mathscr {H}}'\).
Given \(F\in {\mathscr {H}}'\), we seek a solution to the operator equation
where \({\mathscr {L}}:{\mathscr {H}}\to {\mathscr {H}}'\) is a linear operator which is assumed to be a bounded bijection, that is,
We call the operator equation well-posed since (2.35) implies for any given data \(F\in {\mathscr {H}}'\) the existence and uniqueness of the solution \(U\in {\mathscr {H}}\) which depends continuously on the data.
In the following subsections, we describe some problem classes which can be placed into this framework. In particular, these examples will have the format that \({\mathscr {H}}\) is a product space
where each of the Hi,0 ⊆ Hi is a Hilbert space (or a closed subspace of a Hilbert space Hi determined, e.g., by homogeneous boundary conditions). The spaces Hi will be Sobolev spaces living on a domain \({\varOmega }\subset \mathbb {R}^n\) or on (part of) its boundary. According to the definition of \({\mathscr {H}}\), the elements \(V\in {\mathscr {H}}\) will consist of M components V = (v1, …, vM)T, and we define \(\|V\|{ }_{{\mathscr {H}}}^2 := \sum _{i=1}^M \|v_i\|{ }^2_{H_i}\). The dual space \({\mathscr {H}}'\) is then endowed with the norm
where \(\langle V,W\rangle := \sum _{i=1}^M \langle v_i,w_i\rangle _i\) in terms of the dual pairing 〈⋅, ⋅〉i between Hi and \(H_i^{\prime }\).
We next formulate four classes which fit into this format. The first two concern are elliptic boundary value problems with included essential boundary conditions, and elliptic boundary value problems formulated as saddle point problem with boundary conditions treated by means of Lagrange Multipliers. For an introduction into elliptic boundary value problems and saddle point problems together with the functional analytic background one can, e.g., resort to [7]. Based on these formulations, we afterwards introduce certain control problems. A recurring theme in the derivation of the system of operator equation is the minimization of a quadratic functional subject to linear constraints.
2.3.2 Elliptic Boundary Value Problems
Let \(\varOmega \subset \mathbb {R}^n\) be a bounded domain with piecewise smooth boundary ∂Ω := Γ ∪ ΓN. We consider the scalar second order boundary value problem
where n = n(x) is the outward normal at x ∈ Γ, \(\mathbf {a}=\mathbf {a} (\mathbf {x}) \in \mathbb {R}^{n\times n}\) is uniformly positive definite and bounded on Ω and c ∈ L∞(Ω). Moreover, f and g are some given right hand side and boundary data. With the usual definition of the bilinear form
the weak formulation of (2.39) requires in the case g ≡ 0 to find \(y\in {\mathscr {H}}\) where
or
such that
The Neumann-type boundary conditions on ΓN are implicitly satisfied in the weak formulation (2.43), therefore called natural boundary conditions. In contrast, the Dirichlet boundary conditions on Γ have to be posed explicitly, for this reason called essential boundary conditions. The easiest way to achieve this for homogeneous Dirichlet boundary conditions when g ≡ 0 is to include them into the solution space as above in (2.41). In the nonhomogeneous case g≢0 on Γ in (2.39) and Γ≠∅, one can reduce the problem to a problem with homogeneous boundary conditions by homogenization as follows. Let w ∈ H1(Ω) be such that w = g on Γ. Then \(\tilde y:= y-w\) satisfies \(a(\tilde y,v)=a(y,v)-a(w,v) = \langle v,f\rangle - a(w,v) =: \langle v,\tilde f\rangle \) for all \(v\in {\mathscr {H}}\) defined in (2.41), and on Γ one has \(\tilde y =g-w\equiv 0\), that is, \(\tilde y\in {\mathscr {H}}\). Thus, it suffices to consider the weak form (2.43) with eventually modified right hand side. (A second possibility which allows to treat inhomogeneous boundary conditions explicitly in the context of saddle point problems will be discussed below in Sect. 2.3.3.)
The crucial property is that the bilinear form defined in (2.40) is continuous and elliptic on \({\mathscr {H}}\),
see, e.g., [7].
By Riesz’ representation theorem, the bilinear form defines a linear operator \(A:{\mathscr {H}}\to {\mathscr {H}}'\) by
which is under the above assumptions a bounded linear bijection, that is,
Here we only consider the case where A is symmetric. With corresponding alterations, the material in the subsequent sections can also be derived for the nonsymmetric case with corresponding changes with respect to the employed algorithms.
The relation (2.46) entails that given any \(f\in {\mathscr {H}}'\), there exists a unique \(y\in {\mathscr {H}}\) which solves the linear system
derived from (2.43). This linear operator equation where the operator defines a bounded bijection in the sense of (2.46) is the simplest case of a well-posed variational problem (2.35). Adhering to the notation in Sect. 2.3.1, we have here M = 1 and \({\mathscr {L}}=A\).
2.3.3 Saddle Point Problems Involving Boundary Conditions
A collection of saddle point problems or, more general, multiple field formulations including first order system formulations of the elliptic boundary value problem (2.39) and the three field formulation of the Stokes problem with inhomogeneous boundary conditions have been rephrased as well-posed variational problems in the above sense in [35], see also further references cited therein.
Here a particular saddle point problem derived from (2.39) shall be considered which will be recycled later in the context of control problems. In fact, this formulation is particularly appropriate to handle essential Dirichlet boundary conditions.
Recall from, e.g., [7], that the solution \(y\in {\mathscr {H}}\) of (2.43) is also the unique minimizer of the minimization problem
This means that y is a zero for its first order variational derivative of \({\mathscr {J}}\), that is, \(\delta {\mathscr {J}}(y;v)=0\). We denote here and in the following by \(\delta ^M {\mathscr {J}}(v; w_1,\ldots , w_M)\) the M-th variation of \({\mathscr {J}}\) at v in directions w1, …, wM, see e.g., [72]. In particular, for M = 1
is the (Gateaux) derivative of \({\mathscr {J}}\) at v in direction w.
In order to generalize (2.48) to the case of nonhomogeneous Dirichlet boundary conditions g, we formulate this as minimizing J over v ∈ H1(Ω) subject to constraints in form of the essential boundary conditions v = g on Γ. Using techniques from nonlinear optimization theory, one can employ a Lagrange multiplier p to append the constraints to the optimization functional J defined in (2.48). Satisfying the constraint is guaranteed by taking the supremum over all such Lagrange multipliers before taking the infimum. Thus, minimization subject to a constraint leads to the problem of finding a saddle point (y, p) of the saddle point problem
Some comments on the choice of the Lagrange multiplier space and the dual form 〈⋅, ⋅〉Γ in (2.50) are in order. The boundary expression v = g actually means taking the trace of v ∈ H1(Ω) to Γ ⊆ ∂Ω which we explicitly write from now on γv := v|Γ. Classical trace theorems which may be found in [43] state that for any v ∈ H1(Ω) one looses ‘\(\frac {1}{2}\) order of smoothness’ when taking traces so that one ends up with γv ∈ H1∕2(Γ). Thus, when the data g is also such that g ∈ H1∕2(Γ), the expression in (2.50) involving the dual form \(\langle \cdot ,\cdot \rangle _{\varGamma }:= \langle \cdot ,\cdot \rangle _{H^{1/2}(\varGamma ) \times (H^{1/2}(\varGamma ))'}\) is well-defined, and so is the selection of the multiplier space (H1∕2(Γ))′. In case of Dirichlet boundary conditions on the whole boundary of Ω, i.e., the case Γ ≡ ∂Ω, one can identify (H1∕2(Γ))′ = H−1∕2(Γ).
The above formulation (2.50) was first investigated in [2]. Another standard technique from optimization to handle minimization problems under constraints is to append the constraints to J(v) by means of a penalty parameter ε as follows, cf. [3]. For the case of homogeneous Dirichlet boundary conditions, one could introduce the functional \(J(v)+ (2{\varepsilon })^{-1} \|\gamma v\|{ }^2_{H^{1/2}(\varGamma )}\). (The original formulation in [3] uses the term \(\|\gamma v\|{ }_{L_2(\varGamma )}^2\).) Although the linear system derived from this formulation is still elliptic—the bilinear form is of the type \(a(v,v) +{\varepsilon }^{-1} (\gamma v,\gamma v)_{H^{1/2}(\varGamma )}\)—the spectral condition number of the corresponding operator Aε depends on ε. The choice of ε is typically attached to the discretization of an underlying grid with grid spacing h for Ω of the form ε ∼ hα when h → 0 for some exponent α > 0 chosen such that one retains the optimal approximation order of the underlying scheme. Thus, the spectral condition number of the operators in such systems depends polynomially on (at least) h−α. Consequently, iterative solution schemes such as the conjugate gradient method converge as slow as without preconditioning for A, and so far no optimal preconditioners for this situation are known.
It should also be mentioned that the way of treating essential boundary conditions by Lagrange multipliers can be extended to fictitious domain methods which may be used for problems with changing boundaries such as shape optimization problems [46, 49]. There one embeds the domain Ω into a larger, simple domain  , and formulates (2.50) with respect to
, and formulates (2.50) with respect to  and dual form on the changing boundary Γ [52]. One should note, however, that for Γ a proper subset of ∂Ω, there may occur some ambiguity in the relation between the fictitious domain formulation and the corresponding strong form (2.39).
and dual form on the changing boundary Γ [52]. One should note, however, that for Γ a proper subset of ∂Ω, there may occur some ambiguity in the relation between the fictitious domain formulation and the corresponding strong form (2.39).
In order to bring out the role of the trace operator, we define in addition to (2.40) a second bilinear form on H1(Ω) × (H1∕2(Γ))′ by
so that the saddle point problem (2.50) may be rewritten as
Computing zeroes of the first order variations of \({\mathscr {J}}\), now with respect to both v and q, yields the system of equations that a saddle point (y, p) has to satisfy
Defining the linear operator B : H1(Ω) → H1∕2(Γ) and its adjoint B′ : (H1∕2(Γ))′→ (H1(Ω))′ by 〈Bv, q〉Γ = 〈v, B′q〉Γ := b(v, q), this can be rewritten as the linear operator equation from \({\mathscr {H}} := H^1({\varOmega })\times (H^{1/2}(\varGamma ))'\) to \({\mathscr {H}}'\) as follows: Given \((f,g)\in {\mathscr {H}}'\), find \((y,p) \in {\mathscr {H}}\) that solves
It can be shown that the Lagrange multiplier is given by p = −n ⋅a∇y and can here be interpreted as a stress force on the boundary [2].
Let us briefly investigate the properties of B representing the trace operator. Classical trace theorems from, e.g., [43], state that for any f ∈ Hs(Ω), 1∕2 < s < 3∕2, one has

Conversely, for every g ∈ Hs−1∕2(Γ), there exists some f ∈ Hs(Ω) such that f|Γ = g and

Note that the range of s extends accordingly if Γ is more regular. Estimate (2.55) immediately entails for s = 1 that B : H1(Ω) → H1∕2(Γ) is continuous. Moreover, the second property (2.56) means B is surjective, i.e., rangeB = H1∕2(Γ) and \(\ker B'=\{0\}\), which yields that the inf–sup condition

is satisfied.
At this point it will be more convenient to consider (2.54) as a saddle point problem in abstract form on \({\mathscr {H}} = Y\times Q\). Thus, we identify Y = H1(Ω) and Q = (H1∕2(Γ))′ and linear operators A : Y → Y ′ and B : Y → Q′.
The abstract theory of saddle point problems states that existence and uniqueness of a solution pair \((y,p)\in {\mathscr {H}}\) holds if A and B are continuous, A is invertible on \(\ker B \subseteq Y\) and the range of B is closed in Q′, see, e.g., [7, 9, 42]. The properties for B and the continuity for A have been assured above. In addition, we will always deal here with operators A which are invertible on \(\ker B\), which cover the standard cases of the Laplacian (a = I and c ≡ 0) and the Helmholtz operator (a = I and c = 1).
Consequently,
is linear bijection, and one has the mapping property
for any \((v,q)\in {\mathscr {H}}\) with constants depending on upper and lower bounds for A, B. Thus, the operator equation (2.54) is established to be a well-posed variational problem in the sense of Sect. 2.3.1: for given \((f,g)\in {\mathscr {H}}'\), there exists a unique solution \((y,p)\in {\mathscr {H}}=Y\times Q\) which continuously depends on the data.
2.3.4 Parabolic Boundary Value Problems
More recently, weak full space-time formulation for one linear parabolic equation became popular which allow us to consider time just as another space variable as follows.
Let again \({\varOmega }\subset \mathbb {R}^n\) be a bounded Lipschitz domain with boundary ∂Ω, and denote by ΩT := I × Ω with time interval I := (0, T) the time-space cylinder for functions f = f(t, x) depending on time t and space x. The parameter T < ∞ will always denote a fixed final time. Let Y be a dense subspace of H := L2(Ω) which is continuously embedded in L2(Ω) and denote by Y ′ its topological dual. The associated dual form is denoted by \(\langle \cdot ,\cdot \rangle _{Y'\times Y}\) or, shortly 〈⋅, ⋅〉. Later we will use 〈⋅, ⋅〉 also for time-space duality with the precise meaning clear from the context. Norms will be indexed by the corresponding spaces. Following [59], Chapter III, p. 100, let for a.e. t ∈ I there be bilinear forms \(a(t;\cdot ,\cdot ):Y\times Y\to \mathbb {R}\) so that t↦a(t;⋅, ⋅) is measurable on I and that a(t;⋅, ⋅) is continuous and elliptic on Y , i.e., there exists constants 0 < α1 ≤ α2 < ∞ independent of t such that a.e. t ∈ I
Define accordingly a linear operator A = A(t) : Y → Y ′ by
Denoting by \({\mathscr {L}}(V,W)\) the set of all bounded linear functions from V to W, we have by (2.60) \(A(t)\in {\mathscr {L}}(Y,Y')\) for a.e. t ∈ I. Typically, A(t) will be a scalar linear elliptic differential operator of order two on Ω and \(Y=H^1_0({\varOmega })\). We denote by L2(I;Z) the space of all functions v = v(t, x) for which for a.e. t ∈ I one has v(t, ⋅) ∈ Z. Instead of L2(I;Z), we will write this space as the tensor product of the two separable Hilbert spaces, L2(I) ⊗ Z, which, by Theorem 12.6.1 in [1], can be identified. This fact will be frequently employed also in the sequel.
The standard semi-weak form a linear evolution equation is the following, see e.g. [40]. Given an initial condition y0 ∈ H and right hand side f ∈ L2(I;Y ′), find y in some function space on ΩT such that
For \(Y=H^1_0({\varOmega })\), the weak formulation of the first equation includes homogeneous Dirichlet conditions y(t, ⋅)|∂Ω = 0 for a.e. t ∈ I.
The space-time variational formulation for (2.62) will be based on the solution space
equipped with the graph norm
and the Cartesian product space of test functions
equipped for \(v=(v_1,v_2) \in {\mathscr {V}}\) with the norm
Note that v1 = v1(t, x) and v2 = v2(x).
Integration of (2.62) over t ∈ I leads to the variational problem to find for given \(f\in {\mathscr {V}}'\) a function \(y\in {\mathscr {Y}}\)
where the bilinear form \(b(\cdot ,\cdot ):{\mathscr {Y}}\times {\mathscr {V}}\to \mathbb {R}\) is defined by
and the right hand side \( \langle f,\cdot \rangle :{\mathscr {V}}\to \mathbb {R}\) by
for \(v=(v_1,v_2)\in {\mathscr {V}}\). It was proven in [37, Chapter XVIII, §3] that the operator defined by the bilinear form b(⋅, ⋅) is an isomorphism with respect to the spaces \({\mathscr {Y}}\) and \({\mathscr {V}}\). An alternative, shorter proof given in [66] is based on a characterization of bounded invertibility of linear operators between Hilbert spaces and provides detailed bounds on the norms of the operator and its inverse as follows.
Theorem 4
The operator \(B\in {\mathscr {L}}({\mathscr {Y}},{\mathscr {V}}')\) defined by 〈Bw, v〉 := b(w, v) for \(w\in {\mathscr {Y}}\) and \(v\in {\mathscr {V}}\) with b(⋅, ⋅) from (2.68) and spaces \({\mathscr {Y}}\), \({\mathscr {V}}\) defined in (2.63), (2.65) is boundedly invertible: There exist constants 0 < β1 ≤ β2 < ∞ such that
As proved in [66], the continuity constant β2 and the inf–sup condition constant β1 for b(⋅, ⋅) satisfy
where α1, α2 are the constants from (2.60) bounding A(t), and ϱ is defined as
We like to recall from [37, 40] that \({\mathscr {Y}}\) is continuously embedded in \({\mathscr {C}}^0(I;H)\) so that the pointwise in time initial condition in (2.62) is well-defined. From this it follows that the constant ρ is bounded uniformly in the choice of \({\mathscr {Y}}\hookrightarrow H\).
For the sequel, it will be useful to explicitly identify the dual operator \(B^*:{\mathscr {V}}\to {\mathscr {Y}}'\) of B which is defined by
In fact, it follows from the definition of the bilinear form (2.68) on \({\mathscr {Y}}\times {\mathscr {V}}\) by integration by parts for the first term with respect to time, and using the dual A(t)∗ w.r.t. space that
Note that the first term of the right hand side defining B∗ which involves \(\frac {\partial }{\partial t} v_1(t,\cdot )\) is still well-defined with respect to t as an element of \({\mathscr {Y}}'\) on account of \(w\in {\mathscr {Y}}\).
2.3.5 PDE-Constrained Control Problems: Distributed Control
A class of problems where the numerical solution of systems (2.47) is required repeatedly are certain control problems with PDE-constraints described next. Adhering to the notation from Sect. 2.3.2, consider as a guiding model for the subsequent discussion the objective to minimize a quadratic functional of the form
subject to linear constraints
where A : H → H′ is defined as above in (2.61) satisfying (2.46) and f ∈ H is given. Reserving the symbol \({\mathscr {H}}\) for the resulting product space in view of the notation in Sect. 2.3.1, the space H is in this subsection defined as in (2.41) or in (2.42). In order for a solution y of (2.75), the state of the system, to be well-defined, the problem formulation has to ensure that the unknown control u appearing on the right hand side is at least in H′. This can be achieved by choosing the control space \({\mathscr {U}}\) whose norm appears in (2.74) such that it is as least as smooth as H′. The second ingredient in the functional (2.74) is a data fidelity term which tries to match the system state y to some prescribed target state y∗, measured in some norm which is typically weaker than ∥⋅∥H. Thus, we require that the observation space \({\mathscr {Z}}\) and the control space \({\mathscr {U}}\) are such that the continuous embeddings

hold. Mostly one has investigated the simplest cases of norms which occur for \({\mathscr {U}}={\mathscr {Z}}=L_2({\varOmega })\) and which are covered by these assumptions [59]. The parameter ω ≥ 0 balances the norms in (2.74).
Since the control appears in all of the right hand side of (2.75), such control problems are termed problems with distributed control. Although their practical value is of a rather limited nature, distributed control problems help to bring out the basic mechanisms. Note that when the observed data are compatible in the sense that y∗≡ A−1f, the control problem has the trivial solution u ≡ 0 which yields \({\mathscr {J}}(y,u)\equiv 0\).
Solution schemes for the control problem (2.74) subject to the constraints (2.75) can be based on the system of operator equations derived next by the same variational principles as employed in the previous section, using a Lagrange multiplier p to enforce the constraints. Defining the Lagrangian functional
on H × H × H′, the first order necessary conditions or Karush-Kuhn-Tucker (KKT) conditions \(\delta \mathop {\mbox{Lagr}}(x)=0\) for x = p, y, u can be derived as
Here the linear operators S and R can be interpreted as Riesz operators defined by the inner products \((\cdot ,\cdot )_{{\mathscr {Z}}}\) and \((\cdot ,\cdot )_{{\mathscr {U}}}\). The system (2.78) may be written in saddle point form as
on \({\mathscr {H}}:= H\times H \times H'\).
Remark 2
We can also allow for \({\mathscr {Z}}\) in (2.74) to be a trace space on part of the boundary ∂Ω as long as the corresponding condition (2.76) is satisfied [53].
The class of control problems where the control is exerted through Neumann boundary conditions can also be written in this form since in this case the control still appears on the right hand side of a single operator equation of a form like (2.75), see [29].
Well-posedness of the system (2.79) can now be established by applying the conditions for saddle point problems stated in Sect. 2.3.3. For the control problems here and below we will, however, follow a different route which better supports efficient numerical solution schemes. The idea is as follows. While the PDE constraints (2.75) that govern the system are fixed, there is in many applications some ambiguity with respect to the choice of the spaces \({\mathscr {Z}}\) and \({\mathscr {U}}\). L2 norms are easily realized in finite element discretizations, although in some applications like glass cooling smoother norms for the observation \(\|\cdot \|{ }_{{\mathscr {Z}}}\) are desirable [63]. Once \({\mathscr {Z}}\) and \({\mathscr {U}}\) are fixed, there is only a single parameter ω to balance the two norms in (2.74). Modelling the objective functional is therefore an issue where more flexibility may be advantageous. Specifically in a multiscale setting, one may want to weight contributions on different scales by multiple parameters.
The wavelet setting which we describe below allows for this flexibility. It is based on formulating the objective functional in terms of weighted wavelet coefficient sequences which are equivalent to \({\mathscr {Z}}\), \({\mathscr {U}}\) and which, in addition, support an efficient numerical implementation. Once wavelet discretizations are introduced, we formulate below control problems with such objective functionals.
2.3.6 PDE-Constrained Control Problems: Dirichlet Boundary Control
Even more involved as the control problems with distributed control encountered in the previous section are those problems with Dirichlet boundary control which are, however, practically much more relevant.
An illustrative guiding model for this case is the problem to minimize for some given data y∗ the quadratic functional
where, adhering to the notation in Sect. 2.3.2 the state y and the control u are coupled through the linear second order elliptic boundary value problem
The appearance of the control u as a Dirichlet boundary condition in (2.81) is referred to as a Dirichlet boundary control. In view of the treatment of essential Dirichlet boundary conditions in the context of saddle point problems derived in Sect. 2.3.3, we write the PDE constraints (2.81) in the operator form (2.54) on Y × Q where Y = H1(Ω) and Q = (H1∕2(Γ))′. The model control problem with Dirichlet boundary control then reads as follows: Minimize for given data \(y_*\in {\mathscr {Z}}\) and f ∈ Y ′ the quadratic functional
subject to
In view of the problem formulation in Sect. 2.3.5 and the discussion of the choice of the observation space \({\mathscr {Z}}\) and the control space, here we require analogously that \({\mathscr {Z}}\) and \({\mathscr {U}}\) are such that the continuous embeddings

hold. In view of Remark 2, also the case of observations on part of the boundary ∂Ω can be taken into account [54]. Part of the numerical results are for such a situation shown in Fig. 2.4.
Remark 3
It should be mentioned that the simple choice \({\mathscr {U}}=L_2(\varGamma )\) which is used in many applications of Dirichlet control problems is not covered here. There may arise the problem of well-posedness in this case which we briefly discuss. Note that the constraints (2.81) or, in weak form (2.54), guarantee a unique weak solution y ∈ Y = H1(Ω) provided that the boundary term u satisfies u ∈ Q′ = H1∕2(Γ). In the framework of control problems, this smoothness of u therefore has to be required either by the choice of \({\mathscr {U}}\) or by the choice of \({\mathscr {Z}}\) (such as \({\mathscr {Z}}=H^1({\varOmega })\)) which would assure By ∈ Q′. In the latter case, we could relax condition (2.84) on \({\mathscr {U}}\).
In the context of flow control problems, an H1 norm on the boundary for the control has been used in [45].
Similarly as stated at the end of Sect. 2.3.5, we can derive now by variational principles the first order necessary conditions for a coupled system of saddle point problems. Well-posedness of this system can then again be established by applying the conditions for saddle point problems from Sect. 2.3.3 where the inf-sup condition for the saddle point problem (2.54) yields an inf-sup condition for the exterior saddle point problem of interior saddle point problems [51]. However, also in this case, we follow the ideas mentioned at the end of Sect. 2.3.6 and pose a corresponding control problem in terms of wavelet coefficients.
2.3.7 PDE-Constrained Control Problems: Parabolic PDEs
Finally, we consider the following tracking-type control problem constrained by an evolution PDE as formulated in Sect. 2.3.4.
We wish to minimize for some given target state y∗ and fixed end time T > 0 the quadratic functional
over the state y = y(t, x) and the control u = u(t, x) subject to
where B is defined by Theorem 4 and \(f\in {\mathscr {V}}'\) is given by (2.69). The real weight parameters ω1, ω2 ≥ 0 are such that ω1 + ω2 > 0 and ω3 > 0. The space Z by which the integral over Ω in the first two terms in (2.85) is indexed is to satisfy Z ⊇ Y with continuous embedding. Although there is in the wavelet framework great flexibility in choosing even fractional Sobolev spaces for Z, for transparency, we pick here Z = Y . A more general choice only results in multiplications of vectors in wavelet coordinate with diagonal matrices of the form (2.96) below, see [29]. Moreover, we suppose that the operator E is a linear operator \(E:U\to {\mathscr {V}}'\) extending ∫I〈u(t, ⋅), v1(t, ⋅)〉 dt trivially, that is, E ≡ (I, 0)T. In order to generate a well-posed problem, the space U in (2.85) must be chosen to enforce that Eu is at least in \({\mathscr {V}}'\). We pick here the natural case U = Y ′ which is also the weakest possible one. More general cases for both situations which result again in multiplication with diagonal matrices for wavelet coordinate vectors are discussed in [29].
2.4 Wavelets
The numerical solution of the classes of problems introduced above hinges on the availability of appropriate wavelet bases for the function spaces under consideration which are all particular Hilbert spaces. first introduce the three basic properties that we require our wavelet bases to satisfy.
Afterwards, construction principles for wavelets based on multiresolution analysis of function spaces on bounded domains will be given.
2.4.1 Basic Properties
In view of the problem classes considered above, we need to have a wavelet basis for each occurring function space at our disposal. A wavelet basis for a Hilbert space H is here understood as a collection of functions

which are indexed by elements λ from an infinite index set  . Each of the λ comprises different information λ = (j, k, e) such as the refinement scale or level of resolution j and a spatial location \(\mathbf {k}=\mathbf {k}(\lambda )\in \mathbb {Z}^n\). In more than one space dimensions, the basis functions are built from taking tensor products of certain univariate functions, and in this case the third index e contains information on the type of wavelet. We will frequently use the symbol |λ| := j to have access to the resolution level j. In the univariate case on all of \(\mathbb {R}\), ψH,λ is typically generated by means of shifts and dilates of a single function ψ, i.e., ψλ = ψj,k = 2j∕2ψ(2j ⋅−k), \(j,k\in \mathbb {Z}\), normalized with respect to \(\|\cdot \|{ }_{L_2}\). On bounded domains, the structure of the functions is essentially the same up to modifications near the boundary.
. Each of the λ comprises different information λ = (j, k, e) such as the refinement scale or level of resolution j and a spatial location \(\mathbf {k}=\mathbf {k}(\lambda )\in \mathbb {Z}^n\). In more than one space dimensions, the basis functions are built from taking tensor products of certain univariate functions, and in this case the third index e contains information on the type of wavelet. We will frequently use the symbol |λ| := j to have access to the resolution level j. In the univariate case on all of \(\mathbb {R}\), ψH,λ is typically generated by means of shifts and dilates of a single function ψ, i.e., ψλ = ψj,k = 2j∕2ψ(2j ⋅−k), \(j,k\in \mathbb {Z}\), normalized with respect to \(\|\cdot \|{ }_{L_2}\). On bounded domains, the structure of the functions is essentially the same up to modifications near the boundary.
The three crucial properties that we will assume the wavelet basis to have for the sequel are the following.
Riesz Basis Property (R)
Every v ∈ H has a unique expansion in terms of ΨH,

and its expansion coefficients satisfy a norm equivalence, that is, for any  one has
one has

where 0 < cH ≤ CH < ∞. This means that wavelet expansions induce isomorphisms between certain function spaces and sequence spaces. It will be convenient in the following to abbreviate ℓ2 norms without subscripts as  when the index set is clear from the context. If the precise format of the constants does not matter, we write the norm equivalence (2.89) shortly as
when the index set is clear from the context. If the precise format of the constants does not matter, we write the norm equivalence (2.89) shortly as

Locality (L)
The functions ψH,λ are have compact support which decreases with increasing level j = |λ|, i.e.,
Cancellation Property (CP)
There exists an integer \(\tilde d =\tilde d_H\) such that

Thus, integrating against a wavelet has the effect of taking an \(\tilde d\)th order difference which annihilates the smooth part of v. This property is for wavelets defined on Euclidean domains typically realized by constructing ΨH in such a way that it possesses a dual or biorthogonal basis \(\tilde \varPsi _{H} \subset H'\) such that the multiresolution spaces \(\tilde S_j:= {span}\{\tilde \psi _{H,\lambda }:|\lambda |< j\}\) contain all polynomials of order \(\tilde d\). Here dual basis means that \(\langle \psi _{H,\lambda },\tilde \psi _{H,\nu }\rangle =\delta _{\lambda ,\nu }\),  .
.
A few remarks on these properties are in order. In (R), the norm equivalence (2.90) is crucial since it means complete control over a function measured in ∥⋅∥H from above and below by its expansion coefficients: small changes in the coefficients only causes small changes in the function which, together with the locality (L), also means that local changes stay local. This stability is an important feature which is used for deriving optimal preconditioners and driving adaptive approximations where, again, the locality is crucial. Finally, the cancellation property (CP) entails that smooth functions have small wavelet coefficients which, on account of (2.89) may be neglected in a controllable way. Moreover, (CP) can be used to derive quasi-sparse representations of a wide class of operators.
By duality arguments one can show that (2.89) is equivalent to the existence of a biorthogonal collection which is dual or biorthogonal to ΨH,

which is a Riesz basis for H′, that is, for any \(\tilde v = \tilde {\mathbf {v}}^T \,\tilde \varPsi _H\in H'\) one has
see [23, 25, 51]. Here and in the sequel the tilde expresses that the collection \(\tilde \varPsi _H\) is a dual basis to a primal one for the space identified by the subscript, so that \(\tilde \varPsi _H= \varPsi _{H'}\).
Above in (2.89), we have already introduced the following shorthand notation which simplifies the presentation of many terms. We will view ΨH both as in (2.87) as a collection of functions as well as a (possibly infinite) column vector containing all functions always assembled in some fixed unspecified order. For a countable collection of functions Θ and some single function σ, the term 〈Θ, σ〉 is to be understood as the column vector with entries 〈θ, σ〉, θ ∈ Θ, and correspondingly 〈σ, Θ〉 the row vector. For two collections Θ, Σ, the quantity 〈Θ, Σ〉 is then a (possibly infinite) matrix with entries (〈θ, σ〉)θ ∈ Θ,σ ∈ Σ for which 〈Θ, Σ〉 = 〈Σ, Θ〉T. This also implies for a (possibly infinite) matrix C that 〈CΘ, Σ〉 = C〈Θ, Σ〉 and 〈Θ, CΣ〉 = 〈Θ, Σ〉CT.
In this notation, the biorthogonality or duality conditions (2.93) can be reexpressed as
with the infinite identity matrix I.
Wavelets with the above properties can actually obtained in the following way. This concerns, in particular, a scaling depending on the regularity of the space under consideration. In our case, H will always be a Sobolev space Hs = Hs(Ω) or a closed subspace of Hs(Ω) determined by homogeneous boundary conditions, or its dual. For s < 0, Hs is interpreted as above as the dual of H−s. One typically obtains the wavelet basis ΨH for H from an anchor basis  which is a Riesz basis for L2(Ω), meaning that Ψ is scaled such that \(\|\psi _\lambda \|{ }_{L_2({\varOmega })}\sim 1\). Moreover, its dual basis \(\tilde \varPsi \) is also a Riesz basis for L2(Ω). Ψ and \(\tilde \varPsi \) are constructed in such a way that rescaled versions of both bases \(\varPsi ,\tilde \varPsi \) form Riesz bases for a whole range of (closed subspaces of) Sobolev spaces Hs, for \(0 <s< \gamma , \tilde \gamma \), respectively. Consequently, one can derive that for each \(s\in (-\tilde \gamma ,\gamma )\) the collection
which is a Riesz basis for L2(Ω), meaning that Ψ is scaled such that \(\|\psi _\lambda \|{ }_{L_2({\varOmega })}\sim 1\). Moreover, its dual basis \(\tilde \varPsi \) is also a Riesz basis for L2(Ω). Ψ and \(\tilde \varPsi \) are constructed in such a way that rescaled versions of both bases \(\varPsi ,\tilde \varPsi \) form Riesz bases for a whole range of (closed subspaces of) Sobolev spaces Hs, for \(0 <s< \gamma , \tilde \gamma \), respectively. Consequently, one can derive that for each \(s\in (-\tilde \gamma ,\gamma )\) the collection

is a Riesz basis for Hs [23]. This means that there exist positive finite constants cs, Cs such that

holds for each \(s\in (-\tilde \gamma ,\gamma )\). Such a scaling represented by a diagonal matrix Ds introduced in (2.96) will play an important role later on. The analogous expression in terms of the dual basis reads

where \(\tilde \varPsi _s\) forms a Riesz basis of Hs for \(s \in (-\gamma ,\tilde \gamma )\). This entails the following fact. For \(\tau \in (-\tilde \gamma , \gamma )\) the mapping

acts as a shift operator between Sobolev scales which means that
Concrete constructions of wavelet bases with the above properties for parameters \(\gamma ,\tilde \gamma \le 3/2\) on a bounded Lipschitz domain Ω can be found in [33, 34]. This suffices for the above mentioned examples where the relevant Sobolev regularity indices range between − 1 and 1.
2.4.2 Norm Equivalences and Riesz Maps
As we have seen, the scaling provided by D−s is an important feature to establish norm equivalences (2.97) for the range \(s\in (-\tilde \gamma ,\gamma )\) of Sobolev spaces Hs. However, there are several other norms which are equivalent to \(\|\cdot \|{ }_{H^s}\) which may later be used in the objective functional (2.74) in the context of control problems. This issue addresses the mathematical model which we briefly discuss now.
We first consider norm equivalences for the L2 norm. Let as before Ψ be the anchor wavelet basis for L2 for which the Riesz operator \(\mathbf {R}= {\mathbf {R}}_{L_2}\) is the (infinite) Gramian matrix with respect to the inner product \((\cdot ,\cdot )_{L_2}\) defined as
Expanding Ψ in terms of \(\tilde \varPsi \) and recalling the duality (2.95), this entails
R may be interpreted as the transformation matrix for the change of basis from \(\tilde \varPsi \) to Ψ, that is, \(\varPsi =\mathbf {R} \tilde \varPsi \).
For any w = wTΨ ∈ L2, we now obtain the identities
Expanding w with respect to the basis \(\hat \varPsi := {\mathbf {R}}^{-1/2}\varPsi = {\mathbf {R}}^{1/2}\tilde \varPsi \), that is, \(w = \hat {\mathbf {w}}^T \hat \varPsi \), yields \(\|w\|{ }_{L_2}= \|\hat {\mathbf {w}}\|\). On the other hand, we get from (2.97) with s = 0
From this we can derive the condition number κ(Ψ) of the wavelet basis in terms of the extreme eigenvalues of R by defining
where κ(R) also denotes the spectral condition number of R and where the last relation is assured by the asymptotic estimate (2.104). However, the absolute constants will have an impact on numerical results in specific cases.
For a Hilbert space H denote by ΨH a wavelet basis for H satisfying (R), (L), (CP) with a corresponding dual basis \(\tilde \varPsi _H\). The (infinite) Gramian matrix with respect to the inner product (⋅, ⋅)H inducing ∥⋅∥H which is defined by
will be also called Riesz operator. The space L2 is covered trivially by R0 = R. For any function v := vTΨH ∈ H we have then the identity
Note that in general RH may not be explicitly computable, in particular, when H is a fractional Sobolev space.
Again referring to (2.97), we obtain as in (2.105) for the more general case
Thus, all Riesz operators on the applicable scale of Sobolev spaces are spectrally equivalent. Moreover, comparing (2.108) with (2.105), we get
Of course, in practice, the constants appearing in this equation may be much sharper, as the bases for Sobolev spaces with different exponents are only obtained by a diagonal scaling which preserves much of the structure of the original basis for L2.
We summarize these results for further reference.
Proposition 1
In the above notation, we have for any v = vTΨs ∈ Hs the norm equivalences
2.4.3 Representation of Operators
A final ingredient concerns the wavelet representation of linear operators in terms of wavelets. Let H, V be Hilbert spaces with wavelet bases ΨH, ΨV and corresponding duals \(\tilde \varPsi _H\), \(\tilde \varPsi _V\), and suppose that \({\mathscr {L}}:H\to V\) is a linear operator with dual \({\mathscr {L}}':V'\to H'\) defined by \(\langle v,{\mathscr {L}}'w\rangle := \langle {\mathscr {L}} v,w\rangle \) for all v ∈ H, w ∈ V .
We shall make frequent use of this representation and its properties.
Remark 4
The wavelet representation of \({\mathscr {L}}:H\to V\) with respect to the bases \(\varPsi _H,\tilde \varPsi _V\) of H, V ′, respectively, is given by
Thus, the expansion coefficients of \({\mathscr {L}} v\) in the basis that spans the range space of \({\mathscr {L}}\) are obtained by applying the infinite matrix \(\mathbf {L} = \langle \tilde \varPsi _V, {\mathscr {L}}\varPsi _H\rangle \) to the coefficient vector of v. Moreover, boundedness of \({\mathscr {L}}\) implies boundedness of L in ℓ2, i.e.,

Proof
Any image \({\mathscr {L}} v\in V\) can naturally be expanded with respect to ΨV as \({\mathscr {L}} v=\langle {\mathscr {L}} v,\tilde \varPsi _V\rangle \varPsi _V\). Expanding in addition v in the basis ΨH, v = vTΨH yields
As for (2.112), we can infer from (2.89) and (2.111) that

which confirms the claim. 
2.4.4 Multiscale Decomposition of Function Spaces
In this section, the basic construction principles of the biorthogonal wavelets with properties (R), (L) and (CP) are summarized, see, e.g., [24]. Their cornerstones are multiresolution analyses of the function spaces under consideration and the concept of stable completions. These concepts are free of Fourier techniques and can therefore be applied to derive constructions of wavelets on domains or manifolds which are subsets of \(\mathbb {R}^n\).
Multiresolution of L2
Practical constructions of wavelets typically start out with multiresolution analyses of function spaces. Consider a multiresolution \({\mathscr {S}}\) of L2 which consists of closed subspaces Sj of L2, called trial spaces, such that they are nested and their union is dense in L2,
The index j is the refinement level which appeared already in the elements of the index set  in (2.87), starting with some coarsest level \(j_0\in \mathbb {N}_0\). We abbreviate for a finite subset Θ ⊂ L2 the linear span of Θ as
in (2.87), starting with some coarsest level \(j_0\in \mathbb {N}_0\). We abbreviate for a finite subset Θ ⊂ L2 the linear span of Θ as
Typically the multiresolution spaces Sj have the form
for some finite index set Δj, where the set \(\{\varPhi _j\}_{j=j_0}^{\infty }\) is uniformly stable in the sense that
holds uniformly in j. Here we have used again the shorthand notation
and Φj denotes both the (column) vector containing the functions ϕj,k as well as the set of functions (2.115).
The collection Φj is called single scale basis since all its elements live only on one scale j. In the present context of multiresolution analysis, Φj is also called generator basis or shortly generators of the multiresolution. We assume that the ϕj,k are compactly supported with
It follows from (2.116) that they are scaled such that
holds. It is known that nestedness (2.114) together with stability (2.116) implies the existence of matrices \({\mathbf {M}}_{j,0}=(m^j_{r,k})_{r\in \varDelta _{j+1},k\in \varDelta _j}\) such that the two-scale relation
is satisfied. We can essentially simplify the subsequent presentation of the material by viewing (2.119) as a matrix-vector equation which then attains the compact form
Any set of functions satisfying an equation of this form, the refinement or two-scale relation, will be called refinable.
Denoting by [X, Y ] the space of bounded linear operators from a normed linear space X into the normed linear space Y , one has that
is uniformly sparse which means that the number of entries in each row or column is uniformly bounded. Furthermore, one infers from (2.116) that
where the corresponding operator norm is defined as
Since the union of \({\mathscr {S}}\) is dense in L2, a basis for L2 can be assembled from functions which span any complement between two successive spaces Sj and Sj+1, i.e.,
where
The functions Ψj are called wavelet functions or shortly wavelets if, among other conditions detailed below, the union {Φj ∪ Ψj} is still uniformly stable in the sense of (2.116). Since (2.122) implies S(Ψj) ⊂ S(Φj+1), the functions in Ψj must also satisfy a matrix-vector relation of the form
with a matrix Mj,1 of size (#Δj+1) × (#∇j). Furthermore, (2.122) is equivalent to the fact that the linear operator composed of Mj,0 and Mj,1,
is invertible as a mapping from ℓ2(Δj ∪∇j) onto ℓ2(Δj+1). One can also show that the set {Φj ∪ Ψj} is uniformly stable if and only if
The particular cases that will be important for practical purposes are when not only Mj,0 and Mj,1 are uniformly sparse but also the inverse of Mj. We denote this inverse by Gj and assume that it is split into
A special situation occurs when
which corresponds to the case of L2 orthogonal wavelets [36]. A systematic construction of more general Mj, Gj for spline-wavelets can be found in [34], see also [24] for more examples, including the hierarchical basis.
Thus, the identification of the functions Ψj which span the complement of S(Φj) in S(Φj+1) is equivalent to completing a given refinement matrix Mj,0 to an invertible matrix Mj in such a way that (2.126) is satisfied. Any such completion Mj,1 is called stable completion of Mj,0. In other words, the problem of the construction of compactly supported wavelets can equivalently be formulated as an algebraic problem of finding the (uniformly) sparse completion of a (uniformly) sparse matrix Mj,0 in such a way that its inverse is also (uniformly) sparse. The fact that inverses of sparse matrices are usually dense elucidates the difficulties in the constructions.
The concept of stable completions has been introduced in [14] for which a special case is known as the lifting scheme [69]. Of course, constructions that yield compactly supported wavelets are particularly suited for computations in numerical analysis.
Combining the two-scale relations (2.120) and (2.124), one can see that Mj performs a change of bases in the space Sj+1,
Conversely, applying the inverse of Mj to both sides of (2.128) results in the reconstruction identity
Fixing a finest resolution level J, one can repeat the decomposition (2.122) so that SJ = S(ΦJ) can be written in terms of the functions from the coarsest space supplied with the complement functions from all intermediate levels,
Thus, every function v ∈ S(ΦJ) can be written in its single-scale representation
as well as in its multi-scale form
with respect to the multiscale or wavelet basis
Often the single-scale representation of a function may be easier to compute and evaluate while the multi-scale representation allows one to separate features of the underlying function characterized by different length scales. Since therefore both representations are advantageous, it is useful to determine the transformation between the two representations, commonly referred to as the Wavelet Transform,
where
The previous relations (2.128) and (2.129) indicate that this will involve the matrices Mj and Gj. In fact, TJ has the representation
where each factor has the form
Schematically TJ can be visualized as a pyramid scheme

Accordingly, the inverse transform \({\mathbf {T}}_J^{-1}\) can be written also in product structure (2.135) in reverse order involving the matrices Gj as follows:
where each factor has the form
The corresponding pyramid scheme is then

Remark 5
Property (2.126) and the fact that Mj and Gj can be applied in (#Δj+1) operations uniformly in j entails that the complexity of applying TJ or \({\mathbf {T}}_J^{-1}\) using the pyramid scheme is of order \(\mathscr {O}(\#\varDelta _J) =\mathscr {O}(\dim \, S_J)\) uniformly in J. For this reason, TJ is called the Fast Wavelet Transform (FWT). Note that there is no need to explicitly assemble TJ or \({\mathbf {T}}_J^{-1}\).
In Table 2.4 spectral condition numbers for the Fast Wavelet Transform (FWT) for different constructions of biorthogonal wavelets on the interval computed in [62] are displayed.
Since \(\cup _{j\ge j_0} S_j\) is dense in L2, a basis for the whole space L2 is obtained when letting J →∞ in (2.133),

The next theorem from [23] illustrates the relation between Ψ and TJ.
Theorem 5
The multiscale transformations T J are well-conditioned in the sense
if and only if the collection Ψ defined by (2.141) is a Riesz basis for L2, i.e., every v ∈ L2 has unique expansions
where \(\tilde \varPsi \) defined analogously as in (2.141) is also a Riesz basis for L2 which is biorthogonal or dual to Ψ,
such that

We briefly explain next how the functions in \(\tilde \varPsi \), denoted as wavelets dual to Ψ, or dual wavelets, can be determined. Assume that there is a second multiresolution \(\tilde {\mathscr {S}}\) of L2 satisfying (2.114) where
and \(\{\tilde \varPhi _j\}_{j=j_0}^\infty \) is uniformly stable in j in the sense of (2.116). Let the functions in \(\tilde \varPhi _j\) also have compact support satisfying (2.117). Furthermore, suppose that the biorthogonality conditions
hold. We will often refer to Φj as the primal and to \(\tilde \varPhi _j\) as the dual generators. The nestedness of the \(\tilde S_j\) and the stability again implies that \(\tilde \varPhi _j\) is refinable with some matrix \(\tilde {\mathbf {M}}_{j,0}\), similar to (2.120),
The problem of determining biorthogonal wavelets now consists in finding bases \(\varPsi _j,\tilde \varPsi _j\) for the complements of S(Φj) in S(Φj+1), and of \(S(\tilde \varPhi _j)\) in \(S(\tilde \varPhi _{j+1})\), such that
and
holds. The connection between the concept of stable completions and the dual generators and wavelets is made by the following result which is a special case from [14].
Proposition 2
Suppose that the biorthogonal collections \(\{\varPhi _j\}_{j=j_0}^{\infty }\) and \(\{\tilde \varPhi _j \}_{j=j_0}^{\infty }\) are both uniformly stable and refinable with refinement matrices M j,0 , \(\tilde {\mathbf {M}}_{j,0}\) , i.e.,
and satisfy the duality condition (2.147). Assume that \(\check {\mathbf {M}}_{j,1}\) is any stable completion of Mj,0 such that
satisfies (2.126).
Then
is also a stable completion of M j,0 , and \({\mathbf {G}}_j = {\mathbf {M}}_j^{-1} = ({\mathbf {M}}_{j,0},{\mathbf {M}}_{j,1})^{-1}\) has the form
Moreover, the collections of functions
form biorthogonal systems,
so that
In particular, the relations (2.147), (2.156) imply that the collections
are biorthogonal,
Remark 6
It is important to note that the properties needed in addition to (2.159) in order to ensure (2.145) are neither properties of the complements nor of their bases \(\varPsi ,\tilde \varPsi \) but of the multiresolution sequences \({\mathscr {S}}\) and \(\tilde {\mathscr {S}}\). These can be phrased as approximation and regularity properties and appear in Theorem 6.
We briefly recall yet another useful point of view. The operators
are projectors onto
respectively, which satisfy
Remark 7
Let \(\{\varPhi _j\}_{j=j_0}^\infty \) be uniformly stable. The Pj defined by (2.160) are uniformly bounded if and only if \(\{\tilde \varPhi _j\}_{j=j_0}^\infty \) is also uniformly stable. Moreover, the Pj satisfy (2.162) if and only if the \(\tilde \varPhi _{j}\) are refinable as well. Note that then (2.147) implies
In terms of the projectors, the uniform stability of the complement bases Ψj, \(\tilde \varPsi _j\) means that
so that the L2 norm equivalence (2.145) is equivalent to
for any v ∈ L2, where \(P_{j_0-1}=P_{j_0-1}^{\prime } := 0\).
The whole concept derived so far lives from both Φj and \(\tilde \varPhi _j\). It should be pointed out that in the algorithms one actually does not need \(\tilde \varPhi _j\) explicitly for computations.
We recall next results that guarantee norm equivalences of the type (2.89) for Sobolev spaces.
Multiresolution of Sobolev Spaces
Let now \({\mathscr {S}}\) be a multiresolution sequence consisting of closed subspaces of Hs with the property (2.114) whose union is dense in Hs. The following result from [23] ensures under which conditions norm equivalences hold for the Hs-norm.
Theorem 6
Let \(\{\varPhi _j\}_{j=j_0}^\infty \) and \(\{\tilde \varPhi _j\}_{j=j_0}^\infty \) be uniformly stable, refinable, biorthogonal collections and let the Pj : Hs → S(Φj) be defined by (2.160). If the Jackson-type estimate

and the Bernstein inequality

hold for
then for
one has
Recall that we always write Hs = (H−s)′ for s < 0.
The regularity of \(\mathscr {S}\) and \(\tilde {\mathscr {S}}\) is characterized by
Recalling the representation (2.164), we can immediately derive the following fact.
Corollary 2
Suppose that the assumptions in Theorem 6 hold. Then we have the norm equivalence
In particular for s = 0 the Riesz basis property of the Ψ, \(\tilde \varPsi \) relative to L2(2.145) is recovered. For many applications it suffices to have (2.170) or (2.172) only for certain s > 0 for which one only needs to require (2.166) and (2.167) for \(\{\varPhi _j\}_{j=j_0}^\infty \). The Jackson estimates (2.166) of order \(\tilde d\) for \(S(\tilde \varPhi _j)\) imply the cancellation properties (CP) (2.92), see, e.g., [26].
Remark 8
When the wavelets live on \({\varOmega }\subset \mathbb {R}^n\), (2.166) means that all polynomials up to order \(\tilde d\) are contained in \(S(\tilde \varPhi _j)\). One also says that \(S(\tilde \varPhi _j)\) is exact of order \(\tilde d\). On account of (2.144), this implies that the wavelets ψj,k are orthogonal to polynomials up to order \(\tilde d\) or have \(\tilde d\)th order vanishing moments. By Taylor expansion, this in turn yields (2.92).
We will later use the following generalization of the discrete norms (2.165). Let for \(s\in \mathbb {R}\)

which by the relations (2.164) is also equivalent to

In this notation, (2.170) and (2.172) read

In terms of such discrete norms, Jackson and Bernstein estimates hold with constants equal to one [51], which turns out to be useful later in Sect. 2.5.2.
Lemma 1
Let \(\{\varPhi _j\}_{j=j_0}^\infty \) and \(\{\tilde \varPhi _j\}_{j=j_0}^\infty \) be uniformly stable, refinable, biorthogonal collections and let the Pj be defined by (2.160). Then the estimates

and

are valid, and correspondingly for the dual side.
The same results hold for the norm  defined in (2.173).
defined in (2.173).
Reverse Cauchy–Schwarz Inequalities
The biorthogonality condition (2.147) implies together with direct and inverse estimates the following reverse Cauchy–Schwarz inequalities for finite-dimensional spaces [28]. It will be one essential ingredient for the discussion of the LBB condition in Sect. 2.5.2.
Lemma 2
Let the assumptions in Theorem 6 be valid such that the norm equivalence (2.170) holds for \((-\tilde \sigma ,\sigma )\) with \(\sigma ,\tilde \sigma \) defined in (2.169). Then for any v ∈ S(Φj) there exists some \(\tilde v^* = \tilde v^*(v)\in S(\tilde \varPhi _j)\) such that

for any \(0\le s < \min (\sigma ,\tilde \sigma )\).
The proof of this result given in [28] for s = 1∕2 in terms of the projectors Pj defined in (2.160) and corresponding duals \(P_j^{\prime }\) immediately carries over to more general s. Recalling the representation (2.161) in terms of wavelets, the reverse Cauchy inequality (2.178) attains the following sharp form.
Lemma 3 ([51])
Let the assumptions of Lemma 1 hold. Then for every v ∈ S(Φj) there exists some \(\tilde v^* = \tilde v^*(v)\in S(\tilde \varPhi _j)\) such that

for any \(0\le s\le \min (\sigma ,\tilde \sigma )\).
Proof
Every v ∈ S(Φj) can be written as
Setting now
with the same coefficients vj,k, the definition of  yields by biorthogonality (2.159)
yields by biorthogonality (2.159)

Combining this with the observation
confirms (2.179). 
Remark 9
The previous proof reveals that the identity (2.179) is also true for elements from infinite-dimensional spaces Hs and (Hs)′ for which Ψ and \(\tilde \varPsi \) are Riesz bases.
Biorthogonal Wavelets on \(\mathbb {R}\)
The construction of biorthogonal spline-wavelets on \(\mathbb {R}\) from [18] for \(L_2=L_2(\mathbb {R})\) employs the multiresolution framework introduced at the beginning of this section. There the ϕj,k are generated through the dilates and translates of a single function ϕ ∈ L2,
This corresponds to the idea of a uniform virtual underlying grid, explaining the terminology uniform refinements. B-Splines on uniform grids are known to satisfy refinement relations (2.119) in addition to being compactly supported and having L2-stable integer translates. For computations, they have the additional advantage that they can be expressed as piecewise polynomials. In the context of variational formulations for second order boundary value problems, a well-used example are the nodal finite elements ϕj,k generated by the cardinal B-Spline of order two, i.e., the piecewise linear continuous function commonly called the ‘hat function’. For cardinal B-Splines as generators, a whole class of dual generators \(\tilde \phi _{j,k}\) (of arbitrary smoothness at the expense of larger supports) can be constructed which are also generated by one single function \(\tilde \phi \) through translates and dilates. By Fourier techniques, one can construct from \(\phi ,\tilde \phi \) then a pair of biorthogonal wavelets \(\psi ,\tilde \psi \) whose dilates and translates built as in (2.180) constitute Riesz bases for \(L_2(\mathbb {R})\).
By taking tensor products of these functions, one can generate biorthogonal wavelet bases for \(L_2(\mathbb {R}^n)\).
Biorthogonal Wavelets on Domains
Some constructions that exist by now have as a core ingredient tensor products of one-dimensional wavelets on an interval derived from the biorthogonal wavelets from [18] on \(\mathbb {R}\). On finite intervals in \(\mathbb {R}\), the corresponding constructions are usually based on keeping the elements of \(\varPhi _j,\tilde \varPhi _j\) supported inside the interval while modifying those translates overlapping the end points of the interval so as to preserve a desired degree of polynomial exactness. A general detailed construction satisfying all these requirements has been proposed in [34]. Here just the main ideas for constructing a biorthogonal pair \(\varPhi _j,\tilde \varPhi _j\) and corresponding wavelets satisfying the above requirements are sketched, where we apply the techniques derived at the beginning of this section.
We start out with those functions from two collections of biorthogonal generators \(\varPhi _j^{\mathbb {R}}, \tilde \varPhi _j^{\mathbb {R}}\) for some fixed j ≥ j0 living on the whole real line whose support has nonempty intersection with the interval (0, 1). In order to treat the boundary effects separately, we assumed that the coarsest resolution level j0 is large enough so that, in view of (2.117), functions overlapping one end of the interval vanish at the other. One then leaves as many functions from the collection \(\varPhi _j^{\mathbb {R}},\tilde \varPhi _j^{\mathbb {R}}\) living in the interior of the interval untouched and modifies only those near the interval ends. Note that keeping just the restrictions to the interval of those translates overlapping the end points would destroy stability (and also the cardinality of the primal and dual basis functions living on (0, 1) since their supports do not have the same size). Therefore, modifications at the end points are necessary; also, just discarding them from the collections (2.115), (2.146) would produce an error near the end points. The basic idea is essentially the same for all constructions of orthogonal and biorthogonal wavelets on \(\mathbb {R}\) adapted to an interval. Namely, one takes fixed linear combinations of all functions in \(\varPhi _j^{\mathbb {R}},\tilde \varPhi _j^{\mathbb {R}}\) living near the ends of the interval in such a way that monomials up to the exactness order are reproduced there and such that the generator bases have the same cardinality. Because of the boundary modifications, the collections of generators are there no longer biorthogonal. However, one can show in the case of cardinal B-Splines as primal generators (which is a widely used class for numerical analysis) that biorthogonalization is indeed possible. This yields collections denoted by \(\varPhi _j^{(0,1)},\tilde \varPhi _j^{(0,1)}\) which then satisfy (2.147) on (0, 1) and all assumptions required in Proposition 2.
For the construction of corresponding wavelets, first an initial stable completion \(\check {\mathbf {M}}_{j,1}\) is computed by applying Gaussian eliminations to factor Mj,0 and then to find a uniformly stable inverse of \(\check {\mathbf {M}}_j\). Here we exploit that for cardinal B-Splines as generators the refinement matrices Mj,0 are totally positive. Thus, they can be stably decomposed by Gaussian elimination without pivoting. Application of Proposition 2 then gives the corresponding biorthogonal wavelets \(\varPsi _j^{(0,1)}, \tilde \varPsi _j^{(0,1)}\) on (0, 1) which satisfy the requirements in Corollary 2. It turns out that these wavelets coincide in the interior of the interval again with those on all of \(\mathbb {R}\) from [18]. An example of the primal wavelets for d = 2 generated by piecewise linear continuous functions is displayed in Fig. 2.2 on the left. After constructing these basic versions, one can then perform local transformations near the ends of the interval in order to improve the condition or L2 stability constants, see [11, 62] for corresponding results and numerical examples.
Primal wavelets for d = 2 on [0, 1] (left) and on a sphere (right) from [64]
We display spectral condition numbers for the FWT for two different constructions of biorthogonal wavelets on the interval computed in [62] in Table 2.4. The first column denotes the finest level on which the spectral condition numbers of the FWT are computed. The next column contains the numbers for the construction of biorthogonal spline-wavelets on the interval from [34] for the case \(d=2,\tilde d=4\) while the last column displays the numbers for a scaled version derived in [11]. We will see later in Sect. 2.5.1 how the transformation TJ is used for preconditioning.
Along these lines, also biorthogonal generators and wavelets with homogeneous (Dirichlet) boundary conditions can be constructed. Since the \(\varPhi _j^{(0,1)}\) are locally near the boundary monomials which all vanish at 0, 1 except for one, removing the one from \(\varPhi _j^{(0,1)}\) which corresponds to the constant function produces a collection of generators with homogeneous boundary conditions at 0, 1. In order for the moment conditions (2.92) still to hold for the Ψj, the dual generators have to have complementary boundary conditions. A corresponding construction has been carried out in [30] and implemented in [11]. Homogeneous boundary conditions of higher order can be generated accordingly.
By taking tensor products of the wavelets on (0, 1), in this manner biorthogonal wavelets for Sobolev spaces on (0, 1)n with or without homogeneous boundary conditions are obtained. This construction can be further extended to any other domain or manifold which is the image of a regular parametric mapping of the unit cube. Some results on the construction of wavelets on manifolds are summarized in [25]. There are essentially two approaches. The first idea is based on domain decomposition and consists in ‘gluing’ generators across interelement boundaries, see, e.g., [13, 31]. These approaches all have in common that the norm equivalences (2.172) for Hs = Hs(Γ) can be shown to hold only for the range − 1∕2 < s < 3∕2, due to the fact that duality arguments apply only for this range because of the nature of a modified inner product to which biorthogonality refers. The other approach which overcomes the above limitations on the ranges for which the norm equivalences hold has been developed in [32] based on previous characterizations of function spaces as Cartesian products from [15]. The construction in [32] has been optimized and implemented to construct wavelet bases on the sphere in [56, 64], see Fig. 2.2.
Of course, there are also different attempts to construct wavelet bases with the above properties without using tensor products. A construction of biorthogonal spline-wavelets on triangles introduced by [68] has been implemented in two spatial dimensions with an application to the numerical solution of a linear elliptic boundary value problem in [48].
2.5 Problems in Wavelet Coordinates
2.5.1 Elliptic Boundary Value Problems
We now consider the wavelet representation of the elliptic boundary value problem from Sect. 2.3.2. Let for \({\mathscr {H}}\) given by (2.41) or (2.42) \(\varPsi _{{\mathscr {H}}}\) be a wavelet basis with corresponding dual \(\tilde \varPsi _{{\mathscr {H}}}\) which satisfies the properties (R), (L) and (CP) from Sect. 2.4.1. Following the recipe from Sect. 2.4.3, expanding \(y={\mathbf {y}}^T \varPsi _{{\mathscr {H}}}\), \(f={\mathbf {f}}^T \tilde \varPsi _{{\mathscr {H}}}\) and recalling (2.45), the wavelet representation of the elliptic boundary value problem (2.47) is given by
where
Then the mapping property (2.46) and the Riesz basis property (R) yield the following fact.
Proposition 3
The infinite matrix A is a boundedly invertible mapping from  into itself, and there exists finite positive constants cA ≤ CA such that
into itself, and there exists finite positive constants cA ≤ CA such that

Proof
For any \(v\in {\mathscr {H}}\) with coefficient vector v ∈ ℓ2, we have by the lower estimates in (2.89), (2.46) and the upper inequality in (2.94), respectively,
where we have used the wavelet representation (2.111) for A. Likewise, the converse estimate
follows by the lower inequality in (2.94) and the upper estimates in (2.46) and (2.89). The constants appearing in (2.183) are therefore identified as \(c_{\mathbf {A}}:= c_{{\mathscr {H}}}^{2} c_A\) and \(C_{\mathbf {A}}:= c_{{\mathscr {H}}}^2 C_A\). 
In the present situation where A is defined via the elliptic bilinear form a(⋅, ⋅), Proposition 3 entails the following result with respect to preconditioning. Let for  the symbol Λ denote any finite subset of the index set
the symbol Λ denote any finite subset of the index set  . For the corresponding set of wavelets ΨΛ := {ψλ : λ ∈ Λ} denote by SΛ := spanΨΛ the respective finite-dimensional subspace of \({\mathscr {H}}\). For the wavelet representation of A in terms of ΨΛ,
. For the corresponding set of wavelets ΨΛ := {ψλ : λ ∈ Λ} denote by SΛ := spanΨΛ the respective finite-dimensional subspace of \({\mathscr {H}}\). For the wavelet representation of A in terms of ΨΛ,
we obtain the following result.
Proposition 4
If a(⋅, ⋅) is \({\mathscr {H}}\)-elliptic according to (2.44), the finite matrix AΛ is symmetric positive definite and its spectral condition number is bounded uniformly in Λ, i.e.,
where cA, CA are the constants from (2.183).
Proof
Clearly, since AΛ is just a finite section of A, we have ∥AΛ∥≤∥A∥. On the other hand, by assumption, a(⋅, ⋅) is \({\mathscr {H}}\)-elliptic which entails that a(⋅, ⋅) is also elliptic on every finite subspace \(S_\varLambda \subset {\mathscr {H}}\). Thus, we infer \(\|{\mathbf {A}}^{-1}_\varLambda \|\le \|{\mathbf {A}}^{-1}\|\), and we have
Together with the definition \(\kappa _2({\mathbf {A}}_{\varLambda }):= \|{\mathbf {A}}_{\varLambda }\| \, \|{\mathbf {A}}^{-1}_{\varLambda }\|\) we obtain the claimed estimate. 
In other words, representations of A with respect to properly scaled wavelet bases for \({\mathscr {H}}\) entail well-conditioned system matrices AΛ independent of Λ. This in turn means that the convergence speed of an iterative solver applied to the corresponding finite system
does not deteriorate as Λ →∞.
In summary, ellipticity implies stability of the Galerkin discretizations for any set  . This is not the case for finite versions of the saddle point problems discussed in Sect. 2.5.2.
. This is not the case for finite versions of the saddle point problems discussed in Sect. 2.5.2.
Fast Wavelet Transform
Let us briefly summarize how in the situation of uniform refinements, i.e., when S(ΦJ) = S(ΨJ), the Fast Wavelet Transformation (FWT) TJ can be used for preconditioning linear elliptic operators, together with a diagonal scaling induced by the norm equivalence (2.172) [27]. Here we recall the notation from Sect. 2.4.4 where the wavelet basis is in fact the (unscaled) anchor basis from Sect. 2.4.1. Thus, the norm equivalence (2.89) using the scaled wavelet basis ΨH is the same as (2.172) in the anchor basis. Recall that the norm equivalence (2.172) implies that every v ∈ Hs can be expanded uniquely in terms of the Ψ and its expansion coefficients v satisfy
where Ds is a diagonal matrix with entries \({\mathbf {D}}^s_{(j,k),(j',k')} =2^{sj}\delta _{j,j'}\delta _{k,k'}\). For \({\mathscr {H}}\subset H^1({\varOmega })\), the case s = 1 is relevant.
In a stable Galerkin scheme for (2.43) with respect to S(ΨJ) = S(ΨΛ), we have therefore already identified the diagonal (scaling) matrix DJ consisting of the finite portion of the matrix D = D1 for which j0 − 1 ≤ j ≤ J − 1. The representation of A with respect to the (unscaled) wavelet basis ΨJ can be expressed in terms of the Fast Wavelet Transform TJ, that is,
where ΦJ is the single-scale basis for S(ΨJ). Thus, we first set up the operator equation as in Finite Element settings in terms of the single-scale basis ΦJ. Applying the Fast Wavelet Transform TJ together with DJ yields that the operator
has uniformly bounded condition numbers independent of J. This can be seen by combining the properties of A according to (2.46) with the norm equivalences (2.89) and (2.94).
It is known that the boundary adaptations of the generators and wavelets aggravate the absolute values of the condition numbers. Nevertheless, these constants can be greatly reduced by sophisticated biorthogonalizations of the boundary adapted functions [11]. Numerical tests confirm that the absolute constants can further be improved by taking instead of \( {\mathbf {D}}_J^{-1}\) the inverse of the diagonal of 〈ΨJ, AΨJ〉 for the scaling in (2.189) [11, 17, 62]. Table 2.5 displays the condition numbers for discretizations of an operator in two spatial dimensions for boundary adapted biorthogonal spline-wavelets in the case \(d=2,\tilde d=4\) with such a scaling.
2.5.2 Saddle Point Problems Involving Boundary Conditions
As in the previous situation, we first derive an infinite wavelet representation of the saddle point problem introduced in Sect. 2.3.3.
Let for \({\mathscr {H}} = Y\times Q\) with Y = H1(Ω), Q = (H1∕2(Γ))′ two collections of wavelet bases ΨY, ΨQ be available, each satisfying (R), (L) and (CP), with respective duals \(\tilde \varPsi _{Y}\), \(\tilde \varPsi _{Q}\). Similar to the previous case, we expand y = yTΨY and p = pTΨQ and test with the elements from ΨY, ΨQ. Then (2.54) attains the form
where
In view of the above assertions, the operator L is an ℓ2-automorphism, i.e., for every  we have
we have
with constants cL, CL only depending on \(c_{\mathscr {L}},C_{\mathscr {L}}\) from (2.59) and the constants in the norm equivalences (2.89) and (2.94).
For saddle point problems with an operator L satisfying (2.192), finite sections are in general not uniformly stable in the sense of (2.186). In fact, for discretizations on uniform grids, the validity of the corresponding mapping property relies on a suitable stability condition, see e.g. [9, 42]. The relevant facts derived in [28] are as follows.
The bilinear form a(⋅, ⋅) defined in (2.40) is for c > 0 elliptic on all of Y = H1(Ω) and, hence, also on any finite-dimensional subspace of Y . Let there be two multiresolution analyses \(\mathscr {Y}\) of H1(Ω) and \(\mathscr {Q}\) of Q where the discrete spaces are Yj ⊂ H1(Ω) and QΛ =: Qℓ ⊂ (H1∕2(Γ))′. With the notation from Sect. 2.4.4 and in addition superscripts referring to the domain on which the functions live, these spaces are represented by
Here the indices j and ℓ refer to mesh sizes on the domain and the boundary,
The discrete inf–sup condition, the LBB condition, for the pair Yj, Qℓ requires that there exists a constant β1 > 0 independent of j and ℓ such that
holds. We have investigated in [28] the general case in arbitrary spatial dimensions where the Qℓ are not trace spaces of Yj. Employing the reverse Cauchy-Schwarz inequalities from Sect. 2.4.4, one can show that (2.194) is satisfied provided that hΓ(hΩ)−1 = 2j−ℓ ≥ cΩ > 1, similar to a condition which was known for bivariate polygons and particular finite elements [2, 41].
It should be mentioned that the obstructions caused by the LBB condition can be avoided by means of stabilization techniques proposed, e.g., in [67] where, however, the location of the boundary of Ω relative to the mesh is somewhat constrained. Another stabilization strategy based on wavelets has been investigated in [6]. A related approach which systematically avoids restrictions of the LBB type is based on least squares techniques [35].
It is particularly interesting that adaptive schemes based on wavelets like the one in Sect. 2.6.2 can be designed in such a way that the LBB condition is automatically enforced which was first observed in [22]. More on this subject can be found in [26].
In order to get an impression of the value of the constants for the condition numbers for AΛ in (2.185) and the corresponding ones for the saddle point operator on uniform grids (2.192), we mention an example investigated and implemented in [62]. In this example, Ω = (0, 1)2 and Γ is one face of its boundary. In Table 2.5 from [62], the spectral condition numbers of A and L with respect to two different constructions of wavelets for the case d = 2 and \(\tilde d=4\) are displayed. We see next to the first column in which the refinement level j is listed the spectral condition numbers of A with the wavelet construction from [34] denoted by ADKU and with the modification introduced in [11] and a further transformation [62] denoted by AB. The last columns contain the respective numbers for the saddle point matrix L where \(\kappa _2(\mathbf {L}):= \sqrt {\kappa ({\mathbf {L}}^T \mathbf {L})}\).
2.5.3 Control Problems: Distributed Control
We now discuss appropriate wavelet formulations for PDE-constrained control problems with distributed control as introduced in Sect. 2.3.5. Let for any space \(\mathscr {V}\in \{H,{\mathscr {Z}},{\mathscr {U}}\}\) \(\varPsi _{\mathscr {V}}\) denote a wavelet basis with the properties (R), (L), (CP) for \(\mathscr {V}\) with dual basis \(\tilde \varPsi _{\mathscr {V}}\).
Let \({\mathscr {Z}},{\mathscr {U}}\) satisfy the embedding (2.76). In terms of wavelet bases, the corresponding canonical injections correspond in view of (2.96) to a multiplication by a diagonal matrix. That is, let \({\mathbf {D}}_{{\mathscr {Z}}},{\mathbf {D}}_H\) be such that
Since \({\mathscr {Z}}\) possibly induces a weaker and \({\mathscr {U}}\) a stronger topology, the diagonal matrices \({\mathbf {D}}_{{\mathscr {Z}}},{\mathbf {D}}_H\) are such that their entries are nondecreasing in scale, and there is a finite constant C such that
For instance, for \(H=H^\alpha , {\mathscr {Z}}=H^\beta \), or for H′ = H−α, \({\mathscr {U}} = H^{-\beta }\), 0 ≤ β ≤ α, \({\mathbf {D}}_{{\mathscr {Z}}},{\mathbf {D}}_H\) have entries \(({\mathbf {D}}_{{\mathscr {Z}}})_{\lambda ,\lambda } = ({\mathbf {D}}_H)_{\lambda ,\lambda } = ({\mathbf {D}}^{\alpha -\beta })_{\lambda ,\lambda } = 2^{(\alpha -\beta )|\lambda |}\).
We expand y in ΨH and u in a wavelet basis \(\varPsi _{{\mathscr {U}}}\) for \({\mathscr {U}}\subset H'\),
Following the derivation in Sect. 2.5.1, the linear constraints (2.75) attain the form
where
Recall that A has been assumed to be symmetric. The objective functional (2.80) is stated in terms of the norms \(\|\cdot \|{ }_{{\mathscr {Z}}}\) and \(\|\cdot \|{ }_{{\mathscr {U}}}\). For an exact representation of these norms, corresponding Riesz operators \({\mathbf {R}}_{{\mathscr {Z}}}\) and \({\mathbf {R}}_{{\mathscr {U}}}\) defined analogously to (2.106) would come into play which may not be explicitly computable if \({\mathscr {Z}},{\mathscr {U}}\) are fractional Sobolev spaces. On the other hand, as mentioned before, such a cost functional in many cases serves the purpose of yielding unique solutions while there is some ambiguity in its exact formulation. Hence, in search for a formulation which best supports numerical realizations, it is often sufficient to employ norms which are equivalent to \(\|\cdot \|{ }_{{\mathscr {Z}}}\) and \(\|\cdot \|{ }_{{\mathscr {U}}}\). In view of the discussion in Sect. 2.4.2, we can work for the norms \(\|\cdot \|{ }_{{\mathscr {Z}}}\), \(\|\cdot \|{ }_{{\mathscr {U}}}\) only with the diagonal scaling matrices Ds induced by the regularity of \({\mathscr {Z}},{\mathscr {U}}\), or we can in addition include the Riesz map R defined in (2.101). In the numerical studies in [11], a somewhat better quality of the solution is observed when R is included. In order to keep track of the appearance of the Riesz maps in the linear systems derived below, we choose here the latter variant.
Moreover, we expand the given observation function \(y_* \in {\mathscr {Z}}\) as
The way the vector y∗ is defined here for notational convenience may by itself actually have infinite norm in ℓ2. However, its occurrence will always include premultiplication by \({\mathbf {D}}_{{\mathscr {Z}}}^{-1}\) which is therefore always well-defined. In view of (2.110), we obtain the relations
Note that here R = 〈Ψ, Ψ〉 (and not R−1) comes into play since y, y∗ have been expanded in a scaled version of the primal wavelet basis Ψ. Hence, equivalent norms for \(\|\cdot \|{ }_{{\mathscr {Z}}}\) may involve R. As for describing equivalent norms for \(\|\cdot \|{ }_{{\mathscr {U}}}\), recall that u is expanded in the basis ΨU for U ⊂ H′. Consequently, R−1 is the natural matrix to take into account when considering equivalent norms, i.e., we choose here
Finally, we formulate the following control problem in (infinite) wavelet coordinates.
(DCP) For given data  ,
,  , and weight parameter ω > 0, minimize the quadratic functional
, and weight parameter ω > 0, minimize the quadratic functional
over  subject to the linear constraints
subject to the linear constraints
Remark 10
Problem (DCP) can be viewed as (discretized yet still infinite-dimensional) representation of the linear-quadratic control problem (2.74) together with (2.75) in wavelet coordinates in the following sense. The functional \(\check {\mathbf {J}}(\mathbf {y}, \mathbf {u})\) defined in (2.203) is equivalent to the functional J(y, u) from (2.74) in the sense that there exist constants 0 < cJ ≤ CJ < ∞ such that
holds for any y = yTΨH ∈ H, given \(y_* = ({\mathbf {D}}_{{\mathscr {Z}}}^{-1}{\mathbf {y}}_*)^T \varPsi _{{\mathscr {Z}}} \in {\mathscr {Z}}\) and any \(u = {\mathbf {u}}^T\varPsi _{{\mathscr {U}}} \in {{\mathscr {U}}}\). Moreover, in the case of compatible data y∗ = A−1f yielding J(y, u) ≡ 0, the respective minimizers coincide, and y∗ = A−1f yields \(\check {\mathbf {J}}(\mathbf {y},\mathbf {u})\equiv \mathbf {0}\). In this sense the new functional (2.203) captures the essential features of the model minimization functional.
Once problem (DCP) is posed, we can apply variational principles to derive necessary and sufficient conditions for a unique solution. All control problems considered here are in fact simple in this regard, as we have to minimize a quadratic functional subject to linear constraints, for which the necessary conditions are also sufficient. In principle, there are two ways to derive the optimality conditions for (DCP). We have encountered in Sect. 2.3.5 already the technique via the Lagrangian.
We define for (DCP) the Lagrangian introducing the Lagrange multiplier, adjoint variable or adjoint state p as
Then the KKT conditions δLagr(w) = 0 for w = p, y, u are, respectively,


The first system resulting from the variation with respect to the Lagrange multiplier always recovers the original constraints (2.204) and will be referred to as the primal system or the state equation. Accordingly, we call (2.207b) the adjoint or dual system, or the costate equation. The third Eq. (2.207c) is sometimes denoted as the design equation. Although A is symmetric, we continue to write AT for the operator of the adjoint system to distinguish it from the primal system.
The coupled system (2.207) later is to be solved. However, in order to derive convergent iterations and deduce complexity estimates, a different formulation will be advantageous. It is based on the fact that A is according to Proposition 3 a boundedly invertible mapping on ℓ2. Thus, we can formally invert (2.198) to obtain \(\mathbf {y} = {\mathbf {A}}^{-1}\mathbf {f} + {\mathbf {A}}^{-1}{\mathbf {D}}_H^{-1} \mathbf {u}\). Substitution into (2.203) yields a functional depending only on u,
Employing the abbreviations

the functional simplifies to
Proposition 5 ([53])
The functional J is twice differentiable with first and second variation
In particular, J is convex so that a unique minimizer exists.
Setting
the unique minimizer u of (2.210) is given by solving
or, equivalently, the system
By definition (2.212), Q is a symmetric positive definite (infinite) matrix. Hence, finite versions of (2.214) could be solved by gradient or conjugate gradient iterative schemes. As the convergence speed of any such iteration depends on the spectral condition number of Q, it is important to note that the following result.
Proposition 6
The (infinite) matrix Q is uniformly bounded on ℓ2, i.e., there exist constants 0 < cQ ≤ CQ < ∞ such that
The proof follows from (2.46) and (2.196) [29]. Of course, in order to make such iterative schemes for (2.214) practically feasible, the explicit inversion of A in the definition of Q has to be avoided and replaced by an iterative solver in turn. This is where the system (2.207) will come into play. In particular, the third equation (2.207c) has the following interpretation which will turn out to be very useful later.
Proposition 7
If we solve for a given control vector u successively (2.204) for y and (2.207b) for p, then the residual for (2.214) attains the form
Proof
Solving consecutively (2.204) and (2.207b) and recalling the definitions of Z, g (2.209a), (2.212) we obtain

Hence, the residual Qu −g attains the form
where we have used the definition of Q from (2.212). 
Having derived the optimality conditions (2.207), the next issue is their efficient numerical solution. In view of the fact that the system (2.207) still involves infinite matrices and vectors, this also raises the question how to derive computable finite versions. By now we have investigated two scenarios.
The first version with respect to uniform discretizations is based on choosing finite-dimensional subspaces of the function spaces under consideration. The second version which deals with adaptive discretizations is actually based on the infinite system (2.207). In both scenarios, a fully iterative numerical scheme for the solution of (2.207) is designed along the following lines. The basic iteration scheme is a gradient or conjugate gradient iteration for (2.214) as an outer iteration where each application of Q is in turn realized by solving the primal and the dual system (2.204) and (2.207b) also by a gradient or conjugate gradient method as inner iterations.
For uniform discretizations for which we wanted to test numerically the role of equivalent norms and the influence of Riesz maps in the cost functional (2.203), we have used in [12] as central iterative scheme the conjugate gradient (CG) method. Since the interior systems are only solved up to discretization error accuracy, the whole procedure may therefore be viewed as an inexact conjugate gradient (CG) method. We stress already at this point that the iteration numbers of such a method do not depend on the discretization level as finite versions of all involved operators are also uniformly well-conditioned in the sense of (2.215). In each step of the outer iteration, the error will be reduced by a fixed factor ρ. Combined with a nested iteration strategy, it will be shown that this yields an asymptotically optimal method in the amount of arithmetic operations.
Starting from the infinite coupled system (2.207), we have investigated in [29] adaptive schemes which, given any prescribed accuracy ε > 0, solve (2.207) such that the error for y, u, p is controlled by ε. Here we have used a gradient scheme as basic iterative scheme since it somehow simplifies the analysis, see Sect. 2.6.2.
2.5.4 Control Problems: Dirichlet Boundary Control
Having derived a representation in wavelet coordinates for both the saddle point problem from Sect. 2.3.3 and the PDE-constrained control problem in the previous section, it is straightforward to find also an appropriate representation of the control problem with Dirichlet boundary control introduced in Sect. 2.3.6. In order not to be overburdened with notation, we specifically choose the control space on the boundary as \({{\mathscr {U}}}:=Q (=(H^{1/2}(\varGamma ))')\). For the more general situation covered by (2.84), a diagonal matrix with nondecreasing entries like in (2.195) would come into play to switch between \({{\mathscr {U}}}\) and Q. Thus, the exact wavelet representation of the constraints (2.83) is given by the system (2.190), where we exchange the given Dirichlet boundary term g by u in the present situation to express the dependence on the control in the right hand side, i.e.,
The derivation of a representer of the initial objective functional (2.82) is under the embedding condition (2.84)  for v ∈ Y now the same as in the previous section, where all reference to the space H is to be exchanged by reference to Y . We end up with the following minimization problem in wavelet coordinates for the case of Dirichlet boundary control. (DCP) For given data
for v ∈ Y now the same as in the previous section, where all reference to the space H is to be exchanged by reference to Y . We end up with the following minimization problem in wavelet coordinates for the case of Dirichlet boundary control. (DCP) For given data  ,
,  , and weight parameter ω > 0, minimize the quadratic functional
, and weight parameter ω > 0, minimize the quadratic functional
over  subject to the linear constraints (2.217),
subject to the linear constraints (2.217),
The corresponding Karush-Kuhn-Tucker conditions can be derived by the same variational principles as in the previous section by defining a Lagrangian in terms of the functional \(\check {\mathbf {J}}(\mathbf {y},\mathbf {u})\) and appending the constraints (2.198) with the help of additional Lagrange multipliers (z, μ)T, see [53]. We obtain in this case a system of coupled saddle point problems
Again, the first system appearing here, the primal system, are just the constraints (2.198) while (2.95) will be referred to as the dual or adjoint system. The specific form of the right hand side of the dual system emerges from the particular formulation of the minimization functional (2.218). The (here trivial) equation (2.219c) stems from measuring u just in ℓ2, representing measuring the control in its natural trace norm. Instead of replacing μ by u in (2.95) and trying to solve the resulting equations, (2.219c) will be essential to devise an inexact gradient scheme. In fact, since L in (2.198) is an invertible operator, we can rewrite \(\check {\mathbf {J}} (\mathbf {y},\mathbf {u})\) by formally inverting (2.198) as a functional of u, that is, \(\mathbf {J}(\mathbf {u}):= \check {\mathbf {J}} (\mathbf {y}(\mathbf {u}),\mathbf {u})\) as above. The following result will be very useful for the design of the outer–inner iterative solvers
Proposition 8
The first variation of J satisfies
where (u, μ) are part of the solution of (2.219). Moreover, J is convex so that a unique minimizer exists.
Hence, Eq. (2.219c) is just δJ(u) = 0. For a unified treatment below of both control problems considered in these notes, it will be useful to rewrite (2.219c) like in (2.214) as a condensed equation for the control u alone. We formally invert (2.217) and (2.219b) and obtain
with the abbreviations

and

Proposition 9
The vector u as part of the solution vector (y, p, z, μ, u) of (2.219) coincides with the unique solution u of the condensed equations (2.221).
2.6 Iterative Solution
Each of the four problem classes discussed above lead to the problem to finally solve a system
or, equivalently, a linear system
where M : ℓ2 → ℓ2 is a (possibly infinite) symmetric positive definite matrix satisfying
for some constants 0 < cM ≤ CM < ∞ and where b ∈ ℓ2 is some given right hand side.
A simple gradient method for solving (2.224) is
with some initial guess q0. In all of the previously considered situations, it has been asserted that there exists a fixed parameter α, depending on bounds for the second variation of J, such that (2.227) converges and reduces the error in each step by at least a fixed factor ρ < 1, i.e.,
where ρ is determined by
Hence, the scheme (2.227) is a convergent iteration for the possibly infinite system (2.225). Next we will need to discuss how to reduce the infinite systems to computable finite versions.
2.6.1 Finite Systems on Uniform Grids
Let us first consider finite-dimensional trial spaces with respect to uniform discretizations. For each of the Hilbert spaces H, this means in the wavelet setting to pick the index set of all indices up to some highest refinement level J, i.e.,

satisfying  . The representation of operators is then built as in Sect. 2.4.3 with respect to this truncated index set which corresponds to deleting all rows and columns that refer to indices λ such that |λ| > J, and correspondingly for functions. There is by construction also a coarsest level of resolution denoted by j0.
. The representation of operators is then built as in Sect. 2.4.3 with respect to this truncated index set which corresponds to deleting all rows and columns that refer to indices λ such that |λ| > J, and correspondingly for functions. There is by construction also a coarsest level of resolution denoted by j0.
Computationally the representation of operators according to (2.111) is in the case of uniform grids always realized as follows. First, the operator is set up in terms of the generator basis on the finest level J. This generator basis simply consists of tensor products of B-Splines, or linear combinations of these near the boundaries. The representation of an operator in the wavelet basis is then achieved by applying the Fast Wavelet Transform (FWT) which needs \({\mathscr {O}}(N_{J,H})\) arithmetic operations and is therefore asymptotically optimal, see, e.g., [24, 34, 51] and Sect. 2.4.4.
In order not to overburden the notation, let in this subsection the resulting system for N = NJ,H unknowns again be denoted by
where now \(\mathbf {M}:\mathbb {R}^N\to \mathbb {R}^N\) is a symmetric positive definite matrix satisfying (2.226) on \(\mathbb {R}^N\). It will be convenient to abbreviate the residual using an approximation \(\tilde {\mathbf {q}}\) to q for (2.229) as

We will employ a basic conjugate gradient method that iteratively computes an approximate solution qK to (2.229) with given initial vector q0 and given tolerance ε > 0 such that

where K denotes the number of iterations used. Later we specify ε depending on the discretization for which (2.229) is set up. The following scheme CG contains a routine App(ηk, M, dk) which in view of the problem classes discussed above is to have the property that it approximately computes the product Mdk up to a tolerance ηk = ηk(ε) depending on ε, i.e., the output mk of App(ηk, M, dk) satisfies
For the cases where M = A, this is simply the matrix-vector multiplication Mdk. For the situations where M may involve the solution of an additional system, this multiplication will be only approximative. The routine is as follows.
CG [ε, q0, M, b] →qK
-
(i)
Set d0 := b −Mq0 and r0 := −d0. Let k = 0.
-
(ii)
While ∥rk∥ > ε
$$\displaystyle \begin{aligned} \begin{array}{lllrrl} {\mathbf{m}}_k &:=& \mathbf{App}(\eta_k({\varepsilon}), \mathbf{M}, {\mathbf{d}}_k) \\ {} \alpha_k &:=& \displaystyle\frac{({\mathbf{r}}_{k})^T {\mathbf{r}}_{k}}{({\mathbf{d}}_k)^T {\mathbf{m}}_k} &\qquad {\mathbf{q}}_{k+1} &:=& {\mathbf{q}}_k +\alpha_k {\mathbf{d}}_k \\ {} {\mathbf{r}}_{k+1} &:=& {\mathbf{r}}_k +\alpha_k {\mathbf{m}}_k &\qquad \beta_k &:=& \displaystyle\frac{({\mathbf{r}}_{k+1})^T {\mathbf{r}}_{k+1}}{({\mathbf{r}}_k)^T {\mathbf{r}}_k} \\ {} {\mathbf{d}}_{k+1} &:=& -{\mathbf{r}}_{k+1} + \beta_k {\mathbf{d}}_k\\ {} k &:=& k+1 \end{array} \end{aligned} $$(2.233) -
(iii)
Set K := k − 1.
Let us briefly discuss in the case M = A that the final iterate qK indeed satisfies (2.231). From the newly computed iterate qk+1 = qk + αkdk it follows by applying M on both sides that Mqk+1 −b = Mqk −b + αkMdk which is the same as Resd(qk+1) = RESD(qk) + αkMdk. By the initialization for rk used above, this in turn is the updating term for rk, hence, rk = RESD(qk). After the stopping criterion based on rk is met, the final iterate qK observes (2.231).
The routine CG computes the residual up to the stopping criterion ε. From the residual, we can in view of (2.226) estimate the error in the solution as
that is, it may deviate from the norm of the residual from a factor proportional to the smallest eigenvalue of M.
Distributed Control
Let us now apply the solution scheme to the situation from Sect. 2.5.3 where Q now involves the inversion of finite-dimensional systems (2.207a) and (2.207b). The material in the remainder of this subsection is essentially contained in [12].
We begin with a specification of the approximate computation of the right hand side b which also contains applications of A−1.
RHS [ζ, A, f, y∗] →bζ
-
(i)
CG \([\frac {c_{\mathbf {A}}}{2C} \frac {c_{\mathbf {A}}}{C^2 C_0^2} \zeta , \mathbf {0}, \mathbf {A}, \mathbf {f}] \to {\mathbf {b}}_1\)
-
(ii)
CG \([\frac {c_{\mathbf {A}}}{2C} \zeta , \mathbf {0}, {\mathbf {A}}^T, - {\mathbf {D}}_{{\mathscr {Z}}}^{-1} \mathbf {R} {\mathbf {D}}_{{\mathscr {Z}}}^{-1} ({\mathbf {b}}_1 - {\mathbf {y}}_*) ] \to {\mathbf {b}}_2\)
-
(iii)
\({\mathbf {b}}_\zeta := {\mathbf {D}}_H^{-1} {\mathbf {b}}_2\).
The tolerances used within the two conjugate gradient methods depend on the constants cA, C, C0 from (2.46), (2.196) and (2.104), respectively. Since the additional factor cA(CC0)−2 in the stopping criterion in step (i) in comparison to step (ii) is in general smaller than one, this means that the primal system needs to be solved more accurately than the adjoint system in step (ii).
Proposition 10
The result bζ of RHS [ζ, A, f, y∗] satisfies
Proof
Recalling the definition (2.212) of b, step (iii) and step (ii) yield
Employing the upper bounds for \({\mathbf {D}}_{{\mathscr {Z}}}^{-1}\) and R, we arrive at

Accordingly, an approximation mη to the matrix-vector product Qd is the output of the following routine App.
App [η, Q, d] →mη
-
(i)
CG \([\frac {c_{\mathbf {A}}}{3C} \frac {c_{\mathbf {A}}}{C^2 C_0^2} \eta , \mathbf {0}, \mathbf {A}, \mathbf {f} + {\mathbf {D}}_H^{-1}\mathbf {d}] \to {\mathbf {y}}_\eta \)
-
(ii)
CG \([\frac {c_{\mathbf {A}}}{3C} \eta , \mathbf {0}, {\mathbf {A}}^T, -{\mathbf {D}}_{{\mathscr {Z}}}^{-1} \mathbf {R} {\mathbf {D}}_Z^{-1} ({\mathbf {y}}_\eta - {\mathbf {y}}_*)] \to {\mathbf {p}}_\eta \)
-
(iii)
\({\mathbf {m}}_\eta := {\mathbf {g}}_{\eta /3} + \omega {\mathbf {R}}^{-1} \mathbf {d} - {\mathbf {D}}_H^{-1} {\mathbf {p}}_\eta \).
The choice of the tolerances for the interior application of CG in steps (i) and (ii) will become clear from the following result.
Proposition 11
The result mη of App[η, Q, d] satisfies
Proof
Denote by yd the exact solution of (2.207a) with d in place of u on the right hand side, and by pd the exact solution of (2.207b) with yd on the right hand side. Then we deduce from step (iii) and (2.216) combined with (2.104) and (2.196)
Denote by \(\hat {\mathbf {p}}\) the exact solution of (2.207b) with yη on the right hand side. Then we have \({\mathbf {p}}_{\mathbf {d}} -\hat {\mathbf {p}} = -{\mathbf {A}}^{-T} {\mathbf {D}}_Z^{-1} \mathbf {R} {\mathbf {D}}_Z^{-1}({\mathbf {y}}_{\mathbf {d}} - {\mathbf {y}}_\eta )\). It follows by (2.46), (2.104) and (2.196) that
where the last estimate follows by the choice of the threshold in step (i). Finally, the combination (2.239) and (2.240) together with (2.235) and the stopping criterion in step (ii) readily confirms that
□
The effect of perturbed applications of M in CG and more general Krylov subspace schemes with respect to convergence has been investigated in a numerical linear algebra context for a given linear system (2.229) in several papers, see, e.g., [70]. Here we have chosen the ηi to be proportional to the outer accuracy ε incorporating a safety factor accounting for the values of βi and ∥ri∥.
Finally, we can formulate a full nested iteration strategy for finite systems (2.207) on uniform grids which employs outer and inner CG routines as follows. The scheme starts at the coarsest level of resolution j0 with some initial guess \({\mathbf {u}}^{j_0}_0\) and successively solves (2.214) with respect to each level j until the norm of the current residual is below the discretization error on that level.
In wavelet coordinates, ∥⋅∥ corresponds to the energy norm. If we employ as in [12] on the primal side for approximation linear combinations of B-splines of order d (degree d − 1, see Sect. 2.2.1), the discretization error is for smooth solutions expected to be proportional to 2−(d−1)j (compare (2.15)). Then the refinement level is successively increased until on the finest level J a prescribed tolerance proportional to the discretization error 2−(d−1)J is met. In the following, superscripts on vectors denote the refinement level on which this term is computed. The given data \({\mathbf {y}}_*^j\), fj are supposed to be accessible on all levels. On the coarsest level, the solution of (2.214) is computed exactly up to double precision by QR decomposition. Subsequently, the results from level j are prolongated onto the next higher level j + 1. Using wavelets, this is accomplished by simply adding zeros: wavelet coordinates have the character of differences, this prolongation corresponds to the exact representation in higher resolution wavelet coordinates. The resulting Nested-Iteration-Incomplete-Conjugate-Gradient Algorithm is the following.
NEICG [J] →uJ
-
(i)
Initialization for coarsest level j := j0
-
(1)
Compute right hand side \({\mathbf {g}}^{j_0}=({\mathbf {Z}}^T\mathbf {G})^{j_0}\) by QR decomposition using (2.209).
-
(2)
Compute solution \({\mathbf {u}}^{j_0}\) of ( 2.214 ) by QR decomposition.
-
(1)
-
(ii)
While j < J
-
(1)
Prolongate \({\mathbf {u}}^{j} \to {\mathbf {u}}^{j+1}_0\) by adding zeros, set j := j + 1.
-
(2)
Compute right hand side using RHS \([2^{-(d-1)j}, \mathbf {A}, {\mathbf {f}}^j, {\mathbf {y}}_*^j] \to {\mathbf {g}}^j\).
-
(3)
Compute solution of (2.214) using CG \([2^{-(d-1)j}, {\mathbf {u}}^j_0, \mathbf {Q},{\mathbf {g}}^j]\to {\mathbf {u}}^j\).
-
(1)
Recall that step (ii.3) requires multiple calls of App[η, Q, d], which in turn invokes both CG[…, A, …] as well as CG[…, AT, …] in each application.
On account of (2.46) and (2.215), finite versions of the system matrices A and Q have uniformly bounded condition numbers, entailing that each CG routine employed in the process reduces the error by a fixed rate ρ < 1 in each iteration step. Let NJ ∼ 2nJ be the total number of unknowns (for yJ, uJ and pJ) on the highest level J. Employing the CG method only on the highest level, one needs \(\mathscr {O}(J)=\mathscr { O}(\log {\varepsilon })\) iterations to achieve the prescribed discretization error accuracy εJ = 2−(d−1)J. As each application of A and Q requires \(\mathscr {O}(N_J)\) operations, the solution of (2.214) by CG only on the finest level requires \(\mathscr {O}(J\,N_J)\) arithmetic operations.
Theorem 7 ([12])
If the residual (2.216) is computed up to discretization error proportional to 2−(d−1)j on each level j and the corresponding solutions are taken as initial guesses for the next higher level, NEICG is an asymptotically optimal method in the sense that it provides the solution uJ up to discretization error on level J in an overall amount of \({{\mathscr {O}}}(N_J)\) arithmetic operations.
Proof
In the above notation, nested iteration allows one to get rid of the factor J in the total amount of operations. Starting with the exact solution on the coarsest level j0, in view of the uniformly bounded condition numbers of A and Q, one needs only a fixed amount of iterations to reduce the error up to discretization error accuracy εj = 2−(d−1)j on each subsequent level j, taking the solution from the previous level as initial guess. Thus, on each level, one needs \(\mathscr {O}(N_j)\) operations to realize discretization error accuracy. Since the spaces are nested and the number of unknowns on each level grows like Nj ∼ 2nj, by a geometric series argument the total number of arithmetic operations stays proportional to \(\mathscr {O}(N_J)\). 
Numerical Examples
As an illustration of the ingredients for a distributed control problem, we consider the following example taken from [12] with the Helmholtz operator in (2.39) (a = I, c = 1) and homogeneous Dirichlet boundary condition. A non-constant right hand side \(f(x):= 1 + 2.3 \exp (-15|x-\frac {1}{2}|)\) is chosen, and the target state is set to a constant y∗≡ 1. We first investigate the role the different norms \(\|\cdot \|{ }_{{\mathscr {Z}}}\) and \(\|\cdot \|{ }_{{\mathscr {U}}}\) in (2.74), encoded in the diagonal matrices \({\mathbf {D}}_{{\mathscr {Z}}},{\mathbf {D}}_H\) from (2.195), have on the solution. We see in Fig. 2.3 for the choice \({\mathscr {U}}=L_2\) and \({\mathscr {Z}}=H^s(0,1)\) for different values of s varying between 0 and 1 the solution y (left) and the corresponding control u (right) for fixed weight ω = 1. As s is increased, a stronger tendency of y towards the prescribed state y∗≡ 1 can be observed which is, however, deterred from reaching this state by the homogeneous boundary conditions. Extensive studies of this type can be found in [11, 12].
As an example displaying the performance of the proposed fully iterative scheme NEICG in two spatial dimensions, Table 2.6 from [12] is included. This is an example of a control problem for the Helmholtz operator with Neumann boundary conditions. The stopping criterion for the outer iteration (relative to ∥⋅∥ which corresponds to the energy norm) on level j is chosen to be proportional to 2−j. The second column displays the final value of the residual of the outer CG scheme on this level, i.e., \(\|{\mathbf {r}}_K^j\| = \| \text{RESD}({\mathbf {u}}_K^j)\|\). The next three columns show the number of outer CG iterations (#O) for Q according to the App scheme followed by the maximum number of inner iterations for the primal system (#E), the adjoint system (#A) and the design equation (#R). We see very well the effect of the uniformly bounded condition numbers of the involved operators. The last columns display different versions of the actual error in the state y and the control u when compared to the fine grid solution (R denotes restriction of the fine grid solution to the actual grid, and P prolongation). Here we can see the effect of the constants appearing in (2.234), that is, the error is very well controlled via the residual. More results for up to three spatial dimensions can be found in [11, 12].
Dirichlet Boundary Control
For the system of saddle point problems (2.219) arising from the control problem with Dirichlet boundary control in Sect. 2.3.6, also a fully iterative algorithm NEICG can be designed along the above lines. Again the design equation (2.219c) for u serves as the equation for which a basic iterative scheme (2.227) can be posed. Of course, the CG method for A then has to be replaced by a convergent iterative scheme for saddle point operators L like Uzawa’s algorithm. Also the discretization has to be chosen such that the LBB condition is satisfied, see Sect. 2.5.2. Details can be found in [53]. Alternatively, since L has a uniformly bounded condition number, the CG scheme can, in principle, also be applied to LTL. The performance of wavelet schemes on uniform grids for such systems of saddle point problems arising from optimal control is currently under investigation [62].
Numerical Example
For illustration of the choice of different norms for the Dirichlet boundary control problem, consider the following example taken from [62]. Here we actually have the situation of controlling the system through the control boundary Γ on the right hand side of Fig. 2.4 while a prescribed state y∗≡ 1 on the observation boundary Γy opposite the control boundary is to be achieved. The right hand side is chosen as constant f ≡ 1, and ω = 1. Each layer in Fig. 2.4 corresponds to the state y for different values of s when the observation term is measured in Hs(Γy), that is, the objective functional (2.82) contains a term \(\|y-y_*\|{ }_{H^s(\varGamma _y)}^2\) for s = 1∕10, 2∕10, 3∕10, 4∕10, 5∕10, 7∕10, 9∕10 from bottom to top. We see that as the smoothness index s for the observation increases, the state moves towards the target state at the observation boundary.
2.6.2 Adaptive Schemes
In case of the appearance of singularities caused by the data or the domain, a prescribed accuracy may require discretizations with respect to uniform grids to spend a large amount of degrees of freedom in areas where the solution is actually smooth. Hence, although the above numerical scheme NEICG is of optimal linear complexity, the degrees of freedom are not implanted in an optimal way. In these situations, one expects adaptive schemes to work favourably which judiciously place degrees of freedom where singularities occur. Thus, the guiding line for adaptive schemes is to reduce the total amount of degrees of freedom when compared to discretizations on a uniform grid. This does not mean that the previous investigations with respect to uniform discretizations are dispensable. In fact, the above results on conditioning carry over to the adaptive case, the solvers are still linear in the amount of arithmetic operations and, in particular, one expects to recover the uniform situation when the solutions are smooth. Much on adaptivity for variational problems and the relation to nonlinear approximation can be found in [26].
The starting point for adaptive wavelet schemes systematically derived for variational problems in [19,20,21] is the infinite formulation in wavelet coordinates as derived for the different problem classes in Sect. 2.5. These algorithms have been proven to be optimal in the sense that they match the optimal work/ accuracy rate of the wavelet-best N-term approximation, a concept which has been introduced in [19]. The schemes start out with formulating algorithmic ingredients which are then step by step reduced to computable quantities. We follow in this section the material for the distributed control problem from [29]. An extension to Dirichlet control problem involving saddle point problems can be found in [54]. It should be pointed out that the theory is neither confined to symmetric A nor to the positive definite case.
Algorithmic Ingredients
We start out again with a very simple iterative scheme for the design equation. In view of (2.215) and the fact that Q is positive definite, there exists a fixed positive parameter α such that in the Richardson iteration (which is a special case of a gradient method)
the error is reduced in each step by at least a factor
where u is the exact solution of (2.214). As the involved system is still infinite, we aim at carrying out this iteration approximately with dynamically updated accuracy tolerances.
The central idea of the wavelet-based adaptive schemes is to start from the infinite system in wavelet coordinates (2.207) and step by step reduce the routines to computable versions of applying the infinite matrix Q and the evaluation of the right hand side g of (2.214) involving the inversion of A. The main conceptual tools from [19,20,21] are the following.
We first assume that we have a routine at our disposal with the following property. Later it will be shown how to realize this routine in the concrete case.
Res [η, Q, g, v] →rη determines for a given tolerance η > 0 a finitely supported sequence rη satisfying
The schemes considered below will also contain the following routine.
Coarse [η, w] →wη determines for any finitely supported input vector w a vector wη with smallest possible support such that
This ingredient will eventually play a crucial role in controlling the complexity of the scheme although its role is not yet apparent at this stage. A detailed description of Coarse can be found in [19]. The basic idea is to first sort the entries of w by size. Then one subtracts squares of their moduli until the sum reaches η2, starting from the smallest entry. A quasi-sorting based on binary binning can be shown to avoid the logarithmic term in the sorting procedure at the expense of the resulting support size being at most a fixed constant of the minimal size, see [4].
Next a perturbed iteration is designed which converges in the following sense: for every target accuracy ε, the scheme produces after finitely many steps a finitely supported approximate solution with accuracy ε. To obtain a correctly balanced interplay between the routines Res and Coarse, we need the following control parameter. Given (an estimate of) the reduction rate ρ and the step size parameter α from (2.242), let K denote the minimal integer ℓ for which \(\rho ^{\ell -1}(\alpha \ell +\rho )\le \textstyle \frac {1}{10}.\)
Denoting in the following always by u the exact solution of (2.214), a perturbed version of (2.241) for a fixed target accuracy ε > 0 is the following.
Solve \(\,[{\varepsilon },\mathbf {Q},\mathbf {g}, \overline {\mathbf {q}}^0,{\varepsilon }_0 ]\to \overline {\mathbf {q}}_{\varepsilon }\)
-
(i)
Given an initial guess \(\overline {\mathbf {q}}^0\) and an error bound \(\|\mathbf {q}-\overline {\mathbf {q}}^0\|\leq {\varepsilon }_0\); set j = 0.
-
(ii)
If εj ≤ ε, stop and set \(\overline {\mathbf {q}}_{\varepsilon }:= \overline {\mathbf {q}}^j\). Otherwise set \({\mathbf {v}}^0:=\overline {\mathbf {q}}^j\).
-
(ii.1)
For k = 0, …, K − 1 compute Res [ρkεj, Q, g, vk] →rk and
$$\displaystyle \begin{aligned} {\mathbf{v}}^{k+1}:={\mathbf{v}}^k+\alpha {\mathbf{r}}^k. \end{aligned} $$(2.246) -
(ii.2)
Apply Coarse \(\,[\frac {2}{5} {\varepsilon }_j, {\mathbf {v}}^K]\to \overline {\mathbf {q}}^{j+1}\); set \({\varepsilon }_{j+1}:=\frac {1}{2}{\varepsilon }_j\), j + 1 → j and go to (ii).
-
(ii.1)
In the case that no particular initial guess is known, we initialize \(\overline {\mathbf {q}}^0= \mathbf {0}\), set \({\varepsilon }_0 := c_{\mathbf {Q}}^{-1}\|\mathbf {g}\|\) and briefly write then Solve \(\,[{\varepsilon },\mathbf {Q},\mathbf {g}]\to \overline {\mathbf {q}}_{\varepsilon }\).
In a straightforward manner, perturbation arguments yield the convergence of this algorithm [20, 21].
Proposition 12
The iterates \(\overline {\mathbf {q}}^j\) generated by Solve [ε, Q, g] satisfy
where εj = 2−jε0.
In order to derive appropriate numerical realizations of Solve, recall that (2.214) is equivalent to the KKT conditions (2.207). Although the matrix A is always assumed to be symmetric here, the distinction between the system matrices for the primal and the dual system, A and AT, may be helpful.
The strategy for approximating in each step the residual g −Quk, that is, realization of the routine Res for the problem (2.214), is based upon the result stated in Proposition 7. In turn, this requires solving the two auxiliary systems in (2.207). Since the residual only has to be approximated, these systems will have to be solved only approximately. These approximate solutions, in turn, will be provided again by employing Solve but this time with respect to suitable residual schemes tailored to the systems in (2.207). In our special case, the matrix A is symmetric positive definite, and the choice of wavelet bases ensures the validity of (2.46). Thus, (2.242) holds for A and AT so that the scheme Solve can indeed be invoked. Although we conceptually use the fact that a gradient iteration for the reduced problem (2.214) reduces the error for u in each step by a fixed amount, employing (2.207) for the evaluation of the residuals will generate as byproducts approximate solutions to the exact solution triple (y, p, u) of (2.207). Under this hypothesis, we formulate next the ingredients for suitable versions SolvePRM and SolveADJ of Solve for the systems in (2.207). Specifically, this requires identifying residual routines ResPRM and ResADJ for the systems SolvePRM and SolveADJ. The main task in both cases is to apply the operators A, AT, \({\mathbf {D}}_H^{-1}\) and \({\mathbf {R}}^{1/2}{\mathbf {D}}_{{\mathscr {Z}}}^{-1}\). Again we assume for the moment that routines for the application of these operators are available, i.e., that for any \(\mathbf {L} \in \{\mathbf {A},{\mathbf {A}}^T, {\mathbf {D}}_H^{-1},{\mathbf {R}}^{1/2}{\mathbf {D}}_{{\mathscr {Z}}}^{-1}\}\) we have a scheme at our disposal with the following property.
Apply [η, L, v] →wη determines for any finitely supported input vector v and any tolerance η > 0 a finitely supported output wη which satisfies
The scheme SolvePRM for the first system in (2.207) is then defined by

where \(\overline {\mathbf {y}}^0\) is an initial guess for the solution y of \(\mathbf {A}\mathbf {y} = \mathbf {f} + {\mathbf {D}}_H^{-1} \mathbf {v}\) with accuracy ε0. The scheme Res for Step (ii) in Solve is in this case realized by a new routine ResPRM defined as follows.
ResPRM \(\,[\eta ,\mathbf {A}, {\mathbf {D}}_H^{-1} ,\mathbf {f},\mathbf {v},\overline {\mathbf {y}}]\to {\mathbf {r}}_\eta \) determines for any positive tolerance η, a given finitely supported v and any finitely supported input \(\overline {\mathbf {y}}\) a finitely supported approximate residual rη satisfying (2.244),
as follows:
-
(i)
Apply \([\frac {1}{3}\eta ,\mathbf {A},\overline {\mathbf {y}}]\to {\mathbf {w}}_\eta \);
-
(ii)
Coarse \([\frac {1}{3}\eta ,\mathbf {f}]\to {\mathbf {f}}_\eta \);
-
(iii)
Apply \([\frac {1}{3}\eta , {\mathbf {D}}_H^{-1},\mathbf {v}]\to {\mathbf {z}}_\eta \);
-
(iv)
set rη := fη + zη −wη.
By triangle inequality, one can for ResPRM and the subsequent variants of Res show that indeed (2.249) or (2.244) holds.
Similarly, one needs a version of Solve for the approximate solution of the second system (2.207b), \({\mathbf {A}}^T \mathbf {p} = - {\mathbf {D}}_{{\mathscr {Z}}}^{-1}\mathbf {R}{\mathbf {D}}_{{\mathscr {Z}}}^{-1}(\mathbf {y} - {\mathbf {y}}_*)\), which depends on an approximate solution \(\overline {\mathbf {y}}\) of the primal system and possibly on some initial guess \(\overline {\mathbf {p}}^0\) with accuracy ε0. Here we set

As usual we assume that the data f, y∗ are approximated in a preprocessing step with sufficient accuracy. A suitable residual approximation scheme ResADJ for Step (ii) of this version of Solve is the following where the main issue is the approximate evaluation of the right hand side.
ResADJ \(\,[\eta ,\mathbf {A}, {\mathbf {D}}_{{\mathscr {Z}}}^{-1},{\mathbf {y}}_*,\overline {\mathbf {y}},\overline {\mathbf {p}}]\to {\mathbf {r}}_\eta \) determines for any positive tolerance η, given finitely supported data \(\overline {\mathbf {y}},{\mathbf {y}}_*\)and any finitely supported input \(\overline {\mathbf {p}}\) an approximate residual rη satisfying (2.244), i.e.,
as follows:
-
(i)
Apply \([\frac {1}{3}\eta ,{\mathbf {A}}^T,\overline {\mathbf {p}}]\to {\mathbf {w}}_\eta \);
-
(ii)
Apply \([\frac {1}{6}\,\eta , {\mathbf {D}}_{{\mathscr {Z}}}^{-1},\overline {\mathbf {y}}]\to {\mathbf {z}}_\eta \); Coarse \([\frac {1}{6}\, \eta ,{\mathbf {y}}_*]\to ({\mathbf {y}}_*)_\eta \); set dη := (yZ)η −zη; Apply \([\frac {1}{6}\eta , {\mathbf {D}}_{{\mathscr {Z}}}^{-1} ,{\mathbf {d}}_\eta ]\to \hat {\mathbf {v}}_\eta \); Apply \([\frac {1}{6}\eta , \mathbf {R} ,\hat {\mathbf {v}}_\eta ]\to {\mathbf {v}}_\eta \);
-
(iii)
set rη := vη −wη.
Finally, we can define the residual scheme for the version of Solve applied to (2.214). We shall refer to this specification as SolveDCP with corresponding residual scheme is ResDCP. Since the scheme is based on Proposition 7, it will involve several parameters stemming from the auxiliary systems (2.207).
ResDCP \([\eta ,\mathbf {Q},\mathbf {g},\tilde {\mathbf {y}},\delta _y,\tilde {\mathbf {p}},\delta _p,\mathbf {v},\delta _v]\to ({\mathbf {r}}_\eta ,\tilde {\mathbf {y}},\delta _y, \tilde {\mathbf {p}},\delta _p)\) determines for any approximate solution triple \((\tilde {\mathbf {y}},\tilde {\mathbf {p}},\mathbf {v})\) of the system (2.207) satisfying
an approximate residual rη such that
Moreover, the initial approximations \(\tilde {\mathbf {y}},\tilde {\mathbf {p}}\) are overwritten by new approximations \(\tilde {\mathbf {y}},\tilde {\mathbf {p}}\) satisfying (2.251) with new bounds δy and δp defined in (2.253) below, as follows:
-
(i)
SolvePRM \([\frac {1}{3} c_{\mathbf {A}}\,\eta ,\mathbf {A}, {\mathbf {D}}_H^{-1},\mathbf {f},\mathbf {v},\tilde {\mathbf {y}},\delta _y ]\to {\mathbf {y}}_\eta \);
-
(ii)
SolveADJ \([\frac {1}{3}{\eta },\mathbf {A}, {\mathbf {D}}_{{\mathscr {Z}}}^{-1},{\mathbf {y}}_*,{\mathbf {y}}_\eta ,\tilde {\mathbf {p}},\delta _p]\to {\mathbf {p}}_\eta \);
-
(iii)
Apply \([\frac {1}{3}{\eta }, {\mathbf {D}}_H^{-1},{\mathbf {p}}_\eta ]\to {\mathbf {q}}_\eta \); set rη := qη − ωv;
-
(iv)
set \( \xi _y := c_{\mathbf {A}}^{-1}\, \delta _v + \textstyle \frac {1}{3} c_{\mathbf {A}}\eta , ~\xi _p:= c_{\mathbf {A}}^{-2}\,\delta _v +\frac {2}{3}\eta \); replace \(\tilde {\mathbf {y}},\delta _y\) and \(\tilde {\mathbf {p}},\delta _p\) by
$$\displaystyle \begin{aligned} \begin{array}{rll} \tilde{\mathbf{y}} &:=\mbox{\text{COARSE}}[4\xi_y,{\mathbf{y}}_\eta],~~~ & \delta_y :=5\,\xi_y,\\ \tilde{\mathbf{p}} & :=\mbox{\text{COARSE}}[4\xi_p,{\mathbf{p}}_\eta],~~~& \delta_p :=5\,\xi_p. \end{array}\end{aligned} $$(2.253)
Step (iv) already indicates the conditions on the tolerance η and the accuracy bound δv under which the new error bounds in (2.253) are actually tighter. The precise relation between η and δv in the context of SolveDCP is not apparent yet and emerges as well as the claimed estimates (2.252) and (2.253) from the complexity analysis in [29].
Finally, the scheme SolveDCP attains the following form with the error reduction factor ρ from (2.242) and α from (2.241).
Solve DCP \(\,[{\varepsilon },\mathbf {Q},\mathbf {g}]\to \overline {\mathbf {u}}_{\varepsilon } \)
-
(i)
Let \(\overline {\mathbf {q}}^0:= \mathbf {0}\) and \({\varepsilon }_0:= c_{\mathbf {A}}^{-1} (\|{\mathbf {y}}_Z\| + c_{\mathbf {A}}^{-1} \|\mathbf {f}\|)\).Let \(\tilde {\mathbf {y}}:=\mathbf {0}\), \(\tilde {\mathbf {p}}:= \mathbf {0}\) and set j = 0.Define \(\delta _y:=\delta _{y,0}:= c_{\mathbf {A}}^{-1} (\|\mathbf {f}\| + {\varepsilon }_0)\) and \(\delta _p:=\delta _{p,0}:= c_{\mathbf {A}}^{-1} (\delta _{y,0} + \|{\mathbf {y}}_Z\|)\).
-
(ii)
If εj ≤ ε, stop and set \(\overline {\mathbf {u}}_{\varepsilon }:= \overline {\mathbf {u}}^j\), \(\overline {\mathbf {y}}_{\varepsilon }=\tilde {\mathbf {y}}\), \(\overline {\mathbf {p}}_{\varepsilon }=\tilde {\mathbf {p}}\).Otherwise set \({\mathbf {v}}^0:=\overline {\mathbf {u}}^j\).
-
(ii.1)
For k = 0, …, K − 1, compute
-
Res
 \(\,[\rho ^k {\varepsilon }_j, \mathbf {Q}, \mathbf {g}, \tilde {\mathbf {y}},\delta _y, \tilde {\mathbf {p}},\delta _p,{\mathbf {v}}^k, \delta _k]\to ({\mathbf {r}}^k,\tilde {\mathbf {y}},\delta _y,\tilde {\mathbf {p}},\delta _p) \),
\(\,[\rho ^k {\varepsilon }_j, \mathbf {Q}, \mathbf {g}, \tilde {\mathbf {y}},\delta _y, \tilde {\mathbf {p}},\delta _p,{\mathbf {v}}^k, \delta _k]\to ({\mathbf {r}}^k,\tilde {\mathbf {y}},\delta _y,\tilde {\mathbf {p}},\delta _p) \), -
where δ0 := εj and δk := ρk−1(αk + ρ)εj;
-
set
$$\displaystyle \begin{aligned} {\mathbf{v}}^{k+1}:={\mathbf{v}}^k+\alpha {\mathbf{r}}^k.\end{aligned} $$(2.254)
-
(ii.2)
Coarse \(\,[\frac {2}{5} {\varepsilon }_j, {\mathbf {v}}^K]\to \overline {\mathbf {u}}^{j+1}\); set \({\varepsilon }_{j+1}:=\frac {1}{2}{\varepsilon }_j\), j + 1 → j and go to (ii).
By overwriting \(\tilde {\mathbf {y}}\), \(\tilde {\mathbf {p}}\) at the last stage prior to the termination of SolveDCP one has δv ≤ ε, η ≤ ε, so that the following fact is an immediate consequence of (2.253).
Proposition 13
The outputs \(\overline {\mathbf {y}}_{\varepsilon }\) and \(\overline {\mathbf {p}}_{\varepsilon }\) produced by SolveDCP in addition to uε are approximations to the exact solutions y, p of (2.207) satisfying
Complexity Analysis
Proposition 12 states that the routine Solve converges for an arbitrary given accuracy provided that there is a routine Res satisfying the property (2.244). Then we have broken down step by step the necessary ingredients to derive computable versions which satisfy these requirements. What we finally want to show is that the routines are optimal in the sense that they provide the optimal work/accuracy rate in terms of best N-term approximation. The complexity analysis given next also reveals the role of the routine Coarse within the algorithms and the particular choices of the thresholds in Step (iv) of ResDCP.
In order to be able to assess the quality of the adaptive algorithm, the notion of optimality has to be clarified first in the present context.
Definition 1
The scheme Solve has an optimal work/accuracy rate s if the following holds: Whenever the error of best N-term approximation satisfies

then the solution \(\overline {\mathbf {q}}_{\varepsilon }\) is generated by Solve at an expense that also stays proportional to ε−1∕s and in that sense matches the best N-term approximation rate.
Note that this implies that \(\#\mathrm {supp}\,\overline {\mathbf {q}}_{\varepsilon }\) also stays proportional to ε−1∕s. Thus, our benchmark is that whenever the solution of (2.214) can be approximated by N terms at rate s, Solve recovers that rate asymptotically. If q is known, the wavelet-best N-term approximation qN of q is given by picking the N largest terms in modulus from q, of course. However, when q is the (unknown) solution of (2.214) this information is certainly not available.
Since we are here in the framework of sequence spaces ℓ2, the formulation of appropriate criteria for complexity will be based on a characterization of sequences which are sparse in the following sense. We consider sequences v for which the best N-term approximation error decays at a particular rate (Lorentz spaces). That is, for any given threshold 0 < η ≤ 1, the number of terms exceeding that threshold is controlled by some function of this threshold. In particular, set for some 0 < τ < 2

This determines a strict subspace of ℓ2 only when τ < 2. Smaller τ’s indicate sparser sequences. Let Cv for a given \(\mathbf {v}\in \ell _{\tau }^w\) be the smallest constant for which (2.255) holds. Then one has \(|\mathbf {v}|{ }_{\ell _{\tau }^w} := \sup _{n\in \mathbb {N}} n^{1/\tau } v^*_{n} = C_{\mathbf {v}}^{1/\tau },\) where \({\mathbf {v}}^*=(v_n^*)_{n\in \mathbb {N}}\) is a non-decreasing rearrangement of v. Furthermore, \(\|\mathbf {v}\|{ }_{\ell _{\tau }^w} := \|\mathbf {v}\|+ |\mathbf {v}|{ }_{\ell _{\tau }^w}\) is a quasi-norm for \(\ell _{\tau }^w\). Since the continuous embeddings \( \ell _\tau \hookrightarrow \ell _{\tau }^w \hookrightarrow \ell _{\tau + {\varepsilon }} \hookrightarrow \ell _{2}\) hold for τ < τ + ε < 2, \(\ell _{\tau }^w\) is ‘close’ to ℓτ and is therefore called weak ℓτ. The following crucial result connects sequences in \(\ell _{\tau }^w\) to best N-term approximation [19].
Proposition 14
Let positive real numbers s and τ be related by
Then
\(\mathbf {v}\in \ell _{\tau }^w\)
if and only if

The property that an array of wavelet coefficients v belongs to ℓτ is equivalent to the fact that the expansion vTΨH in terms of a wavelet basis ΨH for a Hilbert space H belongs to a certain Besov space which describes a much weaker regularity measure than a Sobolev space of corresponding order, see, e.g., [16, 39]. Thus, Proposition 14 expresses how much loss of regularity can be compensated by judiciously placing the degrees of freedom in a nonlinear way in order to retain a certain optimal order of error decay.
A key criterion for a scheme Solve to exhibit an optimal work/accuracy rate can be formulated through the following property of the respective residual approximation. The routine Res is called τ∗-sparse for some 0 < τ∗ < 2 if the following holds: Whenever the solution q of (2.214) belongs to \(\ell _{\tau }^w\) for some τ∗ < τ < 2, then for any v with finite support the output rη of Res [η, Q, g, v] satisfies

and

where s and τ are related by (2.256), and the number of floating point operations needed to compute rη stays proportional to #supprη.
The analysis in [20] then yields the following result.
Theorem 8
If Res is τ∗-sparse and if the exact solution q of (2.214) belongs to \(\ell _{\tau }^w\) for some τ > τ∗, then for every ε > 0 algorithm Solve [ε, Q, g] produces after finitely many steps an output \(\overline {\mathbf {q}}_{\varepsilon }\) (which, according to Proposition 12, always satisfies \(\|\mathbf {q} - \overline {\mathbf {q}}_{\varepsilon }\| < {\varepsilon }\)) with the following properties: For s and τ related by (2.256), one has

and the number of floating point operations needed to compute \(\overline {\mathbf {q}}_{\varepsilon }\) remains proportional to \(\#{supp} \overline {\mathbf {q}}_{\varepsilon }\).
Hence, τ∗-sparsity of the routine Res implies for Solve asymptotically optimal work/accuracy rates for a certain range of decay rates given by τ∗. We stress that the algorithm itself does not require any a-priori knowledge about the solution such as its actual best N-term approximation rate. Theorem 8 also states that controlling the \(\ell _{\tau }^w\)-norm of the quantities generated in the computations is crucial. This finally explains the role of Coarse in Step (ii.2) of Solve in terms of the following result [19].
Lemma 4
Let \(\mathbf {v}\in \ell _{\tau }^w\) and let w be any finitely supported approximation such that \(\|\mathbf {v} - \mathbf {w}\| \le \frac {1}{5}\eta \) . Then the output w η of Coarse \(\,[\frac {4}{5} \eta , \mathbf {w}]\) satisfies

This can be interpreted as follows. If an error bound for a given finitely supported approximation w is known, a certain coarsening using only knowledge about w produces a new approximation to (the possibly unknown) v which gives rise to a slightly larger error but realizes the optimal relation between support and accuracy up to a uniform constant. In the scheme Solve, this means that by the coarsening step the \(\ell _{\tau }^w\)-norms of the iterates vK are controlled.
It remains to establish that for SolveDCP the corresponding routine ResDCP is τ∗-sparse. The following results from [29] reduce this question to the efficiency of Apply. We say that Apply [⋅, L, ⋅] is τ∗-efficient for some 0 < τ∗ < 2 if for any finitely supported \(\mathbf {v} \in \ell _{\tau }^w\), for 0 < τ∗ < τ < 2, the output wη of Apply [η, L, v] satisfies  and
and  for η → 0. Here the constants depend only on τ as τ → τ∗ and s, τ satisfy (2.256). Moreover, the number of floating point operations needed to compute wη is to remain proportional to #supp wη.
for η → 0. Here the constants depend only on τ as τ → τ∗ and s, τ satisfy (2.256). Moreover, the number of floating point operations needed to compute wη is to remain proportional to #supp wη.
Proposition 15
If the Apply schemes in ResPRM and ResADJ are τ∗-efficient for some τ∗ < 2, then ResDCP is τ∗-sparse whenever there exists a constant C such that \(C\eta \geq \max \,\{\delta _v,\delta _p\}\) and
where v is the current finitely supported input and \(\tilde {\mathbf {y}},\tilde {\mathbf {p}}\) are the initial guesses for the exact solution components (y, p).
Theorem 9
If the Apply schemes appearing in ResPRM and ResADJ are τ∗-efficient for some τ∗ < 2 and the components of the solution (y, p, u) of (2.207) all belong to the respective space \(\ell _{\tau }^w\) for some τ > τ∗, then the approximate solutions yε, pε, uε, produced by SolveDCP for any target accuracy ε, satisfy

and

where the constants only depend on τ when τ approaches τ∗. Moreover, the number of floating point operations required during the execution of SolveDCP remains proportional to the right hand side of (2.260).
Thus, the practical realization of SolveDCP providing optimal work/accuracy rates for a possibly large range of decay rates of the error of best N-term approximation hinges on the availability of τ∗-efficient schemes Apply with possibly small τ∗ for the involved operators.
For the approximate application of wavelet representations of a wide class of operators, including differential operators, one can indeed devise efficient schemes which is a consequence of the cancellation properties (CP) together with the norm equivalences (2.89) for the relevant function spaces. For the example considered above, the τ∗-efficiency of A defined in (2.198) can be shown whenever A is s∗-compressible where τ∗ and s∗ are related by (2.256). One knows that s∗ is the larger the higher the ‘regularity’ of the operator and the order of cancellation properties of the wavelets are. Estimates for s∗ in terms of these quantities for spline wavelets and the above differential operator A can be found in [5]. These were refined and extended to trace operators in [62]. Hence, Theorem 9 guarantees asymptotically optimal complexity bounds for τ > τ∗. This means that the scheme SolveDCP recovers rates of the error of best N-term approximation of order N−s for s < s∗.
When describing the control problem, it has been pointed out that the wavelet framework allows for a flexible choice of norms in the control functional which is reflected by the diagonal matrices \({\mathbf {D}}_{{\mathscr {Z}}}\) and DH in (DCP), (2.203) together with (2.204). The following result states that multiplication by either \({\mathbf {D}}_{{\mathscr {Z}}}^{-1}\) or \({\mathbf {D}}_H^{-1}\) makes a sequence more compressible, that is, they produce a shift in weak ℓτ spaces [29].
Proposition 16
For β > 0, \(\mathbf {p}\in \ell _{\tau }^w\) implies \({\mathbf {D}}^{-\beta }\mathbf {p} \in \ell ^w_{\tau '}\), where \(\frac {1}{\tau '} := \frac {1}{\tau } + \frac {\beta }{d}\).
We can conclude the following. Whatever the sparsity class of the adjoint variable p is, the control u is in view of (2.207c) even sparser. This means also that although the control u may be accurately recovered with relatively few degrees of freedom, the overall solution complexity is in the above case bounded from below by the less sparse auxiliary variable p.
The application of these techniques to control problems constrained by parabolic PDEs can be found in [44]. For an extension of these techniques to control problems involving PDEs with possibly infinite stochastic coefficients which introduce a substantial difficulty, one may consult [57, 58].
References
J.P. Aubin, Applied Functional Analysis, 2nd edn. (Wiley, Hoboken, 2000)
I. Babuška, The finite element method with Lagrange multipliers. Numer. Math. 20, 179–192 (1973)
I. Babuška, The finite element method with penalty. Math. Comput. 27, 221–228 (1973)
A. Barinka, Fast evaluation tools for adaptive wavelet schemes, Ph.D. dissertation, RWTH Aachen, 2004
A. Barinka, T. Barsch, Ph. Charton, A. Cohen, S. Dahlke, W. Dahmen, K. Urban, Adaptive wavelet schemes for elliptic problems — implementation and numerical experiments. SIAM J. Sci. Comput. 23, 910–939 (2001)
S. Bertoluzza, Wavelet stabilization of the Lagrange multiplier method. Numer. Math. 86, 1–28 (2000)
D. Braess, Finite Elements: Theory, Fast Solvers and Applications in Solid Mechanics, 2nd edn. (Cambridge University Press, Cambridge, 2001)
J.H. Bramble, J.E. Pasciak, J. Xu, Parallel multilevel preconditioners. Math. Comput. 55, 1–22 (1990)
F. Brezzi, M. Fortin, Mixed and Hybrid Finite Element Methods (Springer, New York, 1991)
A. Buffa, H. Harbrecht, A. Kunoth, G. Sangalli, Multilevel preconditioning for isogeometric analysis, Comput. Methods Appl. Mech. Eng. 265, 63–70 (2013)
C. Burstedde, Wavelets methods for linear-quadratic, elliptic optimal control problems, Ph.D. dissertation, University of Bonn, Bonn, 2005
C. Burstedde, A. Kunoth, Fast iterative solution of elliptic control problems in wavelet discretizations. J. Comput. Appl. Math. 196(1), 299–319 (2006)
C. Canuto, A. Tabacco, K. Urban, The wavelet element method, part I: construction and analysis. Appl. Comput. Harmon. Anal. 6, 1–52 (1999)
J.M. Carnicer, W. Dahmen, J.M. Peña, Local decomposition of refinable spaces. Appl. Comput. Harmon. Anal. 3, 127–153 (1996)
Z. Ciesielski, T. Figiel, Spline bases in classical function spaces on compact C∞ manifolds: part I and II. Stud. Math. 76, 1–58 and 95–136 (1983)
A. Cohen, Numerical Analysis of Wavelet Methods. Studies in Mathematics and Its Applications, vol. 32 (Elsevier, New York, 2003)
A. Cohen, R. Masson, Adaptive wavelet methods for second order elliptic problems, preconditioning and adaptivity. SIAM J. Sci. Comput. 21, 1006–1026 (1999)
A. Cohen, I. Daubechies, J.-C. Feauveau, Biorthogonal bases of compactly supported wavelets, Commun. Pure Appl. Math. 45, 485–560 (1992)
A. Cohen, W. Dahmen, R. DeVore, Adaptive wavelet methods for elliptic operator equations – convergence rates. Math. Comput. 70, 27–75 (2001)
A. Cohen, W. Dahmen, R. DeVore, Adaptive wavelet methods II – beyond the elliptic case. Found. Comput. Math. 2, 203–245 (2002)
A. Cohen, W. Dahmen, R. DeVore, Adaptive wavelet schemes for nonlinear variational problems. SIAM J. Numer. Anal. 41(5), 1785–1823 (2003)
S. Dahlke, W. Dahmen, K. Urban, Adaptive wavelet methods for saddle point problems — optimal convergence rates. SIAM J. Numer. Anal. 40, 1230–1262 (2002)
W. Dahmen, Stability of multiscale transformations. J. Fourier Anal. Appl. 2, 341–361 (1996)
W. Dahmen, Wavelet and multiscale methods for operator equations. Acta Numer. 6, 55–228 (1997)
W. Dahmen, Wavelet methods for PDEs – some recent developments. J. Comput. Appl. Math. 128, 133–185 (2001)
W. Dahmen, Multiscale and wavelet methods for operator equations, in Multiscale Problems and Methods in Numerical Simulation, ed. by C. Canuto. C.I.M.E. Lecture Notes in Mathematics, vol. 1825 (Springer, Heidelberg, 2003), pp. 31–96
W. Dahmen, A. Kunoth, Multilevel preconditioning. Numer. Math. 63, 315–344 (1992)
W. Dahmen, A. Kunoth, Appending boundary conditions by Lagrange multipliers: analysis of the LBB condition. Numer. Math. 88, 9–42 (2001)
W. Dahmen, A. Kunoth, Adaptive wavelet methods for linear-quadratic elliptic control problems: convergence rates. SIAM J. Control. Optim. 43(5), 1640–1675 (2005)
W. Dahmen, R. Schneider, Wavelets with complementary boundary conditions — function spaces on the cube. Results Math. 34, 255–293 (1998)
W. Dahmen, R. Schneider, Composite wavelet bases for operator equations. Math. Comput. 68, 1533–1567 (1999)
W. Dahmen, R. Schneider, Wavelets on manifolds I: construction and domain decomposition. SIAM J. Math. Anal. 31, 184–230 (1999)
W. Dahmen, R. Stevenson, Element-by-element construction of wavelets satisfying stability and moment conditions. SIAM J. Numer. Anal. 37, 319–325 (1999)
W. Dahmen, A. Kunoth, K. Urban, Biorthogonal spline wavelets on the interval – stability and moment conditions. Appl. Comput. Harmon. Anal. 6, 132–196 (1999)
W. Dahmen, A. Kunoth, R. Schneider, Wavelet least squares methods for boundary value problems. SIAM J. Numer. Anal. 39, 1985–2013 (2002)
I. Daubechies, Orthonormal bases of compactly supported wavelets. Commun. Pure Appl. Math. 41, 909–996 (1988)
R. Dautray, J.-L. Lions, Mathematical Analysis and Numerical Methods for Science and Technology. Evolution Problems, vol. 5 (Springer, Berlin, 2000)
C. de Boor, A Practical Guide to Splines, revised edn. (Springer, New York, 2011)
R.A. DeVore, Nonlinear approximation. Acta Numer. 7, 51–150 (1998)
L.C. Evans, Partial Differential Equations (AMS, Providence, 1998)
V. Girault, R. Glowinski, Error analysis of a fictitious domain method applied to a Dirichlet problem. Jpn. J. Ind. Appl. Math. 12, 487–514 (1995)
V. Girault, P.-A. Raviart, Finite Element Methods for Navier–Stokes Equations (Springer, Berlin, 1986)
P. Grisvard, Elliptic Problems in Nonsmooth Domains (Pitman, New York, 1985)
M.D. Gunzburger, A. Kunoth, Space-time adaptive wavelet methods for optimal control problems constrained by parabolic evolution equations. SIAM J. Control. Optim. 49(3), 1150–1170 (2011)
M.D. Gunzburger, H.C. Lee, Analysis, approximation, and computation of a coupled solid/fluid temperature control problem. Comput. Methods Appl. Mech. Eng. 118, 133–152 (1994)
J. Haslinger, R.A.E. Mäkinen, Introduction to Shape Optimization: Theory, Approximation, and Computation (SIAM, Philadelphia, 2003)
S. Jaffard, Wavelet methods for fast resolution of elliptic problems. SIAM J. Numer. Anal. 29, 965–986 (1992)
J. Krumsdorf, Finite element wavelets for the numerical solution of elliptic partial differential equations on polygonal domains, Diploma thesis (in English), Universität Bonn, Bonn, January 2004
K. Kunisch, G. Peichl, Shape optimization for mixed boundary value problems based on an embedding domain method. Dyn. Contin. Discret. Impuls. Syst. 4, 439–478 (1998)
A. Kunoth, Multilevel Preconditioning (Verlag Shaker, Aachen, 1994)
A. Kunoth, Wavelet methods — elliptic boundary value problems and control problems, in Advances in Numerical Mathematics (Teubner, Leipzig, 2001)
A. Kunoth, Wavelet techniques for the fictitious domain—Lagrange multiplier approach. Numer. Algorithm 27, 291–316 (2001)
A. Kunoth, Fast iterative solution of saddle point problems in optimal control based on wavelets. Comput. Optim. Appl. 22, 225–259 (2002)
A. Kunoth, Adaptive wavelet methods for an elliptic control problem with Dirichlet boundary control. Numer. Algorithm 39(1–3), 199–220 (2005)
A. Kunoth, Multilevel preconditioning for variational problems, in Isogeometric Analysis and Applications, ed. by B. Jüttler, B. Simeon. Lecture Notes in Computational Sciences and Engineering (Springer, 2014), pp. 247–281
A. Kunoth, J. Sahner, Wavelets on manifolds: an optimized construction. Math. Comput. 75, 1319–1349 (2006)
A. Kunoth, Chr. Schwab, Analytic regularity and GPC approximation for control problems constrained by parametric elliptic and parabolic PDEs. SIAM J. Control. Optim. 51(3), 2442–2471 (2013)
A. Kunoth, Chr. Schwab, Sparse adaptive tensor Galerkin approximations of stochastic pde-constrained control problems. SIAM/ASA J. Uncertain. Quantif. 4 (2016), 1034–1059
J.L. Lions, Optimal Control of Systems Governed by Partial Differential Equations (Springer, Berlin, 1971)
J. Maes, A. Kunoth, A. Bultheel, BPX-type preconditioners for 2nd and 4th order elliptic problems on the sphere. SIAM J. Numer. Anal. 45(1), 206–222(2007)
P. Oswald, On discrete norm estimates related to multilevel preconditioners in the finite element method, in Constructive Theory of Functions, ed. by K.G. Ivanov, P. Petrushev, B. Sendov. Proceedings of International Conference Varna 1991 (Bulgarian Academy of Sciences, Sofia, 1992), pp. 203–214
R. Pabel, Wavelet Methods for PDE Constrained Control Problems with Dirichlet Boundary Control (Shaker, Maastricht, 2007). https://doi.org/10.2370/236_232
R. Pinnau, G. Thömmes, Optimal boundary control of glass cooling processes. Math. Methods Appl. Sci. 27, 1261–1281 (2004)
J. Sahner, On the optimized construction of wavelets on manifolds, Diploma thesis (in English), Universität Bonn, Bonn, September 2003
L.L. Schumaker, Spline Functions: Basic Theory, 3rd edn. (Cambridge Mathematical Library, Cambridge University Press, Cambridge, 2007)
Chr. Schwab, R. Stevenson, Space-time adaptive wavelet methods for parabolic evolution equations. Math. Comput. 78, 1293–1318 (2009)
R. Stenberg, On some techniques for approximating boundary conditions in the finite element method. J. Comput. Appl. Math. 63, 139–148 (1995)
R. Stevenson, Locally supported, piecewise polynomial biorthogonal wavelets on non-uniform meshes. Constr. Approx. 19, 477–508(2003)
W. Sweldens, The lifting scheme: a construction of second generation wavelets. SIAM J. Math. Anal. 29, 511–546 (1998)
J. van den Eshof, G.L.G. Sleijpen, Inexact Krylov subspace methods for linear systems. SIAM J. Matrix Anal. Appl. 26, 125–153 (2004)
H. Yserentant, On the multilevel splitting of finite element spaces. Numer. Math. 49, 379–412 (1986)
E. Zeidler, Nonlinear Functional Analysis and its Applications; III: Variational Methods and Optimization (Springer, New York, 1985)
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2018 Springer Nature Switzerland AG
About this chapter
Cite this chapter
Kunoth, A. (2018). Adaptive Multiscale Methods for the Numerical Treatment of Systems of PDEs. In: Lyche, T., Manni, C., Speleers, H. (eds) Splines and PDEs: From Approximation Theory to Numerical Linear Algebra. Lecture Notes in Mathematics(), vol 2219. Springer, Cham. https://doi.org/10.1007/978-3-319-94911-6_2
Download citation
DOI: https://doi.org/10.1007/978-3-319-94911-6_2
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-94910-9
Online ISBN: 978-3-319-94911-6
eBook Packages: Mathematics and StatisticsMathematics and Statistics (R0)


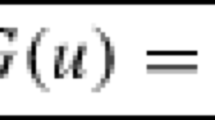




 for any j ≥ j0 with a constant independent of j.
for any j ≥ j0 with a constant independent of j.



