Abstract
We study the coinductive formulation of common knowledge in type theory. We formalise both the traditional relational semantics and an operator semantics, similar in form to the epistemic system S5, but at the level of events on possible worlds rather than as a logical derivation system. We have two major new results. Firstly, the operator semantics is equivalent to the relational semantics: we discovered that this requires a new hypothesis of semantic entailment on operators, not known in previous literature. Secondly, the coinductive version of common knowledge is equivalent to the traditional transitive closure on the relational interpretation. All results are formalised in the proof assistants Agda and Coq.
Access provided by CONRICYT-eBooks. Download conference paper PDF
Similar content being viewed by others
1 Introduction
Common knowledge is a modality in epistemic logic: a group of agents has common knowledge of an event if everyone knows it, everyone knows that everyone knows it, everyone knows that everyone knows that everyone knows it, and so on ad infinitum. Some famous logical puzzles (the muddy children or the cheating husbands problem [8, 9]) involve clever uses of this notion: the solution is based on some information shared by the agents and on their ability to deduce other people’s reasoning in a potentially unlimited reflection.
Type-theoretic logical systems allow the direct definition of coinductive types which may contain infinite objects, constructed by guarded corecursion [2, 7, 11]. By the propositions-as-types interpretation that is standard in type theory, coinductive types are propositions whose proofs may be infinite. Common knowledge can be naturally expressed as a coinductive operator: common knowledge of an event is recursively defined as universal knowledge of it in conjunction with common knowledge of the universal knowledge of it. Although it is well-known that the common knowledge modality is a greatest fixed point [1, 8], and some coinductive methods have been tried with it before [4], our work [6] is the first direct formalisation of this approach.
The traditional frame semantics [12, 14] account of knowledge modalities interprets them as equivalence relations on the set of possible states of the world: the knowledge of an agent is represented as a relation identifying states that cannot be distinguished by the agent. Common knowledge is interpreted as the transitive closure of the union of the knowledge relations for all agents.
The authors of [4] develop an infinitary deductive system with the aim that the system’s derivations serve as justification terms for common knowledge. The derivations are finitely branching trees but, along coinductive lines, branches may be infinitely deep. The authors establish the soundness and completeness of this system with respect to a relational semantics where common knowledge is treated as a transitive closure, but do not employ coinduction as a proof technique which can generate such an infinite proof term from a finite specification.
We instead take an entirely semantic approach, which is shallowly embedded in the logic of a type theory with coinductive types. This is in contrast to a previous type-theoretic formalisation of common knowledge [15] which is deeply embedded in the logic of the Coq proof assistant. This allows Coq to be used as a metatheory to experiment with the target logic, but does not allow for all of the features of Coq’s own logic, such as coinduction, to be used from within the target logic.
Our formulation of epistemic logic is based on an underlying set of states of the world; epistemic propositions are interpreted as events, that is, predicates on states (Sect. 2). Knowledge modalities are then functions over events. Our treatment of these knowledge modalities is similar to the syntactic encoding of epistemic logic in the modal logic system S5 [16]. Its study on the semantics side, as the algebraic structure of knowledge operators, is new (Sect. 3).
We give two main original contributions. Firstly, we prove that the operator semantics is equivalent to the relational semantics (Sect. 4). In formalising the equivalence, we discovered that it is necessary to assume a previously unknown property for operators: preservation of semantic entailment, which states that the knowledge operator preserves the consequences of a possibly infinite set of events (S5 gives this only for finite sets). Secondly, we prove that the coinductive formulation of common knowledge is equivalent to the relational representation as transitive closure, and that the coinductive operator itself satisfies the properties of a knowledge operator (Sect. 5). All these results are formalised in two type-theoretic proof assistants: AgdaFootnote 1 and CoqFootnote 2.
2 Possible Worlds and Events
In this section, we present the semantic framework in which we will be working throughout the paper. Our formalisation of epistemic logic is not axiomatic, but definitional. Instead of postulating a set of axioms for a knowledge modality, we define it using the logic of a proof assistant, like Agda or Coq, along the semantic lines of possible-worlds models. In other words, we work with a shallow embedding of epistemic logic in type theory. (The deep and shallow embedding approaches to the formalisation of logics and domain-specific languages are well-known and widespread. The first exposition of the concepts, but not the terminology, that we can find is by Reynolds [17]. See, for example, [13] for a clear explanation.)
We postulate a set of possible worlds, which we call states. A state encodes all relevant information about the world we are modelling. In the semantics of epistemic logic, a proposition may be true in some states, but false in others, so we interpret a proposition as a predicate over states, called an event.
To avoid confusion with the propositions that are native to the type theory, we shall refer to epistemic propositions only as events from this point on. By the standard propositions-as-types interpretation, we identify type-theoretic propositions with the type of their proofs, adopting an Agda-like notation. That is, we use the type universe \(\mathsf {Set}\) for both data types and propositions.
An event can be seen extensionally as the set of states in which that event occurs, or is true. It is convenient to define set-like operators to combine events and make logical statements about them. In the following, the variable e ranges over events and the variable w ranges over states. We obtain the truth assignment of an event e in a state w by simply applying the event to the state, written \(e \, w\).

The first three operators, \(\sqcap \), \(\sqcup \), and \(\sqsubset \), are binary operations on events: they map two events to the event that is their conjunction, disjunction, and implication, respectively; we can see them set-theoretically as intersection, union, and exponent of sets of states. The fourth, \(\mathop {\sim }\), is a unary operator expressing event negation, set theoretically it is the complement.
The next two operators are relations between two events. The first of the two, \(\subset \), states that the first event logically implies the second, set-theoretically the first is a subset of the second. The next, \(\equiv \), states that two events are logically equivalent, their set extensions being equal. Finally, the operator  expresses the fact that an event is true in all states: that it is semantically forced to be true. On the logical system side, it corresponds to a tautology. The operator \(\subset \) can also be expressed in terms of the equivalence:
expresses the fact that an event is true in all states: that it is semantically forced to be true. On the logical system side, it corresponds to a tautology. The operator \(\subset \) can also be expressed in terms of the equivalence:  .
.
As a simple example, imagine that we are modelling a scenario in which a coin has been tossed and a six-sided die has been rolled. We have these primitive events:

Then, for example, \(D_3 \sqcup D_4\) is the event which is true in those states where the die rolled a 3 or a 4, we might assume  so that there cannot be a state in which the coin landed both heads side up and tails side up, and so on.
so that there cannot be a state in which the coin landed both heads side up and tails side up, and so on.
Now we come to introducing modal operators for knowledge, so let us introduce two agents in our example, Alice and Bob. A modal operator in this setting is a function \(\mathsf {Event}\rightarrow \mathsf {Event}\), so we give each agent an operator of this type, \(\mathsf {K}_A\) and \(\mathsf {K}_B\) respectively. This allows us to also express events such as the following:

But not all operators on events are suitable to represent the knowledge of an agent. In the next section, we will define a class of operators on events that can be considered possible descriptions of an agent’s knowledge. Then, assuming there is a set of agents, each with their own knowledge operator, we give a coinductive definition of another operator expressing their common knowledge.
3 Knowledge Operator Semantics
For the moment we do not consider a set of agents, but just fix a single operator \(\mathsf {K}:\mathsf {Event}\rightarrow \mathsf {Event}\) and specify a set of properties that it must satisfy to be a possible interpretation of the knowledge of an agent. Traditionally, the modal logic system S5 [16] is employed to provide an idealised model for knowledge (modern presentations and historical overviews can be found in [3, 8]). In short, its properties state that agents are perfect reasoners, can only know events which are actually true, and are aware of what they do and do not know. We posit a version of this logic as the properties that the knowledge operator \(\mathsf {K}\) must satisfy.
We discovered that an extra infinitary deduction rule is required to obtain a perfect correspondence with the traditional relational interpretation which we describe in Sect. 4. This cannot be expressed at the level of the syntactic logical system, but it becomes essential at the semantic level of operators on events. It states that the knowledge operator must preserve semantic entailments, even if the conclusion follows from an infinite set of premises. Like other epistemic postulates in the standard literature, this is a strong principle which may be unrealistic to assume for real-world agents, but our discovery shows that it is already an implicit feature of the classical frame semantics.
Definition 1
A family of events indexed on a type X is a function \(E:X\rightarrow \mathsf {Event}\). Given a family of events E, we can generate the event  that is true in those states where all members of the family are true:
that is true in those states where all members of the family are true:

We can map \(\mathsf {K}\) onto the whole family by applying it to every member: We write \(\mathsf {K}\,E\) for the family \(\lambda x. \mathsf {K}\,(E\,x)\). We say that \(\mathsf {K}\) preserves semantic entailment if, for every family \(E : X \rightarrow \mathsf {Event}\) and every event e, we have:

We require that \(\mathsf {K}\) has this property and also satisfies the properties of S5. Some of these are derivable from semantic entailment, but we formulate them all in the definition to clearly reflect the relation with traditional epistemic logic.
Definition 2
An operator on events, \(\mathsf {K}:\mathsf {Event}\rightarrow \mathsf {Event}\), is called a knowledge operator if it preserves semantic entailment and satisfies the event-based version of the properties of S5:
-
1.
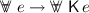
This principle is known as knowledge generalisation (or necessitation in modal logics with an operator \(\square \) that is interpreted as “it is necessary that”). It states that all derivable theorems are known, that is, the agent is capable of applying pure logic to derive tautologies. Here we work on the semantics side: instead of logical formulas, the objects of the knowledge operators are events, that is, predicates on states. We understand an event to be a tautology if it is true in every state. The unfolding of the principle is: \( (\forall w . e \, w) \rightarrow \forall v . \mathsf {K}\, e \, v. \)
-
2.
\(\mathsf {K}\, (e_1 \sqsubset e_2) \subset (\mathsf {K}\, e_1 \sqsubset \mathsf {K}\, e_2)\)
Corresponding to Axiom K, this states that the knowledge operator distributes over implication: The agent is capable of applying modus ponens to what they know. Notice the use of the two operators \(\sqsubset \), mapping two events to the event expressing the implication between the two, and \(\subset \), stating that the second event is true whenever the first one is. If we unfold the definitions, this states that: \( \forall w . \mathsf {K}\, (e_1 \sqsubset e_2) \, w \rightarrow \mathsf {K}\, e_1 \, w \rightarrow \mathsf {K}\, e_2 \, w. \) That is, if in a state w the agent knows that \(e_1\) implies \(e_2\) and also knows \(e_1\), then they know \(e_2\).
-
3.
\(\mathsf {K}\, e \subset e\)
Corresponding to Axiom T, this states that knowledge is true: what distinguishes knowledge from belief or opinion is that when an agent knows an event, that event must actually hold in the present state.
-
4.
\(\mathsf {K}\, e \subset \mathsf {K}\, (\mathsf {K}\, e)\)
Corresponding to Axiom 4, this is a principle of self-awareness of knowledge: agents know when they know something.
-
5.
\(\mathop {\sim }\mathsf {K}\, e \subset \mathsf {K}\, (\mathop {\sim }\mathsf {K}\, e)\)
Corresponding to Axiom 5, this negative version of the principle of self-awareness could be called the Socratic Principle: When an agent does not know something, they at least know that they do not know it.
Lemma 1
The first two properties in the definition of knowledge operator (knowledge generalisation and Axiom K) are consequences of preservation of semantic entailment.
Proof
Assume that \(\mathsf {K}\) preserves semantic entailment.
-
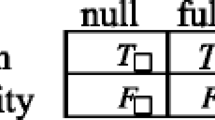
Knowledge generalisation is immediate once we see that
 is equivalent to the semantic entailment from the empty family:
is equivalent to the semantic entailment from the empty family:  .
. -
Axiom K follows from applying preservation of the semantic entailment version of modus ponens (using a family with just two elements):
 .
.
(We have used set notation for the families: they indicate the trivial family indexed on the empty type and a family indexed on the Booleans.) \(\square \)
Let us now return to a setting with a non-empty set of agents, ranged over by the variable a. Each agent has an individual knowledge operator \(\mathsf {K}_a\) satisfying Definition 2. Recall that common knowledge of an event intuitively means that everyone knows it, everyone knows that everyone knows it, everyone knows that everyone knows that everyone knows it, and so on ad infinitum.
We define \(\mathsf {EK}\) to be the “everyone knows” operator expressing universal knowledge of an event:
\(\mathsf {EK}\) is not itself a knowledge operator. It is possible to show that it satisfies knowledge generalisation, Axiom K, and, with at least one agent, Axiom T. It also preserves semantic entailment. The two introspective properties of Axioms 4 and 5, however, are not satisfied in general: if they were, there would be no distinction between universal knowledge and common knowledge.
Common knowledge of an event e intuitively means the infinite conjunction:
This infinite conjunction can be expressed by a coinductive definition saying that common knowledge of e means the conjunction of \(\mathsf {EK}\,e\) and, corecursively, common knowledge of \(\mathsf {EK}\,e\). In Agda or Coq, this can be defined directly by a coinductive operator:
This defines common knowledge at a high level without mentioning states, naturally corresponding to the informal recursive notion. If we unfold the definitions so that we can see the constructor’s type in full, it becomes evident that the definition satisfies the positivity condition of (co)inductive types:
The meaning of the definition is that a proof of \(\mathsf {cCK}\,e\) must have the form of the constructor \(\mathsf {cCK\!-\!intro}\) applied to proofs of \(\mathsf {EK}\,e\) and \(\mathsf {cCK}\,(\mathsf {EK}\, e)\). The latter must in turn be obtained by another application of \(\mathsf {cCK\!-\!intro}\). This process proceeds infinitely, without end. To obtain such a proof, we can give a finite corecursive definition that, when unfolded, generates the infinite structure.
The idea is that when proving that an event e is common knowledge, we must prove \(\mathsf {EK}\,e\) without any extra assumption, but we can recursively use the statement that we are proving in the derivation of \(\mathsf {cCK}\,(\mathsf {EK}\,e)\). This apparently circular process must satisfy a guardedness condition, ensuring that the unfolding is productive. See, for an introduction, Chap. 13 of the Coq book by Bertot and Casteran [2] or the application to general recursion by one of us [5]. We will soon give an example in the proof of Lemma 4.
Since a proof of \(\mathsf {cCK}\, e\) must be constructed by a proof of \(\mathsf {EK}\, e \sqcap \mathsf {cCK}\, (\mathsf {EK}\, e)\), we can derive either conjunct if we have that e is common knowledge. That is, we obtain the following trivial lemmas:
Lemma 2
For every event e we have: \( \mathsf {cCK}\, e \subset \mathsf {EK}\, e. \)
Lemma 3
For every event e we have: \( \mathsf {cCK}\, e \subset \mathsf {cCK}\, (\mathsf {EK}\, e). \)
We now illustrate a proof by coinduction as a first simple example, showing that common knowledge is equivalent to the family of events expressing finite iterations of \(\mathsf {EK}\):
Lemma 4
For every event e, the family \(\mathsf {recEK}\,e\) semantically entails \(\mathsf {cCK}\,e\):

Proof
In a coinductive proof, we are allowed to assume the statement we are proving and use it in a restricted way:
CoInductive Hypothesis CH:

Of course, we cannot just use the assumption CH directly to prove the theorem. We must make at least one step in the proof without circularity.
Unfolding the statement, we need to prove that for every state w we have:
So let us assume that for every natural number n, \(\mathsf {recEK}\,e\,n\,w\) holds.
We must now prove \(\mathsf {cCK}\,e\,w\), which can be derived using the constructor \(\mathsf {cCK\!-\!intro}\) from \(\mathsf {EK}\,e\,w\) and \(\mathsf {cCK}\,(\mathsf {EK}\,e)\,w\).
-
\(\mathsf {EK}\,e\,w\) is just \(\mathsf {recEK}\,e\,0\,w\), which is true by assumption;
-
To prove \(\mathsf {cCK}\,(\mathsf {EK}\,e)\,w\), we now invoke CH, instantiated for the event \(\mathsf {EK}\,e\):

That is:
$$ \forall w. (\forall n. \mathsf {recEK}\,(\mathsf {EK}\,e)\,n\,w) \rightarrow \mathsf {cCK}\,(\mathsf {EK}\,e)\,w $$So we need to prove that for every n, \(\mathsf {recEK}\,(\mathsf {EK}\,e)\,n\,w\). This is trivially equivalent to \(\mathsf {recEK}\,e\,(n+1)\,w\), which is true by assumption. Therefore, Assumption CH allows us to conclude \(\mathsf {cCK}\,(\mathsf {EK}\,e)\,w\), as desired. \(\square \)
Let us observe the structure of this proof. We allowed ourselves to assume the statement of the theorem as a hypothesis. But it can only be used in a limited way. We used it immediately after applying the constructor \(\mathsf {cCK\!-\!intro}\), to prove the recursive branch of it. This is the typical way in which guarded corecursion works: we can make a circular call to the object we are defining immediately under the application of the constructor.
The proof of the implication in the other direction, omitted here, is simply by induction over natural numbers, repeatedly unfolding the definition of common knowledge.
Lemma 5
For every event e and \(n:\mathbb {N}\): \( \mathsf {cCK}\,e \subset \mathsf {recEK}\,e\,n. \)
The equivalence of common knowledge with the family \(\mathsf {recEK}\) gives an immediate proof of the following useful property corresponding to Axiom 4 of S5.
Lemma 6
For every event e, we have: \( \mathsf {cCK}\,e \subset \mathsf {cCK}\,(\mathsf {cCK}\,e). \)
Finally, the coinductive definition of common knowledge satisfies the properties of knowledge operators. We must prove all the S5 properties and preservation of semantic entailment for \(\mathsf {cCK}\).
Theorem 1
Common knowledge, \(\mathsf {cCK}\), is itself a knowledge operator.
Proof
We can give a direct proof of the statement by deriving all the properties of knowledge operators for \(\mathsf {cCK}\). Lemma 6 shows that Axiom 4 holds. Proofs of all other S5 properties and of preservation of semantic entailment are interesting applications of coinductive methods. These proofs are omitted here, but are used in the Coq formalisation.
This theorem is also a consequence of Theorem 4 (equivalence of \(\mathsf {cCK}\) with the relational characterisation) and Theorem 3 (equivalence relations define knowledge operators). This proof is used in the Agda formalisation. \(\square \)
4 Relational Semantics
In this section, we present the traditional frame semantics of epistemic logic, the knowledge operators being introduced through equivalence relations on states. We prove that a knowledge operator semantics can be generated from an equivalence relation and vice versa, additionally showing that these transformations form an isomorphism.
Two states may differ by a number of events: some events may be true in one of the states, but false in the other. If an agent has no knowledge of any of these discriminating events, only knowing events which are common to both states, then those states are indistinguishable as far as the agent is aware. We say that these states are epistemically accessible from one another: if the world were in one of those states, the agent would consider either state to be plausible, not having sufficient knowledge to inform them precisely in which state the world is actually in.
To say that an agent has knowledge of an event in a particular state is then to say that the event holds in all states that the agent finds epistemically accessible from that state. We formalise this notion by defining a transformation from relations on states to unary operators on events:
Care must be taken to distinguish this notation from the notation of earlier sections where each agent a had a knowledge operator \(\mathsf {K}_a\) directly postulated. When talking in terms of the relational semantics, we do not take these operators as primitive. Here, \(\mathsf {K}_{[R]}\) refers to the operator generated when transforming some relation \(R : \mathsf {State}\rightarrow \mathsf {State}\rightarrow \mathsf {Set}\).
It is a well known result in modal logic that applying this transformation to an equivalence relation yields a knowledge operator satisfying the properties of S5. We establish this fact here, assuming only the needed properties of the relation (see [10] for a more extensive listing of which relational properties imply which modal axioms). The proofs are omitted, but can be adapted from standard expositions. They are also present in the Agda and Coq formalisations.
Lemma 7
If R is a relation on states, then the operator \(\mathsf {K}_{[R]}\) has the following properties.
-
\(\mathsf {K}_{[R]}\) satisfies knowledge generalisation:

-
\(\mathsf {K}_{[R]}\) satisfies Axiom K: \(\mathsf {K}_{[R]} \, (e_1 \sqsubset e_2) \subset \mathsf {K}_{[R]} \, e_1 \sqsubset \mathsf {K}_{[R]} \, e_2\)
-
If R is reflexive, then \(\mathsf {K}_{[R]}\) satisfies Axiom T: \(\mathsf {K}_{[R]} \, e \subset e\)
-
If R is transitive, then \(\mathsf {K}_{[R]}\) satisfies Axiom 4: \(\mathsf {K}_{[R]} \, e \subset \mathsf {K}_{[R]} \, (\mathsf {K}_{[R]} \, e)\)
-
If R is symmetric and transitive, then \(\mathsf {K}_{[R]}\) satisfies Axiom 5: \(\mathop {\sim }\mathsf {K}_{[R]} \, e \subset \mathsf {K}_{[R]} \, (\mathop {\sim }\mathsf {K}_{[R]} \, e)\)
To complete a proof that \(\mathsf {K}_{[R]}\) is a knowledge operator, we have to show in addition that it preserves semantic entailment. As is the case with knowledge generalisation and Axiom K, this does not require any hypothesis on the properties of R.
Lemma 8
For every family \(E:X\rightarrow \mathsf {Event}\) and every event e, we have:

Proof
Let us assume that  (Assumption 1).
(Assumption 1).
We must prove  , that is, unfolding the definitions of
, that is, unfolding the definitions of  and \(\subset \), for every state w, \(\forall x. \mathsf {K}_{[R]}\,(E\,x)\,w \rightarrow \mathsf {K}_{[R]}\,e\,w\), where x ranges over the index of the family E. So let us assume that \(\forall x. \mathsf {K}_{[R]}\,(E\,x)\,w\) (Assumption 2). We must then prove that \(\mathsf {K}_{[R]}\,e\,w\).
and \(\subset \), for every state w, \(\forall x. \mathsf {K}_{[R]}\,(E\,x)\,w \rightarrow \mathsf {K}_{[R]}\,e\,w\), where x ranges over the index of the family E. So let us assume that \(\forall x. \mathsf {K}_{[R]}\,(E\,x)\,w\) (Assumption 2). We must then prove that \(\mathsf {K}_{[R]}\,e\,w\).
Unfolding the definition of \(\mathsf {K}_{[R]}\), our goal becomes \(\forall v. w\,R\,v\rightarrow e\,v\). So let v be any state such that \(w\,R\,v\) (Assumption 3). We must prove that \(e\,v\).
To prove this goal we apply directly Assumption 1, which states (when unfolded) that \(\forall v. (\forall x. (E\,x)\,v)\rightarrow e\,v\). Therefore, to prove the goal, we just have to show that \(\forall x. (E\,x)\,v\).
For any index x, Assumption 2 tells us that \(\mathsf {K}_{[R]}\,(E\,x)\,w\), that is, by definition of \(\mathsf {K}_{[R]}\), \(\forall v. w\,R\,v\rightarrow (E\,x)\,v\). But since our choice of v satisfies \(w\,R\,v\) by Assumption 3, we have that \((E\,x)\,v\), as desired. \(\square \)
We can then put the two lemmas together to satisfy Definition 2.
Theorem 2
If R is an equivalence relation on states, then \(\mathsf {K}_{[R]}\) is a knowledge operator.
The inverse transformation, taking a knowledge operator and returning a relation on states is:
This transformation always results in an equivalence relation, as \(\leftrightarrow \) is itself an equivalence relation. In fact, if we admit classical reasoning, one direction of the implication is sufficient.
Lemma 9
If \(\mathsf {K}\) is a knowledge operator, then \(\lambda w.\lambda v.\forall e.\mathsf {K}\, e \, w \rightarrow \mathsf {K}\, e \, v\) is an equivalence relation.
As an immediate corollary, it is equivalent to \(\lambda w . \lambda v . \forall e . \mathsf {K}\, e \, w \leftrightarrow \mathsf {K}\, e \, v\).
Proof
Reflexivity and transitivity are trivial. To show symmetry, we first assume, for some states w and v, that \(\forall e . \mathsf {K}\, e \, w \rightarrow \mathsf {K}\, e \, v\) and, for some event e, \(\mathsf {K}\, e \, v\). We want to prove that \(\mathsf {K}\, e \, w\).
Suppose, towards a contradiction, that \(\lnot (\mathsf {K}\, e \, w)\), which can also be written as \((\mathop {\sim }\mathsf {K}\, e) \, w\). By Axiom 5, we have \(\mathsf {K}\,(\mathop {\sim }\mathsf {K}\, e) \, w\). By instantiating the first assumption with event \(\mathop {\sim }\mathsf {K}\, e \), we deduce that \(\mathsf {K}\,(\mathop {\sim }\mathsf {K}\, e) \, v\). By Axiom T, this implies \((\mathop {\sim }\mathsf {K}\, e) \, v\), which can be written as \(\lnot (\mathsf {K}\, e \, v)\), contradicting the second assumption: our supposition \(\lnot (\mathsf {K}\, e \, w)\) must be false. We conclude, by excluded middle, that \(\mathsf {K}\, e \, w\) is true, as desired. \(\square \)
We now prove that the mappings of knowledge operators to equivalence relations and vice versa are actually inverse: we can equivalently work with either representation of knowledge. The proofs are mostly straightforward applications of the properties of S5 and equivalence relations, except one direction, for which we added the assumption of preservation of semantic entailment. We give the proof of this.
In order to do this we first characterise the transformations of \(\mathsf {K}\) using event families generated by \(\mathsf {K}\) on a fixed state w. Choose as index set the set of events that are known in w: \(X = \{e \mid \mathsf {K}\,e\,w\}\) (in Coq or Agda, we use the dependent sum type \(\varSigma e . \mathsf {K}\,e\,w\) whose elements are pairs \(\langle e, h\rangle \) of an event e and a proof h of \(\mathsf {K}\,e\,w\)); the family itself is just the application of \(\mathsf {K}\). Formally:
Intuitively, \(\mathsf {KFam}^{w}\) is the total amount of knowledge in state w. Set-theoretically it is \(\{\mathsf {K}\,e \mid \mathsf {K}\,e\,w\}\). One observation, whose proof we omit here, is that \(R_{[\mathsf {K}]}\,w\,v\) is equivalent to  . Another observation will allow us to replace \(\mathsf {K}_{[R_{[\mathsf {K}]}]}\,e\,w\) with an expression involving \(\mathsf {KFam}^{w}\).
. Another observation will allow us to replace \(\mathsf {K}_{[R_{[\mathsf {K}]}]}\,e\,w\) with an expression involving \(\mathsf {KFam}^{w}\).
Lemma 10
For every event e and state w, the proposition \(\mathsf {K}_{[R_{[\mathsf {K}]}]}\,e\,w\) is equivalent to  .
.
Proof
We just unfold the definitions and use the previous lemma:

\(\square \)
Lemma 11
For every knowledge operator \(\mathsf {K}\) and every event e, we have:
Proof
Assume, for some state w, that \(\mathsf {K}_{[R_{[\mathsf {K}]}]}\,e\,w\). We must prove \(\mathsf {K}\,e\,w\).
By Lemma 10, the assumption is equivalent to  . Since \(\mathsf {K}\) preserves semantic entailment, we also have
. Since \(\mathsf {K}\) preserves semantic entailment, we also have  .
.
We just need to prove that all elements of the family \(\mathsf {K}\,\mathsf {KFam}^{w}\) are true in state w to deduce that \(\mathsf {K}\,e\,w\) holds, as desired. But in fact, given an index \(\langle e', h\rangle \) for the family \(\mathsf {KFam}^{w}\), with h being a proof of \(\mathsf {K}\,e'\,w\), this goal becomes \( \mathsf {K}\,(\mathsf {KFam}^{w}\,\langle e', h\rangle )\,w = \mathsf {K}\,(\mathsf {K}\,e')\,w \) which can be dispatched by applying Axiom 4 to h. \(\square \)
The other three directions of the isomorphisms are straightforward applications of the properties of knowledge operators and equivalence relations.
Theorem 3
For every knowledge operator \(\mathsf {K}\), \(\mathsf {K}_{[R_{[\mathsf {K}]}]}\) is equivalent to \(\mathsf {K}\): for every event e and every state w, \( \mathsf {K}_{[R_{[\mathsf {K}]}]}\,e\,w \leftrightarrow \mathsf {K}\,e\,w. \)
For every equivalence relation on states R, \(R_{[\mathsf {K}_{[R]}]}\) is equivalent to R: for every pair of states w and v, \( R_{[\mathsf {K}_{[R]}]}\,w\,v \leftrightarrow R\,w\,v. \)
In this section we proved that the traditional frame semantics of epistemic logic is equivalent with our notion of knowledge operator. This isomorphism validates our discovery of the property of preservation of semantic entailments and shows that it was already implicitly present in the relational view.
5 Equivalence with Relational Common Knowledge
This section shows that the coinductive definition of common knowledge is equivalent to the traditional characterisation as transitive closure of the union of all the agents’ accessibility relations. We use the isomorphism of Theorem 3 to treat equivalence relations on states and their corresponding knowledge operators interchangeably.
We first equip our agents with individual knowledge operators by postulating an equivalence relation \(\simeq _a : \mathsf {State}\rightarrow \mathsf {State}\rightarrow \mathsf {Set}\) for each agent a as their epistemic accessibility relation. The knowledge operator for an agent a is then \(\mathsf {K}_{[\simeq _a]}\), which we shall write in shorthand as \(\mathsf {K}_a\).
Our formulation of the “everyone knows” operator, \(\mathsf {EK}\), and the coinductive common knowledge operator, \(\mathsf {cCK}\), are as they appear in Sect. 3. The only difference is in the underlying definition of \(\mathsf {K}_a\), which had previously been taken as primitive and assumed to satisfy the knowledge operator properties outlined in Definition 2. The relations \(\simeq _a\) are equivalence relations, so we can conclude that this new formulation of \(\mathsf {K}_a\) also satisfies these properties by Theorem 2.
The relational definition of the common knowledge operator is given by its own relation: the transitive closure of the union of all accessibility relations \(\simeq _a\). We write this relation as \(\propto \). It is defined inductively as follows:
Lemma 12
\(\propto \) is an equivalence relation.
Proof
Transitivity is immediate by definition of constructor \(\mathop {\propto \!\!\mathsf {-trans}}\). Reflexivity follows from the reflexivity of the agents’ underlying accessibility relations included in \(\propto \) by constructor \(\mathop {\propto \!\!\mathsf {-union}}\) (it is essential that there is at least one agent). Symmetry is proved by induction on the proof of \(\propto \): the base case follows from the symmetry of the single agents’ accessibility relation, while the recursive case is straightforward from the proof of transitivity and the inductive hypotheses. \(\square \)
We can intuitively grasp how it gets us to common knowledge in the following way. Observe that in an agent a’s accessibility relation, if each state were alone in its own equivalence class, then a would be omniscient, able to perfectly distinguish each state from all others. If a were to forget an event, however, then all of those states which differ only by that event would collapse into an equivalence class together. In general, the fewer the number of equivalence classes in \(\simeq _a\), the fewer the number of events a knows.
Taking the union of all agents’ accessibility relations is essentially taking the union of their ignorance. This gets us as far as a relational interpretation of \(\mathsf {EK}\), which is not necessarily transitive. We take the transitive closure to reobtain an equivalence relation, further expanding the ignorance represented by the relation, but ensuring that we have the introspective properties of Axioms 4 and 5 that are essential to common knowledge.
It is as if there were a virtual, maximally-ignorant agent whose accessibility relation is \(\propto \), knowing only those events which are common knowledge among all agents and nothing more. With this in mind, we can define the relational common knowledge operator, \(\mathsf {rCK}\), in the same way that we defined each agent’s knowledge operator:
By Theorem 3 and Lemma 12, we can conclude that \(\mathsf {rCK}\) satisfies all of the knowledge operator properties: We can also verify that it has properties corresponding to the two trivial properties of \(\mathsf {cCK}\), Lemmas 2 and 3.
Lemma 13
For every event e we have: \( \mathsf {rCK}\, e \subset \mathsf {EK}\, e. \)
Proof
Unfolding the statement, we need to prove that for every state w we have:
So we assume the first statement, \(\forall v . w \propto v \rightarrow e \, v\), and we also assume we have an agent a and state u such that \(w \simeq _a u\).
We are left to show that e holds in u. By the definition of constructor \(\mathop {\propto \!\!\mathsf {-union}}\), given \(w \simeq _a u\), we can derive that \(w \propto u\), and then, instantiating our first assumption with state u, we obtain \(e \, u\) as desired. \(\square \)
Lemma 14
For every event e we have: \( \mathsf {rCK}\, e \subset \mathsf {rCK}\, (\mathsf {EK}\, e). \)
Proof
Unfolding the statement, we need to prove that for every state w we have:
As in the previous proof, we have the assumption that for any state v such that \(w \propto v\), e holds in v, so to reach our conclusion \(e \, t\) we can prove that \(w \propto t\). We have the additional assumptions \(w \propto u\) and \(u \simeq _a t\).
From the latter, by \(\mathop {\propto \!\!\mathsf {-union}}\) we derive \(u \propto t\). Then by the transitive property of \(\propto \), constructor \(\mathop {\propto \!\!\mathsf {-trans}}\), we conclude \(w \propto t\). \(\square \)
With these results, we are now able to prove the first direction of the equivalence of \(\mathsf {rCK}\) and \(\mathsf {cCK}\).
Lemma 15
For every event e we have: \( \mathsf {rCK}\, e \subset \mathsf {cCK}\, e. \)
Proof
The conclusion of this theorem is an application of the coinductive predicate \(\mathsf {cCK}\), so we may proceed by coinduction, assuming the statement as our coinductive hypothesis CH : \(\forall e . \mathsf {rCK}\, e \subset \mathsf {cCK}\, e\)
Unfolding the application of \(\subset \), we need to prove that, for every state w, \( \mathsf {rCK}\, e \, w \rightarrow \mathsf {cCK}\, e \, w. \) So we assume \(\mathsf {rCK}\, e \, w\), and use constructor \(\mathsf {cCK\!-\!intro}\) to derive the conclusion \(\mathsf {cCK}\, e \, w\), generating the proof obligations \(\mathsf {EK}\, e \, w\) and \(\mathsf {cCK}\, (\mathsf {EK}\,e) \, w\).
-
\(\mathsf {EK}\, e \, w\) comes from Lemma 13 applied to assumption \(\mathsf {rCK}\, e \, w\).
-
To prove \(\mathsf {cCK}\, (\mathsf {EK}\, e) \, w\) we invoke assumption CH, instantiating it with event \(\mathsf {EK}\, e\), leaving us to prove \(\mathsf {rCK}\, (\mathsf {EK}\, e) \, w\). This is the conclusion of Lemma 14, which we can apply to assumption \(\mathsf {rCK}\, e \, w\) to complete the proof. \(\square \)
We need an additional property of \(\mathsf {cCK}\) before we are able to complete the other direction of the equivalence proof. The property is related to Axiom 4 of knowledge operators, for example, for an agent a’s knowledge operator \(\mathsf {K}_a\):
Unfolding \(\subset \) and the outermost application of \(\mathsf {K}_a\) in the conclusion yields the principle:
That is, if we have that \(\mathsf {K}_a \, e\) holds at some state w, and we also have that \(w \simeq _a v\) for some state v, then we can conclude that \(\mathsf {K}_a \, e\) holds at state v too. We call this transporting the agent’s knowledge across the relation \(\simeq _a\).
Since \(\mathsf {rCK}\) is also a knowledge operator, defined in the same way as \(\mathsf {K}_a\) but for a different equivalence relation, this transportation principle must hold for it too: relational common knowledge of an event can be transported from one state to another provided that those states are bridged by \(\propto \). The additional property of \(\mathsf {cCK}\) that we are to prove is that it too can be transported across \(\propto \).
Lemma 16
For every two states w and v and event e we have:
Proof
We assume \(\mathsf {cCK}\, e \, w\) and proceed by induction on \(w \propto v\):
-
If \(w \propto v\) is constructed by \(\mathop {\propto \!\!\mathsf {-union}}\), then there is some agent a for whom \(w \simeq _a v\) holds. We can apply Lemma 6, the Axiom 4 property for \(\mathsf {cCK}\), to obtain \(\mathsf {cCK}\, (\mathsf {cCK}\, e) \, w\), and then, by Lemma 2, it follows that \(\mathsf {EK}\, (\mathsf {cCK}\, e) \, w\). Since all agents know this, we can instantiate this fact with agent a to conclude that a must know it: \( \mathsf {K}_a \, (\mathsf {cCK}\, e) \, w \). We use the transportation principle of \(\mathsf {K}_a\) to transport \(\mathsf {K}_a \, (\mathsf {cCK}\, e)\) from state w to state v as these states are bridged by \(w \simeq _a v\). Then, as a knows \(\mathsf {cCK}\, e\) at state v, by Axiom T, it must actually hold in state v.
-
If \(w \propto v\) is constructed by \(\mathop {\propto \!\!\mathsf {-trans}}\), then there is some state u for which \(w \propto u\) and \(u \propto v\) hold. By induction hypothesis, we also have \(\mathsf {cCK}\, e \, w \rightarrow \mathsf {cCK}\, e \, u\) and \(\mathsf {cCK}\, e \, u \rightarrow \mathsf {cCK}\, e \, v \). We can simply use the transitivity of implication, induction hypotheses, and our assumption \(\mathsf {cCK}\, e \, w\) to reach our goal. \(\square \)
Lemma 17
For every event e we have: \( \mathsf {cCK}\, e \subset \mathsf {rCK}\, e. \)
Proof
Unfolding the statement we are to prove, for every event e and state w: \( \mathsf {cCK}\, e \, w \rightarrow \forall v . w \propto v \rightarrow e \, v. \)
We assume \(\mathsf {cCK}\, e \, w\) and \(w \propto v\). By Lemma 16 and these assumptions, we can then transport \(\mathsf {cCK}\, e\) from state w to v: \(\mathsf {cCK}\, e \, v\). From this, we can derive \(\mathsf {EK}\, e \, v\) by Lemma 2. Since everyone knows e at state v, and our set of agents is non-empty, there must be some agent who knows e at v. By Axiom T, e must actually hold at v. \(\square \)
Combining Lemmas 15 and 17 gives the full equivalence.
Theorem 4
For all events e, \( \mathsf {rCK}\, e \equiv \mathsf {cCK}\, e, \) that is, \( \mathsf {K}_{[\propto ]} \, e \equiv \mathsf {cCK}\, e. \)
6 Conclusion
We presented a type-theoretic formalisation of epistemic logic and a coinductive implementation of the common knowledge operator. This was done through a shallow embedding: we formulated knowledge operators as functions on events, which are predicates on a set of possible worlds or states.
The coinductive version of common knowledge has some advantages with respect to the traditional relational version.
-
It is a straightforward formulation of the intuitive definition: common knowledge of an event means that everyone knows it and the fact that everyone knows it is itself common knowledge.
-
It can be formulated at a higher level, using only the knowledge operators of each agent and the connectives of epistemic logic: the coinductive definition of \(\mathsf {cCK}\) does not mention states.
-
It gives us a new reasoning tool in the form of guarded corecursion. We demonstrated its power in several proofs in this paper and in the previous work on Aumann’s Theorem.
We proved that our coinductive formulation is equivalent to two other versions:
-
The traditional one as transitive closure of the union of the accessibility relations of all agents;
-
The recursive family of iterations of the “everyone knows” operator.
In the process of investigating this subject we discovered that knowledge operators obtained from equivalence relations satisfy a previously unknown property of preservation of semantic entailment in addition to the properties of S5. We proved that this fully characterises knowledge operators and gives an isomorphism between them and equivalence relations.
References
Barwise, J.: Three views of common knowledge. In: Vardi, M.Y. (ed.) Proceedings of the 2nd Conference on Theoretical Aspects of Reasoning about Knowledge, Pacific Grove, CA, March 1988, pp. 365–379. Morgan Kaufmann (1988)
Bertot, Y., Castéran, P.: Interactive Theorem Proving and Program Development. Coq’Art: The Calculus of Inductive Constructions. Springer, Heidelberg (2004). https://doi.org/10.1007/978-3-662-07964-5
Blackburn, P., de Rijke, M., Venema, Y.: Modal Logic. Cambridge University Press, New York (2001)
Bucheli, S., Kuznets, R., Struder, T.: Two ways to common knowledge. Electron. Notes Theor. Comput. Sci. 262, 83–98 (2010)
Capretta, V.: General recursion via coinductive types. Log. Methods Comput. Sci. 1(2), 1–18 (2005). https://doi.org/10.2168/LMCS-1(2:1)2005
Capretta, V.: Common knowledge as a coinductive modality. In: Barendsen, E., Geuvers, H., Capretta, V., Niqui, M. (eds.) Reflections on Type Theory, Lambda Calculus, and the Mind, pp. 51–61. ICIS, Faculty of Science, Radbout University Nijmegen (2007). Essays Dedicated to Henk Barendregt on the Occasion of his 60th Birthday
Coquand, T.: Infinite objects in type theory. In: Barendregt, H., Nipkow, T. (eds.) TYPES 1993. LNCS, vol. 806, pp. 62–78. Springer, Heidelberg (1994). https://doi.org/10.1007/3-540-58085-9_72
Fagin, R., Halpern, J.Y., Vardi, M.Y., Moses, Y.: Reasoning About Knowledge. MIT Press, Cambridge (1995)
Gamow, G., Stern, M.: Puzzle Math. Viking Press, New York (1958)
Garson, J.: Modal logic. In: Zalta, E.N. (ed.) The Stanford Encyclopedia of Philosophy. Metaphysics Research Lab, Stanford University (2016)
Giménez, E.: Codifying guarded definitions with recursive schemes. In: Dybjer, P., Nordström, B., Smith, J. (eds.) TYPES 1994. LNCS, vol. 996, pp. 39–59. Springer, Heidelberg (1995). https://doi.org/10.1007/3-540-60579-7_3
Hintikka, J.: Knowledge and Belief. Cornell University Press, Ithaca (1962)
Keller, C., Werner, B.: Importing HOL light into Coq. In: Kaufmann, M., Paulson, L.C. (eds.) ITP 2010. LNCS, vol. 6172, pp. 307–322. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-14052-5_22
Kripke, S.A.: A completeness theorem in modal logic. J. Symb. Logic 24(1), 1–14 (1959)
Lescanne, P.: Common knowledge logic in a higher order proof assistant. In: Voronkov, A., Weidenbach, C. (eds.) Programming Logics. LNCS, vol. 7797, pp. 271–284. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-37651-1_11
Lewis, C.I., Langford, C.H.: Symbolic Logic. The Century Co., New York (1932)
Reynolds, J.C.: User-defined types and procedural data structures as complementary approaches to data abstraction. In: Gries, D. (ed.) Programming Methodology. MCS, pp. 309–317. Springer, New York (1978). https://doi.org/10.1007/978-1-4612-6315-9_22
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2018 Springer International Publishing AG, part of Springer Nature
About this paper
Cite this paper
Baston, C., Capretta, V. (2018). The Coinductive Formulation of Common Knowledge. In: Avigad, J., Mahboubi, A. (eds) Interactive Theorem Proving. ITP 2018. Lecture Notes in Computer Science(), vol 10895. Springer, Cham. https://doi.org/10.1007/978-3-319-94821-8_8
Download citation
DOI: https://doi.org/10.1007/978-3-319-94821-8_8
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-94820-1
Online ISBN: 978-3-319-94821-8
eBook Packages: Computer ScienceComputer Science (R0)




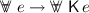
 is equivalent to the semantic entailment from the empty family:
is equivalent to the semantic entailment from the empty family:  .
. .
.
