Multi-network User Identification via Graph-Aware Embedding

Abstract

User identification is widely used in anomaly detection, recommendation system and so on. Previous approaches focus on extraction of features describing users, and the learners try to emphasize the differences between different user identities. However, one applicable user identification scenario occurs in the circumstance of social network, where features of users are not acquirable while only relationships between users are provided. In this paper, we aim at the later situation, i.e., the Network User Identification, where features of users cannot be extracted in social network applications. We consider the information limitation of the single network and focus on utilizing the multiple relationships between identities from multi-networks. Different from the existing common subspace methods in Cross-Network User Identification, we propose a more discriminative Graph-Aware Embedding (GAEM) method for modeling the relationships as well as the transformation between different social networks explicitly in one unified framework. As a consequence, we can get more accurate predictions of the user identities directly based on the learned transferring model with GAEM. The experimental evaluations on real-world data demonstrate the superiorities of our proposed method comparing to the state-of-the-art.

This work was supported by NSFC (61773198).

1 Introduction

With the increasing popularity of social media platforms, more and more people are encouraged to participate in online social networks. Meanwhile, the problem of user identification becomes attractive and has been widely researched recently [9]. However, traditional user identification aims to predict links between user identities and in this case, the essential task turns into recovering the similar closures among identities. These paradigms are almost performed in single social network while neglecting the fact that people take participate in many networks, such as Facebook, Instagram and Twitter, simultaneously. How to identify the accounts of the same user across different social platforms is a desirable, newly proposed problem. In this paper, we named the later task as “multi-network user identification” (MUI). MUI has obviously practical significance in many web applications [8, 26].

Features used in user identification become a crucial fact affecting the performance, especially in single network user identification. Many researchers have been devoted to solving the problem of feature learning/engineering in UI [19]. However, these approaches adopted by existing solutions are always based on the collected profile features or content features, leaving the following essential challenges without considering [22]: Difficulties on obtaining profile features for privacy policies; Incompletion of profile features, owing to many reasons, i.e., law terms, users willings, distributed data storage; Sparsities of content features, due to the divergence of user activity patterns.

The structural information of the social networks, alternatively, can be utilized directly and efficiently for user identification across multiple online social networks and this information can be relatively easy to be obtained (usually permitted by carriers API). There are some structural information based methods proposed, which discover unmatched pair-wise user identities in an iterative way from seed matched pair-wise user identities [30, 33]. This type of structural information utilization generally use iterative strategy for spreading over linkages, and named by “propagation” methods. The propagation methods, however, are time-consuming and require more parameters on controlling the information spreading over linkages and is sensitive to linkage noises. To better address the mentioned issues, researchers proposed the embedding methods which first learn the latent features with the information of structure preserved, including TSVM [13], LINE [24], and then identify users based on different distance metric. Nevertheless, most existing graph embedding algorithms are step-by-step. Therefore, [23] built a hypergraph to model high-order relations, and proposed a novel subspace learning algorithm to project seed matching pairs to a node to ensure the aforementioned constraint. However, it needs auxiliary profile information.

In this paper, we focus on the second paradigm of structural information utilization approaches and propose a more discriminative Graph-Aware Embedding (GAEM) method aim at the MUI problem. The proposed GAEM models the relationships as well as the transformation between different social networks in one unified framework. As a consequence, we can identify the user identities across different social platforms using the network structural information only. Especially, rather than utilizing the raw data, we construct more discriminative weighted graphs by exploring the shared neighborhood structures of the vertices globally. Meanwhile, we can predict the transformation among different weighted graphs and ensure the consistency between the transferred weighted graphs, simultaneously. Besides, inspired by the rank constraint, we utilize the rank of the transformation as a rank regularization to improve the construction of the transformation and weighted graph. We empirically validate the effectiveness of our framework, and our model achieves significantly better performance on various tasks.

The rest of this paper starts from the introduction of related work. Then we propose our approach, followed by experiments and conclusion.

2 Related Work

The GAEM approach can identify the user identity across multiple networks in semi-supervised scenarios via the weighted graph embedding. Therefore our work is closely related to: user identity identification and graph embedding.

User identity identification problem was first formalized as connecting corresponding identities across communities in [28]. Considering social network diversity and information asymmetry, previous research can be categorized into three types considering the different feature extraction: profile based, content based and network structure based. User profile based methods aim to collect tagging information provided by users or user profiles from several social networks (e.g., user-name, profile picture, description, location, occupation, etc.), and represent the profiles in vectors [29], then construct models with the new feature representation [16, 17]; Content based methods aim to utilize the personally identifiable information from public pages of user-generated content [1, 14]. However, previous profile or content based methods always collect specific information of the users, and face serious challenges if required data are not available, i.e., missing features, data sparsity or false data, etc. Alternatively, recent methods have been focused on utilizing the structural network information, [15] unifies learning the latent features of user identities collectively in source and target networks. Nevertheless, the solution is iterative one-to-one mapping method.

Naturally, the local structures are represented by the observed links in the networks, which capture the first-order proximity between the vertices [24]. Most existing graph embedding algorithms are designed to preserve this kind of proximity [3, 25]. However, the observed first-order proximity in real-world data is always not sufficient for preserving the global network structures, while many legitimate linkages in the real-world network are actually not observed, which can be denoted as second-order proximity. As a complement, many works explore the second-order proximity between the vertices, which is not determined through the observed linkage but through the shared neighborhood structures of the vertices [21, 24]. Nevertheless, these graph embedding methods can not directly handle the user identification.

In this paper, we utilize the network information across different social platforms, which can be directed, undirected or weighted, to identify holistic unmatched user identities simultaneously. Specially, we construct the discriminative weighted graph by exploring the shared neighborhood structures of the vertices globally, and learn the transformation to make the transferred weighted graphs consistent. Meanwhile, a rank regularization is also proposed, and the implementation can be optimized effectively.

3 Proposed Method

3.1 Notations

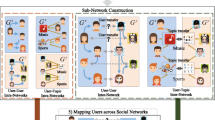
Our method can predict the user identities across multiple networks from different social platform, and we consider the case of two networks for simplicity here. Suppose the two relation networks are represented as $X^1 \in \mathbb {R}^{d_1 \times d_1}$, i.e., the Facebook network, and $X^2 \in \mathbb {R}^{d_2 \times d_2}$, i.e., the Twitter network, where $X_{ij}^v$ denotes the link value between the $i{-}$th instance and $j{-}$th instance of the $v{-}$th network, and $X_{ij}^v \not = 0$ if there is a linkage between $i{-}$th instance and $j{-}$th instance, $X_{ij}^v = 0$ otherwise, it is notable that $X^v$ can be directed, undirected or weighted. Meanwhile, the problem in our setting can be seen as a transductive problem, we have $N_1$ matched pair-wise users denoted by $\{(\mathbf{x}_{i}^1, \mathbf{x}_{j}^2)\}$ in advance, i.e., the blue dotted lines, and $N_2$ unmatched pair-wise users, i.e., the red dotted lines, the number of all practical matched pair-wise users is $N = N_1 + N_2$, $N \le \min (d_1,d_2)$, and GAEM aims to identify the unmatched user identities.

3.2 Graph-Aware Embedding (GAEM)

Naturally, the user linkage network $X^v$ can be seen as a graph $G^v = (V^v,E^v)$, $V^v= \{\mathbf{x}^v_i\}_{i = 1}^{d_v}$ corresponds to the set of vertices and $E^v = \{(\mathbf{x}_i^v,\mathbf{x}_j^v)\}$ denotes to the set of edges from $\mathbf{x}_i^v$ to $\mathbf{x}_j^v$ iff $X_{ij}^v \not = 0$. The observed links in the network can be considered as the local structures, which denote the first-order proximity between the vertices. However, the first-order proximity is insufficient for preserving the global network structures. As a complement, the second-order proximity between the vertices are used, which determined by shared neighborhood structures of the vertices, and the nodes with shared neighbors are likely to be similar.

Therefore, given the raw network $X^v$, inspired from [31], a weighted graph $\hat{G}^v = (V^v,\hat{E}^v,W^v)$ can be reconstructed to characterize the global structure of the raw relation network, $V^v= \{\mathbf{x}^v_i\}_{i = 1}^{d_v}$ corresponds to the set of vertices as above, and the $\hat{E}^v = \{(\mathbf{x}_i^v,\mathbf{x}_j^v)\}_{\mathbf{x}_i^v \in KNN(x_j^v)}$ denotes the set of edges from $\mathbf{x}_i^v$ to $\mathbf{x}_j^v$ iff $x_i^v$ is among the K-nearest neighbors of $x_j^v$. Furthermore, $W^v = [W_{ij}^v] \in \mathbb {R}^{d_v \times d_v}$ represents the nonnegative weight matrix, where $W_{ij}^v = 0$ iff $(\mathbf{x}_i^v,\mathbf{x}_j^v) \not \in \hat{E}^v$. Meanwhile, the $j{-}$th column $W_{j\cdot }^v = \{W_{1j}^v,W_{2j}^v,\cdots ,W_{d_vj}^v\}$ is determined by following problem:

$$\begin{aligned}&\min \limits _{W_{\cdot j}^v} \Vert \mathbf{x}_j^v - \sum _{(\mathbf{x}_i^v,\mathbf{x}_j^v)\in E^v}W_{ij}^v\mathbf{x}_i^v\Vert ^2 \nonumber \\ \textit{s.t.}\quad&\sum _{(\mathbf{x}_i^v,\mathbf{x}_j^v)\in \hat{E}^v}W_{ij}^v = 1, W_{ij}^v\ge 0 \end{aligned}$$

(1)

Conceptually, the $W_{ij}^v$ characterizes the relative importance of neighbor example $\mathbf{x}_i^v$ in reconstructing $x_j^v$. Here the loss term can take any convex forms and we use linear least square loss here for simplicity.

With the embedded weighted matrix $W^v$ in Eq. 1, and the known matched links $\{\mathbf{x}_{i}^1,\mathbf{x}_{j}^2\}$, we aim to predict the unmatched user identities. Specially, considering that different networks share the similar global structure, the objective is to learn a transfer matching matrix $M \in \mathbb {R}^{\min (d_v) \times max(d_v)}$, in which $M_{ij} =1$ iff the link $\{\mathbf{x}_{i}^1,\mathbf{x}_{j}^2\}$ is matched, $M_{ij} = 0$ otherwise. Without any loss of generalizations, we assume $d_1 \le d_2$ in the remaining of this paper, thus $M \in \mathbb {R}^{d_1 \times d_2}$. The transformation of the larger weighted matrix can be written as $M(MW^2)^T$, note that the M transfers the disordered weighted matrix $W^2$ in rows and columns. After the transformation, the weighted matrices of different networks should be similar, which can be represented as $\ell (W^v, M)$.

In practical case, the ideal transformation M, gives identical outputs for consistent weighted matrix, and consequently make the rank of M equal to N, which is the number of practical matched pair-wise users, and we define $RC(M) = rank(M)$ here, it is notable that RC(F) reflects the prediction compatibility among the weighted matrices. Thus, rank consistency can be used as a regularization in the learning framework, which is helpful to achieve compatible and consistent transformation upon the achieved weighted matrix. The keys of the proposed method are the reconstructed weighted matrices, the transfer matching matrix and rank regularization, which boost the performance of weighted matrices construction and the learning transfer matching matrix simultaneously. Benefited from these, we can bridge the loss of weighted matrices construction and the gap of transferred weighted matrices in a unified framework:

$$\begin{aligned} \min \limits _{W^v,M}&\sum _{v}\ell _v(X^v,W^v) + \ell (W^v,M) + \lambda RC(M) \nonumber \\ \textit{s.t.}\quad&M_{i,j} \in \{0,1\},\sum _{(\mathbf{x}_i^v,\mathbf{x}_j^v)\in \hat{E}^v}W_{ij}^v = 1, W_{ij}^v\ge 0 \end{aligned}$$

(2)

The first term $\ell _v(X^v,W^v)$ denotes the loss of the construction of each weighted matrix. Furthermore, $W^1$ and $W^2$ are disordered while the construction on each network is self-adaptive. The second term $\ell (W^v,M)$, is the loss of transferred weighted matrices, which leverages the consistency constraint of the weighted matrices on each linkage network. The last term RC(M), is the rank regularization on transfer matrix M, which constrains the degree of freedom. $\lambda > 0$ is the balance parameter.

Specifically, objective function $\ell _v(X^v,W^v)$ in Eq. 2 can be generally represented as the form in Eq. 1, the $\ell (W^v,M)$ can be any convex loss function here, and we use square loss here for simplicity. Thus, the Eq. 2 can be re-formed as:

$$\begin{aligned} \min \limits _{W^v,M}&\sum _{v}\sum _{j=1}^{d_v}\Vert \mathbf{x}_j^v - \sum _{\mathbf{x}_i^v \in KNN(x_j^v)}W_{ij}^v\mathbf{x}_i^v\Vert ^2 \nonumber \\&+\, \Vert W^1-M(MW^2)^T\Vert _F^2 + \lambda RC(M)\\ \textit{s.t.} \quad&M_{i,j} \in \{0,1\}, \sum _{(\mathbf{x}_i^v,\mathbf{x}_j^v)\in \hat{E}^v}W_{ij}^v = 1, W_{ij}^v\ge 0 \nonumber \end{aligned}$$

(3)

3.3 Optimization

The 2nd term in Eq. 3 involves the product of the weighted matrix $W^2$ and the transformation M, which makes the formulation not joint convex. Consequently, the formulation cannot be optimized easily. We provide the optimization process below:

Fix M, Optimize $W^v$: According to the constraint $\sum _{(\mathbf{x}_i^v,\mathbf{x}_j^v)\in \hat{E}^v}W_{ij} = 1$, the Eq. 1 can be re-written as:

$$\begin{aligned} \min \limits _{W^v_{\cdot j}}&{W^v_{\cdot j}}^T G_j^v W^v_{\cdot j}\\ \textit{s.t.}\quad&\mathbf{1}^\top W^v_{\cdot j} = 1, W_{i,j}\ge 0 \end{aligned}$$

Here, $G_j^v \in \mathbb {R}^{d_v \times d_v}$ is the local Gram matrix for $\mathbf{x}_j$ with elements $(G_j^v)_{mn} = (\mathbf{x}_j - \mathbf{x}_m)^\top (\mathbf{x}_j - \mathbf{x}_n)$. Apparently, when M and $W^2$ are fixed, the 3rd term of Eq. 3 is not related to $W^1$, besides, it is NP-hard to directly learn the binary $M_{i,j} \in \{0,1\}$, thus, we relax to $M_{i,j} \in [0,1]$. Eventually, Eq. 3 can be equivalently written as:

$$\begin{aligned} \min \limits _{W^1_{\cdot j}}&{W^1_{\cdot j}}^T (G_j^1+I)W^1_{\cdot j}-2{M(MW^2)^T_{\cdot j}}^T W^1_{\cdot j} \nonumber \\ \textit{s.t.}\quad&M_{i,j} \in [0,1], \mathbf{1}^\top W^1_{\cdot j} = 1, W_{i,j}\ge 0 \end{aligned}$$

(4)

Here I is the identity matrix with the same size of $G_j^1$. Equation 4 corresponds to a standard quadratic programming (QP) problem whose optimal solution can be obtained by any off-the-shelf QP solver. The weighted matrix $W^1$ is constructed by solving column-wisely. Similarly, when M and $W^1$ are fixed, the Eq. 3 can be equivalently written as:

$$\begin{aligned} \min \limits _{W^2_{\cdot j}}&{W^2_{\cdot j}}^T (G^2+\hat{M})W^2_{\cdot j} - 2{(M^TW^1M)^T_{\cdot j}} W^2_{\cdot j} \nonumber \\ \textit{s.t.}\quad&M_{i,j} \in [0,1], \mathbf{1}^\top W^2_{\cdot j} = 1, W_{i,j}\ge 0 \end{aligned}$$

(5)

Where $\hat{M} = M^TMM^TM$. Equation 5 also corresponds to a standard quadratic programming (QP) problem as Eq. 4.

From the aspect of weighted matrix construction, we treat the extra transferred weighted matrix as supervision to help to construct the discriminative weighted matrix $W^v$, i.e., we consider the transferred weighted matrices should have consistently global structure in this step.

Fix $W^v$, Optimize M: Apparently, when $W^v$ are fixed, the 1st term of Eq. 3 is not related to M, thus Eq. 3 can be equivalently written as:

$$\begin{aligned} \min \limits _{M}&||W^1-M(MW^2)^T||_F^2 + \lambda RC(M) \nonumber \\ \textit{s.t.}\quad&M_{i,j} \in [0,1] \end{aligned}$$

(6)

Note that the rank norm minimization is NP-hard, and inspired by [6], the nuclear norm usually acts as a convex surrogate. Specifically, given a matrix $X \in \mathbb {R}^{m \times n}$, its singular value are assumed as $\sigma _i, i =1,\cdots ,\min (m,n)$, which are ordered from large to small. Thus, the nuclear norm can be defined as $\Vert X\Vert _* = \sum _{i=1}^{\min (m,n)}\sigma _i$, and the nuclear norm has been widely used in various scenarios in rank norm minimization problem [10].

Nevertheless, blindly minimize the rank will break the natural structure of M. Therefore, a directional optimization approach, which conduct the RC(M) until converging to N during the minimization procedure is desired. According to [2, 27], we use truncated nuclear norm as a surrogate function of the RC(M) operator:

Definition 1

Given a matrix $X \in \mathbb {R}^{m \times n}$, the truncated nuclear norm $\Vert X\Vert _r$ is defined as the sum of $\min (m,n)-r$ minimum singular values, i.e., $\Vert X\Vert _r = \sum _{i=r+1}^{min(m,n)}\sigma _i(X)$.

Different from traditional nuclear norm minimization, which preserves all the singular values, truncated nuclear norm minimizes the singular values with first r largest ones unchanged, which is more close to the true rank definition. Specially, if $\Vert X\Vert _r = 0$, there are only r non-zero singular values for X, and this explicitly indicates the rank of X is less than or equals to r. Practically, in order to impel the RC(F) directional to the practical matched users, it is clear to set $r = N$.

The truncated nuclear norm can be re-formulated as the equivalent form by the following theorem [11]:

Theorem 1

Given a matrix $X \in \mathbb {R}^{m \times n}$ and any non-negative integer r ($r \le \min (m,n)$), for any matrix $A \in \mathbb {R}^{r \times m}$ and $B \in \mathbb {R}^{r \times n}$ such that $AA^\top = I_r, BB^\top = I_r$, where $I_r \in \mathbb {R}^{r \times r}$ is identity matrix. Truncated nuclear norm can be reformulated as:

$$\begin{aligned} \Vert X\Vert _r = \Vert X\Vert _* - \max \mathrm{{Tr}}(AXB^\top ) \end{aligned}$$

(7)

If the singular value decomposition of matrix X is $X = U\varSigma V^\top$ where $\varSigma$ is the diagonal matrix of singular values sorted in descending order and $U \in \mathbb {R}^{m \times n}, V \in \mathbb {R}^{n \times n}$. The optimal solution for the trace term in the above equation has a closed form solution: $A = (\mathbf{u}_1,\mathbf{u}_2,\cdots ,\mathbf{u}_r)^\top$ and $B = (\mathbf{v}_1,\mathbf{v}_2,\cdots ,\mathbf{v}_r)^\top$, corresponds to the first r columns of left and right singular vectors.

With Theorem 1, we can reformulate the Eq. 6 as:

$$\begin{aligned} \arg \min \limits _{M}&\Vert W^1-M(MW^2)^T||_F^2 + \lambda (\Vert M\Vert _* - maxTr(AMB^T)) \nonumber \\ \textit{s.t.} \quad&A^TA = I, B^TB = I \end{aligned}$$

(8)

Because of the non-convexity of truncated nuclear norm, alternative approach can be utilized for the optimization. A simple solution to Eq. 8 is alternating descent method. We can fix M and optimize A, B via SVD on M first, and then fix A and B to optimize M. When A and B are fixed, the subproblem is convex.

A and B can be obtained by SVD on M, which are the left and right singular vectors corresponding to the maximum N singular values. As the number of actually required singular vectors is rather small, partial SVD can be used [4]. The most computational cost step, however, is the subproblem for solving M in Eq. 8. We will give a detailed investigation on employing Accelerate Proximal Gradient Descent Method (APG) [2] for solving this subproblem in the following.

Note that when A and B are fixed, the problem is composed of two convex parts, i.e., a smooth loss term $P_1(M)$ and a non-smooth trace norm $P_2(M)$:

$$\begin{aligned} P_1(M) = L(M) - \mathrm{{Tr}}(AMB^\top ), P_2(M) = \Vert M\Vert _* \end{aligned}$$

(9)

APG is suitable for solving Eq. 9 [12], which optimizes on a linearized approximation version of the original problem. In the $t{-}$th iteration, if we denote the current optimization variable as $M^t$, then we can linearize the smooth part $P_1(\cdot )$ respect to $M^t$ as:

$$\begin{aligned} \small Q(M)&=\, P_1(M^t) + \mathrm{{Tr}}({<}\nabla P_1(M^t),M-M^t{>}) + \frac{L}{2}\Vert M-M^t\Vert _F^2 + P_2(F) \nonumber \\&=\, L(M) + \frac{L}{2}\Vert M-M^t\Vert _F^2 + \lambda \Vert M\Vert _* - \mathrm{{Tr}}(AMB^\top ) \nonumber \\&\quad + \mathrm{{Tr}}({<}\nabla P_1(M^t),M-M^t{>}) \end{aligned}$$

(10)

where $\nabla P_1(M^t) = - \big ((W^1 - M^t(M^tW^2)^\top )M^t(W^2+{W^2}^\top ) + \lambda A^\top B\big )$. Here L is the Lipschitz coefficient, which can be estimated by line search strategy [2]. Minimizing Q(M) w.r.t. M is equivalent to solving:

$$\begin{aligned} \hat{M} = \arg \min \limits _{M} \lambda \Vert M\Vert _* + \frac{L}{2}\Vert M - (M^t - \frac{1}{L}\nabla P_1(M^t))\Vert _F^2 \end{aligned}$$

(11)

APG updates the optimal solution in Eq. 11 at each iteration. Given the following theorem [6] about the proximal operator for nuclear norm:

Theorem 2

For each $\tau \ge 0$ and $Y \in \mathbb {R}^{m \times n},$ we have

$$\begin{aligned} D_{\tau }(Y) = \arg \min \limits _{X} \frac{1}{2}\Vert X - Y\Vert _F^2 + \tau \Vert X\Vert _* \end{aligned}$$

(12)

Here, $D_{\tau }(Y)$ is a matrix shrinkage operator for matrix Y, which can be calculated by SVD of Y. If SVD of Y is $Y = U\varSigma V^\top$, then

$$\begin{aligned} D_{\tau }(Y) = UD_{\tau }(\varSigma ) V^\top \quad D_{\tau }(\varSigma ) = diag(max(\sigma _i - \tau ,0)). \end{aligned}$$

(13)

we can solve Eq. 11 in a closed form:

$$\begin{aligned} \hat{M} = \mathfrak {D}_L(M^t) \mathrel {\mathop =^\mathrm{def}} D_{\frac{\lambda }{L}}(M^t - \frac{1}{L}\nabla P_1(M^t)) \end{aligned}$$

(14)

4 Experiment

4.1 Datasets and Configurations

Data Sets: In this paper, we use the datasets from webpage networks and the social networks in our empirical investigations.

The WebKB dataset [5] contains webpages collected from 4 universities: Wisconsin, Washington, Cornell and Texas (denoted as Wins., Wash., Corn. and Texas in tables) and described with two networks: the content and the citation. The content represents the documents-words matrix, containing 0/1 values, and can be indicated as the similarity relationships between the documents. On the other hand, the citation denotes the number of citation links between documents, which can be acted as another network structure. The ground-truth mapping of WebKB across these two networks is in the documents-mapping. To demonstrate the generalization ability, we also demonstrate our method on different social networks. The social networks collection consists of four popular online social networking sites: LiveJournal (LJ), Flickr (FL), Last.fm (LF), and MySpace (MS) as [32]. We use the linked user accounts dataset from [7, 20] as the ground truth. The data was originally collected by [20] through Google Profiles service by allowing users to integrate different social network services. Five subsets are constructed from social networks, i.e., flickr-lastfm; flickr-myspace; livejournal-lastfm, livejournal-myspace and livejournal-flickr.

For all datasets in our experiments, we randomly select $\{20\%, 40\%,$ $60\%, 80\%\}$ for matched pair-wise examples, and the remains are unmatched for prediction. We repeat this for 30 times, the acc. and std. of predictions are recorded as classification performance. The parameter $\lambda$ in the training phase is tuned in $\{ 10^{-2},\cdots , 10^2\}$. The number of k-nearest neighbors is set 15. Empirically, when the variations between the objective value of Eq. 3 is less than $10^{-5}$ in iteration, we treat GAEM converged.

Compare Algorithms: Our method solves the problem of user identities identification across networks. Thus, we choose five state-of-the-art user linkage identify classifiers: HYDRA [16], COSNET [32], ULink [17], NS [18], IONE [15]. Note that the HYDRA and COSNET utilize both the profile information and network structure, and we consider the raw network structure information as the profile features in our setting, on the other hand, ULink is difficult to handle the sparse network information, and we use the embedded features by Isomap as the input. Moreover, NS and IONE directly take the network structure as input. Besides, our method is also related to graph embedding. Thus, we construct the weighted matrix with four graph embedding methods: Baseline (BL), Isomap [25], Deepwalk [21], Weight [31], the first two methods, i.e., BL, Isomap, only consider the local structure, while remaining two methods, i.e., Deepwalk, Weight, consider the global structure. It is notable that these methods can not unify the weighted matrix construction and transformation together, thus, we calculates the weighted matrices and then optimize the transformation M separately.

Fig. 1.

Webpage linkage comparison for batch data setting (with ratio between between the ground-truth matching pairs to non-matching pairs being 4:1)

Fig. 2.

Social Networks comparison for batch data setting (with ratio between the ground-truth matching pairs to non-matching pairs being 3:1)

4.2 Experiment Results

Multiple-Network Identity Identification: To demonstrate the effectiveness of our proposed method. For both the webpage networks and social networks datasets, We fix the ratio of the number of matched pair-wise users at $80\%$ firstly, and record the avg. ± std. of the GAEM and compared methods in Figs. 1 and 2.

Figure 1 clearly reveals that on all webpage datasets, the average accuracies of GAEM are the best. Further more, while comparing to the graph embedding methods, the methods considering the global structure proximity, i.e., DeepWalk, Weight, are superior to the local structure proximity based methods, i.e., BL, Isomap, on the majority of datasets, which indicates that global structure proximity is more efficient and different social networks share the similar global structure, and it confirms to the real significance. On the other hand, the performance of previous user identity linkage methods are not well performed, note that these methods require the specific collected or designed features, specifically, ULink is a supervised method, which can not utilize the network structure information; HYDRA maximizes the structure consistency by modeling the core social network behavior consistency, and the performance hinges heavily upon the availability of the consistent structure, where the consistency is calculated by extra profile features, it performs worse than GAEM in the cases where raw features can not possess consistent structure, COSNET is found to be in a similar situation as HYDRA, as for NS and IONE methods, these methods also require additional information and are sensitive to the parameters. Thus, GAEM is well performed considering the global structure proximity with the network information. To demonstrate the generalization ability, we conduct more experiments, Fig. 2 records the prediction accuracies (avg. ± std.) of the GAEM and compared methods on five social network datasets, and Fig. 2 reveals that on the social network datasets, the average accuracies of GAEM are also competitive with the compared methods, the average accuracies are the best on three datasets, i.e., flickr-lastfm; flickr-myspace; livejournal-lastfm.

Fig. 3.

Influence of number of matched pair-wise users of Webpage linkage comparison

Influence of Number of Matched Pair-Wise Users: In order to explore the influence of the number of initial matched pair-wise users on performance, more experiments are conducted. In this section, the parameters in each investigation are fixed as the optimal values, the $\lambda$ in GAEM is set 1, while the ratio of initial matched pair-wise users varies in $\{20\%,40\%,60\%,80\%\}$. Due to the page limits, results on only 4 datasets, i.e., Wins., Wash., Corn., and Texas, and the results are recorded in Fig. 3. From these figures, it clearly shows that GAEM achieves the best performance when the ratio is larger than $40\%$ on most datasets. Besides, we can also find that GAEM achieves an optimal performance fast, and the accuracy of GAEM increases faster than compared methods.

Fig. 4.

Objective function value convergence and corresponding classification accuracy vs. number of iterations of GAEM with matched pair-wise users ratio at $80\%$

Empirical Investigation on Convergence: To investigate the convergence empirically, the objective function value, i.e., the value of Eq. 3 and the classification performance of GAEM in each iteration are recorded. Due to the page limits, results on only 4 datasets mentioned above, are plotted in Fig. 4. It clearly reveals that the objective function value decreases as the iterations increase, and the classification performance is stable after several iterations. Moreover, these additional experimental results indicate that our GAEM can converge very fast, i.e., GAEM converges after 3 rounds.

5 Conclusion

The user identification problem in the multi-network environment is a challenging problem. Previous efforts mainly focus on the predefined profile or content features in the learning approaches, while leaving the data incompleteness and sparsities unconsidered. These approaches, meanwhile, are difficult to handle the information of structures provided by multi-networks. In this paper, we propose the Graph-Aware Embedding (GAEM) approach, which utilizes the more general social networks information and identifies the accounts of the same user by exploiting useful information from the networks. We construct the more discriminative weighted graph instead of the raw linkage network, while predicting the transformation among different weighted graphs simultaneously. As a consequence, we can get more accurate predictions of the user identities directly obtained from the learned transformation matrix, experimental evaluations on real-world applications demonstrate the superiority of our proposed method over the compared methods. How to extend multiple platforms and the scalability with improved performance are interesting future works.