Evolution of Risk-Statuses in One Model of Tax Control

Abstract

Nowadays information is an important part of social life and economic environment. One of the principal elements of economics is the system of taxation and therefore tax audit. However total audit is expensive, hence fiscal system should choose new instruments to force the tax collections. In current study we consider an impact of information spreading about future tax audits in a population of taxpayers. It is supposed that all taxpayers pay taxes in accordance with their income and individual risk-status. Moreover we assume that each taxpayer selects the best method of behavior, which depends on the behavior of her social neighbors. Thus if any agent receives information from her contacts that the probability of audit is high, then she might react according to her risk-status and true income. Such behavior forms a group of informed agents which propagate information further then the structure of population is changed. We formulate an evolutionary model with network structure which describes the changes in the population of taxpayers under the impact of information about future tax audit. The series of numerical simulation shows the initial and final preferences of taxpayers depends on the received information.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

8.1 Introduction

The tax system is one of the most important mechanisms of state regulation. A significant part of this system is tax control, which provides receiving taxes and fees in the state budget. For a wide class of models, such as [4, 6, 16, 25], which describe tax control with static game-theoretical attitude, “the threshold rule” was formulated. This rule defines the value of auditing probability which is critical for the decision of taxpayers to evade taxation or not. However, in real life it is difficult to implement tax inspections with the threshold probability because this process requires large investments from the tax authority, while it has substantially limited budget. Hence, the tax authority needs to find a way to stimulate the population to pay taxes in accordance with their true level of income.

Previous studies [18, 22] have shown that information dissemination has a significant impact on the behavior of agents in various environments, such as the urban population, the social network, labor teams, etc. Taking into account previous research [1,2,3], the current paper studies the propagation of information about upcoming tax inspections as a way to stimulate the population to pay taxes honestly. This approach allows tax authority to optimize the collection of taxes within the strong limitation of budget.

Let’s suppose that the population of taxpayers is heterogeneous in its perception of such information. Additionally to previous research [9, 10] susceptibility of each agent depends on its risk-status, due to her natural propensity to risk. Economic environment of each individual also impacts on the perceiving of incoming information. In contrast to many different works, where information spreads during random matches of agents, here we consider only structured population and we suppose that information can be transferred only between connected agents. Social connections of each taxpayer can be described mathematically by using networks of various modifications. We also assume that tax authority injects information about future audits to the population and thereby the share of Informed agents is formed. Agents from the Informed group can spread it over their network of contacts and thereby the structure of population is changed. According to all these reasons we formulate an evolutionary model on the network which describes the variation of taxpayers’ behavior. We estimate the initial and final distribution of taxpayers which prefer to evade taxation in series of numerical simulations. Numerical experiments include two different approaches that characterize the evolutionary process: special imitation rule for evolutionary game on the network and Markov’s chain which define random process on the network.

The paper is organized as follows. Section 8.2 presents the mathematical model of tax audit in classical formulation. Section 8.3 introduces an idea of risk propensity of taxpayers. Section 8.4 shows the dynamic model of tax control, which includes the knowledge about additional information and presents two different approaches to find a solution. Numerical examples are presented in Sect. 8.5.

8.2 Static Model of Tax Audit

As a basic model we consider a game-theoretical static model of tax control, in which the players are the tax authority and n taxpayers as a basis for the following study. Every taxpayer has true income ξ and declares income η after each tax period, η ≤ ξ.

As it was studied in the classical works, such as [6, 25], to simplify the model, we suppose, that the total set of taxpayers is divided into the groups of low level income agents and high level income agents. Obviously, the number of partitions can be increased, but it does not effect on the following arguments and conclusions. In other words, taxpayers’ incomes can take only two values: ξ ∈{L, H}, where L is the low level and H is the high level of income (0 ≤ L < H). Declared income η also can take values from the mentioned binary set η ∈{L, H}.

Thus, in this model there are three different groups of taxpayers, depending on the relation η(ξ) between true and declared incomes:

• 1. η(ξ) = L(L);

• 2. η(ξ) = H(H);

• 3. η(ξ) = L(H).

Obviously that the taxpayers from the first and the second groups declare their income correspondingly to its true level and they do not try to evade. The third group is the group of tax evaders. In other words, this group is of interest of the tax authority.

The tax authority audits those taxpayers, who declared η = L, with the probability P _L every tax period. Let’s suppose that tax audit is absolutely effective, i.e. it reveals the existing evasion. The proportional case of penalty is considered: when the tax evasion is revealed, the evader must pay (θ + π)(ξ − η), where constants θ and π are the tax and the penalty rates correspondingly. For the agents from the studied groups the payoffs are:

$$\displaystyle \begin{aligned}u \left(L(L)\right) = (1-\theta) \cdot L; \end{aligned} $$

(8.1)

$$\displaystyle \begin{aligned}u \left(H(H)\right) = (1-\theta) \cdot H; \end{aligned} $$

(8.2)

$$\displaystyle \begin{aligned}u \left(L(H)\right) = H - \theta L - P_L(\theta+\pi)(H - L). \end{aligned} $$

(8.3)

The fraction of audited taxpayers is P _L. It’s obvious that either the agents from the first group (who actually have true income ξ = L) or the evaders from the third group are both in this fraction of audited taxpayers.

The total set of the taxpayers is divided into the next groups: wealthy taxpayers, who pay taxes honestly (η(ξ) = H(H)), insolvent taxpayers (η(ξ) = L(L)) and wealthy evaders (η(ξ) = L(H)). The diagram, presented in Fig. 8.1a, illustrates this distribution.

Fig. 8.1

Auditing of the different groups of the taxpayers

In Fig. 8.1, cases: b, c, d, the little circle, inscribed in the diagram, corresponds to the fraction of audited taxpayers. Let’s call it an “audited circle”. Only those, who declared η = L, are in the interest for auditing. Therefore, the mentioned circle is inscribed into the sectors, which correspond to the situations η(ξ) = L(H) and η(ξ) = L(L).

On one hand in Fig. 8.1b the case, when either evaders or simply insolvent taxpayers are audited, is considered. In Fig. 8.1c the “audited circle” is contained in the area, which satisfies the condition η(ξ) = L(H). This is the optimistic situation, when every audit reveals the existing tax evasion. On the other hand, the Fig. 8.1d illustrates the pessimistic case, when none of the audits reveals the evasion, because only insolvent taxpayers, declared their true income η(ξ) = L(L), are audited. Certainly, all presented diagrams illustrate only some boundary ideal cases, however the tax authority’s aim is obviously to lead the real situation closer to the illustration in Fig. 8.1c.

Hence, the following arguments, related to the searching of possible tax evasions, apply to the third group of the agents, declared η(ξ) = L(H). Thereby, precisely this group is expedient to be considered as the studied population, speaking in the terms of the evolutionary games.

Risk neutral taxpayers’ behaviour supposed to be absolutely rational: their tax evasion is impossible only if the risk of punishment is so high that the tax evader’s profit is less or equal to his expected post-audit payments (in the case when his evasion is revealed):

$$\displaystyle \begin{aligned} P_L(\theta+\pi)(H-L) \ge \theta(H-L). \end{aligned}$$

Therefore, the critical value of audit probability P _L (due to the taxpayer’s decision to evade or not) is

$$\displaystyle \begin{aligned} P_{L}^{*}=\frac{\theta}{\theta + \pi}. \end{aligned} $$

(8.4)

For this type of models the optimal solution is usually presented in the form of the “threshold rule” in various modifications (see, for example, [6] or [25]). In [4] this rule is formulated so that the optimal value $P_{L}^{*}$ of the auditing probability is defined from (8.4), and for the risk neutral taxpayer the optimal strategy is

$$\displaystyle \begin{aligned} \eta^*(\xi)=\left\{ \begin{array}{ll} H, & P_L \ge P_{L}^{*}; \\ L, & P_L < P_{L}^{*}. \end{array} \right. \end{aligned} $$

(8.5)

Nevertheless there are some problems which should be fixed to make the static model described above close to real-life process. The first problem is that the players are supposed to be risk neutral. However in real life there are also risk averse and risk loving economic agents. Another problem is that we consider the game with complete information. It is assumed that the taxpayers know (or can estimate) the value of the auditing probability, but, by considering the static model, we do not take into account the method of receiving information. The third problem is that the auditing with optimal probability (8.4) is excessively expensive and the tax authority usually has strongly limited budget, thus, the actual value of P _L should be substantially less than $P_{L}^{*}$ in real life. By taking into consideration all mentioned reasons, we formulate an extended model of tax audit which includes an information component and an evolutionary process of adaptation of taxpayers to the changes in the economic environment.

8.3 Model with Different Risk-Statuses

Now let’s consider the homogeneous population of n taxpayers, where agents possess one of three risk-statuses: risk averse, risk neutral and risk loving agents. Let’s restrict the considered population by the subpopulation of taxpayers with high level H of income. This restriction is natural because there is no reason and ability to evade for the taxpayers with low level L of income, independently on their risk-status.

The size of this subpopulation is n _H (n _L + n _H = n, where n _L is a number of the taxpayers with income level L). Now let ν _a be the share of risk averse agents with income H ($\nu _a = \frac {n_a}{n_H}$), ν _n be the share of risk neutral agents with high-level income ($\nu _n = \frac {n_n}{n_H}$) and ν _l be the share of risk loving agents with income H ($\nu _l= \frac {n_l}{n_H}$) respectively. Naturally, ν _a + ν _n + ν _l = 1 (or, equivalent equation, n _a + n _n + n _l = n _H).

We also assume that each risk-status has its “threshold of sensitivity”. This term means that each taxpayer with income H compares the real and critical values of the auditing probability P _L before to make a decision to evade or to pay taxes honestly. Based on the results obtained for the static model 8.2 it is obvious that for the risk neutral agent this threshold value is $P_{L}^{*}$ from the Eq. (8.4). Let $\underline {P_L}$ and $\overline {P_L}$ be the sensitivity thresholds for the risk averse and risk loving agents correspondingly. These values satisfy the inequality [17]:

$$\displaystyle \begin{aligned} 0 \le \underline{P_L} < {P_L}^* < \overline{P_L} \le 1. \end{aligned}$$

It is natural to suppose that the agents’ behavior depends on their statuses. Here, risk-status defines the relation between obtained information about future auditing and agent’s own sensitivity threshold. If the information of tax audit is absent then we assume that initially the population is sure that the probability of future audits takes its values from the interval $( \underline {P_L}, {P_L}^*)$.

This value is less than the threshold for the risk neutral agents, therefore, they evade of taxation, moreover, risk loving taxpayers, which are sure in small possibility of auditing, also do not pay. The only payers are agents with risk-averse status form the considered subpopulation. In this situation the total tax revenue is

$$\displaystyle \begin{aligned} TTR_1 = n_L \theta L + n_H \left( \nu_a \theta H + (1- \nu_a)\left(\theta \, L + P_L \,(\theta+\pi)(H - L)\right)\right) - n \, P_L \, c , \end{aligned} $$

(8.6)

where c is the cost of one audit.

8.4 The Evolutionary Model on the Network

In Sect. 8.2 we have discussed that it is extremely expensive to audit taxpayers with the optimal probability (8.4). Thus the tax authority needs to find additional ways to stimulate taxpayers’ fees. One of these ways is the injection of information about future auditing (which possibly can be false) into the population of taxpayers. Following [9,10,11], in current study we discuss that information contains a message “$P_L \ge P_{L}^{*}$”. We suppose that the dissemination of such information over the population will impact on the behavior of taxpayers and their risk-statuses. The cost of unit of information is c _inf. We assume that c _inf is significantly less than the auditing casts (c _inf ≪ c). Every taxpayer who receives the information can use it by choosing the strategy to pay or not to pay taxes due to her true income level. Additionally, in contrast to the standard approach of evolutionary games [21, 26], in which it is assumed that meetings between agents occur randomly in the population, here we will consider only the connected agents. For example, any taxpayer has a social environment such as family, relatives, friends, neighbors. Communicating with them, agents choose opponents at random to transmit information, but taking into account the existing connections. Thus, to describe possible interactions between agents, the population can be represented by a network where the nodes are taxpayers transmitting information to each other during the process of communication and links are the connections between them. Earlier such approach was considered in [9].

Therefore, the taxpayer’s decision about her risk-status (risk averse, risk neutral or risk loving) depends on two important factors: her own (natural) risk propensity and the behavior of her neighbors in the population (those with whom she communicates). As a result of the dissemination of information, the entire population of agents is divided into two subgroups: those who received and used the information (the share n _inf), and those who do not intend to use the information (the share n _noinf), or, we can say, those who have a propensity to perceive or not to perceive the received information. Thus, at the initial time moment this population can be presented as a sum of the mentioned shares:

$$\displaystyle \begin{aligned} n = n_{inf} (t_0) + n_{noinf} (t_0), \end{aligned}$$

but at each following moment the ratio of the fractions n _inf(t) and n _noinf(t) will differ from the previous one.

If one taxpayer from a subgroup of those who use information meets another one from the same subgroup, they will get the payoffs (U _inf, U _inf). In this case both of them know the same information and pay, hence their payoff is defined from the Eq. (8.2). Similarly, if the taxpayer who does not perceive the information (and therefore wants to evade) meets the same taxpayer, they will get the payoffs (U _ev, U _ev), which are defined from the Eq. (8.3).

We denote the taxpayer’s propensity to perceive the information as δ, 0 ≤ δ ≤ 1, and consider a case when the uninformed taxpayer meets the informed taxpayer. As a result of such meeting, uninformed taxpayer obtains information and should pay the payoff (8.2) with probability δ if she believes in this information, or the payoff (8.3) if she does not believe.

In the current study we use evolutionary game approach to describe the dynamic nature of such economic process. Thus, we have a well-mixed population of economic agents (taxpayers), where the instant communications between taxpayers can be defined by two-players bimatrix game [21]. For the cases, when taxpayers of different types meet each other, the matrix of payoffs can be written in the form:

where A is the strategy of taxpayer if she is informed (she perceives the information) and B is the strategy of taxpayer if she is uninformed.

Suppose that at a finite time moment T the system reached its stationary state. Then let’s denote by ν _inf the share of those who used the received information and paid taxes according to their true income level ($\nu _{inf} = \nu _{inf} (T) =\frac {n_{inf} (T)}{n}$), while the share of those who evades taxation despite information received is denoted by ν _ev ($\nu _{ev} = \nu _{ev} (T) =\frac {n_{ev} (T)}{n}$).

Hence the total income received from taxation of the entire population is

$$\displaystyle \begin{aligned} \begin{array}{ll} TTR_2 = n_L \theta L + n_H & \left( \nu_{inf} \theta H + \nu_{ev} \left(\theta L + P_L(\theta+\pi)(H-L) \right) \right) - \\ & - n(P_L \, c + \nu_{inf}^0 c_{inf}), \end{array} \end{aligned} $$

(8.7)

where $\nu _{inf}^0 = \nu _{inf}(t_0)$.

The papers [12, 14, 15] have studied the game of a large number of agents and obtained the results which can be used to give precise quantitative predictions and proper stability analysis of equilibria.

In this paper we present a comparative analysis of two evolutionary approaches applied to the model of tax control. The first approach is to define propagation information as a random process on the network and use the model by De Groot [7] as a mathematical tool. The second approach is built on the special stochastic imitation rule for evolutionary dynamics on the network [20, 21]. Now let’s examine how these ideas can be applied to the modeling of dynamic processes on networks.

8.4.1 The Model Based on the Markov Process on the Network

Now let’s refuse the assumption that agents can estimate the choice of each strategy absolutely correctly. This refusion allows us to consider a model of random dissemination of information about the probability of future auditing. One of the first models describing this problem is the model by De Groot [7], then similar attitude was also studied in [8] and [5].

Based on the previous research we consider a direct network G = (N, P), where N is the set of economic agents (for the present study N = {1, …, n}), and P is a stochastic matrix of connections between agents: p _ij is an element of the matrix P which characterizes the connection between agents i and j. p _ij > 0 in the case when there exists a social connection between taxpayers i and j, (i, j ∈ N). The value of this parameter is close to 1 if the ith agent has a reason to assume that the agent j has an expert knowledge about the probability of auditing, and otherwise it is close to 0.

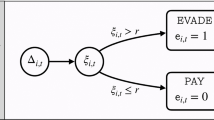
Let’s assume that at the initial time moment each agent has a certain belief, $f_i^0$ about the value of the auditing probability. Moreover, we suppose that she decides to evade taxation, comparing $f_i^0$ with the threshold of sensitivity P _L ^∗, in this case if $f_i^0 < {P_L}^*$ then the ith agent evades paying taxes, else if the threshold rises, then she prefers not to risk.

Interaction of agents leads to the updating of their knowledge on the auditing probability at each iteration:

$$\displaystyle \begin{aligned} f_i^k = \sum_{j=1}^{n} p_{ij} f_j^{k - 1}. \end{aligned}$$

The interaction continues infinitely or until the moment when for some k the condition $f_i ^ k \approx f_i ^ {k-1}$ holds for every i.

Now, we assume that information centers can be artificially introduced into the natural population of agents, which is presented as a network. Here, as information centers (further principals) we set the agents who seek to convince the other agents that value of the auditing probability is equal to some determined value.

The role of such information center can be performed by any of the agents j. Let S be the set of agents for which the condition p _ij > 0, i ≠ j, (it is clear because this inequality is formulated for pairs of different agents). We assign the parameter α _j, which expresses the degree of confidence of the value $f_j^{\,0}$, with this agent j. Then the updated elements of the jth row of the matrix P will have the following form:

$$\displaystyle \begin{aligned} p_{ij} = \left\{ \begin{array}{ll} \alpha_j, & i=j \\ \frac{1 - \alpha_j}{|S|}, & i \in S\\ 0, & i \notin S, i \neq j \end{array} \right. \end{aligned} $$

(8.8)

Described model can be used, for example, to present a goal of the tax authority to overstate the value of the auditing probability. In this case, the parameters of the information center have the following form: $f_j^0 = 1$, α _j ≈ 1.

8.4.2 The Model Based on the Proportional Imitation Rule

In the current paragraph we present a different approach to describe the sequence of changes in the population of taxpayers. Let G = (N, L) denote an indirect network, where N is a set of economic agents (N = {1, …, n} as in Sect. 8.4.1) and L ⊂ N × N is an edge set. Each edge in L represents two-player symmetric game between connected taxpayers. The taxpayers choose strategies from a binary set X = {A, B} and receive payoffs according to the matrix of payoffs in Sect. 8.4. Each instant time moment agents use a single strategy against all opponents and thus the games occurs simultaneously. We define the strategy state by x(T) = (x ₁(t), …, x _n(t))^T, x _i(t) ∈ X. Here x _i(t) ∈ X is a strategy of taxpayer i, $i = \overline {1, n}$, at time moment t. Aggregated payoff of agent i is defined as in [20]:

$$\displaystyle \begin{aligned} u_i = \omega_i\sum_{j\in M_i} a_{x_i(t), x_j(t)}, \end{aligned} $$

(8.9)

where $a_{x_i(t), x_i(t)}$ is a component of payoff matrix, M _i := {j ∈ L : {i, j}∈ L} is a set of neighbors for taxpayer i, weighted coefficient ω _i = 1 for cumulative payoffs and $\omega _i=\frac {1}{|M_i|}$ for averaged payoffs. Vector of payoffs of the total population is u(t) = (u ₁(t), …, u _n(t))^T.

The state of population is changed according to the rule, which is a function of the strategies and payoffs of neighboring agents:

$$\displaystyle \begin{aligned} x_i(t+1)=f(\{x_j(t), u_j(t):j\in N_i\cup\{i\}\}). \end{aligned} $$

(8.10)

Here we suppose that taxpayer changes her behavior if at least one neighbor has better payoff. As the example of such dynamics we can use the proportional imitation rule [21, 26], in which each agent chooses a neighbor randomly and if this neighbor received a higher payoff by using a different strategy, then the agent will switch with a probability proportional to the payoff difference. The proportional imitation rule can be presented as:

$$\displaystyle \begin{aligned} p\,(x_i(t+1)=x_j(t)):=\left[\frac{\lambda}{|M_i|}(u_j(t)-u_i(t))\right]_0^1 \end{aligned} $$

(8.11)

for each agent i ∈ L where j ∈ M _i is a uniformly randomly chosen neighbor, λ > 0 is an arbitrary rate constant, and the notation $[z]^1_0$ indicates $\max (0,\min (1, z))$.

Below we present two cases of the changing rule [10, 11]:

• Case 1. Initial distribution of agents is nonuniform. When agent i receives an opportunity to revise her strategy then she considers her neighbors as one homogeneous player with aggregated payoff function. This payoff function is equal to the mean value of payoffs of players who form a homogeneous player. It is assumed that the agent meets any neighbor with uniform probability, then mixed strategy of such homogeneous player is a distribution vector of pure strategies of included players. If payoff function of homogeneous player is better, then player i changes her strategy to the most popular strategy of her neighbors.

• Case 2. Initial distribution of agents is uniform. In this case agent i keeps her own strategy.

8.5 Numerical Simulations

In this section we present numerical examples to support the approaches described in Sects. 8.4.1 and 8.4.2. Based on these simulation we analyze the following factors of influence on the population of taxpayers:

• 1. the structure of the network: we use grid and random structures of graphs;

• 2. the way of information dissemination: we consider the processes based on the Markov processes and the proportional imitation rule;

• 3. the initial distribution of risk-status in the population, i.e. what part of the population has a certain propensity to risk;

• 4. the value of the information injection, i.e. the portion of Informed agents at the initial time moment.

In all experiments we use the distribution of the income among the population of Russian Federation in 2017 [23] (see Table 8.1).

Table 8.1 The distribution of income among taxpayers

According to the model we suppose that only two level of income is accessible for each taxpayer: low and high (L and H). After the unification of groups with different levels of income according to the economic reasons, we calculate the average levels of income L and H (the mathematical expectations of the uniform and Pareto distributions—see 8.7) and receive the corresponding shares of the population (see Table 8.2).

Table 8.2 Two modeled groups and average income

For all experiments we fix the following values of parameters:

• share of risk-averse taxpayers in population is ν _a = 17% due to the psychological research [19];

• tax and penalty rates are θ = 0.13 due to the income tax rate in Russia [24], π = 0.065 (for bigger values of π, we obtain even bigger values of optimal audit probability P _L ^∗);

• optimal value of the probability of audit is P _L ^∗ = 0.67;

• actual value of the probability of audit is P _L = 0.1;

• unit cost of auditing is c = 7455 (minimum wage in St. Petersburg [23]);

• unit cost of information injection is c _inf = 10% ^∗ c = 745.5;

• under the implementation of the approximate equality $f_i ^ k \approx f_i ^ {k-1}$ from the Sect. 8.4.1 we have that the inequality $|f_i^k - f_i^{k-1}| < 10^{-3}$ holds.

As we described in Sect. 8.4, we use the network G to define the structure of population. The number of considered taxpayers is defined from the Table 8.2. If, for example, the size of the total population is n = 30, the size of subpopulation with income level H is n _H = 0.57 ⋅ n = 17.10, when n = 25 we obtain that n _H = 14.25 and so on. For the network we use the relation $\frac {\lambda }{|M_i|}=1$ and vary values of other parameters in different examples.

Let the number of nodes in the population be n = 30. For the initial model, which does not include the process of information dissemination the value of total tax revenue (8.6) is TTR ₁ = 50, 935.26. For the network of n = 25 nodes TTR ₁ = 42, 446.05.

For the model which takes into account dissemination of information, we apply two algorithms: the first is based on the Markov process on the network (see Sect. 8.4.1), the second is based on the proportional imitation rule (Sect. 8.4.2).

Several results of numerical modeling of the Markov process in the network are presented in Figs. 8.2, 8.3, 8.4, and 8.5. Blue dots correspond to evaders and yellow dots correspond to those who pay honestly, respectively. The value of TTR ₂ exceeds TTR ₁ by almost two times, thus the existence of an information center is actual because the number of evaders has decreased.

Fig. 8.2

Markov process. Agents are considered in pairs. Direct link from one to the other is formed with a probability of 1/20, n = 25. Initial state is (ν _inf, ν _ev) = (1, 24)

Fig. 8.3

Markov process. Stationary state is (ν _inf, ν _ev) = (22, 3). Total tax revenue TTR ₂ = 83, 624.94

Fig. 8.4

Markov process. Agents are considered in pairs. Direct link from one to the other is formed with a probability of 1/10, n = 25. Initial state is (ν _inf, ν _ev) = (1, 24)

Fig. 8.5

Markov process. Stationary state is (ν _inf, ν _ev) = (20, 5). Total tax revenue TTR ₂ = 78, 901.06

For the second algorithm we compute the payoff functions of taxpayers U _inf = 43, 500, U _ev = 47, 643.75.

The results of numerical simulation obtained from the proportional imitation rule are shown in Figs. 8.6, 8.7, 8.8, 8.9, 8.10, and 8.11. Despite the fact that the probability of information perception is high (δ = 0.9), the network structure is such that most agents become evaders, and the total tax revenue is significantly reduced. From the experiments it follows that the value of TTR ₂ is significantly lower than the value of TTR ₁.

Fig. 8.6

Grid. Probability of perception information δ = 0.9, n = 25. Initial state is (ν _inf, ν _ev) = (23, 2)

Fig. 8.7

Grid. Probability of perception information δ = 0.9, n = 25. Stationary state is (ν _inf, ν _ev) = (0, 25). Total tax revenue TTR ₂ = 15, 261.31

Fig. 8.8

Random. Probability of perception information δ = 0.9, n = 30. Initial state is (ν _inf, ν _ev) = (28, 2)

Fig. 8.9

Random. Probability of perception information δ = 0.9, n = 30. Stationary state is (ν _inf, ν _ev) = (3, 27). Total tax revenue TTR ₂ = 25, 101.19

Fig. 8.10

Ring. Probability of perception information δ = 0.9, n = 30. Initial state is (ν _inf, ν _ev) = (13, 17)

Fig. 8.11

Ring. Probability of perception information δ = 0.9, n = 30. Stationary state is (ν _inf, ν _ev) = (0, 30). Total tax revenue TTR ₂ = 29, 197.88

From the series of numerical experiments by using two alternative algorithms for the model of tax control which takes into account the risk statuses of economical agents we can summarize the following.

Firstly, the algorithm based on proportional imitation rule (see Sect. 8.4.2) is not very effective for the considered model. In contrast to the previous study (see. [10] or [11]), where we considered the average income of each agent, in the current paper the structure of the network influences on the population of taxpayers such as the imitation of behavior of nearest neighbor increases the share of evaders, even with a high probability of information perception and a relatively small number of the evaders at the initial moment. Therefore, the total revenue of the system is significantly reduced. Hence we can conclude that if the income of taxpayers is differentiated than we need to apply an alternative approach to estimate the effectiveness of the propagated information.

In contrast, the new approach considers the algorithm which is based on the Markov process (see Sect. 8.4.1). And the second conclusion is that the mentioned algorithm is effective. In the framework of this attitude only one agent injects information and hence she can be considered as an information center in the network. This approach significantly minimizes the costs of spreading information over the population of taxpayers. Thus the total revenue of the system is increased depending on the structure of the population and a number of connections between the information center and the outer network.

8.6 Conclusion

In the study presented above we have investigated the problem of tax control taking into account two important factors: the difference between propensity to risk of the economical agents and the propagation of the information about possible tax inspections among the population of taxpayers. We used two different approaches to illustrate the process of propagation of information on network such as Markov process and stochastic imitation rule for evolutionary dynamics. For the mentioned models we presented mathematical formulations, analysis of the agents’ behavior and series of numerical experiments. Numerical simulation demonstrates the differences between the initial and final distribution of honest taxpayers and evaders and estimates the profit of tax authority in the case of using information as a tool to stimulate tax collection. We also can summarize that if agents behave accordingly to the proportional imitation rule then numerical simulation has demonstrated that the injected information in the population of taxpayers and the process of it’s propagation is not effective. Whereas if the propagation process is described by Markov process with one authorized center then the described model is valid.

Appendix

In Appendix we present additional information about probability distribution, used in this paper. Let’s recall that the density f(x) and function F(x) of the uniform distribution of the value X on the interval (b − a, b + a) are defined by the next way [13]:

$$\displaystyle \begin{aligned} f(x)= \left\{ \begin{array}{lcr} \displaystyle{\frac{1}{2a}}, & \qquad \mbox{if }\ & |x-b|\le a, \\ \vspace{-10pt}\\ 0, & \qquad \mbox{if }\ & |x-b|>a, \end{array} \right. \end{aligned} $$

$$\displaystyle \begin{aligned} F(x)= \left\{ \begin{array}{lcr} 0, &\qquad \mbox{if }\ & x<b-a, \\ \vspace{-10pt}\\ \displaystyle{\frac 1{2a}(x-b+a)}, &\qquad \mbox{if }\ &|x-b| \le a, \\ \vspace{-10pt}\\ 1, &\qquad \mbox{if }\ & x>b+a, \end{array} \right. \end{aligned} $$

The mathematical expectation MX of the uniform distribution is MX = b.

The Pareto distribution [13], which is often used in the modeling and prediction of an income, has the next density

$$\displaystyle \begin{aligned} f(x)= \left\{ \begin{array}{lcr} \displaystyle{ \frac{a b^a}{{x}^{ a+1}}}, &\qquad \mbox{if }\ & x\ge b, \\ \vspace{-10pt}\\ 0, &\qquad \mbox{if }\ &x<b, \end{array} \right. \end{aligned} $$

function

$$\displaystyle \begin{aligned} F(x)= \left\{ \begin{array}{lcr} \displaystyle{1-\left(\frac{b}{x}\right)^a}, &\qquad \mbox{if }\ &x\ge b, \\ \vspace{-10pt}\\ 0, &\qquad \mbox{if }\ &x<b, \end{array} \right. \end{aligned} $$

and the mathematical expectation $MX=\displaystyle {\frac {a}{(a-1)}} \cdot b$.

The scatter of income levels in the group with the highest income may be extremely wide. Therefore, as a value of parameter of the distribution we consider a = 2: higher or lower values significantly postpone or approximate average value to the lower limit of income.