Keywords

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

3.1 Introduction

In the present paper we consider a non-antagonistic positional (feedback) differential two-person game (see, for example, [1, 3, 12]), for which emphasis is placed on the case where each of the two players, in addition to the normal (nor), type of behavior oriented on maximizing their own functional, can use other types of behavior introduced in [5, 9], such as altruistic (alt), aggressive (agg) and paradoxical (par) types. It is assumed that during the game, players can switch their behavior from one type to another. The idea of using the players to switch their behavior from one type to another in the course of the game was applied to the game with cooperative dynamics in [9] and for the repeated bimatrix 2 × 2 game in [6], which allowed to obtain new solutions in these games.

It is also assumed that in the game each player chooses the indicator function determined over the whole time interval of the game and takes values in the set {nor, alt, agg, par}, simultaneously with the choice of the positional strategy. Player’s indicator function shows the dynamics for changing the type of behavior that this player adheres to. Rules for the formation of controls are introduced for each pair of behaviors of players.

The formalization of positional strategies in the game is based on the formalization and results of the general theory of positional (feedback) differential games [4, 10, 11]. The concept of the BT-solution is introduced.

The idea to switch players’ behavior from one type to another in the course of the game is somewhat similar to the idea of using trigger strategies [2]. This is indicated by the existence of punishment strategies in the structure of decision strategies. However, there are significant differences. In this paper, we also use more complex switching, namely, from one type of behavior to another, changing the nature of the problem of optimization—from non-antagonistic games to zero-sum games or team problem of control and vice versa.

An example of a game with dynamics of simple motion on a plane and a phase constraint in two variants is proposed. In the first variant we assume that the first and second players can exhibit altruism towards their partner for some time periods. In the second variant, in addition to the assumption of altruism of the players, we also assume that each player can act aggressively against other player for some periods of time, and a case of mutual aggression is allowed. In both variants sets of BT-solutions are described. This paper is a continuation of [6,7,8].

3.2 Some Results from the Theory of Non-antagonistic Positional Differential Games (NPDG) of Two Persons

The contents of this section can be found in [4]. In what follows, we use the abbreviated notation NPDG to denote non-antagonistic positional (feedback) differential game.

Let the dynamics of the game be described by the equation

$$\displaystyle \begin{aligned} \dot {x}=f(t,x,u,v),\;\;t \in [t_{0},\vartheta],\;\; x(t_{0})=x_{0}, \end{aligned} $$
(3.1)

where x ∈ R n, u ∈ P ∈ comp(R p), v ∈ Q ∈ comp(R q); 𝜗 is the given moment of the end of the game.

Player 1 (P1) and Player 2 (P2) choose controls u and v, respectively.

Let G be a compact set in R 1 × R n whose projection on the time axis is equal to the given interval [t 0, 𝜗]. We assume, that all the trajectories of system (3.1), beginning at an arbitrary position (t ∗, x ∗) ∈ G, remain within G for all t ∈ [t ∗, 𝜗].

It is assumed that the function f : G × P × Q↦R n is continuous over the set of arguments, satisfies the Lipschitz condition with respect to x, satisfies the condition of sublinear growth with respect to x and satisfies the saddle point condition in the small game [10, 11]

$$\displaystyle \begin{aligned} \max\limits_{u\in P}\min\limits_{v\in Q}s^{T}f(t,x,u,v)=\min\limits_{v\in Q}\max\limits_{u\in P}s^{T}f(t,x,u,v) \end{aligned} $$
(3.2)

for all (t, x) ∈ G and s ∈ R n.

Both players have information about the current position of the game (t, x(t)). The formalization of positional strategies and the motions generated by them is analogous to the formalization introduced in [10, 11], with the exception of technical details [4].

Strategy of Player 1 is identified with the pair U = {u(t, x, ε), β 1(ε)}, where u(⋅) is an arbitrary function of position (t, x) and a positive precision parameter ε > 0 and taking values in the set P. The function β 1 : (0, ∞)↦(0, ∞) is a continuous monotonic function satisfying the condition β 1(ε) → 0 if ε → 0. For a fixed ε the value β 1(ε) is the upper bound step of subdivision the segment [t 0, 𝜗], which Player 1 applies when forming step-by-step motions. Similarly, the strategy of Player 2 is defined as V = {v(t, x, ε), β 2(ε)}.

Motions of two types: approximated (step-by-step) ones and ideal (limit) ones are considered as motions generated by a pair of strategies of players. Approximated motion x [⋅, t 0, x 0, U, ε 1, Δ 1, V, ε 2, Δ 2] is introduced for fixed values of players’ precision parameters ε 1 and ε 2 and for fixed subdivisions \(\varDelta _{1}=\{t_{i}^{(1)}\}\) and \(\varDelta _{2}=\{t_{j}^{(2)}\}\) of the interval [t 0, 𝜗] chosen by P1 and P2, respectively, under the conditions δ(Δ i)≤ β i(ε i), i = 1, 2. Here \(\delta (\varDelta _{i})=\max\limits _{k}(t_{k+1}^{(i)}-t_{k}^{(i)}).\) A limit motion generated by the pair of strategies (U, V ) from the initial position (t 0, x 0) is a continuous function x[t] = x[t, t 0, x 0, U, V ] for which there exists a sequence of approximated motions

$$\displaystyle \begin{aligned} \{x[t,t_{0}^{k},x_{0}^{k},U,\varepsilon_{1}^{k},\varDelta_{1}^{k},V,\varepsilon_{2}^{k},\varDelta_{2}^{k}]\} \end{aligned}$$

uniformly converging to x[t] on [t 0, 𝜗] as \( k\rightarrow \infty ,\quad \varepsilon _{1}^{k}\rightarrow 0,\quad \varepsilon _{2}^{k}\rightarrow 0, \quad t_{0}^{k}\rightarrow t_{0}, \) \( x_{0}^{k}\rightarrow x_{0, \quad}\delta (\varDelta _{i}^{k})\leq \beta _{i}(\varepsilon _{i}^{k}) \).

The control laws (U, ε 1, Δ 1) and (V, ε 2, Δ 2) are said to be agreed with respect to the precision parameter if ε 1 = ε 2. Agreed control laws generate agreed approximate motions, the sequences of which generate agreed limit motions.

A pair of strategies (U, V ) generates a nonempty compact (in the metric of the space C[t 0, 𝜗]) set X(t 0, x 0, U, V ) consisting of limit motions x[⋅, t 0, x 0, U, V ].

Player i chooses his control to maximize the payoff functional

$$\displaystyle \begin{aligned} I_{i}=\sigma_{i}(x(\vartheta)),\quad i=1,2 \end{aligned} $$
(3.3)

where σ i : R n↦R 1 are given continuous functions.

Thus, an non-antagonistic positional (feedback) differential game (NPDG) is defined.

Now we introduce the following definitions [4].

Definition 3.1

A pair of strategies (U N, V N) is called a Nash equilibrium solution (NE–solution) of the game, if for any motion x ∗[⋅] ∈ X(t 0, x 0, U N, V N), any moment τ ∈ [t 0, 𝜗], and any strategies U and V  the following inequalities hold

$$\displaystyle \begin{aligned} \max_{x[\cdot]}\sigma_{1}(x[\vartheta,\tau,x^{\ast}[\tau],U,V^{N}])\leq \min_{x[\cdot]}\sigma _{1}(x[\vartheta,\tau,x^{\ast}[\tau],U^{N},V^{N}]), \end{aligned} $$
(3.4)
$$\displaystyle \begin{aligned} \max_{x[\cdot]}\sigma_{2}(x[\vartheta,\tau,x^{\ast}[\tau],U^{N},V])\leq \min_{x[\cdot]}\sigma _{2}(x[\vartheta,\tau,x^{\ast}[\tau],U^{N},V^{N}]). \end{aligned} $$
(3.5)

where the operations min are performed over a set of agreed motions, and the operations max by sets of all motions.

Definition 3.2

An NE-solution (U P, V P) which is Pareto non-improvable with respect to the values I 1, I 2 (3.3) is called a P(NE)-solution.

Now we consider auxiliary zero-sum positional (feedback) differential games Γ 1 and Γ 2. Dynamics of both games is described by the Eq. (3.1). In the game Γ i Player i maximizes the payoff functional σ i(x(𝜗)) (3.3) and Player 3 − i opposes him.

It follows from [10, 11] that both games Γ 1 and Γ 2 have universal saddle points

$$\displaystyle \begin{aligned} \{u^{(i)}(t,x,\varepsilon),\quad v^{(i)}(t,x,\varepsilon)\},\quad i=1,2 \end{aligned} $$
(3.6)

and continuous value functions

$$\displaystyle \begin{aligned} \gamma_{1}(t,x),\quad \gamma_{2}(t,x) \end{aligned} $$
(3.7)

The property of strategies (3.6) to be universal means that they are optimal not only for the fixed initial position (t 0, x 0) ∈ G but also for any position (t ∗, x ∗) ∈ G assumed as initial one.

It is not difficult to see that the value of γ i(t, x) is the guaranteed payoff of the Player i in the position (t, x) of the game.

In [4] the structure of NE- and P(NE)-solutions was established. Namely, it was shown that all NE- and P(NE)-solutions of the game can be found in the class of pairs of strategies (U, V ) each of which generates a unique limit motion (trajectory). The decision strategies that make up such a pair generating the trajectory x ∗(⋅) have the form

$$\displaystyle \begin{aligned} U^{0}=\{u^{0}(t,x,\varepsilon), \ \beta^{0}_{1}(\varepsilon)\}, \ \ V^{0}=\{v^{0}(t,x,\varepsilon), \ \beta^{0}_{2}(\varepsilon)\}, \end{aligned} $$
(3.8)
$$\displaystyle \begin{aligned} u^{0} \left( t,x,\varepsilon \right)= \left\{ \begin{array}{l} u^{\ast}\left(t,\varepsilon\right), \quad\left\Vert x-x^{\ast}(t)\right\Vert < \varepsilon\varphi\left( t\right) \\ u^{(2)}(t,x,\varepsilon), \quad\left\Vert x-x^{\ast}(t)\right\Vert\geq\varepsilon\varphi\left( t\right) \end{array}, \right. \end{aligned}$$
$$\displaystyle \begin{aligned} v^{0} \left( t,x,\varepsilon \right)= \left\{ \begin{array}{l} v^{\ast}\left(t,\varepsilon \right), \quad\left \Vert x-x^{\ast}(t)\right \Vert < \varepsilon \varphi \left( t \right) \\ v^{(1)}(t,x,\varepsilon), \quad\left\Vert x-x^{\ast}(t) \right \Vert\geq \varepsilon \varphi \left( t\right), \end{array} \right. \end{aligned}$$

for all t ∈ [t 0, 𝜗], ε > 0. In (3.8) we denote by u ∗(t, ε), v ∗(t, ε) families of program controls generating the limit motion x ∗(t). The function φ(⋅) and the functions \(\beta ^{0}_{1}(\cdot )\) and \(\beta ^{0}_{2}(\cdot )\) are chosen in such a way that the approximated motions generated by the pair (U 0, V 0) from the initial position (t 0, x 0) do not go beyond the εφ(t) -neighborhood of the trajectory x ∗(t). Functions u (2)(⋅, ⋅, ⋅) and v (1)(⋅, ⋅, ⋅) are defined in (3.6). They play the role of punishment strategies for exiting this neighborhood.

Further, for each NE- and P(NE)-trajectories x ∗(t) the following property holds.

Property 3.1

The point t = 𝜗 is the maximum point of the value function γ i(t, x) (3.7) computed along this trajectory, that is,

$$\displaystyle \begin{aligned} \gamma_{i}(t,x^{\ast}(t))\leq\gamma_{i}(\vartheta,x^{\ast}(\vartheta)),\;t_{0}\leq t\leq \vartheta,\;i=1,2 \end{aligned} $$
(3.9)

3.3 A Non-antagonistic Positional Differential Games with Behavior Types (NPDGwBT): BT-Solution

Now we assume that in addition to the usual normal (nor) type of behavior aimed at maximizing own functionals (3.3), players can use other types of behavior, namely, altruistic, aggressive and paradoxical types [5, 9].

These three types of behavior can be formalized as follows:

Definition 3.3

We say that Player 1 is confined in the current position of the game by altruistic (alt) type of behavior if his actions in this position are directed exclusively towards maximizing the functional I 2 (3.3) of Player 2.

Definition 3.4

We say that Player 1 is confined in the current position of the game by aggressive (agg) type of behavior if his actions in this position are directed exclusively towards minimizing the functional I 2 (3.3) of Player 2.

Definition 3.5

We will say that Player 1 is confined in the current position of the game by paradoxical (par) type of behavior if his actions in this position are directed exclusively towards minimizing own payoff I 1 (3.3).

Similarly, we define the altruistic and aggressive types of Player 2 behavior towards Player 1, as well as the paradoxical type of behavior for Player 2.

Note that the aggressive type of player behavior is actually used in NPDG in the form of punishment strategies contained in the structure of the game’s decisions (see, for example, [4]).

The above definitions characterize the extreme types of behavior of players. In reality, however, real individuals behave, as a rule, partly normal, partly altruistic, partly aggressive and partly paradoxical. In other words, mixed types of behavior seem to be more consistent with reality.

If each player is confined to “pure” types of behavior, then in the considered game of two persons with dynamics (3.1) and functionals I i (3.3) there are 16 possible pairs of types of behavior: (nor, nor), (nor, alt), (nor, agg), (nor, par), (alt, nor), (alt, alt), (alt, agg), (alt, par), (agg, nor), (agg, alt), (agg, agg), (agg, par), (par, nor), (par, alt), (par, agg), (par, par). For the following four pairs (nor, alt), (alt, nor), (agg, par) and (par, agg) the interests of the players coincide and they solve a team problem of control. For the following four pairs (nor, agg), (alt, par), (agg, nor) and (par, alt) players have opposite interests and, therefore, they play a zero-sum differential game. The remaining eight pairs define a non-antagonistic differential games.

The idea of using the players to switch their behavior from one type to another in the course of the game was applied to the game with cooperative dynamics in [9] and for the repeated bimatrix 2 × 2 game in [6], which allowed to obtain new solutions in these games.

The extension of this approach to non-antagonistic positional differential games leads to new formulation of problems. In particular, it is of interest to see how the player’s gains, obtained on Nash solutions, are transformed. The actual task is to minimize the time of “abnormal” behavior, provided that the players’ gains are greater than when the players behave normally.

Thus, we assume that players can switch from one type of behavior to another in the course of the game. Such a game will be called a non-antagonistic positional (feedback) differential game with behavior types (NPDGwBT).

In NPDGwBT we assume that simultaneously with the choice of positional strategy, each player also chooses his indicator function defined on the interval \(t\in \left [ t_{0},\vartheta \right ]\) and taking the value in the set {nor, alt, agg, par}. We denote the indicator function of Player i by the symbol α i : [t 0, 𝜗]↦{nor, alt, agg, par}, i = 1, 2. If the indicator function of some player takes a value, say, alt on some time interval, then this player acts on this interval as an altruist in relation to his partner. Note also that if the indicator functions of both players are identically equal to the value nor on the whole time interval of the game, then we have a classical NPDG.

Thus, in the game NPDGwBT Player 1 controls the choice of a pair of actions {position strategy, indicator function} (U, α 1(⋅)), and player 2 controls the choice of a pair of actions (V, α 2(⋅)).

As mentioned above, for any pair of types of behavior three types of decision making problems can arise: a team problem, a zero-sum game, and a non-antagonistic game. We will assume that the players for each of these three problems are guided by the following Rule 3.1.

Rule 3.1

If on the time interval (τ 1, τ 2) ⊂ [t 0, 𝜗] the player’s indicator functions generate a non-antagonistic game, then on this interval players choose one of P(NE)-solutions of this game. If a zero-sum game is realized, then as a solution, players choose the saddle point of this game. Finally, if a team problem of control is realized, then players choose one of the pairs of controls such that the value function γ i(t, x) calculated along the generated trajectory is non-decreasing function, where i is the number of the player whose functional is maximized in team problem.

Generally speaking, the same part of the trajectory can be tracked by several pairs of players’ types of behavior, and these pairs may differ from each other by the time of use of abnormal types.

It is natural to introduce the following Rule 3.2.

Rule 3.2

If there are several pairs of types of behavior that track a certain part of the trajectory, then players choose one of them that minimizes the time of using abnormal types of behavior.

We now introduce the definition of the solution of the game NPDGwBT. Note that the set of motions generated by a pair of actions {(U, α 1(⋅)), (V, α 2(⋅))} coincides with the set of motions generated by the pair (U, V ) in the corresponding NPDG.

Definition 3.6

The pair \(\{(U^{0}, \alpha _{1}^{0}(\cdot )),(V^{0}, \alpha _{2}^{0}(\cdot ))\}\), consistent with Rule 3.1, forms a BT-solution of the game NPDGwBT if there exists a trajectory x BT(⋅) generated by this pair and there is a P(NE)-solution in the corresponding NPDG game generating the trajectory x P(⋅) such that the following inequalities are true

$$\displaystyle \begin{aligned} \sigma_{i}(x^{BT}(\vartheta))\geq\sigma_{i}(x^{P}(\vartheta)),\;\;i=1,2, \end{aligned} $$
(3.10)

where at least one of the inequalities is strict.

Definition 3.7

The BT-solution \(\{(U^{0}, \alpha _{1}^{0}(\cdot )),(V^{0}, \alpha _{2}^{0}(\cdot ))\}\), which is Pareto non-improvable with respect to the values I 1, I 2 (3.3), is called P(BT)-solution of the game NPDGwBT.

Problem 3.1

Find the set of BT-solutions.

Problem 3.2

Find the set of P(BT)-solutions.

In the general case, Problems 3.1 and 3.2 have no solutions. However, it is quite expected that the use of abnormal behavior types by players in the game NPDGwBT can in some cases lead to outcomes more preferable for them than in the corresponding game NPDG only with a normal type of behavior. An example of this kind is given in the next section.

3.4 Example

Let equations of dynamics be as follows

$$\displaystyle \begin{aligned} \dot{x}=u+v,\;\;\;x,u,v\in R^{2},\;\|u\|\leq1,\;\|v\|\leq1,\;\; 0\leq t\leq \vartheta ,\;\;x(0)=x^{0}, \end{aligned} $$
(3.11)

where x is the phase vector; u and v are controls of Players 1 and 2, respectively. Let payoff functional of Player i be

$$\displaystyle \begin{aligned} I_{i}=\sigma_{i}(x(\vartheta))=18-\|x(\vartheta)-a^{(i)}\|,\ \ i=1,2. \end{aligned} $$
(3.12)

That is, the goal of Player i is to bring vector x(𝜗) as close as possible to the target point a (i).

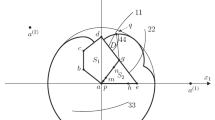
Let the following initial conditions and values of parameters be given: 𝜗 = 5.0, x 0 = (0, 0), a (1) = (10, 8), a (2) = (−10, 8) (Fig. 3.1).

Fig. 3.1
figure 1

Attainability set

Full size image

The game has the following phase restrictions. The trajectories of the system (3.11) are forbidden from entering the interior of the set S, which is obtained by removing from the quadrilateral Oabc the line segment Oe. The set S consists of two parts S 1 and S 2, that is, S = S 1 ∪ S 2.

Coordinates of the points defining the phase constraints:

$$\displaystyle \begin{aligned} a=(-4.5,3.6),\; b=(0,8),\; c=(6.5,5.2),\; O=(0,0),\;e=(3.25, 6.6). \end{aligned} $$
(3.13)

It can be verified that the point a lies on the interval Oa (2) , the point c lies on the interval Oa (1) , and the point e lies on the interval bc. We also have |a (1) b| = |a (2) b| = 10.

Attainability set of the system (3.11) constructed for the moment 𝜗 consists of points of the circle of radius 10 located not higher than the three-link segment aOc and also bounded by two arcs connecting the large circle with the sides ab and bc of the quadrilateral. The first arc is an arc of the circle with center at the point a and radius r 1 = 10 −|Oa| = |ad 2|. The second (composite) arc consists of an arc of the circle with center at the point e and radius r 2 = 10 −|Oe| = |ed 1| and an arc of the circle with center at the point c and radius r 3 = 10 −|Oc| (Fig. 3.1).

Results of approximate calculations: r 1 = 4.2372, r 2 = 2.6432, r 3 = 1.6759, d 1 = (0.8225, 7.6457), d 2 = (−1.4704, 6.5623). In addition, we have: |Oa (1)| = |Oa (2)| = 12.8062.

In Fig. 3.1 the dashed lines represent arcs of the circle L with center at the point b and radius r 4 = |Oa (1)|−|a (1) b| = 12.8062 − 10 = 2.8062. These arcs intersect the sides ab and bc at the points p 1 = (2.5773, 6.8898) and p 2 = (−2.0065, 6.0381), respectively. By construction, the lengths of the two-links a (1) bp 2 and a (2) bp 1 are equal to each other and equal to the lengths of the segments Oa (1) and Oa (2).

The value functions γ 1(t, x) and γ 2(t, x), 0 ≤ t ≤ 𝜗, x ∈ R 2∖S , of the corresponding auxiliary zero-sum games Γ 1 and Γ 2 in this example will be as follows

$$\displaystyle \begin{aligned} \gamma_{i} \left( t,x \right) = \left\{ \begin{array}{l} 18 -\|(x-a^{(i)}\|, \quad xa^{(i)}\bigcap int S= \emptyset \\ 18 - \rho_{S}\left(x,a^{(i)}\right), \quad otherwise \end{array}, \right. \end{aligned} $$
(3.14)

where i = 1, 2, and \(\rho _{S} \left ( x, a^{(i)} \right )\) denotes the smallest of the two distances from the point x to the point a (i), one of which is calculated when the set S is bypassed clockwise and the other counterclockwise.

At first we solve the game NPDG (without abnormal behavior types). One can check that in the game NPDG the trajectory x(t) ≡ 0, t ∈ [0, 5], (stationary point O) is a Nash trajectory. Further, the trajectories constructed along the line Oe, are not Nash ones, since none of them is satisfied condition (3.9). This is also confirmed by the fact that the circle of radius |a (1) e| with the center at the point a (1) has no points in common with the circle L (see Fig. 3.1). Obviously, these are not Nash and all the trajectories that bypass the set S 1 on the right. Are not Nash and all trajectories that bypass the set S 2 on the left, since a circle of radius |a (2) a| with the center at the point a (2) also has no points in common with the circle L. As a result, it turns out that the mentioned trajectory is the only Nash trajectory, and, consequently, the only P(NE)-trajectory; the players’ gains on it are I 1 = I 2 = 5.1938.

Let us now turn to the game NPDGwBT, in which each player during certain periods of time may exhibit altruism and aggression towards other player, and the case of mutual aggression is allowed.

We consider two variants of the game.

Variant I

We assume that players 1 and 2 together with a normal type of behavior, can exhibit altruism towards their partner during some time intervals.

Variant II

In addition to the assumption of altruism of the players, we assume that each player can act aggressively against another player for some periods of time, and a case of mutual aggression is allowed.

In the attainability set, we find all the points x for which inequalities hold

$$\displaystyle \begin{aligned} \sigma_{i}(x)\geq\sigma_{i}(O), \;i=1,2,\;\; \sigma_{1}(x)+\sigma_{2}(x)>\sigma_{1}(O)+\sigma_{2}(O) \end{aligned} $$
(3.15)

Such points form two sets D 1 and D 2 (see Fig. 3.1). The set D 1 is bounded by the segment p 1 d 1, and also by the arcs p 1 q 1 and q 1 d 1 of the circles mentioned above. The set D 2 is bounded by the segment p 2 d 2, and also by the arcs d 2 q 2 and q 2 p 2 of the circles mentioned. On the arc p 1 q 1, the non-strict inequality (3.15) for i = 2 becomes an equality, and on the arc q 2 p 2, the non-strict inequality (3.15) becomes an equality for i = 1. At the remaining points sets D 1 and D 2 , the non-strict inequalities (3.15) for i ∈{1, 2} are strict.

Now within the framework of Variant I we construct a BT-solution leading to the point d 2 ∈ D 2. Consider the trajectory Oad 2; the players’ gains on it are I 1 = 5.9436, I 2 = 9.3501, that is, each player gains more than on single P(NE)-trajectory. How follows from the foregoing, the trajectory Oad 2 is not Nash one. However, if it is possible to construct indicator functions-programs of players that provide motion along this trajectory, then a BT-solution will be constructed.

On the side Oa, we find a point g equidistant from the point a (1) if we go around the set S clockwise, or if we go around S counterclockwise. We obtain g = (−3.6116, 2.8893). Further, if we move along the trajectory Oad 2 with the maximum velocity for t ∈ [0, 5], then the time to hit the point g will be t = 2.3125, and for the point a will be t = 2.8814. It can be verified that if we move along this trajectory on the time interval [0, 2.3125] then the function γ 1(t, x) (3.14) decreases monotonically and the function γ 2(t, x) increases monotonically; for motion on the interval t ∈ [2.3125, 2.8814], both functions γ 1(t, x) and γ 2(t, x) increase monotonically; finally, when driving on the remaining interval t ∈ [2.8814, 5.0], then the function γ 1(t, x) increases monotonically, and the function γ 2(t, x) decreases.

We check that on the segment Og of the trajectory the pair (alt, nor), which defines a team problem of control, is the only pair of types of behavior that realizes motion on this segment in accordance with Rule 3.1; this is the maximum shift in the direction of the point a (2) . In the next segment ga there will already be four pairs of “candidates” (nor, nor), (alt, nor), (nor, alt) and (alt, alt)), but according to Rule 3.2 the last three pairs are discarded; the remaining pair determines a non-antagonistic game, and the motion on this segment will be generated by P(NE)-solution of the game. Finally, for the last segment ad 2, the only pair of types of behavior, that generates motion on the segment in accordance with Rule 3.1, there will be a pair (nor, alt) that defines a team problem of control; the motion represents the maximum shift in the direction of the point d 2.

Thus, we have constructed the following indicator function-programs of players

$$\displaystyle \begin{aligned} \alpha_{1}^{(1)}(t)=\{alt, t\in [0,2.3125);\;\; nor, t\in [2.3125,5]\}, \end{aligned} $$
(3.16)
$$\displaystyle \begin{aligned} \alpha_{2}^{(1)}(t)=\{nor, t\in [0,2.8814);\;\;alt, t\in [2.8814,5] \}. \end{aligned} $$
(3.17)

We denote by (U (1), V (1)) the pair of players’ strategies that generates the limit motion Oad 2 for t ∈ [0, 5] and is consistent with the constructed indicator functions. Then we obtain the following assertion.

Theorem 3.1

In Variant I , the pair of actions \(\{(U^{(1)}, \alpha _{1}^{(1)}(\cdot )),(V^{(1)}, \alpha _{2}^{(1)}(\cdot ))\}\) (3.16), (3.17) provides the P(BT)-solution.

We turn to the Variant II, in which, in addition to assuming the altruism of the players, it assumed that players can use an aggressive type of behavior. We construct a BT-solution, leading to the point d 1 ∈ D 1.

Let us find the point m equidistant from the point a (2) if we go around the set S 2 clockwise, or if we go around S 2 counterclockwise. We also find a point n equidistant from the point a (1) as if we were go around the set S 1 clockwise, or if we go around S 1 counterclockwise. The results of the calculations: m = (1.7868, 3.6285), n = (0.3190, 0.6478).

Consider the trajectory Oed 1; the players’ gains on it are I 1 = 8.8156, I 2 = 7.1044, that is, the gains of both players on this trajectory are greater than the gains on the single P(NE)-trajectory. As follows from the above, the trajectory Oed 1 is not Nash one. Therefore, if it is possible to construct indicator functions-programs of players that provide motion along this trajectory, then a BT-solution will be constructed.

First of all find that if we move along the trajectory Oed 1 with the maximum velocity for t ∈ [0, 5], the time to hit the point n will be t = 0.3610, the point m will be t = 2.0223, and the point e will be t = 3.6784. It is easy to verify that for such a motion along the trajectory Oed 1 on the interval t ∈ [0, 0.3610], both functions γ 1(t, x) and γ 2(t, x) (3.14) decrease monotonically; for motion on the interval t ∈ [0.3610, 2.0223], the function γ 2(t, x) continues to decrease, and the function γ 1(t, x) increases; for motion on the interval t ∈ [1.9135, 3.9620], both functions increase; finally, on the remaining interval t ∈ [3.9620, 5], the function γ 2(t, x) continues to increase, and the function γ 1(t, x) decreases.

We check that on the segment On of the trajectory, the pair (agg, agg), which determines the non-antagonistic game, is the only pair of types of behaviors that realizes motion on the segment in accordance with Rule 3.1; this is the motion generated by the P(NE)-solution, the best for both players. In the next segment nm, two pairs of types of behaviors realize motion on the segment according to Rule 3.1, namely (nor, alt) and (agg, alt); however, according to Rule 3.2, only the pair (nor, alt) remains; it defines a team problem of control in which the motion represents the maximum shift in the direction of point m. There are already four pairs of “candidates” (nor, nor), (alt, nor), (nor, alt) and (alt, alt) on the segment me, but according to Rule 3.2 the last three pairs are discarded; the remaining pair defines a non-antagonistic game and the motion on this segment is generated by the P(NE)-solution of the game. Finally, for the last segment ed 1, the only pair of types of behaviors is the pair (alt, nor), which defines a team problem of control; the motion represents the maximum shift in the direction of the point d 1.

Thus, we have constructed the following indicator function-programs of players

$$\displaystyle \begin{aligned} \alpha_{1}^{(2)}(t)=\{agg, t\in [0,0.3610);\;\;\;nor, t\in [0.3610,3.6784);\; alt, t\in [3.6784,5] \}, \end{aligned} $$
(3.18)
$$\displaystyle \begin{aligned} \alpha_{2}^{(2)}(t)=\{agg, t\in [0,0.3610);\;\; alt, t\in [0.3610,2.0223);\;\; nor, t\in [2.0223,5]\}. \end{aligned} $$
(3.19)

We denote by (U (2), V (2)) the pair of players’ strategies that generate the limit motion Oed 1 for t ∈ [0, 5] and is consistent with the constructed indicator functions. Then we obtain the following assertion.

Theorem 3.2

In Variant II , the pair of actions \(\{(U^{(2)}, \alpha _{1}^{(2)}(\cdot )),(V^{(2)}, \alpha _{2}^{(2)}(\cdot ))\}\) (3.18), (3.19) provides the P(BT)-solution.

Remark 3.1

It is obvious that Theorem 3.1 is also true for Variant II.

Following the scheme of the proofs of Theorems 3.1 and 3.2 (and also taking into account Remark 3.1), we arrive at the following Theorems.

Theorem 3.3

In Variant I , the set D 2 consists of those and only those points that are endpoints of the trajectories generated by the BT-solutions of the game.

Theorem 3.4

In Variant II , the sets D 1 and D 2 consist of those and only those points that are the ends of the trajectories generated by the BT-solutions of the game.

3.5 Conclusion

Realized idea of using the players to switch their behavior from one type to another in the course of the game is somewhat similar to the idea of using trigger strategies [2]. This is indicated by the existence of punishment strategies in the structure (8) of decision strategies. However, there are significant differences. In this paper, we also use more complex switching, namely, from one type of behavior to another, changing the nature of the problem of optimization—from non-antagonistic games to zero-sum games or team problem of control and vice versa. And these switchings are carried out according to pre-selected indicator function-programs.

Each player controls the choice of a pair of actions positional strategy, indicator function. Thus, the possibilities of each player in the general case have expanded (increased) and it is possible to introduce a new concept of a game solution (P(BT)-solution) in which both players increase their payoffs in comparison with the payoffs in Nash equilibrium in the game without switching types of behavior.

For players, it is advantageous to implement P(BT)-trajectory; so they will follow the declared indicator function-programs (3.16), (3.17) or (3.18), (3.19).