Keywords

1 Introduction

First derived by Landau [6] as the grazing collision limit of the Boltzmann equation, the Fokker–Planck–Landau (FPL) or Landau equation is a collisional kinetic model that describes the non-equilibrium dynamics of charged particles in a plasma [16].

Let \(f=f(t,x,v)\) be the density distribution function of particles, where t is the time, x is the space, and v is the velocity. The FPL equation with the mean-field term (also known as the Vlasov–Poisson–Landau equation) reads

$$\begin{aligned} \partial _t f + v\cdot \nabla _x f + E(t,x)\cdot \nabla _v f = Q(f,f), \quad t>0, \ x\in \varOmega \subset \mathbb {R}^{d_x}, \ v\in \mathbb {R}^{d_v}, \end{aligned}$$
(1)

where E(t, x) is the electric field given by

$$\begin{aligned} E(t,x)=-\nabla _x \phi (t,x), \end{aligned}$$
(2)

and \(\phi (t,x)\) is a self-consistent electrostatic potential function satisfying the Poisson equation

$$\begin{aligned} \varDelta _x \phi (t,x) =\mu (x)- \int _{\mathbb {R}^{d_v}} f(t,x,v)\,\mathrm {d}{v}, \end{aligned}$$
(3)

where \(\mu (x)\) is a neutralizing background satisfying

$$\begin{aligned} \int _{\mathbb {R}^{d_x}}\mu (x)\,\mathrm {d}{x} = \int _{\mathbb {R}^{d_x}}\int _{\mathbb {R}^{d_v}} f(t,x,v)\,\mathrm {d}{v}\,\mathrm {d}{x}. \end{aligned}$$
(4)

Q(f, f) on the right-hand side of (1) is the FPL collision operator that models binary interactions among particles:

$$\begin{aligned} Q(f,f)(v)=\nabla _v \cdot \int _{\mathbb {R}^{d_v}} A(v-v_*)[f(v_*)\nabla _v f(v) - f(v)\nabla _{v_*}f(v_*)] \,\mathrm {d}{v}_*. \end{aligned}$$
(5)

Here A(w) is a semi-positive definite matrix defined by

$$\begin{aligned} A(w)=\varPsi (w)\left( I-\frac{w\otimes w}{|w|^2}\right) , \end{aligned}$$
(6)

where I is the identity matrix. For inverse power law potentials, \(\varPsi (w)=|w|^{\gamma +2}\) with \(-3\le \gamma \le 1\). The case \(\gamma =-3\) corresponds to the Coulomb interaction which is of primary importance in plasma applications.

The collision operator Q(f, f) possesses some important physical properties: it preserves mass, momentum, and energy

$$\begin{aligned} \int _{\mathbb {R}^{d_v}} Q(f,f)\phi (v)\,\mathrm {d}{v} =0,\quad \phi (v)=1,v,|v|^2; \end{aligned}$$
(7)

and satisfies the entropy dissipation inequality (the H-theorem)

$$\begin{aligned} \int _{\mathbb {R}^{d_v}} Q(f,f)\log f \,\mathrm {d}{v} \le 0. \end{aligned}$$
(8)

The equality only holds when f attains the local equilibrium (Maxwellian)

$$\begin{aligned} f(v)=M(v)=\frac{\rho }{(2\pi T)^{d_v/2}}e^{-\frac{(v-u)^2}{2T}}, \end{aligned}$$
(9)

where \(\rho ,u,T\) are the density, bulk velocity, and temperature defined as

$$\begin{aligned} \rho =\int _{\mathbb {R}^{d_v}}f\,\mathrm {d}{v}, \quad u=\frac{1}{\rho }\int _{\mathbb {R}^{d_v}}vf\,\mathrm {d}{v}, \quad T=\frac{1}{d_v\rho }\int _{\mathbb {R}^{d_v}}(v-u)^2f\,\mathrm {d}{v}. \end{aligned}$$
(10)

Equation (1) needs to be supplemented with appropriate initial condition

$$\begin{aligned} f(0,x,v)=f^0(x,v), \end{aligned}$$
(11)

where \(f^0\) can be chosen as, for example, the local equilibrium (9). For boundary condition, a commonly used one is the Maxwell boundary condition: For any boundary point \(x\in \partial \varOmega \), let n(x) be the unit inward normal vector to the boundary, then the inflow boundary condition is specified as

$$\begin{aligned} f(t,x,v) = g(t,x,v), \quad v\cdot n>0, \end{aligned}$$
(12)
$$\begin{aligned} g(t,x,v):=(1-\alpha ) f(t,x,v-2(v\cdot n)n)+ \frac{\alpha }{(2\pi )^{\frac{d_v-1}{2}}T_w^{\frac{d_v+1}{2}}}e^{-\frac{v^2}{2T_w}}\int _{v\cdot n<0} f(t,x,v)|v\cdot n|\,\mathrm {d}{v}, \end{aligned}$$
(13)

where \(T_w=T_w(t,x)\) is the temperature of the wall (boundary). The constant \(\alpha \) (\(0\le \alpha \le 1\)) is the accommodation coefficient with \(\alpha =1\) corresponding to the purely diffusive boundary, and \(\alpha =0\) the purely specular reflective boundary.

In the past decades, the FPL equation (1) has been studied extensively both theoretically and numerically. The readers are referred to [16] for a review of the main mathematical aspects, and the recent paper [1] and references therein for relevant numerical methods. In spite of the vast amount of existing research, the study of the FPL equation has mostly remained deterministic and ignored uncertainty. In reality, however, there are many sources of uncertainties that can arise in this equation: imprecise measurements for initial boundary conditions and physical parameters; incomplete knowledge of the fundamental interaction mechanism between particles; and so on. Understanding the impact of these uncertainties is critical to the simulations of complex plasma systems and will allow scientists and engineers to obtain more reliable predictions and perform better risk assessment. The goal of this paper is to develop an efficient stochastic numerical method for uncertainty quantification (UQ) of the FPL equation (1).

The basic framework of our work is built on a probabilistic approach which models the uncertain parameters as random variables. In the FPL equation (1), this amounts to consider the distribution function

$$\begin{aligned} f=f(t,x,v,z), \quad z\in I_z\in \mathbb {R}^d, \end{aligned}$$
(14)

now depending on an extra argument z—a d-dimensional random vector with support \(I_z\) collecting all possible uncertainties in the system. For instance, one may consider \(z=(z^\mu ,z^{\text {ini}},z^{\text {bdry}})\), where \(z^\mu \), \(z^{\text {ini}}\), \(z^{\text {bdry}}\) denote, respectively, the random parameters arising from

  • the neutralizing background (3): \(\mu =\mu (x,z^\mu )\);

  • the initial condition (11): \(f(0,x,v,z)=f^0(x,v,z^{\text {ini}})\) for \(x\in \varOmega \);

  • the boundary condition (12): \(f(t,x,v,z)=g(t,x,v,z^{\text {bdry}})\) for \(x\in \partial \varOmega \).

We will further assume the components of z are already mutually independent random variables obtained through some dimension reduction technique, e.g., Karhunen–Loève expansion [9], and do not pursue the issue of random input parameterization in this paper.

To properly model the propagation of uncertainties, we adopt the generalized polynomial chaos-based stochastic Galerkin (gPC-sG) method, which is widely used in the UQ simulations nowadays [2, 3, 10, 13, 17, 18]. Simply speaking, this method seeks to approximate the unknown function f via an orthogonal polynomial series:

$$\begin{aligned} f(t,x,v,z) \approx \sum _{k=1}^Kf_k(t,x,v)\varPhi _k(z):=f^K(t,x,v,z),\, f_k(t,x,v) = \int _{I_z}f(t,x,v,z)\varPhi _k(z)\pi (z)\,\mathrm {d}{z}, \end{aligned}$$
(15)

where \(\{\varPhi _k(z)\}\) is a set of d-variate polynomials of degree up to m which satisfy

$$\begin{aligned} \int _{I_z} \varPhi _j(z)\varPhi _k(z)\pi (z)\,\mathrm {d}{z}=\delta _{jk},\quad 1\le j,k \le K, \end{aligned}$$

with \(\pi (z)\) being the probability distribution of z and \(\delta _{jk}\) the Kronecker delta function. The number of basis functions is \(K=\left( {\begin{array}{c}m+d\\ m\end{array}}\right) \). Equipped with this gPC representation, one then proceeds as follows: (1) Substitute the expansion (15) into the original equation and conduct a Galerkin projection. This usually results in a system of coupled deterministic equations for the gPC coefficients \(\{f_k\}_{k=1}^K\) requiring different treatment from the corresponding deterministic equation. (2) Solve the gPC system. (3) Use \(\{f_k\}_{k=1}^K\) to reconstruct the solution in \(I_z\) via (15), or construct the solution statistics directly, e.g., the mean and standard deviation can be retrieved as

$$\begin{aligned} \mathbb {E}[f]=f_1, \quad S[f]=\sqrt{\sum _{k=2}^K f_k^2}. \end{aligned}$$
(16)

For the FPL equation, the main difficulty associated with solving the gPC-sG system lies in the evaluation of the nonlinear collision operator. Similar to the work [5], we propose a fast algorithm to efficiently compute the collision operator under the Galerkin projection. The acceleration is achieved by combining a singular value decomposition (SVD) of the collision kernel with the fast spectral method in the deterministic case [11].

In the cases where the random domain \(I_z\) is high-dimensional, i.e., d is large, the usual gPC-sG method may fail to be affordable since the number of basis functions \(K=\left( {\begin{array}{c}m+d\\ m\end{array}}\right) \) is too large. To circumvent this difficulty, we use the sparse wavelet basis as in our previous work [15]. We use N-level hierarchical piecewise polynomial functions of degree at most m as basis functions in one dimension and use a standard sparse grid construction to obtain basis functions in d-dimensional random spaces. With this basis, one can achieve an accuracy of \(O(N^d 2^{-N(m+1)})\) with \(K=O((m+1)^d2^NN^{d-1})\) basis functions. The accuracy is \(O(K^{-(m+1)}(\log K)^{(m+2)(d-1)})\) in terms of K. This method is much more efficient than the usual gPC-sG method if d is large.

When using the sparse grid method, K can still be too large to make an SVD of order K affordable. Thus the following two difficulties arise. The first one is that one can no longer afford the SVD approach for the collision operator. To avoid it, we notice the sparsity of a basis-related tensor \(S_{b,ijk}\) proved in [15]. As a result, one can compute the collision operator directly with low computational cost. The second difficulty is that a direct computation of the numerical flux for the mean-field term requires a diagonalization of constant flux matrices of order K. To avoid this diagonalization, we utilize the local Lax–Friedrichs splitting [7]. In this way, one can compute the second-order upwind flux without diagonalization of the flux matrices.

The rest of this paper is organized as follows. Section 2 describes in detail the gPC-sG method for the FPL equation with uncertainty. Section 3 discusses the spatial and time discretization. In Sect. 4, we give a consistency analysis of the gPC-sG method for the collision operator. In Sect. 5, we give a sparse wavelet method for problems with high-dimensional random inputs. Extensive numerical results are presented in Sect. 6. Finally, the paper is concluded in Sect. 7.

2 The gPC-sG Method for the FPL Equation with Uncertainties

In this section, we describe the gPC-sG method for the FPL equation with uncertainty. We start by substituting the truncated gPC expansion (15) into Eq. (1). Upon a standard Galerkin projection, this yields a system of equations for the gPC coefficients \(f_k\):

$$\begin{aligned} \begin{aligned} \partial _t f_k(t,x,v) +&v\cdot \nabla _x f_k(t,x,v) + \nabla _v \cdot \int _{I_z} E(t,x,z) f^K(t,x,v,z) \varPhi _k(z)\pi (z)\,\mathrm {d}{z} \\&= Q_k(f^K,f^K)(t,x,v), \quad 1\le k\le K, \end{aligned} \end{aligned}$$
(17)

where \(Q_k(f^K,f^K)\), the kth mode of the collision operator, is defined as

$$\begin{aligned} Q_k(f^K,f^K):=\int _{I_z}Q(f^K,f^K)(t,x,v,z)\varPhi _k(z)\pi (z)\,\mathrm {d}{z}. \end{aligned}$$
(18)

To simplify the forcing term, note that

$$\begin{aligned} E_k(t,x)=-\nabla _x \phi _k(t,x),\quad \varDelta _x \phi _k(t,x) =\mu _k(x)- \int _{\mathbb {R}^{d_v}} f_k(t,x,v)\,\mathrm {d}{v}, \end{aligned}$$
(19)

where \(\mu _k(x) = \int _{I_z}\mu (x,z)\varPhi _k(z)\pi (z)\,\mathrm {d}{z}\) are the gPC coefficients of the neutralizing background \(\mu \). Then the integral term in (17) becomes

$$\begin{aligned} \int _{I_z}\left( \sum _{i=1}^K E_i(t,x)\varPhi _i(z)\right) \left( \sum _{j=1}^K f_j(t,x,v)\varPhi _j(z)\right) \varPhi _k(z)\pi (z)\,\mathrm {d}{z} =\sum _{j=1}^K A_{kj}(t,x)f_j(t,x,v), \end{aligned}$$
(20)

with

$$\begin{aligned} A_{kj}(t,x):=\sum _{i=1}^K S_{ijk}E_i(t,x), \quad S_{ijk}=\int _{I_z}\varPhi _i(z)\varPhi _j(z)\varPhi _k(z)\pi (z)\,\mathrm {d}{z}. \end{aligned}$$
(21)

To simplify the collision term, we define the bilinear FPL collision operator as

$$\begin{aligned} Q(f,g)(v)=\nabla _v \cdot \int _{\mathbb {R}^{d_v}} A(v-v_*)(f(v_*)\nabla _v g(v) - f(v)\nabla _{v_*}g(v_*)) \,\mathrm {d}{v}_*, \end{aligned}$$
(22)

Then the collision term (18) can be expressed as

$$\begin{aligned} Q_k(f^K,f^K)=\sum _{i,j=1}^K S_{ijk}Q(f_i,f_j). \end{aligned}$$
(23)

Due to the double summation in (23), a direct evaluation of the collision operator \(Q_k\) would be very expensive. To reduce the computational cost, we follow the approach proposed in [5]. Specifically, we pre-compute the singular value decomposition (SVD) of the matrix \(\{S_{ijk}\}_{ij}\) for each k:

$$\begin{aligned} S_{ijk}=\sum _{r=1}^{R_k}U_{ir}^k V_{rj}^k, \end{aligned}$$
(24)

where \(R_k\) is the numerical rank of the matrix. Plugging (24) into (23) and rearranging terms give

$$\begin{aligned} Q_k(f^K,f^K)=\sum _{r=1}^{R_k}Q\left( g^k_r,h^k_r\right) , \quad g^k_r:=\sum _{i=1}^K U_{ir}^k f_i, \quad h^k_r:=\sum _{j=1}^K V_{rj}^k f_j. \end{aligned}$$
(25)

Therefore, we reduce the original double summation into a single one. To compute the bilinear term \(Q\left( g^k_r,h^k_r\right) \), we apply the fast spectral method introduced in [11] for the deterministic FPL collision operator. See Appendix for a brief description of this method. The numerical complexity of such a computation is \(O(N_v^{d_v}\log N_v)\) where \(N_v\) is the number of mesh points in each velocity direction, and \(d_v\) is the dimension of the velocity space. Thus, for each k, the cost of computing \(Q_k\) is \(O(R_k N_v^{d_v}\log N_v)\) with \(R_k\le K\), and \(K=\left( {\begin{array}{c}m+d\\ m\end{array}}\right) \) is the dimension of d-variate polynomials of degree up to m (note that the direct evaluation of \(Q_k\) based on (23) requires \(O(K^2N_v^{2d_v})\) operations).

The initial data is given by

$$\begin{aligned} f_k(0,x,v)=f^0_k(x,v)=\int _{I_z}f^0(x,v,z)\varPhi _k(z)\pi (z)\,\mathrm {d}{z}. \end{aligned}$$
(26)

The Maxwell boundary condition is given by

$$\begin{aligned} f_k(t,x,v) = g_k(t,x,v),\quad x\in \partial \varOmega , \quad v\cdot n>0, \end{aligned}$$
(27)

with n the inward normal of \(\partial \varOmega \), and

$$\begin{aligned} g_k(t,x,v):= \int _{I_z}g(t,x,v,z)\varPhi _k(z)\pi (z)\,\mathrm {d}{z}. \end{aligned}$$
(28)

We consider the case where the wall temperature \(T_w\) and the accommodation coefficient \(\alpha \) may depend on z. We assume that \(\alpha (z) = \sum _{k=1}^K \alpha _k\varPhi _k(z)\). Then

$$\begin{aligned} \begin{aligned} g(t,x,v,z):=&(1-\alpha (z)) f^K(t,x,v-2(v\cdot n)n,z) \\+&\frac{\alpha (z)}{(2\pi )^{\frac{d_v-1}{2}}T_w(x,z)^{\frac{d_v+1}{2}}}e^{-\frac{v^2}{2T_w(x,z)}}\int _{v\cdot n<0} f^K(t,x,v,z)|v\cdot n|\,\mathrm {d}{v}. \end{aligned} \end{aligned}$$
(29)

Substitute into (28), one gets

$$\begin{aligned} \begin{aligned} g_k =&\sum _{j=1}^K\left( \int _{I_z}(1-\alpha (z))\varPhi _k(z)\varPhi _j(z)\pi (z)\,\mathrm {d}{z} \right) f_j(t,x,v-2(v\cdot n)n) \\&+ \sum _{j=1}^K D_{kj}(x,v)\int _{v\cdot n<0} f_j(t,x,v)|v\cdot n|\,\mathrm {d}{v}, \end{aligned} \end{aligned}$$
(30)

where

$$\begin{aligned} D_{kj}(x,v) = \int _{I_z}\frac{\alpha (z)}{(2\pi )^{(d_v-1)/2}T_w(x,z)^{(d_v+1)/2}}e^{-\frac{|v|^2}{2T_w(x,z)}} \varPhi _k(z)\varPhi _j(z) \pi (z)\,\mathrm {d}{z}, \end{aligned}$$
(31)

is a matrix that is time-independent hence can be pre-computed.

3 The Spatial and Time Discretization

In order to solve the Galerkin system (17), we split it into three steps:

$$\begin{aligned} \left\{ \begin{array}{l} \displaystyle \partial _t f_k + v\cdot \nabla _x f_k =0,\\ \displaystyle \partial _t f_k + \sum _{j=1}^K A_{kj}(t,x)\cdot \nabla _vf_j =0,\\ \displaystyle \partial _t f_k = Q_k(f^K, f^K). \end{array}\right. \end{aligned}$$
(32)

Note that each \(A_{kj}\) is a vector of length \(d_v\). To achieve second-order accuracy in time, we use the Strang splitting and the second-order Runge–Kutta method for each step. For the transport step, we employ a second-order MUSCL scheme with the minmod slope limiter [7]. For the forcing step, we discuss the case \(d_v=1\) for simplicity. The general case follows by computing the fluxes dimension by dimension. In the case \(d_v=1\), for each fixed x, since \((A_{kj})\) is a symmetric matrix depending on x but not on v, the equation becomes a system of linear hyperbolic equations in v with constant characteristic speeds which can be solved by upwind schemes. Thus we can diagonalize the matrix A, find the Riemann invariants, and use the MUSCL scheme on each Riemann invariant. To be precise, suppose A is written as

$$A=P^{-1}DP,$$

where \(P=(P_{kj})\) is an invertible matrix, and D is a diagonal matrix. Then the forcing step equations can be written as

$$\partial _t \bar{f}_k + D_{kk}\partial _v\bar{f}_k =0,$$

where \(\bar{f}_k=\sum _{j=1}^{K}P_{kj}f_j\). These equations in \(\bar{f}_k\) are hyperbolic with constant characteristic speeds and therefore can be solved by the MUSCL scheme. And then \(f_k\) is computed by

$$f_k=\sum _{j=1}^{K}(P^{-1})_{kj}\bar{f}_j.$$

For the collision step, we use the fast algorithm mentioned above to compute \(Q_k\).

To choose the time step \(\varDelta t\), we notice first that it has to satisfy the CFL condition from the transport step, which is \(\varDelta t\le \frac{\varDelta x}{R_v},\) where \(R_v\) is the largest possible characteristic speed. In addition, it has to satisfy the CFL condition from the forcing step, which is \(\varDelta t\le \frac{\varDelta v}{C_1},\) where the constant \(C_1=\max _{x,z}|E(t,x,z)|\) is the maximum of the electric field. Furthermore, due to the parabolic nature of the FPL collision operator, one has the following constraint for the collision step \(\varDelta t\le \frac{\varDelta v^2}{C_2},\) where the constant \(C_2\sim \max _{x,z}\int _{\mathbb {R}^{d_v}} A(v-v_*)f(t,x,v_*,z)\,\mathrm {d}{v}_*\) is the maximum of the strength of diffusion of the collision operator. Thus one should choose \(\varDelta t\) to satisfy the three restrictions.

4 Consistency Analysis of the gPC-sG Method for the Collision Operator

Here we give a consistency analysis of the gPC-sG method for the FPL collision operator. For simplicity, the random variable z is assumed to be one-dimensional in this section.

Suppose the exact solution to the spatial homogeneous FPL equation

$$\begin{aligned} \partial _t f = Q(f,f), \end{aligned}$$
(33)

is

$$\begin{aligned} f(t,v,z)=\sum _{k=1}^\infty f_k(t,v)\varPhi _k(z), \quad f_k(t,v) = \int _{I_z} f(t,v,z)\varPhi _k(z)\pi (z)\,\mathrm {d}{z}. \end{aligned}$$
(34)

Given the gPC approximation of f:

$$\begin{aligned} f\approx f^K(t,v,z) =\sum _{k=1}^K f_k(t,v)\varPhi _k(z), \end{aligned}$$
(35)

To analyze the consistency of the gPC-sG method, one substitutes the exact solution f into the scheme

$$\begin{aligned} \partial _t f_k \approx Q_k(f^K,f^K), \end{aligned}$$
(36)

and estimate the difference of the LHS and the RHS. Since f solves Eq. (33), one has

$$\begin{aligned} \partial _t f_k = Q_k(f,f). \end{aligned}$$
(37)

Thus it suffices to analyze \(Q_k(f,f)-Q_k(f^K,f^K)\), the numerical truncation error of the collision operator. We will use the following lemma proved by Pareschi et al. [12]:

Lemma 1.

Let \(g,h\in L^2_v\), then

$$\begin{aligned} \Vert Q(g,h)\Vert _{L^2_v}\le C \Vert h\Vert _{L^1_v}\Vert g\Vert _{H^2_v}. \end{aligned}$$
(38)

We estimate the error of collision operator as follows:

$$\begin{aligned}&|Q_k(f,f)-Q_k(f^K,f^K)|^2\\= & {} \left| \int _{I_z} [Q(f,f)-Q(f^K,f^K)]\varPhi _k(z)\pi (z)\,\mathrm {d}{z}\right| ^2\\\le & {} \int _{I_z}|Q(f,f)-Q(f^K,f^K)|^2\pi (z)\,\mathrm {d}{z} \int _{I_z}|\varPhi _k(z)|^2\pi (z)\,\mathrm {d}{z}.\\ \end{aligned}$$

Notice

$$\begin{aligned} |Q(f,f)-Q(f^K,f^K)|^2&= |Q(f,f-f^K)-Q(f^K-f,f^K)|^2\\&\le 2[|Q(f,f-f^K)|^2 + |Q(f^K-f,f^K)|^2], \end{aligned}$$

Then one gets

$$\begin{aligned} |Q_k(f,f)-Q_k(f^K,f^K)|^2\le 2\int _{I_z} \left[ |\bar{Q}(f,f-f^K)|^2+|\bar{Q}(f^K-f,f^K)|^2\right] \pi (z)\,\mathrm {d}{z}. \end{aligned}$$
(39)

Integrating in v and using the lemma, we get

$$\begin{aligned}&\Vert Q_k(f,f)-Q_k(f^K,f^K)\Vert ^2_{L^2_v}\\\le & {} C\int _{I_z}(\Vert f^K\Vert _{L^1_v}^2 \Vert f-f^K\Vert _{H^2_v}^2 + \Vert f-f^K\Vert _{L^1_v}^2 \Vert f\Vert _{H^2_v}^2)\pi (z)\,\mathrm {d}{z}\\\le & {} C\int _{I_z}(\Vert f-f^K\Vert _{H^2_v}^2+\Vert f-f^K\Vert _{L^1_v}^2)\pi (z)\,\mathrm {d}{z}, \end{aligned}$$

where C will be a generic positive constant in the sequel. The second inequality above is obtained by assuming that the \(L^1_v\) and \(H^2_v\) norms of f are bounded, and those norms of \(f^K\) are uniformly bounded in K. Also, notice that

$$\begin{aligned} \Vert f-f^K\Vert \le C_N K^{-N},\quad \forall N\ge 1, \end{aligned}$$
(40)

in which the norms are \(L^1_v\) or \(H^2_v\). The term \(C_N K^{-N}\) comes from the spectral accuracy of the projection operator, assuming that \(f\in H^{N+2}_v\). Plug into (40), we end up with the estimate

$$\begin{aligned} \Vert Q_k(f,f)-Q_k(f^K,f^K)\Vert ^2_{L^2_v}\le C_N K^{-2N} . \end{aligned}$$
(41)

which shows the spectral consistency of the gPC-sG method for the collision operator.

Remark 1.

In the proof, we assume that the \(L^1_v\) and \(H^2_v\) norms of f are bounded, and those norms of \(f^K\) are uniformly bounded in K. The regularity of f for the FPL equation without the forcing term is proved by Guo [4] assuming that the initial data is close enough to the global Maxwellian in a suitable Sobolev space. The result was extended to the equation with external force by Li and Yu [8]. No result is known for the equation we consider, where the force is self-consistent. Furthermore, the regularity of \(f^K\) is completely open. However, numerically we always observe the boundedness of these norms. Therefore, these assumptions are reasonable.

5 A Remark on High-Dimensional Random Spaces

If the random space is high-dimensional, the usual gPC expansion, which requires \(K=\left( {\begin{array}{c}m+d\\ d\end{array}}\right) \) basis functions where m is the maximal degree of polynomials and d is the dimension of the random space, can be prohibitively expensive. To handle this difficulty, we adopt the sparse technique we proposed in [15]. Using locally supported piecewise polynomials and a hierarchical construction, this technique gives a basis with \(K=O((m+1)^d2^NN^{d-1})\) basis functions, where N is the number of hierarchical levels, and m is the maximal degree of polynomials. The accuracy is \(O(N^d2^{-N(m+1)})\), which is \(O(K^{-(m+1)}(\log K)^{(m+2)(d-1)})\) in terms of K.

With this sparse basis, the number of basis can still be moderately large so that the SVD method for the collision operator as well as the diagonalization of the forcing term matrix A in (32) are no longer affordable. To avoid the SVD for the collision operator computation, we follow [15] and compute \(Q_k = \sum _{i,j=1}^K S_{ijk}Q(f_i,f_j)\) directly. The following sparsity result was proven: The number of pairs (i, j) for which there is at least one k with \(S_{ijk}\ne 0\) is no more than \(O((m+1)^{2d}2^{2N}N^{d+1})\), compared to the total number of pairs \(O((m+1)^{2d}2^{2N}N^{2d-2})\). Only for such pairs it is required to compute \(Q(f_i,f_j)\), and thus the computational cost for \(Q_k\) is still greatly reduced if N and d are large.

To avoid the diagonalization of the forcing term matrix A, we discuss the case \(d_v=1\) for simplicity. The cases with larger \(d_v\) can be treated dimension by dimension. In the case of \(d_v=1\), we use the local Lax–Friedrichs splitting for the second equation of (32) as follows:

$$\begin{aligned} \partial _t \mathbf {f} + \frac{1}{2}(A(x)-\beta (x)\mathscr {I}) \partial _v \mathbf {f} + \frac{1}{2}(A(x)+\beta (x)\mathscr {I}) \partial _v \mathbf {f} = 0, \end{aligned}$$
(42)

where \(\mathbf {f}=(f_1,\dots ,f_K)\), \(\mathscr {I}\) is the identity matrix of order K, and \(\beta (x)\) is a local (in each cell) upper bound of the absolute values of the eigenvalues of the symmetric matrix A(x). The eigenvalues of the first flux matrix \((A(x)-\beta (x)\mathscr {I})\) are all negative, while those of the second one are all positive. Thus one can use a second-order upwind scheme with the minmod slope limiter on each flux terms without diagonalizing the matrices.

6 Numerical Results

In all the numerical examples here, except for the Landau damping, we take the physical domain to be the one-dimensional (\(d_x=1\)) interval [0, 1] and the velocity domain to be two-dimensional (\(d_v=2\)). In all the examples, except for the six-dimensional random domain example, we take the periodic boundary condition. We discretize the physical domain into \(N_x\) grid points uniformly:

$$x_j=\left( j-\frac{1}{2}\right) \varDelta x,\quad \varDelta x=\frac{1}{N_x},\quad j=1,\dots ,N_x.$$

The velocity domain is truncated into \([-R_v,R_v]^2\) and discretized into \(N_v\) points in each dimension:

$$v_{j_1,j_2}=\left( -R_v+(j_1-\frac{1}{2}\varDelta v),-R_v+(j_2-\frac{1}{2}\varDelta v)\right) ,\quad \varDelta v=\frac{2R_v}{N_v},\quad j_1,j_2=1,\dots ,N_v.$$

\(R_v\) is big enough so \([-R_v,R_v]^2\) contains the support of the solution.

We assume the random variable z obeys uniform distribution on \([-1,1]^d\). In the first three examples, we take \(d=1\). In the fourth example, we take \(d=2\). These examples are computed by the gPC-sG method with the gPC basis being the normalized Legendre polynomials. For the last example, \(d=6\), and we use the sparse method given in the previous section.

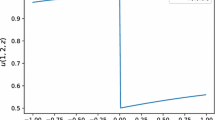
6.1 Random Initial Data: A Shock Tube Problem

We take the random initial data to be the equilibrium with macroscopic quantities

$$\left\{ \begin{array}{l} \rho _l=1+0.2\left( \frac{z+1}{2}\right) ,\quad u_l=0,\quad T_l=1,\quad x\le 0.5,\\ \rho _r=0.125,\quad u_r=0,\quad T_r=0.25,\quad x>0.5.\\ \end{array}\right. $$

We take

$$N_x=100,\quad N_v=32,\quad R_v=6,\quad K=7,\quad \varDelta t=0.001,$$

and compute the solution at \(t=0.1\) by the sG method. The result is compared with the solution by the stochastic collocation (sC) method with the same parameters and \(N_z=10\) Gauss–Legendre quadrature points; see Fig. 1. To implement the sC method, we take \(N_z\) Gauss–Legendre quadrature points \(\{z_j\}_{j=1}^{N_z}\) in the random domain and then solve the (deterministic) FPL equation at each \(z_j\). Finally, the mean and standard deviations of any quantity f are computed by

$$\begin{aligned} \mathbb {E}[f] = \sum _{j=1}^{N_z}f(z_j)w_j,\quad S[f] = \sqrt{\sum _{j=1}^{N_z}f(z_j)^2w_j-(\mathbb {E}[f])^2}, \end{aligned}$$
(43)

where \(w_j\) is the quadrature weight of the point \(z_j\). For the sC method, we verified that the solution with \(N_z=20\) quadrature points is indistinguishable with the solution with \(N_z=10\) quadrature points. Therefore, the \(N_z=10\) solution is good enough as a reference solution. This is also true for other numerical examples except the last one.

One can see from Fig. 1 that the results of two methods agree well. This shows that the sG method has good accuracy.

Fig. 1
figure 1

Random initial data: expectation and standard deviation of macroscopic quantities. Solid line: sC, \(N_x=100,\ N_v=32,\ R_v=6,\ N_z=10,\ \varDelta t=0.001\). Dots: sG, \(N_x=100,\ N_v=32,\ R_v=6,\ K=7,\ \varDelta t=0.001\)

Full size image

6.2 The Landau Damping

We use the Landau damping to test our sG method for the forcing term. For simplicity, we omit the collision term. The physical space is the interval \([0,4\pi ]\) with periodic boundary condition, and the velocity domain is one-dimensional. The random initial condition is

$$f^0(x,v)=\frac{1}{\sqrt{2\pi }}(1+(0.5+0.1z)\cos (0.5x))e^{-\frac{|v|^2}{2}}.$$

We take

$$N_x=64,\quad N_v=128,\quad R_v=6,\quad K=7,\quad \varDelta t=0.03,$$

for the sG method and compare with the sC method with the same parameters and \(N_z=10\). We compare the expectation and standard deviation of the magnitude of the electric field for t from 0 to 9.

It can be seen from Fig. 2 that the results from two methods agree well, which shows the accuracy of the sG method. Since the uncertainty is small, the expectation is similar to the result of [14]. The standard deviation in both examples also shows oscillation in time, and this needs further theoretical explanations.

Fig. 2
figure 2

Landau damping: expectation and standard deviation. Solid line: sC, \(N_x=64,\ N_v=128,\ R_v=6,\ N_z=10,\ \varDelta t=0.03\). Dots: sG, \(N_x=64,\ N_v=128,\ R_v=6,\ K=7,\ \varDelta t=0.03\). Upper curve: expectation. Lower curve: standard deviation

Full size image

6.3 A Random Neutralizing Background

We take the deterministic initial data as the equilibrium with macroscopic quantities

$$\begin{aligned} \rho = (2+\sin (2\pi x))/3,\quad u = (0.2,0),\quad T = (3+\cos (2\pi x))/4, \end{aligned}$$
(44)

and the random background as

$$\begin{aligned} \mu (x,z) = \frac{2}{3}(1+0.2z\sin (4\pi x)). \end{aligned}$$
(45)

We take

$$\begin{aligned} N_x=100,\quad N_v=32,\quad R_v=8,\quad K=7,\quad \varDelta t=0.001, \end{aligned}$$
(46)

and compare the solution by the sC method with the same parameters and \(N_z=10\) Gauss–Legendre quadrature points at \(t=0.1\). One can see from Fig. 3 that the results of two methods agree well, even for the standard deviations whose magnitude is small. This shows that the sG method can efficiently handle the uncertainties from the neutralizing background.

Fig. 3
figure 3

Random background: expectation and standard deviation of macroscopic quantities. Solid line: sC, \(N_x=100,\ N_v=32,\ R_v=8,\ N_z=10,\ \varDelta t=0.001\). Dots: sG, \(N_x=100,\ N_v=32,\ R_v=8,\ K=7,\ \varDelta t=0.001\)

Full size image

6.4 An Example with a Two-Dimensional Random Variable

To demonstrate that our sG method is efficient for more than one random dimension, we give a test of our method on an example with two-dimensional random domain \(I_{z_1,z_2}=[-1,1]^2\). The gPC basis is taken to be \(\{\varPhi _{k_1}(z_1)\varPhi _{k_2}(z_2)\}\) where \(\varPhi _k(z)\) is the normalized Legendre polynomial of degree k, and \(k_1+k_2\le m\). The initial data is given by

$$f^0(x,v)=\frac{\rho ^0(x)}{4\pi T^0(x)}\left( e^{-\frac{|v-u^0(x)|^2}{2T^0(x)}}+e^{-\frac{|v+u^0(x)|^2}{2T^0(x)}}\right) ,$$

where

$$\left\{ \begin{array}{l} \displaystyle \rho ^0(x,z)=\frac{1}{3}\left( 2+\sin (2\pi x)+\frac{1}{2}\sin (4\pi x)z_1+\frac{1}{3}\sin (6\pi x)z_2\right) ,\\ \displaystyle u^0=(0.2,0),\\ \displaystyle T^0(x,z)=\frac{1}{4}\left( 3+\cos (2\pi x)+\frac{1}{2}\cos (4\pi x)z_1+\frac{1}{3}\cos (6\pi x)z_2\right) .\\ \end{array}\right. $$

The numerical parameters are

$$N_x=100,\quad N_v=32,\quad R_v=6,\quad m=5,\quad \varDelta t=0.001,$$

and the result is compared at \(t=0.1\) with the sC method with the same parameters and \(N_z=10\) collocation points in each dimension. The result is shown in Fig. 4. It can be seen that the results of the two methods agree well, which shows the accuracy of the sG method for two-dimensional random domains.

Fig. 4
figure 4

Two-dimensional test with random initial data: expectation and standard deviation of macroscopic quantities. Solid line: sC, \(N_x=100,\ N_v=32,\ R_v=6,\ N_z=10,\ \varDelta t=0.001\). Dots: sG, \(N_x=100,\ N_v=32,\ R_v=6,\ m=5,\ \varDelta t=0.001\)

Full size image

6.5 An Example with a Six-Dimensional Random Domain

We finally give an example with a six-dimensional random domain. To deal with the high-dimensionality, we use the sparse sG method mentioned in Sect. 5.

Fig. 5
figure 5

Six-dimensional random domain example, using sparse sG: expectation and standard deviation of macroscopic quantities. \(N_x = 100,\ N_v = 32, \ R_v=8, \ \varDelta t = 0.001,\ m=0,\ N=3\)

Full size image

We take the initial data as the equilibrium with

$$\begin{aligned}&\rho (x,z) = 1 + \exp (-100(x-0.5)^2)\sin (10(x-0.5))(0.5+0.1z_2), \nonumber \\&\quad u(x,z) = 0,\quad T = 1 + 0.5\exp (-100(x-0.4-0.01z_1)^2), \end{aligned}$$
(47)

and boundary data as the Maxwell boundary with

$$\begin{aligned} T_w = 1+0.2z_3,\quad \alpha = 0.5 + 0.3z_4. \end{aligned}$$
(48)

The random background is given by

$$\begin{aligned} \mu (x,z) = 1+0.1z_5\sin (2\pi x) + 0.2z_6\cos (2\pi x). \end{aligned}$$
(49)

We choose numerical parameters as

$$N_x = 100,\quad N_v = 32,\quad R_v = 8,\quad \varDelta t = 0.001.$$

We use the sparse basis with \(m=0,\ N=3\) to solve the equation, and the result is shown in Fig. 5. One can clearly see that near the center of the domain, the mean and standard deviation of the density and the temperature are diffused due to the kinetic transport term, and those of the velocity exhibit more complicated behavior due to the forcing term. The most interesting phenomena is that near the left boundary, the effect of the boundary condition is not influential on the mean, but is dominating the standard deviation. In fact, for all the three standard deviations, one can see that the uncertainty comes from boundary and propagates into the domain. Note that for this example with six random dimensions, with the sparse approach, only 138 basis functions are needed.

7 Conclusion

In this paper, we propose a gPC-based stochastic Galerkin method for the Fokker–Planck–Landau equation with random uncertainties. By a gPC expansion and Galerkin projection, we convert the FPL equation with uncertainty into a system of deterministic equations. We prove the consistency of the gPC-sG method for the collision operator as well as accelerate the computation of the collision kernel by a singular value decomposition combined with a fast spectral method. We adopt the sparse method from [15] to handle high-dimensional random inputs. To avoid the expensive SVD operations, we take advantage of the sparsity of the tensor \(S_{b,ijk}\) for the computation of the collision operator and use a flux splitting for the mean-field term. Numerical results show the efficiency of the stochastic Galerkin method.