Keywords

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

The diversity of physical properties of doped fullerides has not been explained so far at a microscopic level despite the intensive experimental and theoretical studies conducted in recent decades. A variety of fullerene-based organic compounds have been synthesized with metals [1], hydrogen [2, 3], halogens [4,5,6], and benzene [7] that form a new class of organic conductors and semiconductors with tunable parameters. In polycrystalline C60 doped with alkali metals , at temperatures under 33 K superconductivity has been observed [8,9,10,11,12,13] with critical temperatures varying from 2.5 K for Na2KC60 to 33 K for RbCs2C60. Along with the phonon mechanism of Cooper pairing [14, 15], purely electronic pairing mechanism has been proposed [16]. To date, superconductivity of molecular conductors remains an open problem. According to the theoretical band structure calculations (see [17] for a review), fullerides with integer band-filling parameter n should be Mott–Hubbard insulators because all of them possess large enough intra-atomic Coulomb correlation. At the same time, the doped systems A3C60 (where A = K, Rb, Cs) turn out to be metallic at low temperatures [1]. It has been noted in papers [18, 19] that for a proper description of the metallic behavior of A3C60 (with x = 3 corresponding to the half filling of conduction band), the orbital degeneracy of the energy band is to be taken into account.

Adding to fullerene C60 the radicals containing metals of platinum group creates fullerene-based ferromagnetic materials [1]. Another example of ferromagnetic system in which neither component per se is ferromagnetic, are stacked Pd/C60 bilayers [20]. A purely organic compound TDAE-C60 (TDAE stands for tetrakis(dimethylamino)ethylene) represents a pronounced example of ferromagnetic behavior [21,22,23] of unclear nature. Studies of polymerized fullerenes [24,25,26] are promising as well. Distinct from polycrystalline fulleride, where fullerene molecules are bound weakly by van der Waals forces, in such polymers a chemical binding is realized. In temperature interval from 300 K to 500 K the polymerized fullerene C60 has the features of semiconductor with 2.1 eV energy gap [27].

Solid-state fullerenes (fullerides) are molecular crystals with intra-molecular interaction much stronger than intermolecular one. In a close packing structure each fullerene molecule has 12 nearest neighbors. Such structures are of two types, namely, base-centered cubic and hexagonal ones [28,29,30]. At low temperatures, the cubic О h crystal lattice symmetry does not correspond to the icosahedral Y symmetry of individual C60 molecules. There are four C60 molecules per unit cell of fulleride lattice, arranged in tetrahedra so that molecules’ orientations in every tetrahedron are identical. The tetrahedra form a simple cubic lattice. At ambient temperatures, solid fullerides have one of closely packed lattices [31, 32] and are semiconductors with band gap of 1.5–1.95 eV for C60 [33, 34], 1.91 eV for C70 [35], 0.5–1.7 eV for C78 [36], 1.2–1.7 eV for C84 [37,38,39]. Electrical resistivity of polycrystalline C60 [37, 40, 41] decreases monotonically with temperature and energy gap depends on the external pressure. Experimental studies of fulleride films [42] have shown nonexponential dependences with characteristic relaxation times of τ~5 ⋅ 10−8 s. The absence of temperature dependence in the temperature region 150–400 K favors the carrier localization and the recombination mechanism related to electron tunneling between the localized states. Transition from electronic to hole conductivity is proven by change of Hall coefficient sign. Such a transition is inherent, for example, to half-filled conduction band of K3C60.

In single-particle approximation, neglecting electron correlations, the following spectrum has been calculated [43]: 50 of 60 pz electrons of a neutral molecule fill all orbitals up to L = 4. The lowest L = 0,1,2 orbitals correspond to icosahedral states ag, t1u, hg. All states with greater L values undergo the icosahedral-field splitting. There are ten electrons in partially filled L = 5 state. Icosahedral splitting (L = 5 → hu + t1u + t2u) of these 11-fold degenerate orbitals leads to the electronic configuration shown in Fig. 6.1.

Fig. 6.1
figure 1

Single-electron energy levels of fullerene С60 (from paper [44]). The highest occupied molecular orbital (НОМО) and the lowest unoccupied molecular orbital (LUМО) are of particular importance

Full size image

Microscopic calculations and experimental data show that the completely filled highest occupied molecular orbital is of hu symmetry, and LUМО (threefold degenerate) has t1u symmetry. The HOMO–LUMO gap is caused by icosahedral perturbation in L = 5 shell, with experimentally found value of about 1 eV [45]. t1g (LUMO+1) state formed by L = 6 shell is 1 eV above the t1u LUМО. Different phases of the alkali fullerides are formed at changes of temperature, alkali metal concentration, or lattice structure. In particular, metallic or insulating phases occur at different fillings n of LUMO in С60 (n can take values from 0 to 6).

For a detailed theoretical study of electrical and magnetic properties of doped fullerides a model is to be formulated, which takes into account orbital degeneracy of energy levels, Coulomb correlation, as well as correlated hopping of electrons in narrow energy bands. The proper treatment of these interactions is important for a consistent description of a competition between on-site Coulomb correlation (characterized by Hubbard parameter U) and delocalization processes (translational motion of electrons is determined by bare bandwidth and energy levels’ degeneracy). Section 6.2 is devoted to the formulation of such model. Energy spectrum of electronic subsystem and the ground-state energy have been calculated within the Green function approach in Sect. 6.3. A generalization of the magnetization and Curie temperature calculations [46, 47] has been developed, which allows us to extend the phase diagram of the model and discuss driving forces for ferromagnetic state stabilization observed in TDAE-doped fullerides and polymerized fullerides. The competition of itinerant behavior enhanced by the external pressure application and localization due to the correlation effects is discussed.

2 Theoretical Model of Doped Fulleride Electronic Subsystem

Within the second quantization formalism, the Hamiltonian of interacting electrons (with spin-independent interaction V ee(r − r') in crystal field V ion(r)) may be written as

$$ H={H}_0+{H}_{i\kern0.1em n\kern0.1em t}, $$
(6.1)
$$ {H}_0=\sum \limits_{\sigma}\int {d}^3{rc}_{\sigma}^{+}(r)\kern0.22em \left[-\frac{\mathrm{\hslash}}{2m}\Delta +{V}^{\mathrm{ion}}(r)\right]{c}_{\sigma }(r), $$
$$ {H}_{i\kern0.1em n\kern0.1em t}=\sum \limits_{\sigma, {\sigma}^{\prime }}\int {d}^3r\int {d}^3{r}^{\prime}\kern0.1em {V}^{ee}\left(r-{r}^{\prime}\right)\kern0.1em {n}_{\sigma }(r)\kern0.1em {n}_{\sigma^{\prime }}\left({r}^{\prime}\right). $$

Here \( {c}_{\sigma}^{+}(r) \), c σ (r) are field operators of electron with spin σ creation and annihilation, respectively, \( {n}_{\sigma }(r)={c}_{\sigma}^{+}(r)\kern0.1em {c}_{\sigma }(r) \). Interaction term is diagonal with respect to spatial coordinates r, r'; therefore, it depends only on the electron fillings of the sites interacting, with energy V ee(r − r'). The lattice potential V ion(r) causes the splitting of initial band into multiple sub-bands numbered by index λ. For noninteracting electrons description, Bloch wave functions ψ λ k (r) and band energies є λk of corresponding states are used. Let us introduce Wannier functions, localized at position R i :

$$ {\varphi}_{\lambda \kern0.1em i}(r)=\frac{1}{\sqrt{N}}\sum \limits_k{e}^{-i\kern0.1em k\kern0.1em {R}_i}{\psi}_{\lambda \kern0.1em k}, $$

where N is the number of lattice sites. Electron creation and annihilation operators \( {a}_{i\kern0.1em \lambda \kern0.1em \sigma}^{+} \), a i λ σ on lattice site i in band λ can be introduced:

$$ {a}_{i\kern0.1em \lambda \kern0.1em \sigma}^{+}=\int {d}^3r{\varphi}_{\lambda \kern0.1em i}(r){\widehat{c}}_{\sigma}^{+}(r), $$
$$ {a}_{i\kern0.1em \lambda \kern0.1em \sigma }=\int {d}^3r{\varphi}_{\lambda \kern0.1em i}(r){\widehat{c}}_{\sigma }(r), $$

with the inverse transform

$$ {\widehat{c}}_{\sigma}^{+}(r)=\sum \limits_{i\kern0.1em \sigma }{\varphi}_{\lambda \kern0.1em i}^{\ast }(r){a}_{i\kern0.1em \lambda \sigma}^{+}, $$
$$ {\widehat{c}}_{\sigma }(r)=\sum \limits_{i\kern0.1em \sigma }{\varphi}_{\lambda \kern0.1em i}^{\ast }(r){a}_{i\kern0.1em \lambda \kern0.1em \sigma }. $$

In this way a general Hamiltonian can be rewritten in Wannier (site) representation as

$$ H=\sum \limits_{\lambda ij\sigma}{t}_{i j\lambda}{a}_{i\lambda \sigma}^{+}{a}_{i\lambda \sigma}+\frac{1}{2}\sum \limits_{\alpha \beta \gamma \delta}\sum \limits_{i j kl}\sum \limits_{\sigma {\sigma}^{\prime }}{J}_{i j kl}^{\alpha \beta \gamma \delta}{a}_{i\alpha \sigma}^{+}{a}_{j\beta {\sigma}^{\prime}}^{+}{a}_{l\delta {\sigma}^{\prime }}{a}_{k\gamma \sigma}, $$
(6.2)

where the matrix elements are defined by formulae

$$ {t}_{i\kern-0.1em j\lambda}=\int {d}^3r{\varphi}_{\lambda \kern0.1em i}^{\ast}\left(r-{R}_i\right)\left[-\frac{\hslash }{2m}\Delta +{V}^{\mathrm{ion}}(r)\right]\kern0.1em {\varphi}_{\lambda \kern0.1em j}\left(r-{R}_j\right), $$
(6.3)
$$ {J}_{i\kern-0.1em jkl}^{\alpha \beta \gamma \delta}=\int {d}^3r\int {d}^3{r}^{\prime }{V}^{ee}\left(r-{r}^{\prime}\right){\phi}_{i\alpha}^{\ast}\left(r-{R}_i\right){\phi}_{j\beta}^{\ast}\left({r}^{\prime }-{R}_j\right){\phi}_{l\delta}\left({r}^{\prime }-{R}_l\right){\phi}_{k\gamma}\left(r-{R}_k\right) $$
(6.4)

Note that the Hamiltonian in Wannier representation is nondiagonal, which is essential feature of strongly correlated electron systems and requires specific theoretical approaches for energy spectrum calculation. By analogy to the nondegenerate model [48, 49], we obtain the following Hubbard-type Hamiltonian for orbitally degenerate band with matrix elements of electron interactions describing correlated electron hoppings:

$$ {\displaystyle \begin{array}{l}H=-\mu \sum \limits_{i\lambda \sigma}{a}_{i\lambda \sigma}^{+}{a}_{i\lambda \sigma}+{\sum \limits_{i j\lambda \sigma}}^{\prime }{a}_{i\lambda \sigma}^{+}\left({t}_{i j}+\sum \limits_{k^{\prime}\lambda^{\prime }}J\left({i\lambda k}^{\prime }{\lambda}^{\prime }{j\lambda k}^{\prime }{\lambda}^{\prime}\right){n}_{k\prime \lambda \prime}\right){a}_{j\lambda \sigma}+\\ {}+U\sum \limits_{i\lambda}{n}_{i\lambda \uparrow }{n}_{i\lambda \downarrow }+\frac{U^{\prime }}{2}\sum \limits_{i\sigma \lambda \lambda^{\prime }}{n}_{i\lambda \sigma}{n}_{i\lambda \prime \overline{\sigma}}+\frac{\left({U}^{\prime }-{J}_0\right)}{2}\sum \limits_{i\sigma \lambda \lambda^{\prime }}{n}_{i\lambda \sigma}{n}_{i\lambda \prime \sigma }+\\ {}+\frac{1}{2}J\sum \limits_{i j\lambda \lambda^{\prime}\sigma \sigma^{\prime }}{a}_{i\lambda \sigma}^{+}{a}_{j\lambda \prime \sigma \prime}^{+}{a}_{i\lambda \sigma \prime }{a}_{j\lambda \prime \sigma },\end{array}} $$
(6.5)

where μ is chemical potential, \( {n}_{i\lambda \sigma}={a}_{i\lambda \sigma}^{+}{a}_{i\lambda \sigma} \) is number operator of electrons of spin σ in orbital λ of site i, \( \overline{\sigma} \) denotes spin projection opposite to σ, n iλ  = niλ↑ niλ↓; t ij is electron hopping integral from site j to site i (interorbital hoppings are neglected),

$$ J\left( i\lambda k{\lambda}^{\prime } j\lambda k{\lambda}^{\prime}\right)=\int \int {\varphi}_{\lambda}^{\ast}\left(r-{R}_i\right){\varphi}_{\lambda}\left(r-{R}_j\right)\frac{e^2}{\left|r-{r}^{\prime}\right|}{\left|{\varphi}_{\lambda^{\prime }}\left({r}^{\prime }-{R}_k\right)\right|}^2 drd{r}^{\prime } $$
(6.6)

(ϕ λ are Wannier functions),

$$ U=\int \int {\left|{\varphi}_{\lambda}\left(r-{R}_i\right)\right|}^2\frac{e^2}{\left|r-{r}^{\prime}\right|}{\left|{\varphi}_{\lambda}\left({r}^{\prime }-{R}_i\right)\right|}^2 drd{r}^{\prime } $$
(6.7)

is on-site Coulomb correlation, assumed to have the same magnitude for all orbitals,

$$ {J}_0=\int \int {\varphi}_{\lambda}^{\ast}\left(r-{R}_i\right){\varphi}_{\lambda^{\prime }}\left(r-{R}_i\right)\frac{e^2}{\left|r-{r}^{\prime}\right|}{\varphi}_{\lambda^{\prime}}^{\ast}\left({r}^{\prime }-{R}_i\right){\varphi}_{\lambda}\left({r}^{\prime }-{R}_i\right) drd{r}^{\prime } $$
(6.8)

is on-site Hund’s rule exchange integral, which stabilizes states |λ ↑ λ ′↑〉 and |λ ↓ λ ′↓〉, forming the atomic moments. Values of U, U ′, and J0 are related by condition [50]

$$ {U}^{\prime }=U-2{J}_0. $$

Intersite exchange coupling is parameterized as

$$ J=J\left( i\lambda j{\lambda}^{\prime } j\lambda i{\lambda}^{\prime}\right)=\int \int {\varphi}_{\lambda}^{\ast}\left(r-{R}_i\right){\varphi}_{\lambda}\left(r-{R}_j\right)\frac{e^2}{\left|r-{r}^{\prime}\right|}{\varphi}_{\lambda}^{\ast}\left(r-{R}_j\right){\varphi}_{\lambda}\left(r-{R}_i\right) drd{r}^{\prime }. $$
(6.9)

Intra-site Coulomb repulsion U and intersite exchange J are two principal energy parameters of the model. In fullerides, the competition between the Coulomb repulsion and delocalization processes (translation motion of electrons) determines the metallic or insulating state realization [51].

For fullerides, magnitude of U may be estimated from different methods. Within the local density approximation the Coulomb repulsion of 3.0 eV was obtained [52, 53]. From experimental data of paper [54] based on the electron affinity to ion \( {C}_{60}^{-} \) the value 2.7 eV has been obtained. In solid state closely spaced C60 molecules cause screening, which leads to the repulsion energy reduction to 0.8–1.3 eV [52, 53]. Auger spectroscopy and photo-emission spectroscopy gave values in the 1.4–1.6 eV range [44, 55]. It is worthwhile to note that electrons of the same spin projection spend less energy to sit on the same site than those of antiparallel spins; thus, orbitally degenerated levels are filled in accordance to Hund’s rule. Experiments [55] give for singlet-triplet splitting a value of 0.2 eV ± 0.1 eV; in paper [45], U2 is taken to be 0.05 eV.

We reduce the term \( {\sum \limits_{i j k\lambda {\lambda}^{\prime}\sigma}}^{/}J\left( i\lambda k{\lambda}^{\prime } j\lambda k{\lambda}^{\prime}\right)\kern0.1em {a}_{i\lambda \sigma}^{+}{n}_{k{\lambda}^{\prime }}{a}_{j{\lambda}^{\prime}\sigma } \) in Hamiltonian (6.5) to

$$ {\displaystyle \begin{array}{l}{\sum \limits_{i j\lambda \sigma}}^{\prime}\left(J\left( i\lambda \kern0.1em i\lambda \kern0.1em j\lambda \kern0.1em i\lambda \right){a}_{i\lambda \sigma}^{+}{a}_{j\lambda \sigma}{n}_{i\kern0.1em \overline{\sigma}}+h.c.\right)+{\sum \limits_{i j\lambda \overline{\lambda}\sigma}}^{\prime}\left(J\left( i\lambda \kern0.1em i\overline{\lambda}\kern0.1em j\lambda \kern0.1em i\overline{\lambda}\right){a}_{i\lambda \sigma}^{+}{a}_{j\lambda \sigma}{n}_{i\overline{\lambda}}+h.c.\right)\\ {}+{\sum \limits_{i j\lambda \lambda \prime \sigma}}^{\prime}\sum \limits_{\begin{array}{l}k\ne i\\ {}k\ne j\end{array}}\left(J\left( i\lambda \kern0.1em k\lambda \kern0.1em j\lambda \kern0.1em {k\lambda}^{\prime}\right){a}_{i\lambda \sigma}^{+}{a}_{j\lambda \sigma}{n}_{k\lambda \prime}\right)\end{array}} $$

(here \( \overline{\lambda} \) denotes the orbital other than λ). The first and the third sums in this expression generalize the correlated hopping, introduced for nondegenerate model (see, e.g., [49]). The second sum describes the correlated hopping type, which is a peculiarity of orbitally degenerated systems. Among such processes one can distinguish three distinct types of hopping, of which the first and the second are influenced by the occupancies of sites between which hopping takes place and the third one depends on neighboring sites’ filling. The latter can be taken into account in a mean-field type approximation:

$$ {\sum \limits_{i j\lambda {\lambda}^{\prime}\sigma}}^{\prime}\sum \limits_{\begin{array}{l}k\ne i\\ {}k\ne j\end{array}}J\left( i\lambda \kern0.1em k{\lambda}^{\prime}\kern0.1em j{\lambda}^{\prime}\kern0.1em k{\lambda}^{\prime}\right){a}_{i\lambda \sigma}^{+}{a}_{j\lambda \sigma}{n}_{k{\lambda}^{\prime }}\cong n{\sum \limits_{i j\lambda \sigma}}^{\prime}\kern0.1em {T}_1\left( i j\right){a}_{i\lambda \sigma}^{+}{a}_{j\lambda \sigma}, $$

where n =  < n iα  + n iβ  + n iγ > is mean number of electrons per site,

$$ {T}_1\left( i j\right)=\sum \limits_{\begin{array}{l}k\ne i\\ {}k\ne j\end{array}}J\left( i\lambda \kern0.1em k{\lambda}^{\prime}\kern0.1em j\lambda \kern0.1em k{\lambda}^{\prime}\right) $$

and we assume that J(iλ kα jλ kα) = J(iλ kβ jλ kβ) = J(iλ kγ jλ kγ) and T1(ij) is the same for all orbitals. If α-, β-, and γ-orbital states are equivalent, one can take:

$$ J\left( i\lambda \kern0.1em i\overline{\lambda}\kern0.1em j\lambda \kern0.1em i\overline{\lambda}\right)={t}_{\alpha \alpha}^{\prime}\left( i j\right)={t}_{\beta \beta}^{\prime}\left( i j\right)={t}_{\gamma \gamma}^{\prime}\left( i j\right)={t}_{i\kern0.1em j}^{\prime }, $$
$$ J\left( i\lambda \kern0.1em i\lambda \kern0.1em j\lambda \kern0.1em i\lambda \right)={t}_{\alpha \alpha}^{{\prime\prime}}\left( i j\right)={t}_{\beta \beta}^{{\prime\prime}}\left( i j\right)={t}_{\gamma \gamma}^{{\prime\prime}}\left( i j\right)={t}_{i\kern0.1em j}^{{\prime\prime} }. $$

The Hamiltonian takes its final form

$$ {\displaystyle \begin{array}{l}H=-\mu \sum \limits_{i\lambda \sigma}{a}_{i\lambda \sigma}^{+}{a}_{i\lambda \sigma}+U\sum \limits_{i\lambda}{n}_{i\lambda \uparrow }{n}_{i\lambda \downarrow }+\frac{U^{\prime }}{2}\sum \limits_{i\lambda \sigma}{n}_{i\lambda \sigma}{n}_{i{\lambda}^{\prime}\overline{\sigma}}+\\ {}+\frac{\left({U}^{\prime }-{J}_0\right)}{2}\sum \limits_{i\lambda {\lambda}^{\prime}\sigma }{n}_{i\lambda \sigma}{n}_{i{\lambda}^{\prime}\sigma }+{\sum \limits_{i j\lambda \sigma}}^{\prime }{t}_{i j}(n){a}_{i\lambda \sigma}^{+}{a}_{j\lambda \sigma}+\\ {}+{\sum \limits_{i j\lambda \overline{\lambda}\sigma}}^{\prime}\left({t}_{i\kern0.1em j}^{\prime }{a}_{i\lambda \sigma}^{+}{a}_{j\lambda \sigma}{n}_{i\overline{\lambda}}+h.c.\right)+{\sum \limits_{i j\lambda \sigma}}^{\prime}\left({t}_{i\kern0.1em j}^{{\prime\prime} }{a}_{i\lambda \sigma}^{+}{a}_{j\lambda \sigma}{n}_{i\lambda \overline{\sigma}}+h.c.\right)\\ {}+\frac{1}{2}\sum \limits_{i j\lambda \sigma {\sigma}^{\prime }}J(ij){a}_{i\lambda \sigma}^{+}{a}_{j\lambda {\sigma}^{\prime}}^{+}{a}_{i\lambda {\sigma}^{\prime }}{a}_{j\lambda \sigma},\end{array}} $$
(6.10)

with effective concentration-dependent hopping integral t ij (n) = t ij  + nT1(ij). Estimations of bare half bandwidth (w = z|t pj |, z being the number of nearest neighbors to a site) are 0.5–0.6 eV from data of paper [17] and 0.6 eV from paper [45].

3 Results and Discussion

For calculation of single-particle electron spectrum we apply the Green function method. The equation for single-particle Green function is

$$ E\left\langle \left\langle {a}_{p\alpha \uparrow }|{a}_{p^{\prime}\alpha \uparrow}^{+}\right\rangle \right\rangle =\frac{\delta_{p{p}^{\prime }}}{2\pi }+\left\langle \left\langle \left[{\alpha}_{p\alpha \uparrow },H\right]|{a}_{p^{\prime}\alpha \uparrow}^{+}\right\rangle \right\rangle . $$
(6.11)

Taking into account the Hamiltonian (6.10) structure, in the commutator from the above equation we approximate nondiagonal terms in a mean-field manner as

$$ {\displaystyle \begin{array}{l}\sum \limits_{i j\lambda \sigma {\lambda}^{\prime }}{t}_{i j}^{\prime }(n)\left(\left[{a}_{p\alpha \uparrow },{a}_{i\lambda \sigma}^{+}{a}_{j\lambda \sigma}{n}_{i{\lambda}^{\prime }}\right]+\left[{a}_{p\alpha \uparrow },{a}_{i\lambda \sigma}^{+}{a}_{j\lambda \sigma}{n}_{j{\lambda}^{\prime }}\right]\right)=\\ {}=\sum \limits_j{t}_{p j}^{\prime}\left(\left\langle {n}_{p\beta}\right\rangle +\left\langle {n}_{p\gamma}\right\rangle \right){a}_{j\alpha \uparrow }+\sum \limits_{j\sigma}{t}_{p j}^{\prime}\left(\left\langle {a}_{p\beta \sigma}^{+}{a}_{j\beta \sigma}\right\rangle +\left\langle {a}_{p\gamma \sigma}^{+}{a}_{j\gamma \sigma}\right\rangle \right){a}_{p\alpha \uparrow }+\\ {}+\sum \limits_j{t}_{p j}^{\prime}\left(\left\langle {n}_{j\beta}\right\rangle +\left\langle {n}_{j\gamma}\right\rangle \right){a}_{j\alpha \uparrow }+\sum \limits_{j\sigma}{t}_{p j}^{\prime}\left(\left\langle {a}_{j\beta \sigma}^{+}{a}_{p\beta \sigma}\right\rangle +\left\langle {a}_{j\gamma \sigma}^{+}{a}_{p\gamma \sigma}\right\rangle \right){a}_{p\alpha \uparrow }.\end{array}} $$
(6.12)

In a general case, averaged value of electron number operator depends on orbital 〈n iλ 〉 = n λ ,

$$ {\beta}_{\lambda}^{\prime }=\sum \limits_{j\sigma, {\lambda}^{\prime}\ne \lambda }{t}_{pj}^{\prime}\left\langle {a}_{p{\lambda}^{\prime}\sigma}^{+}{a}_{j{\lambda}^{\prime}\sigma }+h.c.\right\rangle . $$
(6.13)

According to the terminology of work [56], we classify the quantity \( {\beta}_{\lambda}^{\prime } \) as orbital-dependent shift of the band center.

Analogously, we process terms

$$ {\displaystyle \begin{array}{l}\sum \limits_{i j\lambda \sigma}{t}_{i j}^{{\prime\prime}}\left(\left[{a}_{p\alpha \uparrow },{a}_{i\lambda \sigma}^{+}{a}_{j\lambda \sigma}{n}_{i\lambda \overline{\sigma}}\right]+\left[{a}_{p\alpha \uparrow },{a}_{i\lambda \sigma}^{+}{a}_{j\lambda \sigma}{n}_{j\lambda \overline{\sigma}}\right]\right)=\\ {}=2\left(\sum \limits_j{t}_{p j}^{{\prime\prime}}\left\langle {n}_{p\alpha \downarrow}\right\rangle {a}_{j\alpha \uparrow }+\sum \limits_j{t}_{p j}^{{\prime\prime}}\left\langle {a}_{p\alpha \downarrow}^{+}{a}_{j\alpha \downarrow}\right\rangle {a}_{p\alpha \uparrow}\right)\end{array}} $$
(6.14)

and introduce notations n λσ  = 〈n jλσ 〉 and

$$ {\beta}_{\lambda \sigma}^{{\prime\prime} }=2\sum \limits_j{t}_{p j}^{{\prime\prime}}\left\langle {a}_{p\lambda \overline{\sigma}}^{+}{a}_{j\lambda \overline{\sigma}}\right\rangle . $$
(6.15)

According to the terminology of paper [56], we classify the quantity \( {\beta}_{\lambda \sigma}^{{\prime\prime} } \) as spin-dependent shift of the sub-band center.

Then the commutator (6.14) can be represented in the form

$$ 2{n}_{\lambda \sigma}\sum \limits_j{t}_{pj}^{{\prime\prime} }{a}_{j\alpha \uparrow }+{\beta}_{\lambda \sigma}^{{\prime\prime} }. $$

For the exchange interaction we have

$$ \frac{1}{2}J\sum \limits_{i j\lambda {\lambda}^{\prime}\sigma {\sigma}^{\prime }}\left[{a}_{p\alpha \uparrow}^{+},{a}_{i\lambda \sigma}^{+}{a}_{j{\lambda}^{\prime }{\sigma}^{\prime}}^{+}{a}_{i\lambda {\sigma}^{\prime }}{a}_{j{\lambda}^{\prime}\sigma}\right]=J\sum \limits_{j{\lambda}^{\prime }{\sigma}^{\prime }}{a}_{j{\lambda}^{\prime }{\sigma}^{\prime}}^{+}{a}_{p\alpha {\sigma}^{\prime }}{a}_{j{\lambda}^{\prime}\uparrow }. $$
(6.16)

Averaging this expression, one has to take into account that \( \left\langle {a}_{j\lambda \sigma}^{+}{a}_{p\overline{\lambda}\sigma}\right\rangle =0 \) because the electron transfer between different orbitals is excluded \( \left\langle {a}_{j\lambda \sigma}^{+}{a}_{j\lambda \overline{\sigma}}\right\rangle =\left\langle {S}_{j\lambda}^{\pm}\right\rangle =0 \), then we have

$$ J\sum \limits_{\sigma}\left\langle {a}_{j\alpha \sigma}^{+}{a}_{p\alpha \sigma}\right\rangle \sum \limits_j{a}_{j\alpha \uparrow }- zJ\left({n}_{\alpha \uparrow }+{n}_{\beta \uparrow }+{n}_{\gamma \uparrow}\right){a}_{p\alpha \uparrow .} $$

Other commutators in Eq. (6.11) are trivial. Hence, the equation of motion in the mean-field approximation takes the form

$$ {\displaystyle \begin{array}{l}\left\{E+\mu -{\beta}_{\alpha}^{\prime }-{\beta}_{\alpha \uparrow}^{{\prime\prime} }-{Un}_{\alpha \downarrow }-2{U}^{\prime }{n}_{\beta \downarrow }-2\left({U}^{\prime }-{J}_0\right){n}_{\beta \uparrow }+ zJ\left({n}_{\alpha \uparrow }+{n}_{\beta \uparrow }+{n}_{\gamma \uparrow}\right)\right\}\left\langle \left\langle {a}_{p\alpha \uparrow }|{a}_{p^{\prime}\alpha \uparrow}^{+}\right\rangle \right\rangle =\\ {}=\frac{\delta_{p{p}^{\prime }}}{2\pi }+\sum \limits_j\left\{{t}_{p j}(n)-4{t}_{p j}^{\prime }{n}_{\overline{\lambda}}-2{t}_{p j}^{{\prime\prime} }{n}_{\lambda \downarrow }+J\sum \limits_{\sigma}\left\langle {a}_{j\alpha \sigma}^{+}{a}_{p\alpha \sigma}\right\rangle \right\}\left\langle \left\langle {a}_{j\alpha \uparrow }|{a}_{p^{\prime}\alpha \uparrow}^{+}\right\rangle \right\rangle .\end{array}} $$
(6.17)

Let us introduce notations

$$ {\tilde{\mu}}_{\lambda \sigma}=\mu -{\beta}_{\lambda}^{\prime }-{\beta}_{\lambda \sigma}^{{\prime\prime} }-{Un}_{\lambda \overline{\sigma}}-2{U}^{\prime }{n}_{\overline{\lambda}\overline{\sigma }}-2\left({U}^{\prime }-{J}_0\right){n}_{\overline{\lambda}\sigma }+ zJ\sum \limits_{\lambda }{n}_{\lambda \sigma}, $$
(6.18)

for the renormalized chemical potential and

$$ {\alpha}^{\lambda \sigma}=1-{\tau}_1n-4{\tau}^{\prime }{n}_{\overline{\lambda}}-2{\tau}^{{\prime\prime} }{n}_{\lambda \overline{\sigma}}-\frac{zJ}{w}\sum \limits_{j\sigma}\left\langle {a}_{j\alpha \sigma}^{+}{a}_{p\alpha \sigma}\right\rangle . $$
(6.19)

for the correlation band narrowing factor.

Here, dimensionless parameters of correlated hopping \( {\tau}^{\prime }={t}_{pj}^{\prime }/\left|{t}_{pj}\right| \); \( {\tau}^{{\prime\prime} }={t}_{pj}^{{\prime\prime} }/\left|{t}_{pj}\right| \) are introduced. In absence of the correlated hopping τ1 = 0, τ ′ = τ ″ = 0.

After the Fourier-transform, we obtain for the Green function

$$ {\left\langle \left\langle {a}_{p\lambda \sigma}|{a}_{p^{\prime}\lambda \sigma}^{+}\right\rangle \right\rangle}_{\overrightarrow{k}}=\frac{1}{2\pi}\frac{1}{E-{E}^{\lambda \sigma}\left(\overrightarrow{k}\right)}, $$
(6.20)

where the energy spectrum is

$$ {E}^{\lambda \sigma}\left(\overrightarrow{k}\right)=-{\tilde{\mu}}_{\lambda \sigma}+{\alpha}^{\lambda \sigma}t\left(\overrightarrow{k}\right). $$
(6.21)

The chemical potential is to be calculated from the equation

$$ {n}_{\lambda \sigma}=\frac{1}{N}\sum \limits_{\overrightarrow{k}}\underset{-\infty }{\overset{\infty }{\int }}{J}_{\overrightarrow{k}}^{\lambda \sigma}(E) dE, $$
(6.22)

where the spectral density of the Green function is defined by the expression

$$ {J}_{\overrightarrow{k}}^{\lambda \sigma}=\frac{}{}\delta \left(E-{E}^{\lambda \sigma}\left(\overrightarrow{k}\right)\right){\left[1+\exp \left(\left(E-{\tilde{\mu}}_{\lambda \sigma}\right)/\theta \right)\right]}^{-1}. $$
(6.23)

where θ = kT. In case of arbitrary density of electronic states ρ(ε) for nonzero temperatures one has

$$ {n}_{\lambda \sigma}=\underset{-w}{\overset{w}{\int }}\rho \left(\varepsilon \right){\left[1+\exp \left(\left({E}^{\lambda \sigma}\left(\overrightarrow{k}\right)-{\tilde{\mu}}_{\lambda \sigma}\right)/\theta \right)\right]}^{-1} d\varepsilon . $$
(6.24)

The ground-state energy can be calculated by the method of work in [57] as

$$ {\displaystyle \begin{array}{l}{E}_0=\frac{1}{2N}\sum \limits_{\overrightarrow{k}\lambda \sigma}\underset{-\infty }{\overset{\infty }{\int }}\left({t}_{\overrightarrow{k}}(n)+{E}^{\lambda \sigma}\left(\overrightarrow{k}\right)\right){J}_{\overrightarrow{k}}^{\lambda \sigma}(E) dE=\\ {}\kern1em =\frac{1}{2N}\sum \limits_{\overrightarrow{k}\lambda \sigma}\left({t}_{\overrightarrow{k}}(n)+{E}^{\lambda \sigma}\left(\overrightarrow{k}\right)\right){\left[1+\exp \left(\left({E}^{\lambda \sigma}\left(\overrightarrow{k}\right)-{\tilde{\mu}}_{\lambda \sigma}\right)/\theta \right)\right]}^{-1}.\end{array}} $$
(6.25)

For arbitrary density of states (at T = 0 K) one has

$$ {E}_0=\frac{1}{2}\sum \limits_{\lambda \sigma}\underset{-w}{\overset{\varepsilon^{\lambda \sigma}}{\int }}\rho \left(\varepsilon \right)\left(\left(1-{\tau}_1n\right)\varepsilon +{E}^{\lambda \sigma}\left(\varepsilon \right)\right) d\varepsilon . $$
(6.26)

Single-electron states occupation numbers are related by the constraints

$$ \sum \limits_{\lambda \sigma}{n}_{\lambda \sigma}=n,\kern1em \sum \limits_{\lambda}\left({n}_{\lambda \uparrow }-{n}_{\lambda \downarrow}\right)=m, $$

in the case of no orbital ordering, we have nλ↑ = (n + m)/3, nλ↓ = (n − m)/3.

In the case of rectangular density of states, the ground-state energy can be calculated analytically:

$$ {E}_0=-\sum \limits_{\lambda \sigma}\left\{\left(1-{\tau}_1n+{\alpha}^{\lambda \sigma}\right)\left(1-{n}_{\lambda \sigma}\right){n}_{\lambda \sigma}\frac{w}{2}+{\tilde{\mu}}_{\lambda \sigma}\frac{n_{\lambda \sigma}}{2}\right\}, $$
(6.27)

where

$$ {\tilde{\mu}}_{\lambda \sigma}=\mu -{\beta}_{\lambda}^{\prime }-{\beta}_{\lambda \sigma}^{{\prime\prime} }-\left(U+2{U}^{\prime}\right)\frac{n-{\eta}_{\sigma }m}{3}-2\left({U}^{\prime }-{J}_0\right)\frac{n+{\eta}_{\sigma }m}{3}+ zJ\left(n+{\eta}_{\sigma }m\right), $$
$$ {\alpha}^{\lambda \sigma}=1-{\tau}_1n-\frac{8}{3}{\tau}^{\prime }n-\frac{2}{3}{\tau}^{{\prime\prime}}\left(n-{\eta}_{\sigma }m\right)-\frac{2}{3}\frac{zJ}{w}\left(n-\frac{1}{3}\left({n}^2+{m}^2\right)\right), $$

η σ  = 1 for spin-up electrons and −1 otherwise. In these calculations we take into account that

$$ \frac{zJ}{w}\sum \limits_{j\sigma}\left\langle {a}_{j\alpha \sigma}^{+}{a}_{p\alpha \sigma}\right\rangle =-\frac{zJ}{w}\sum \limits_{j\sigma}\frac{t_{p j}}{\left|{t}_{p j}\right|}\left\langle {a}_{j\alpha \sigma}^{+}{a}_{p\alpha \sigma}\right\rangle =\frac{zJ}{w}\sum \limits_{\sigma }{n}_{\alpha \sigma}\left(1-{n}_{\lambda \sigma}\right) $$
(6.28)

and

$$ {\beta}_{\lambda}^{\prime }=4\sum \limits_{j\sigma}{t}_{pj}^{\prime}\left\langle {a}_{j\overline{\lambda}\sigma}^{+}{a}_{p\overline{\lambda}\sigma}\right\rangle =-4{\tau}^{\prime}\sum \limits_{\sigma}\underset{-w}{\overset{w}{\int }}\rho \left(\varepsilon \right)\varepsilon d\varepsilon . $$
(6.29)

For the rectangular density of states

$$ {\beta}_{\lambda}^{\prime }=-\frac{8}{3}{\tau}^{\prime }w\left(n-\frac{1}{3}\left({n}^2+{m}^2\right)\right). $$
(6.30)

Analogously,

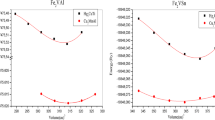
$$ {\beta}_{\lambda \uparrow}^{{\prime\prime} }=\frac{2}{9}{\tau}^{{\prime\prime} }w\left(n\left(3-n\right)-{\eta}_{\sigma }m\left(3-2n\right)-{m}^2\right). $$
(6.31)

Thus, the model is parameterized and dependences of the ground-state energy of the considered model E0 on energy parameters U, J H , zJ, correlated hopping parameters τ1, τ ′, τ ″, electron concentration n, and magnetization m can be studied numerically. Using the expression (6.27), one can obtain the equilibrium value of system magnetization m GS , which is a zeroth-order approximation in magnetization calculation at nonzero temperature. In case of the second-order transition, one obtains equation for the Curie temperature at arbitrary density of states

$$ {\theta}_c=6\underset{-w}{\overset{w}{\int }}\rho \left(\varepsilon \right)\left(A+ B\varepsilon \right)\exp \left({E}^{\ast }/{\theta}_c\right){\left(\exp \left({E}^{\ast }/{\theta}_c\right)+1\right)}^{-2} d\varepsilon, $$
(6.32)

where E ∗ is paramagnetic spectrum. The chemical potential is determined by the condition

$$ n=3\underset{-w}{\overset{w}{\int }}\rho \left(\varepsilon \right){\left(\exp \left({E}^{\ast }/{\theta}_c\right)+1\right)}^{-1} d\varepsilon . $$
(6.33)

Equations (6.32) and (6.33) generalize corresponding results for nondegenerate case [47] on triple orbital degeneracy of energy levels and allow modeling of the Curie temperature at various densities of electronic states in a wide range of the model energy parameters values for electron concentrations 0 < n < 3 (which corresponds to doped fullerides AnC60 and TDAE-C60). Behavior of Curie temperature appears to be closely related to the ground-state magnetization concentrational dependence. The correlated hopping reduces the obtained values of the Curie temperature considerably.

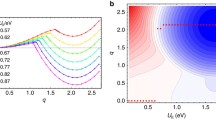
In Fig. 6.2, the concentration dependence of Curie temperature is shown in different scenarios, corresponding to different acting mechanisms of correlated hopping of electrons, both second-type correlated hopping parameters considered to have the same magnitude τ2 = τ ′ = τ ″. One can see that the correlated hopping, which is known [49] to suppress conductance, enhances ferromagnetic tendencies greatly. Applicability of the particular scenario to a given fulleride requires further studies and will be considered elsewhere. On a qualitative level, taking into account the correlated hopping allows to obtain reasonable estimates for Curie temperature within the considered model of triply degenerate band with intersite exchange small enough to be characteristic for polymerized fullerenes [58] and αTDAE-C60 [59]. We note that the system remains semiconducting at Coulomb interaction energies greater than the bandwidth at integer average occupation number of a site in this model [19].

Fig. 6.2
figure 2

Curie temperature dependence of band filling at U/w = 1.2, J0/w = 0/35. Curve 1 corresponds to zJ/w = 0.25 and τ1 = τ2 = 0; 2: zJ/w = 0.1 and τ1 = τ2 = 0.05; 3: zJ/w = 0.1; and τ1 = 0.05, τ2 = 0.07

Full size image

Thus, both ferromagnetic ordering and semiconducting behavior [21] can be observed. Simultaneous taking into account of triple orbital degeneracy of energy levels and correlated hopping of electrons makes standard methods of theoretical treatment complicated to apply, though it gives a clue for description of ferromagnetic behavior of doped fullerides. At the same time, the approach used in this investigation has its own shortcomings [47], namely, it overestimates numerical values for Curie temperature. This is rewarded by the natural description of the electron–hole asymmetry, which is clearly seen from curves 2 and 3 in Fig. 6.2. As expected, Hund’s rule coupling affects the Curie temperature considerably (see Fig. 6.3); however, in the absence of the correlated hopping, the values of J0/w required for a ferromagnetic solution are too large to be the case of the doped fullerides.

Fig. 6.3
figure 3

Curie temperature dependence on J0/w for quarter-filling of the band at U/w = 1.2 and zJ/w = 0.05. Curve 1 corresponds to the absence of correlated hopping; 2: τ1 = 0.1, τ2 = 0; 3: τ1 = 0.1, τ2 = 0.1

Full size image

In Fig. 6.3, there is a region of sharp critical temperature increase at increasing J0/w (this region corresponds to a partial spin polarization of the system) and a region of linear proportionality between Curie temperature and J0/w (this region corresponds to saturated ferromagnetic state). The competition of itinerant behavior and localization due to the correlation effects can be enhanced by the external pressure application renormalizing the effective band width. This effect is particularly important near the critical value of J0/w parameter. In our opinion, based on estimations of papers [17, 45, 55], curve 3 can be used as a reasonable model for the pressure-driven transition to ferromagnetic state.

From Fig. 6.4 one can see that the change of electron concentration qualitatively changes tendencies in the present model, which is yet another example of electron–hole asymmetry. In the present approach, the difference between ferromagnetic order stabilization by the correlated hopping for scenarios 1,2 and destabilization for 3,4,5 can be attributed to the different consequences of sub-bands’ narrowing caused by the correlated hopping in energy band picture at electron concentrations n = 1 and n = 3.

Fig. 6.4
figure 4

Curie temperature dependence on the correlated hopping parameter τ2 at U/w = 1, zJ/w = 0.05, J0/w = 0.4. Curve 1 corresponds to n = 1, τ1 = 0; curve 2: n = 1, τ1 = 0,1; curve 3: n = 3, τ1 = 0,05; curve 4: n = 3, τ1 = 0,08; curve 5: n = 3, τ1 = 0,1

Full size image

4 Conclusions

The general model for electronic subsystem of doped fullerides can describe both semiconducting behavior and magnetic order onset, if Coulomb correlation, intersite exchange interaction, correlated hopping of electrons, and orbital degeneracy of energy levels are all taken into account. In such a model, the magnetization and Curie temperature calculations allow us to extend the model phase diagram and discuss driving forces for ferromagnetic state stabilization observed in polymerized fullerenes and tetrakis(diethylamino)ethylene-fullerene. Curie temperature dependence on integer electron concentration at realistic values of the Coulomb correlation strength and Hund’s rule coupling, associated with orbital degeneracy of energy levels, is strongly asymmetrical with respect to half-filling. Hund’s rule coupling stabilizes ferromagnetic ordering in quarter-filled band. There is a region of sharp critical temperature increase at increasing Hund’s rule coupling parameter corresponding to a partial spin polarization of the system and a region of saturated ferromagnet state. The balance of itinerant behavior and localization due to the correlation effects can be shifted by the external pressure application renormalizing the effective band width.