Abstract
Checking the semantic equivalence of operations is an important task in software development. For instance, regression testing is a routine task when software systems are developed and improved, and software package managers require the equivalence of operations in different versions of a package within the same major version. In order to support a good automation of this process, a solid foundation is required. It has been shown that the notion of equivalence is not obvious when non-deterministic features are present. In this paper, we discuss a general notion of equivalence in functional logic programs and develop a practical method to check it. Our method can be integrated in a property-based testing tool which is used in a software package manager to check the semantic versioning of software packages.
Access provided by CONRICYT-eBooks. Download conference paper PDF
Similar content being viewed by others
1 Motivation
Functional logic languages combine the most important features of functional and logic programming in a single language (see [4, 14] for recent surveys). In this paper we consider Curry [18], a contemporary functional logic language which conceptually extends Haskell with common features of logic programming. Hence, Curry combines the demand-driven evaluation of functions with non-deterministic evaluation of operations defined by overlapping rules. As discussed in [6], the combination of these features poses new issues for defining the equivalence of expressions. Actually, three different notions of equivalence can be distinguished:
-
1.
Ground equivalence: Two expressions are equivalent if they have the same results when their variables are replaced by ground terms.
-
2.
Computed-result equivalence: Two expressions are equivalent if they have the same outcomes, i.e., variables in expressions are considered as free variables which might be instantiated during the evaluation process.
-
3.
Contextual equivalence: Two expressions are equivalent if they produce the same outcomes in all possible contexts.
Ground equivalence seems reasonable for functional programs since free variables are not allowed in expressions to be evaluated in functional programming. For instance, consider the Boolean negation defined by

The expressions not (not x) and x are ground equivalent, which can be checked easily by instantiating x to True and False, respectively, and evaluating both expressions. However, these expressions are not computed-result equivalent w.r.t. the narrowing semantics of functional logic programming: the expression not (not x) evaluates to the two outcomes {x = False} False and {x = True} True,Footnote 1 whereas the expression x evaluates to the single result \(\mathtt {\{\}\, x}\) without instantiating the free variable x. Due to these differences, Bacci et al. [6] states that ground equivalence is “the (only possible) equivalence notion used in the pure functional paradigm.” As we will see later, this is not true since contextual equivalence is also relevant in non-strict functional languages.
The previous example shows that the evaluation of ground equivalent expressions might result in answers with different degrees of instantiation. However, the presence of logic variables and non-determinism might also lead to different results when ground equivalent expressions are put in a same context. For instance, consider the following contrived example [6] (a more natural example will be shown later):

The expressions f x and g x are computed-result equivalent since the only computed result is {x = A} C A. Now consider the following operation:

Then the expression k (f x) x evaluated lazily produces \({\mathtt {\{x=B\}\,\,B}}\), whereas the expression k (g x) x produces no values. In fact, the evaluation of g x instantiates (narrows) x to A, and k (C A) A is irreducible. Hence, the ground and computed-result equivalent expressions are not contextually equivalent.
The equivalence of operations is important when existing software packages are further developed, e.g., refactored or implemented with more efficient data structures. In this case, we want to ensure that operations available in the API of both versions of a software package are equivalent, as long as we do not introduce intended API changes. For this purpose, software package management systems associate version numbers to software packages. In the semantic versioning standard,Footnote 2 a version number consists of major, minor, and patch number, separated by dots, and an optional pre-release specifier. For instance, 2.0.1 and 3.2.1-alpha.2 are valid version numbers. An intended and incompatible change of API operations is marked by a change in the major version number. Thus, operations available in two versions of a package with identical major version numbers should be equivalent. Unfortunately, most package managers do not check this equivalence but leave it as a recommendation to the package developer.
Improving this situation is the motivation for our work. We want to develop a tool to check the equivalence of two operations. Since we aim to integrate this kind of semantic versioning checking in a practical software package manager [16], the tool should be fully automatic. Thus, we are going to test equivalence properties rather than verify them. Although this might be unsatisfactory from a theoretical point of view, it could be quite powerful from a practical point of view and might prevent wasting time to prove incorrect properties. For instance, property-based test tools like QuickCheck [8] provide great confidence in programs by checking program properties with many test inputs. For instance, we could check the equivalence of two operations f and \(f'\) by checking the equation \(f\;x = f'\;x\) with many values for x. The previous discussion of equivalence criteria shows that this property checks only the ground equivalence of f and \(f'\). However, in the context of semantic versioning checking, ground equivalence is too restricted since equivalent operations should deliver the same results in any context. Therefore, contextual equivalence is desired. Actually, this kind of equivalence has been proposed in [5] as the only notion to state the correctness of an implementation w.r.t. a specification in functional logic programming. Unfortunately, the automatic checking of contextual equivalence with property-based test tools does not seem feasible due to the unlimited number of possible contexts. Therefore, Bacci et al. [6] state: “In a test-based approach...the addition of a further outer context would dramatically alter the performance.” Therefore, the authors abandon the use of a standard property-based test tool in their work.
In this paper we show that we can use such tools for contextual equivalence (and, thus, semantic versioning) checking if we use an appropriate encoding of test data. For this purpose, we develop some theoretical results that allow us to reduce the contexts to be considered for equivalence checking. From these results, we show how property-based testing can be used for this purpose. Based on these results, we extend an existing property-based test tool for functional logic programs [15] to test the equivalence of operations. This is the basis of a software package manager with semantic versioning checking [16].
In the next section, we review the main concepts of functional logic programming and Curry. Section 3 defines our notion of equivalence which is used in Sect. 4 to develop practically useful characterizations of equivalent operations. Section 5 shows how to use these criteria in a property-based testing tool. Section 6 discusses some related work before we conclude.
2 Functional Logic Programming and Curry
We briefly review those elements of functional logic languages and Curry that are necessary to understand the contents of this paper. More details can be found in surveys on functional logic programming [4, 14] and in the language report [18].
Curry is a declarative multi-paradigm language combining in a seamless way features from functional and logic programming. The syntax of Curry is close to Haskell [23]. In addition to Haskell, Curry allows free (logic) variables in conditions and right-hand sides of rules. Thus, expressions in Curry programs contain operations (defined functions), constructors (introduced in data type declarations), and variables (arguments of operations or free variables). Function calls with free variables are evaluated by a possibly non-deterministic instantiation of demanded arguments [2]. In contrast to Haskell, rules with overlapping left-hand sides are non-deterministically (and not sequentially) applied.
Example 1
The following example shows the definition of a non-deterministic list insertion operation in Curry:

For instance, the expression insert 0 [1,2] non-deterministically evaluates to one of the values [0,1,2], [1,0,2], or [1,2,0]. Based on this operation, we can easily define permutations:

Thus, perm [1,2,3,4] non-deterministically evaluates to all 24 permutations of the input list.
Non-deterministic operations, which are interpreted as mappings from values into sets of values [13], are an important feature of contemporary functional logic languages. Using non-deterministic operations as arguments could cause a semantical ambiguity. Consider the operations

Standard term rewriting produces, among others, the derivation

whose result is (presumably) unintended. Therefore, González-Moreno et al. [13] proposed the rewriting logic CRWL as a logical foundation for declarative programming with non-strict and non-deterministic operations. This logic specifies the call-time choice semantics [19] where values of the arguments of an operation are set, though not computed, before the operation is evaluated. In a lazy strategy, this is naturally obtained by sharing. For instance, the two occurrences of coin in the derivation above are shared so that “double coin” has only two results: 0 or 2. Since standard term rewriting does not conform to the intended call-time choice semantics, other notions of rewriting have been proposed to formalize this idea, like graph rewriting [11, 12] or let rewriting [21]. In this paper, we use a simple reduction relation that we sketch without giving all details (which can be found in [21]).
In the following, we ignore free (logic) variables since they can be considered as syntactic sugar for non-deterministic data generator operations [3]. Thus, a value is an expression without operations or free variables. To cover non-strict computations, expressions can also contain the special symbol \(\bot \) to represent undefined or unevaluated values. A partial value is a value containing occurrences of \(\bot \). A partial constructor substitution is a substitution that replaces variables by partial values. A context \(\mathcal{{C}}[\cdot ]\) is an expression with some “hole”. The reduction relation we use throughout this paper is defined as follows (conditional rules are not considered for the sake of simplicity):

The first rule models call-time choice: if a rule is applied, the actual arguments of the operation must have been evaluated to partial values. The second rule models non-strictness by allowing the evaluation of any subexpression to an undefined value (which is intended if the value of this subexpression is not demanded). As usual, \(\mathrel {\buildrel * \over \rightarrow }\) denotes the reflexive and transitive closure of this reduction relation. The equivalence of this rewrite relation and CRWL is shown in [21].
3 Equivalent Operations
As discussed above, equivalence of operations can be defined in different ways. Ground equivalence and computed result equivalence only compare the values of applications. This is too weak since some operations have no finite values.
Example 2
Consider the following operations that generate infinite lists of numbers:

Since these operations do not produce finite values, we cannot detect any difference when comparing only computed results. However, they behave different when put into some context, e.g., an operation that selects the second element of a list:

Now, snd (ints1 0) and snd (ints2 0) evaluate to 1 and 2, respectively.
Therefore, we do not consider these operations as equivalent. This motivates the following notion of equivalence for possibly non-terminating and non-deterministic operations.Footnote 3
Definition 1
(Equivalence). Let \(f_1,f_2\) be operations of type \(\tau \rightarrow \tau '\). \(f_1\) is equivalent to \(f_2\) iff, for any expression \(E_1\), \(E_1 \mathrel {\buildrel * \over \rightarrow }v\) iff \(E_2 \mathrel {\buildrel * \over \rightarrow }v\), where v is a value and \(E_2\) is obtained from \(E_1\) by replacing each occurrence of \(f_1\) with \(f_2\).
This notion of equivalence conforms with the usual notion of contextual equivalence in programming languages (e.g., see [25] for a tutorial). It was already proposed in [5] as the notion of equivalence for functional logic programs and also defined in [6] as “contextual equivalence” for functional logic programs.
Thus, ints1 and ints2 are not equivalent. Moreover, even terminating operations that always compute same results might not be equivalent if put into some context.
Example 3
Consider the definition of lists sorted in ascending order:

We can use this definition and the definition of permutations above to provide a precise specification of sorting a list by computing some sorted permutation:

We might try to obtain an even more compact formulation by defining the “sorted” property as an operation that is the (partial) identity on sorted lists:

Then we can define another operation to sort a list by composing perm and idSorted:

Although both sort and sort’ compute sorted lists, they might behave differently in a same context. For instance, suppose we want to compute the minimum of a list by returning the head element of the sorted list:

Then head (sort [3,2,1]) returns 1, as expected, but head (sort’ [3,2,1]) returns 1 as well as 2. The latter unintended value is obtained by computing the permutation [2,3,1] so that head (idSorted [2,3,1]) returns 2, since the list rest idSorted [3,1] is not evaluated due to non-strictness.
This example shows that our strong notion of equivalence is reasonable. However, testing this equivalence might require the generation of arbitrary contexts. Therefore, we show in the next section how to avoid this context generation.
4 Refined Equivalence Criteria
The definition of equivalence as stated in Definition 1 covers the intuition that equivalent operations can be interchanged at any place in an expression without changing its value. Proving such a general form of equivalence could be difficult. Therefore, we define another form of equivalence that is based on an operation to observe the computed results of the corresponding operations.
Definition 2
(Observable equivalence). Let \(f_1,f_2\) be operations of type \(\tau \rightarrow \tau '\). \(f_1\) is observably equivalent to \(f_2\) iff, for all operations g of type \(\tau ' \rightarrow \tau ''\), all expressions e and values v, \(g~(f_1~e) \mathrel {\buildrel * \over \rightarrow }v\) iff \(g~(f_2~e) \mathrel {\buildrel * \over \rightarrow }v\).
We can expect that proving observable equivalence is easier than equivalence since we trade a context made of an arbitrary expression with multiple occurrences of a function f with a single function call with a single occurrence of f. Fortunately, the next theorem shows that proving observable equivalence is sufficient in general.
Theorem 1
Let \(f_1,f_2\) be operations of type \(\tau \rightarrow \tau '\). \(f_1\) and \(f_2\) are equivalent iff they are observably equivalent.
Proof
It is trivial that equivalence implies observable equivalence. Hence, we assume that \(f_1\) and \(f_2\) are observably equivalent, i.e., for all operations g of type \(\tau ' \rightarrow \tau ''\), all expressions e and values v, \(g~(f_1~e) \mathrel {\buildrel * \over \rightarrow }v\) iff \(g~(f_2~e) \mathrel {\buildrel * \over \rightarrow }v\). We show by induction on the number n of occurrences of the symbol \(f_1\) the following claim:
If \(E_1\) is an expression with n occurrences of \(f_1\), \(E_2\) is obtained from \(E_1\) by replacing each occurrence of \(f_1\) with \(f_2\), and v is a value, then \(E_1 \mathrel {\buildrel * \over \rightarrow }v\) iff \(E_2 \mathrel {\buildrel * \over \rightarrow }v\).
Base case (\(n=0\)): Since \(E_1\) contains no occurrence of \(f_1\), \(E_2 = E_1\) and the claim is trivially satisfied.
Inductive case (\(n>0\)): Assume the claim holds for \(n-1\) and \(E_1\) contains n occurrences of \(f_1\) and \(E_1 \mathrel {\buildrel * \over \rightarrow }v\) for some value v. We have to show that \(E_2 \mathrel {\buildrel * \over \rightarrow }v\) (the opposite direction is symmetric) where \(E_2\) is obtained from \(E_1\) by replacing each occurrence of \(f_1\) with \(f_2\). Let p be a position in \(E_1\) with \(E_1|_p = f_1~e\) and e does not contain any occurrence of \(f_1\). Since \(E_1 \mathrel {\buildrel * \over \rightarrow }v\), by definition of \(\mathrel {\buildrel * \over \rightarrow }\), there is a partial value \(t_1\) with \(f_1~e \mathrel {\buildrel * \over \rightarrow }t_1\) and \(E_1[t_1]_p \mathrel {\buildrel * \over \rightarrow }v\). We define a new operation g by

where x is a variable that does not occur in \(E_1\). Hence \(g~(f_1~e) \mathrel {\buildrel * \over \rightarrow }g~t_1 \rightarrow E_1[t_1]_p \mathrel {\buildrel * \over \rightarrow }v\). Our assumption implies \(g~(f_2~e) \mathrel {\buildrel * \over \rightarrow }v\). By definition of \(\mathrel {\buildrel * \over \rightarrow }\), there is a partial value \(t_2\) with \(g~(f_2~e) \mathrel {\buildrel * \over \rightarrow }g~t_2 \rightarrow E_1[t_2]_p \mathrel {\buildrel * \over \rightarrow }v\). Since \(E_1[t_2]_p\) contains \(n-1\) occurrences of \(f_1\), the induction hypothesis implies that \(E_2[t_2]_p \mathrel {\buildrel * \over \rightarrow }v\). Therefore,  . \(\square \)
. \(\square \)
A proof that two operations are observably equivalent could still be difficult since we have to take all possible observation operations into account. However, the next result shows that it is sufficient to verify that two operations yield always the same partial values on identical inputs.
Theorem 2
Let \(f_1,f_2\) be operations of type \(\tau \rightarrow \tau '\). If, for all expressions e and partial values t, \(f_1~e \mathrel {\buildrel * \over \rightarrow }t\) iff \(f_2~e \mathrel {\buildrel * \over \rightarrow }t\), then \(f_1\) and \(f_2\) are equivalent.
Proof
By Theorem 1 it is sufficient to show the observable equivalence of \(f_1\) and \(f_2\). Hence, let g be an operation of type \(\tau ' \rightarrow \tau ''\), e an expression and v a value with \(g~(f_1~e) \mathrel {\buildrel * \over \rightarrow }v\). We have to show that \(g~(f_2~e) \mathrel {\buildrel * \over \rightarrow }v\) (the other direction is symmetric). By definition of \(\mathrel {\buildrel * \over \rightarrow }\), there is some partial value t with \(f_1~e \mathrel {\buildrel * \over \rightarrow }t\) and \(g~t \mathrel {\buildrel * \over \rightarrow }v\). By the assumption of the theorem, \(f_2~e \mathrel {\buildrel * \over \rightarrow }t\). Hence, \(g~(f_2~e) \mathrel {\buildrel * \over \rightarrow }g~t \mathrel {\buildrel * \over \rightarrow }v\). \(\square \)
Note that the consideration of all partial result values is essential to establish equivalence. For instance, consider the operations sort and sort’ defined in Sect. 3. Although sort and sort’ compute the same values, we have that \({\texttt {sort' [2,3,1]} \mathrel {\buildrel * \over \rightarrow }{2:}\bot }\) but sort [2,3,1] cannot be derived to \({\mathtt {2:\bot }}\). Actually, we have seen that sort and sort’ are not equivalent.
The following result is the converse of Theorem 2. It shows that not only having the same partial values is a sufficient condition for the equivalence of function, but also a necessary condition. For partial values t and u, we write \(t < u\) iff t is obtained by one or more applications of the Bot rule to u. It follows that if u is a partial value of an expression e, then any \(t < u\) is also a partial value of e. If t is a partial value, we denote by \(\bar{t}\) an expression obtained from t by replacing any instance of \(\bot \) in t with a fresh variable.
Theorem 3
Let \(f_1,f_2\) be operations of type \(\tau \rightarrow \tau '\). If, for some expression e, the partial values of \(f_1~e\) differ from those of \(f_2~e\), then \(f_1\) and \(f_2\) are not equivalent.
Proof
We construct a function g that, under the statement hypothesis, witnesses the non-equivalence of \(f_1\) and \(f_2\). Let \(T_1\) be the set of partial values of \(f_1~e\) and \(T_2\) the set of partial values of \(f_2~e\). W.l.o.g., we assume that there exists some partial value \(t \in T_1\) such that \(t \not \in T_2\). Let g be defined by the single rule:
Then, \(g~(f_1~e) \mathrel {\buildrel * \over \rightarrow }g~t \rightarrow 0\), whereas we show that  . Suppose the contrary. Then, it must be that \(f_2~e \mathrel {\buildrel * \over \rightarrow }u\) with u is an instance of \(\bar{t}\). This implies \(t < u\), which in turn implies \(t \in T_2\). \(\square \)
. Suppose the contrary. Then, it must be that \(f_2~e \mathrel {\buildrel * \over \rightarrow }u\) with u is an instance of \(\bar{t}\). This implies \(t < u\), which in turn implies \(t \in T_2\). \(\square \)
The next corollary is useful to avoid the consideration of all argument expressions in equivalence proofs.
Corollary 1
Let \(f_1,f_2\) be operations of type \(\tau \rightarrow \tau '\). If, for all partial values t and \(t'\), \(f_1~t \mathrel {\buildrel * \over \rightarrow }t'\) iff \(f_2~t \mathrel {\buildrel * \over \rightarrow }t'\), then \(f_1\) and \(f_2\) are equivalent.
Proof
Assume that \(f_1~t \mathrel {\buildrel * \over \rightarrow }t'\) iff \(f_2~t \mathrel {\buildrel * \over \rightarrow }t'\) holds for all partial values t and \(t'\). Consider an expression e and a partial value \(t_1\) such that \(f_1~e \mathrel {\buildrel * \over \rightarrow }t_1\). By definition of \(\mathrel {\buildrel * \over \rightarrow }\), there is a partial value \(t_0\) with \(e \mathrel {\buildrel * \over \rightarrow }t_0\) and \(f_1~t_0 \mathrel {\buildrel * \over \rightarrow }t_1\). Our assumption implies \(f_2~t_0 \mathrel {\buildrel * \over \rightarrow }t_1\). Hence \(f_2~e \mathrel {\buildrel * \over \rightarrow }f_2~t_0 \mathrel {\buildrel * \over \rightarrow }t_1\). Since the other direction is symmetric, Theorem 2 implies the equivalence of \(f_1\) and \(f_2\). \(\square \)
Hence, we have a sufficient criterion for equivalence checking which does not require the enumeration of arbitrary contexts. Instead, it is sufficient to test the equivalence on all partial values. Such a test can be performed by property-based test tools, as shown in the next section.
One may wonder whether the consideration of values instead of partial values is enough for equivalence checking. The next example shows that the answer is negative.
Example 4
Consider the following operations that take and return Booleans.

Functions f1 and f2 behave identically on every input value. However, f1 \(\mathtt {\bot }\) has no value, whereas f2 \(\mathtt {\bot }\) has value True. Thus, values as arguments are not as discriminating as partial values to expose a difference in behavior, whereas partial values are as discriminating as expressions. Actually, f1 and f2 are not equivalent: consider the operation failed which has no value.Footnote 4 Then f2 failed has value True whereas f1 failed has no value.
Corollary 1 requires to compare all partial result values and not just computed results. The former is more laborious since an expression might evaluate to many partial values even if it has a single value. For instance, consider the list generator

The expression fromTo 1 5 evaluates to the single value [1,2,3,4,5]. According to the reduction relation defined in Sect. 2, the same expression reduces to the partial values \(\mathtt {\bot }\), \(\mathtt {\bot :\bot }\), \(\mathtt {1:\bot }\), \(\mathtt {\bot :\bot :\bot }\), \(\mathtt {1:\bot :\bot }\), \(\mathtt {\bot :2:\bot }\), \(\mathtt {1:2:\bot }\), ... If operations are non-terminating, it is necessary to consider partial result values in general. For instance, ints1 0 and ints2 0 do not evaluate to a value but they evaluate to the different partial values \({{\mathtt {0:1:\bot }}}\) and \({\mathtt {0:2:\bot }}\), respectively, which shows the non-equivalence of ints1 and ints2 by Corollary 1. Thus, one may wonder whether for “well behaved” operations it suffices to consider only result values. This good behavior is captured by the property that a function returns a value for any argument value, see Definition 3. Unfortunately, the answer is negative.
Definition 3
(Terminating, totally defined). Let f be an operation of type \(\tau \rightarrow \tau '\). f is terminating if, for all values t of type \(\tau \), any rewrite sequence \(f~t \rightarrow t_1 \rightarrow t_2 \rightarrow \cdots \) is finite. f is totally defined if, for all values t of type \(\tau \), rewrite rule \(\mathsf {Fun}\) is applicable to f t.
Requiring termination as a condition of good behavior is necessary, as the operations ints1 and ints2 show. Total definedness is also necessary, as can be seen by this example:

g1 and g2 are terminating but head is not totally defined. Actually, both g1 0 and g2 0 have no value but they are not equivalent: head (g1 0) and head (g2 0) evaluate to 1 and 2, respectively.
Example 5
Functions h1 and h2, defined below, are totally defined and terminating. For any Boolean value t, h1 t and h2 t produce the same value result, namely t. However, h1 and h2 are not observably equivalent when applied to argument failed as witnessed by g.

Note that we have to use partial input values for equivalence tests even if all relevant operations are terminating and totally defined. This has been shown in Example 4, since both operations of this example are terminating and totally defined.
Now we have enough refined criteria to implement an equivalence checker with a property-based checking tool.
5 Property-Based Checking
Property-based testing is a useful technique to obtain reliable software systems. Testing cannot verify the correctness of programs, but it can be performed automatically and it might prevent wasting time when attempting to prove incorrect properties. If proof obligations are expressed as properties, i.e., Boolean expressions parameterized over input data, and we test these properties with a lot of input data, we have a higher confidence in the correctness of the properties. This motivates the use of property testing tools which automate the checking of properties by random or systematic generation of test inputs. Property-based testing has been introduced with the QuickCheck tool [8] for the functional language Haskell and adapted to other languages, like PrologCheck [1] for Prolog, PropEr [22] for the concurrent functional language Erlang, and EasyCheck [7] and CurryCheck [15] for the functional logic language Curry. If the test data is generated in a systematic (and not random) manner, like in SmallCheck [26], GAST [20], EasyCheck [7], or CurryCheck [15], these tools can actually verify properties for finite input domains. In the following, we show how to extend the property-based test tool CurryCheck to support equivalence checking of operations.
Properties can be defined in source programs as top-level entities with result type Prop and an arbitrary number of parameters. CurryCheck offers a predefined set of property combinators to define properties. In order to compare expressions involving non-deterministic operations, CurryCheck offers the property  which has the type a \({\mathtt {\rightarrow }}\) a \({\mathtt {\rightarrow }}\) Prop. It is satisfied if both arguments have identical result sets. For instance, we can state the requirement that permutations do not change the list length by the property
which has the type a \({\mathtt {\rightarrow }}\) a \({\mathtt {\rightarrow }}\) Prop. It is satisfied if both arguments have identical result sets. For instance, we can state the requirement that permutations do not change the list length by the property

Since the left argument of  evaluates to many (expectedly identical) values, it is relevant that
evaluates to many (expectedly identical) values, it is relevant that  compares result sets (rather than multi-sets). This is reasonable from a declarative programming point of view, since it is irrelevant how often some result is computed.
compares result sets (rather than multi-sets). This is reasonable from a declarative programming point of view, since it is irrelevant how often some result is computed.
Corollary 1 provides a specific criterion for equivalence testing: Two operations f1 and f2 are equivalent if, for any partial argument value, they produce the same partial result value. Since partial values cannot be directly compared, we model partial values by extending total values with an explicit \(\bot \) constructor. For instance, consider the data types used in Sect. 1. Assume that they are defined by

We define their extension to partial values by renaming all constructors and adding a \(\bot \) constructor to each type:

In order to compare the partial results of two operations, we introduce operations that return the partial value of an expression w.r.t. a given partial value, i.e., the expression is partially evaluated up to the degree required by the partial value (and it fails if the expression has not this value). These operations can easily be implemented for each data type:

Now we can test the equivalence of f and g by evaluating both operations to the same partial value. Thus, a single test consists of the application of each operation to an input x and a partial result value p together with checking whether these applications produce p:

To check this property, CurryCheck systematically enumerates partial values for x (see below how this can be implemented) and values for p. During this process, CurryCheck generates the inputs x = failed and  for which the property does not hold. This shows that f and g are not equivalent.
for which the property does not hold. This shows that f and g are not equivalent.
In a similar way, we can model partial list result values and test whether sort and sort’, as defined in Sect. 3, are equivalent. If the domain of list elements has three values (like the standard type Ordering with values LT, EQ, and GT), CurryCheck reports a counter-example (a list with three different elements computed up to the first element) with the 89th test. The high number of tests is due to the fact that test inputs as well as partial output values are enumerated to test each property.
The number of test cases can be significantly reduced by a different encoding. Instead of enumerating operation inputs as well as partial result values, we can enumerate operation inputs only and use a non-deterministic operation which returns all partial result values of some given expression. For our example types, these operations can be defined as follows:

Now we can test the equivalence of f and g by checking whether both operations have the same set of partial values for a given input:

CurryCheck returns the same counter-example as before. This is also true for the permutation sort example, but now the counter-example is found with the 11th test.
Due to the reduced search space of our second implementation of equivalence checking, we might think that this method should always be preferred. However, in case of non-terminating operations, it is less powerful. For instance, consider the operations ints1 and ints2 of Example 2. Since ints1 0 has an infinite set of partial result values, the equivalence test with pvalOf operations would try to compare sets with infinitely many values. Thus, it would not terminate and does not yield a counter-example. However, the equivalence test with peval operations returns a counter-example by fixing a partial term (e.g., a partial list with at least two elements) and evaluating ints1 and ints2 up to this partial list.
Based on these considerations, equivalence checking is implemented in CurryCheck as follows. First, CurryCheck provides a specific “operation equivalence” property denoted by  . Hence,
. Hence,

denotes the property that f and g are equivalent operations. In contrast to other properties like  , which are implemented by some Curry code [7], the property
, which are implemented by some Curry code [7], the property  is just a markerFootnote 5 which will be transformed by CurryCheck into a standard property based on the results of Sect. 4. For this purpose, CurryCheck transforms the property above as follows:
is just a markerFootnote 5 which will be transformed by CurryCheck into a standard property based on the results of Sect. 4. For this purpose, CurryCheck transforms the property above as follows:
-
1.
If both operations f and g are terminating, then the sets of partial result values are finite so that these sets can be compared in a finite amount of time. Thus, if T is the result type of f and g, the auxiliary operation
 (and similarly for all types on which T depends) is generated as shown above and the following property is generated:
(and similarly for all types on which T depends) is generated as shown above and the following property is generated: 
-
2.
Otherwise, for each partial value, CurryCheck tests whether both operations compute this result. Thus, if T is the result type of f and g, the auxiliary operation
 (and similarly for all types on which T depends) is generated as shown above and the following property is generated:
(and similarly for all types on which T depends) is generated as shown above and the following property is generated: 
In order to decide between these transformation options, CurryCheck uses the analysis framework CASS [17] to approximate the termination behavior of both operations. If the termination property of both operations can be proved (for this purpose, CASS uses an ordering on arguments in recursive calls), the first transformation is used, otherwise the second. If the termination cannot be proved but the programmer is sure about the termination of both operations, he can also mark the property with the suffix ’TERMINATE to tell CurryCheck to use the first transformation.
Example 6
Consider the recursive and non-recursive definition of the McCarthy 91 function:

Since CASS is not able to check the termination of mc91r, we annotate the equivalence property so that CurryCheck uses the first transformation:

Due to the results of Sect. 4, the generated properties must be checked with all partial input values. In the default mode, CurryCheck generates (total) values for input parameters of properties. However, CurryCheck also supports the definition of user-defined generators for input parameters (see [15] for details). For instance, one can define a generator for partial Boolean values by

CurryCheck automatically defines generators for partial values of all data types occurring in equivalence properties.
According to the results of Sect. 4, checking the above properties allows us to find counter-examples for non-equivalent operations if the domain of values is finite (as in the example of Sect. 1) or we enumerate enough test inputs. An exception are specific non-terminating operations. For instance, consider the contrived operations

where the evaluation of loop does not terminate. The non-equivalence of k1 and k2 can be detected by evaluating them to \({\mathtt {[\bot ,True]}}\) and \({\mathtt {[\bot ,False]}}\), respectively. Since a systematic enumeration of all partial values might generate the value \({\mathtt {[True,\bot ]}}\) before \({\mathtt {[\bot ,True]}}\), CurryCheck might not find the counter-example due to the non-termination of loop (since CurryCheck performs all tests in a sequential manner). Fortunately, this is a problem which rarely occurs in practice. Not all non-terminating operations are affected by this problem but only operations that loop without producing any data. For instance, the non-equivalence of ints1 and ints2 of Example 2 can be shown with our approach. Such operations are called productive in [16]. Intuitively, productive operations always generate some data after a finite number of steps.
In order to avoid such non-termination problems when CurryCheck is used in an automatic manner (e.g., by a software package manager), CurryCheck has an option for a “safe” execution mode. In this mode, operations involved in an equivalence property are analyzed for their productivity behavior. If it cannot be proved that an operation is productive (by approximating their run-time behavior with CASS), the equivalence check for this operation is ignored. This ensures the termination of all equivalence tests. The restriction to productive operations is not a serious limitation since, as evaluated in [16], most operations occurring in practical programs are actually productive. If there are operations where CurryCheck cannot prove productivity but the programmer is sure about this property, the property can be annotated with the suffix ’PRODUCTIVE so that it is also checked in the safe mode.
Example 7
Consider the definition of all prime numbers by the sieve of Eratosthenes:

After looking at the first four values of this list, a naive programmer might think that the following prime generator is much simpler:

Testing the equivalence of these two operations is not possible in the safe mode, since the productivity of primes depends on the fact that there are infinitely many prime numbers. Hence, a more experienced programmer would annotate the equivalence test as

so that it will be tested even in the safe mode and CurryCheck finds a counter-example (evaluating the result list up to the first five elements) to this property.
6 Related Work
Equivalence of operations was defined for functional logic programs in [5]. There, this notion is applied to relate specifications and implementations. Moreover, it is shown how to use specifications as dynamic contracts to check the correct behavior of implementations at run-time, but static methods to check equivalence are not discussed.
Bacci et al. [6] formalized various notions of equivalence, as reviewed in Sect. 1, and developed the tool AbsSpec which derives specifications, i.e., equations up to some fixed depth of the involved expressions, from a given Curry program. Although the derived specifications are equivalent to the implementation, their method cannot be used to check the equivalence of arbitrary operations (and AbsSpec does no longer work at the time of this writing).
QuickSpec [9] has similar goals as AbsSpec but is based on a different setting. QuickSpec infers specifications in form of equations from a given functional program but it uses a black box approach, i.e., it uses testing to infer program properties. Thus, it can be seen as an intermediate approach between AbsSpec and our approach: similarly to our approach, QuickSpec uses property-based testing to check the correctness of specifications, but it is restricted to functional programs, which simplifies the notion of equivalence.
Our method to check equality of computed results for all partial values is also related to test properties in non-strict functional languages [10]. Thanks to the non-deterministic features of Curry, our approach does not require impure features like isBottom or unsafePerformIO, which are used in [10] to compare partial values.
Partial values as inputs for property-based testing are also used in Lazy SmallCheck [26], a test tool for Haskell which generates data in a systematic (not random) manner. Partial input values are used to reduce the number of test cases: if a property is satisfied for a partial value, it is also satisfied for all refinements of this partial value so that it is not necessary to test these refinements. Thus, Lazy SmallCheck exploits partial values to reduce the number of test cases for total values, where in our approach partial values are used to avoid testing with all possible contexts and to find counter examples which might not be detected with total values only. In contrast to our explicit encoding of partial values, which is possible due to the logic features of Curry, Lazy SmallCheck represents partial values as run-time errors which are observed using imprecise exceptions [24].
The use of property-based testing to check the equivalence of operations in a software package manager with support for semantic versioning is proposed in [16]. This approach concentrates on ensuring the termination of equivalence checking by introducing the notion of productive operations. However, for terminating operations only ground equivalence is tested so that the proposed semantic versioning checking method is more restricted than in our case. The results presented in this paper can be used to generalize this semantic versioning tool.
7 Conclusions
We have presented a method to check the equivalence of operations defined by a functional logic program. This method is useful for software package managers to provide automatic semantic versioning checks, i.e., to compare two different versions of a software package, or to check the correctness of an implementation against a specification. Since we developed our results for a non-strict functional logic language, the same techniques can be used to test equivalence in purely functional languages, e.g., for Haskell programs.
We have shown that the general equivalence of operations, which requires that the same values are computed in all possible contexts, can be reduced to checking or proving equality of partial results terms. Our results support the use of automatic property-based test tools for equivalence checking. Although this method is incomplete, i.e., it does not formally ensure equivalence, it provides a high confidence and prevent wasting time in attempts to prove incorrect equivalence properties. Moreover, the presented results could also be helpful for manual proof construction or using proof assistants.
For future work, we will integrate our method in the software package manager CPM [16]. Furthermore, it is interesting to explore how automatic theorem provers can be used to verify specific equivalence properties.
Notes
- 1.
Note that functional logic languages compute a substitution as well as a value as a result.
- 2.
- 3.
The extension to operations with several arguments is straightforward. For the sake of simplicity, we formally define our notions only for unary operations.
- 4.
A possible definition is: failed = head [].
- 5.
CurryCheck also ensures that both arguments of
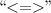 are defined operations, otherwise an error is reported.
are defined operations, otherwise an error is reported.
References
Amaral, C., Florido, M., Santos Costa, V.: PrologCheck – property-based testing in Prolog. In: Codish, M., Sumii, E. (eds.) FLOPS 2014. LNCS, vol. 8475, pp. 1–17. Springer, Cham (2014). https://doi.org/10.1007/978-3-319-07151-0_1
Antoy, S., Echahed, R., Hanus, M.: A needed narrowing strategy. J. ACM 47(4), 776–822 (2000)
Antoy, S., Hanus, M.: Overlapping rules and logic variables in functional logic programs. In: Etalle, S., Truszczyński, M. (eds.) ICLP 2006. LNCS, vol. 4079, pp. 87–101. Springer, Heidelberg (2006). https://doi.org/10.1007/11799573_9
Antoy, S., Hanus, M.: Functional logic programming. Commun. ACM 53(4), 74–85 (2010)
Antoy, S., Hanus, M.: Contracts and specifications for functional logic programming. In: Russo, C., Zhou, N.-F. (eds.) PADL 2012. LNCS, vol. 7149, pp. 33–47. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-27694-1_4
Bacci, G., Comini, M., Feliú, M.A., Villanueva, A.: Automatic synthesis of specifications for first order Curry. In: Principles and Practice of Declarative Programming (PPDP 2012), pp. 25–34. ACM Press (2012)
Christiansen, J., Fischer, S.: EasyCheck — test data for free. In: Garrigue, J., Hermenegildo, M.V. (eds.) FLOPS 2008. LNCS, vol. 4989, pp. 322–336. Springer, Heidelberg (2008). https://doi.org/10.1007/978-3-540-78969-7_23
Claessen, K., Hughes, J.: QuickCheck: a lightweight tool for random testing of Haskell programs. In: International Conference on Functional Programming (ICFP 2000), pp. 268–279. ACM Press (2000)
Claessen, K., Smallbone, N., Hughes, J.: QuickSpec: guessing formal specifications using testing. In: Fraser, G., Gargantini, A. (eds.) TAP 2010. LNCS, vol. 6143, pp. 6–21. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-13977-2_3
Danielsson, N.A., Jansson, P.: Chasing bottoms: a case study in program verification in the presence of partial and infinite values. In: Kozen, D. (ed.) MPC 2004. LNCS, vol. 3125, pp. 85–109. Springer, Heidelberg (2004). https://doi.org/10.1007/978-3-540-27764-4_6
Echahed, R., Janodet, J.-C.: On constructor-based graph rewriting systems. Research report IMAG 985-I, IMAG-LSR, CNRS, Grenoble (1997)
Echahed, R., Janodet, J.-C.: Admissible graph rewriting and narrowing. In: Proceedings of the Joint International Conference and Symposium on Logic Programming (JICSLP 1998), pp. 325–340 (1998)
González-Moreno, J.C., Hortalá-González, M.T., López-Fraguas, F.J., Rodríguez-Artalejo, M.: An approach to declarative programming based on a rewriting logic. J. Logic Program. 40, 47–87 (1999)
Hanus, M.: Functional logic programming: from theory to Curry. In: Voronkov, A., Weidenbach, C. (eds.) Programming Logics. LNCS, vol. 7797, pp. 123–168. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-37651-1_6
Hanus, M.: CurryCheck: checking properties of curry programs. In: Hermenegildo, M.V., Lopez-Garcia, P. (eds.) LOPSTR 2016. LNCS, vol. 10184, pp. 222–239. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-63139-4_13
Hanus, M.: Semantic versioning checking in a declarative package manager. In: Technical Communications of the 33rd International Conference on Logic Programming (ICLP 2017). OpenAccess Series in Informatics (OASIcs), pp. 6:1–6:16 (2017)
Hanus, M., Skrlac, F.: A modular and generic analysis server system for functional logic programs. In: Proceedings of the ACM SIGPLAN 2014 Workshop on Partial Evaluation and Program Manipulation (PEPM 2014), pp. 181–188. ACM Press (2014)
Hanus, M. (ed.): Curry: an integrated functional logic language (vers. 0.9.0) (2016). http://www.curry-language.org
Hussmann, H.: Nondeterministic algebraic specifications and nonconfluent term rewriting. J. Logic Program. 12, 237–255 (1992)
Koopman, P., Alimarine, A., Tretmans, J., Plasmeijer, R.: Gast: generic automated software testing. In: Peña, R., Arts, T. (eds.) IFL 2002. LNCS, vol. 2670, pp. 84–100. Springer, Heidelberg (2003). https://doi.org/10.1007/3-540-44854-3_6
López-Fraguas, F.J., Rodríguez-Hortalá, J., Sánchez-Hernández, J.: A simple rewrite notion for call-time choice semantics. In: Proceedings of the 9th ACM SIGPLAN International Conference on Principles and Practice of Declarative Programming (PPDP 2007), pp. 197–208. ACM Press (2007)
Papadakis, M., Sagonas, K.: A PropEr integration of types and function specifications with property-based testing. In: Proceedings of the 10th ACM SIGPLAN Workshop on Erlang, pp. 39–50 (2011)
Peyton Jones, S. (ed.): Haskell 98 Language and Libraries—The Revised Report. Cambridge University Press, Cambridge (2003)
Peyton Jones, S., Reid, A., Henderson, F., Hoare, T., Marlow, S.: A semantics for imprecise exceptions. In: Proceedings of the ACM SIGPLAN 1999 Conference on Programming Language Design and Implementation (PLDI 1999), pp. 25–36. ACM Press (1999)
Pitts, A.M.: Operational semantics and program equivalence. In: Barthe, G., Dybjer, P., Pinto, L., Saraiva, J. (eds.) APPSEM 2000. LNCS, vol. 2395, pp. 378–412. Springer, Heidelberg (2002). https://doi.org/10.1007/3-540-45699-6_8
Runciman, C., Naylor, M., Lindblad, F.: SmallCheck and Lazy SmallCheck: automatic exhaustive testing for small values. In: Proceedings of the 1st ACM SIGPLAN Symposium on Haskell, pp. 37–48. ACM Press (2008)
Acknowledgments
The authors are grateful to Finn Teegen for constructive remarks to an initial version of this paper, and to the anonymous reviewers for their helpful comments to improve this paper. This material is based in part upon work supported by the National Science Foundation under Grant No. 1317249.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2018 Springer International Publishing AG, part of Springer Nature
About this paper
Cite this paper
Antoy, S., Hanus, M. (2018). Equivalence Checking of Non-deterministic Operations. In: Gallagher, J., Sulzmann, M. (eds) Functional and Logic Programming. FLOPS 2018. Lecture Notes in Computer Science(), vol 10818. Springer, Cham. https://doi.org/10.1007/978-3-319-90686-7_10
Download citation
DOI: https://doi.org/10.1007/978-3-319-90686-7_10
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-90685-0
Online ISBN: 978-3-319-90686-7
eBook Packages: Computer ScienceComputer Science (R0)





 (and similarly for all types on which
(and similarly for all types on which 
 (and similarly for all types on which
(and similarly for all types on which 
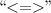 are defined operations, otherwise an error is reported.
are defined operations, otherwise an error is reported.