Topology Optimization Using GPGPU

Abstract

In this paper we present a matrix-free geometric multigrid method for solving a linear system of equations needed at every iteration of the topology optimization process. The multigrid solver is parallelized on an Nvidia graphics card using CUDA, therefore reducing simulation time drastically. This enables users to derive optimal topologies represented with a high number of elements while having low execution time. Computational domain is discretized with a regular structured hexahedral mesh. To improve the accuracy of the non-conformal discretizazion, the Dirichlet boundary conditions are imposed in a weak form using Nitsche method.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

Additive manufacturing is driving a revolution in manufacturing [17]. With this technique we can produce objects by successively adding thin layers of material. Nowadays this procedure is used to obtain a wide variety of items such as plastic prototypes for engineers and designers, customized medical devices such as dental implants, hip implants, or hearing aids. Significant breakthrough was the use of additive manufacturing in aerospace industry [7], which meant that less material could be used compared to conventional production techniques. Therefore, the production costs were reduced, and the lighter aircraft components lead to significant fuel savings.

Since additive manufacturing results in nearly infinite design spaces, the importance of topology optimization [1] is constantly growing. Topology optimization represents an optimal placement of material within a given design space, boundary conditions, and loads in order to satisfy the prescribed objective functions. During the design process, topology optimization enables engineers to explore different design solutions that meet the design requirements with optimum material usage while preserving required structural integrity.

In recent years a lot of research was invested in exploring and establishing the theory of topology optimization. The application field of topology optimization has expanded beyond structural analysis to include fluid flow, acoustics, heat transfer, nanophotonic devices, and material designs [4]. However, most of the research was carried out for 2D models. Due to high computational costs, performing topology optimization on 3D models may require hours, or in some cases even days, which hinders rapid prototyping design process. Ideally, the designer would like to have almost instantaneous feedback when exploring the design space. Not as much research was conducted in improving computational efficiency as it was done for establishing the theory of topology optimization, hence it stays still an open topic for the research [13]. Therefore, in this paper we investigate the use of the multi-core architecture such as GPU (Graphics Processing Unit) by utilizing parallel programming framework CUDA (Compute Unified Device Architecture) [11]. Since the optimization process comes with a high computational price of performing the finite-element method (FEM) analysis at each optimization step, the main focus of this work is to develop an efficient solver for performing FEM analysis. In order to accomplish this, several steps are taken. The computational domain under consideration is discretized with the help of hexahedral elements, yielding a system of linear equations. This enables the use of highly efficient matrix-free geometric multigrid methods [10] for solving the linear system of equations. Geometric multigrid algorithm is adapted in such a way that it maps to GPU hardware [5], therefore resulting in execution times far superior to those when solving the problem on CPU.

2 Previous Work

The goal of this section is to give a short overview of previous research conducted in the field of topology optimization with a focus on computational efficiency. In one of the earliest works [2] in this field, parallel computing in combination with domain decomposition was used. Test geometries were discretized using approximately 196,000–884,000 elements depending on the test model. System of linear equations was solved by using the preconditioned conjugate gradient method. Simulations for several test cases were performed on a Cray T3E using 16–24 processors depending on the test case, with solution times ranging from 4 to 43 h. A lot of improvements in numerical algorithms and in hardware were introduced since then, reducing simulation times drastically.

One of the first works demonstrating the use of GPU in topology optimization was presented in [14]. Here, the most time consuming part of the topology optimization process, which is solving a system of linear equations, is parallelized on GPU using CUDA. The author implemented a matrix-free conjugate gradient method with modifications to the single precision computation, necessary due to the hardware limitations. The investigated GPU was a GeForce GTX280 with 1 GB device memory and 240 CUDA cores each running at 1.30 GHz. The GPU execution time was up to 60 times faster in comparison to CPU. For a test case with resolution of nearly 1,000,000 elements and a lower class GPU such as GeForce 9600M GT with 32 CUDA cores, each running at 0.78 GHz, the authors reported simulation time under 2 h.

In a more recent work [16], the author used the Jacobi-preconditioned conjugate-gradient method for solving the system of linear equations on a GPU. The author was using hexahedral elements which conform the boundary. The used hardware was the Nvidia GeForce GTX 480 with 480 CUDA cores and 1.5 GB of device memory. Numerical results for several test cases were presented which we will discuss in the Results section.

3 Finite Element Formulation

Discretization of the computational domain is performed using hexahedral elements. CAD (Computer-Aided Design) geometry in STEP (Standard for the Exchange of Product model data) format is passed as an input and discretized using the Open CASCADE (Computer Aided Software for Computer Aided Design and Engineering) [12] library. Using hexahedral elements implies that we do not have to perform element rotation in space nor any other transformation. Every hexahedral element has an identical stiffness matrix which can be analytically pre-computed.

3.1 Linear Elasticity Equations

Elastic deformation of a continuum body on the domain $\varOmega$ with Dirichlet $\varGamma _D$ and Neumann $\varGamma _N$ boundaries is described by the following equations [3, 18]:

$$\begin{aligned} \nabla \cdot \sigma +f&= 0 \qquad \qquad \forall x \in \varOmega \end{aligned}$$

(3.1.1)

$$\begin{aligned} \sigma&= C : \varepsilon&\qquad \qquad \forall x \in \varOmega \end{aligned}$$

(3.1.2)

$$\begin{aligned} \varepsilon&= \dfrac{1}{2}\cdot (\nabla u + (\nabla u)^\top )&\qquad \qquad \forall x \in \varOmega \end{aligned}$$

(3.1.3)

$$\begin{aligned} u&= \hat{u}&\qquad \qquad \forall x \in \varGamma _D \end{aligned}$$

(3.1.4)

$$\begin{aligned} \sigma \cdot n&= t&\qquad \qquad \forall x \in \varGamma _N \end{aligned}$$

(3.1.5)

where $\sigma$ and $\varepsilon$ represent stress and strain tensor respectively. f represents the force term, C is the elasticity tensor, $\hat{u}$ is the prescribed displacement on the Dirichlet boundary, n is a normal vector to the Neumann boundary, t is a traction vector. After obtaining the weak form from Eq. (3.1.1) we use tri-linear shape functions to approximate our solution ${\mathbf {u}}_{h}$ of the problem:

$$\begin{aligned} {\mathbf {u}}_{h} = \sum \limits ^i N_{i}(\mathbf {x})\cdot {\mathbf {u}}_{i} \end{aligned}$$

(3.1.6)

where $N_{i}(\mathbf {x})$ represent the shape functions that span the finite dimensional space $\mathbb {V}_{h}$, and ${\mathbf {u}}_{i}$ are coefficients associated with shape functions. The element stiffness matrix $\mathbf {K}_{e}$ obtained from discretization can be written as:

$$\begin{aligned} \mathbf {K}_{e} = \int \limits _{\varOmega _{e}} \mathbf {B}_{e}^\top \mathbf {C} \mathbf {B}_{e} d\varOmega \end{aligned}$$

(3.1.7)

where $\mathbf {B}_{e}$ represents the strain-displacement matrix and $\mathbf {C}$ is the elasticity matrix. The element stiffness matrix $\mathbf {K}_{e}$ is computed only once and we use it for all elements in our computational domain.

3.2 Per Node Equations

Following the work of [5], we do not want to assemble and store the full stiffness matrix. We rather operate on per node equations. That is, each node is assigned with 3 degrees of freedom, and with 27 $3\times 3$ matrices which represent the interaction of the node with its neighbors. These matrices are extracted from the element stiffness matrix $\mathbf {K}_{e}$ which we precomputed. In order to show the assembling process of the aforementioned per node equations, let us set up the per element equations in the following manner:

$$\begin{aligned} \sum \limits _{j=1}^{8}\mathbf {k}_{i,j}^{e_{k}} \cdot {\mathbf {u}}_{j}^{e_{k}} = \mathbf {f}_{i}^{e_{k}}&\qquad \qquad i = 1,\dots ,8. \end{aligned}$$

(3.2.1)

We sum over all 8 nodes of a hexahedral element $e_{k}$, where $\mathbf {k}_{i,j}^{e_{k}}$ represents $3\times 3$ block matrix extracted from k-th element stiffness matrix, and associated with each node j. ${\mathbf {u}}_{j}^{e_{k}}$ is the corresponding displacement and $\mathbf {f}_{i}^{e_{k}}$ is the force term acting on the given element. Equation (3.2.1) for a given node i represents the influence of an element $e_{k}$ on the displacement of the node i. Since this node is shared by the 8 adjacent elements, we add up equations yielding from all k elements as well. Thus, we obtain the per node equations:

$$\begin{aligned} \sum \limits ^{(1,1,1)}_{i = (-1,-1,-1)} \mathbf {M}_{i}^{nod} {\mathbf {u}}_{nod+i} = \mathbf {f}_{nod}, \end{aligned}$$

(3.2.2)

where nod represents discrete coordinates of the node. By adding vector i to the discrete coordinates of the node we visit all the neighboring nodes. Here, $\mathbf {M}^{nod}$ is an array of 27 block matrices corresponding to the observed node and subindex i determines the block matrix corresponding to the neighbor of node. ${\mathbf {u}}_{nod+i}$ are the displacements of the corresponding nodes and $\mathbf {f}_{nod}$ is the force term. For more details on the equation assembly process the reader may refer to the works [5, 8].

4 Multigrid Solver

Since the bottleneck of the optimization process is the performance of FEM analysis on each iteration step, we propose a multigrid method based on the work of [5]. Multigrid methods [10], used to provide fast numerical solvers especially for elliptic partial differential equations, can greatly improve simulation times if implemented efficiently. In this work we implemented a CUDA based matrix-free geometric multigrid method. We used a standard multigrid V-cycle with Gauss-Seidel relaxation.

4.1 Per Node Equations Assembly for All Levels

Each level of the multigrid hierarchy is organized in such a way that if there is at least one active fine grid cell that is covered by the coarse grid cell, we consider the cell on the coarse level to be active as well. Before we start performing the V-cycle, we assemble per-node equations for all simulation levels [5, 8]. On the finest level we assemble equations using precomputed element stiffness matrix, afterwards we use Galerkin coarse grid operator to assemble equations on the coarser levels.

4.2 Gauss-Seidel Relaxation

To apply the smoothing step to our linear system of equations we use a Gauss-Seidel smoother. We first divide the set of nodes in 8 groups, such that we could perform smoothing in parallel, as suggested in [5, 8]. With respect to our per node equations the smoothing step can be formulated as:

$$\begin{aligned} {\mathbf {u}}^{k+1}_{nod} = {\mathbf {u}}^{k}_{nod} + \omega \cdot (\mathbf {M}_{0,0,0}^{nod})^{-1}\cdot \left( \!\mathbf {f}_{nod} {-} \sum _{i=(-1,-1,-1)}^{(0,0,-1)} \mathbf {M}_{i}^{nod} {\mathbf {u}}^{k+1}_{nod+i}- \sum _{i=(0,0,0)}^{(1,1,1)} \mathbf {M}_{i}^{nod} {\mathbf {u}}^{k}_{nod+i}\!\right) \end{aligned}$$

(4.2.1)

where ${\mathbf {u}}^{k}_{nod}$ is the current value, and ${\mathbf {u}}^{k+1}_{nod}$ is the updated value of displacement at a given node, and $\omega$ is a relaxation coefficient.

5 Topology Optimization Formulation

In our work we decided to use SIMP (Solid Isotropic Microstructure with Penalization) approach for performing the topology optimization. This method is proposed as “artificial density approach” by [1]. The domain is discretized with hexahedral elements, where to each hexahedra a density variable $\rho$ is assigned. These density variables are used as design variables in the optimization process for meeting the desired objective function requirements. The main advantage of the SIMP method over other methods is an easy implementation and a well established theoretical foundation. The topology optimization problem formulation is given by:

$$\begin{aligned} \begin{aligned} \underset{\rho }{\text {minimize}} \quad&c(\rho ) = \mathbf {f}^\top {\mathbf {u}} = {\mathbf {u}}^\top \mathbf {K}(\rho ) {\mathbf {u}} \\ \text {subject to} \quad&\dfrac{V(\rho )}{V_{0}} = \alpha \\ \quad&\mathbf {K}(\rho ){\mathbf {u}} = \mathbf {f} \\ \quad&0 < \rho _{min} \le \rho \le 1. \end{aligned} \end{aligned}$$

That is, we wish to minimize the compliance $c(\rho )$ subjected to a volume constraint of a given volume fraction $\alpha$, being the ratio between the material volume $V(\rho )$ and the design domain volume $V_{0}$. Displacement and force vectors are denoted respectively ${\mathbf {u}}$ and $\mathbf {f}$. The element stiffness matrix is denoted as $\mathbf {K}(\rho )$. For solving the aforementioned optimization process we use the Optimality Criteria method. Identical to work of [1, 15], we update our density design variables $\rho$ as follows:

$$\begin{aligned} \rho _{e}^{new}= {\left\{ \begin{array}{ll} \text {max}(\rho _{min},\rho _{e} - \delta \rho )\\ \begin{aligned} &{}\,\,\,\,\text {if} &{}\rho _{e}B^{\eta }_{e}\le \text {max}(\rho _{min},\rho _{e} - \delta \rho )\\ \end{aligned}\\ \text {min}(1,\rho _{e} + \delta \rho )\\ \begin{aligned} &{}\,\,\,\,\text {if} &{}\text {min}(1,\rho _{e} + \delta \rho )\le \rho _{e}B^{\eta }_{e}\\ \end{aligned}\\ \rho _{e}B^{\eta }_{e} \\ \begin{aligned} &{} \,\,\,\, \text {if} &{} \text {max}(\rho _{min},\rho _{e} - \delta \rho )<\rho _{e}B^{\eta }_{e}<\text {min}(1,\rho _{e} + \delta \rho )\\ \end{aligned}\\ \end{array}\right. } \end{aligned}$$

(5.0.1)

where the element density $\rho _{e}$ is our design variable, $\delta \rho$ is a non-negative increment of design variable, and the exponent $\eta = 1/2$ is a numerical damping coefficient. The update value $B_{e}$ is given by the optimality condition:

$$\begin{aligned} B^{\eta }_{e} = \dfrac{-\partial c/ \partial \rho _{e} }{\lambda \partial V/ \partial \rho _{e} } \end{aligned}$$

(5.0.2)

where $\lambda$ is a Lagrangian multiplier that we obtain by applying a bi-section algorithm. From the equation (5.0.2) we compute the sensitivity of the objective function as:

$$\begin{aligned}&\dfrac{\partial c}{\partial \rho _{e} } =- p(\rho _{e})^{p-1}{\mathbf {u}}^\top _{e}\mathbf {K}_{0}{\mathbf {u}}_{e}\end{aligned}$$

(5.0.3)

$$\begin{aligned}&\dfrac{\partial V}{\partial \rho _{e} } = 1. \end{aligned}$$

(5.0.4)

6 Imposing Dirichlet Boundary Conditions

With the use of non-conformal hexahedral elements, as typically used in topology optimization problems, the challenge of accurately imposing boundary conditions arises. Different from tetrahedral meshes that conform the boundary, hexahedral meshes are embedding the boundary. Hence, it is necessary to enforce Dirichlet boundary conditions in a weak sense. By adding the terms to the weak formulation of the elasticity equation we impose values on the embedded boundary. Identical to the work of [3, 18], the strong formulation of the linear elasticity problem is transformed into the weak form using the principle of minimum of potential energy. The total potential energy $\varPi _{tot}$ of the body at rest is the sum of the internal $\varPi _{int}$ and the external $\varPi _{ext}$ potential energy:

$$\begin{aligned} \varPi _{tot} = \varPi _{int} + \varPi _{ext} \end{aligned}$$

(6.0.1)

where

$$\begin{aligned} \varPi _{int}&= \dfrac{1}{2}\int \limits _{\varOmega } \varepsilon ({\mathbf {u}}):\mathbf {C}:\varepsilon ({\mathbf {u}})d\varOmega \end{aligned}$$

(6.0.2)

$$\begin{aligned} \varPi _{ext}&= \int \limits _{\varOmega } {\mathbf {u}} \cdot \mathbf {f} d\varOmega + \int \limits _{\varGamma _{N}} {\mathbf {u}} \cdot \mathbf {t} d\varGamma . \end{aligned}$$

(6.0.3)

After finding the first variation of the total potential energy, and setting it to zero, we obtain the weak formulation:

$$\begin{aligned} \int \limits _{\varOmega } \varepsilon (\mathbf {v}):\mathbf {C}:\varepsilon ({\mathbf {u}})d\varOmega = \int \limits _{\varOmega } \mathbf {v} \cdot \mathbf {f} d\varOmega + \int \limits _{\varGamma _{N}} \mathbf {v} \cdot \mathbf {t} d\varGamma \end{aligned}$$

(6.0.4)

where $\mathbf {v}$ are the test functions and ${\mathbf {u}}$ are the shape functions.

6.1 Nitsche Terms

Following the works of [3, 6, 18] constraint potentials are added to the total energy potential $\varPi _{tot}$. The Nitsche constraint potential is obtained by using a combination of Langrange Multiplier Method and Penalty Method:

$$\begin{aligned} \varPi _{Lagrange}&= \int \limits _{\varGamma _{D}} \lambda \cdot ({\mathbf {u}}-\hat{{\mathbf {u}}}) d\varGamma \end{aligned}$$

(6.1.1)

$$\begin{aligned} \varPi _{Penalty}&= \dfrac{1}{2}\cdot \beta \int \limits _{\varGamma _{D}} ({\mathbf {u}}-\hat{{\mathbf {u}}})^2 d\varGamma \end{aligned}$$

(6.1.2)

where $\lambda$ is defined as in [18]:

$$\begin{aligned} \lambda = -\mathbf {C}:\varepsilon ({\mathbf {u}})\cdot \mathbf {n}. \end{aligned}$$

(6.1.3)

The $\beta$ from equation (6.1.2) is typically chosen [6] as the ratio of the area of the embedded surface $\varGamma _e$ and the volume of the partial hexahedron $H_e$, cut by the embedded surface:

$$\begin{aligned} \beta \ge \dfrac{measure(\varGamma _e)}{measure(H_e)}\, . \end{aligned}$$

(6.1.4)

Having added the constraint energy potentials (6.1.1) and (6.1.2) to the total potential energy, we find the minimum of the potential by setting the first variation to zero. Hence we obtain the weak formulation with the Nitsche terms:

$$\begin{aligned} \int \limits _{\varOmega } \varepsilon ({\mathbf {u}}):\mathbf {C}&:\varepsilon ({\mathbf {u}})d\varOmega - \int \limits _{\varGamma _{D}} (\varepsilon (\mathbf {v}):\mathbf {C})\cdot \mathbf {n}\cdot {\mathbf {u}} d\varGamma - (\varepsilon ({\mathbf {u}}):\mathbf {C})\cdot \mathbf {n}\cdot \mathbf {v} d\varGamma + \beta \int \limits _{\varGamma _{D}} \mathbf {v} \cdot {\mathbf {u}} d\varGamma \nonumber \\&=\int \limits _{\varOmega } \mathbf {v} \cdot \mathbf {f} d\varOmega + \int \limits _{\varGamma _{N}} \mathbf {v} \cdot \mathbf {t} d\varGamma - \int \limits _{\varGamma _{D}} (\varepsilon (\mathbf {v}):\mathbf {C})\cdot \mathbf {n}\cdot \hat{{\mathbf {u}}} d\varGamma + \int \limits _{\varGamma _{D}} \mathbf {v} \cdot \hat{{\mathbf {u}}} d\varGamma . \end{aligned}$$

(6.1.5)

After discretization [18], we have the following formulation for a hexahedral element with the embedded interface:

$$\begin{aligned}&\int \limits _{\varOmega _{e}} \mathbf {B}_{e}^\top \mathbf {C} \mathbf {B}_{e} d\varOmega - \int \limits _{\varGamma _{D}^e} \mathbf {B}_{e}^\top \mathbf {C} \cdot \mathbf {n}\cdot \mathbf {N} d\varGamma - \int \limits _{\varGamma _{D}^e} \mathbf {N}^\top \cdot \mathbf {n}^\top \cdot \mathbf {C} \mathbf {B}_{e} d\varGamma + \beta \int \limits _{\varGamma _{D}} \mathbf {N}^\top \cdot \mathbf {N} d\varGamma \nonumber \\&\qquad \qquad =\int \limits _{\varOmega } \mathbf {N}^\top \cdot \mathbf {f} d\varOmega + \int \limits _{\varGamma _{N}} \mathbf {N}^\top \cdot \mathbf {t} d\varGamma - \int \limits _{\varGamma _{D}} \mathbf {B}_{e}^\top \mathbf {C}\cdot \mathbf {n}\cdot \hat{{\mathbf {u}}} d\varGamma + \int \limits _{\varGamma _{D}} \mathbf {N}^\top \cdot \hat{{\mathbf {u}}} d\varGamma . \end{aligned}$$

(6.1.6)

Additional terms in this equation with respect to the original discretization are used to enforce Dirichlet boundary conditions by modifying the original system of linear equations.

7 Results

In this section we intend to present some of the results computed with the help of our topology optimization tool. All of the following simulations were carried out on a machine with Intel Core i7-4710HQ processor running at 2.5 GHz, RAM memory of 8GB, and commodity graphics card GeForce GTX 860M with 640 CUDA cores and 4 GB of GDDR5 memory.

7.1 GE Challenge

General Electric (GE) raised an open challenge [9] where a jet engine bracket was to be optimized to withstand the working loads while having minimum mass. Ten selected designs were produced from a titanium alloy using a direct metal laser melting (DMLM) machine, which uses a laser beam to fuse layers of metal powder into a final shape [9]. Afterwards, the parts were sent to the destruction testing. We wish to present our design solution which resembles some of the winning designs.

Fig. 1

Initial design of jet engine bracket provided by the GE challenge [9]

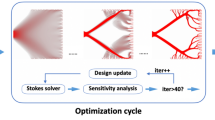
Initial geometry shown in Fig. 1 is discretized with the help of approximately 950,000 hexahedral elements. Topology optimization on GPU was carried out in 14.4 s for the total of 9 iterations. Performing FEM analysis on average took 0.9 s. Optimized topology is illustrated in Fig. 2.

Fig. 2

Jet engine bracket, part of the GE challenge [9], optimized with volume fraction of $\alpha = 0.35$. The initial geometry is shown as a transparent body

Fig. 3

Optimal topology of a bridge

7.2 Bridge Design

For a design domain of a rectangular cuboid shape, subjected to the forces acting perpendicular to the mid-plane of the design domain, we obtain the optimal bridge topology which is illustrated in Fig. 3a. Optimization domain was discretized using 400,000 hexahedral elements, and simulation was carried out in 10.32 s. For a comparison, in the work [16] for a similar test case of mid-plane loaded bridge with 113,000 degrees of freedom, the author reported execution time of 36.2 s when using GPU. With our solver we achieved better execution time for approximately 4 times higher mesh resolution.

Fig. 4

Cantilever optimized for volume fraction $\alpha = 0.35$

Fig. 5

Cube embedded within the hexahedral mesh

Fig. 6

Different approaches for enforcing boundary conditions at the interface of the elements cut by the cube. The vertical axis denotes the displacement along z axis. The horizontal axis denotes z coordinate of the cube hexahedral mesh

Another bridge structure is shown in Fig. 3b. It was modelled using 465,000 hexahedral elements. The simulation was carried out in only 6.5 s.

7.3 Cantilever

In this example we consider cantilever discretized using 740,000 hexahedral elements, and optimized in 13.8 s. The resulting topology is shown in Fig. 4. For a similar case of a loaded cantilever in work [2], discretized with 245,760 elements, authors reported solution time of approximately 3.9 h. In another variation of a loaded cantilever in work [16], the author reported computing time of 4 min for 324,000 elements when using GPU.

7.4 Dirichlet Boundary Conditions

We demonstrate the results with imposed zero Dirichlet boundary conditions by the Nitsche method on a cube object. For this test case the cube with dimensions $2.5\times 2.5\times 2.5$ mm is discretized with 6 hexahedral elements in each direction and of side length 0.5 mm. Evenly distributed vertical forces are acting on the upper surface of the cube. As it can be seen in Fig. 5, the cube is embedded within the hexahedral mesh.

Zero Dirichlet boundary condition is imposed on embedded bottom surface of the cube. Figure 6a shows that zero displacement along z axis is located exactly at the midpoint of the hexahedral element when using the Nitsche method. On the other hand, when we use a strong method that assigns the same value to all the nodes of the boundary elements, displacement is constant across the whole hexahedral element as shown in Fig. 6b.

Thus, we observe that Nitsche method allows us to prescribe boundary conditions for boundary non-conforming meshes in a much more precise way compared to the strong method. As we have seen in the example where our mesh did not conform to the boundary, with the help of Nitsche method we were able to enforce zero displacement exactly at the intersection of the hexahedral elements and the Dirichlet boundary of the cube.