Abstract
We address the problem of transforming typed functional programs into relational form. In this form, a program can be run in various “directions” with some arguments left free, making it possible to acquire different behaviors from a single specification. We specify the syntax, typing rules and semantics for the source language as well as its relational extension, describe the conversion and prove its correctness both in terms of typing and dynamic semantics. We also discuss the limitations of our approach, present the implementation of the conversion for the subset of OCaml and evaluate it on a number of realistic examples.
Access provided by CONRICYT-eBooks. Download conference paper PDF
Similar content being viewed by others
Keywords
These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.
1 Introduction
Relational programming is an attractive technique, based on the idea of constructing programs as relations. While in general some relational effects can be reproduced with a number of languages for logic programming, such as Prolog, MercuryFootnote 1, or CurryFootnote 2, in a narrow sense relational programming amounts to writing relational specifications in miniKanren [10]. miniKanrenFootnote 3, initially designed as a small relational DSL, embedded in Scheme/Racket, was later implemented for a number of general-purpose host languages, including Scala, Haskell, Standard ML and OCaml.
With relational approach, it becomes possible to give simple and elegant solutions for the problems, otherwise considered as tricky, tough, tedious, or boring [6]. For example, relational interpreters can be used to derive quines—programs, which reduce to themselves, as well as twines or thrines (pairs or triples of programs, reducing to each other) [8]; a straightforward relational description of simply typed lambda calculus [3] inference rules works both as type inferencer and inhabitation problem solver [5]; relational list sorting can be used to generate all permutations [13], etc.
On the other hand, writing relational specifications can sometimes be a tricky and error-prone task. Fortunately, many specifications can be written systematically by “generalizing” a certain functional program. From the very beginning, the conversion from functional to relational form was considered as an element of relational programming thesaurus [10]. However, the traditional approach—unnesting—was formulated for an untyped case, worked only for specifically written programs and was never implemented.
We present a generalized form of relational conversion, which can be applied to typed terms in general form. We study the relational conversion for a small ML-like language (essentially, a certain subset of OCaml), equipped with Hindley-Milner type system with let-polymorphism [15]. We start from retelling the syntax, typing rules, and operational semantics, and then extend the source language with a conventional set of relational constructs. This set corresponds to existing typed embedding of miniKanren into OCaml [13]. We then present typing rules and develop operational semantics for this relational extension; to our knowledge, this is the first attempt to specify formal semantics for miniKanren. Next, we develop formal rules for relational conversion and prove, that these rules respect both typing and semantics. Finally, we describe the implementation of a relational converter and demonstrate its application for a number of problems, for some of which we present a relational solution for the first time.
We would like to express our gratitude to William Byrd and the anonymous reviewers for their constructive remarks, which, we believe, led to the improvement of the presentation.
2 Relational Programming in miniKanren
In the context of this paper, we will use a certain concrete implementation of miniKanren—a shallow DSL for OCamlFootnote 4, called OCanren [13]. OCanren corresponds to miniKanren with disequality constraints [1], and (modulo typing) follows the original implementation [11, 12]. Here we describe the external view on OCanren, giving the only intuitive meaning of its constructs; the formal description will be presented in Sect. 3.2. We also use a simplified syntax, which is a little bit different from the concrete syntax in actual implementation, but assumed to be easier to read.
The central notion of miniKanren is goal; in OCanren a goal can be an arbitrary expression of reserved goal type, which we denote \(\mathfrak G\). There are only five syntactic forms of goals (denoted below as \(g, g_1, g_2\), etc.):
-
conjunction \(g_1\wedge g_2\);
-
disjunction \(g_1\vee g_2\);
-
fresh variable introduction
 ;
; -
unification \(t_1\;\equiv \;t_2\);
-
disequality constraint \(t_1\;\not \equiv \;t_2\).
Two last forms of goals constitute a basis for goal construction; here \(t_1\) and \(t_2\) are terms. In OCanren a term is an arbitrary expression of polymorphic logic type \(\alpha ^o\). The postfix notation \(\Box ^o\) is a traditional way to denote relational entities, and we will use it for types as wellFootnote 5.
The simplest expression of logic type is a variable, bound in  . Another example is a primitive value, injected into the logic domain with a built-in primitive “\(\uparrow \)”, such as \(\uparrow \!3\) (of type
. Another example is a primitive value, injected into the logic domain with a built-in primitive “\(\uparrow \)”, such as \(\uparrow \!3\) (of type  ) or
) or  (of type
(of type  ). Other types (pairs, lists, user-defined algebraic datatypes, etc.) can be used in relational specifications as well, being injected by the same primitive. For example, expression
). Other types (pairs, lists, user-defined algebraic datatypes, etc.) can be used in relational specifications as well, being injected by the same primitive. For example, expression  has the type
has the type  ,
,  —the type
—the type  , etc. The subtle part is that (since the unification only works for logical types) the placement of “\(^o\)” determines the granularity of unification. Indeed, a logical variable can only be placed where logical type is expected. Thus, in unification one can use a value of type
, etc. The subtle part is that (since the unification only works for logical types) the placement of “\(^o\)” determines the granularity of unification. Indeed, a logical variable can only be placed where logical type is expected. Thus, in unification one can use a value of type  as a whole, but in order to control the contents of the pair relationally, the type
as a whole, but in order to control the contents of the pair relationally, the type  is required. This makes it impossible to reuse some built-in or standard types in relational code—for example, predefined list type is not flexible enough, since it does not allow the tail of the list to be logical. Instead, logical list type has to be introduced:
is required. This makes it impossible to reuse some built-in or standard types in relational code—for example, predefined list type is not flexible enough, since it does not allow the tail of the list to be logical. Instead, logical list type has to be introduced:

With logical list type, we can implement some relations for lists:

Here we defined relational list concatenation  , a canonical example in the field. This ternary relation is constructed, using case analysis and recursion:
, a canonical example in the field. This ternary relation is constructed, using case analysis and recursion:
-
1.
If the first list is empty, then the second and the third lists must be equal.
-
2.
Otherwise, the first list can be split into a head and a tail, and two fresh variables
 and
and  are needed to denote them. We also need a fresh variable
are needed to denote them. We also need a fresh variable  to denote the list, such that appending
to denote the list, such that appending  to
to 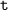 equals
equals  . To ensure this property, we use a recursive call to
. To ensure this property, we use a recursive call to  . Finally, we acquire the final result by consing
. Finally, we acquire the final result by consing  and
and  .
.
The definition of  takes three logical lists
takes three logical lists  ,
,  and
and  as arguments, and constructs a goal, which can be executed or combined with other goals. In the former case, a stream of answers is returned. An element of the stream contains the description of certain constraints for logical variables, which have to be respected in order for the relation to hold. We denote the running primitive “\(\leadsto \)”, so
as arguments, and constructs a goal, which can be executed or combined with other goals. In the former case, a stream of answers is returned. An element of the stream contains the description of certain constraints for logical variables, which have to be respected in order for the relation to hold. We denote the running primitive “\(\leadsto \)”, so

returns an empty stream, since there is no list  , such that appending
, such that appending  and
and  gives empty list, while
gives empty list, while

discovers the expected constraint for the variable  .
.
As it can be seen from the type, relational concatenation is polymorphic, like its functional counterpart. However, the query

ends with a run-time error due to inability to unify closures. This is a fundamental limitation in original miniKanren as well, as it deals only with first-order syntactic unification [2]. This example demonstrates, that, unlike pure OCaml, the typing in OCanren is somewhat weak. In order to restore the strong typing, some of the type variables have to be bounded to range over only non-functional types. The lack of direct support for bounded polymorphism [9] in OCaml makes this step problematic. Our experience, however, shows, that in practice this deficiency rarely gets in the way. In the following development, we assume, that in polymorphic types some type variables may be implicitly bounded by the set of non-function types, and these boundings are respected in all instantiations of those type variables.
Finally, we describe the unnesting technique [10], which was introduced as a method for manual transformation of functional programs into relational form. Unnesting introduces a new name for each nested subexpression; now, when the value of each subexpression is bound to a certain variable, the conversion is straightforward: each pattern-matching construct is transformed into a disjunction, new names, introduced in pattern bindings and unnestings, are transformed into  variables, and each converted function is supplied with the additional argument, unified with the result. As a result we consider, again, the list concatenation function (see Fig. 1a). The result of unnesting is shown on Fig. 1b, while the final relational form—on Fig. 1c.
variables, and each converted function is supplied with the additional argument, unified with the result. As a result we consider, again, the list concatenation function (see Fig. 1a). The result of unnesting is shown on Fig. 1b, while the final relational form—on Fig. 1c.
However, not every definition can be converted to a relational form by unnesting. Consider, for example, the definition on Fig. 2a. Unnesting would transform this program into the form, shown on Fig. 2b, which is obviously invalid, since it unifies a function f with a logical variable r. In order to apply unnesting, one needs to \(\eta \)-expand the definition of g, making the functional nature of its return type syntactically visible. We stress, that relational conversion, described in Sect. 4, is essentially different from unnesting. In particular, we use \(\eta \)-expansion in a very limited manner (only in one case).
3 The Source Language and Relational Extension
Our development of relational conversion is based on the idea of transforming a program in a functional language into a program in relational extension of that language. In the context of miniKanren, this approach looks quite natural, since miniKanren itself, as a DSL, reuses many important features (for example, function definitions) from a host language.
In this section, we present a formal description of a small functional language, taken as a source for relational conversion. We describe its syntax, typing rules, and semantics, and then extend it with relational constructs. We specify the typing rules and semantics for the extension as well.
3.1 The Source Language
The syntax of our source functional language is shown on Fig. 3. It consists of a lambda calculus, enriched with constructors with fixed arities \(C^n\), patterns p and pattern-matching constructs, and expressions for recursive/non-recursive let-bindings. Among the constructors we distinguish two nullary interpreted constructors  and
and  , and add a boolean equality operator “\(=\)”.
, and add a boolean equality operator “\(=\)”.
In a pattern matching, we only allow shallow patterns (which is not an essential limitation) and do not allow wildcards (which is important—converting wildcard pattern matching into relational form would require essentially different projections).
Our language is equipped with Hindley-Milner type system, and we present the typing rules in a conventional syntax-directed form on Fig. 4. Besides type variables and function types, our system contains a number of implicitly defined algebraic datatypes \(T^k\), and we stipulate, that each constructor \(C^n\) belongs to the exactly one datatype. In the rule Constr\(_T\), we assume that type \(t^C\) has the form \(T^k(t_1,\dots , t_k)\), where each of the types \(t_i\) is recovered from the types \(t_i^C\) of arguments of constructor \(C^n\) and, moreover, these types agree in the sense of constructor application. Similarly, in the rule Match\(_T\), the types of all \(C_i^{k_i}(x^i_1,\dots , x^i_{k_i})\) are expected to be equal \(t^C\), and \(t^{C_i}_j\) is a type of j-th argument of constructor \(C_i\), used in the pattern. The rule Eq\(_T\) specifies that both operands of equality operator must have the same (but arbitrary) type. Thus, we can call this operator “polymorphic equality” (Fig. 5).
We describe the semantics of our language in the form of transition system. The transition relation
describes a one step of evaluation of expression e with a stack of contexts \(\mathcal S\), which results in a new stack \(\mathcal S^\prime \) and a new expression \(e^\prime \). A context is an expression with a unique hole; informally speaking, a stack of contexts describes a path in the expression being evaluated from the topmost construct to the point, where the evaluation currently is taking place. For a context C and an expression e, we denote by C[e] a complete expression with no holes, which is obtained by plugging e into the unique hole of C. From each state \(\langle {C_1:C_2:\dots :C_k,e}\rangle \) we can build an expression \(C_k[\dots [C_2[C_1[e]]]\dots ]\), which represents an intermediate result of evaluation according to a small-step semantics. This form of semantic description originates from Felleisen-style [16] approach for small-step semantics, and we’ve chosen it since it can be naturally extended for a relational case.
Our semantics describes call-by-value left-to-right evaluation; in the rules \(\textsc {Beta}\), \(\textsc {Mu}\), \(\textsc {LetVal}\), \(\textsc {LetRec}\) and \(\textsc {MatchVal}\), we perform capture-avoiding substitutions, which respect the names in abstractions and let-bindings. In the rule \(\textsc {MatchVal}\) we assume, that at most one pattern matches the scrutinee—this is an important difference from the usual semantics of pattern matching, when the patterns are examined in a top-down manner until the matching succeeds. In the rules \(\textsc {EqTrue}\) and \(\textsc {EqFalse}\) we assume, that the values v, \(v_1\), \(v_2\) do not have the forms \(\lambda x\dots \) or \(\mu f\dots \).
Finally, for a closed expression e and a value v, we write \(e \leadsto ^f v\), iff
where \(\epsilon \)—an empty stack, and “\(\rightarrow ^*\)” is a reflexive-transitive closure of “\(\rightarrow \)”.
3.2 Relational Extension
The relational extension adds five conventional miniKanren expressions for constructing goals; the syntax is shown on Fig. 6. Since relational constructs are added to regular functional ones, it becomes possible to construct expressions like  , etc. In order to rule such pathological expressions out, we devised an extension for the type system of the source language. In fact, this approach follows the actual implementation for OCaml, where a careful choice of types for representing terms and goals made it possible to reject the majority of non-well-formed programs at compile-time.
, etc. In order to rule such pathological expressions out, we devised an extension for the type system of the source language. In fact, this approach follows the actual implementation for OCaml, where a careful choice of types for representing terms and goals made it possible to reject the majority of non-well-formed programs at compile-time.
Our extension for the type system introduces one interpreted datatype constructor \(\Box ^o\) with one data constructor \(\uparrow \)—a polymorphic type and a constructor for logical terms. In addition, we introduce an interpreted type of goals \(\mathfrak G\), which is distinct from all other types. The typing rules for the relational extension are shown on Fig. 7. These rules describe rather expected typing: in unification and disequality constraints only terms of the same logical type can be used, and conjunction and disjunction can only be taken for goals. Note, in our extension a term can be calculated as a result of arbitrary expression in initial functional language (as long as this expression has expected logical type), but such “higher-order” terms will never appear as a result of relational conversion, so, in fact, relational extension we describe here defines a richer language, than we actually need.
The semantics of extended language is shown on Fig. 8. First, the state is extended: besides the stack of contexts and current expression it now contains a set of used semantic variables \(\varSigma \) and a logical state \(\sigma \). Semantic variables are allocated and substituted for syntactic logic variable occurrences, when  expression is evaluated (see rule Fresh). Logical states are affected, when unification or disequality constraint is evaluated; we explain them in details below. All existing rules for the initial language are considered rewritten to propagate newly added components of states unchanged. Then, we modify the substitution to respect names, bound in
expression is evaluated (see rule Fresh). Logical states are affected, when unification or disequality constraint is evaluated; we explain them in details below. All existing rules for the initial language are considered rewritten to propagate newly added components of states unchanged. Then, we modify the substitution to respect names, bound in  as well. Next, we consider two new kinds of values: a semantic variable and a special value
as well. Next, we consider two new kinds of values: a semantic variable and a special value  . The former is a result of evaluation for a free logic variable, the latter—the result of evaluation for a succeeded goal.
. The former is a result of evaluation for a free logic variable, the latter—the result of evaluation for a succeeded goal.
We also extend the definition of context to handle the new kinds of expressions. In unification and disequality constraint, the terms are evaluated left-to-right. Conjunction and disjunction, however, evaluate nondeterministically: in disjunction only one subgoal is chosen (see rules DisjL and DisjR), a conjunction can evaluate either left, or right subgoal first (see rules ConjStartL and ConjStartR). When chosen subgoal is evaluated to the value  , the other subgoal starts its evaluation (rules ConjL and ConjR). We have chosen a nondeterministic variant for the semantics, since different existing miniKanren implementations use (a little bit) different search, and we do not want to depend on the implementation details. An opposite side of this solution is that for a concrete program and a concrete miniKanren implementation, the result of the evaluation might not coincide with that, prescribed by the semantics: in some concrete implementation a program can diverge, while nondeterministic semantics may still define a certain scenario to complete with a result. We argue, that in this case, it will always be possible to rewrite a program or/and interpreter to converge according to that scenario.
, the other subgoal starts its evaluation (rules ConjL and ConjR). We have chosen a nondeterministic variant for the semantics, since different existing miniKanren implementations use (a little bit) different search, and we do not want to depend on the implementation details. An opposite side of this solution is that for a concrete program and a concrete miniKanren implementation, the result of the evaluation might not coincide with that, prescribed by the semantics: in some concrete implementation a program can diverge, while nondeterministic semantics may still define a certain scenario to complete with a result. We argue, that in this case, it will always be possible to rewrite a program or/and interpreter to converge according to that scenario.
Finally, we describe the structure of a logical state and the implementation of unification and disequality constraint. The development is mainly based on the existing implementation [1] and standard approaches for implementing unification [2, 14]. We, therefore, assume the familiarity of the reader with the following notions:
-
substitution (\(\theta \));
-
application of substitution \(\theta \) to a term t (\(t\,\theta \));
-
composition of substitutions (\(\theta \theta ^\prime \));
-
most general unifier of two terms (\(mgu\,(t_1, t_2)\)).
A logical state contains two components
where \(\theta \) is a substitution, \(\varTheta ^-\)—a set of negative substitutions, describing disequality constraints, which can potentially be violated. The initial state contains undefined substitution and empty set:
The effect of unification is described by the following primitive:
First, it calculates the most general unifier for the terms under consideration w.r.t. current substitution:
If there is no such \(\rho \), the unification fails, and the evaluation terminates unsuccessfully. Otherwise, \(\rho \) has to be checked against the disequality constraints, represented by \(\varTheta ^-\) (if \(\varTheta ^-\) is empty, the check succeeds immediately).
Being a substitution, \(\rho \) at the same time can be considered as the following unification problem: we can try to unify a pair of terms
where \(\{\mathfrak s_i\} = dom\,(\rho )\). We pick every substitution \(\theta ^-\in \varTheta ^-\) and calculate the \(mgu\,(t_l\,\theta ^-, t_r\,\theta ^-)\). There are three possible outcomes:
-
1.
The unification fails. This means, that disequality constraint, represented by \(\theta ^-\), can no longer be violated. We remove \(\theta ^-\) from \(\varTheta ^-\) and continue with the next disequality constraint.
-
2.
The unification succeeds with the empty substitution. This means, that disequality constraint, represented by \(\theta ^-\), is violated. The check stops, and the whole top-level unification fails.
-
3.
The unification succeeds with a non-empty substitution \(\theta ^{\prime -}\). This means, that in order not to violate disequality constraint, represented by \(\theta ^-\), \(\theta ^{\prime -}\) has to be respected. We replace \(\theta ^-\) with \(\theta ^{\prime -}\) in \(\varTheta ^-\) and continue with the next disequality constraint.
If the disequality check succeeds, by the end we have a modified set \(\varTheta ^{\prime -}\), and we assume
The evaluation of disequality constraint is performed in a similar manner using the primitive
First, the \(mgu\,(t_1\,\theta ,\,t_2\,\theta )\) is calculated. Again, there are three possible cases:
-
1.
The unification fails. This means, that disequality constraint is satisfied.
-
2.
The unification succeeds with the empty substitution. This means, that disequality constraint is violated.
-
3.
The unification succeeds with a non-empty substitution \(\theta ^{\prime -}\). This means, that this substitution describes the disequality constraint, which has to be respected in the future, so we add it to \(\varTheta ^-\).
If disequality constraint succeeds, we obtain a (potentially) modified set \(\varTheta ^{\prime -}\), and we assume
Finally, for a closed goal g and a logical state \(\sigma \), we define \(g \leadsto ^r \sigma \), iff

where “\(\leadsto ^*\)” is a reflexive-transitive closure of “\(\leadsto \)”.
One may notice, that the typing rules for the relational extension add nothing more than some interpreted types and symbols w.r.t. the type system of the substrate language. Thus, it is rather expected, that the relational extension inherits all its useful properties (like progress and type preservation). Surprisingly, this is not completely so. Indeed, the only value for goals is  , but, obviously, not every goal succeeds (for example,
, but, obviously, not every goal succeeds (for example,  always fails). Thus, our relational extension lacks the progress property—a decently typed non-value goal sometimes cannot make a step. This makes no harm in the context of the paper; in any case, a failure value for goals can be added to the language together with the failure propagation rules.
always fails). Thus, our relational extension lacks the progress property—a decently typed non-value goal sometimes cannot make a step. This makes no harm in the context of the paper; in any case, a failure value for goals can be added to the language together with the failure propagation rules.
4 Relational Conversion
Before we describe the relational conversion itself, we formulate some limitations for the source programs. Functional programs tend to operate with higher-order values, while miniKanren is limited by a first-order unification. Therefore, it would be unreasonable to expect, that arbitrary functional program can be converted into a relational form (at least using reasonably simple transformations).
We introduce the set of ground types \(\mathcal G\):
Informally, a value of a ground type cannot contain closures. Then we formulate the following limitations for the programs to be converted into a relational form:
-
all constructor parameter types must be type variables;
-
constructors and polymorphic equality can only be applied to the values of ground types;
-
all
 -expressions must be of ground types.
-expressions must be of ground types.
The first condition means, that all algebraic datatypes (which we consider as defined implicitly, see Sect. 3.1) have to be fully-polymorphic. The first two limitations then allow us to specify the polymorphism restriction for relational programs, which we mentioned informally in Sect. 2: all type variables are bounded to range only over ground types (this condition, of course, is sufficient, but not necessary).
The third limitation is not essential and introduced only to simplify the presentation. If a  -expression does not have a ground type, it can always be transformed to have one by applying \(\eta \)-expansion:
-expression does not have a ground type, it can always be transformed to have one by applying \(\eta \)-expansion:

where \(\bar{x}\) is a vector of new variables, different from those in e, \(e_i\), and \(p_i\). In fact, our implementation, described in Sect. 5, performs this expansion as long as a non-ground type  -expression is encountered. This is the single case when we actually inspect types and perform \(\eta \)-expansion.
-expression is encountered. This is the single case when we actually inspect types and perform \(\eta \)-expansion.
The general idea behind the conversion can be illustrated on a type level: an expression of type t in the source language is transformed into the expression of type  in relational extension, where the transformation
in relational extension, where the transformation  is defined as follows:
is defined as follows:

In other words, an expression of a ground type is converted into a goal-returning function. The informal semantics of this function is to make its argument respect a certain contract. As the argument can have some free variable occurrences, the goal tries to substitute these variables with some values in order to respect the contract this goal represents. For example, a constant  is converted into a function
is converted into a function  .
.
The conversion itself is described in terms of transformation  , see Fig. 9. The first five rules simply propagate the conversion through the expression; the last three actually do the work. These rules themselves may look complicated, but the idea is rather simple.
, see Fig. 9. The first five rules simply propagate the conversion through the expression; the last three actually do the work. These rules themselves may look complicated, but the idea is rather simple.
In the case of constructor we know, that all expressions \(e_i\) have ground types. Thus, their relational images are goal-returning functions. We create a set of fresh variables (one for each expression) and pass them as arguments to these functions to associate them with the values of the expressions. The result of conversion for the constructor application itself has to be a goal-returning function as well. We surround expression constructed so far with abstraction and unify its argument q with the constructor, applied to corresponding logical variables. We also apply logical constructor \(\uparrow \) to respect the typing rule for unification.
The rule for pattern-matching conversion operates similarly. First, the scrutinee must have a ground type (since it is matched against constructors). We create a fresh variable \(q_e\) and associate it with the value of the scrutinee exactly as in the previous case. Then, for each branch we create a number of fresh variables (one for each variable in the pattern for the branch) and express pattern-matching in terms of unification, using these variables and corresponding constructor. Finally, the body \(e_i\) of the branch is an expression with free variables, corresponding to those in the pattern. We, therefore, convert \(e_i\) and surround the result with lambdas, closing all these variables. To pass the bindings \(q^i_j\) for pattern variables to the body, we apply this function to goal-returning functions \(({\equiv }{q^i_j})\). This, again, gives us a goal-returning function, which we apply to the topmost result variable q.
The last rule follows the same pattern: both arguments of polymorphic equality are transformed into goal-returning functions, and we know, that the arguments of these functions are of some ground type. We apply these functions to fresh variables and perform case analysis. Note, this is the only case when we actually use disequality constraints (Fig. 9).
An interesting property of relational conversion is that it does not change terms, which do not use constructors, equality, and pattern-matching. Thus, a lot of useful higher-order functions—application, composition, fixed point, etc.—are already relational and can be used in relational specifications.
Another observation is that our transformation is compositional (a relational image of application is an application of relational images). This means, that relational conversion is compatible with separate compilation—multiple source files can be converted independently without losing the possibility to work properly when combined.
Then, it is interesting, that the result of relational conversion runs in a forward direction deterministically. Thus, relational conversion imposes only a constant-time slowdown in a forward direction.
Finally, we formulate the following properties for relational conversion:
-
Static correctness: if an expression e has a type t in the source language, then
 has a type
has a type  in relational extension. In other words, relational conversion transforms properly typed programs into properly typed. Proof is by structural induction (and trivial).
in relational extension. In other words, relational conversion transforms properly typed programs into properly typed. Proof is by structural induction (and trivial). -
Partial semantic correctness: if an expression e has a ground type t and \(e \leadsto ^f v\) for some value v, then
 , and \(\theta (\mathfrak {s})=v\), where \(\mathfrak {s}\) is a semantic variable, associated with x on the first step of the relational evaluation.
, and \(\theta (\mathfrak {s})=v\), where \(\mathfrak {s}\) is a semantic variable, associated with x on the first step of the relational evaluation.
In order to prove the complete correctness, we need some means to interpret the results of relational derivation with free variables in functional case. This is a subject of future research.
5 Implementation and Application
We implemented relational conversion for the subset of OCaml language, using the infrastructure of the original compiler. In its current form, the converter takes the whole file and converts every definition into relational form, but in future, we consider to implement a more flexible approach, when only some definitions are converted, being attributed for this purpose in some way. Our converter rewrites the original abstract syntax tree, annotated with the types, inferred by the compiler, into relational form, using the set of combinators from OCanren. Note, the semantics of OCaml is different from the semantics of source language we presented in Sect. 3.1: in OCaml, the order of reductions in application and binary operators is unspecified (unlike left-to-right in our case), pattern-matching in OCaml is performed in a top-down manner (and, thus, there can be more than one pattern matching the scrutinee), etc. We, therefore, trust an end user to apply relational conversion only to programs, for which these differences play no role.
Our preliminary evaluation discovered two problems. First, the converter used to generate a lot of abstractions, many of which could be applied immediately. We additionally implemented an optimization pass, which performs administrative reductions where possible. This optimization greatly improves the quality of converted programs in terms of both readability and performance. Next, in our initial implementation, too many values were functionalized and, as a result, massively recalculated with essential performance degradation. We improved the implementation by identifying the important specific case and handling it with a little different transformation.
As the first example of the conversion we consider the implementation of concatenation function for lists (see Fig. 10a). In Sect. 2, we already saw the canonical version of relational concatenation. The result of relational conversion, however, is slightly different (see Fig. 10b). The main difference comes from the functionalization of primitive values: while conventional  operates on logical lists, the converted variant uses a goal-returning functions. Thus, the conventional
operates on logical lists, the converted variant uses a goal-returning functions. Thus, the conventional  for arguments
for arguments  ,
,  and
and  can be expressed using the converted one as
can be expressed using the converted one as  .
.
In the next subsections, we consider more elaborated and interesting examples. From now on, we refrain from presenting the complete source and converted code and consider only the signatures and some interesting queries.
5.1 Higher-Order Lambda Interpreter
As we mentioned in Sect. 1, one of the important application domains for miniKanren is the implementation of relational interpreters [5, 6, 8]. Writing relational interpreter, as a rule, amounts to a careful rewriting of functional implementation in miniKanren. In this regard, obtaining a relational interpreter automatically from a functional specification looks a natural idea.
In our case, we generalize this idea a little bit: we build a relational interpreter for a family of languages—essentially, the lambda calculus with various reduction orders. The construction of this interpreter was inspired by Felleisen-style semantic description [16]. Our interpreter takes as its first argument a function, which decomposes a term, passed as a second argument, into a redex and a context (if possible). After the decomposition, the interpreter performs beta-reduction on the redex and reconstructs the term by plugging the result back into the context. These steps are repeated until the decomposition is no longer possible (or infinitely). This approach brings us a few benefits: first, various reduction orders can be expressed by changing only the decomposition function, and next, we demonstrate the applicability of our technique for a higher-order case.
The signatures of relevant functions are

where  and
and  are the types of the terms (in de Bruijn form) and context-term pairs respectively;
are the types of the terms (in de Bruijn form) and context-term pairs respectively;  is a higher-order interpreter, all other functions define corresponding reduction orders. Relational counterparts for these definitions, provided by the conversion, are shown below:
is a higher-order interpreter, all other functions define corresponding reduction orders. Relational counterparts for these definitions, provided by the conversion, are shown below:

Note, due to the compositionality of the conversion, the type of functions, representing reduction orders, still corresponds to the type of the first argument of the interpreter.
The interpreter, constructed by our tool, can be run in a forward direction (for readability purposes, we use here a symbolic quoted representation of the terms instead of concrete datatype constructor-based):

As it is expected from relational interpreter, it equally can be run in the opposite direction, returning for a term a (potentially infinite) stream of terms, reducing to it:

This interpreter can be extended to the subset of Scheme, with which the quines/twines/thrines benchmarks [8] can be reproduced.
5.2 Hindley-Milner Type Inference
Our next example is the type inference for Hindley-Milner type system [15]. Interestingly enough, that while typing rules for STLC can be directly expressed in relational terms, providing the solutions for type inference, type checking, and type inhabitation problems at the same time, for not so different Hindley-Milner system with let-polymorphism, the problem becomes much harder. The most robust existing relational solution requires the extension of miniKanren with nominal constructs [7], while the correctness of other implementations in conventional miniKanren is still a matter of discussion [4].
On the other hand, in terms of functional programming, this task is rather a textbook exercise. We implemented a simple version of syntax-directed type inference and converted it into the relational form; the signatures for the original and converted implementations are shown below:

For this example, we use a conventional representation of terms with named variables. In a forward direction, our relational implementation works, as expected, as a type inferencer—given a term it infers its type:

In a reverse direction, relational type inferencer is capable of finding the inhabitants of a specified type:

Note, the first query diverges, providing no results (which is rather expected since the type is un-inhabited). This is a long-time known phenomenon of miniKanren—the search can diverge, when no answers exist; relational specifications, which always stop in this case, are called refutationally complete [5]. Given example demonstrates, that our derived relational specification is not refutationally complete, which is not a rarity in the relational world; making it refutationally complete is a separate task.
It may appear at first glance, that using relational Hindley-Milner inferencer for solving inhabitance problem is superfluous, since the inhabitance for Hindley-Milner is equivalent to inhabitance for STLC. However, with relational inferencer we may solve some problems, which are distinct from both pure inference and pure inhabitance:

In this query, we supplied an incomplete term with a hole (\(\Box \)) and some type, and as a result, we’ve got a term to plug into the hole in order for the complete term to have that type. Note, the term we’ve got as a result cannot be typed in STLC, since the variable  is applied there twice with different types of arguments.
is applied there twice with different types of arguments.
A final observation: we do not claim to completely solve the problem of relational implementation of Hindley-Milner type system. Even though our converted relational implementation behaves as expected, it still not ideal—indeed, in functional implementation we had to implement unification on types, which does not make use of built-in unification in miniKanren and, to some extent, doubles the work. We, therefore, do not consider this approach as an ideal solution.
5.3 miniKanren with Disequality Constraints
Our final example is an implementation of miniKanren in miniKanren. Although there already exist a few similar implementations, written directly in miniKanren, our version is different, since it supports disequality constraints. We consider this as an important distinction—first, the presence of disequality constraints makes the language much more expressible, and next, implementing disequality constraints directly in miniKanren is a very tedious and error-prone task. On the other hand, providing relationally converted version amounts only to repeating a well-known and rather compact original implementation [1].
The signatures for functional and relational miniKanren implementations are as follows:

Here  stands for the type, representing the goals,
stands for the type, representing the goals,  —for the type of substitutions. Again, our relational miniKanren interpreter works in both directions. As a more interesting query, we consider the following:
—for the type of substitutions. Again, our relational miniKanren interpreter works in both directions. As a more interesting query, we consider the following:

Here we specified an incomplete relational program (specifically, a relational addition of numbers in Peano form). The hole (\(\Box \)) replaces one of the branches, and expected substitution describes the results of addition. Our relational interpreter, converted from functional implementation, turned out to be capable of finding the correct subgoal—“ ”—to be placed into the hole.
”—to be placed into the hole.
6 Conclusion
We presented an approach for converting typed functional programs into relations. Relational conversion in many cases allows us to avoid tedious recoding of functional specifications into relational form and to concentrate on writing relational specifications only when their reconstruction from functions is impossible or undesirable. Our implementation works for the subset of OCaml; we evaluated it for a number of interesting examples and acquired some new relational solutions.
There is a number of directions for future research. First, a performance evaluation is desirable—at present time we do not know, what slowdown factor is. Another problem is a development of an approach to prove complete correctness (or refute this claim).
Notes
- 1.
- 2.
- 3.
- 4.
- 5.
In the real implementation the terms have a more complex two-parametric type, which encodes a tagging, needed to be performed when the results of the relational program are returned into the functional world; these details, however, are irrelevant to the objectives of the paper, and we stick with the simplified version.
References
Alvis, C.E., Willcock, J.J., Carter, K.M., Byrd, W.E., Friedman, D.P.: cKanren: miniKanren with constraints. In: Proceedings of the 2011 Annual Workshop on Scheme and Functional Programming, October 2011
Baader, F., Snyder, W.: Unification theory. In: Handbook of Automated Reasoning. Elsevier Science Publishers B.V., Amsterdam (2001)
Barendregt, H.P.: Lambda calculi with types. In: Handbook of Logic in Computer Science, vol. 2, pp. 117–309. Oxford University Press Inc., New York (1992)
Byrd, W.E.: Private communication
Byrd, W.E.: Relational programming in miniKanren: techniques, applications, and implementations. Ph.D. thesis, Indiana University, September 2009
Byrd, W.E., Ballantyne, M., Rosenblatt, G., Might, M.: A unified approach to solving seven programming problems (functional pearl). Proc. ACM Program. Lang. 1(ICFP), 8:1–8:26 (2017)
Byrd, W.E., Friedman, D.P.: \(\alpha \)Kanren: a fresh name in nominal logic programming. In: Proceedings of the 2007 Annual Workshop on Scheme and Functional Programming, pp. 79–90 (2007)
Byrd, W.E., Holk, E., Friedman, D.P.: miniKanren, live and untagged: quine generation via relational interpreters (programming pearl). In: Proceedings of the 2012 Annual Workshop on Scheme and Functional Programming, Scheme 2012, pp. 8–29. ACM, New York (2012)
Cardelli, L., Wegner, P.: On understanding types, data abstraction, and polymorphism. ACM Comput. Surv. 17(4), 471–523 (1985)
Friedman, D.P., Byrd, W.E., Kiselyov, O.: The Reasoned Schemer. The MIT Press, Cambridge (2005)
Hemann, J., Friedman, D.P.: \(\mu \)Kanren: a minimal functional core for relational programming. In: Proceedings of the 2013 Annual Workshop on Scheme and Functional Programming (2013)
Hemann, J., Friedman, D.P., Byrd, W.E., Might, M.: A small embedding of logic programming with a simple complete search. SIGPLAN Not. 52(2), 96–107 (2016)
Kosarev, D., Boulytchev, D.: Typed embedding of a relational language in OCaml. In: ACM SIGPLAN Workshop on ML (2016)
Lassez, J.-L., Maher, M.J., Marriott, K.: Unification revisited. In: Foundations of Deductive Databases and Logic Programming, pp. 587–625. Morgan Kaufmann Publishers Inc., San Francisco (1988)
Pierce, B.C.: Types and Programming Languages, 1st edn. The MIT Press, Cambridge (2002)
Wright, A., Felleisen, M.: A syntactic approach to type soundness. Inf. Comput. 115(1), 38–94 (1994)
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2018 Springer International Publishing AG, part of Springer Nature
About this paper
Cite this paper
Lozov, P., Vyatkin, A., Boulytchev, D. (2018). Typed Relational Conversion. In: Wang, M., Owens, S. (eds) Trends in Functional Programming. TFP 2017. Lecture Notes in Computer Science(), vol 10788. Springer, Cham. https://doi.org/10.1007/978-3-319-89719-6_3
Download citation
DOI: https://doi.org/10.1007/978-3-319-89719-6_3
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-89718-9
Online ISBN: 978-3-319-89719-6
eBook Packages: Computer ScienceComputer Science (R0)





 ;
; and
and  are needed to denote them. We also need a fresh variable
are needed to denote them. We also need a fresh variable  to denote the list, such that appending
to denote the list, such that appending  to
to 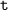 equals
equals  . To ensure this property, we use a recursive call to
. To ensure this property, we use a recursive call to  . Finally, we acquire the final result by consing
. Finally, we acquire the final result by consing  and
and  .
.







 -expressions must be of ground types.
-expressions must be of ground types.
 has a type
has a type  in relational extension. In other words, relational conversion transforms properly typed programs into properly typed. Proof is by structural induction (and trivial).
in relational extension. In other words, relational conversion transforms properly typed programs into properly typed. Proof is by structural induction (and trivial). , and
, and 