A Comparison Between Threshold Ergodic Sets and Stochastic Simulation of Boolean Networks for Modelling Cell Differentiation

Abstract

Recently a cell differentiation model based on noisy random Boolean networks has been proposed. This mathematical model is able to describe in an elegant way the most relevant features of cell differentiation. Noise plays a key role in this model; the different stages of the differentiation process are emergent dynamical configurations deriving from the control of the intracellular noise level. In this work we compare two approaches to this cell differentiation framework: the first one (already present in the literature) is focused on a network analysis representing the average wandering of the system among its attractors, whereas the second (new) approach takes into consideration the dynamical stories of thousands of individual cells. Results showed that under a particular noise condition the two approaches produce comparable results. Therefore both can be used to model the cell differentiation process in an integrative and complementary manner.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

Cell differentiation is the process by which the development of specialized cell types takes place, starting from a single cell (the zygote). The development of different cell types is the result of highly complex dynamics between intracellular, intercellular, external and inherited signals [4, 5]. Intracellular interactions are captured in gene regulatory networks (GRNs): complex networks that regulate the gene expression. Each cell type presents a particular pattern of gene expression.

Boolean networks (BNs) [6] are models of gene regulatory networks and are prominent examples of complex dynamical systems. Recently a cell differentiation model based on Boolean networks subject to noise has been proposed [11, 12]. This model reproduces the generic abstract features of the differentiation process, such as the attainment of different degrees of differentiation, deterministic and stochastic differentiation, reversibility, induced pluripotency and cell type change [12]. The model considers the asymptotic behaviours of noisy random Boolean networks, where (intracellular) noise is modelled as the transient flip of a node value. Attractors of BNs are unstable with respect to noise even at low level [10]. In fact, even if the flips last for a single time step sometimes we observe transitions from an attractor to another one. The main abstraction introduced in the model presented in [11, 12] is the Threshold Ergodic Set (TES). TESs represent the asymptotic states of the BNs subject to noise. The various steps of the differentiation process are represented by TES landscapes, which are the emergent results of intracellular noise changes. This model offers a way to mitigate the intrinsic complexity of the analysis of stochastic systems: by applying it we are able to analyse a noisy random Boolean network and produce a static global picture of the all possible differentiation pathways that it can express. So, the main characteristics of the differentiation are captured by TES-based differentiation trees, TES-trees in the following.

The generic abstract properties of the model have been already shown to match those of the real biological phenomenon. However, we remark that (i) the results produced by this model depend on the specific noise mechanism implemented and therefore the properties enlighten by the TES model might differ from those observed in the dynamics of real biological cells, as noise acting on them might perturb them in different ways; and (ii) the differentiation picture the TES model produces summarises all the possible outcomes of the BN dynamics that may happen under this specific noise mechanism and so it might not represent in sufficient detail individual cell dynamics. For these reasons, we compared the properties of the TES model with the actual dynamical simulation of the BN subject to random external perturbations with the aim of assessing to what extent the two approaches exhibit comparable results and their respective strengths and weaknesses.

The paper is organised as follows. In Sect. 2 we introduce the differentiation model. In Sect. 3 the approach based on stochastic simulations of Boolean networks is illustrated. The experimental setting is described in Sect. 4. Results and discussion are presented in Sects. 5 and 6, respectively.

2 TES Differentiation Model

The cell differentiation model we consider in this work has been presented in  [11, 12]. This abstract model¹ is able to describe the most relevant features of the differentiation process, which are the following:

• 1. Different degrees of differentiation: totipotent, pluripotent, multipotent and fully differentiated cells.

• 2. Stochastic differentiation: a population of identical cells can generate different cell types, in a stochastic way.

• 3. Deterministic differentiation: activation or deactivation of specific genes or group of genes can trigger the development of a multipotent cell into a well-defined type.

• 4. Limited reversibility: a cell can come back to a previous stage under the action of appropriate signals.

• 5. Induced pluripotency: fully differentiated cells can come back to a pluripotent state by modifying the expression level of some genes.

• 6. Induced change of cell type: the expression of few transcription factors can convert one cell type into another.

This differentiation model is based on noisy random Boolean networks. A Boolean network (BN) is a genetic regulatory network (GRN) model, and a complex dynamical system, introduced by Kauffman [6]. A BN is a discrete-state and discrete-time dynamical system whose structure is defined by a directed graph in which each node represents a gene; genes are binary devices that have incoming arcs from other nodes if these last influence the activation of that gene. The most studied BN models are characterized by synchronous dynamics and deterministic functions. With such dynamics, the reachable asymptotic states are fixed points and cyclic attractors.

This differentiation model takes into account only intracellular noise, since it deals with a single cell as a closed system. It is generic and in principle can support different definitions of noise; however in this contribution we adopt the noise type originally presented in [11, 12]. Hence, we investigate the asymptotic dynamics of BNs subject to noise modelled by the transient flip of a randomly chosen node which lasts for a single time step (a logic negation of node’s state). After the transient flip the BN evolves according to its usual deterministic rules until an attractor is found. This noise type represents the smallest stochastic perturbation that can affect a Boolean network; even in this configuration we can observe jumps from an attractor to another one. By perturbing each node of each phase of each attractor found (one at a time), and checking in which attractor the dynamics lead we can compute the attractor transition matrix (ATM). This procedure is described in [8, 12, 13]. The ATM summarises the observed transitions between attractors and gives us an estimate of the probabilities with which such transitions can occur; a measure of the system’s robustness respect to a random flip of an arbitrary state.

The Threshold Ergodic Set (TES) is the key concept introduced on ATM: indeed, cell types are modelled by TESs. A TES$_\theta$ is a set of attractors in which the dynamics of the network remains trapped, under the hypothesis that attractor transitions with probability less than threshold $\theta$ are not feasible². TESs are computed from the ATM, by iteratively removing the entries with value less than a threshold $\theta$, which is progressively increased from 0 to 1. The TES-trees are constructed following this procedure: TES$_0$ represents the level 0 and each subsequent level is created if the current threshold applied to the ATM produces a different TES-landscape with respect to the previous one. In this way we capture, in a static representation, all the possible differentiation dynamics of a BN subject to noise. The threshold abstraction plays an important role, as it is a mathematical concept strictly related with the noise level in the cell: it scales with the reciprocal of the noise level. High levels of noise (low threshold values) correspond to pluripotent cell states, where the BN trajectory can wander freely among the attractors; conversely, low levels of noise (high thresholds) induce low probabilities to jump between attractors, thus representing the case of specialised cells [11, 12].

3 Stochastic Simulation Approach

The main contribution introduced by the previous model is that the differentiation process is strongly correlated with the intracellular noise level. From the model point of view we know how the threshold is related to noise, see [11], and in addition we know that pluripotent cells have a more intrinsic noise level than the more specialized ones [9]. But the threshold and above all its variation mechanism introduced in the model (with which we model the differentiation process) are externally controlled. In fact the threshold represents an abstraction of the mechanisms implemented by the real cell to control noise. The identification of autogenous mechanisms, somehow bound to cell’s dynamics, through which achieve a threshold self-regulation is subject of ongoing work. As first step to identify the biological mechanisms that affect noise level, and in turn the threshold, we can take in exam a system with different types of noise and noise levels and we can verify if the system is able to reproduce the TES phenomenology. In fact, the approach to cell differentiation previously presented might not capture the real asymptotic configurations of real cells if the cellular system is subject to a noise implemented in a different way with respect to the original model. For example, a real cell dynamics might quickly diverge from the TES model’s prevision if its dynamics is such that:

• more than one noise events can occur simultaneously in an asymptotic state;

• noise events occur in its transients.

In addition, the TES-based differentiation trees are constructed following a specific process of threshold variation on the ATM. This process allows us to observe all the differentiation pathways the GRN model is capable of expressing, under a particular noise setting.

To verify to what extent can the TES model predict the entire spectrum of scenarios produced by the dynamics of a system subject to intrinsic noise, we perform time evolutions of Boolean networks subject to different noise levels and we compare these two approaches. Noise levels are represented by distinct frequencies of random perturbations. In such a way, we have the means for counting—for each noise level—the number of differences between the outcomes obtained with the TES model and the stochastic simulations. In the following we call a story a single time evolution of a BN subject to random perturbations. Considering that we are interested in the asymptotic behaviour of the BN dynamics we count the jumps between attractors obtained in each story and we compare them with each level of the TES-based differentiation tree, computed using the TES-model approach on the same BN. We call an incompatibility a jump between attractors that would not be allowed given the TES-landscape of a tree’s level.

4 Experimental Setting

The Boolean networks used in the experiments have $n = 100$ nodes and $k = 2$ distinct inputs per node assigned randomly (self-loops are not allowed). Boolean functions have been set by assigning a 1 in the node truth table so as to attain exactly a frequency of 0.5 across all the truth tables (for $k=2$, this corresponds to the critical value [1]). The rationale behind this choice is that in preliminary results, by setting the bias for each boolean function, in some instances the average overall bias calculated on all nodes could have a non-negligible standard deviation from the desired mean value. Because we want to estimate the differences between the model and the stochastic simulations, we did not want the results to be affected by variance in network dynamic regime. So we use an exact bias, following this procedure for generating networks: we generate a vector of length equal to the sum of the number of Boolean functions’ entries of all nodes in the network ($2 ^{k} * n$), we assign half the values to 1 and half to 0 and we use a random permutation of this vector to define the Boolean functions.

The BN is subject to a synchronous dynamics, i.e. all nodes update their state in parallel and functions are applied deterministically. Given that the typical time needed to transcribe a gene is equal to 25–50 s in yeasts and 2–3 min in mammalians (see reference BNID 111611 [7]); we assume 1 min as a plausible mean value for a BN’s synchronous step of update. In addition, analysing the cell’s average life span in humans (see reference BNID 101940 [7]) we set to $5\times 10^4$ the number of steps for a BN run, in order to model an upper bound of plausible mean cell lifetimes (approximately one month). The only stochastic component resides in the noise, which has been simulated as a temporary flip of the value of a node applied with probability $\nu$; hence, at each step of the temporal evolution of the network, $\nu n$ nodes are flipped on average. We ran experiments with $\nu$ so as to have on average one flip every $\tau$ steps, with $\tau \in \{1,5,10,15,20,50,100,200,500,10^3,5\times 10^3,10^4,2\times 10^4,5\times 10^4\}$. In the following, we will denote the corresponding noise probabilities as $\nu _\tau$. Note that the higher $\tau$, the lower the probability $\nu$ applied to each node. This noise mechanism emulates possible temporary fluctuations in the expression level of genes and may occur both during stationary phases (i.e. along attractors of the BN) and transients. We run experiments with 30 random BNs; for each of them we compute the ATM and then the TES-tree, following the procedures mentioned in Sect. 2. A typical TES-tree is depicted in Fig. 1. The time evolution of each BN was also simulated 100 times (100 stories), each one of them starting from a random initial state. We collected the trajectories of the BNs and computed statistics on the compatibility between the stories and the TES-tree, besides other ancillary statistics on the overall dynamics of the BNs.

Fig. 1.

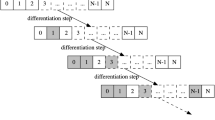
An example of a TES-tree. Levels are numbered from 0, the topmost, to n, the lowermost; $n=6$ in this example. TES of level 1 has a diamond shape whereas TESs of level n have an hexagonal one. Labels on the edges indicate the minimum threshold value at which any TESs of the previous level splits or reduces. Continuous lines denote paths along the differentiation tree that can be followed by increasing the threshold at minimum steps (these values are directly obtained by the ATM). Dashed lines denote the paths that can instead be followed if the threshold was increased by larger steps.

Fig. 2.

Distribution of the median values of the incompatibilities between the level 1 and level n of the TES-trees and stochastic simulations with the probabilities to flip a node $\nu$ so as to have on average one flip every 1, 5, 10, 15, 20 steps. Noise probabilities $\nu _\tau$ expressed with different colours (Color figure online).

5 Results

In this section we provide the results obtained. The comparison between TES-trees and simulations with stochastic noise is mainly based on counting the transitions between attractors that are observed in the stochastic simulation but that are not allowed by the ATM, given a probability threshold $\theta$. That is, the analysis of what we have called incompatibilities between the two approaches for modelling cell differentiation. For each value of $\nu _\tau$, we counted the incompatibilities observed in all the 100 stories w.r.t. the lowest non-zero value of $\theta$ (level 1 of the TES-tree) and the highest one, where all TESs are single attractors (level n of the TES-tree). These two particular levels are taken as representative elements able to summarise the trend of incompatibilities since level 1 represents the first TES with not trivial constraints and level n is the most constrained one. Results are summarised in Figs. 2, 3 and 4. In these figures the boxplots graphically represent distributions of the median values of the overall incompatibilities (computed on all 30 BNs) with respect to a particular noise level; different noise levels are represented by distinct colours. For each noise level two boxplots are plotted, one for the incompatibilities with respect to the level 1 and one for the level n.

Fig. 3.

Distribution of the median values of the incompatibilities between the level 1 and level n of the TES-trees and stochastic simulations with the probabilities to flip a node $\nu$ so as to have on average one flip every 50, 100, 200, 500 steps. Noise probabilities $\nu _\tau$ expressed with different colours (Color figure online).

Fig. 4.

Distribution of the median values of the incompatibilities between the level 1 and level n of the TES-trees and stochastic simulations with the probabilities to flip a node $\nu$ so as to have on average one flip every 1000, 5000, 10000, 20000, 50000 steps. Noise probabilities $\nu _\tau$ expressed with different colours (Color figure online).

As expected, the higher $\nu _\tau$ (corresponding to low values of $\tau$), the higher the number of these incompatibilities. Moreover, this increases with $\theta$; which corresponds to the increase of the TES-tree’s depth. Despite the discrepancy which is apparent at high noise levels, we observe that already for medium noise levels, i.e. not higher than $\nu _{200}$, the incompatibilities are limited and tend to be negligible towards low noise levels.

As previously stated, we could observe marked differences between model and simulations if the actual noise presents in the stories is different from that hypothesized by the model. Hence, we analyze the dynamics of the stochastic simulations and we count the number of noise events occurred during transients and the multiple flips in attractors. With multiple flips we mean the occurrence of more than one node value change at a time. Situations both not covered in the model and which could represent the main causes of divergence between the two approaches. In Figs. 5, 6, 7 and 8 each distribution summarises the median values of the property in exam; the median value for each BN computed across the 100 stories of a particular noise level. Hence, we have one boxplot for each distribution of medians. These statistics show that noise events in transients and multiple flips decrease in an exponential way as noise decreases. This trend is more evident in Figs. 6 and 8, which have logarithmic scales. We can note that under noise level $\nu _{100}$ the number of multiple flips and noise during transients become negligible with respect to the number of steps considered in the stories (i.e. $5\times 10^4$). We must remark that although the flip of a gene is the smallest stochastic perturbation that can affect a Boolean network it biologically reproduces a fairly intense event, much stronger than molecular fluctuations. Hence, the noise level $\nu _{200}$ (250 noise events on average in a story) identified as the convergence point between the two approaches could even be a too high noise level for a real cell’s life span. This observation contextualizes the results obtained in a biological framework and it highlights the relevant noise levels in which a real cell can operate.

The results obtained support the statement that there exists a significant noise level under which the two models are in agreement. Therefore, (i) under this threshold they can be both used to model differentiation phenomena—and their observations can be combined—and (ii) the new dynamic simulations may add interesting pieces of information on the heterogeneities of the possible individual configurations.

Fig. 5.

Distribution of the median values of the number of noise events occurred during transients in stochastic simulations (stories), for different noise levels. Noise levels expressed by the $\nu _\tau$ values in the x axis.

Fig. 6.

Detail of Fig. 5 on logarithmic scale.

Fig. 7.

Distribution of the median values of the number of multiple flips occurred in the attractors in stochastic simulations (stories), for different noise levels. Noise levels expressed by the $\nu _\tau$ values in the x axis.

Fig. 8.

Detail of Fig. 7 on logarithmic scale.

6 Conclusion

In this paper we have compared two approaches for modelling cell differentiation, both based on random Boolean networks subject to noise. One approach is represented by the well-known model based on TES concept, the other is grounded in time evolutions of BNs subject to different noise levels. The analysis of the emerging differences between these two approaches suggests that there is a specific noise level under which the two models produce similar results. This result has important implications because it shows that both approaches can be used to model cell differentiation and in addition their outcomes can be, at least in part, complementary. Indeed, the new approach could be used to determine the distribution of the extra-cellular noise, due to the intra-cellular events. Moreover this work produced, on the one hand, another proof of robustness of the TES-based differentiation model and, on the other, since the stochastic simulations of BN require less computational cost than the TES model they can be used as an alternative and exploitable approach to conceive more performing automatic procedure for generating biologically plausible cell differentiation model based on BNs [2, 3].