Keywords

1 Introduction

This work deals with the problem of modelling oscillatory phenomena by suitable systems of differential equations, together with providing a proper numerical scheme for an accurate and efficient approximation of their solutions. A special emphasis is here given to a significant case study: the well-known Belousov-Zhabotinsky (BZ) reaction. The BZ is a striking example of a self-organizing chemical system, and thanks to its characteristics, it became a widely employed model also in other fields. For instance, in biology BZ can be considered a simple analogue of periodic phenomena (metabolic cycles, circadian clocks, etc) and in mathematics and physics it is an ideal example of complex nonlinear dynamical system [1]. There are several models to describe the complex kinetics of the BZ reaction, being the Oregonator, the most used [1,2,3].

In [4] this system has been integrated by employing an adapted numerical scheme which exploits information obtained by observing time series of experimental data. It has been shown that this problem-oriented approach is more accurate and stabler than general-purpose numerical methods, which could require a strong reduction in stepsize in order to accurately follow the behaviour of the exact solution. In this paper, we focus on the nature of the operator, in order to improve the matching of the numerical solution of the Oregonator with the time series.

In Field, Körös and Noyes approach, the time evolution of BZ reactions is treated as a continuous and deterministic process. In many cases, this is sufficient to study the qualitative behaviour of the system. However, the reaction-rate equations may be unable to describe the fluctuations in the molecular population levels within the study, for instance, of ecological systems, microscopic biological systems and nonlinear systems characterised by chemical instability. Therefore, in some cases it may be more convenient to employ a stochastic approach, which derives from some physical considerations. Firstly, molecular population levels change in a discrete manner, so the time evolution of a chemically reacting system is not a continuos process. Moreover, it is impossible to predict the exact molecular population levels at a certain time unless the exact positions and velocities of all the molecules in the system are known [5, 6]. The stochastic formulation of chemical kinetics basically takes into account that the collisions in a system of molecules in thermal equilibrium occur essentially in a random way. However, it is based on the so-called master equation which is often mathematically intractable. For this reason, we suggest to add a stochastic term to the deterministic system in order to obtain a model which is still simple to integrate like the reaction-rate equations, but it can lead to a numerical solution more similar to the time series. In the resulting model, the time evolution of the system is described by a system of Itô stochastic differential equations, where the stochastic term is characterised by a Wiener process and an arbitrary function empirically chosen. The deterministic term of this system is integrated by employing a one-step numerical method, whereas the stochastic term is approximated through Monte Carlo simulations. The numerical solution is compared to the time series of the experiment performed in [7] on an unstirred ferroin catalysed BZ system.

In summary, we describe the main aspects of Belousov-Zhabotinsky reaction in Sect. 2, Sect. 3 is devoted to the development of the new stochastic model to describe the kinetics of this reaction, while Sect. 4 shows some numerical experiments and Sect. 5 exhibits the conclusions.

2 The Belousov Zhabotinsky Reaction

The Belousov-Zhabotinsky reaction is probably the simplest closed macroscopic system that can be maintained far from equilibrium by an internal source of free energy homogeneously distributed in space [8,9,10,11]. Being outside of thermodynamical equilibrium, BZ can display several exotic dynamical regimes: periodic, aperiodic and chaotic oscillations [12,13,14], Turing structures and pattern formation [15, 16], autocatalysis and bistability [17]. At present, most of the research involving the BZ reaction deals with stimuli-responsive smart materials [18,19,20] and with the simulation of complex biological communication [21,22,23]. In this work, we attempt to reproduce the periodic oscillatory regime generally manifested by the BZ in homogeneous well-stirred reactors.

BZ reaction involves an organic substrate that is oxidised by bromate ions in an acidic medium and is generally catalysed by one-electron metal-ion oxidants with standard reduction potentials of 1–1.5 V, for example metal ions complexes (ferroin, cerium sulphate, etc.) [1, 3] (and references therein). Under proper conditions, the system exhibits self-sustained temporal oscillations in the concentrations of the catalysts, visible through a color change in the solution (more drastic for the iron). The oscillations stem from two concurrent processes: at the beginning the metal ion is reduced and the concentration of bromide ions (\([\mathrm {Br^{-}}]\)) is high (Process I); then bromides are consumed up to a certain critical value and the metal ion is oxidised (Process II); finally, the metal ion reacts to produce bromide ions and reverts to its reduced state again. However, from the kinetics point of view, the oscillations are caused by an Hopf instability deriving from the nonlinear chemical mechanism (autocatalysis + inhibition) and occurring in the reaction. The most widely accepted model to describe BZ reaction has been proposed by Field and Noyes in [24] and it has been derived from the more complicated Field-Körös-Noyes mechanism [25] which is based on 11 reactions involving 15 chemical species that lead to a system of 7 coupled nonlinear first-order ordinary differential equations. In order to theoretically analyse oscillations, bistability and traveling waves, it is sufficient to consider the following reduced formulation of the FKN mechanism [26]:

$$\begin{aligned} \begin{aligned} A + Y&\xrightarrow {k_1} X+P, \\ X + Y&\xrightarrow {k_2} 2P, \\ A + X&\xrightarrow {k_3} 2X+2Z,\\ 2X&\xrightarrow {k_4}A+P, \\ B+Z&\xrightarrow {k_5}\frac{1}{2}f \, Y, \\ \end{aligned} \end{aligned}$$

where the main chemical elements are:

$$\begin{aligned} \begin{array}{llll} X=\mathrm {HBrO_2} &{}\text { (bromous acid), } &{} P=\mathrm {HOBr} &{} \text { (hypobromous acid), } \\ Y=\mathrm {Br^{-}} &{}\text { (bromide ion), } &{} A=\mathrm {BrO_3^-} &{}\text { (bromate ion), } \\ Z=\mathrm {Me^{(n+1)+}} &{} \text { (metal ion in oxidized state), } \quad &{} B &{} \text { (organic substrate)}, \end{array} \end{aligned}$$

and f is a stoichiometric factor which represents the number of bromide ions produced when metal ions are reduced. The concentrations of A, B and P are generally maintained constant, whereas the concentrations of intermediates X, Y and Z vary periodically. The kinetics of the system can be described by the following set of 3 differential equations [3]

$$\begin{aligned}&\frac{d x^*}{ dt^*} = k_1 \, a \, y^* -k_2\,x^*y^*+k_3\,a \, x^*-2k_4 (x^*)^2, \end{aligned}$$
(1a)
$$\begin{aligned}&\frac{d y^*}{ dt^*} = -k_1 \, a \, y^* -k_2 \,x^*y^* + \dfrac{f}{2}\, k_5 \, b \, z^*, \end{aligned}$$
(1b)
$$\begin{aligned}&\frac{d z^*}{ dt^*} =2 k_3 \, a \, x^*-k_5 \, b \, z^*, \end{aligned}$$
(1c)

which is called Oregonator and involves the concentrations of the aforementioned chemical elements. We refer to such concentrations by using letters in lower case henceforth. As highlighted in [27], the Oregonator is not only the simplest model for Belousov-Zhabotinsky reaction but also the most popular to study the period and the amplitude of observed oscillations.

The oscillations in the exact solution of the Oregonator are strongly dependent on the values of the involved parameters, especially \(k_5\) and f. Indeed, if \(k_5 = 0\), the bromide ion (\(\mathrm {Br^{-}}\)) concentration decays to zero according to the Eq. (1b), so the system cannot oscillate. Moreover, oscillations occur only if \(0.5< f < 2.414\), whereas for \(f < 0.5\) and \(f > 2.414\) the system is in a stable steady state, being Process II or Process I dominant, respectively (see [1] and references therein).

In order to integrate the Oregonator (1), we consider its dimensionless form, as follows:

$$\begin{aligned} \epsilon \frac{d x}{ dt}&= q \, y-x \, y + x\, (1-x), \end{aligned}$$
(2a)
$$\begin{aligned} \epsilon '\frac{d y}{ dt}&= -q \, y -x\, y+ f \, z, \end{aligned}$$
(2b)
$$\begin{aligned} \frac{d z}{ dt}&=x-z, \end{aligned}$$
(2c)

where

$$\begin{aligned} \begin{aligned}&x=\frac{2k_4}{k_3 a}x^*, \quad y=\frac{k_2}{k_3 a}y^*, \quad z=\frac{k_4k_5b}{(k_3a)^2}z^*, \quad t=t^*k_5 b, \\&\epsilon =\frac{k_5b}{k_3a}, \quad \epsilon '=\frac{2k_4k_5b}{k_2k_3a}, \quad q=\frac{2k_1k_4}{k_2k_3}, \end{aligned} \end{aligned}$$
(3)

or, in a more compact form,

$$\begin{aligned} \dfrac{d r}{d t} = F (r;\,q,\, f,\, \epsilon ,\, \epsilon '), \end{aligned}$$
(4)

where \(r=[x, y, z]^T\) and \(F (r;\,q,\,f,\, \epsilon ,\, \epsilon ') = \left[ \begin{array}{c} \frac{1}{\epsilon }\,(q \, y-x \, y + x\, (1-x)) \\ \frac{1}{\epsilon '}\,(-q \, y -x\, y+ f \, z)\\ x-z \end{array} \right] \).

3 Stochastic Adaptation of the Oregonator

We aim to develop a simple stochastic variant of the deterministic system (4) in order to better describe the fluctuations usually observed in time series of experimental data. For this purpose, we add a stochastic term to the reaction-rate Eq. (4), as follows

$$\begin{aligned} \dfrac{d R}{d t} = F (R; q, f, \epsilon , \epsilon ') + \lambda \, G(R) \, dW, \end{aligned}$$
(5)

where R(t) is a three-dimensional stochastic process describing the concentrations of the key chemical elements, \(F (R; q, f, \epsilon , \epsilon ')\) is the deterministic forcing term, \(\lambda \) is the amplitude of the stochastic term, G(R) is an arbitrary function and W(t) is a Wiener process. We recall that a standard Wiener process is a stochastic process \(\left\{ W(t), \, t \in [0, T] \right\} \) such that \(W(0)=0\) with probability 1, the function \(\varPhi :t \rightarrow W(t)\) is continuous with probability 1, the increments are independent and behave as the random variable \(\sqrt{t-s} \; \mathcal {N}(0, 1)\), i.e. a normally distributed random variable with zero-mean and variance equal to \(t-s\).

Equation (5) is a system of Itô stochastic differential equations, whose solution R(t) is a stochastic process depending on an initial value

$$\begin{aligned} R(0)=R_0, \end{aligned}$$
(6)

a deterministic integral and an Itô stochastic integral.

In order to integrate (5) in [0, T], we discretize the interval by selecting equidistant \(N+1\) points, as follows

$$\begin{aligned} 0=t_0< t_1< \dots < t_N=T, \end{aligned}$$

and we employ a one-step stochastic numerical method having this general formulation

$$\begin{aligned} R_{n+1}=R_n + h (\alpha \, F(R_{n+1}) + \beta \, F(R_n)) + \, G(R_n) \, \left( W(t_{n+1})-W(t_n))\right) , \end{aligned}$$
(7)

where h is the integration stepsize. For the simulation of the Wiener increments, we employ Monte Carlo simulations, i.e. we generate a standard normally distributed variable through the Matlab routine randn and we approximate the Wiener increments multiplying this variable with \(\sqrt{h}\).

4 Numerical Experiments

We take into account the experiment performed in [7] on an unstirred ferroin catalysed BZ system, where the organic substrate is the malonic acid (\(B=\) MA) and the catalyst is the redox couple ferriin/ferroin (\(\mathrm {Fe(phen)_3^{3+}/Fe(phen)_3^{2+}}\)).

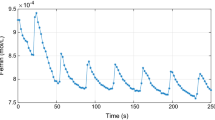
In [7] time series are recorded spectrophotometrically at wavelengths equal to \(510 \, \text {nm}\) (ferroin) and \(630 \, \text {nm}\) (ferriin), where the molar extinction coefficients are equal to \(1.1 \times 10^{4} \, \text {mol}^{-1} \text {dm}^3 \text {cm}^{-1}\) and \(620 \, \text {mol}^{-1} \text {dm}^3 \text {cm}^{-1}\), respectively. Employing these data, we construct the corresponding time series of the concentration of the ferriin, i.e. the catalyst in its oxided state, which is the third component of the solution of the Oregonator (5). The resulting time series shows an initial exponential decay trend corresponding to the start of the reaction (see Fig. 1) and followed by periodic oscillations.

In order to model this chemically reacting system, we consider the system of Itô stochastic differential equations (5) in a region of the plane \(k_5-f\) where the solution is known to oscillate. With regards to the choice of G(R), we select different functions. Firstly, we have considered a linear noise depending on the parameters of the problem

(8)

This choice is convenient because the function evaluations are not highly demanding in terms of computational cost. Another possible G-function has a logarithmic expression:

(9)

Since we observe an oscillatory behaviour in time series (Fig. 1), we next consider a simple trigonometric noise

(10)

but, as will be shown in Table 1, it may be more convenient to adopt a trigonometric G-function depending on the parameters of the problem, as follows:

(11)

We have solved system (5) in [0, 250] combined with these different noises, provided by the initial conditions

$$\begin{aligned} x(0) = 0.0013,\quad y(0) = 0.2834,\quad z(0) = 0.1984, \end{aligned}$$
(12)

and the following values for the parameters

$$\begin{aligned} f = 1, \quad q = 3.52 \cdot 10^{-5}, \quad \epsilon = 0.3779, \quad \epsilon '=7.56 \cdot 10^{-4}. \end{aligned}$$
(13)

We remark that the concentrations in (12) are in their dimensionless form. We employ a one-step method to integrate the deterministic part and Monte Carlo simulations to treat the stochastic term. In particular, we have integrated the deterministic term through explicit Euler method, obtaining the Euler-Maruyama method

$$\begin{aligned} R_{n+1}=R_n + h \, F(R_n) + G(R_n) \, \left( W(t_{n+1})-W(t_n) \right) . \end{aligned}$$
(14)

However, this method is strongly unstable for every choice of the G functions and amplitude \(\lambda \) due to the stiffness of the problem. For this reason, we integrate the deterministic term through the implicit trapezoidal rule, as follows:

$$\begin{aligned} R_{n+1}=R_n + \dfrac{h}{2} \left( F(R_n)+F(R_{n+1}) \right) + G(R_n) \, \left( W(t_{n+1})-W(t_n))\right) . \end{aligned}$$
(15)

We remark that the implicitness of this stochastic method is only in the deterministic part.

Fig. 1.
figure 1

Time series of concentration of ferriin related to the experiment carried out in [7] on an unstirred ferroin catalyzed BZ system.

Full size image
Table 1. Minimum error computed in the last point with 100 simulations as difference between the value assumed in the last point by the numerical solution obtained by the scheme (15) for \(h = 0.06\) and with different functions G and the corresponding value observed in time series.
Full size table
Fig. 2.
figure 2

Numerical solution of stochastic Oregonator (5) having initial conditions (12) and parameters (13) computed by the method (15) which integrates the deterministic term with the implicit trapezoidal rule and treats the stochastic part through Monte Carlo simulations. Different choices for the amplitude \(\lambda \) and the function G are considered and the adopted stepsize is \(h=0.06\).

Full size image

Table 1 reports the relative errors computed by comparing the value assumed by the numerical solution in the last point of the interval and the corresponding value observed in time series. In case of non-zero amplitude of the stochastic term, i.e. when the system (5) does not reduce to the deterministic formulation (4), we have run 100 simulations for each G function and amplitude \(\lambda \) because of the random nature of the Wiener increments and we have computed the minimum error obtained. We observe that the accuracy generally improves when we add the stochastic term to the model and it is higher for the logarithmic noise (9) and the parameter-dependent trigonometric one (11) than for the linear (8) and the first trigonometric case (10). Moreover, increasing the amplitude \(\lambda \) of the stochastic term, the errors related to the stochastic models become higher, but they are still smaller than the error obtained with the deterministic formulation of the problem. Therefore, it may be convenient to add a stochastic term, but its amplitude has to be small enough, so that the noise does not cover the solution.

The solution of the deterministic model (see Fig. 2(a)) has a regular profile having only two oscillations, so it differs more from the time series than the solutions of stochastic models. Indeed, the numerical solution of the stochastic model combined with a trigonometric noise (see Fig. 2(d)) has a regular profile with three oscillations, but it is still far from time series. The choices of a linear noise (Fig. 2(b)) or a logarithmic noise (Fig. 2(c)) lead to solutions which are more oscillatory, so they are qualitatively more similar to time series. However, the solution obtained with a linear noise exhibits some spurious oscillations due to the noise and that one computed with a logarithmic noise has a highly irregular profile. As it regards Fig. 2(e), we can observe that the profile of the solution quantitatively matches very well with the time series and, moreover, the peaks are distributed similarly as in the pattern of the time series, which makes this kind of choice of the diffusion term in the stochastic model very promising. Clearly, the noisy behaviour observable in Fig. 2(e) is given by a single realization of the stochastic process solution that may be replaced, in future investigations, by a more regular and smooth mean behaviour over several realizations. We remark that in the figures the variable concentrations of ferriin (z) and time (t) have been recasted according to the positions (3) by employing the values

$$\begin{aligned} k_2 = 1.11 \cdot 10^{6},\quad k_3 = 15.54, \quad k_4 = 1.11 \cdot 10^{3}, \quad k_5 = 1. \end{aligned}$$

5 Conclusion

In this work, we have presented a new stochastic model to describe the kinetics of Belousov-Zhabotinsky reaction, assumed here as an experimental benchmark for proposing an adapted numerical scheme for differential models of oscillatory phenomena. Indeed, following the idea of adapting numerical schemes to time series presented in [4] (coming from [28,29,30,31,32,33,34] and references therein), we have adapted in this work also the model to describe better the available experimental data. In particular, we have considered the well-known deterministic model developed by Fields, Körös and Noyes and we have added a stochastic term, leading to a system of Itô stochastic differential equations. In this system, the stochastic term is characterized by an arbitrary function selected empirically. The resulting system has been integrated by a combination of known time-stepping methods for the integration of the deterministic part and Monte Carlo simulations for the numerical treatment of the stochastic term. The numerical solution has been compared with the time series related to the experiment carried out in [7] on an unstirred ferroin-catalysed BZ system. Numerical experiments show an high improvement in accuracy and a slight enhancement in the preservation of the qualitative behaviour observed in time series. It is important to highlight that our proposed approach can be assumed as a general setting for handling oscillatory problems in many different contexts: for instance, in the description of chemical oscillators in compartmentalized systems like microemulsions that feature nano-sized reactors [35]. Future developments of this research will be focused on taking these preliminary results as starting point to also fit the data into the model under a qualitative point of view, rather than only quantitative. In this sense, as it is clearly visible in the experiments, the passage from deterministic to stochastic models has been crucial and it seems promising to proceed in this direction.