Controlling Chemical Chaos in the Belousov-Zhabotinsky Oscillator

Abstract

Chaos is ubiquitous in Nature and represents one of the most fascinating expressions of real world complexity. Depending on the specific context, the onset of chaotic behaviours can be undesirable, thus, controlling the mechanisms at the basis of chaotic dynamics represents a cutting-edge challenge in many areas, including cardiology, information processing, hydrodynamics and optics, to name a few. In this work we review our recent results showing how, in chemical reactions, the active interplay between a nonlinear kinetics and hydrodynamic instabilities can be exploited as a general mechanism to induce and control chemical chaos. To this end, we consider as a model system the Belousov-Zhabotinsky (BZ) reaction. Thanks to a chemo-hydrodynamic coupling, the reaction can undergo chaotic oscillations when carried out in batch conditions. Chaos appears and disappears by following Ruelle-Takens-Newhouse scenario both in the cerium- and ferroin-catalyzed BZ systems. Here, we present experimental evidence that the transition to chemical chaos can be directly controlled by tuning either kinetic or hydrodynamic parameters of the system. Experiments were simulated by using a reaction-diffusion-convection (RDC) model where the nonlinear reaction kinetics are coupled to the Navier-Stokes equations. Numerical solutions of the RDC model clearly indicate that natural convection can feedback on the spatio-temporal evolution of the concentration fields and, in turn, changes bulk oscillation patterns. Distinct bifurcations in the oscillation patterns are found when the Grashof numbers (governing the entity of convective flows into the system) and the diffusion coefficients of the chemical species are varied. The consumption of the initial reagents is also found to be a critical phenomenon able to modulate the strength of the RDC coupling and drive order-disorder transitions.

1 Introduction

The term “chaos” identifies deterministic aperiodic behaviours sensitive to initial conditions [1]. This means that the same chaotic system will evolve in two exponentially divergent stories when starting from two infinitesimally different initial conditions. Also popular among non-scientists as butterfly effect, this feature implies the long-term unpredictability of chaotic systems; in fact, though these systems are governed by deterministic rules, their macroscopic initial states cannot be known with infinite precision. In this framework, we can include the failure of the economic and weather forecasts and we can also understand why the onset of chaos is often considered undesirable, such as in the case of transitions from regular rhythm to chaotic electrical activity in the cardiac tissue, which preludes to ventricular fibrillations. In contrast, in several contexts chaos turns to be useful. An example is the realm of artificial intelligence where the complexity of chaotic sequences can be exploited as a source of information to develop fundamental logics [2, 3] or to encrypt messages [4]. Independently of the context, it is always desirable to understand and control chaotic instabilities and their underlying mechanisms.

In this perspective chemical systems have traditionally played a key role. In particular, chemical oscillators, whereby the concentration of some intermediates of the reaction changes periodically in time, have been widely used as relatively simple model systems for studying chaotic dynamics [5]. The Belousov-Zhabotinsky (BZ) reaction [6, 7] is the prototype of chemical oscillators. It consists of a mixture of a bromate salt, an oxidizable substrate (malonic acid in the most common recipe) and a redox catalyst (typically ferroin or cerium complexes) in a strongly acidic medium. The reaction proceeds easily at room temperature and pressure and it can stay far-from-equilibrium for a long time thanks to the slow depletion of the reactants. When stirred, the reaction shows periodic oscillations between the reduced and the oxidized state of the catalyst (and other intermediates); if the same solution is poured into a Petri dish forming a shallow layer, oxidation waves (concentric or spiral waves) periodically form and develop through the medium as a result of the spatial synchronization and spreading of the chemical oscillations driven by diffusion (see an example in Fig. 1b).

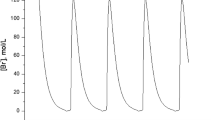
A minimal kinetic scheme that can describe the BZ oscillatory mechanism is the FKN model [5, 8]. According to this scheme there are 3 fundamental processes that cyclically alternate during the reaction. The first two steps involve the depletion of bromide ions () and the autocatalytic production that, in turn, oxidises the catalyst. In the third step (the reset of the clock), the catalyst is brought back to the reduced form via a reaction with the organic species of the system (typically malonic acid) and, simultaneously, new ions are produced. The switching among the three steps is ruled by the concentration of bromides, that alternatively crosses a threshold dictated by the experimental conditions (reactants concentration, temperature, etc.) and initiate either the oxidative or the reducing process. Oscillations are visible following a chromatic periodic change from red to blue when the ferroin is used as the redox catalyst. Nevertheless, in order to follow the dynamics quantitatively, spectrophotometric or potentiometric recordings are the most convenient techniques. Large-amplitude periodic oscillations in the solution absorbance typically appear in the spectrophotometric recordings when the solution is well-stirred. However, it was found that, if stirring is stopped, periodic oscillations dynamically transform into aperiodic and eventually chaotic oscillations (see Fig. 1a) [9, 10]. This phenomenon can be reproduced in a wide range of conditions and represents a sort of fingerprint of the system. Chaotic oscillations occur and vanish by following a Ruelle-Takens-Newhouse (RTN) route, that involves a sequence of Hopf bifurcations going from periodicity to quasi-periodicity and eventually to chaos [11].

Fig. 1.

(a) Examples of spectrophotometric recordings of the Ce(IV)-catalyzed BZ reaction in a batch unstirred reactor. On the left the typical oscillations characterizing a well-stirred solution while on the right the evolution of the unstirred reaction. The red box identifies the characteristic aperiodic transient between the two periodic regions. [MA] = 0.3 M, [] = 0.09 M, [] = 1 M, [Ce(IV)] = 4 mM. (b) Example of concentric chemical waves developing in the ferroin-catalyzed BZ medium. (c) Scheme of the complex interplay between nonlinear kinetics and transport phenomena, sustaining density-driven chemo-hydrodynamic patterns and the transition to chemical chaos. (Color figure online)

The physical basis of the onset of chaos was found to be an active interplay between the nonlinear kinetics and transport phenomena (typically diffusion and convection). In fact, the nonlinear kinetics, when coupled to diffusion, induces the spontaneous formation of chemical waves that, in turn, bear concentration inhomogeneities and density gradients. In the presence of the gravitational field, unfavourable density gradients initiate buoyancy-driven convective flows that couple back with the reaction evolution and the reaction-diffusion patterns. This loop, sketched in Fig. 1c, is also called chemo-hydrodynamic coupling [12] and is known to promote complex behaviours and the formation of new stationary or dynamical patterns [13,14,15].

In this paper, we show how to master the system dynamics, including self-sustained chaos, by tuning the coupling between chemistry and transport phenomena. In fact, chemically-driven convection induced by an oscillatory reaction can be controlled through a simple adjustment of experimental conditions (reactants concentration, temperature, etc.) and physical properties (viscosity, reactor geometry, etc.), that act either on the kinetics or on the hydrodynamics of the system, in order to select and maintain over time a chosen dynamical reaction regime (periodic, aperiodic or chaotic). Experimental results are guided and supported by numerical simulations and interpreted in terms of a general reaction-diffusion-convection model that can be generalised and applied to similar problems.

2 Experimental Approach

2.1 Experimental

In our experiments we used both the cerium- and the ferroin-catalyzed BZ systems. Malonic acid (, MA), sodium bromate (), sulfuric acid (), ferroin (, Fe) and cerium sulfate (, Ce(IV)) were purchased from Sigma Aldrich. All reagents were of analytical quality and were used without further purification. Deionised water from reverse osmosis was used to prepare all the solutions.

The kinetics of the BZ reaction has been studied at 25.0 $^\circ$C. The typical recipe for the cerium-catalyzed system was [Ce(IV)] = 0.004 M, [MA] = 0.30 M, [] = 0.09 M, [] = 1 M while the following concentrations [MA] = 0.74 M, [] = 0.28 M, [] = 0.35 M, [Fe] = 0.93 mM were used for the ferroin-catalyzed sytem.

The reaction dynamics was monitored by recording via a UV-vis spectrophotometer the absorption of (i) Ce(IV) for the cerium-catalyzed system at $\lambda _{max}=320$ nm ($\epsilon \sim$ 5600 M$^{-1}$ cm$^{-1}$) and (ii) the ferriin, the oxidized form of ferroin, at $\lambda _{max}=630$ nm ($\epsilon \sim$ 620 M$^{-1}$ cm$^{-1}$) for the ferroin-catalyzed BZ system. 3.0 mL of the reactive solution were prepared in a beaker, stirred for twenty minutes and finally transferred into a quartz cuvette for spectrophotometric data acquisition. Each kinetic measurement has been repeated at least three times in order to check the reproducibility of the experimental results. The time series obtained in this way were analyzed by means of the Fast Fourier Transform (FFT).

2.2 Hydrodynamic Control

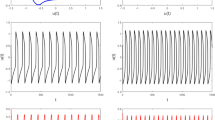
Influence of Stirring. An immediate and straightforward control over the chemo-hydrodynamic coupling responsible for chaos, is to restart stirring during the development of the aperiodic transient [10, 16]. In this way we can suppress the onset of natural convection as we eliminate the concentration gradients at the origin of the buoyancy-driven hydrodynamic instabilities. When stirred, the system behaves as a unique oscillator with regular high-amplitude oscillations. If stirring is stopped again, the system dynamics undergoes a new transition to the aperiodic regimes. This is illustrated in Fig. 2. We expect that a similar behaviour can also be obtained if the reaction is carried-out in parabolic flights (see as an example the experiments run in microgravity with the Iodide-Arseneous-Acid (IAA) reaction [17]), where periodic conditions of microgravity eliminate and decouple intermittently the contribution of buoyancy-driven convection to the system dynamics.

Fig. 2.

Effect of stirring when ferroin catalysed BZ reaction undergoes a transition to chemical chaos. Reproduced from [10] with permission of the copyright owner.

Influence of the Reactor Size. Hydrodynamic instabilities are also known to be sensitive to the size of the spatial domain where they occur and can be avoided working with reactors below a critical size. A spectrophotometric study on the dynamic behaviour of the BZ system in unstirred batch conditions was then carried out by using cuvettes with different path length, specifically in the range 1 to 0.02 cm [18]. It was shown that there is a critical threshold, namely 0.05 cm, below which the transition to aperiodic oscillations cannot be observed any more and just periodic oscillations develop as the possibility for the onset of convection is also hindered by narrowing the reactor (see Fig. 3).

Fig. 3.

Effect of the reactor size in the dynamics of the BZ reaction in batch and unstirred reactors.

Fig. 4.

Relative viscosity, $\eta _{rel}$, of the ferroin-catalyzed BZ solution and related effect in the chemical oscillator dynamics when the reaction is carried out in batch conditions and without stirring. [MA] = 0.74 M, [] = 0.28 M, [] = 0.35 M; the inset shows the zoom of the region 0 < [SDS] $< 1\times 10^{-2}$ M.

Influence of the Medium Viscosity. A further control of the system dynamics can be obtained by changing the medium viscosity. In our check experiments this was obtained for example by adding different amounts of an organic polymer, namely poly-ethylene-glycol (PG), to the reactive solution [16] or by using a surfactant, sodium dodecyl sulphate (SDS) [19, 20], both able to increase the hydrodynamic inertia of the medium to contrast convective motions without affecting the chemical kinetics. In particular, differently to the case of the zwitterionic surfactant N-tetradecyl-N,N-dimethylamine oxide that causes an induction period prior to the onset of regular oscillations [19, 21], SDS only slightly alter the kinetics of the BZ reaction, without changing the oscillation mechanism and without introducing new dynamical features [22], even above the critical micelle concentration (CMC). To maximise the effect of the surfactant on the viscosity of the solutions, we thus varied SDS concentration above CMC.

Both PG and SDS, by suppressing the possibility for the onset of hydrodynamic motions, can in parallel prevent the system from a transition to chemical chaos. The percentage of PG and the concentration of SDS are related to the kinematic viscosity and this can effectively act as a direct control parameter in the bifurcation sequence from chaotic to periodic regimes. Once more, it was found that this route to periodicity obeys a RTN scenario. To give an example of this result, we report in Fig. 4 the transition scenario from chaos to periodicity obtained by increasing the concentration of SDS in the range [1, 250] mM, which causes an increase of viscosity up 10% as compared to the surfactant-free BZ system.

Fig. 5.

A ternary bifurcation diagram describing possible dynamical regimes in a Ce(IV)-catalyzed closed unstirred BZ system as a function of the volume fraction of three initial reactants: malonic acid, potassium bromate and Ce(IV). The green, yellow and red zones identify periodic, quasi-periodic and chaotic domains, respectively. The black boundary zone corresponds to initial compositions where no oscillations occur. Reproduced from [24] with permission of the copyright owner. (Color figure online)

2.3 Chemical Control

In order to show that not only hydrodynamics but also chemistry plays a crucial role in the appearance of chemical chaos, a large number of experiments were carried out by varying different relative initial concentration of the reactants of the BZ oscillator. As shown by Pojman et al. [23], the concentration of the main reactants can be treated as a pseudo-bifurcation parameter in batch conditions. A systematic screening of the ternary parameter-space was performed [24] by varying the relative concentration of the redox catalyst (here CeSO$_4$), NaBrO$_3$ and malonic acid. It was found that by changing the initial composition of the system the oscillatory dynamics and, hence, the transition to chaos, could be controlled to a large extent. This is illustrated in the ternary diagram shown in Fig. 5. When the relative concentration of the reactants is that circumscribed by the red region, chaos can appear after the periodic behaviour following a RTN route. Yellow areas indicate conditions where only quasi-periodicity can develop and, finally, green region are related to situations in which only periodic behaviours were observed.

The ionic strength of the solution is a further tool to control the dynamics of the system through chemistry. In fact, it was demonstrated that by adding an inert electrolyte to the solution (, , etc.) the chemical potential of the reactants could be tuned to prevent or induce the chaotic regime [25].

3 Numerical Approach

The experimental approach discussed so far could be strengthen by means of a theoretical/numerical implementation. In fact, the modelling strategy helped us in the interpretation of the experimental results and now serves as powerful planning instrument to predict new routes for chaos control.

3.1 Model

We modeled the system as a two-dimensional vertical slab (i.e. a vertical cut of the real three-dimensional spectrophotometric cuvette, perpendicular to a virtual spectrophotometric beam) in the coordinate system (x, y), with the gravitational field $\mathbf {g}=(0,-g)$ oriented against the vertical axis y. As shown in previous work, this two-dimensional description is a reliable approximation to the three-dimensional problem [26,27,28,29]. A set of reaction-diffusion-convection (RDC) equations is derived by coupling the chemical kinetics to diffusion through Fick’s terms and to natural convection by means of the Navier-Stokes equations.

The reaction-diffusion-convection (RDC) system is (i) formulated in the Boussinesq approximation, (ii) written in the vorticity-stream function ($\omega -\psi$) form, (iii) conveniently scaled on the chemical time scale $t_0$ (see [5]) and on the characteristic space scale of the problem, $x_0$. Finally, since the BZ reaction is not highly exothermic and thermal gradients are rapidly smoothed, we formulated the problem under the isothermal approximation.

The resulting model is

$$\begin{aligned} \frac{\partial c_i}{\partial t} + D_{\nu }\left( u\frac{\partial c_i}{\partial x} + v\frac{\partial c_i}{\partial y}\right) - D_i \nabla ^2 c_i = k_i(c_i, \bar{\lambda }) \;\,\,\;\,\,\, i=1,2 \end{aligned}$$

(1)

$$\begin{aligned} \frac{\partial \omega }{\partial t} + D_{\nu }\left( u\frac{\partial \omega }{\partial x} +v\frac{\partial \omega }{\partial y}\right) -D_{\nu }\nabla ^2\omega =-D_\nu \sum _i Gr_i\frac{\partial c_i}{\partial x} \end{aligned}$$

(2)

$$\begin{aligned} \frac{\partial ^2 \psi }{\partial x^2}+\frac{\partial ^2 \psi }{\partial y^2}=-\omega \end{aligned}$$

(3)

$$\begin{aligned} u =\frac{\partial \psi }{\partial y} \end{aligned}$$

(4)

$$\begin{aligned} v = -\frac{\partial \psi }{\partial x} \end{aligned}$$

(5)

$D_{\nu } = \nu {t_0}/x_0^2=58.5$ is the dimensionless viscosity ($\nu$ being the medium kinematic viscosity); $D_i = D{t_0}/x_0^2=0.00350$ is the dimensionless diffusivity (D being the dimensional diffusivity of the two oscillating species). $u = U/v_0$ and $v = V/v_0$ are dimensionless horizontal and vertical components of the velocity field scaled over the velocity scale $v_0 = x_0/t_0$.

$Gr_i = gx_0^3\delta \rho _i/\rho _0\nu ^2$ is the Grashof number for the i-th species, g is the gravitational acceleration, $\rho _0$ is the reference density of the medium and $\delta \rho _i = \frac{\partial \rho }{\partial c_i}$ is the density variation due to the change of the concentration of the i-th species with respect to the reference conditions (reduced state) of the reactive mixture. The Grashof number is a measure of the sensitivity of a species to produce convective motions in virtue of isothermal density changes and, in a sense, controls the strength of the RDC coupling within the system. $\omega$ is the vorticity, defined as the rotor of the velocity vector (u, v), while the stream function $\psi$ is defined by Eqs. (4) and (5).

The kinetic functions $k_i(c_i, \bar{\lambda })$ are derived from the Oregonator model [5] and have the form

$$\begin{aligned} k_1(c_i, \bar{\lambda }) = \frac{\text {d}c_1}{\text {d}\tau }= & {} \frac{1}{\epsilon _1}\left( \frac{(q a - c_1)}{(q a + c_1)}fbc_2 + c_1(a-c_1) \right) \end{aligned}$$

(6)

$$\begin{aligned} k_2(c_i, \bar{\lambda }) = \frac{\text {d}c_2}{\text {d}\tau }= & {} a c_1-b c_2 \end{aligned}$$

(7)

where $i =1,2$, $c_1$ is the concentration of bromous acid, $c_2$ is the concentration of the oxidized form of the catalyst and $\bar{\lambda } = \epsilon _1, q, f, a, b$ the set of kinetic parameters. The initial distributions of the chemical species are set as

$$\begin{aligned} c_1(0) = \ 0.8 \ if \ 0< \theta < 0.5 \end{aligned}$$

(8)

$$\begin{aligned} = \ c_{1(ss)} \ \text {elsewhere} \end{aligned}$$

(9)

$$\begin{aligned} c_2(0) = c_{2(ss)} + \frac{\theta }{8 \pi f} \end{aligned}$$

(10)

(where $c_{2(ss)} =c_{1(ss)} = q(f+1)/(f-1)$ and $\theta$ is the polar coordinate angle) to mimic inhomogeneous concentration profiles that typically occur in unstirred systems. These specific functions were used by Jahnke et al. [30] to initiate spiral waves in an analogous reaction-diffusion system. q and $\epsilon$ are kinetic parameters accounting for the excitability of the system and f is a stoichiometric factor included in the resetting step of the oscillatory scheme. This parameter allows one to set the system in an oscillatory regime when it ranges [0.5, 1+$\sqrt{2}$] and we use $f=1.6$; q is fixed to 0.01; $\epsilon =0.01$; a and b are the concentration of the bromate salt and the malonic acid, respectively. In our study we set $b=1$ while a was used a chemical control parameter.

The PDE system (1–5) was numerically solved over a $100 \times 100$ points grid (mesh-point separation $h_x = 0.50$), using the alternating direction finite difference method [31]. We imposed no-slip boundary conditions for the fluid velocity and no-flux boundary conditions for chemical concentrations at the walls of the slab. A small time step $h_t$ has to be used due to the stiff nature of the kinetic equations. $h_t = 1\times 10^{-6}$ was tested to be a good value.

In the experiments the output of the spectrophotometric recordings is the average of the absorbance of the reactive solution over the spatial domain scanned by the spectrophotometric beam as a function of the time. In order to have an observable comparable to the experimental data, we build up time series by reporting at each integration time step the mean concentration of the oscillatory intermediates averaged over the solving grid ($\langle c_1 \rangle$ and $\langle c_2 \rangle$). The resulting signals are then analyzed by means of the FFT and attractor’s reconstruction.

3.2 Hydrodynamic Control

We focus now on the direct transition from periodic to chaotic regimes under hydrodynamic control, namely by changing the Grashof numbers of the chemical species [26]. This gives a picture of the direct transition to chaos in the unstirred BZ reaction (shown in Fig. 1) if one assumes that, after stirring is stopped, residual advective motions relax, concentration patterns (typically waves) with related density gradients can build-up and initiate convective motions with progressively growing intensity. In this regime the chemical oscillator is in the far-from-equilibrium branch, where the depletion of the initial reactants is negligibly slow and the system can maintain quasi-stationary conditions like if it was open.

Periodic regime. In Fig. 6a we show a limit cycle, with a fundamental frequency $\omega _1 = 0.747$ Oregonator frequency units, obtained in the absence of convection (i.e. with $Gr_i = 0.00$). Periodicity is still found when the chemo-hydrodynamic coupling is strengthened, by increasing both Grashof numbers to 9.40. The related attractor projection ($\langle c_1 \rangle$, $\langle c_2 \rangle$) and the time series are shown in Fig. 6(b), left and centre panels, respectively. To show the attractor change, we keep fixed the region framing the phase portrait. The oscillatory dynamics of $\langle c_1 \rangle$ and $\langle c_2 \rangle$ present one fundamental frequency $\omega _1 = 0.396$, different from that observed in panel (a). This confirms that convection is actively coupled with the reaction-diffusion system. Note that, due hydrodynamic inertia, the new solution presents a longer period with respect to the case where convection is at rest.

Fig. 6.

(a) Characterization of the periodic dynamics of the RDC system for $Gr_1=Gr_2=0.00$: (left) trajectories described by the system in the phase space projection ($\langle c_1 \rangle$, $\langle c_2 \rangle$) ($\langle c_1 \rangle \in [0.02,0.20]$ and $\langle c_2 \rangle \in [0.06,0.12]$); (centre) time series describing $\langle c_2 \rangle$ dynamics in the time-frame [100, 200] Oregonator time units; (right) FFT amplitude spectrum. (b) The same analysis is performed for $Gr_1=Gr_2=9.40$.

Quasi-periodic regime. As the Grashof numbers are increased to 9.80 a quasiperiodic behavior is found (see Fig. 7). This can be inferred by the attractor reconstruction (left), the time series (centre) and quantitatively revealed by the related Fourier amplitude spectrum (right). In the latter, two characteristic fundamental frequencies ($\omega _1$, $\omega _2$) and their linear combinations are shown. These frequencies, which ratio $\omega _1/\omega _2$ is an irrational number, characterize the toroidal flow of the system represented in the phase-space projection ($\langle c_1 \rangle$, $\langle c_2 \rangle$).

Fig. 7.

Quasi-periodic regime for $Gr_1=Gr_2=9.80$: phase space trajectories in the phase space projection ($\langle c_1 \rangle$, $\langle c_2 \rangle$) with $\langle c_1 \rangle \in [0.02,0.20]$ and $\langle c_2 \rangle \in [0.06,0.12]$ (left), time series describing $\langle c_2 \rangle$ dynamics in the time-frame [100:200] Oregonator time units (centre) and related Fourier amplitude spectrum (right) (a = $\omega _2$ − $\omega _1$, b = 3$\omega _2$ − 3$\omega _1$, c = 6$\omega _2$ − 7$\omega _1$, d = $\omega _1$ + 1/2$\omega _1$, e = 4$\omega _2$ − 4$\omega _1$, f = 7$\omega _2$ − 8$\omega _1$, g = $\omega _1$ + $\omega _2$).

Chaotic regime. If the Grashof numbers are further increased, namely to 12.10, an aperiodic behavior (see Fig. 8a) associated with the strange attractor in Fig. 8c, is observed. As shown in Fig. 8a, the time series manifest sensitivity to initial conditions consistent with one of the signatures for chaotic dynamics. To test for chaos, we have also calculated the largest Lyapunov exponents, $\lambda$, using the Rosenstein algorithm from TISEAN package [32]. The value $\lambda = 0.018$ was extracted from linear regression of the curves S($\epsilon$,m,t) for m = 5–9 shown Fig. 8d.

Fig. 8.

Chaotic dynamics for $Gr_1=Gr_2=12.10$: (a) time series describing $\langle c_2 \rangle$ evolutions for two different initial conditions in the time-frame [100:200] Oregonator time units; (b) FFT amplitude spectrum of the signal in panel (a); (c) strange attractor of this chaotic regime obtained in the phase-space ($\langle c_1 \rangle$, $\langle c_2 \rangle$, vorticity); (d) Computation of the maximum Lyapunov exponent by means of the Rosestein algorithm. The value of $\lambda = 0.018$ is obtained by the linear regression of the curves S($\epsilon$,m,t) for m = 5–9, in the zone between 0–40 iterations.

3.3 Chemical Control

As mentioned in Sect. 2.3, we can use the initial concentration of reactants as a bifurcation pseudo-parameter [23, 24] to modify and control chemically the system dynamics. An inverse transition chaos-periodicity consistent with a RTN scenario was indeed induced keeping constant the Grashof numbers and decreasing the sodium bromate concentration, i.e. parameter a [33]. The chaotic regime, occurring for $a= 1$, has been extensively characterized in Sect. 3.2 and [26]. A bifurcation to quasi-periodicity takes place for $a = 0.97$ and it is characterized in Fig. 9(a, b). Quasi-periodicity is confirmed by the Fourier amplitude spectrum, showing two incommensurable fundamental frequencies ($\omega _1 = 0.39$, $\omega _2 = 0.54$) and their harmonic combinations. Note that these frequencies match the values $\omega _1 = 0.39$, $\omega _2 = 0.54$ of the quasi-periodic regime obtained in the direct transition under hydrodynamic control.

When a is decreased to 0.95 a supercritical Hopf bifurcation leading to a bi-periodic solution can be detected. In the corresponding FFT’s amplitude spectrum (Fig. 9c), the main frequency $\omega _1$ can be still identified and subharmonic frequencies of the type $n \; \times \frac{\omega _1}{2}$ (where n is an integer) clearly emerge. According to the FFT’s spectrum, the corresponding attractor exhibits a double-period, visible in the inset of Fig. 9d.

Figure 9f shows a limit cycle characterized by the main frequency $\omega _1$ (see the related FFT spectrum in Fig. 9e) obtained when a reaches the value 0.93. The FFT’s analysis reveals a supercritical Pichfork bifurcation, leading to a unique oscillation period.

As a whole, this transition scenario under chemical control can describe the inverse route from chaos to periodicity observed in Fig. 1a.

Fig. 9.

Attractor reconstruction in the phase-space section ($\langle c_1 \rangle$, $\langle c_2 \rangle$, with $\langle c_1 \rangle \in [0.02,0.20]$, $\langle c_2 \rangle \in [0.06,0.12]$) and FFT amplitude spectra of the simulated dynamical regimes in the transition from chaotic to periodic oscillations controlled by the concentration of the initial reactant a. (a–b), $a = 0.97$ a quasi-periodic regime; (c–d), $a = 0.95$ a bi-periodic regime; (e–f), $a =0.93$ a periodic regime.

4 Concluding Discussion

To summarize, we discussed the active interplay of nonlinear kinetics with related chemically-driven transport phenomena as a general mechanism for devising a self-sustained chaotic generator. The route to chaos in this context can be controlled by tuning the strength of the chemo-hydrodynamic coupling either via chemical or hydrodynamic parameters. We have supported this idea by means of experimental examples and also formalized it with a reaction-diffusion-convection model which allows the numerical description and prediction of the chaotic dynamics.

This theoretical framework guided us in the interpretation of the transition from periodicity to chaos and viceversa observed in experiments. In particular, it was found that the reaction evolves through two main phases, characterized by a longer time scale with respect to chemical oscillations. In a first phase, the concentration of the reactants is in large excess with respect to the intermediates and the reactant depletion can be neglected. In this phase, the system is mainly under hydrodynamic control and convection drives the system to chaos. In a second phase, the system evolves to the ultimate thermodynamic equilibrium. The main reactants consumption cannot be neglected any more and the reactants concentration acts as a bifurcation parameter towards regular periodic oscillations.

Conceptually, the results obtained with this experimental system and the related theoretical model have a general value and can also be extended to spatiotemporal phenomena [34]. The modularity of the RDC model permits to fit our findings to isomorphic problems; by changing the kinetics terms, for example, we can study other nonlinear chemical systems or face more complex mechanisms such those that lead and control low-dimensional spatio-temporal turbulence in cardiac arrhythmias.

Also, chaotic dynamics are themselves rich sources of information [4]. In the realm of artificial intelligence chemo-hydrodynamic systems could be thus exploited as generators of chaotic signals for implementing fundamental logics and as a controllable contaminator in protocols for encrypting messages. Similar studies have already been initiated by using externally-forced chemo-hydrodynamic oscillations, which feature suitable output to develop fundamental operations based on fuzzy logic [2, 3].