Formation of Sand Bedforms Under Surface Waves

Abstract

Surface waves often generate bedforms at the seabed. Small structures such as ripples with a typical wavelength between ten centimeters and one meter are very common structures in the coastal zone. The formation of these structures under nonlinear surface waves is considered in this chapter. Under regular waves, two modes of pattern formation from a flatbed in a wave flume are reported for well-sorted grains and mixtures of grains. Sand ripples can form uniformly or from isolated ripples spreading on the bed while growing. In this latter case, front propagation speed is measured and a simple model based on the quintic complex Ginzburg-Landau equation can explain features of front propagation on the granular bed. The profile of surface waves propagating in shoaling water approaches the solitary waveform before wave breaking. The main characteristics of solitary waves are presented. The effect of the high nonlinearity of these waves may be very significant on bedforms induced in the nearshore zone. The interaction between solitary waves and a sandy bed is reported. Sandy ripples induce a strong energy dissipation of solitary waves. When solitary waves propagate on the background of a standing harmonic wave, bars are formed with crests located beneath the nodes of the harmonic surface wave. In the case of harmonic standing waves alone, the bar crests are positioned beneath the antinodes of the harmonic surface wave. Grains with different densities may be found on the seabed. The concentration of light sedimenting particles on ripple crests is explained by a simple theoretical model.

1 Introduction

Bedforms are often generated on the seabed. These sedimentary structures result from a complex interaction between the flow and the sediments. The knowledge of the size of these structures is necessary for the estimate of their equivalent roughness, of the bed shear stress, and of the sediment transport. Numerous studies have been carried out on sand bedforms induced by surface waves. However, due to the complexity of the involved processes, many questions remain unsolved, in particular, in the case of nonlinear surface waves. Nonlinearity may generally not be neglected for surface waves. The formation of sand bedforms under weakly nonlinear waves is first considered in this chapter. In other respects, long waves such as tsunamis often behave like solitary, highly nonlinear waves. After a brief introduction on these waves, the interaction between solitary waves and a sandy bed will be considered.

2 Ripple Pattern Formation Under Regular Surface Waves

In a wave flume, ripple pattern formation from an initial plane bottom depends on the forcing conditions applied to grains. Two distinct modes are identified and characterized by two nondimensional parameters: the Reynolds number Re = U _∞ a/$\nu$ and the Froude number $Fr = U_{\infty } /\sqrt {(s - 1)gd_{50} } ,$ where a and U _∞ are the fluid particle semi-excursion and the fluid velocity amplitude at the edge of the bed boundary layer, respectively, s is the relative density of sediment, g the gravity, and v the water kinematic viscosity. Either ripples form on the whole bed or several isolated rippled zones named patches first appear. In the latter case, ripples grow from a defect of small amplitude on the initial flat bottom. This mode of formation is exhibited in Fig. 1 for well-sorted sands and also for mixing of sands [1].

Fig. 1

Example of bed image in grayscale for mixing of sands forming by patch for n = 2000 cycles (d _m  = 350 $\upmu$m; Re = 4715; Fr = 1.7)

The two modes of pattern formation are represented in the (Fr, Re) plane (Fig. 2) for tests performed with sands (111 $\upmu$m < d ₅₀  < 375 $\upmu$m) [2] and PVC particles (d ₅₀  = 170 $\upmu$m) [12]. The dotted line on Fig. 2 delineates the domain of the two modes of pattern formation. For a fixed Re number, if Froude number remains lower than a critical Froude number Fr_c, ripples form from localized sites and the perturbation necessary to initiate ripple growth must be of finite amplitude, whereas if Fr > Fr_c, a perturbation of infinitesimal amplitude is enough to trigger ripple formation and ripples can form spontaneously on the whole bottom. A rough estimate of the number of cycles for observation of isolated systems of ripples before invasion on the whole bottom n _c is represented on Fig. 3. The dimensionless bed shear stress (Shields parameter) is defined with Jonsson formulae [3] for the skin friction factor f _w by: $\uptheta$ $\uptheta$ = 0.5 f _w Fr², and $\uptheta$ _c is the critical Shields number. When the deviation to the threshold for ripple formation ($\uptheta$ − $\uptheta$ _c ) increases, the amplitude of the perturbation necessary to destabilize the bottom decreases, the number of observed initial sites of ripples nucleation increases and the time of observation of these ripple patches decreases.

Fig. 2

Delineation of the two modes of pattern formation in the (Re, Fr) plane

Fig. 3

Number of cycles for observation of isolated systems of ripples before invasion on the whole bottom n _c as a function of the deviation to the threshold of ripple formation

2.1 Dynamics of Propagation Fronts

Experimental determination

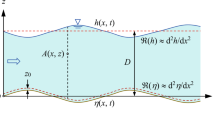
Ripples form by a mechanism of amplification of initial perturbations of small amplitude. When ripples form from isolated nucleation sites, the front propagation on the granular bed plays an important role in the pattern formation processes. The work performed with A. B. Ezersky [2] was focused on a test with a well-sorted sand with a slow dynamics (Test B, Re = 5512; Fr = 2.2), where isolated systems of ripples can be observed for more than 1000 excitation cycles before total invasion on the whole bed. For each patch, the two fronts are processed separately. Fourier spectrum of the bed elevation signal $\eta$(x, t) is calculated for a selected y-transverse line along the x-longitudinal direction in the front zone and harmonics are filtered to conserve only $\eta_{m} (x,t),$ the slow-varying amplitude, and $\phi (x,t),$ the slow-varying phase. After the filtering process, we get: $\eta (x,t) = \eta_{m} (x,t)\,\cos \,(kx + \phi (x,t)).$ In the next step of the processing, Hilbert transform is processed and the module of the complex amplitude $a(x)$ and unwrapped phase $\phi (x)$ of the envelope wave of the front are extracted. The wavefront is localized in the region, where a transition from a low amplitude to a high nearly constant value is detected. The chosen detection threshold is fixed to 15% of the maximum amplitude of the selected patch. An example of detected mean ripple fronts is presented in Fig. 4. The upflow $v_{p - }$ and down flow front $v_{p + }$ velocities designate, respectively, a front propagation in the direction opposite to the surface wave propagation and in the same direction of surface waves. Fronts propagate linearly with time with a good regression coefficient and a greater velocity for the fronts propagating in the direction of surface waves. The difference between the two mean front velocities has been attributed to the drift along the direction wave propagation induced by surface waves in the bed boundary layer [4].

Fig. 4

Longitudinal position of detected ripple fronts for Test B (Re = 5512, Fr = 2.2) as a function of number of excitation cycles. Estimated front propagation velocities

$$ \begin{array}{*{20}l} {\left( {{\text{P}}_{1} } \right):v_{p - } = - 0.23{\text{ mm s}}^{ - 1} ;} \hfill & {v_{p + } = + 0.62{\text{ mm s}}^{ - 1} ;} \hfill \\ {\left( {{\text{P}}_{2} } \right):v_{p - } = - 0.19{\text{ mm s}}^{ - 1} ;} \hfill & {v_{p + } = + 0.53{\text{ mm s}}^{ - 1} ;} \hfill \\ {\left( {{\text{P}}_{3} } \right):v_{p - } = - 0.16{\text{ mm s}}^{ - 1} ;} \hfill & {v_{p + } = + 0.45{\text{ mm s}}^{ - 1} } \hfill \\ \end{array} $$

Model for propagation of ripple fronts

The quintic complex Ginzburg-Landau equation was used to model the propagation of sandy ripples fronts:

$$ \frac{\partial A}{\partial t} = \left( {1 + ic_{1} } \right)\frac{{\partial^{2} A}}{{\partial x^{2} }} + \varepsilon A + \left( {1 + ic_{3} } \right)\left| A \right|^{2} A - \left( {1 - ic_{5} } \right)\left| A \right|^{4} A $$

(1)

where A is the complex amplitude of sand ripples, ε is criticality and $c_{1} ,c_{2} ,c_{3}$ are real coefficients. Equation (1) is a model equation for subcritical bifurcation as observed for sand ripple dynamics. Indeed, experiments showed us that there is a threshold value of the amplitude: an amplification of the perturbations occurs for amplitudes more than a threshold value and a decay with time is observed for amplitudes less than threshold value. The analytical solution of Eq. (1) [5] can be expressed in the form: $A = e^{ - i\omega t} a(\xi )e^{i\varphi (\xi )} ,\xi = x \mp Vt$, where V is the front velocity and $\omega$ the frequency of sand ripples. The analytical solution for the amplitude and phase of propagating fronts (see [1] for more details) can be written as follows:

$$ a = a_{N} \frac{{e^{{K_{L \mp \xi } }} }}{{\sqrt {1 + e^{{2K_{L \mp \xi } }} } }} $$

(2)

and

$$ \phi = q_{N} \xi - \frac{{\left( {q_{N} - q_{L} } \right)}}{{K_{L \mp \xi } }}lna $$

(3)

The ξ sign “+” corresponds to a front, which propagates in the positive direction, $K_{L + } < 0,a(x = - \infty ,t = 0) = a_{N}$ is the limit of the exponential growth, $a(x = + \infty ,t = 0) = 0,$ and the sign “−” corresponds to a front propagating in the opposite direction: $K_{L - } > 0,a(x = - \infty ,t = 0) = 0,$ $a(x = + \infty ,t = 0) = a_{N}$. In the phase expression (Eq. 3), $q_{L} ,q_{N}$ may be considered as the contributions to the wave number for waves of bottom profile with infinitesimal and finite amplitudes.

Excluding the linear growing phase in space for a given instant, Eq. 3 can be simplified in the form $\phi (x) = \frac{{q_{L} - q_{N} }}{{K_{L \pm } }}\,\ln \,a,$ predicting a theoretical local linear dependence between the wave phase and logarithm of the wave amplitude $a(x).$

Experimental data were used to check if this correlation occurs for wavefronts in sand ripples. The linear dependence between lna and ${\varphi }$ was found and the coefficients $\frac{{q_{L} - q_{N} }}{{K_{L \pm } }}$ were estimated at different instants for one patch and for fronts propagating in both directions. This result validates the model prediction.

2.2 Ripple Growth in Pattern

Complex demodulation by Hilbert transformation was used to extract geometric characteristics of each ripple and to build distributions of ripple characteristics of patterns while they form. Three examples of growth of dominant ripple wavelength in the pattern are presented in Fig. 5. For the test performed with light PVC particles (Test A, Re = 214; Fr = 1.4; d = 1.35; D ₅₀  = 0.17 mm), ripples form on the whole bottom from an initial network of short fragments of three-dimensional ripples and they grow by coalescence processes. Ripples initially formed are rolling-grain ripples. During this stage, the pattern is characterized by a constant dominant ripple length and a low steepness (h/L < 0.1) in agreement with Sleath empirical criterion [6]. For Test B conducted with a well-sorted sand characterized by a pattern formation from nucleation sites, rolling-grain ripples are not detected. Vortex ripples grow with an exponential relaxation law. The equilibrium length is reached before the whole bottom is covered by ripples. Thus, the selection of the dominant equilibrium wavelength is not significantly influenced by the initial mode of pattern growth. A similar exponential relaxation law is found in the case of a mixing of sands (Test C, Fr = 2.2, Re = 4640, median diameter d _m  = (d ₁₆ .d ₅₀ .d ₈₄ )^1/3 = 350 $\upmu$m). Grain heterogeneity does not influence significantly the growth law for pattern dominant length.

Fig. 5

Dominant ripple wavelength versus the number of excitation cycles for Test A: solid diamonds, Re = 214, Fr = 1.4, PVC particles; Test B: open diamonds, Re = 5512, Fr = 2.2, well-sorted sand and Test C: solid triangles, Re = 4640, Fr = 2.2, sand mixture

3 Sand Bedforms Induced by Strongly Nonlinear Surface Waves

3.1 Solitary Waves

Solitary waves have been the object of attention from Prof. Alexander Ezersky. The solitary water wave, localized wave that propagates along one space direction only with undeformed shape has been experimentally discovered in 1834 by John Scott Russell. A model equation representing the dynamics of solitary waves was obtained by Korteweg and de Vries [7]. This well-known KdV equation, which has been obtained for shallow water under the assumption of wave propagation in one direction, may be written as follows:

$$ \frac{\partial \eta }{\partial t} + V_{0} \frac{\partial \eta }{\partial x} + \frac{3}{2}\frac{{V_{0} }}{H}\eta \frac{\partial \eta }{\partial x} + \frac{1}{6}V_{0} H^{2} \frac{{\partial^{3} }}{{\partial x^{3} }} = 0 $$

(4)

where η is the displacement of free surface, t the time, $V_{0} = \sqrt {gH}$ the velocity of surface waves of infinitely small amplitude in shallow water, H the water depth, and x the wave propagation direction. The localized solution resulting from the balance of nonlinearity and dispersion has the form of a single hump as observed by Russell:

$$ \eta_{s} \left( {x - V_{s} t} \right) = A_{s} { \cos }h^{ - 2} \left( {\sqrt {\frac{{3A_{s} }}{{4H^{3} }}} \left( {x - V_{s} t} \right)} \right) $$

(5)

$$ V_{s} = V_{0} \left( {1 + \frac{{A_{s} }}{2H}} \right) $$

(6)

where V _s is the velocity of the solitary wave which depends linearly on its amplitude, $A_{s} .$ The duration of this wave is proportional to $A_{s}^{ - 1/2} .$

As an oscillatory wave moves into shoaling water, the wave amplitude becomes higher, the trough becomes flatter, and the surface profile approaches the solitary waveform before wave breaking [8]. The cnoidal wave theory approaches the solitary wave theory as the wavelength becomes very long. In other respects, long waves such as tsunamis and waves resulting from large displacements of water caused by landslides and earthquakes often behave like solitary waves. Ezersky et al. [9] studied the generation of solitary waves (solitons) in a 10 m long hydrodynamic resonator used in shallow water. Surfaces waves were produced by an oscillating paddle at one end of the flume, and a near-perfect reflection took place at the other end. The frequency of the wavemaker was chosen close to the resonant frequency of the mode whose wavelength is equal to the flume length. For small values of the amplitude of displacement of the wavemaker, only standing harmonic waves are generated in the channel. For values of this amplitude greater than a critical value, pulses propagating from one end of the flume to the other end are excited on the background of the standing wave. The characteristics of such pulses are close to those of the theoretical soliton. In particular, the soliton width decreases with increasing values of its amplitude, as illustrated in Fig. 6. Moreover, these pulses resulting from the excitation of high harmonics are not altered by collision with other pulses. They are called solitons by Ezersky et al. [9]. The KdV equation does not describe the interaction of contra-propagative waves. The Boussinesq equations can be used to depict counter-propagating solitary waves.

Fig. 6

Schematic comparison between the size of two theoretical solitons (solutions of the KdV equation)

3.2 Formation of Sand Bedforms Under Solitary Waves

The effect of the high nonlinearity of solitary waves may be very significant on bedforms induced in the nearshore zone. Let us consider the formation of sand bedforms under solitary waves.

Numerous studies have been carried out on bedforms under linear or weakly nonlinear waves [6, 10,11,12,13]. In the nearshore zone, bars consisting of ridges of sediments running roughly parallel to the shore are common features on sandy beaches. These structures provide a possible mechanism of natural beach protection from the energy of incident waves. The mode of sediment transport has a key role on the bar position under partially standing waves, the bars having spacing equal to half the surface wavelength. This spacing corresponds to the Bragg condition for which strong reflection of the incident waves may occur. The bar position is a very significant parameter as far as the ability of bars to reflect wave incident energy is concerned. The effect of solitary waves on the bar position, and more generally on bedforms generation has been carefully studied by Prof. A. E. Ezersky. Experimental and theoretical work has been carried out at this aim. As far as the experimental work is concerned, Ezersky chose to use the original method of solitary waves generation in a hydrodynamic resonator described in the previous section and considered the interaction between solitary waves and a loose sandy bed. When high nonlinear waves are excited in the resonator, small ripples form rapidly everywhere in the flume, except in the central part, where the bed remains flat as illustrated in Fig. 7. This region corresponds to the zone of collision of counter-propagating solitons, which have horizontal velocities of opposite sign, leading to a horizontal velocity close to zero in the collision zone [14]. The value of bed shear stress is then close to zero, anyway below the critical value $\theta_{c}$ for incipient motion given by Soulsby and Whitehouse [15]:

Fig. 7

Sketch of ripples formation under solitary waves propagating on the background of a standing harmonic wave

$$ \theta_{c} = \frac{0.24}{{D_{*} }} + 0.055\left[ {1 - { \exp }\left( { - 0.020D_{*} } \right)} \right] $$

(7)

where $D_{*} = \left[ {g\left( {s - 1} \right)/v^{2} } \right]^{1/3} D,s$ is the sediment relative density, D, the sediment median diameter, and ν the kinematic viscosity. A strong interaction between the sandy bed and the free surface occurs, as shown in Fig. 8, where the temporal evolution of the free surface $\eta$ at the reflective end of the flume is depicted with a sketch of the sand distribution in the flume. The level 0 mm corresponds to the water level at rest. The peaks in the free surface elevation correspond to the passage of solitary waves. Neglecting the interaction of contra-propagative waves, the free surface displacement at the fixed end of the flume can be described by

Fig. 8

Interaction between the free surface and the sandy bed. Frequency of the oscillating paddle: f = 0.173 Hz. Amplitude of the horizontal displacement of the oscillating paddle averaged over depth: a = 6 cm. H = 0.26 m; s = 2.65; D = 0.15 mm. a and b Beginning of the test, just after the solitary waves formation. c and d After ripple formation

$$ \eta \left( t \right) = 2\eta_{s} \left( t \right) + 2A_{0} { \sin }\left( {\omega t - \varphi_{s} } \right) $$

(8)

where ω is the angular pulsation of the flow, $A_{0}$ the harmonic wave amplitude, and $\varphi_{s}$ the phase shift between the soliton and the harmonic waves. The sandy bed is initially flat (Fig. 8b).

Figure 8c, d shows that after about 27 min, that is when the dimensionless time $\tau = t\omega \, \cong \,1760$, the bed is rippled and the peak values of the free surface are significantly lower than at the beginning of the test. This results from the dissipation at the now rippled bed.

The variation of the soliton amplitude $A_{s}$ with the time t is depicted in Fig. 9 for the same test as in Fig. 8. The decrease of $A_{s}$ is particularly marked during the beginning of ripple formation. The temporal variations of the ripple height h and wavelength L, averaged over the flume length, are exhibited in Figs. 10 and 11, respectively. The ripple dimensions forming on the bed increase for increasing values of time, when the soliton amplitude decreases, as shown in Fig. 8. Let us consider the soliton energy $E_{s}$:

Fig. 9

Variation of the amplitude of the solitary wave with time. Same test conditions as for Fig. 8

Fig. 10

Variation of the mean ripple height with time. Same test conditions as for Fig. 8

Fig. 11

Variation of the mean ripple wavelength with time. Same test conditions as for Fig. 8

$$ E_{s} = \int\limits_{ - \infty }^{ + \infty } {\eta_{s}^{2} dx \sim A_{s}^{3/2} } $$

(9)

Taking into account the energy dissipation due to ripples, the temporal variation of the soliton energy may be written as follows:

$$ \frac{{dE_{s} }}{dt} = \frac{3}{2}\frac{{\omega A_{0} }}{H}E_{s} \,{ \cos }\,\varphi_{s} - \left( {\beta + \alpha h} \right)E_{s} $$

(10)

In this equation, β is a coefficient describing the part of the damping of the soliton, which is independent of the scale of the perturbations, and α a phenomenological coefficient for the dissipation of the soliton due to sand ripples. This part of dissipation is supposed to be proportional to the ripple height, as a linear function is the simplest parameterization.

Once the ripples are formed, two sand accumulation zones progressively appear (Fig. 12). At the equilibrium state, that is for $t\, \cong \,60$ h, they form bars with crests located beneath the nodes of the harmonic surface wave. In the case of harmonic standing waves (without solitons), the bar crests are positioned beneath the antinodes of the surface elevation when the suspended load transport is dominant [16]. In the present case, where solitons are excited on the background of a standing harmonic wave, ripples generate vortices, which lift into suspension a lot of sand, leading to a significant amount of suspended load transport. Present bar positions may be explained by the variation of the time window between the passage of the contra-propagating solitons with the distance along the flume [17].

Fig. 12

Sand accumulation zones with superimposed ripples. Same test conditions as for Fig. 8. Equilibrium state; z: altitude from the flume bottom

Grains with different physical characteristics (size, shape, and density) are often found on the seabed. This led Ezersky to study the segregation of sedimenting grains of different densities on a rippled bed under a velocity field induced by solitary waves. These waves were excited in a hydrodynamic resonator as described above in the section “solitary waves”. The hydrodynamic forcing was stopped, the water waves damped, and sedimentation of suspended particles occurred. The grain mixture consisted of particles of different densities: sand grains (s = 2.65) and PVC grains (s = 1.35). It was found that light particles (PVC grains) accumulate on the ripple crests. This can be explained as follows. Taking into account the Stokes force and neglecting the turbulent drag, the grain velocity $\vec{V}$ may be obtained from the flow velocity $\vec{U}$ [18]:

$$ \vec{V} = \vec{U} + \frac{{S_{t} }}{\omega }\frac{{\rho_{w} }}{{\rho_{gr} }}\frac{{d\vec{U}}}{dt} + \left( {\frac{{\rho_{gr} - \rho_{w} }}{{\rho_{w} }}} \right)\vec{g} - \frac{{S_{t} }}{\omega }\frac{{d\vec{V}}}{dt} $$

(11)

where $S_{t} = D^{2} \rho_{gr} \omega /18v\rho_{w}$ is the Stokes number, $\rho_{w}$ the fluid density, and $\rho_{gr}$ the grain density. For small values of the Stokes number, it is possible to use $S_{t}$ as an expansion parameter for the grain velocity:

$$ \vec{V} = \vec{V}^{\left( 0 \right)} + S_{t} \vec{V}^{\left( 1 \right)} + S_{t}^{2} \vec{V}^{\left( 2 \right)} + \cdots $$

(12)

Let us consider in the first approximation a very simple model defined in the vicinity of each sand crest by the stream function $\psi = - a\left( {\alpha x + z} \right)z,$ with α a nondimensional coefficient and a a coefficient corresponding to an angular frequency. While the flow direction changes periodically, a stationary hyperbolic point takes place. After some transformation, the time-averaged velocity of particles may be expressed in the horizontal direction in the following way:

$$ \left\langle {V_{x} } \right\rangle = - x\left( {\frac{{s^{{\prime }} }}{2}a_{0} \alpha_{0} e^{ - \gamma t} + \frac{{S_{t} }}{4\omega }a_{0}^{2} \alpha_{0}^{2} e^{ - 2\gamma t} } \right) $$

(13)

where $s^{{\prime }} = 1 - \rho_{w} /\rho_{gr} ,$ γ is the rate of exponential decay of surface waves, $a_{0}$ and $\alpha_{0}$ the amplitudes of a and α, respectively. The expression of $\left\langle {V_{x} } \right\rangle$ is such as whatever the side of the ripple crest, where the particles are, the grains move toward the ripple top. The sand grains which are heavier than the PVC grains settle faster than the PVC grains. When most sand grains have settled on the bottom, only PVC grain concentrate near the ripple crests.

4 Conclusions

Seabed is rarely flat. Sand bedforms are very common. Many studies have been carried out on these sedimentary structures, in particular under the assumption of linear waves. However, the nonlinearity of surface waves cannot be neglected in most of practical cases, and the physical processes involved in the bedforms generation, in this case, are poorly understood. Prof. A.B. Ezersky carried out pioneering work in this field, and he has significantly contributed to the emergence of new approaches. The interaction between a sandy bed and extreme waves propagating in the shoaling zone is one of the subjects he outlined the need for further work, owing to the significance of the practical applications for the evolution of the shore. In order to bring a contribution to this topic, a PhD project was launched in October 2016 between the LOMC (CNRS, University Le Havre Normandie) and M2C (CNRS, University Caen Normandie) laboratories, started in the end of 2016 with the financial support of the Normandie Regional Council. A PhD was hired and Prof. A. E. should have been his co-advisor together with us.