1 Introduction

Since the early works of Bénard [1] and von Karmàn [2], the regular pattern of the vortex street behind circular cylinders at low Reynolds numbers \( (30 < Re = U_{\infty } d/\nu < 180) \) has always attracted considerable attention of researchers because of its theoretical interest as well as practical importance. Here, \( U_{\infty } \) is the velocity of the oncoming flow, d is the diameter of the cylinder and \( \nu \) is the kinematic viscosity of the fluid. From a theoretical point of view, flows over a bluff body represents an important class of problems within the domain of fluid mechanics, which involves different phenomena such as wake characteristics, vortex shedding, drag, and lift coefficients. A large number of theoretical investigations have been developed in terms of the concepts of absolute and convective instabilities. The inception of wake instability has been described in the framework of the Stuart-Landau model [3, 4]. This problem has also been significantly studied as the circular cylinder is the most widely used shape in various engineering applications making appearances in aeronautical, chemical, civil, electrical, nuclear, offshore, and wind engineering [5]. A very large number of results concerning vortex shedding have already been discussed in the literature and several reviews for the wake of a cylinder are available, [6–8].

Most of the authors agree that over the laminar state of flow, there is a transition from a 2D steady to a 2D periodic wake at \( Re_{c} = 45 \) and a 3D transition at a Reynolds number \( Re_{c} \) between 150 and 210. Over the 2D laminar vortex regime, a universal \( St - Re \) number relationship is found when parallel and oblique shedding is considered, Hammache and Gharib [9]. Here, \( St = f d/U_{\infty } \) is the Strouhal number, where f is the frequency of eddy shedding.

The majority of researches concerning this flow has been mainly devoted to the case, where the cylinder and the oncoming flow are at the same temperature. In comparison, the case of heat input on the cylinder wake has received little attention. This situation is also of great importance as it is also related to a large class of engineering applications like hot-wire anemometry, cooling of electronic equipment, combustion devices, heat exchangers and chemical reactors, etc.

The wake behavior downstream a heated cylinder is generally more complicated. Depending on the value of the ratio between buoyancy and inertial forces, characterized by the Richardson number \( Ri = Gr/Re^{2} \), the heat transfer can be controlled by forced convection, mixed convection or free convection. Here, \( Gr = g\beta (T_{w} - T_{\infty } )d^{3} /\nu^{2} \) is the Grashof number, g is the acceleration of gravity, \( \beta \) is the coefficient of thermal expansion, \( T_{w} \) and \( T_{\infty } \) are the temperatures of the heated cylinder and the free stream, respectively. When mixed or free convection is present, the influence of heating also depends on orientation of the flow direction with respect to the direction of gravity. The case of a horizontal heated cylinder embedded in an incoming flow directed either horizontally or vertically—upward or downward—involves various phenomena [10–17].

To limit the scope of the material, the primary focus of this chapter is restrained to the study of the heated cylinder in the forced convection regime, i.e., when the Richardson number \( Ri \ll 1 \).

For a horizontal heated cylinder with a horizontal oncoming flow, even in absence of buoyancy effects, the wake is already complicated. Due to the presence of heat transfer, the fluid temperature varies, which causes variations of its physical properties as density \( \varrho \), kinematic viscosity, \( \nu \), and thermal diffusivity a. The choice of a reference temperature for the kinematic viscosity of fluid \( \nu \) in order to calculate the reference Reynolds number for describing the flow regime is a crucial issue for studying the flow around a heated cylinder. It is important to point out that, 30 years ago, it did not exist any consistent analysis to select this reference temperature. Therefore, it was not possible to determine the value of the Reynolds number of a heated cylinder over the laminar regime and to anticipate on the steady or periodic nature of the flow regime around and downstream the cylinder.

Most of the previous studies concerning the horizontal heated cylinder exposed to a horizontal air cross-flow rather were focused on the determination of semiempirical correlations to characterize the forced convective heat transfer. From these approaches, a large number of \( Nu - Re \) relationships have been proposed in the literature, Mc Adams (1954) [18–24].

The Nusselt number \( Nu \) is defined as \( Nu = h d/\lambda \), where h is the mean heat transfer coefficient over the whole cylinder surface and \( \lambda \) is the thermal conductivity of the fluid. Some of these relations are also function of the Prandtl number \( Pr = \nu /a \) and can be used for fluids other than air. In these relations, the Reynolds number is dependent on the temperature through the temperature dependence of the kinematic viscosity \( \nu = \mu /\rho \). Depending on the authors, various reference temperatures were selected. Fluid properties were calculated either at the film temperature, defined as \( T_{film} = (T_{w} + T_{\infty } )/2 \) [20–24], or the dynamic viscosity \( \mu \) at the film temperature and the density \( \rho \) at the free stream temperature, Mc Adams [19].

In addition to the value of the mean heat transfer coefficient, local heat transfer coefficient around the circumference of the cylinder was measured by Eckert and Soehngen [25]. On the other hand, information concerning the velocity and temperature fields in the forced regime over this low Reynolds numbers range was scarce. One of the main reason for this situation was linked to the experimental difficulties of performing accurate velocity and temperature measurements at low velocities in a wake of small dimensions.

In this context, extensive experiments on the laminar wake of a heated cylinder have been carried out since 1988 at Rouen and Nizhny Novgorod in order to improve the knowledge of this flow. Initially, these researches were conducted in an independent way until some cooperation has been developed between the two laboratories via the support of CNRS. These experiments have used a wide variety of specific measurements techniques including visualization, hot-wire, cold wire, LDA, PIV, acoustic scattering. The first researches on this subject have shown that the structure of the wake downstream a heated cylinder was very sensitive to the heat input. It was found that even in absence of buoyancy effects, heat was never a passive contaminant [26, 27].

In order to get a better knowledge of the phenomenon, further researches have been led to identify and quantify the conditions controlling the flow regime in the wake of a heated cylinder, namely:

  • How the heat input modifies the transition from a 2D periodic to a 2D steady wake or vice versa?

  • How the vortex shedding frequency varies with the heat input?

  • Is it possible to find out an effective Reynolds number and an effective temperature for characterizing the flow regime?

  • These are some of the questions discussed in the chapter.

This chapter is organized as follows. After a brief description of the onset of vortex street in isothermal conditions, the history of the effective Reynolds number and effective temperature concepts is presented in Sect. 2. The experimental determination of the effective temperature is discussed in Sect. 3. The physical reality of the effective temperature is examined in Sect. 4 in relation to similarities of the flow dynamic and heat transfer at the same effective Reynolds numbers. Some limitations of this approach are discussed in Sect. 5.

2 The Isothermal Bénard–Kárman Vortex Street

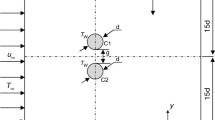
In the case of a horizontal unheated cylinder exposed to a horizontal cross-flow, as presented in Fig. 1, the description of the flow is commonly characterized by the Reynolds number \( Re \):

Fig. 1
figure 1

Schematic of horizontal flow arrangement around a heated cylinder with wall temperature \( T_{w} \) higher than the free stream temperature \( T_{\infty } \)

Full size image
$$ Re = U_{\infty } d/\nu_{0} $$
(1)

For unheated cylinders, the onset of the vortex shedding appears at a Reynolds number \( Re_{c0} \) defined by:

$$ Re_{c0} = U_{c} d/\nu_{0} $$
(2)

where \( U_{c} \) is the critical velocity.

As shown in Table 1, the critical Reynolds number \( Re_{c0} \) of a cylinder determined in isothermal conditions ranges from 40 to 49. For Reynolds numbers \( Re > Re_{c0} \), the wake becomes unstable which generates the vortex shedding phenomenon in which vortices are shed alternately at each side of the cylinder at a given frequency f. A cross-sectional view of the vortex shedding illustrates in Fig. 2 the development of the Bénard–Kárman street.

Table 1 Values of the critical Reynolds number for unheated cylinder
Full size table
Fig. 2
figure 2

Flow visualization of the vortex street behind a ribbon located in a water flow

Full size image

For a ribbon, the critical Reynolds number was found to be \( Re_{c0} = 32 \), LeMasson [32]. The Strouhal number \( St = f d/U_{\infty } \) is commonly used to characterize the vortex shedding. For the isothermal case, the \( St - Re \) relations given by Roshko [34]

$$ St = A - B/Re\quad {\text{with}}\,A = 0.212\,{\text{and}}\,B = 4.452 $$
(3)

or Williamson and Brown [35]:

$$ St = A^{{\prime }} - B^{{\prime }} /\sqrt {Re} \quad {\text{with}}\,A^{{\prime }} = 0.2665\,{\text{and}}\,B^{{\prime }} = 1.0175 $$
(4)

are often used.

3 The Heated Bénard–Kárman Vortex Street

In the case of a horizontal heated cylinder exposed to a horizontal cross-flow, the description of the flow is commonly characterized by the Reynolds number \( Re \) and the overheat ratio \( \eta \) defined from the cylinder temperature \( T_{w} \) and the free stream temperature \( T_{\infty } \) by:

$$ \eta = \Delta T_{w} /T_{\infty } , $$
(5)

where:

$$ \Delta T_{w} = (T_{w} - T_{\infty } ) $$
(6)

When the cylinder is heated, temperature differences generated within the fluid lead to variations of its physical properties: viscosity \( \nu \), density \( \rho \), thermal diffusivity a. The temperature variations also modify the value of the Prandtl number \( Pr = \nu /a \), which controls the relative thickness of the momentum and thermal layers.

3.1 Background and History of the Effective Reynolds Number Concept

An extensive review of the literature revealed that previous experimentalists had already mentioned that cylinder heating stabilizes the wake flow. It would appear that this result was first mentioned by Freymuth, Berger (private communication). The same result was also briefly cited in the report of the IUTAM symposium on concentrated vortex motions in fluids [36]. In this symposium, Uberoi presented some experimental results on the formation and properties of the vortex wake behind a heated circular cylinder. He found that with increasing cylinder temperature, the critical Reynolds number for the cylinder itself increases and the Strouhal number of the periodic vortex shedding decreases.

The same interest concerning the periodic or steady character of the near-heated wake was found in experiments of dispersion of heat in turbulent flows [37–41]. In these experiments, heat was injected in turbulent flow by means of a fine wire heated by direct current. The initial instantaneous wake was supposed to be a steady laminar wake in relation to the increase of the kinematic viscosity. However, for the authors, the precise value of the effective temperature to be used for the physical properties of fluid was no clear. It is worth to note, as for the \( Nu - Re \) relationships, the authors rather used the wire temperature \( T_{w} \) [26], Crum and Hanratty (1970), or the film temperature \( T_{film} \) [32, 34, 28] to identify an effective kinematic viscosity in order to calculate an effective Reynolds number.

The previous examples show that while, in air, the phenomenon of stabilization of the wake owing to a heat input was already well-known, there was no clear answer to the question of how to determine the effective Reynolds number of a heated cylinder. In order to clarify this issue, detailed and controlled experimental studies of the thermal wake of a horizontal heated cylinder have been carried out at Rouen [27, 42, 43].

By using fine cold wire, authors measured the wake temperature downstream a horizontal heated wire (d = 0.254 mm). In air, with a constant free stream velocity, the experiments showed that the heat input \( P/l \) could significantly alter characteristics of vortex shedding. Total suppression could be achieved by increasing the power per unit length \( P/l \) sufficiently. An example of suppression of vortex shedding is presented in Fig. 3. Measurements of temperature fluctuations in the near heated wake showed that \( I_{\theta } = \left( {\overline{{\theta^{'2} }} } \right)^{1/2}/\overline{\Delta \theta } \) the intensity of temperature fluctuations, canceled when \( P/l \) reaches a critical value. The minimum heat input needed to suppress the vortex shedding increases when \( (Re - Re_{c0} ) \) increased. The influence of heating on the frequency f of vortex shedding in air appears in Fig. 4, where \( f/f_{0} \) has been plotted as a function of \( P/l \). Here, \( f_{0} \) is the frequency of vortex shedding in the absence of heating. Cylinder heating caused a decrease in frequency similar to that observed when the free velocity decreased in an unheated flow.

Fig. 3
figure 3

The effect of heating on the intensity of temperature fluctuations measured in the heated wake of the cylinder showing the suppression of vortex shedding in air [27]

Full size image
Fig. 4
figure 4

The effect of heating on the vortex shedding frequency f for the cylinder in air, f 0 is the frequency measured in isothermal conditions [27]

Full size image

At the same time, similar experiments performed at Nizhny Novgorod by Ezersky [26] led to the same results. By using vertical heated wires (d = 0.1–0.8 mm), hot-wire measurements indicated that an increase in the temperature of a streamlined cylinder provided a decrease in shedding frequency and eventually led to suppression of periodic shedding of vortices. The characteristics of temperature fluctuations observed for increasing cylinder temperature and the characteristics of velocity fluctuations observed in the wake of a decreasing flow velocity were similar for moderate heating.

For both experiments, this stabilizing effect was attributed to the increase in kinematic air viscosity \( \nu \) and the apparent decrease of the Reynolds number. Further analysis of this phenomenon showed a broad similarity of the near-wake flows in isothermal and non-isothermal conditions. This led the authors to the definition of an effective Reynolds number \( Re_{eff} \) associated with an effective temperature \( T_{eff} \) [27, 42]. The effective Reynolds number was proposed on the basis of a similarity hypothesis that the onset of vortex shedding occurs at the same value of the critical effective Reynolds number for all heated and unheated cylinders. At the transition, the critical Reynolds numbers \( Re_{c0} \) and \( Re_{c,eff} \) were the same for both unheated and heated cases:

$$ Re_{c0} = Re_{c,eff} $$
(7)
$$ U_{c} d/\nu_{0} = U d/\nu_{eff} , $$
(8)

where \( \nu_{eff} = \nu \left( {T_{eff} } \right) \) is the effective viscosity. By knowing the temperature dependence of the air kinematic viscosity \( \nu \), it was then possible to deduce the effective temperature \( T_{eff} \). The determination of this effective temperature \( T_{eff} \) is presented in Sect. 3.2 for various experiments.

Another possible explanation for this thermal effect was also proposed by Lecordier et al. [42], suggesting that the control could result of a slight change of the location of the separation point due to the increase of the dynamic viscosity of the fluid. However, additional experiments realized with a heated ribbon showed the same result, in a situation, where the separation point of the bluff body is fixed, [44].

At the same time, a different interpretation of this phenomenon was given by Yu and Monkewitz [45]. These authors linked the suppression of vortex shedding, through heat addition to the near wake, to the reduction of absolute instability due to the decrease of the density in the near wake. In their stability analysis, using similar profiles for velocity and temperature, calculations for constant or temperature-dependent viscosity did not lead to significant differences. These authors concluded that “the change in the stability characteristics brought about by heating the cylinder was the result of a subtly modified interaction between the two mixing layers via the inertial terms and not a viscous effect”. For a heated circular cylinder [4] showed suppression of vortex shedding up to twice the critical Reynolds number based on free stream temperature. Following the analysis of Yu and Monkewitz [45], they related this control to ratio of average density in the recirculation region to free stream density. These authors had to point out that in their experiment, buoyancy effects could be considerable.

In the presence of these two plausible interpretations related to the predominant role either of kinematic viscosity or density, new experiments were carried out at Rouen in water with heated cylinder and ribbon. This choice was related to the opposite dependence of kinematic viscosity with temperature for water and air. As shown in Fig. 5, in water the reverse tendency was observed indicating that the heating of the cylinder destabilizes the flow. The minimum heat input needed to generate the vortex shedding increased when \( (Re_{c} - Re) \) increases. In parallel, as shown in Fig. 6, the cylinder heating increased the frequency of vortex shedding, [32, 34, 28, 29–31, 33, 35]. This dominant viscous effect supported by the opposite behavior observed for air and water was confirmed numerically by Socolescu et al. [46].

Fig. 5
figure 5

The effect of heating on the intensity of temperature fluctuations measured in the heated wake of the ribbon, showing the onset of vortex shedding in water [32]

Full size image
Fig. 6
figure 6

The effect of heating on the vortex shedding frequency f for the cylinder in water. f0 is the frequency measured in isothermal conditions, [32]

Full size image

Since then, a large amount of experimental and numerical investigations has closely confirmed the influence of these thermal effects on the wake flow behind a heated circular cylinder operating in the forced convection regime. For the case of air, Yahagi [47] studied experimentally the heated wake behind a cylinder at a very high overheat ratio \( \eta = 3.66 \). He observed a decrease of the vortex shedding frequency when cylinder temperature increased, indicating that the local kinematic viscosity plays a key role in the vortex structure. As a result, the vortex frequency of the heated cylinder could be expressed as a function of the Strouhal and Reynolds numbers, when the local kinematic viscosity was reasonably estimated by taking into account the effect of the cylinder heating.

Wang and his collaborators have brought a large body of information concerning the determination of the effective temperature in air [33, 48, 49, 50] (see Sect. 3.2). Their results were concerned also with the validity of the \( St - Re_{eff} \) relationship [33]. Other studies focused on the heat transfer and showed that a representative temperature could also be used to describe the heat transfer correlation as well [51]. More recently, consistently with the known effect of flow stabilization by cylinder heating, they showed that cylinder cooling destabilizes the wake flow in air [52]. Sabanca and Durst [53], were the first to obtain numerically the decrease of the wake frequency with heating in absence of free convection effects. Shi et al. [54] investigated numerically the influence of the overheat ratio on characteristic quantities of the 2D horizontal flow past a heated cylinder. They showed the strong stabilizing effect on the flow due to the increase in the kinetic viscosity of air. The Strouhal number \( St \) at various overheat ratios could be satisfactorily correlated by the effective Reynolds number based on the effective temperature given by Wang et al. [33]. Baranyi et al. [55] investigated experimentally and numerically the effect of heat transfer on the flow around a heated cylinder. Results for heated and unheated cylinders in terms of \( St - Re \) relationships agreed reasonably well with Williamson [8] results providing the use of an effective temperature depending on the overheat ratio. For the case of water, Vit et al. [56] confirmed experimentally that cylinder heating in water increases the frequency. They showed that the concept of effective temperature, originally suggested for heated cylinders in air, can be also used for heated cylinders in water. Pech [57] studied numerically the impacts of heating for flow of water and air. Computations showed that the Strouhal number decreases with temperature increase in the case of air and increases in case of water. The separation angle also showed some dependence on temperature ratios.

3.2 Experimental Determination of the Effective Temperature

As mentioned above, the concepts of effective Reynolds number and effective temperature were introduced on the assumption that onset of vortex shedding is the same for both heated and unheated cases, i.e., \( Re_{c0} = Re_{c,eff} = U d/\nu_{eff} \).

Here, the effective viscosity \( \nu_{eff} = \nu (T_{eff} ) \) is used to account for the thermal effect. The effective temperature \( T_{eff} \) is related to the cylinder temperature \( T_{w} \) by the following relation:

$$ T_{eff} = T_{\infty } + c \left( {T_{w} - T_{\infty } } \right), $$
(9)

where \( 0 \le c \le 1 \) is a constant. The ratio of viscosities is then given by:

$$ \nu_{eff } /\nu_{0} = \left( {T_{eff} /T_{\infty } } \right)^{1,777} = \left( {1 + c\,\eta } \right)^{1,777} , $$
(10)

where the power-law exponent of the dynamic viscosity of air is given by [58]. However, various methods have been used to determine experimentally the effective temperature.

Determination of the effective temperature at the transition

The more simple method consists of deducing \( T_{eff} \) at the transition from the definition of \( Re_{c,eff} \):

$$ U_{c} d/\nu_{0} = U d/\nu_{eff} $$
(11)

where \( U_{c} \) is the critical velocity determined without heating and U is the critical velocity with the heated cylinder. From (11) the ratio \( \nu_{eff } /\nu_{0} \) is calculated and the relative effective temperature \( T_{eff } /T_{\infty } \) can be deduced from (12):

$$ T_{eff } /T_{\infty } = (U/U_{c } )^{0.563} $$
(12)

and the value c from the relation (9). Using this method, the experiments carried out by Hamma [27] and Lecordier et al. [42] with a 0.254 mm diameter heated wire led to c-values: 0.275 and 0.3. Dumouchel et al. [59, 60] with a 1 mm diameter tube found c-values: 0.27 and 0.24. Wang et al. [33] showed that their experimental results with \( c = 0.28 \) satisfies the concept of constant critical Reynolds number for the temperature ratio \( T_{w } /T_{\infty } \) up to 2.

The value of the effective temperature \( T_{eff } \) can be also determined at the transition in an instationnary situation. When the heating is sufficient to stabilize the wake, it is possible to observe, on the temperature signal \( T_{s} (t) \) measured in the wake, the apparition of vortices after the electric power is put off at \( t = 0 \), as shown in Fig. 7. The decrease in the cylinder temperature \( T_{w} (t) \) is controlled with the thermal inertia of the heated cylinder and involves the decrease in the wake temperature \( T_{s} (t) \). When the vortices appear at \( t = t_{app} \) the effective temperature can be deduced from the measurement of \( T_{s} (t_{app.} ) \). With this method, Hamma [27] found a value \( c = 0.275 \).

Fig. 7
figure 7

Temperature signal measured in the heated wake. After suppression of the heating at t = 0, the onset of vortex shedding occurs at t = tapp [27]

Full size image

Determination of the effective temperature from a universal \( \varvec{St} - \varvec{Re}_{{\varvec{eff}}} \) relationship

When the heat input is not sufficient to suppress the vortex shedding, it is then possible to determine the effective temperature from frequency measurements. Assuming that the effective Reynolds concept is also valid for the \( St - Re_{eff} \), the effective temperature can be deduced from the best fit found between the \( St - Re_{eff} \) curve and the St–Re relation of the isothermal case. This method of determination of \( T_{eff} \) was used by Vit et al. [56] due to experimental difficulties to detect the critical Reynolds in their experiment in water. Using the St–Re relation given by Williamson and Brown [35], the best fitting of all \( St - Re \) data onto one \( St - Re_{eff} \) curve was obtained for \( c = 0.97. \)

Other authors have also deduced the effective temperature assuming the validity of the \( St - Re_{eff} \) relationship at some particular values. By measuring the same frequency f both downstream an unheated cylinder and a heated cylinder, Lecordier et al. [42] determined two values of Strouhal numbers \( St_{0} = f d/U_{0} \) and \( St_{eff} = f d/U \). Using the relation of Roshko [24] with A = 0.212, they deduced the ratio \( \nu_{eff } /\nu_{0} \):

$$ \nu_{eff } /\nu_{0} = (U/U_{0} )((1 - St_{eff} /A)/(1 - St_{0} /A)) $$
(13)

The relative effective temperature \( T_{eff } /T_{\infty } \) deduced from this relation gave \( c = 0.30 \). Ezersky [26] used a similar approach by considering at constant velocity \( U, \) the variation of the Strouhal number \( St \) with the overheat ratio \( \eta \). By using the relation of Roshko [34],

$$ St = f d/U = A - B/Re_{eff} $$
(14)
$$ St = A - B\nu_{g} (T_{eff} )/Ud $$
(15)
$$ \partial St/\partial \eta = - (B/Ud)\partial \nu_{g} (1 + c\eta )/\partial \eta $$
(16)
$$ \partial St/\partial \eta = - 1.777(Bc/Re_{0} )(1 + c\eta )^{0.777} $$
(17)

With B=4.494, experiments carried out with 0.1 mm and 0.8 mm diameter heated wires led to c-values: 0.23 and 0.255.

The values of c are listed in Table 2. If we exclude the value given by Baranyi et al. [55], it appears that the mean value of c is about 0.275, very close to the c-value 0.28 determined by Wang et al. [33] and commonly accepted for the effective temperature in air. The higher value proposed by Baranyi et al. [56] could be due to the fact that their experiments were related to the transitional regimes in modes A and B, instead of to the laminar regime as mentioned by Trávníček and Wang [61]. In water, the c-value is 0.97 in relation with the higher value of the Prandtl number in water.

Table 2 Experimental values of c for the heated cylinder in air and water
Full size table

Fedorchenko et al. [49] have shown that assuming small \( c\Delta T_{w}^{*} \) values, the c-value for any dilute gas is related to an exponent n of the kinematic viscosity–temperature power law by a simple formula \( c = 1/2n \). They deduced a linear increase of the critical Reynolds number in the heated case given by the relation:

$$ Re_{c} = Re_{c0 } T_{film}^{*} $$
(18)

and arrived at the important conclusion that the effective Reynolds number can be determined for any dilute gas without knowing the particular c-value. Here, \( \Delta T_{w}^{*} = \Delta T_{w} /T_{\infty } \) and \( T_{film}^{*} = T_{film} /T_{\infty } \).

However, when higher values of \( c\Delta T_{w }^{*} \) are considered, the effective Reynolds number is given by the nonlinear expression:

$$ Re_{c} = Re_{c0 } (1 + 2c\Delta T_{film}^{*} )^{1.777} $$
(19)

Figure 8 shows \( Re_{c} /Re_{c0 } \)—\( T_{film}^{*} \) dependence for air according to relations (18) and (19). The solid line is the linear prediction given by relation (18) [48]. Dashed lines are the prediction given by using relation (19) for the c-values 0.24 and 0.3. The points are experimental data of Wang et al. [33], Hamma [27], Dumouchel et al. [59]. For air, whatever the selected c-value, the linear assumption seems sufficient for overheat ratio lower than 0.4. For higher overheat ratio, the nonlinear character appears and depends on the selected c-value.

Fig. 8
figure 8

Variation of \( Re_{c} /Re_{c0 } \) with \( T_{film}^{*} \)

Full size image

It is worth to note that in water the linear assumption would be only valid for overheat ratio lower than 0.03. This could complete the issue raised by Fedorchenko et al. [49].

3.3 Interpretation of the Effective Temperature

It is worth to note that the effective temperature \( T_{eff} \) is much lower than the film temperature \( T_{film} \) generally used to take into account the influence of temperature on fluid properties on \( Nu - Re \) relationships. As mentioned by Dumouchel et al. [60], in air the effective temperature \( T_{eff} \) is close to the temperature of the recirculation zone and is not just an artificial value. Temperature measurements obtained at Rouen, in air and water, in the near wake for both heated cylinder and ribbon are shown in Fig. 9, [27, 60, 62]. The values of \( \Delta T_{max} /\Delta T_{w} \) have been plotted as a function of \( x/d \). In air, the relative maximum temperature in the near wake is between 0.2 and 0.3, the range of values found in c. Temperatures measured at \( x/d = 1.25 \) by Yahagi [47] are also presented. They are very close to the \( \Delta T_{eff} /\Delta T_{w} \) values calculated by Wang et al. [33] for this experiment. In water, the values of \( \Delta T_{max} /\Delta T_{w} \) in the near wake are higher than in air. They reach 0.5–0.6 at \( x/d = 1 \) and are consistent with the rather high value of \( c = 0.97 \) measured by Vit et al. (2006). A comparison of the results obtained for heat transfer, in air and water, require to account for the values of Prandtl number \( Pr \). The Prandtl number of air and water, at the free stream temperature, are about 0.7 and 7. Experimental and numerical studies have shown that just behind the heated cylinder the velocity fields, in air, oil, and water, at the same effective Reynolds number are similar [44, 63]. Conversely, the corresponding thermal fields are very different. In air, a relatively thick thermal layer near the cylinder transforms into a thinnest layer in oil. In the near wake of a heated cylinder in oil, the isotherms show a small temperature protuberance in the vicinity of the separation point [63]. This situation can also explain the strong double-peaked character of the temperature profiles observed in the near wake in water, Lecordier et al. [62].

Fig. 9
figure 9

Variation of \( \Delta T_{max} /\Delta T_{w} \) in the near wake of heated cylinder and ribbon

Full size image

In air, recent numerical simulation of Xin et al. [64] showed that heating different places of cylinder surface results in different control effects. The stabilization effect was found stronger for heating on the leeward side. This can be related to the results of Strykowski and Sreenivasan [65], Paranthoën and Lecordier [66], where the use of a heated secondary cylinder located just at the end of the recirculation zone allows to suppress the vortex shedding phenomenon. In this case, for the same value of \( (Re - Re_{c0} ) \), the power per unit length needed to suppress the vortices was about one hundred times lower in this second situation.

3.4 Similarities of the Heated Wake in Relation to \( \varvec{Re}_{{\varvec{eff}}} \)

Concerning the dynamics of the flow, some similarities were found with the effective Reynolds number concept for the global quantities such as Strouhal number \( St \).

Wang et al. [33] found experimentally that their experimental data of the parallel vortex shedding (PVS) mode fell on a “universal” \( St - Re_{eff} \) curve over a wide range of overheat ratio. This result was confirmed numerically by Shi et al. [54]. Wu et al. [67] showed that similar trend also can be found for the vortex shedding frequency of Oblique Vortex Shedding (OVS) mode. Moreover, the onsets of OVS that results in discontinuities in the \( St{-}Re_{eff} \) relationships were found at about the same effective Reynolds number for both isothermal and non-isothermal cases.

In accordance with the similarity of this global quantity \( St \) with \( Re_{eff} \), Shi et al. [54] indicated the existence of a local similarity in the dimensionless viscous force over the cylinder surface for flows with the same effective Reynolds number. This local similarity was also observed in the rear portion of the cylinder for the dimensionless pressure force. Moreover, the results indicated that the same effective Reynolds number also characterizes the velocity field in the proximity of the cylinder and in the near-wake region with good accuracy.

Extensive measurements of velocity carried out downstream of a heated circular cylinder or ribbon have shown the influence of heat input on the velocity field in the near wake [44]. In presence of the heating in air, the heated mean longitudinal velocity profiles were slightly wider than the isothermal profiles. This behavior was also characterized in each section by a decrease of the centerline mean longitudinal velocity and of the RMS values of the transverse velocities in comparison with the isothermal case. By considering the effective Reynolds number \( Re_{eff} \), some characteristics of the heated or unheated wake were found in close agreement. For example, for the same values of \( Re_{eff} \), the length of the wake bubble \( s* \), the evolutions of the normalized RMS transverse velocity \( \sigma_{v}^{*} \) were found similar in both isothermal and non-isothermal cases. Furthermore, detailed comparison of experimental results showed that, in similar effective Reynolds numbers conditions, the interaction between the two shear layers at the end of the recirculation zone was roughly the same. Following the analysis of Abernathy and Kronauer, Gerrard [68, 69], this interaction could be calculated, at the end of the recirculation zone, as the ratio \( I \) between the rate of circulation in the shear layer and the shear layer spacing \( \Delta \) [44, 70].

$$ I = \left| {\frac{{d\Gamma }}{dt}} \right|/\Delta = \frac{{(\partial U/\partial y)_{max} }}{\Delta } \delta {\text{U}}(\Delta /2) $$

In this term, \( \delta \) is the shear layer thickness.

For better comparison between experiments with the cylinder and the ribbon in air and in water \( I \) was normalized by using the frequency of vortex shedding \( f_{{Re_{c} }} \) and the velocity \( {\text{U}}(\Delta /2)_{{Re_{c} }} \) determined at the critical Reynolds number:

$$ I^{*} = \frac{{(\partial U/\partial y)_{max} \delta {\text{U}}(\Delta /2)}}{\Delta }\frac{1}{{f_{{Re_{c} }} {\text{U}}(\Delta /2){\text{U}}(\Delta /2)_{{Re_{c} }} }} $$

In Fig. 10, this normalized interaction term \( I* \) has been plotted as a function of \( (Re_{eff} - Re_{c} ) \). As shown in this figure, the results obtained from cylinder and ribbon experiments in air and water agree reasonably well. Vortex shedding is present when the normalized interaction term \( I* \) is larger than a threshold value of about 5.5–6. In air, in presence of heating, the value of \( I* \) decreases with increasing heating and suppression of vortices could occur when this threshold value is reached. In water, the opposite trend was observed.

Fig. 10
figure 10

Variation of the normalized interaction term for heated and unheated cylinders and ribbons versus \( (Re_{eff} - Re_{c} ), \) [32, 71]

Full size image

The same unanimity for the choice of \( T_{eff} \) was not observed for the global heat transfer aspect characterized by the Nusselt number \( Nu \). Shi et al. [54] found that the calculated values of \( Nu \) were well correlated with the relation of Collis and Williams (1956) when the fluid properties were evaluated at the film temperature \( T_{film} \). The temperature loading factor \( (T_{film} /T_{\infty } )^{ - 0.17} \) was needed to take into account the variation of the overheat ratio. Dumouchel et al. [60] showed that it was possible to plot \( Nu \) as a continuous function of either \( (Re_{film} )^{0,45} \) or \( (Re_{eff} )^{0,45} \) under the condition to use a temperature loading factor \( (T_{film} /T_{\infty } )^{ - 0.25} \), close to the value of Collis and Williams [24], or \( (T_{eff} /T_{\infty } )^{0.28} \), respectively. They noted that the change of slope of the heat transfer curve appeared more clearly in the \( Nu \) \( (T_{eff} /T_{\infty } )^{0.28} \)—\( Re_{eff} \) formulation as \( Re_{eff} \) characterize the regime of the wake. Wang and Trávníček [51] proposed a different correlation method based on the “representative” Reynolds number deduced from “representative temperature” defined as \( T_{rep} = T_{\infty } + 0.36 (T_{w} - T_{\infty } ). \) By introducing this “representative” Reynolds number \( Re_{rep} \) linear correlation equations were successfully derived.

Shi et al. [54] compared these different approaches by examining the local similarity of the Nusselt number. For steady conditions, they observed a better local similarity on the correlation concept of Collis and Williams [24]. For the unsteady regime, a local similarity was observed except for the rear part of the cylinder. These results suggested that the front part of the cylinder from the stagnation point up to the separation point could be only dependent on the thermal boundary layer around the cylinder characterized by \( Re_{film} \). Conversely, the downstream part of the cylinder, from the separation point up to the rear stagnation point would depend on the wake by the influence of the recirculation zone and would be characterized by \( Re_{eff} \). A similar analysis has been made by various authors [20, 23, 72] who proposed a correlation in the following form: \( Nu = a Re_{film}^{0.5} + b Re_{film}^{0.67} \), where the first term represents the heat transfer through the laminar boundary layer on the front part of the cylinder and the second term, the heat transfer of the rear portion. This second term could depend on \( Re_{eff} \).

4 Limits of the Effective Reynolds Number Approach

As shown in the previous examples, the effective Reynolds number concept allows to take into account the influence of the thermal effect on the heated wake. However, there seems to be some evidence that some phenomena appearing when the cylinder is strongly heated cannot be only reduced to renormalization of the Reynolds number, even in the absence of buoyancy forces. When the effective Reynolds number approach works, the spectral characteristics of temperature fluctuations observed for increasing cylinder temperature and the characteristics of velocity fluctuations observed in the wake of a decreasing flow velocity have to be similar. However, some experiments [73–76] showed that such similarity only exists for a range of heating power. Over a definite range of \( P/l \) values, spectra of temperature fluctuations or acoustic wave scattering became essentially nonsymmetrical relative to the maximal values, whereas at higher and lower heating, power spectra had the same symmetrical shape for all Reynolds numbers. Signal amplitude \( A(t) \) and phase \( \phi (t) \), extracted from the time series of temperature fluctuations using Hilbert transformation, showed that for the regime of nonsymmetrical power spectrum, a sequence of defects occurred in the time series of temperature fluctuations. For a such defect, the amplitude dropped down to zero and the phase decreased by about \( 2\pi \) and one period was lost in such an impulse, which explains the nonsymmetrical spectra [74]. The visualizations of the heated wake for \( Re = 89 \), showed that these defects existed over the range \( 2.02 \le T_{w}^{*} \le 2.6 \) [76]. Outside this range, no defects were formed either at small or at large heating power. For large heating, the wake was stabilized as \( Re_{eff} < Re_{c} \). It is worth to note that, in isothermal conditions, similar defects have already been observed for the Reynolds numbers range 160 < \( Re\, < \,230 \) [77]. This kind of defects may also be excited artificially, at smaller Reynolds numbers \( (Re = 140) \) by creating on the cylinder a zone of larger diameter, Williamson [8]. These defects caused by heating arising at lower Reynolds numbers might result from the instability described by [78]. They showed that for a single vortex, flexible modes are excited when a large enough difference existed between the core and periphery densities. For a strongly heated cylinder, the motion of temperature stratified and, hence, density stratified vortices could become important and differ from the motion of a homogeneous fluid, even in the absence of buoyancy forces. The generation of these modes connected with the motion of a density stratified fluid under the action of centrifugal forces may change the wake dynamics fundamentally. It seems that there are no studies mentioning the existence of the defects arising in the street at certain heating intensities.

5 Conclusion

This chapter is concerned with a review of the heated Bénard–Kármán street in relation to the effective Reynolds number concept. From the literature, it is clear that this laminar flow regime is strongly dependent on the level of heating and, even in absence of buoyancy effects, heat is never a passive contaminant. The results obtained in the pioneer works of [26, 42] have been fully confirmed. In air, the frequency of vortex shedding is found to decrease with heating while the opposite trend is observed in water. This is due to the increase in the kinematic viscosity of air and the decrease in the kinematic viscosity of water with increasing overheat ratio. This phenomenon has led to the definition of an effective Reynolds number \( Re_{eff} \) that is associated to an effective temperature \( T_{eff} = T_{\infty } + c(T_{w} - T_{\infty } ) \). This concept assumes that the critical Reynolds numbers in isothermal and no isothermal situations is the same. In relation to the respective values of Prandtl number \( Pr \), c-values of 0.28 for air and 0.97 for water have been found. The values of the corresponding effective temperature were found close to the near-wake temperature.

The underlying physics of the concept of effective temperature was revealed with the similarities of global (Strouhal number, drag coefficient, etc.) or local (dimensionless viscous force on the cylinder surface, dimensionless pressure force in the rear portion of the cylinder surface, etc.) flow characteristics found with the same \( Re_{eff} \). Concerning the Nusselt number, in air, there is no consensus on the choice of the temperature selected for use in the \( Nu - Re \) relationships. The film temperature \( T_{film} \) or the representative temperature \( T_{rep} \) are both used by authors to characterize fluid properties for the steady and the periodic wake regimes. It is worth noting that at least for the rear part of the heated cylinder, the correlation ought to take into account the effective temperature linked to the flow regime.

However, when the cylinder is strongly heated, there exists some range of heating power within which defects are able to grow in a vortex street against the background of a periodic structure. In this case, the phenomena cannot be only reduced to renormalization of the Reynolds number.

Over the past three decades, many advances have been made in the understanding of the wake downstream a heated cylinder in the periodic laminar regime. Nevertheless, the complexity of this flow should continue to motivate the development of further numerical simulations and experimental works. These studies could help resolve some of the problems associated with small scales in the heated turbulent flows. Up to now, these researches have especially concerned the case of air flows and, to a lesser extent, the case of water flows. They could be extended to fluid flows at various Prandtl numbers.