Numerical Study of Nonlinear Fluid–Structure Interaction of an Excited Panel in Viscous Flow

Abstract

Vibration of flexible panel induced by flow and acoustic processes in a duct can be used for silencer design, but it may conversely generate noise if structural instability is induced. Therefore, a complete understanding of fluid–structure interaction is important for effective noise reduction. A new time-domain numerical methodology has been developed for the calculation of the nonlinear fluid–structure interaction of an excited panel in internal viscous flow. This paper reports its validation with two experiments. The first aims to validate that the methodology is able to capture flow-induced structural instability and its acoustic radiation. The second one is to show that the methodology captures the aeroacoustic–structural interaction in a low-frequency silencer and its response correctly. The importance of inclusion of viscous effect in both cases is also discussed.

1 Introduction

A good understanding of the fluid–structure interaction is important in the design of effective flow duct noise control in many aeronautic, automotive, and building service engineering systems. When the flow unsteadiness and/or the duct geometry are changed, acoustic waves are generated which may propagate back to the source region and modify the flow process generating it. Such aeroacoustic processes always appear in the flow duct. Since the duct wall is constructed by thin panels, it may be excited to vibrate by the aeroacoustic processes and in turn modify the source aeroacoustic processes. There is a nonlinear coupling between the aeroacoustics of the fluid and the structural dynamics of the panel. If the design of flow duct noise control is developed with only one media (fluid or panel) in the consideration, it may be completely counteracted by the dynamics occurring in another media through the nonlinear coupling. A complete understanding of the nonlinear fluid–structure interaction and its acoustics is necessary for devising an effective design.

To control the noise generation and its propagation in air flow ducts, a thick layer of acoustic liner is commonly used that covers the duct to absorb noise and prevent the noise in the duct breaks through the duct walls and annoy the people in the surrounding. However, this kind of noise control method is not effective in low frequency range. A drum-like silencer concept was introduced by Huang [1] in which the nonlinear fluid–structure interaction of flexible panels was used to control low-frequency noise. Huang reported that this design is effective in low frequency range and claimed it gives low-pressure loss when flow is present. However, the effect of mean flow is not considered in his theoretical study [1]. Later, Fan et al. [2, 3] attempted to study numerically the aeroacoustic–structural response of the panel in this design in an inviscid flow framework. The presence of inviscid mean flow produces a completely different response from the case without flow. The fluid–structure interaction was found to play a very important role in the noise reduction. The silencer performance was found strongly reduced in the presence of flow. In real application, viscous flow effect may be another important factor that affects the silencing performance. The viscous flow may excite the flexible panel to vibrate and cause structural instability. An experimental study by Liu [4] on the similar design showed that the instability of the panel can be induced. Probably additional noise will be generated by the vibration which reduces the effectiveness of the silencer. Therefore, it is necessary to investigate the nonlinear fluid–structure interaction in viscous flow.

A numerical methodology that facilitates better understanding of fluid–structure interaction in viscous compressible duct flow for advancing design of silencer with flexible panel has recently been developed. In order to minimize the error generated by the numerical coupling procedure that connects the fluid and structure domains, a treatment that combines all governing equations of different physical domains and solved by a single solver is introduced. The new methodology has to be proven able to resolve the nonlinear fluid–structure interaction and its acoustic problems important to achieving a better design of the drum-like silencer concept for practical use. This paper reports the results of such validation with calculations of two pertinent experiments.

2 A Brief of the Numerical Methodology

The aeroacoustic–structural interaction problem involves the interplay between the flow dynamics, acoustics, and structural dynamics. The effects of all three parts play equally important roles. Since acoustic motion is a kind of unsteady flow motions that a fluid medium supports [5], both the acoustic field and its source unsteady flow must be calculated and accurately resolved simultaneously by the numerical model for fluid medium. In addition, the inherent nonlinear interaction between the acoustics and the unsteady flow must be accurately accounted for solving the problem. The generated acoustic waves inside a duct experience multiple reflection and scattering which may then propagate back and alter the unsteady flow dynamics and the panel structural vibration. These nonlinear interactions cannot be ignored. Thus, direct aeroacoustic simulation (DAS) approach [6, 7] is adopted in modeling the aeroacoustics in fluid medium. At the fluid–structure interface, both flow and panel structural responses are simultaneously involved so proper governing equations that describe these responses are needed. They are however usually not available. Therefore, the responses at the interface are resolved by iterating the aeroacoustic and panel dynamic models by Newton’s method. Here only the key components in the formulation of the numerical methodology are described. The details of their numerical implementation are referred to Fan [8].

2.1 Aeroacoustic Model

In DAS, the aeroacoustics of the fluid medium is modeled by solving the two-dimensional compressible Navier–Stokes equations together with ideal gas law for calorically perfect gas. The normalized Navier–Stokes equations without source can be written in the strong conservation form as,

$$\begin{aligned} \frac{\partial \varvec{U}}{\partial t}+\frac{\partial \left( \varvec{F}-\varvec{F}_{v}\right) }{\partial x}+\frac{\partial \left( \varvec{G}-\varvec{G}_{v}\right) }{\partial y}=0, \end{aligned}$$

(1)

where $\varvec{U} = [\rho \quad \rho u \quad \rho v \quad \rho E]$, $\varvec{F} = [\rho u \quad \rho u^{2}+p \quad \rho uv \quad (\rho E+p)u]$, $\varvec{G} = [\rho v \quad \rho uv \quad \rho v^{2}+p \quad (\rho E+p)v]$, $\varvec{F}_{v} = (1/Re)[0 \quad \tau _{xx} \quad \tau _{xy} \quad \tau _{xx}u+\tau _{xy}v-q_{x}]$, $\varvec{G}_{v} = (1/Re)[0 \quad \tau _{xy} \quad \tau _{yy} \quad \tau _{xy}u+\tau _{yy}v-q_{y}]$, $\rho$ is the density of fluid, u and v are the velocities in x and y-directions, respectively, t is the time, normal and shear stresses $\tau _{xx}=(2/3)\mu \left( 2\partial u/\partial x-\partial v/\partial y\right)$, $\tau _{xy}=\mu \left( 2\partial u/\partial y-\partial v/\partial x\right)$, $\tau _{yy}=(2/3)\mu \left( 2\partial v/\partial y-\partial u/\partial x\right)$, $\mu$ is the viscosity, total energy $E=p/\rho (\gamma -1)+(u^{2}+v^{2})/2$, pressure $p=\rho T/\gamma M^{2}$, T is temperature, heat flux $q_{x}=\left[ \mu /(\gamma -1){Pr}M^{2}\right] \left( \partial T/\partial x\right)$, $q_{y}=\left[ \mu /(\gamma -1){Pr}M^{2}\right] \left( \partial T/\partial y\right)$, the specific heat ratio $\gamma =1.4$, the reference Mach number $M=\hat{u}_{\textit{0}}/\hat{c}_{\textit{0}}$ where $\hat{u}_{\textit{0}}$ is the reference velocity, $\hat{c}_{\textit{0}}=(\gamma \hat{R}\hat{T}_{\textit{0}})^{1/2}$, the specific gas constant for air $\hat{R}=287.058\,\mathrm {J/(kg K)}$, the reference Reynolds number ${Re}=\hat{\rho }_{\textit{0}}\hat{c}_{\textit{0}}\hat{L}_{\textit{0}}/\hat{\mu }_{\textit{0}}$, and Prandtl number ${Pr}=\hat{c}_{p,\textit{0}}\hat{\mu }_{\textit{0}}/\hat{k}_{\textit{0}}=0.71$. All the dimensional quantities are indicated with caret.

The conservation element and solution element (CE/SE) method [9] is adopted to solve the DAS governing equations. It has been proven that the inherently low dissipation of CE/SE method allows accurate calculation of the acoustic and flow fluctuations which usually exhibit large disparity in their energy and length scales [7]. Its numerical framework relies solely on strict conservation of physical laws and emphasis on the unified treatment of fluxes in both space and time. Lam [7] showed that CE/SE method is capable of resolving the low Mach number interactions between the unsteady flow and acoustic field accurately by calculating the benchmark aeroacoustic problems with increasing complexity. The formulation of the CE/SE method is not given in this paper. The details can be referred to in the works of Lam [7].

2.2 Structural Dynamic Model

The one-dimensional dynamic response of the flexible panel can be modeled by the simplified nonlinear Von Karman’s theory on Kelvin foundation [10, 11]. The panel is assumed to be of uniform small thickness $h_p=\hat{h}_{p}/\hat{L}_{p}$ and initially flat. Using the same set of reference parameters adopted in the aeroacoustic model, the normalized governing equation for panel displacement $w(x)=\hat{w}/\hat{L}_{\textit{0}}$ can be written as,

$$\begin{aligned} {D}\dfrac{\partial ^{4}{w}}{\partial {x}^{4}} - ({T}_{x}+{N}_{x})\dfrac{\partial ^{2}{w}}{\partial {x}^{2}} + {\rho }_{p}{h}_{p}\dfrac{\partial ^{2}{w}}{\partial {t}^{2}} + {C}\dfrac{\partial {w}}{\partial {t}} + K_p{w} = {{p}_{ex}}, \end{aligned}$$

(2)

where ${N_x} = ({E_p}{h_p}/2 L_p)\int \nolimits _{0}^{L_p}\left( \partial w/\partial x\right) ^2 dx$, $D=\hat{D}/(\hat{\rho }_{\textit{0}}\hat{c}_{\textit{0}}^{2}\hat{L}_{\textit{0}}^3)$ is the bending stiffness, ${T}_{x}=\hat{T}_{x}/(\hat{\rho }_{\textit{0}}\hat{c}_{\textit{0}}^{2}\hat{L}_{\textit{0}})$ is the external tensile stress resultant per unit length in the tangential direction, ${N}_{x}$ is the internal tensile stress in the tangential direction induced by stretching, $E_p=\hat{E}_p\hat{c}_{\textit{0}}^2/(\hat{\rho }_{\textit{0}}\hat{L}_{\textit{0}}^4)$ is the modulus of elasticity, ${L}_{p}=\hat{L}_{p}/\hat{L}_{\textit{0}}$ is the length of panel, ${\rho }_{p}=\hat{\rho }_{p}/\hat{\rho }_{\textit{0}}$ is the density of panel, $C=\hat{C}/(\hat{\rho }_{\textit{0}}\hat{c}_{\textit{0}})$ is the structural damping coefficient, ${K}_{p}=\hat{K}_{p}\hat{L}_{\textit{0}}/(\hat{\rho }_{\textit{0}}\hat{c}_{\textit{0}})$ is the stiffness of foundation, and ${{p}_{ex}}=\hat{{p}_{ex}}/(\hat{\rho }_{\textit{0}} \hat{c}_{\textit{0}}^2)$ is the net pressure exerted on the panel surface.

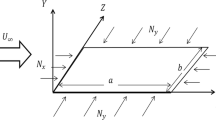
To satisfy the tangency condition, four equivalent relationships between the fluid at the interface and the panel can be derived [12]. They are equivalents of stress, acceleration, velocity, and displacement. When the fluid element size and the normal velocity are small ($M<0.3$) [13], the local viscous effect and compressibility of fluid can be ignored. Therefore, the normal pressure difference can be simply given by Newton’s second law as $\partial p/\partial \eta = -\rho (\partial v_\eta /\partial t) = -\rho \ddot{w}$ (Fig. 1). Then, the panel acceleration is found as $\ddot{w} = -(\partial p/\partial \eta )/\rho$. The panel velocity and displacement can also be obtained by integrating $\ddot{w}$ and $\dot{w}$ over time, i.e., $\dot{w} = \int \ddot{w} dt$ and $w = \int \dot{w} dt$.

Fig. 1

Small fluid volumes on two sides of the flexible panel

2.3 Boundary Conditions

All solid surfaces obey the tangency condition and the normal pressure gradient condition. At no-slip boundary surface, zero tangential velocity $v_\xi = 0$ is applied. Isothermal condition $T = T_{\textit{0}}$ is applied to all solid surfaces, and zero normal velocity $v_\eta = 0$ is applied to all rigid surfaces. At the fluid–panel interface, the normal velocities are set as $\dot{w}$. Pinned conditions are prescribed at both edges for the flexible panel where the displacement and bending moment are set zero, i.e., $w = \partial ^{2}{w}/\partial {x}^{2} = 0$.

2.4 Fluid–Panel Coupling

During the time-marching of the numerical solution, aeroacoustics and structural responses occur at the fluid–panel interface. Consider two adjacent infinitely small control volumes of fluid on both sides of flexible panel and their total stress on the normal direction as shown in Fig. 1 in which $\xi$ and $\eta$ are the tangential and normal directions of the undeflected panel surface, respectively. $\delta$ and l are defined as the size of the fluid volume in normal direction without and with panel deflection, respectively. p is the pressure acting from the surrounding on the surface of the fluid volume. The viscosity-induced normal force may be expressed as $\tau _{\eta \eta }=(2/3)\mu \left( 2\partial v_{\eta }/\partial \eta -\partial v_{\xi }/\partial \xi \right)$, where $v_{\xi }$ and $v_{\eta }$ are the fluid velocities in tangential and normal directions [14]. On the no-slip panel surface, $\partial v_{\xi }/\partial \xi = 0$ and $\tau _{\eta \eta } = \left( 4/3\right) \mu \left( {\partial v_{\eta }}/{\partial \eta }\right)$. When the fluid is driven by the panel, the additional forces applied within the fluid volume are the difference in stresses over the control volume given by $(p_{uface}-\tau _{\eta \eta ,uface})-(p_{upper}-\tau _{\eta \eta ,upper})$ and $(p_{lface}-\tau _{\eta \eta ,lface})-(p_{lower}-\tau _{\eta \eta ,lower})$. Meanwhile, the net external force applied to the panel is ${p}_{ex} = (p_{lface}-\tau _{\eta \eta ,lface})-(p_{uface}-\tau _{\eta \eta ,uface})$.

Since variation of viscous stress with fluid volume is very small compared to the pressure, it can be assumed that $\tau _{\eta \eta ,uface}-\tau _{\eta \eta ,upper} = \tau _{\eta \eta ,lface}-\tau _{\eta \eta ,lower} = 0$. The additional force per unit volume can thus be written as $(p_{uface}-p_{upper})/l_{upper}$ and $(p_{lface}-p_{lower})/l_{lower}$, and the corresponding mechanical power is $v_{\eta ,upper}(p_{uface}-p_{upper})/l_{upper}$ and $v_{\eta ,lower}(p_{lface}-p_{lower})/l_{lower}$, respectively. These forces arising from the vibrating fluid–panel interface are responsible for driving the aeroacoustics solution in the neighborhood of the panel. Therefore, it is better to resolve their effects by expressing them as a source term $\varvec{Q}$ in the homogeneous Eq. 1 originally for fixed domain boundary. Thus, the DAS governing equation can now be written as,

$$\begin{aligned} \dfrac{\partial \varvec{U}}{\partial t}+\dfrac{\partial \left( \varvec{F}-\varvec{F}_{v}\right) }{\partial x}+\dfrac{\partial \left( \varvec{G}-\varvec{G}_{v}\right) }{\partial y} = \varvec{Q}, \end{aligned}$$

(3)

where $\varvec{Q} = [-\sin \theta Q' \quad \cos \theta Q' \quad v_{\eta } Q' \quad 0]$, $Q_{upper}' = (p_{uface} - p_{upper})/l_{upper}$ and $Q_{lower}' = (p_{lower} - p_{lface})/l_{lower}$. This modified equation is solved together with the dynamic equation (Eq. 2) by means of an iterative method to resolve the nonlinear fluid–panel coupling. This new approach appears to give a faster convergence than before. The details of the implementation of the numerical treatment of resolving fluid–panel coupling are referred to Fan [8].

3 Flow-Induced Structural Instability

In order to validate the capability of the numerical methodology of solving fluid–panel interaction, the experimental study carried out by Liu [4] on the instability of flexible panel installed on the wall of a duct carrying a low-speed uniform $\hat{U} = 35~\text {m/s}$ is selected as the benchmark for the validation. In the experiment, a 0.025-mm-thick steel sheet was flush-mounted in a section of rigid flow duct and backed by a rigid cavity as shown in Fig. 2. The entire test section was installed in a closed-loop acoustic wind tunnel. When the flow was turned on, the vibrating velocity of the sheet was measured. The same set of physical parameters are taken for the present calculation: the panel and cavity length $\hat{L}_p = 300~\text {mm}$, the duct width and cavity height $\hat{H} = 100~\text {mm}$, the upstream and downstream length are $1250~\text {mm}$ and $750~\text {mm}$, respectively, the panel density $\hat{\rho }_p = 7800~{{\text {kg}}/{\text {m}}^3}$, the panel thickness $\hat{h}_p = 0.025~\text {mm}$, Young’s modulus $\hat{E}_p = 193~\text {GPa}$, the panel tension $\hat{T}_x = 40~\text {N}$, and the mean flow speed $\hat{U} = 35~\text {m/s}$. Since the background noise level within the entire wind tunnel was highly suppressed in its design, the panel vibration was found solely induced by the unsteady viscous effects on its surface flow. All variables are normalized by $\hat{L}_{\textit{0}}=$ panel length $\hat{L}_{p}$, ambient acoustic velocity $\hat{c}_{\textit{0}}=340\,\text {m/s}$, time $\hat{t}_{\textit{0}}=\hat{L}_{\textit{0}}/\hat{c}_{\textit{0}}$, ambient density $\hat{\rho }_{\textit{0}}=1.225\,{{\text {kg}}/{\text {m}}^{3}}$, pressure $\hat{\rho }_{\textit{0}}\hat{c}_{\textit{0}}^{2}$, and ambient temperature $\hat{T}_{\textit{0}}$. Uniform mesh is used with grid sizes $dx = 0.02$ and $dy = 0.0067$ for both x and y directions.

Fig. 2

Schematic configuration of the experiment setting of Liu [4] (not-to-scale)

Before carrying out the calculation of panel instability, it is important to realize how accurate the aeroacoustic model can capture the background mean velocity profile of the duct flow. It is because under the action of fluid viscosity a wrong velocity profile on duct wall would induce a wrong wall shear stress which might in turn drive a wrong panel instability mode. Liu [4] reported in his work a structural instability experiment at $\hat{U} = 35~\text {m/s}$ but only provided a mean velocity profile measurement at $\hat{U} = 30~\text {m/s}$. So an additional case with $\hat{U} = 30~\text {m/s}$ has to be calculated for appropriate comparison with the experimental data in Fig. 3. The figure shows the numerical velocity profile agrees favorably well with experimental data. The normalized velocity boundary thickness from calculation is 0.039 which agrees very well with that of 0.037 obtained from the experiment. In the very close proximity to duct wall, i.e., $y/H \le 0.02$, the two profiles overlap fully. It provides further support that the aeroacoustic model is able to generate correct mean velocity profile for initiating the flow-induced panel structural instability observed in experiment.

Fig. 3

Mean velocity profile at the inlet. —–, numerical result; – – –, experimental data

Liu [4] reported the emergence of dynamic instability, known as flutter, of the panel in his experiment with duct flow velocity $\hat{U} = 35~\text {m/s}$. In essence when the panel deflection gets large enough, the panel will exhibit a post-flutter oscillation known as limit cycle oscillation. Such phenomenon arises when the effective panel stiffness is so strengthened by panel deformation up to a level that is strong enough to balance the external force exciting the panel oscillation. The time traces of vibrating velocity at two locations, at $x = -0.17$ and 0, obtained from numerical calculation are shown in Fig. 4. After the onset of instability, the amplitudes of panel vibration grow and become saturated after $t \approx 200$. Eventually they enter into time stationary states after $t \approx 800$, and the limit cycle oscillations occur. Axial mode analysis established in Fan et al. [2] is conducted to derive the spatial responses of panel vibration during limit cycle oscillation (Fig. 5). Evidently, the panel response is dominated by the second in vacuo bending mode with $k = 1$. Its first and second harmonics are also resolved.

Fig. 4

Time traces of vibrating velocity. a At $x = -0.17$. b At $x = 0$

Fig. 5

Panel spatial response. a The modal spectrum of panel velocity. b The distributions of panel velocity amplitude

Figure 6 shows a comparison of the arithmetic average of the calculated vibration spectra distributed along the panel with the corresponding one reported in experiment. The numerical result shows a favorable agreement with the experimental data. The first numerical peak emerges at frequency $f_{\textit{0}} = 0.07$ which shows a $-13.5 \%$ frequency shift compared to the experiment result. The difference may be attributed to the limitation of one-dimensional assumption in the calculation of panel dynamics (Eq. 2). The lack of vibration freedom along spanwise direction tends to promote panel resonant vibrations at low frequencies as easily seen from existing analytical solutions [15]. The overall vibration amplitude at dominant frequency appears to be much stronger than that observed in experiment. This might be due to the fact that in experiment the distribution of vibration amplitude over the two-dimensional panel was not uniform so certain canceling effects prevailed in the averaging of spectra. Furthermore, it is easy to observe in Fig. 6 that there are two peaks showing up in the experimental spectrum but not in the calculation. After careful investigation, their emergence is found that related to the excitation of wind tunnel duct acoustic modes during the execution of experiment.

Fig. 6

Frequency spectrum of the vibration velocity on the whole panel. —, numerical result with viscous flow; $\cdots \cdots$, numerical result with inviscid flow; – – –, experimental data; $- \cdot - \cdot -$, duct mode frequencies

The frequency of acoustic resonance within an open-ended duct with rectangular cross section can be estimated from the equation [16, 17] as $f_{{n_1},{n_2},{n_3}} = (c_{\textit{0}}/2) [ {n_1}^2/ ( {l_1} + 2l'' )^2 + {n_2}^2/{l_2}^2 + {n_3}^2/{l_3}^2 ]^{1/2}$, where $c_{\textit{0}}$ is the speed of sound, ${l_1}$, ${l_2}$, and ${l_3}$ are the length, height, and width of the duct, respectively, ${n_1}$, ${n_2}$, and ${n_3}$ are the mode numbers along respective directions, and $l''$ is the end correction. When resonance occurs, the fluid medium at each open end oscillates and the pressure there is not constant. Thus, the effective length for resonant oscillation inside the duct will be a bit longer than its physical length [16, 17] and an end correction is required. For ${k}{a}<0.5,$ the end correction can be approximately determined as ${l}'' = 0.613{a}$ [17], where ${a}=({S}/\pi )^{1/2}$ is the characteristic dimension of the duct cross section with area S, and ${k}=2\pi /\lambda$. The normalized length of the wind tunnel duct section from the nozzle to the diffuser is 7.67 which gives the frequency of the second mode $f_{{2},{0},{0}} = 0.13$. This value matches exactly the second peak in the experimental spectrum in Fig. 6. Besides, Liu [4] opened two openings, each with dimension $50~\text {mm}\times 50~\text {mm}$, upstream and downstream of the test section in his experiment so as to simulate a mean pressure drop along test section similar to those commonly observed in practical ventilating systems. However, that way might introduce extra possibility of open-ended duct resonance between these two new openings. According to Liu [4], the normalized separation between two openings was approximately 5.56. It is not difficult to determine the frequency of second resonant duct mode as $f_{{2},{0},{0}} = 0.18$. Coincidently, this value matches exactly the third peak observed in the experimental spectrum in Fig. 6. Therefore, it is not surprised to see the two identified resonant duct modes, rather than flow-induced instability, might effectively excite the panel to give the two peaks in the spectrum. In our numerical calculation, both the duct inlet and outlet are modeled with truly anechoic boundary conditions so resonance along duct length is impossible. On the other hand, the mean pressure drop in time stationary solution is similar to that in realistic systems so no additional opening is required. These explain why no similar extra peak is observed in the numerical spectrum.

Using inviscid flow assumption, the same problem is also calculated to highlight the importance of fluid viscosity in the onset of flow-induced structural instability. In essence, $\varvec{F}_{v}=\varvec{G}_{v}=0$ are set in Eq. 1 and impose sliding condition on all duct walls and panel surface in the calculation. Evident in Fig. 6, the inviscid solution gives the worst agreement with the experiment. Its first peak occurs at a frequency $f = 0.065$ which is $19.8\%$ lower than that observed in the experiment, a much larger difference with viscous solution. Furthermore, several more peaks show up in the inviscid spectrum but none of them agrees with experimental data. It is also interesting to see it is the inviscid second peak, rather than the first one, which dominates the spectrum. All these observed discrepancies may be attributed to the fact that duct wall boundary layer does not develop due to the lack of fluid viscosity and the pressure along the duct maintains more or less constant. This also leads to stronger net normal force acting on the panel than in viscous calculation. All these changes altogether contribute to a different exciting force, so a different structural instability result prevails.

The flow-induced vibrating panel radiates acoustic waves to upstream and downstream. The acoustic pressure fluctuation along the duct centerline within one period of the dominant frequency, $t_{\textit{1}} = 1/f_{\textit{0}}=14.3$, is shown in Fig. 7. The upstream radiation is in the form of simple plane wave and is much stronger than the downstream radiation. The acoustic power W radiated by the panel can be determined by integrating the acoustic intensity passing through duct cross section enclosing the panel [18], as $W = \int _{0}^{H} ( \bar{\rho }u' + p'\bar{u}/c^2 ) ( p'/\bar{\rho } + \bar{u}u' + \bar{v}v' ) dy$, where $\bar{\rho }$, $\bar{u}$, $\bar{v}$ are the mean values of density and velocities in x- and y-directions, respectively, and $p'$, $u'$, $v'$ are their fluctuations. The average acoustic powers over $t_1$ in upstream and downstream are $-1.5\times 10^{-9}$ (through $x=-2.5$) and $3.6\times 10^{-8}$ (through $x=2.5$), respectively. The acoustic power radiated to upstream is 5.9 db larger.

Fig. 7

Pressure fluctuation along the duct centerline within one period of the dominant vibrating frequency, $t_{\textit{1}} = 1/f_\textit{0}$

In addition to acoustic radiation, the excited panel also produces flow fluctuations at the same frequency which convect downstream. When the fluid impinges the lower wall, it is forced to turn its direction from negative to positive y; for example, at $x\approx 1.3$ in Fig. 8a, an high-pressure zone is created as shown in the same location (Fig. 8b). On the contrary, a low-pressure zone is created on the wall following fluid motion toward the wall, for example at $x\approx 1$. Together with the acoustic wave, the convecting flow fluctuations create a staggered pressure distribution downstream of the panel.

Fig. 8

Snapshot at $t/t_{\textit{1}} = 0.2$. a Velocity fluctuation in y-direction. b Pressure fluctuation

4 Aeroacoustic–Structural Interaction in Practical Silencer Design

An experimental study of the transmission loss of a drum-like silencer installed in a low-speed duct [19] is selected as the benchmark case for the evaluation of the accuracy of the numerical methodology in solving aeroacoustic–structural interaction in realistic situation. According to Fan et al. [2], aeroacoustic–structural interaction refers to a nonlinear problem to which the unsteady flow, acoustics, and structural dynamics contribute equally in a fully coupled manner. The acoustical performance of the drum-like silencer in the selected experimental study fits this context of aeroacoustic–structural interaction very well. The noise reduction of the silencer cannot be deduced accurately by resolving the flow–structure interaction first.

Figure 9 shows a two-dimensional computational domain that replicates key features of the silencer design in the experiment. The silencer is constructed as two opposing side branch cavities each of which is covered by a flexible panel. An acoustic wave propagates along the duct from left to right along with the flow. Each panel responds to the excitation of the convected acoustic wave and vibrates. The induced vibration reflects the incident acoustic wave and modifies the dynamics of flow in its vicinity. As seen from a previous study assuming inviscid duct flow [2], such aeroacoustic–structural interaction plays a critical role in determining the effectiveness of acoustic reflection by the panels and consequently the overall silencer transmission loss performance. However, viscous flow prevails in all practical situation and the effect of viscosity is not understood. The same set of experiment parameters are taken for the calculation: the panel and cavity length $\hat{L}_p = 500~\text {mm}$, the duct width and cavity height $\hat{H} = 100~\text {mm}$, the upstream and downstream length are 1000 and $870~\text {mm}$, respectively, and the panel mass per unit area $\hat{\rho }_p\hat{h}_p = 0.17~{{\text {kg}}/{\text {m}}^2}$. The range of frequency of interest goes from 20 to $1000~\text {Hz}$. The normalization used in the calculation is same as that in Sect. 3. The ambient density, pressure, and temperature are fixed at the outlet. No-slip condition is applied for all rigid duct walls and flexible panel surfaces. A broadband incident acoustic plane wave covering frequency range f from 0.0294 to 1.4706 with a resolution $\varDelta {f}=0.0147$ is introduced into the duct domain. Its excitation function is expressed as $p'_{inc} = p_A \sum \nolimits _{n=1}^{99} \sin ( 2\pi t f_n + \theta _n )$, where $p_A = 4.5\times 10^{-4}$ $({\sim }110\,\text {dB})$ is constant to all $f_n$, and $\theta _n$ is uniformly distributed random phase generated by random number generation function in MATLAB. A uniform flow profile is applied at the inlet to let the duct boundary layer develop freely. A full rigid duct case is first calculated to develop the proper mean flow profile in the whole flow field. The steady solution is then used as the initial condition for the calculation with flexible panel. The initial pressure in the cavity is set as same as the mean pressure in the duct over the panel to avoid large deflection of the panel by the static pressure that affects the panel response. In the mesh, uniform grid distribution is used for both x and y directions with $dx = 0.02$ and $dy = 0.0033$.

Fig. 9

Schematic configuration of the drum-like silencer (not-to-scale)

The instantaneous distribution of vibrating velocities of a tensioned panel with $T_x = 0.108$ ($8213.38~\text {N}$) excited by an acoustic wave convecting with a flow $M=0.026$ ($\hat{U} = 9~\text {m/s}$) was measured in the experiment [19]. Figure 10 shows a comparison between the calculated transmission loss TL with excitation frequencies $f = 0.294$ ($200~\text {Hz}$) and 0.618 ($420 ~\text {Hz}$) and the experimental data. The numerical results have good agreement with the experimental data at both frequencies. The maximum difference is 5.2 and $10.8 \%$ in the results of $f = 0.294$ and 0.618, respectively.

Fig. 10

Comparison of instantaneous distribution of vibrating velocities with $T_x = 0.108$ and $M=0.026$. a $f = 0.294$ ($200 \text {Hz}$). b $f = 0.618$ ($420 \text {Hz}$). —, numerical result; – – –, experimental data

Fig. 11

Comparison of the TL spectra of numerical results to experimental data. —, numerical result with viscous flow; $- \cdot - \cdot -$, numerical result with inviscid flow; $\bigcirc$, experimental data; – – –, duct mode frequency $f_{{2},{0},{0}}$

A comparison of the calculated transmission loss TL with $T_x = 0.116$ ($8821.78\text {N}$) and $M=0.045$ ($\hat{u}_{\textit{0}} = 15\,\text {m/s}$) and the experimental data is illustrated in Fig. 11. An excellent agreement between the numerical result with viscous flow and the experimental data is found except the peak at $f=0.36$. It is underpredicted by approximately $5~\text {db}$. The difference at this frequency can be explained by an investigation of possible wind tunnel duct modes. In the experiment, the test section outlet is connected to a diffuser. The sudden change in area there may cause acoustic reflection. On the other hand, as confirmed in our previous study (Fan et al. [2]), the panel leading edge is responsible for the reflection of incident wave to upstream due to the sharp area change created by the vibrating panel. Reflection of upstream going acoustic wave to downstream is also possible. If the duct section between these two locations is taken as an open-ended duct, it is not difficult to see that its length equal to 2.74 gives a frequency of the second mode $f_{{2},{0},{0}} = 0.36$, which matches the observed peak in the experiment well. In the presence of his mode inside the wind tunnel, the nodal point was just $15 \text {mm}$ away from the microphone in the experiment. The microphone then received a very weak acoustic signal that an over-estimated transmission loss was deduced. However, the numerical calculation does not suffer such duct mode problem. All these observations show clearly that the experimental TL at $f = 0.36$ in Fig. 11 is erroneous and not reliable. However, the data at other frequencies is still trustworthy because neither matches any other possible open-ended wind tunnel duct modes. If the data at $f = 0.36$ is ignored, the maximum difference between numerical and experimental TL is only $0.5~\text {db}$. Such excellent agreement firmly establishes the strong capability of the present numerical methodology in capturing the nonlinear aeroacoustic–structural interaction in the problem correctly. The other difference in the TL levels might be attributed to two reasons. One is due to the fact that the present two-dimensional calculation does not replicate fully the three dimensionality of the experiment. Some three-dimensional panel vibration and duct acoustic modal behaviors are not properly included. Another is the mesh is not fine enough to capture small-scale flow instability. Any acoustic reactive response caused by the panel vibration in response to such instability in the experiment cannot be captured fully.

The importance of the inclusion of viscous effect is also highlighted in Fig. 11 in which a comparison of TL derived from viscous and inviscid solutions is also shown. They show similar overall trends, but the inviscid solution shows obvious overprediction at around $f = 0.5$–0.6 and at the peak at $f = 0.32$. The difference between inviscid solution and experimental data at the peak is as large as $5.7~\text {db}$.

5 Concluding Remarks

A numerical methodology has been introduced to study the nonlinear fluid–structure interaction and its acoustics in internal viscous flow. It is solving the coupled governing equations that include both fluid and structural dynamics at the fluid–structure interface. Two experimental studies are selected as the benchmark cases for validation of the methodology.

The first case is to study the flow-induced structural instability of a thin flexible panel flush-mounted in a duct and backed by cavity. Under a subsonic flow, the vibration of the panel is induced and becomes the limit cycle oscillation. The numerical result has a favorable agreement with the experimental data that validated the capability of the numerical methodology for capturing the fluid–structural interaction. An interesting acoustic response is found that the upstream radiation by the panel vibration is $5.9~\text {db}$ larger than the downstream in terms of acoustic power. The result also shows the viscous effect strongly affects the structural response and inviscid assumption can lead to incorrect result.

Another case is a study on a practical silencer design that makes use of a flexible duct segment constructed by elastic panels. Both acoustic and structural responses are validated with excellent agreement with the experiment. On the other hand, the viscous solution also gives a more accurate prediction than the inviscid solution on the aeroacoustic–structural responses.