Stochastic Models of Tumor Induced Angiogenesis

Abstract

Angiogenesis is a complex multiscale process by which diffusing vessel endothelial growth factors induce sprouting of blood vessels that carry oxygen and nutrients to hypoxic tissue. There is strong coupling between the kinetic parameters of the relevant branching—growth—anastomosis stochastic processes of the capillary network, at the microscale, and the family of interacting underlying biochemical fields, at the macroscale. A hybrid mesoscale tip cell model involves stochastic branching, fusion (anastomosis) and extension of active vessel tip cells with reaction-diffusion growth factor fields. Anastomosis prevents indefinite proliferation of active vessel tips, precludes a self-averaging stochastic process and ensures that a deterministic description of the density of active tips holds only for ensemble averages over replicas of the stochastic process. Evolution of active tips from a primary vessel to a tumor adopts the form of an advancing soliton that can be characterized by ordinary differential equations for its position, velocity and a size parameter. A short review of other angiogenesis models and possible implications of our work is also given.

1 Introduction

The growth of blood vessels out of a primary vessel or angiogenesis is a complex multiscale process responsible for organ growth and regeneration, tissue repair, wound healing and many other natural operations in living beings [1,2,3,4,5]. Angiogenesis is triggered by lack of oxygen (hypoxia) experienced by cells in some tissue. Such cells segregate growth factors that diffuse and reach a nearby primary blood vessel. In response, the vessel wall opens and issues endothelial cells that move towards the hypoxic region, build capillaries and bring blood, oxygen and nutrients to it. Once blood and oxygen have reached the hypoxic region, segregation of growth factors stops, anti-angiogenic substances may be segregated and a regular vessel network may have been put in place, after pruning capillaries with insufficient blood flow. In normal functioning, angiogenic and anti-angiogenic activities balance. Imbalance may result in many diseases including cancer [6]. In fact, after a tumor installed in tissue reaches some 2 mm size, it needs additional nutrients and oxygen to continue growing. Its hypoxic cells segregate growth factors and induce angiogenesis. Unlike normal cells, cancerous ones continue issuing growth factors and attracting blood vessels, which also supply them with a handy transportation system to reach other organs in the body.

Tumor-induced angiogenesis research started with J. Folkman’s pioneering work in 1971 [6]. In addition to vast experimental research [7], models and theory [8] substantially contribute to understanding angiogenesis and developing therapies. In angiogenesis, events happening in cellular and subcellular scales unchain endothelial cell motion and proliferation and build millimeter scale blood sprouts and networks thereof [2,3,4,5]. Models range from very simple to extraordinarily complex and often try to illuminate some particular mechanism; see the review [8]. Realistic microscopic models involve postulating mechanisms and a large number of parameters that cannot be directly estimated from experiments, but they often yield qualitative predictions that can be tested. An important challenge is to extract mesoscopic and macroscopic descriptions of angiogenesis from the diverse microscopic models.

During angiogenesis, the relevant branching, growth and anastomosis (vessel fusion) stochastic processes of the capillary network at the microscale are strongly coupled to the interacting underlying biochemical and mechanical fields at the macroscale. In Sect. 2, we consider a hybrid mesoscale tip cell model that involves stochastic branching, anastomosis and extension of active vessel tip cells with reaction-diffusion growth factor fields [9]. Numerical simulations of the model show that anastomosis prevents indefinite proliferation of active vessel tips [10]. Then fluctuations about the mean of the density of active tips are not small and the stochastic process is not self-averaging. However, as shown in Sect. 3, it is possible to obtain a deterministic description of the density of active tips for ensemble averages over replicas of the stochastic process. The deterministic description consists of an integro-partial differential equation for the density of active vessel tips coupled to a reaction-diffusion equation for the growth factor [9, 10]. As shown in Sect. 4, the evolution of active tips from a primary vessel to a tumor adopts the form of an advancing soliton-like wave that can be characterized by ordinary differential equations for its position, velocity and a size parameter [11, 12]. These results may pave the way to assess optimal control of angiogenesis and therapies based on it.

What are the implications of our work? As described in Sect. 5, there are other models related to ours in which the vessel extension is described by random walks [13, 14], and our methodology may be used to extract deterministic descriptions for the density of active tips amenable to analysis. We could also seek to extend microscopic cellular Potts models (described in Sect. 6) to mesoscales and study them using our methods. The role of blood flow in remodeling vascular networks is briefly considered in Sect. 7. Further remarks are included in our conclusions in Sect. 8.

2 Langevin Tip Cell Models

Tip cell models assume that the tip cells are motile and non-proliferating whereas stalk cells build the blood vessel following the trajectories of the former. Assuming that the tip cells form point particles, their trajectories constitute the blood vessels advancing toward the tumor. In 1991, Stokes and Lauffenburger considered the capillary sprouts as particles of unit mass subject to chemotactic, friction and white noise forces [15, 16]. The distribution of tumor angiogenic factors (TAF) issuing from a small circular tumor is a known stationary non-uniform function. Associated to each sprout, its cell density satisfies a rate equation that takes into account proliferation, elongation, redistribution of cells from the parent vessel, branching and anastomosis. They did not consider the depletion effect that advancing sprouts would have on the TAF concentration. Later tip cell models combined a continuum description of fields influencing cell motion (chemotaxis, haptotaxis, ...) with random walk motion of individual sprouts that experience branching and anastomosis. Capasso and Morale [17] used ideas from these approaches to propose a hybrid model of Langevin-Ito stochastic equations for the sprouts undergoing chemotaxis, haptotaxis, branching and anastomosis coupled to reaction-diffusion equations for the continuum fields. In this model, the evolution of the continuum fields is influenced by the growing capillary network through smoothed (or mollified) versions thereof [18]. Capasso and Morale also attempted to derive a continuum equation for the density of moving tip cells from the stochastic equations but could not account for branching and anastomosis [17]. In what follows, we present a simplified hybrid model that ignores haptotaxis and derive a deterministic description for the density of active tips [9, 10, 19]. As in the Capasso-Morale model, the influence of haptotaxis can be included by adding reaction-diffusion equations for fibronectin and matrix-degrading enzymes [20]. The influence of blood circulation through the newly created blood vessels and secondary branching therefrom can be modeled as in [21].

Fig. 1

Network of blood vessels simulated by the stochastic model of tumor induced angiogenesis. The level curves of the density of the tumor angiogenic factor (vessel endothelial growth factor) are also depicted [11]

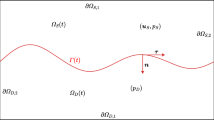
We shall consider a slab geometry as indicated in Fig. 1, which is the result of a numerical simulation of the stochastic model. The extension of the ith capillary sprout with position $\mathbf {X}^i(t)$ and velocity $\mathbf {v}^i(t)$ is given by the nondimensional Langevin-Ito stochastic equation

$$\begin{aligned} d\mathbf {X}^i(t)= & {} \mathbf {v}^i(t)\,dt \nonumber \\ d\mathbf {v}^i(t)= & {} \beta \left[ -\mathbf {v}^i(t) + \mathbf {F} \left( C(t,\mathbf {X}^i(t))\right) \right] dt + \sqrt{\beta }\, d\mathbf {W}^i(t) \end{aligned}$$

(1)

for $t > T^i$ ($T^i$ is the random birth time of the ith tip). Here $C(t,\mathbf {x})$ is the TAF concentration. At time $T^i$, the velocity of the newly created tip is selected out of a normal distribution with mean $\mathbf {v}_0$ and variance $\sigma _v^2$, while the probability that a tip branches from one of the existing ones during an infinitesimal time interval $(t,t + dt]$ is proportional to

$$\begin{aligned} \sum _{i=1}^{N(t,\omega )}\alpha (C(t,\mathbf {X}^i(t)))dt. \end{aligned}$$

(2)

Here $N(t,\omega )$ is the number of tips at time t for a realization $\omega$ of the stochastic process and

$$\begin{aligned} \alpha (C)=\frac{A\, C}{C+1}, \end{aligned}$$

(3)

where A is a positive constant. We ignore secondary angiogenesis from newly formed capillaries [21]. The tip i disappears at a later random time $\varTheta ^i$, either by reaching the tumor or by anastomosis, i.e., by meeting another capillary. At time t, anastomosis for the ith tip occurs at a point $\mathbf {x}$ such that $\mathbf {X}^i(t)=\mathbf {x}$ and $\mathbf {X}^j(s)=\mathbf {x}$ for another tip that was at $\mathbf {x}$ previously, at time $s<t$. In (1), $\mathbf {W}^i(t)$ are i.i.d. Brownian motions, and $\beta$ (friction coefficient) is a positive parameter [9, 10, 12]. The chemotactic force $\mathbf {F}$ controlling tip cell migration in response to the TAF released by tumor cells is

$$\begin{aligned} \mathbf {F}(C)= & {} \frac{\delta _1}{1 + \varGamma _1 C} \nabla _x C\,, \end{aligned}$$

(4)

where $\delta _1$, and $\varGamma _1$ are positive parameters. The TAF diffuses and is consumed by advancing vessel tips according to [10]

$$\begin{aligned} \frac{\partial C}{\partial t}(t,\mathbf {x})= & {} \kappa _c\varDelta _x C(t,\mathbf {x})- \chi _c C(t,\mathbf {x})\left| \sum _{i=1}^{N(t,\omega )}\mathbf {v}^i(t)\,\delta _{\sigma _x}(\mathbf {x}-\mathbf {X}^i(t))\right| . \end{aligned}$$

(5)

Here $\kappa _c$ and $\chi _c$ are positive parameters, while $\delta _{\sigma _x}$ is a regularized delta function (e.g., a Gaussian with standard deviation $\sigma _x$). We are assuming that extending the vessel consumes TAF. As the vessel extends a length $|\mathbf {v}^i(t)|\, dt$ during the time interval between t and $t+dt$, the consumption should be proportional to $|\mathbf {v}^i(t)|$. The difference between the sum of the vector lengths and that indicated in (5) is negligible for the parameters and geometry considered in this paper (it amounts to having a coefficient 1.28 times larger than $\chi _c$ in the previous equation). Having the length of the flux vector as in (5) is convenient. Initial and boundary conditions for the TAF field C have been proposed in [9, 10].

The concentration of all vessels per unit volume in the physical space, at time t (i.e., the vessel network $\mathbf {X}(t,\omega )$) is [10]

$$\begin{aligned} \delta (\mathbf {x}-\mathbf {X}(t,\omega ))= \int \limits _0^t\sum _{i=1}^{N(s,\omega )}\delta _{\sigma _x}(\mathbf {x}-\mathbf {X}^i(s,\omega ))\, ds. \end{aligned}$$

(6)

3 Deterministic Description

We shall see that we can understand the results of numerical simulations of the stochastic process described in the previous section by first finding a deterministic description of the density of active tips. The latter evolves in the form of a slowly varying soliton-like wave that we can analyze. Without performing numerical simulations of the stochastic process, we could guess that such a deterministic description could hold whenever the number of active tips arising from branching becomes very large. In such a case, we could use the law of large numbers to achieve such a description. This was the point of view adopted in the papers [9, 17]. However, anastomosis kills off so many active vessel tips that their number hardly grows to a hundred. Then we need a different point of view in order to derive a deterministic description. The alternative is the Gibbsian idea of considering an ensemble of replicas of the original stochastic process and carrying out arithmetic averages over the number of replicas.

We can find a deterministic description of the stochastic model for the densities of active vessel tips and the vessel tip flux, defined as ensemble averages over a sufficient number $\mathscr {N}$ of replicas (realizations) $\omega$ of the stochastic process:

$$\begin{aligned} p_{\mathscr {N}}(t,\mathbf {x},\mathbf {v})= & {} \frac{1}{\mathscr {N}}\sum _{\omega =1}^\mathscr {N}\sum _{i=1}^{N(t,\omega )}\delta _{\sigma _x}(\mathbf {x}-\mathbf {X}^i(t,\omega ))\, \delta _{\sigma _v}(\mathbf {v}-\mathbf {v}^i(t,\omega )),\end{aligned}$$

(7)

$$\begin{aligned} \tilde{p}_{\mathscr {N}}(t,\mathbf {x})= & {} \frac{1}{\mathscr {N}}\sum _{\omega =1}^\mathscr {N}\sum _{i=1}^{N(t,\omega )}\delta _{\sigma _x}(\mathbf {x}-\mathbf {X}^i(t,\omega )), \end{aligned}$$

(8)

$$\begin{aligned} \mathbf {j}_{\mathscr {N}}(t,\mathbf {x})= & {} \frac{1}{\mathscr {N}}\sum _{\omega =1}^\mathscr {N}\sum _{i=1}^{N(t,\omega )}\mathbf {v}^i(t,\omega )\delta _{\sigma _x}(\mathbf {x}-\mathbf {X}^i(t,\omega )). \end{aligned}$$

(9)

As $\mathscr {N}\rightarrow \infty$, these ensemble averages tend to the tip density $p(t,\mathbf {x},\mathbf {v})$, the marginal tip density $\tilde{p}(t,\mathbf {x})$, and the tip flux $\mathbf {j}(t,\mathbf {x})$, respectively.

Fig. 2

Marginal density of active vessel tips resulting from an average over 400 replicas of the stochastic process according to Eq. (8) at four different times: a 12 h, b 24 h, c 32 h, and d 36 h. At these times, the numbers of active tips are (a) 56, (b) 69, (c) 72, and (d) 66, [10]

Fig. 3

Marginal density of active vessel tips at the x axis resulting from an average over 400 replicas of the stochastic process as in Fig. 2. The primary vessel at $x=0$ issues a pulse that marches toward the tumor at $x=1$, [10]

Figures 2 and 3 show the outcomes of typical simulations of ensemble averaged marginal densities: The two-dimensional lump shown in Fig. 2 is created at the primary vessel at $x=0$ and marches to the tumor at $x=1$. Its profile along the x axis is the soliton-like wave shown in Fig. 3.

Reference [10] shows that the angiogenesis model has a deterministic description based on the following equation for the density of vessel tips, $p(t,\mathbf {x},\mathbf {v})$,

$$\begin{aligned}&\frac{\partial p}{\partial t}(t,\mathbf {x},\mathbf {v})=\alpha (C(t,\mathbf {x}))\, p(t,\mathbf {x},\mathbf {v})\delta _{\sigma _v}(\mathbf {v}-\mathbf {v}_0) - \varGamma \, p(t,\mathbf {x},\mathbf {v}) \int \limits _0^t \tilde{p}(s,\mathbf {x})\, ds \nonumber \\&\quad - \mathbf {v}\cdot \nabla _x p(t,\mathbf {x},\mathbf {v}) - \beta \nabla _v \cdot [(\mathbf {F}(C(t,\mathbf {x}))-\mathbf {v}) p(t,\mathbf {x},\mathbf {v})] + \frac{\beta }{2} \varDelta _{v} p(t,\mathbf {x},\mathbf {v}), \qquad \quad \end{aligned}$$

(10)

$$\begin{aligned}&\tilde{p}(t,\mathbf {x})=\int p(t,\mathbf {x},\mathbf {v}')\, d \mathbf {v'}. \end{aligned}$$

(11)

The two first terms on the right hand side of (10) correspond to vessel tip branching—from Eqs. (2) and (3)—and anastomosis, respectively. While the branching term follows from (2) and (3) in a straightforward manner, deducing the anastomosis integral term is the real breakthrough from past work achieved in [9]. The anastomosis coefficient, $\varGamma$, has to be fitted by comparison of the numerical solution of the deterministic equations and ensemble averages of the stochastic description, [10]. The other terms on the right hand side of (10) are in the Fokker-Planck equation that corresponds to the Langevin equation (1) in the usual manner [22]. While the branching term follows directly from the stochastic branching process, anastomosis occurs when a moving vessel tip at time $t>0$ encounters a preexisting vessel whose tip was at the same place at an earlier time $s<t$. At time t, a moving vessel tip can reach an area $d\mathbf {x}$ about $\mathbf {x}$ that is either unoccupied or occupied by another vessel. In the latter case, it anastomoses. The occupation time density of the area $d\mathbf {x}$ about $\mathbf {x}$ is proportional to $\int _0^t\tilde{p}(s,\mathbf {x})\,ds$—the ensemble average of the vessel network density (6). Then the rate of anastomosis should be proportional to $p(t,\mathbf {x},\mathbf {v})$ times this occupation time density [10]. Equation (5) becomes

$$\begin{aligned} \frac{\partial C}{\partial t}(t,\mathbf {x})=\kappa _c\varDelta _x C(t,\mathbf {x})- \chi _c C(t,\mathbf {x})\,| \mathbf {j}(t,\mathbf {x})|, \end{aligned}$$

(12)

where $\mathbf {j}(t,\mathbf {x})$ is the current density (flux) vector at any point $\mathbf {x}$ and any time $t\ge 0$,

$$\begin{aligned} \mathbf {j}(t,\mathbf {x})= \int \mathbf {v}' p(t,\mathbf {x},\mathbf {v}')\, d \mathbf {v'}. \end{aligned}$$

(13)

Carpio and collaborators have shown that the deterministic system of Eqs. (10)–(12) together with appropriate boundary and initial conditions has a unique solution that depends smoothly on parameters [23, 24].

Figure 4 shows that the outcome of a numerical simulation of the deterministic description is similar to that of the stochastic process.

Fig. 4

Marginal density of active vessel tips resulting from a numerical simulation of the deterministic equations with appropriate boundary conditions for the same times as in Fig. 2 [9, 10]. Better agreement between both descriptions requires fine tuning of the boundary conditions

4 Soliton and Collective Coordinates

In the overdamped limit of negligible inertia in (1), we obtain the simpler Langevin-Ito equation: $d\mathbf {X}^i(t)\approx \mathbf {F}(C(t,\mathbf {X}^i(t)))\, dt+ \beta ^{-1/2}d\mathbf {W}^i(t)$ [11]. By using the Chapman-Enskog perturbation method whose details are explained in [12], it is then possible to derive the following reduced equation for the marginal tip density,

$$\begin{aligned} \frac{\partial \tilde{p}}{\partial t}+\nabla _x\cdot (\mathbf {F}\tilde{p})-\frac{1}{2\beta }\varDelta _x\tilde{p}=\mu \,\tilde{p} - \varGamma \tilde{p}\int _0^t\tilde{p}(s,\mathbf {x})\, ds, \end{aligned}$$

(14)

$$\begin{aligned} \mu =\frac{\alpha }{\pi }\left[ 1+\frac{\alpha }{2\pi \beta (1+\sigma _v^2)}\ln \left( 1+\frac{1}{\sigma _v^2}\right) \right] . \end{aligned}$$

(15)

The drift terms in Eq. (14) are those corresponding to the simpler Langevin-Ito equation for $\mathbf {X}^i(t)$ that results in the overdamped limit. The birth and death terms are obtained by integration of the corresponding ones on right hand side of (10) over velocity. However, the perturbation procedure changes the coefficient $\alpha (C)$ to the related function $\mu (C)$ in (15) [12]. Equation (14) has the following soliton-like solution for constant $\mathbf {F}=(F_x,F_y)$, $\mu$, and zero diffusion, $1/\beta =0$:

$$\begin{aligned} \tilde{p}_s=\frac{(2K\varGamma +\mu ^2)c}{2\varGamma (c-F_x)}{\text {sech}}^2\left[ \frac{\sqrt{2K\varGamma +\mu ^2}}{2(c-F_x)}(x-X(t))\right] ,\quad \dot{X}\equiv \frac{dX}{dt}=c, \end{aligned}$$

(16)

where K is a constant. In fact [11], consider $\tilde{p}_s= {\partial }P(x-ct)/\partial t=-c\, P'(\xi )$, $\xi =x-ct$, which, inserted in (14) with $1/\beta =0$, yields

$$(F_x-c)P''=\mu P'-\varGamma PP'\Longrightarrow (c-F_x)P'=\frac{\varGamma }{2} P^2-K-\mu P.$$

Setting $P=\nu \tanh (\lambda \xi )+\mu /\varGamma$, we find $\nu ^2=(\mu ^2+2K\varGamma )/\varGamma ^2$ and $2\nu \lambda (c-F_x)/\varGamma =-\nu ^2$, thereby obtaining

$$\begin{aligned} P=\frac{\mu }{\varGamma }-\frac{\sqrt{2K\varGamma +\mu ^2}}{\varGamma }\tanh \left[ \frac{\sqrt{2K\varGamma +\mu ^2}}{2(c-F_x)}(\xi -\xi _0)\right] . \end{aligned}$$

Here $\xi _0$ is a constant of integration. Thus $\tilde{p}_s=\partial P/\partial t=-c P'$ is given by (16).

Numerical simulations on a slab geometry show that the marginal tip density evolves toward (16) after an initial stage [11, 12]. It is an open problem to prove this stability result even for a one-dimensional version of Equation (14) on the whole real line and having constant values of $\mathbf {F}$ and $\mu$.

A small diffusion and slowly varying continuum field C produce a moving soliton whose shape and speed are slowly changing. We can find them by deducing evolution equations for the collective coordinates K, c, and X [11, 12]. Then the marginal density profile at $y=0$ can be reconstructed from (16) with spatially averaged $F_x$ and $\mu$ [12]. Note that $\tilde{p}_s$ is a function of $\xi =x-X$ and also of $\mathbf {x}$ and t through $C(t,\mathbf {x})$,

$$\begin{aligned} \tilde{p}_s=\tilde{p}_s\left( \xi ;K,c,\mu (C),F_x\left( C,\frac{\partial C}{\partial x}\right) \right) . \end{aligned}$$

(17)

We assume that the time and space variations of C, which appear when $\tilde{p}_s$ is differentiated with respect to t or x, produce terms that are small compared to $\partial \tilde{p}_s/\partial \xi$. As explained in [12], we shall consider that $\mu (C)$ is approximately constant, ignore $\partial C/\partial t$ because the TAF concentration varies slowly (the dimensionless coefficients $\kappa _c$ and $\chi _c$ appearing in the TAF equation (12) are very small according to Table 2 of [12]) and ignore $\partial ^2\tilde{p}_s/\partial i\partial j$, where $i,j=K,\, F_x$. We now insert (16) into (14), thereby obtaining

$$\begin{aligned}&\left( F_x-\dot{X}\right) \frac{\partial \tilde{p}_s}{\partial \xi }+\frac{\partial \tilde{p}_s}{\partial K} \dot{K}+\frac{\partial \tilde{p}_s}{\partial c}\dot{c} -\frac{1}{2\beta }\left( \frac{\partial ^2\tilde{p}_s}{\partial \xi ^2} +2\frac{\partial ^2\tilde{p}_s}{\partial \xi \partial F_x}\frac{\partial F_x}{\partial x}+ \frac{\partial \tilde{p}_s}{\partial F_x}\varDelta _xF_x\right) \nonumber \\&+\tilde{p}_s\nabla _x\cdot \mathbf {F}+\frac{\partial \tilde{p}_s}{\partial F_x}\left( \frac{\partial F_x}{\partial t}+\mathbf {F}\cdot \nabla _xF_x\right) =\mu \tilde{p}_s -\varGamma \tilde{p}_s\int _0^t\tilde{p}_s dt. \end{aligned}$$

(18)

Equation. (14) with $1/\beta =0$ and constant $\mathbf {F}$ and $\mu$ has the soliton solution (16). Using this fact, we can eliminate the first term on the left hand side of (18) and also the right hand side thereof. Equation (18) then become

$$\begin{aligned}&\frac{\partial \tilde{p}_s}{\partial K} \dot{K}+\frac{\partial \tilde{p}_s}{\partial c}\dot{c}=\mathscr {A}, \end{aligned}$$

(19)

$$\begin{aligned}&\mathscr {A}= \frac{1}{2\beta }\frac{\partial ^2\tilde{p}_s}{\partial \xi ^2}-\tilde{p}_s\nabla _x\cdot \mathbf {F}-\frac{\partial \tilde{p}_s}{\partial F_x}\left( \mathbf {F}\cdot \nabla _xF_x-\frac{1}{2\beta }\varDelta _xF_x\right) +\frac{1}{\beta }\frac{\partial ^2\tilde{p}_s}{\partial \xi \partial F_x}\frac{\partial F_x}{\partial x}. \end{aligned}$$

(20)

We now find collective coordinate equations (CCEs) for K and c. As the lump-like angiton moves on the x axis, we set $y=0$ to capture the location of its maximum. On the x axis, the profile of the angiton is the soliton (16). We first multiply (19) by $\partial \tilde{p}_s/\partial K$ and integrate over x. We consider a fully formed soliton far from primary vessel and tumor. As it decays exponentially for $|\xi |\gg 1$, the soliton is considered to be localized on some finite interval $(-\mathscr {L}/2,\mathscr {L}/2)$. The coefficients in the soliton formula (16) and the coefficients in (20) depend on the TAF concentration at $y=0$, therefore they are functions of x and time and get integrated over x. The TAF concentration varies slowly on the support of the soliton, and therefore we can approximate the integrals over x by [12]

$$\begin{aligned}&\int \limits _\mathscr {I} F(\tilde{p}_s(\xi ;x,t),x) dx \approx \frac{1}{\mathscr {L}}\int _\mathscr {I}\left( \int \limits _{-\mathscr {L}/2}^{\mathscr {L}/2} F(\tilde{p}_s(\xi ;x,t),x) d\xi \right) dx. \end{aligned}$$

(21)

The interval $\mathscr {I}$ over which we integrate should be large enough to contain most of the soliton, of extension $\mathscr {L}$. Thus the CCEs hold only after the initial soliton formation stage. Near the primary vessel and near the tumor, the boundary conditions affect the soliton and we should exclude intervals near them from $\mathscr {I}$. We shall specify the integration interval $\mathscr {I}$ below. Acting similarly, we multiply (19) by $\partial \tilde{p}_{s}/\partial c$ and integrate over x. From the two resulting formulas, we then find $\dot{K}$ and $\dot{c}$ as fractions. The factors $1/\mathscr {L}$ cancel out from their numerators and denominators. As the soliton tails decay exponentially to zero, we can set $\mathscr {L}\rightarrow \infty$ and obtain the following CCEs [12]

$$\begin{aligned} \dot{K}=\frac{\int _{-\infty }^\infty \frac{\partial \tilde{p}_s}{\partial K}\mathscr {A}d\xi \int _{-\infty }^\infty \left( \frac{\partial \tilde{p}_s}{\partial c}\right) ^2d\xi - \int _{-\infty }^\infty \frac{\partial \tilde{p}_s}{\partial c}\mathscr {A}d\xi \int _{-\infty }^\infty \frac{\partial \tilde{p}_s}{\partial K}\frac{\partial \tilde{p}_s}{\partial c} d\xi }{\int _{-\infty }^\infty \left( \frac{\partial \tilde{p}_s}{\partial K}\right) ^2d\xi \int _{-\infty }^\infty \left( \frac{\partial \tilde{p}_s}{\partial c}\right) ^2d\xi -\left( \int _{-\infty }^\infty \frac{\partial \tilde{p}_s}{\partial c}\frac{\partial \tilde{p}_s}{\partial K}d\xi \right) ^2}, \end{aligned}$$

(22)

$$\begin{aligned} \dot{c}=\frac{\int _{-\infty }^\infty \frac{\partial \tilde{p}_s}{\partial c}\mathscr {A}d\xi \int _{-\infty }^\infty \left( \frac{\partial \tilde{p}_s}{\partial K}\right) ^2d\xi - \int _{-\infty }^\infty \frac{\partial \tilde{p}_s}{\partial K}\mathscr {A}d\xi \int _{-\infty }^\infty \frac{\partial \tilde{p}_s}{\partial K}\frac{\partial \tilde{p}_s}{\partial c} d\xi }{\int _{-\infty }^\infty \left( \frac{\partial \tilde{p}_s}{\partial K}\right) ^2d\xi \int _{-\infty }^\infty \left( \frac{\partial \tilde{p}_s}{\partial c}\right) ^2d\xi -\left( \int _{-\infty }^\infty \frac{\partial \tilde{p}_s}{\partial c}\frac{\partial \tilde{p}_s}{\partial K}d\xi \right) ^2}. \end{aligned}$$

(23)

In these equations, all terms varying slowly in space have been averaged over the interval $\mathscr {I}$. The last term in (20) is odd in $\xi$ and does not contribute to the integrals in (22) and (23) whereas all other terms in (20) are even in $\xi$ and do contribute. The integrals appearing in (22) and (23) are calculated in [12]. The resulting CCEs are

$$\begin{aligned}&\dot{K}= \frac{(2K\varGamma +\overline{\mu }^2)^2}{4\varGamma \beta (c-\overline{F_x} )^2} \frac{ \frac{4\pi ^2}{75}+\frac{1}{5}+\left( \frac{2\overline{F_x}}{5 c}-\frac{2\pi ^2}{75}-\frac{9}{10}\right) \frac{\overline{F_x}}{c}}{\left( 1-\frac{4\pi ^2}{15}\right) \left( 1-\frac{\overline{F_x}}{2c}\right) ^2} \nonumber \\&\quad -\frac{2K\varGamma +\overline{\mu }^2}{\varGamma c\left( 2-\frac{\overline{F_x}}{c}\right) }\left( c\overline{\nabla _x\cdot \mathbf {F}} +\overline{\mathbf {F}\cdot \nabla _x F_x}-\frac{\overline{\varDelta _xF_x}}{2\beta }\right) , \end{aligned}$$

(24)

$$\begin{aligned}&\dot{c}=-\frac{7(2K\varGamma +\overline{\mu }^2)}{20\beta (c-\overline{F_x})}\frac{1-\frac{4\pi ^2}{105}}{\left( 1-\frac{4\pi ^2}{15}\right) \left( 1-\frac{\overline{F_x}}{2c}\right) } +\frac{\overline{\mathbf {F}\cdot \nabla _x F_x} -(c-\overline{F_x})\overline{\nabla _x\cdot \mathbf {F}}-\frac{\overline{\varDelta _xF_x}}{2\beta }}{2-\frac{\overline{F_x}}{c}}, \end{aligned}$$

(25)

$$\begin{aligned}&\overline{g(x,y)}= \frac{1}{\mathscr {I}} \int _{\mathscr {I}}g(x,0)\, dx, \end{aligned}$$

(26)

in which the functions of C(t, x, y) have been averaged over the interval $\mathscr {I}$ after setting $y=0$. We expect the CCEs (24) and (25) to describe the mean behavior of the soliton whenever it is far from primary vessel and tumor.

Fig. 5

Comparison of the marginal tip density profile $\tilde{p}(t,x,0)$ (obtained from the stochastic description averaged over 400 replicas) to that of the moving soliton, [11]

Both deterministic or stochastic simulations show that the soliton is formed after some time $t_0=0.2$ (10 h) following angiogenesis initiation. To find the soliton evolution afterwards, we need to solve the CCEs (24) and (25), in which the spatial averages depend on an interval $x\in \mathscr {I}$, which should exclude regions affected by boundaries. We calculate the spatially averaged coefficients in (24) and (25) by: (i) approximating all differentials by second order finite differences, (ii) setting $y=0$, and (iii) averaging the coefficients from $x=0$–0.6 by taking the arithmetic mean of their values at all grid points in the interval $\mathscr {I}=(0,0.6]$. For $x>0.6$, the boundary condition at $x=1$ influences the outcome and therefore we leave values for $x>0.6$ out of the averaging [12]. The initial conditions for the CCEs are set as follows. $X(t_0)=X_0$ is the location of the marginal tip density maximum, $\tilde{p}(t_0,x=X_0,0)$. We find $X_0=0.2$ from the stochastic description. We set $c(t_0)=c_0=X_0/t_0$. $K(t_0)=K_0$ is determined so that the maximum marginal tip density at $t=t_0$ coincides with the soliton peak. This yields $K_0=39$. Solving the CCEs (24) and (25) with these initial conditions and using (16), we obtain the curves depicted in Fig. 5.

5 Random Walk Tip Cell Models

These models describe the extension of blood vessels by random walks biased by chemotaxis or haptotaxis instead of using Langevin equations. The first such model, due to Anderson and Chaplain [13], is based on a reaction-diffusion description of angiogenesis. They consider a continuity equation for the density of endothelial cells (ECs) n (with zero-flux boundary conditions) coupled to equations for the TAF and fibronectin densities, C and f, respectively. In nondimensional form, these equations are [13]:

$$\begin{aligned}&\frac{\partial n}{\partial t}=D\varDelta n - \nabla \cdot \left( \frac{\chi }{1+\alpha C}n\nabla C\right) - \nabla \cdot (\rho n\nabla f),\end{aligned}$$

(27)

$$\begin{aligned}&\frac{\partial f}{\partial t}=\beta n- \gamma n f, \end{aligned}$$

(28)

$$\begin{aligned}&\frac{\partial C}{\partial t}=- \eta n C. \end{aligned}$$

(29)

Here all parameters are positive. The three terms on the right hand side of (27) correspond to diffusion of ECs, chemotaxis and haptotaxis, respectively. Note that chemotaxis has the same form in this equation as in (10) with p replaced by n. Haptotaxis follows the gradient of fibronectin in the extracellular matrix. Note that proliferation and death of ECs are not contemplated by (27). In the next step, these equations are solved by an explicit Euler method in time and finite differences. The resulting equation for $n(t,x,y)\approx n_{l,m}^q$,

$$\begin{aligned} n_{l,m}^{q+1}=n_{l,m}^qW_0+n_{l+1,m}^qW_1+n_{l-1,m}^qW_2+n_{l,m+1}^qW_3+n_{l,m-1}^qW_4, \end{aligned}$$

(30)

has the same form as a master equation for a random walk [22], except that the “transition probabilities” $W_0$ (staying), $W_1$ (moving to the left), $W_2$ (moving to the right), $W_3$ (moving downwards), and $W_4$ (moving upwards) are not normalized. However, this is easily fixed by defining

$$\begin{aligned} \mathscr {W}_i=\frac{W_i}{\sum _{j=0}^4 W_j}, \quad i=0,1,\ldots , 4, \end{aligned}$$

(31)

as new transition probabilities. The random walk associated to these transition probabilities represents extension of vessel tips and replaces the Langevin equation (1). Branching and anastomosis are introduced as in the Langevin tip cell model, except that the tips have to wait some maturity time after branching before they are allowed to branch again. It should be straightforward to find equations for the density of active vessel tips by using the theory described in previous sections.

The Anderson-Chaplain idea is easy to implement starting from continuum models of angiogenesis (and therefore it can be immediately generalized by including more taxis mechanisms, influence of antiangiogenic factors [25], etc), but it has the drawback of having to rely on the finite difference grid or lattice. A few years later, Plank and Sleeman proposed non-lattice models independent of the grid [14] using biased circular random walk models previously introduced by Hill and Häder for swimming microorganisms [26]. If $\theta (t)$ is a continuous random walk on the unit circle biased by chemo and haptotaxis [14], the trajectory of the corresponding tip cell is

$$\begin{aligned} \frac{d\mathbf {x}}{dt}= v_0\, (\cos \theta (t),\sin \theta (t)). \end{aligned}$$

(32)

Thus the tip cells have the same speed $v_0$, directions given by $\theta (t)$ and their trajectories do not have to follow points on a lattice. While branching and anastomosis are modeled as in Sect. 2, the extensions of vessel tips are described by (32) and the biased circular random walk instead of Langevin equations. The master equation for the circular random walk is [14]

$$\begin{aligned}&\frac{dP_n}{dt}=\hat{\tau }_{n-1}^+P_{n-1}+\hat{\tau }_{n+1}^-P_{n+1}-(\hat{\tau }_{n}^++\hat{\tau }_{n}^-) P_{n},\end{aligned}$$

(33)

$$\begin{aligned}&\hat{\tau }_{n}^\pm = 2\lambda \frac{\tau \left( n\delta \pm \frac{\delta }{2}\right) }{\tau \left( n\delta +\frac{\delta }{2}\right) +\tau \left( n\delta -\frac{\delta }{2}\right) }. \end{aligned}$$

(34)

As $\delta \rightarrow 0$ and $n\rightarrow \infty$ so that $n\delta =\theta$, the master equation (33) becomes the Fokker-Planck equation [14]

$$\begin{aligned} \frac{\partial P}{\partial t}(t,\theta )=D\frac{\partial }{\partial \theta }\left[ P(t,\theta )\frac{\partial }{\partial \theta }\left( \ln \frac{P(t,\theta )}{\tau (\theta )}\right) \right] , \end{aligned}$$

(35)

with $D=\lambda \delta ^2$ for $P(t,\theta )=P(t,n\delta )=P_n(t)$. Chemo and haptotaxis are included in the model through the transition probability

$$\begin{aligned}&\tau (\theta )=\frac{\exp [d_C\cos (\theta -\theta _C)+d_f\cos (\theta -\theta _f)]}{\int _{-\pi }^\pi \exp [d_C\cos (s-\theta _C)+d_f\cos (s-\theta _f)]\, ds},\end{aligned}$$

(36)

$$\begin{aligned}&\tan \theta _C=\frac{\nabla C}{|\nabla C|},\quad \tan \theta _f=\frac{\nabla f}{|\nabla f|}. \end{aligned}$$

(37)

Here $\tau (\theta )$ is the stationary probability density of the Fokker-Planck equation (35). Comparisons between numerical simulations of the Anderson-Chaplain and Plank-Sleeman models are carried out in [14].

The random walk models of this Section get their input from continuum equations for EC, TAF and fibronectin densities, but the moving vessel tips characterized by the random walks do not affect the continuum fields. Their outcomes are numerical simulations of the stochastic processes, without further elaboration. In contrast to this somewhat artificial setting, the Langevin tip cell model of Sect. 2 is a hybrid model in which active vessel tips and continuum fields are fully coupled. Furthermore, we can derive an equivalent deterministic description from the Langevin tip cell model and analyze it in terms of a soliton-like attractor. This latter elaboration has also been carried out for a Langevin tip cell model that includes chemotaxis and haptotaxis [20]. It may also be worked out for the random walk models in an appropriate limit, as their governing master equation then becomes a Fokker-Planck equation (corresponding to a Langevin-Ito equation) [22].

6 Cellular Potts Models

In all the previous models, the cells are treated as point particles. For a more precise view of haptotaxis, i.e., the motion of ECs over the extracellular matrix (ECM), we need to consider adhesion and deformation of the cells. This requires a more microscopic view than that offered by tip cell models or by more complicated models that distinguish between tip and stalk ECs and add extra dynamics for them [8].

Often times, ECs and ECM are modeled by a cellular Potts model (CPM) with Monte Carlo dynamics coupled to continuum fields (elastic fields, TAF, ...) [27]. Space in these models consists of a lattice whose cells (lattice sites) may be in finitely many different states, denoted by type $\tau$ and representing ECs, matrix fibers, tissue cells and interstitial fluid. To account for individual entities (ECs, fibers, etc), each entity is further associated with a unique identifying number, denoted by $\sigma$, that is assigned to every lattice site occupied by it. At every Monte Carlo time step, the cell surface (represented by connected lattice vertices) is updated according to a set of cell behavior rules (e.g., target cell shape and size) that are translated in an energy change. Typically, we select randomly a cell $\mathbf{x}$, assign its type, $\tau (\mathbf {x})$, to a randomly chosen neighbor $\mathbf{x}'$, and update accordingly the total energy of the system, H. Using the Metropolis algorithm, a given update is accepted with probability one if the change in the total energy of the system, $\varDelta H$, is reduced and it is accepted with probability $e^{-\beta \varDelta H}$ otherwise ($1/\beta$ is the Monte Carlo temperature). The energy in [27] is

$$\begin{aligned}&H = \sum _\mathrm{sites} J_{\tau ,\tau '} (1-\delta _{\sigma \sigma '})+ \sum _\mathrm{cells}\gamma _\tau (a_\sigma -A_\sigma )^2 - \sum _\mathrm{cells} \sum _\mathrm{sites} \mu _{\sigma } C(t,\mathbf {x}). \end{aligned}$$

(38)

The first term in Eq. (38) is the contribution to total energy resulting from cell-cell and cell-medium adhesion. The second term allows deformation of cells with volume $a_\sigma$ about a target volume (area in 2D space) $A_\sigma$, depending on the Potts parameters $\gamma _\tau$. The target volume is twice that of the initial volume and it corresponds to the volume at which a cell undergoes mitosis, thereby creating a new cell. Thus cell proliferation is contemplated in this CPM. A variation of the last term in (38) is

$$\begin{aligned} \varDelta H_\mathrm{chem}=-\mu _\sigma [C(t,\mathbf {x})-C(t,\mathbf {x}')], \end{aligned}$$

(39)

where $\mathbf {x}$ and $\mathbf {x}'$ are two randomly picked neighboring lattice cells, $\mu _\sigma >0$ is the chemical potential, and Eq. (39) represents chemotaxis favoring motion directed along the TAF gradient. The TAF concentration satisfies a reaction-diffusion equation [27]. The parameters appearing in the model are chosen in such a way that the progression of blood vessels occurs in the time scale observed in experiments [27].

Under this framework, each entity (ECs, ECM, ...) has a finite volume, a deformable shape and competes for space. ECs proliferate. Intercellular interactions occur only at the cells surface and have a cell-type-dependent surface (or adhesion) energy $J_{\tau ,\tau '}$, which is a measure of the coupling strength between the entities $\tau$ and $\tau '$. Other CPMs include an ECM strain-dependent term that favors cell extension in the direction of principal strain (durotaxis). The force exerted by the ECs on the ECM is calculated by finite elements [28]. In more complicated models, each cell contains agents that signal to other cells and adhesion is modeled by a CPM [29].

As in the case of random walk tip cell models, there is a connection between CPM and a deterministic formulation for a density. In [30], Alber et al. have written a discrete time master equation for the probability density $P(t,\mathbf {r},\mathbf {L})$ that a cell with its center of mass at $\mathbf{r}$ occupy a rectangle with sides $\mathbf {L}=(l_x,l_y)$ at time t. It is based on a CPM with energy given by (38), but with a target perimeter instead of the target area. The corresponding term in the energy is

$$\begin{aligned} H_\mathrm{perim}=\sum _\mathrm{cells}[\gamma _{x} (l_{x}-L_{x})^2+\gamma _{y} (l_{y}-L_{y})^2]. \end{aligned}$$

(40)

Here cells are always rectangles and do not proliferate nor die. Assuming that cells contain many lattice sites, they change little at each Monte Carlo step. Assuming further that cell-cell interactions are always binary, the authors derive a Fokker-Planck equation for $P(t,\mathbf {r},\mathbf {L})$. These formulations would have to be extended to CPMs that include cell proliferation and be connected to mesoscopic angiogenesis models: from cell densities to densities of active vessel tip cells.

7 Blood Flow and Vascular Network

Once a vascular network is being created, blood flows through the capillaries, anastomosis enhances flow in some of them and secondary angiogenesis may start in new vessels. Pries and coworkers have modeled blood flow in a vascular network and the response thereof to changing conditions such as pressure differences and wall stresses [31, 32]. This response may remodel the vascular network by changing the radii of certain capillaries, and altering the distribution of blood flow [31, 32]. McDougall, Anderson and Chaplain [33] have used this formulation to add secondary branching from new capillaries induced by wall shear stress to the original random walk tip cell model [13]. Blood flows according to Poiseuille’s law, mass is conserved, there are empirical expressions for blood viscosity and for the wall shear stresses, and radii of capillaries adapt to local conditions. Secondary vessel branching may occur after the new vessel has reached a certain level of maturation and before a basal lamina has formed about it [21, 33]. During such a time interval, the probability of secondary branching increases with both the local TAF concentration and the magnitude of the shear stress affecting the vessel wall. McDougall et al’s. model can be used to figure out how drugs could be transported through the blood vessels and eventually reach a tumor [21, 33]. In dense vessel networks, secondary branching may have little effect on the number of active tips at a given time, as anastomosis could eliminate secondary branches quickly. Thus we may ignore secondary branching when considering the density of active tips in such networks. Of course we cannot ignore it when describing blood flow and network remodeling.

One missing feature of angiogenesis models that take blood flow into account seems to be pruning. It is known that capillaries with insufficient blood circulation may atrophy and disappear. Pruning such blood vessels is an important mechanism to achieve a hierarchical vascular network such as that observed in retinal vascularization during development [3, 4]. Global optimization and adaptation in developing networks has been recently shown to lead to highly optimized transport vascular systems [34, 35]. It would be interesting to adapt these studies to angiogenesis.

8 Conclusions

Angiogenesis is a complex multiscale process by which diffusing vessel endothelial growth factors induce sprouting of blood vessels that carry oxygen and nutrients to hypoxic tissue. Cancerous tumor cells profit from this process to prosper, grow and eventually migrate to other organs. Mathematical models contemplate different aspects of angiogenesis. Here we have reviewed recent work on a simple tip cell model that encompasses vessel extension driven by chemotaxis and described by Langevin equations, stochastic tip branching and vessel fusion (anastomosis). From the stochastic description, we have derived a deterministic integropartial differential equation for the density of active tip cells coupled with a reaction-diffusion equation for the growth factor. The associated initial-boundary value problem is well posed. It is important to note that anastomosis prevents proliferation of active tips and therefore the deterministic description is based on ensemble averages over replicas of the stochastic process. Numerical simulations of both (deterministic and stochastic) descriptions show that the density of active tips adopts the shape of a two-dimensional soliton-like wave (angiton) after a formation stage. We have found an analytical formula for the one-dimensional projection of the soliton and ordinary differential equations for variables that provide its velocity, position and size. These equations also characterize the advance of the vessel network for single replicas. Much more work needs to be carried out to solve mathematical issues arising from our results, both from analysis of the deterministic description and from establishing more precise conditions for its validity. The description of the soliton should be extended to the true two-dimensional soliton (angiton) that appears in the numerical simulations and to the case of a more general geometry than that of the slab. Fluctuations cannot be ignored in the case of ensemble averages, and future work predicting the evolution of a real vessel network should include confidence bands about averages. Anti-angiogenic treatments need to be improved [1, 2], and, in this respect, having better models and theories about their solutions should help. Therapies are related to optimal control of angiogenesis and they require accurate mathematical models, validated by comparison with real data (inverse problems—statistics of random geometric structures).

We have also related the specific model we study to other tip cells models in the literature that describe vessel extension by reinforced random walks instead of stochastic differential equations. Our methodology may be adapted to these other models as Langevin equations arise from reinforced random walks in appropriate limits. All these models describe mesoscales in which cells are just point particles, thereby ignoring their shapes and a microscopic description thereof. Other models consider the evolution of individual endothelial cells of variable shape and extension through cellular Potts models, but the continuation of these models toward the mesoscale has barely begun. Extending the analysis carried out for our mesoscopic stochastic tip cell model to microscopic models is a challenge for the future. Blood circulation through the angiogenic network favors certain vessels, others that do not have enough perfusion shrink and disappear and secondary branching may occur. Future work could delve deeper in the topics of vessel remodeling, pruning, formation of optimal vascular networks and transport of medicals through them.

Apart from the specific application to angiogenesis, we have presented in this paper methodological contributions for a sound mathematical modeling of stochastic vessel networks: (a) the use of stochastic distributions, and their mean densities, describing the vessels, which are random objects of Hausdorff dimension one, cf (6); (b) reduction of vessel distributions to integrals over time of active tip distributions, which are random objects of zero Hausdorff dimension, cf (8); (c) characterization of the attractor of the density of active tips as a soliton whose position, velocity and size are given as solutions of ordinary differential equations, cf (16), (22) and (23). In our system, which is strongly out of equilibrium, this attractor plays a similar role to the stable stationary equilibrium distribution of many physical systems.