Keywords

1 Introduction

The push towards thin-film technology has been driven largely by predictions of future economic viability [1,2,3,4]. Traditional single-crystal solar cells, such as Si and GaAs, demonstrate very high efficiencies (20–30%), but the production of crystalline material is expensive. The original reason thin-film materials were pursued was because they use much less material, which is directly related to the cost of production. Two of the leading thin-film materials are CdTe and CuInGaSe\(_{2}\), chosen because their direct bandgaps require a smaller absorption length than Si (requires less thickness for optimum performance). CdTe is a nearly ideal material for terrestrial solar cell production, as its band gap of 1.45 eV (room temperature) yields the maximum theoretical efficiency for a solar cell, of about 32% (see Fig. 1 for the Schockley-Queisser limit for single cell under AM1.5 illumination.) The current record one-of-a-kind laboratory research cell was fabricated in 2017 by First Solar (FSLR) and has an efficiency of 22.1% [5].

Fig. 1
figure 1

Schockley-Queisser limit

Full size image

Despite overwhelming advances in thin-film CdTe technology in recent years, performance of thin-film CdTe devices is still a subject to various metastable phenomena that could be characterized by temperature-dependent time constants (activation energies). Most of these metastable changes in CdTe are known to be reversible and require different recovery procedures; however, based on experimental and theoretical investigations at First Solar, metastabilities in CdTe device cannot be explained solely by electronic capture-emission phenomena assuming fixed distributions of point defects.

Many of the physical properties of crystalline solids are determined by the presence of native or foreign point defects. In pure compound crystals the native defects are atoms missing from lattice sites where, according to the crystal structure, atoms should be (vacancies); atoms present at sites where atoms should not be (interstitials); and atoms occupying sites normally occupied by other atoms (substitutional). In addition, there may be defects in the electronic structure: quasi-free electrons in the conduction band or electrons missing from the valence band (holes). In impure or doped crystals there are also defects involving the foreign atoms. These may occupy normal lattice sites (substitutional foreign atoms) or interstitial sites (interstitial foreign atoms). In elemental crystals similar point defects occur; only misplaced atoms are missing.

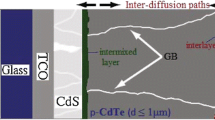
In addition to point defects, the performance of CdTe solar cells is affected by extended defects which include dislocations, stacking faults, grain boundaries (GBs) and inclusions of second phases. Dislocations and GBs are well known to attract impurities, and to promote diffusion [6]. Such effects might be expected to lead to instability in devices, or to have an influence on the thermal processing conditions chosen to fabricate certain devices. An example is the inter-diffusion of CdTe and CdS in polycrystalline solar cells for which the grain boundary diffusion coefficient has been measured [7]. Grain boundary segregation is well known in metals (e.g. Cu in Pb [8]), the driving force being strain reduction at the boundary plane. Decoration of grain and twin boundaries in CdTe with Te inclusions is widely reported. Minor component impurities in CdTe have also been shown to segregate out to grain boundary regions [9] and to dislocation arrays [10].

The electrical states associated with grain boundaries and dislocations can have a number of adverse effects on the performance of CdTe solar cells. Firstly, the deep states associated with extended defects can promote undesirable recombination. Secondly, grain boundaries act as charge transport barriers. This is attributed to the grain boundary manifold being a charged interface, causing it to present an electrical barrier to current transport. Such barriers have been observed directly for CdTe using the so-called ‘remote’ electron beam induced current (EBIC) method [11] and are considered responsible for limiting effects in polycrystalline solar cells [12]. Thirdly, grain boundaries and dislocations may act as conduits for current transport rather than barriers. The impact of the grain boundaries is likely to depend on their position in the layer; near surface grain boundaries are likely to be Te-rich (i.e. conducting) on account of the etching used to prepare contacts, whereas those remote from the free surface may nevertheless act as recombination centers.

In today’s thin-film CdTe technology, Cu is the key dopant that defines major performance parameters such as open-circuit voltage (Voc), short-circuit current (Jsc), and fill-factor (FF) by affecting built-in potential of the junction, collection efficiency, and resistivity of the back contact [13]. However, fast diffusion of Cu from the back contact toward the main junction is believed to contribute to degradation observed in long-term stability studies [14]. It was determined that while modest amounts of Cu enhance cell performance, excessive amounts degrade device quality and reduce performance [15]. Evolution of Cu-related point defects and complexes in CdTe grains and at grain boundaries (GBs) is expected to cause pronounced effect on device performance leading to observed metastable phenomena.

Interactions of Cu in CdTe involve multiple intrinsic and extrinsic point defects and complexes, and as a result, cannot be analyzed in isolation from the rest of the system. Although the other defects in CdTe system could be assumed relatively slow diffusors at typical operating and storage conditions of CdTe device, direct measurement of their distributions is very challenging. Moreover, rapid development of technology involves frequent changes of film growth/activation conditions and, therefore, resulting setup for Cu-related point defects and complexes. All of the above makes quantitative understanding of metastable phenomena in CdTe device virtually impossible with the off-the-shelf tools that researchers have currently.

2 Theoretical Model

As already noted in the Introduction part of this book chapter, the evolution of Cu-related point defects and complexes in CdTe grains and at GBs is expected to cause a pronounced effect on device performance leading to observed metastable phenomena. Interactions of Cu in CdTe involve multiple intrinsic and extrinsic point defects and complexes, and, as a result, cannot be analyzed in isolation from the rest of the system. Understanding the fundamentals behind performance and metastability of CdTe devices requires a model that captures and describes most relevant processes at the lowest level specific to CdTe system and could be confirmed with experiment.

We consider such a model in a form of a self-consistent system of time-dependent reaction-diffusion equations [16,17,18] describing the interactions and the evolution of point defects and complexes coupled with the Poisson equation (see Fig. 2). Because device performance is uniquely defined by device geometry, band-structure of semiconductors, and distributions of charge and recombination centers, the Unified Solver has to be able to simulate macroscopic device characteristics such as current, capacitance and quantum efficiency as a function of the applied bias, DC light intensity, and ambient temperature. Such capabilities establish a tighter link between the microscopic core of the model and macroscopic experimental verification. The core of the solution is a multi-level solver that combines macroscopic diffusion-reaction equations describing sub-systems of the point defects with the global Poisson equation to form a closed system that is solved in time domain and quasi-3D space utilizing grains of specific shape. The characteristic length scale of the features is large enough that the semi-classical approximation (implicitly assumed by using reaction-diffusion equations) is valid. The developed Unified Solver offers flexibility in choosing (turning “on” and “off”) models and reactions that involve selected point defects and complexes in individual materials or domains.

The species under investigation are described by sets of low-level parameters that include their formation energy, ionization energies and diffusion coefficients for different charged states, solubility limits, grain boundary segregation parameters. The evolution of the system for a given set of stressors (temperature, light, and bias) is calculated based on provided initial conditions (distributions). The solver outputs the distributions of charged and neutral dopants and recombination states. Given the device geometry and band structure of semiconductors, the solver uses these distributions to simulate I-V, C-V and QEV trends that could be confirmed experimentally on real device structures.

Fig. 2
figure 2

Schematic block-diagram that illustrates the use of the Unified Solver to tune the model and study CdTe device metastability

Full size image

2.1 Physical Model

A specific example of importance is the penetration of Cu into CdTe absorber using a high temperature diffusion anneal. The Cu penetration involves several processes, including the Cu-Cd exchange reaction and the drift/diffusion of mobile defects, namely \({\text {Cu}}_{i}^{+}\) and \({\text {Cd}}_{i}^{+2}\). To simulate such reaction-diffusion process we use a standard multi-compartment approach [19], which assumes the reactions to happen inside the finite homogeneous compartments (well-stirred reactors), while the mass transfer between compartments happens via pure drift/diffusion process without any effect of defect reactions. Within this multi-compartment approach, we can describe the reactions using the standard chemical kinetics formalism in application to the defect chemistry in solid state.

We write the main Cu-Cd exchange reaction of the Cu penetration process as a bimolecular exchange reaction facilitated by knock-off:

$$\begin{aligned} {Cu^{-}_{Cd} + Cd^{+2}_i \mathop {\rightleftharpoons }^{K^{f}}_{K^{b}} Cu_i^+ + Cd_{Cd}} \end{aligned}$$
(1)

where \(K^f\) and \(K^b\) are reaction rate constants. In the forward exchange reaction (1), the double donor interstitial Cd defect (\({\text {Cd}}_{i}^{+2}\)) reacts with the acceptor substitutional Cu defect (Cu\(_{Cd}^{-}\)), kicks-out Cu into an interstitial position and occupies its place forming regular Cd-on-cation-site lattice atom (Cd\(_{Cd}\)). Such exchange reaction is one of the three types of elementary bimolecular defect reactions, while two others being the formation of a complex pair defect of two isolated point defects and the recombination of interstitial point defect with vacancy [20]. The rate of such bimolecular exchange reaction is proportional to the concentrations of both reactants (Cu\(_{Cd}^{-}\) and Cd\(_{i}^{+2}\)).

The backward reaction, knock-off of Cd by Cu\(_{i}^{+}\), is treated as monomolecular with only one reactant (Cu\(_{i}^{+}\)) because in the uniform binary CdTe matrix in the diluted concentrations approximation, this backward reaction does not require the reactants (Cu\(_{i}^{+}\) and Cd\(_{Cd}\)) to find each other (the regular Cd lattice atoms are available nearby any Cu\(_{i}\)). Therefore, the rate of the backward reaction (1) is proportional only to the concentration of one reactant \({\text {Cu}}_{i}^{+}\).

The above considerations allow us to define the reaction rates (\(R^f\), \(R^b\)) in the following form:

$$\begin{aligned} \left\{ \begin{array}{l} {R_{}^{f} =K_{}^{f} [Cu_{_{Cd} }^{-} ][Cd_{_{i} }^{+2} ]} \\ {R_{}^{b} =K_{}^{b} [Cu_{_{i} }^{+} ]} \end{array}\right. \end{aligned}$$
(2)

where the superscripts f and b indicate the forward and backward reactions, [X] is the concentration of defect X and \(K^{f,b}\) is the corresponding reaction rate constant.

As no reliable experimental methods exist for determination of the rates of the reactions between individual point defects, we use first principles-based analysis to estimate these reaction rates. Following the standard approach for defect chemistry in solids, we consider two major contributions to the Gibbs free energy of point defects, namely the formation enthalpy and the configuration entropy. The calculation of the formation enthalpy of different atomic configurations in the supercell approach allows analyzing the potential energy landscapes and finding the most favorable states of single neutral and charged defects as well as the minimum energy pathways for single reactions. The inclusion of the configuration entropy changes in defect reactions allows accounting for the effect of temperature and defect concentrations on the reaction rates. More details on first-principles calculations can be found in recent works [20, 21].

Analysis of the potential energy landscape for reacting \(\text {Cu}_{Cd}^{-}\) and \({\text {Cd}}_{i}^{+2}\) defects shows that the highest energy barrier in the forward reaction (1) is the \({\text {Cd}}_{i}^{+2}\) diffusion barrier and the formation enthalpy of the products is lower than that of reactants [20, 22]. This allows us to write the forward rate constant as a steady-state rate constant of diffusion-controlled reaction between non-interacting uniformly distributed species (see e.g. [22]). To derive the backward rate constant we use the principle of the detailed balance:

$$\begin{aligned} \left\{ \begin{array}{l} {K^{f} =4\pi DR_{capt}} \\ {K^{b} =K^{f} K^{eq} C_{s} } \end{array}\right. \end{aligned}$$
(3)

In Eq. (3), \(R_{capt}\) represents the capture radius of reactants, here for reaction between the attractive oppositely charged defects with charges q\(_{1}\), q\(_{2}\) we use the Onsager capture radius [23]; D is the sum of diffusivities of reactants dominated by the diffusivity of mobile \({\text {Cd}}_{i}^{+2}\) defect in our case; is equilibrium constant of reaction (1), \(\varDelta \)H is the change of formation enthalpy in the forward reaction; \(C_{s} =1.48\times 10^{22} \) cm\(^{-3}\) is the concentration of regular lattice sites in CdTe. This approach of calculating the reaction constants delivers equilibrium distribution of defects if the simulation time is long enough.

The overall time-space evolution of point defects involved in Cu penetration is described by the following set of reaction-diffusion equations:

$$\begin{aligned} \left\{ \begin{array}{l} {\frac{d[Cu_{{i} }^{+} ]}{dt} =-\nabla \cdot J_{Cu_{i}^{+} } +R^{f} -R^{b} } \\ {\frac{d[Cd_{{i} }^{+2} ]}{dt} =-\nabla \cdot J_{Cd_{i}^{+2} } -R^{f} +R^{b} } \\ {\frac{d[Cu_{{Cd} }^{-} ]}{dt} =-R^{f} +R^{b} } \end{array}\right. \end{aligned}$$
(4)

Note that in Eq. (4), diffusion of \(Cu_{Cd} \) has been ignored due to very small diffusion coefficient [22]. The fluxes \(J_{X} \,\)in Eq. (4) result from both the diffusion due to concentration gradients and from the drift due to external electrostatic field:

$$\begin{aligned} J_{X} =-D_{X} \nabla [X]+\upsilon _{X} [X] \end{aligned}$$
(5)

Assuming Boltzmann statistics (valid for diluted concentrations) and the charge \(\theta \) carried by the defect, its drift velocity \(\upsilon _{x} \) in electric field F equals to \(\mu _{X} F\), where mobility \(\mu _{X} \) is expressed via diffusion coefficient using Einstein relation \(\mu _{X} =\theta \frac{D_{X} }{kT} \). In other words:

$$\begin{aligned} \upsilon _{X} =\theta \frac{D_{X} }{kT} F \end{aligned}$$
(6)

The ionization states of the defects can be calculated from first principle calculations. The diffusion coefficients of point defects have temperature dependence provided by Arrhenius expression:

$$\begin{aligned} D=D_{0} \exp \left( -\frac{\varDelta E_{D} }{kT} \right) \end{aligned}$$
(7)

where \(D_{0} \) and \(\varDelta E_{D} \) are diffusivity prefactor and the energy barrier of elementary diffusion jumps, respectively. These parameters for many important point defects in CdTe have been recently calculated from first principles in works [22, 24, 25].

The electric field in the film is determined not only by the electron/hole concentrations, but also by the ionized defect distributions inside the grain and its boundaries (surfaces), and can be found by solving the Poisson equation:

$$\begin{aligned} \nabla \cdot \left( \varepsilon _{S} \nabla V\right) =-q\left( p-n+[Cu_{_{i} }^{+} ]+2[Cd_{_{i} }^{+2} ]-[Cu_{_{Cd} }^{-} ]\right) \end{aligned}$$
(8)

In Eq. (8), p stands for the hole concentration, n is the electron concentration and \(\varepsilon _{S} \) is the spatially varying dielectric constant of the materical that comprise the CdTe solar cell.

Boundary conditions for diffusion-reaction Eq. (8) are provided by the sink of defects near the boundary given by:

$$\begin{aligned} J_{Gb} =-\sigma _{X} \left( C_{X} -C_{eq} \right) . \end{aligned}$$
(9)

In Eq. (9), \(\sigma _{X} \) is the recombination/generation rate and \(C_{eq} \) is the equilibrium concentration of the defect at the boundary. Usually, the velocity \(\sigma _{X} \) is proportional to the diffusion constant of the defect. In most cases, when the strong sink of defects at grain boundary is assumed, \(C_{eq} \) is considered to be constant. Beyond this approximation, the effect of grain boundary segregation has to be taken into account. The accumulation of impurity atoms at boundaries changes the chemical potential and hence makes \(C_{eq} \) floating. By introducing the floating chemical potential of impurities, the properties of the grain boundary could be taken into account. According to theories of grain boundary segregation, the bulk concentration at grain surface is given by:

$$\begin{aligned} C_{surface} (t)=\exp \left( -\frac{\varDelta G}{kT} \right) \frac{C_{s}^{b} (t)}{1-C_{s}^{b} (t)} . \end{aligned}$$
(10)

Eq. (10) provides connection between the impurity concentrations at grain boundary and bulk by introducing \(\varDelta G\)—the atomic energy difference between the grain boundary and in the bulk. \(C_{s}^{b} \) in Eq. (10) represents the fraction of the grain boundary sites occupied by impurity atoms.

One can generalize the above notation and compactly write the Poisson and the diffusion-reaction equations as:

$$\begin{aligned} -\nabla \cdot (\varepsilon _s \nabla V)=q(p-n+\sum _i\theta _iX_i)&\nonumber \\ \partial _tp-\nabla \cdot (D_p\nabla p + \mu _p p\nabla \phi )= R(n,p)&\nonumber \\ \partial _tn-\nabla \cdot (D_n\nabla n + \mu _n n\nabla \phi )= R(n,p)&\nonumber \\ \partial _tX_i-\nabla \cdot (D_i\nabla X_i + \mu _i\theta _i X_i\nabla \phi )= R_i(\bar{X})&\end{aligned}$$
(11)

where \(X_i\) is the concentration of the ith type of defect and \({\theta }_i\) is the charge of the ith-type of defect. We also define \(\phi =V+V_{bi}\) where \(V_{bi}\) corresponds not only to the usual built-in-voltage, but also includes terms that account for heterojunctions. In future analysis this term will include effects due to the change in chemical potentials for charge carriers in grain boundaries, to account for different materials, or both. (Note that for neutral particles (\({\theta }_i=0\)) this will require including a term in the fourth equation which is not proportional to \(\theta \)). We assume that \(V_{bi}\) is constant with respect to time and therefore does not require an additional partial differential equation.

2.2 Numerical Methods

The major challenge in numerically solving the system of diffusion-reaction equations that are coupled to a global Poisson equation solver—given by the Eq. (11)—is the presence of vastly different time and spatial scales. For example, Cu is a fast diffusor, whereas the diffusion of Cl occurs on a longer time scale and both of these are slow compared to energetically favorable ionization reactions.

For the 2D case, we have previously developed a Unified Solver based on the first order implicit Euler method for the time integration and a Slotboom Finite Element method in space [19].

2.2.1 Time Splitting

Leaving aside for a moment the issue of space discretization, we developed a time discretization scheme which allows us to decouple the equations (in the sense that each equation can be solved independently for a given time step). In particular, there are two types of coupling. The electrical coupling is the most involved, with every (charged) defect appearing in Poisson’s equation and the derivative of the potential appearing in each of the (charged) defect equations. This drift term involves only a single species of defect, but is nonlocal in space. The other coupling is through the \(R_i(\hat{X})\) term, which simultaneously couples all of the reaction-diffusion equations, but acts locally in space.

The usual first step in the numerical solution of Eq. (11) is to use a Gummel-type iteration alternating between calculation of Poisson’s equation and the reaction-diffusion equation [26]. This replaces the solution of a large system of coupled equations by the repeated solution of many smaller equations. When the number of degrees of freedom is large (as is usually the case in 2D or 3D), the iterative scheme will solve the system more efficiently for any reasonable iteration tolerance.

As first step we reformulate the transport equations, using so-called Slotboom variables of the form \(u_i=e^{\frac{{\theta }_i{\phi }_i}{U_T}}X_i\). This transforms the transport equations for the defects into

$$\begin{aligned} {\partial }_tX_i-\nabla \cdot \left( {\mu }_iU_Te^{-\frac{{\theta }_i{\phi }_i}{U_T}}\nabla u_i\right) =0 \end{aligned}$$
(12)

The advantage of the formulation is that the spatial differential operator is self-adjoint in the variables \(u_i\), yielding a stable disretization of the transport equation for large electric fields and, consequently, large spatial variations in the potential \(\phi \). We note that the Slotboom variables, \(u_i\), will exhibit a large dynamic range due to the exponential in the variable transform. Thus, the primary variables will always be the concentrations \(X_i\) and the transport equations will always be discretized in the form

$$\begin{aligned} {\partial }_tX_i-\nabla \cdot \left( {\mu }_iU_Te^{-\frac{{\theta }_i{\phi }_i}{U_T}}\nabla \left( e^{\frac{{\theta }_i{\phi }_i}{U_T}}X_i\right) \right) =0 \end{aligned}$$
(13)

where the spatial derivatives are approximated numerically by differentiating \(u_i=e^{\frac{{\theta }_i{\phi }_i}{U_T}}X_i\).

We utilize an operator splitting (a fractional step-method) for the time discretization of the defect equations, separating the diffusion from the reaction terms. The operator splitting method is of the following form: Given \(X_i\) at time \(t_K\) and a time step \({\varDelta }t\)

  • Step 1: Solve

    $$\begin{aligned} {{\partial }_tX_i}^{\left( 1\right) }-\nabla \cdot \left( {\mu }_iU_Te^{-\frac{{\theta }_i{\phi }_i}{U_T}}\nabla \left( e^{\frac{{\theta }_i{\phi }_i}{U_T}}{X_i}^{\left( 1\right) }\right) \right) =0,\ \end{aligned}$$
    (14)

    for\(\ t_k\le t\le t_k+\varDelta t,\ {\ X_i}^{\left( 1\right) }\left( t_k\right) =X_i(t_k)\)

  • Step 2: Solve

    $$\begin{aligned} {{\partial }_tX_i}^{(2)}=R_i\left( {\mathop {X}\limits ^{\rightharpoonup }}^{\left( 2\right) }\right) ,\ \ \ for\ t_k\le t\le t_k+\varDelta t,\ {\ X_i}^{\left( 2\right) }\left( t_k\right) ={\ X_i}^{\left( 1\right) }\left( t_k+\varDelta t\right) \end{aligned}$$
    (15)

  • Step 3: Set

    $$\begin{aligned} X_i\left( t_k+\varDelta t\right) ={\ X_i}^{\left( 2\right) }\left( t_k+\varDelta t\right) \end{aligned}$$
    (16)

A simple Taylor expansion argument yields that the above method is first order in the time step \({\Delta }_t\). A second order method can be obtained immediately by using a standard modification such as Strang splitting [19], but the advantages of the approach are limited by the nature of the Gummel iteration.

The advantage of the operator splitting approach is the following: An optimal simultaneous implementation of the transport and the reaction terms would result in the solution of a block sparse matrix vector multiplication problem. The matrix will be \(NN_{grid}\times N\ N_{grid}\) where N is the number of defects and \(N_{grid}\) is the number of grid points or finite elements. Each block has size \(N\times N\) and refers to interactions of defects at a single point in space. Depending on the reaction network structure, each block may be fully dense. For a regular triangular finite element mesh (or a rectilinear finite difference or finite volume grid), the matrices will be block-pentadiagonal with a bandwidth of \(N \cdot \sqrt{N_{grid}}\) with \(N_{grid}\) the number of gridpoints or finite elements. Many algorithms exist for solving such banded sparse systems, but a reasonable lower bound for the computational complexity for an \(M\times M\) matrix with bandwidth K is O(KM). For our matrix, this gives a computation time of \(O\left( N^2N^{\frac{3}{2}}_{grid}\right) \). Whereas a simultaneous implementation may be computationally feasible in one spatial dimension, the operator splitting approach is essential in higher dimensions when \(N_{grid}\) is the product of the number of grid points in each direction.

In contrast to the above mentioned approach, using the splitting method we need to solve N different matrix-vector multiplication problems for \(N_{grid}\times N_{grid}\) matrices which have the usual banded structure of a 2D finite element problem. (Many defects exist at lattices cites and do not diffuse, reducing the number of required solves.) Using the same estimates as above, we predict a speed up factor of N. However, modern linear algebra packages have optimized solvers for matrices with structures arriving from discretizing PDEs and our pentadiagional matrices will be solved with complexities approaching \(O\left( N_{grid}{\mathrm {log} \left( N_{grid}\right) }\right) \). For large values of \(N_{grid}\), the speed-up here is considerable. Indeed, the speed-up also occurs in 1D where fast tridiagonal solvers will run in \(O(3\ N_{grid})\) time.

We must still deal with Poisson’s equation, but since it too is linear in \(X_i\), we can consider it in the same step as the diffusion equation for the \(X_i\), retaining the decoupled structure. Note that we are left with significant freedom in the structure of the iteration. In particular, we note that the reaction equation does not a-priori respect the boundary conditions of the problem. For realistic final results, we should therefore choose to calculate the diffusion step last, or proceed by using the Strang-splitting method discussed above. The general time-splitting scheme is shown in Fig. 3.

Fig. 3
figure 3

Flow-chart of the Unified Solver. Device simulation is performed for each time step to obtain self-consistent and real-time electric field and carrier distributions during the diffusion-reaction simulation. Device simulation for IV, QE and CV is presented in dashed line box and is currently employed for the modeling of Cu-related metastabilities of CdTe solar cells

Full size image

2.2.2 Drift-Diffusion Implementation

Due to our choice of splitting methods above, our spatial discretization scheme can be optimized for solving only the following problem:

$$\begin{aligned} {\partial }_tX_i-\nabla \cdot \left( {\mu }_iU_Te^{-\frac{{\theta }_i{\phi }_i}{U_T}}\nabla u_i\right) =0 \end{aligned}$$
(17)

This spatial discretization of the problem is flexible, since none of its properties are dictated by the time-splitting scheme discussed above. In 1D, Scharfetter-Gummel [26] is appropriate (and in some cases optimal). The 1D version of the Unified Solver (obviously without grain boundaries) has already been demonstrated [27, 28].

In 2D, however, many of the schemes in the literature [29] do not work as well as desired. Any scheme which relies upon a-priori knowledge information about the structure of the devices runs into significant difficulties when the doping can change throughout time. The doping at many points in the device changes from p-type to n-type over time. In particular, schemes which require edges perpendicular to the direction of the electric field will not deal well with the nonlinear wave-fronts associated with grain boundary diffusion, let alone complicated grain boundary geometries. To handle these complicated geometries, we choose to use a finite element method for the 2D Unified Solver. Instead of relying upon an elaborate grid scheme, we directly discretize the Slotboom variables and use the properties of the scheme to allow exponential fitting of the charge carriers and defects between nodes.

2.2.2.1 Spatial Discretization

In order to deal with the complicated geometries which arise from the grain boundaries, we seek to solve this equation using finite elements. In the usual way [30], we will triangulate our domain \(\mathrm {\Omega }=\bigcup {T_h}\) with small triangles on the grain boundaries to handle large changes in the gradients. We then take the approximations \(u_i\in V_h\) of \(u_i\), which are piecewise linear on the triangles, and continuous on the whole domain, but still satisfy the boundary conditions. Multiplying our equation by a test function v in the same space and integrating over the domain yields:

$$\begin{aligned} \int \limits _{\mathrm {\Omega }}{{\partial }_t}X_ivdx=\int _{\mathrm {\Omega }}{\nabla }\cdot \left( {\mu }_iU_Te^{-\frac{{\theta }_i{\phi }_i}{U_T}}\nabla u_i\right) vdx \end{aligned}$$
(18)

Integrating by parts and separating the terms allows us to calculate the stiffness and mass matrices:

$$\begin{aligned} {\varvec{A}}_i:=\sum _{K\in T_h}{{\mu }_i}U_T\int _K{-}e^{-\frac{{\theta }_i{\phi }_i}{U_T}}\nabla {\psi }_j\cdot \nabla {\psi }_ldx \end{aligned}$$
(19)
$$\begin{aligned} \varvec{M}_i:=\sum _{K\in T_h}{\int _K{{\psi }_j}}{\psi }_ldx \end{aligned}$$
(20)

Details can be found in any finite element method introduction [30]. Combining the previous results, we can reformulate our PDE by:

$$\begin{aligned} \int _{\mathrm {\Omega }}{{\partial }_t}X_ivdx=\int _{\mathrm {\Omega }}{\nabla }\cdot \left( {\mu }_iU_Te^{-\frac{{\theta }_i{\phi }_i}{U_T}}\nabla u_i\right) vdx \nonumber \\ {\varvec{vM}}({\partial }_tX_{\varvec{i}})=\varvec{v}A_{\varvec{i}}\varvec{u}\mathrm {\ }\forall v\in V_h \end{aligned}$$
(21)

One advantage of finite elements is that zero-flux boundary conditions are incorporated naturally. Because we normally want to conserve atomic species during a simulation, we choose to use zero-flux conditions for all defects. For the carriers we use Ohmic front and back contacts and the matrices \({\varvec{A}}_i\) must be modified. The only complication over traditional methods [29, 30] is that if the doping changes over time, the boundary conditions must also be updated.

In the usual manner for finite elements, we can assume that this relationship holds for all admissible functions v and write the equation as a function of u and X only. Inserting the definition of u to close the equation yields:

$$\begin{aligned} \varvec{M}({\partial }_tX_{\varvec{i}})=A_{\varvec{i}}\left( X_{\varvec{i}}e^{\frac{{\theta }_i\varvec{\phi }}{U_T}}\right) \end{aligned}$$
(22)

Note that for piecewise linear finite elements, the exponential inside the stiffness matrix \(\varvec{A}\) will be evaluated at the barycenter of the finite elements. In contrast, the exponential on the left-hand side must be evaluated at the grid points. Thus, for each entry of the stiffness matrix, this will yield exponentials of the form:

$$\begin{aligned} e^{-\displaystyle \frac{{\theta }_i{\phi }_i({\hat{x}}_K)}{U_T}}e^{\displaystyle \frac{{\theta }_i{\phi }_i(P_i)}{U_T}}=e^{\displaystyle \frac{{\theta }_i({\phi }_i(P_i)-{\phi }_i({\hat{x}}_K))}{U_T}}. \end{aligned}$$
(23)

Note that this form bears great resemblance to the 1D Scharfetter-Gummel exponential [26]. It plays a similar role in allowing a linear problem to approximate exponential fitting between nodes. We can finish the solution by assuming implicit Euler for the time derivative:

$$\begin{aligned} {M}\frac{1}{{\varDelta }t}({{X}}^{k+1}_i-{X_{\varvec{i}}}^k)=A_{\varvec{i}}\left( {X_{\varvec{i}}}^{k+1}e^{\frac{{\theta }_i\varvec{\phi }}{U_T}}\right) \end{aligned}$$
(24)
$$\begin{aligned} \left( \frac{{M}}{{\varDelta }t}-A_{\varvec{i}}\varvec{\phi }\right) {X_{\varvec{i}}}^{k+1}=\frac{{M}}{{\varDelta }t}{X_{\varvec{i}}}^k \end{aligned}$$
(25)

where the matrix \(\varvec{\phi }=\mathrm {diag}\left( e^{\frac{{\theta }_i\varvec{\phi }}{U_T}}\right) \). As discussed previously, this scales the stiffness matrix so that \(A_{\varvec{i}}\varvec{\phi }\) is no longer symmetric). Formally, our solution is given by:

$$\begin{aligned} {X_{\varvec{i}}}^{k+1}={\left( \frac{\varvec{M}}{{\varDelta }t}-A_{\varvec{i}}\varvec{\phi }\right) }^{-1}\frac{\varvec{M}}{{\varDelta }t}{X_{\varvec{i}}}^k \end{aligned}$$
(26)

(In practice, we will always work with the matrix equation directly instead of actually inverting the matrix.)

2.2.2.2 Reaction Step

The system of ordinary differential equations, \({\partial }_tX_i\,\mathrm {=}\,R_i\mathrm {(}\hat{x}\mathrm {)}\), in Step 2 of the operator splitting algorithm is actually quite involved. In general we will have an arbitrary number of defects and an arbitrary number of reactions. However, these reactions are all of two very specific forms, either representing the bimolecular reaction of two defects or the formation/decay of a single defect. We therefore consider only binary reactions of the form \({1 + 2 \rightleftharpoons 3 + 4}, {1 + 2 \rightleftharpoons 3}, {1 \rightleftharpoons 2 + 3}\) the reaction terms can be written as a quadratic form:

$$\begin{aligned} R_i\left( {{\mathop {X}\limits ^{\rightharpoonup }}}\right) =\ {\mathop {X}\limits ^{\rightharpoonup }}^TA_i{{\mathop {X}\limits ^{\rightharpoonup }}}+b^T_i\mathop {X}\limits ^{\rightharpoonup } \end{aligned}$$
(27)

with the matrices \(A_i\) and the column vectors \(b_i\) containing the reaction rates. Increasing the number of defects may increase the total number of possible reactions, but only 3 or 4 defects will be involved in any particular reaction.

There are two strategies for implementing individual reactions. Each reaction can be implemented independently or simultaneously.

  • A sequential implementation would involve solving each reaction independently. The jth reaction generates a matrix \(A_{i,j}\) and a vector \(b_{i,j}\). Note that for bimolecular reactions \(A_{i,j}\) has two nonzero entries and \(b_{i,j}\) is the zero vector. For formation/decay reactions, both \(A_{i,j}\) and \(b_{i,j}\) have one nonzero entry each. For each j, we have the following ODE:

    $$\begin{aligned} {\partial }_tX_i=R_i\left( \hat{x}\right) = {\mathop {X}\limits ^{\rightharpoonup }}^T\left( t_k\right) A_{i,j}{{\mathop {X}\limits ^{\rightharpoonup }\left( t\right) }}+b^T_{i,j}\mathop {X}\limits ^{\rightharpoonup }, \end{aligned}$$
    (28)

    Each of these reactions can be solved using implicit Euler—see section “Iteration by Reaction”.

  • A simultaneous implementation of the reaction equations will require the numerical solution of the ODE system by, for example, the implicit Euler method together with a Newton method for the large quadratic system. The Jacobian \(\frac{\partial \mathop {R}\limits ^{\rightharpoonup }}{\partial \mathop {X}\limits ^{\rightharpoonup }}\), can then be easily computed from Eq. (27).

In both cases, there is no need to use a higher order method since the operator splitting method described in Section A is only of first order.

2.2.2.3 Iteration by Reaction

Because every considered reaction is of either single molecule formation/dissociation or bimolecular type, we can solve every reaction network using just the explicit formulas given below. Simply iterating through all possible reactions in any order gives a first order unconditionally stable method for the reaction step. Experimental results demonstrate that changing this order has no significant impact on the results for the case of copper migration.

For more complex reaction networks complications can occur. These are discussed elsewhere [28].

  1. 1.

    Single Molecule

    Let us consider the reaction given by the rate \(R^{2,3}_1\):

    $$\begin{aligned}&{\partial }_tX_1=K^1_{2,3}X_2X_3-K^{2,3}_1X_1 \nonumber \\&{\partial }_tX_2=K^{2,3}_1X_1-K^1_{2,3}X_2X_3 \nonumber \\&{\partial }_tX_3=K^{2,3}_1X_1-K^1_{2,3}X_2X_3 \end{aligned}$$
    (29)

    This could, for instance, represent the knock-off equation in Eq. (1) where interstitial Copper (\(X_1=[Cu_i]\)) replaces lattice Cadmium, resulting in Copper atom at a Cadmium site (\(X_2=[Cu_{Cd}]\)) and an interstitial Cadmium (\(X_3=[Cd_i]\)).

    Note that the right hand sides are identical (up to a sign) and that the quantities \((X_1+X_2)\) and \((X_1+X_3)\) are conserved (corresponding to conservation of copper and conservation of lattice sites in our example). In particular, if the superscript refers to the time-step, we have that \(X^{k+1}_1+X^{k+1}_2=X^k_1+X^k_2\) and \(X^{k+1}_1+X^{k+1}_3=X^k_1+X^k_3\). We will use these equations to decouple the ODEs. First, let us use the Implicit Euler method to write the first ODE for the time step k as an algebraic expression:

    $$\begin{aligned} \frac{1}{{\varDelta }t}\left( X^{k+1}_1-X^k_1\right) =K^1_{2,3}X^{k+1}_2X^{k+1}_3-K^{2,3}_1X^{k+1}_1. \end{aligned}$$
    (30)

    Since \(\Delta t\) should be small, we multiply it out to avoid numerically unstable division by a small number. Using conservation laws, we can also write \(X^{k+1}_2\) and \(X^{k+1}_3\) in terms of \(X^{k+1}_1\) and the known values of X as time step k:

    $$\begin{aligned} X^{k+1}_2=X^k_1+X^k_2-X^{k+1}_1 \end{aligned}$$
    (31)
    $$\begin{aligned} X^{k+1}_3=X^k_1+X^k_3-X^{k+1}_1 \end{aligned}$$
    (32)

    Substitution yields:

    $$\begin{aligned} X^{k+1}_1-X^k_1=K^1_{2,3}\Delta t\left( X^k_1+X^k_2-X^{k+1}_1\right) \left( X^k_1+X^k_3-X^{k+1}_1\right) -K^{2,3}_1\Delta tX^{k+1}_1 \end{aligned}$$
    (33)

    Careful examination reveals that this is a quadratic equation for \(X^{k+1}_1\). Rearrangement and expansion yields the three coefficients as:

    (34)

    We can then use the quadratic formula to yield:

    $$\begin{aligned} X^{k+1}_1=\frac{-B\pm \sqrt{B^2-4AC}}{2A}=\frac{2C}{\sqrt{B^2-4AC}-B}. \end{aligned}$$
    (35)

    We note that the middle expression has A in the denominator, but that since A is proportional to \(\Delta t\) it may be small. We therefore rearrange the expression to avoid numerical division by a small number. Because B is always negative for positive concentrations, we can also determine the appropriate sign of the square root to obtain our final solution. Finally, since \(X^{k+1}_1\) is now known, we can immediately substitute back into our conservation laws to obtain \(X^{k+1}_2\) and \(X^{k+1}_3\).

  2. 2.

    Bimolecular

    Let us consider the reaction \(R^{3,4}_{1,2}\):

    $$\begin{aligned}&{\partial }_tX_1=K^{1,2}_{3,4}X_3X_4-K^{3,4}_{1,2}X_1X_2 \nonumber \\&{\partial }_tX_2=K^{1,2}_{3,4}X_3X_4-K^{3,4}_{1,2}X_1X_2 \nonumber \\&{\partial }_tX_3=K^{3,4}_{1,2}X_1X_2-K^{1,2}_{3,4}X_3X_4 \nonumber \\&{\partial }_tX_4=K^{3,4}_{1,2}X_1X_2-K^{1,2}_{3,4}X_3X_4. \end{aligned}$$
    (36)

    This could correspond to interstitial Copper (\(X_1=[\mathrm {C}{\mathrm {u}}_{\mathrm {i}}]\)) interacting with Zinc on a Cadmium lattice cite (\(X_2=[\mathrm {Z}{\mathrm {n}}_{\mathrm {Cd}}]\)), resulting in interstitial Zinc (\(X_3=[\mathrm {Z}{\mathrm {n}}_{\mathrm {i}}]\)) and Copper on a Cadmium site (\(X_4=[\mathrm {C}{\mathrm {u}}_{\mathrm {Cd}}]\)). Following the method of the previous section, we can develop three conservation laws and rearrange:

    $$\begin{aligned}&X^{k+1}_2=X^k_2-X^k_1+X^{k+1}_1 \nonumber \\&X^{k+1}_3=X^k_3+X^k_1-X^{k+1}_1 \nonumber \\&X^{k+1}_4=X^k_4+X^k_1-X^{k+1}_1 \end{aligned}$$
    (37)

    Discretizing the equation for \(X_1\) using the Implicit Euler method and substituting the conservation laws will yield a quadratic equation for \(X^{k+1}_1\) in the same manner as in the previous section. The coefficients are:

    (38)
2.2.2.4 Comparison with Newton’s Method

Particular care needs to be taken in order to have a computationally stable steady-states. These states are vital for standard device simulation results such as IV and CV measurements. By the principle of detailed balance, at equilibrium every individual reaction will be in equilibrium. This indicates that we will obtain a stable equilibrium for any iteration order. As noted above, the iteration scheme works well for the copper diffusion case.

However, some problems can occur in far from equilibrium conditions. This behavior becomes even more noticeable when one defect is unstable and has multiple dissociation pathways. For this case, whichever dissociation reaction occurs first in the iteration will occur preferentially to the later reaction, regardless of the relative size of the reaction rates.

This behavior does not occur for the Newton iteration scheme. Because the reactions are considered simultaneously, each reaction pathway will occur with relative frequency exactly governed by the ratio of the reaction rates. In practice, we find that the Newton method is vastly superior for complicated reaction networks. Furthermore, the method does not present a significant computational issue because the reactions are local in space and the Jacobian can be generated independently for each grid point.

3 Verification of 1D Unified Solver

3.1 Verification of 1D Device Simulation Routine Versus SCAPS Device Simulator

As discussed in Sect. 2, in 1D version of the Unified Solver, the device simulation is performed on each time step to obtain self-consistent electric field and carrier distributions during the diffusion-reaction simulation. Besides, the device simulation routine serves to obtain the steady-state electric current during the simulation of current-voltage characteristics of the device. The device simulation routine can use the defect profiles obtained from the consistent solution of 1D kinetic reaction-diffusion problem as well as the artificially set uniform or nonuniform defect profiles similar to other solar cell simulators. In order to verify the accuracy of the device simulation routine, we performed its rigorous comparison with the widely used in the community SCAPS solar cell simulation code [31].

In order to perform such comparison, we used the same device structures (highly p-doped back layer, lightly p-doped CdTe layer, highly n-doped front layer), properties of materials, light absorption spectra and illumination spectra both in 1D Unified Solver and SCAPS solar cell simulator. By comparing the simulated energy bands, distributions of free carrier in the dark and under the stress conditions, as well as JV curves for different doping levels and recombination rates, we conclude that the device simulation routine of 1D Unified Solver reliably produces accurate solution of the drift-diffusion problem for free carriers under different bias conditions (Fig. 4).

Fig. 4
figure 4

Comparison of band diagram (left) and the IV curve calculated with 1D Unified Solver (dashed lines) and SCAPS solar cell simulator (solid lines) for one of the test device structures considered in this study

Full size image

3.2 Verification of the Defect Reaction-Diffusion Model on Experimental Data

3.2.1 Experiment on Cu Penetration

In order to verify the reaction-diffusion model of Cu penetration into CdTe, experimental study of Cu migration in single crystal CdTe was done at First Solar Inc. (Perrysburg, OH). In this experiment, a thin Cu-containing ZnTe layer was deposited on sx-CdTe substrates provided by JX Nippon. After deposition, to drive Cu into CdTe, anneals with different durations were performed at 250, 300 and \(350\,^{\circ }\text {C}\).

Measured Cu profiles show strong dependence on the annealing temperature and duration: Cu penetrates deeper into CdTe as we increase the annealing time/duration (Fig. 5). The high concentration of Cu appearing in the first 0.5 \(\upmu \)m is the residual Cu concentration from the ZnTe layer. Abnormally high concentration of Cu (>10\(^{18}\) \(\text {cm}^{-3}\)) in the region (0.5 < x < 1 m) obtained after very high annealing temperatures (\(350\,^{\circ }\text {C}\)) or long annealing durations (20 min at \(300\,^{\circ }\text {C}\)), was ascribed to the broadening of ZnTe or formation of ZnCdTe, caused by Zn diffusion [32] and will not be further addressed here.

Another important finding in this experiment is a dip of Cu concentration at the edge of CdTe adjacent to ZnTe, while the peak of the Cu concentration in the CdTe layer is situated 1–2 m beneath the interface. This is interpreted as a back diffusion of Cu during the cool down process (SIMS measurements are performed at room temperature after cooling down the sample).

Fig. 5
figure 5

Atomic Cu profiles achieved with different annealing recipes. Black pentagrams represent the control sample without any annealing. Solid lines represent the simulated Cu profiles

Full size image

3.2.2 Simulation

To model this experiment, we created a simulation domain with 15 \(\upmu \)m of initially undoped CdTe and 0.5 \(\upmu \)m of p-doped ZnTe:Cu layer. \(10^{21}\) cm\(^{-3}\) initial concentration of Cu\(_{i}\) was defined in ZnTe:Cu source layer and a constant 10\(^{17}\) cm\(^{-3}\) p-type doping was maintained in this layer during the entire simulation. A 0.45 eV difference in standard formation energy of Cu\(_{i}\) in CdTe and ZnTe layers (more favorable in ZnTe) was used to obtain the best correspondence of the Cu concentration difference across the interface as achieved by different annealing recipes. This energy difference is in a qualitative agreement with the results of first principles calculations. We used Neumann boundary conditions for both ends of the simulation domain to maintain the conservation of all defects. For carrier transport properties and material properties we used widely accepted values of polycrystalline CdTe [33]. Although better carrier lifetime and material quality can be expected in sx-CdTe [34], there should be no considerable impact on the resulting Cu profiles since no (or negligible) electric current flows through the samples during the annealing process. To simulate this experiment on Cu penetration, we included the primary exchange reaction (1) as well as diffusion of Cu\(_{i}\) and Cd\(_{i}\) into the reaction-diffusion model.

The original built-in electric field between highly p-type doped ZnTe and intrinsic CdTe layers prevents \({\text {Cu}}^+_{i}\) from moving into the CdTe region in large amount. When a small amount of \({\text {Cu}}_{i}\) is able to diffuse into CdTe, it quickly knocks Cd atoms off generating an immobile \(\text {Cu}_{Cd}^{-}\) acceptor and mobile \({{\text {Cd}}_{i}^{2+}}\) donor (backward reaction (1). Part of \({{\text {Cd}}_{i}^{2+}}\) is drifted into ZnTe layer under the same built-in electric field across the interface and, as a result, p-type region starts to form in CdTe. We note that since the charge is conserved in all reactions, achieving p-type doping without \({{\text {Cd}}_{i}^{2+}}\) moving out of CdTe is very difficult within this model. We found that during the annealing process, the concentration of \({\text {Cu}}_{Cd}\) does not show a monotonic increase, a saturation effect is observed instead.

The saturation behavior can be explained by analyzing the distribution of defect concentrations and the band diagram during annealing (Fig. 5 left bottom). As Cu forms acceptors in CdTe, an electric field is generated between the Cu occupied p-type region and the intrinsic CdTe region without Cu, which again prevents further movement of Cu\(_{i}\) into the intrinsic region of CdTe. Once the distribution of defects gets close to the balance of all involved reactions, such as 0.5 < x < 6 m region in Fig. 6, less Cu\(_{Cd}\) will be generated. Hence more Cu\(_{i}\) can travel through this saturated region to occupy Cd sites in the newly formed p-i junction area (x > 6 m in Fig. 6).

Fig. 6
figure 6

Left: Simulated profiles of major Cu-related defects and free carriers (top panel) and band diagram in the ZnTe:Cu/sx-CdTe structure after 3 min of annealing at 350 \(^{\circ }\)C (bottom panel). Right: Simulated profiles of major Cu-related defects in the sample after 3 min annealing at 350 \(^{\circ }\)C and an extra 12 min cooling process

Full size image

As we have mentioned before, the measured Cu profiles after cooldown show a dip at CdTe/ZnTe interface. Here we analyze how such dip is formed according to our model. As we cool down a sample to room temperature, Cu\(_{i}\) starts to diffuse back into ZnTe due to the 0.45 eV difference in the standard formation energies of Cu\(_{i}\) between CdTe and ZnTe, and reaction (1), which is out of equilibrium now begins to produce more Cu\(_{i}\) by kick-out Cu\(_{Cd}\) with available Cd\(_{i}\). After reaction (1) consumes most of the Cd\(_{i}\), additional Cd\(_{i}\) from ZnTe penetrates into CdTe and continues to kick-out Cu\(_{Cd}\) to reach the new equilibrium among involved reactions. Since only the interface region can get supplemental Cd\(_{i}\), Cu reduction is more obvious near the interface (Fig. 6 right). As temperature further decreases, both reaction and diffusion rates become quite slow. However, this process is not be completely stopped right after the cooling process. Experimental evidence of Cu movements in CdTe devices stressed at 65 \(^{\circ }\)C has been reported recently [35].

Another important outcome of this simulation is the insight into the formation and evolution of doping during the annealing and cooldown. At high temperature, a partial compensation between Cu\(_{Cd}^{-}\) and \({{\text {Cd}}_{i}^{2+}}\) is achieved as the atomic Cu concentration is around 2 \(\times \) 10\(^{17}\) cm\(^{-3}\) while the hole concentration is one order of magnitude less (see the line with diamonds (green in the online version) in Fig. 6 left, labeled as “Free Holes”). In addition, partial ionization of the Cu\(_{Cd}\) acceptors plays a role in the compensation mechanism since the acceptor level of Cu\(_{Cd}\) is not that shallow. About 90% of Cu\(_{Cd}\) acceptors in the saturated area are ionized at 350 \(^{\circ }\)C according to detailed results from our simulation. After cooldown, the free carrier concentration drops below 3 \(\times \) 10\(^{15}\) cm\(^{-3}\) level (Fig. 6 right) with only a smaller reduction in atomic concentration of Cu at room temperature. More importantly, the new compensation is mostly achieved between Cu\(_{Cd}^{-}\) and \({{\text {Cu}}_{i}^+}\). Therefore during cooling, the compensation mechanism is changed in this case. The observed change is a complex process determined by diffusion, drift, reactions, and temperature-dependent Fermi-Dirac statistics both for free carriers and Cu\(_{Cd}\) acceptors. Again, the resulting room temperature hole density depends crucially not only on donor-acceptor compensation but also on the possibility of the ionization of Cu\(_{Cd}\) acceptors.

Simulated free carrier concentration in the saturation region after cooldown are about an order of magnitude higher than the carrier concentration in poly-crystalline Cu, Cl-treated CdTe solar cells from Colorado State University [35] (Fig. 7). This difference stems from a number of factors: the difference in annealing temperatures and Cu concentration in ZnTe source, not accounting for defect interactions in our simulations, additional doping compensation by Cl and even the effect of grain boundaries on the measured CV doping profiles in px-CdTe films. Therefore, even though, our simulation provides a qualitative understanding of the formation and compensation of doping in CdTe, it is expected that more targeted experiments and simulations will be performed in the future to explain the peculiarities of doping formation in px-CdTe.

Fig. 7
figure 7

Simulated and experimental free carrier concentrations versus atomic Cu concentration at room temperature. Green pentagrams are measured free carrier concentrations in px-CdTe solar cells fabricated by Colorado State University

Full size image

Table 1 shows the comparison of diffusion parameters used to obtain the best correspondence with experimental curves (Fig. 5) and parameters calculated from first principles. It is seen, that in our 1D simulation, the diffusion barrier height of the major specie responsible for Cu penetration (Cu\(^+_{i}\)) is about 0.26 eV higher that theoretically predicted one. We attribute this discrepancy to the fact that we did not account for the interactions between the defects and the formation of complexes, which may influence the overall diffusion kinetics. This effect is worth investigating in the future studies.

Table 1 Fitted diffusion parameters with calculated theoretically in work [25] (in parenthesis)
Full size table

We conclude that the Cu penetration mechanism implemented in the developed reaction-diffusion model is capable to reproduce the experimental dependence of the Cu profile on the annealing conditions, to reproduce some specific features of experimental atomic Cu profiles (dip at the CdTe/ZnTe interface), as well as to provide a theoretical insight into the process of formation and compensation of Cu doping in CdTe layer.

4 Modeling of Light Soaking Effect in CdTe Solar Cells

Nearly all PV technologies exhibit changes in device performance under extended illumination, or “light soaking”, although the magnitude and the trend of these changes are not always the same among different technologies. Experiments on both commercial modules and research cells based on CdTe technology have shown improvement of cell performance under light stress conditions for up to 20 h [36]. Many accredited such phenomena to the passivation of traps and migration of Cu ions, however no simulations were previously done to confirm any of these mechanisms. We use the developed 1D Solver to simulate self-consistently the effects of illumination, bias and temperature on the evolution of defect profiles during stress and the resulting performance changes of the device.

In this simulation, we employ a simplified dopant compensation model. Namely, 10\(^{16}\) cm\(^{-3}\) Cu\(_{Cd}^{-}\), 0.4 \(\times \) 10\(^{16}\) cm\(^{-3}\) \({{\text {Cu}}_{i}^+}\) and 0.5 \(\times \) 10\(^{16}\) cm\(^{-3}\) background donor is assumed as the initial defect distribution in this simulation, resulting in \(\sim \)10\(^{15}\) cm\(^{-3}\) equilibrium hole concentration in the quasi-neutral region of CdTe absorber layer (typical doping in px-CdTe absorber). We use a standard ZnTe/CdTe/CdS device structure with common electronic properties.

The light stress is typically performed after the dark storage of solar devices. Therefore, in order to prepare the initial system for light soaking simulations, first, we simulate the equilibrium of the defects in CdTe cells under dark without any bias at 65 \(^{\circ }\)C (Fig. 8 (left)). In equilibrium, most of the \({{\text {Cu}}_{i}^{+}}\) is pushed away from the depletion region, due to the built-in potential of the p-n diode. As a result, more uncompensated acceptors appear in the junction area. Cu\(_{Cd}\) acceptor is partially ionized in the quasi-neutral region, while it is completely ionized in the depletion region due to low density of holes in that area.

Under light stress condition under applied forwards bias of 0.8 V (maximum power point), the defect equilibrium changes in the following way: (1) \({{\text {Cu}}_{i}^{+}}\) moves closer to the main junction due to the forward bias, reducing the uncompensated acceptor doping density in the depletion region, (2) part of ionized defects (\({{\text {Cu}}_{i}^{+}}\) and Cu\(_{Cd}^{-}\)) are converted into the neutral state after capture of light-generated free carriers, (3) the zero-bias depletion region width increases because of the reduced p-doping in the junction area (Fig. 8 (right)), (4) carrier collection efficiency improves, thus increasing the performance.

Fig. 8
figure 8

Simulated concentrations of defects and free carriers and device energy bands in the dark (left) and under light soak conditions (right) at 65 \(^{\circ }\)C

Full size image

In order to isolate the effect of ionization degree change due to excess carriers capture on \({{\text {Cu}}_{i}^{+}}\) and \(\text {Cu}_{Cd}^{-}\) defects and the effect defect drift under the applied voltage bias, we simulate different stress conditions with different combinations of illumination and forward bias (Table 2). Figure 9 shows the efficiency changes of the solar cells as a function of soaking time with different modes. The results of our simulations suggest that both \({\text {Cu}}_{i}^{+}\) migration towards the junction area and the injection of excess holes in the depletion region can cause the enhancement of device performance. Simulations with defect migration resulted in the strongest performance enhancement effect. Moreover, the effect of defect migration in the dark and with applied forward bias is almost the same as the overall effect of applied light and forward bias.

Table 2 List of stress conditions
Full size table

The kinetics of the performance increase upon such dark to light switching depends on the diffusivity of mobile species involved in the transformation. Using high Cu\(_i^+\) diffusion coefficient (9 \(\times \) 10\(^{-10}\) cm\(^2\)/s at 65 \(^{\circ }\)C) calculated from the first-principles [25], only 0.03 h of light stress is enough for device to reach a new steady-state (see Soak A of Fig. 9). Experimentally observed performance transients often happen on multi-hour timescale [37, 38]. By decreasing the diffusion coefficient of Cu\(_i^+\) down to 10\(^{-13}\) cm\(^2\)/s, we were able to obtain better agreement with the experimentally observed 10 h long device performance stabilization. This indicates that while our model correctly captures the response of the system to the external stress, the actual kinetic mechanisms behind the redistribution of species may be more complex than simple diffusion of Cu\(_i^+\). This result provides the evidence that more complicated diffusion mechanisms beyond simple diffusion of Cu\(_i^+\) may be involved in the defects redistribution in CdTe. For example, the formation of pair complex defects can influence the diffusivities of species by slowing down the fast diffusion of interstitials as well as introducing additional mechanisms of diffusion of weakly mobile substitutional defects [20]. We expect that inclusion of such advanced mechanisms into reaction-diffusion simulations will allow to reproduce, understand and even predict the kinetics of transient performance changes of the real devices.

Fig. 9
figure 9

Device performance changes as a function of soaking time with various conditions

Full size image

5 Conclusions

In summary, we have implemented (in MATLAB) self-consistent 2D numerical solvers for simulating defects reactions and migration in CdTe material. We have verified the 2D solver using the widely used code for solar cell simulation (SCAPS) as well as the experimental data on Cu penetration into CdTe. By doing so, we have shown that the Cu penetration mechanism based on the Cu-Cd exchange reaction and implemented in 2D reaction-diffusion solver is able to reproduce the experimental dependence of Cu profiles in CdTe on the annealing temperature and time. Using the developed 2D reaction-diffusion solver, we have revealed the new mechanism of a transient response of CdTe-based solar cell to the applied light-bias conditions. According to our simulations, the experimentally observed performance enhancement under illumination and/or applied forward bias may be, at least partially, caused by the migration of defects changing the distribution of doping profile in the absorber. Based on simulation results, we discuss the possible explanations for limited incorporation and compensation mechanisms of Cu dopants inside CdTe bulk as well as the possible defect migration mechanisms beyond the simple diffusion of interstitials. We expect that the discrepancies between simulations and experiments will be reduced by inclusion more detailed defect chemistry models with all important defects and interactions between them and making use of more complicated 2D simulation framework that includes the effects of grain boundaries.