Keywords

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

Entanglement of geometric objects is an important and fascinating phenomenon. On one hand it leads to deep mathematical problems, which are studied within branches of mathematics such as topology; several Fields medals have been awarded for such work, in particular in knot theory. On the other hand entanglement is common in Nature and plays a role in physical, chemical, and biological systems. Nobel prizes related to topology have been awarded in 2016 in physics and chemistry. Topology, and entanglement in particular, are important, because they take into account not just local, but global properties of systems under consideration. This sheds new light on such systems and often requires developing new tools to analyze them.

The study of topology and entanglement is particularly interesting when it concerns real physical systems, and at the same time poses theoretical and mathematical challenges. This is the case of entangled proteins, whose studies we summarize in this work. On one hand, it is unbelievable that such complicated structures would evolve accidentally, so there must be some physical and biological role of entanglement. On the other hand, the study of entangled proteins poses new mathematical challenges, for example a description of knots on open chains. Entangled proteins have been very actively studied in recent years, along with the development of new mathematical tools that enable their characterization.

In this work we summarize studies of entangled proteins, which in recent years have gained the status of a new branch of interdisciplinary research, involving biophysics, biochemistry, mathematics, and computer science. Historically knotted proteins attracted attention first, so – after a brief introduction on what we mean by entanglement in general – we discuss first their properties. Subsequently we discuss properties of other entangled structures identified in proteins: slipknots, links, and lassos. We present both theoretical and mathematical tools to describe such structures, as well as their biological role and physical features.

2 Entanglement in Proteins

Proteins are long chains made of amino acids. They are often described in terms of primary, secondary, and tertiary structure. However such a description does not take into account an important feature of a protein chain that we refer to as entanglement. To describe it, it is sufficient to represent a protein as a one-dimensional chain, or a polygonal shape made of a series of segments spanned between consecutive C\(_{\alpha }\) atoms. From a mathematical perspective, when such a one-dimensional chain is embedded in a three-dimensional space, it can non-trivially wind around itself. By the entanglement we understand a pattern of such winding.

There is a branch of mathematics called knot theory, which studies properties of entangled chains. However the most important feature of chains studied in knot theory is that they are closed, i.e. they don’t have loose ends. Such entangled closed chains are called knots, and – apart from closing the chain – they resemble knots that we know from our daily life. Similarly as in daily life, one can also consider knots in open chains, especially if the ends of such chains are long enough – however such knots are not uniquely defined, and they can be untied by a sequence of smooth manipulations (which do not involve cutting of the chain). On the other hand, knots on closed chains cannot be untied without cutting a chain – therefore they can be uniquely defined, and a given type of a knot can be assigned to a given entangled configuration. In this sense knots, as understood mathematically, are referred to as topological objects.

It turns out that protein chains can also be knotted [5, 29, 32, 42, 43, 71, 76] – at least in the imprecise sense of knotting that we use in daily life. As proteins do have loose ends, it is not possible to assign types of knots uniquely to their configurations. Nonetheless, it often happens that termini of a protein are long enough, so that a type of a knot can be assigned to a protein, at least approximately. For this reason one can take advantage of various tools and techniques from knot theory when studying entangled proteins. On the other hand, these tools should be used carefully and they are often insufficient to characterize configurations of open chains – some additional information should also be provided in this case, and some new techniques are necessary to study knotted proteins. As within the last decade it turned out that knotted proteins are much more common than originally believed, such techniques have been developed, as we will discuss in what follows. Knotted proteins are the first class of entangled structures that we discuss in this work – a simple example of a knot formed in an open chain (which could be a protein backbone) is shown in Fig. 8.1.

Fig. 8.1
figure 1

Several classes of entangled structures identified in proteins (from left to right): knots, slipknots, links, lassos. Here we present only one basic example from each of those classes – more complicated examples are discussed in what follows

Full size image

One interesting feature of entangled proteins is that they can form configurations which are trivial from the topological and knot theory viewpoint, however – in appropriate sense – they are still entangled. One example of such a configuration is called a slipknot [32, 63]. It consists of two loops, one threaded through the other, as shown in Fig. 8.1. If two termini of a slipknot are pulled, the two loops disentangle; equivalently, after connecting two termini of a slipknot in the simplest possible way (e.g. by extending them far away), the configuration represents mathematically trivial knot. As in knot theory a slipknot configuration would be regarded as trivial, some novel tools are necessary to describe its geometry – and this is an important task, because it turns out that the entanglement of the two loops of a slipknot has interesting consequences and affects proteins’ properties. Proteins with slipknots are the second class of entangled structures that we discuss in this work.

So far we have briefly explained what we mean by entanglement of open chains. However the pattern of entanglement can be more involved once additional linkages, such as disulfide (or other) bridges are taken into account. When such bonds are present, then proper loops in a protein chain can be also considered (i.e. closed loops formed by only a part of the whole chain). In principle such proper loops might themselves be knotted, which however has not been observed to date. Nonetheless, when two or more loops are present in a given chain, they can be entangled and form structures called links in knot theory [11], see Fig. 8.1. Such links are non-trivial topological objects and can be classified using knot theory tools. Links that are formed on chains with disulfide linkages we call as deterministic, because they are made of closed loops and their topology is uniquely determined. In addition, one can also consider links made of several chains that form a dimer, trimer, etc., after their termini are connected (e.g. closed on a large sphere) – we call such links as probabilistic. Proteins with links are the third class of entangled structures discussed in what follows.

Once disulfide bridges are taken into account, one can also consider configurations where one or two termini of a protein chain pierce through a loop closed by such a bridge. Such configurations are called lassos [13, 45], see Fig. 8.1. Even though they can be regarded as topologically trivial and – similarly to knots in open chains – cannot be uniquely defined, they also have interesting biological and physical consequences. Lassos are the last class of entangled structures that we discuss in this work.

One important conclusion of the work summarized here is that, first of all, entangled structures exist in proteins – even though for a long time it was believed that they are too complicated to form [42]. Another very important result is that the entanglement has certain biological and physical role. Moreover, studies of entangled proteins pose new challenges in mathematics, computer science, and other related disciplines. For all these reasons the new, interdisciplinary field of entangled proteins is rapidly growing, and despite many fascinating results found in last years, we have no doubts that a lot more is still to be discovered.

3 Proteins with Knots and Slipknots

The first class of entangled proteins that we discuss are proteins with knots. As mentioned above, because proteins have loose ends, it is not possible to identify uniquely knots formed by their chains. It is however possible to identify such knots using probabilistic methods. In this section we present basic properties of knots in mathematical sense, discuss how to describe knots and slipknots in proteins using this language, and summarize which (families of) knotted proteins have been identified to date. We also briefly discuss folding mechanisms and how the presence of knots affects the function of proteins.

3.1 Classification and Description of Knots

To present mathematical knots on closed chains it is useful to project them on a two-dimensional plane. A type of a knot is then encoded in a pattern of crossings formed by the projection of the chain. It is always possible to minimize the number of such crossings by smooth transformations of the chain, which do not involve cutting it. On the level of the two-dimensional diagram such transformations can be reduced to three elementary operations, referred to as Reidemeister moves, see Fig. 8.2. Various topological types of knots can be classified in terms of equivalence classes (with respect to Reidemeister moves) of their diagrams. It is also very useful to introduce so called knot invariants – various mathematical objects, such as numbers or some functions, which can be uniquely assigned to a given knot type (so that they do not change under Reidemester moves). Knot invariants are used to distinguish and classify knots: they can be computed for two given knots, and if the results are different, it means that these knots have different topological type. One ultimate goal of research in knot theory is to construct an invariant which would distinguish all knots, i.e. if it would take the same value for two knots, it would mean that these two knots are of the same type. Such an invariant is still not known, however invariants that we know these days are sufficient to distinguish relatively simple knots found in proteins.

Fig. 8.2
figure 2

Reidemeister moves

Full size image

The simplest knot invariant is the minimal number of crossings in a two-dimensional knot diagram obtained from the projection of a knot; this is simply called the number of crossings. For a trivial knot (i.e. unknotted loop), which is denoted \(0_1\), this number is zero. There is no knot with one or two crossings, i.e. any such configuration can be smoothly reduced to, and represents the unknot. There is one knot with three crossings, called the trefoil and denoted \(3_1\), and one knot with four crossings, called the figure-eight knot and denoted \(4_1\). There are two different topological types of knots with five crossings, denoted \(5_1\) and \(5_2\), and three types of knots with six crossings \(6_1\), \(6_2\) and \(6_3\). Some of the knots mentioned here (in fact those identified in proteins to date) are shown in Fig. 8.3. The number of different knots with fixed number of crossings grows very rapidly; for example there are 21 knots with eight crossings, and 165 knots with ten crossings. In the notation we just mentioned the main number denotes the number of crossings, and the subscript labels different knots (with a given crossing number) – so that, for example, \(3_1\) denotes a unique (the only one) knot with three crossings.

In addition, each knot may arise in two forms, which differ only by the mirror image. Sometimes we distinguish the mirror image by adding plus or minus sign in the notation of the knot; for example two versions (mirror images) of the trefoil knot are denoted \(3_1^+\) and \(3_1^-\). For some knots their mirror image is identical to the original knot – for example \(4_1\) knot has this property.

Fig. 8.3
figure 3

Unknot (denoted \(0_1\), left) and examples of non-trivial knots (in closed chains), which have been identified in proteins to date: trefoil (denoted \(3_1\)), figure-8 knot (denoted \(4_1\)), \(5_2\) knot, and Stevedore’s knot (denoted \(6_1\)). Below each knot its Alexander polynomial is given

Full size image

The number of crossings is not a strong invariant – it identifies uniquely only the unknot, trefoil, and figure-eight knot, and for more crossings there are many different, inequivalent topological types of knots with the same number of crossings. For this reason more powerful knot invariants are introduced. There is a large family of knot invariants known as knot polynomials, which are much stronger, i.e. they have different values for more knots, and thus they enable to distinguish more knots. Such polynomials may depend on one or more variables. For example, the so called Alexander polynomial \(\Delta (q)\) and Jones polynomial J(q) depend on one variable q. More intricate HOMFLY-PT polynomial P(a, q) [21, 50] depends on two variables, and reduces to Alexander and Jones polynomials respectively for \(a=1\) and \(a=q^2\). These polynomials can be determined from a two-dimensional diagram of a knot, and – as we explain in what follows – we also use them to identify knots in proteins. Alexander polynomials for knots identified in proteins are given in Fig. 8.3.

One challenge in analyzing knots in proteins is the fact that protein chains are open. To assign a type of knot to an open chain formed by a protein, one may transform it into a closed chain by joining its termini. The problem is that such an operation is not unique, and various knot types may be created depending on how two termini are connected. One simple way to form a closed loop is to connect two termini by a straight segment. However such an operation may lead to other knot than intuitively seen, especially in case when the termini are located far from each other and the entangled region. It is therefore more reasonable to connect the termini to two points – or the same point – on a large sphere surrounding a protein [18, 43], see Fig. 8.4. This gives more reasonable results, however the resulting type of knot may still depend on the details of the method and it is not unique (e.g. it may depend on the choice of such a point or points on a sphere). The best way to cope with this problem is to choose many equally distributed points on a sphere, and – connecting the termini through all those points – compute probability of forming various knots. This is the method that we often use in order to determine a type of a protein knot – for example, after connecting the termini as mentioned above, we calculate the knot polynomial which determines the knot type [29]. We also introduce the minimal probability, typically of the order of 40%, necessary to regard a given structure as knotted (in other words, if a probability of detecting each type of a knot by connecting the termini in various ways is smaller than this 40%, we regard the structure as unknotted). Unless otherwise stated, in case one particular knot type is assigned to a protein, this means that this knot is formed with the highest probability. Influence of the knot detection method on the type and probability of identified knots was analyzed among others in [14, 73].

Fig. 8.4
figure 4

To assign a knot type to an open chain one can either connect two termini to two points on a large sphere surrounding this chain (left), or to connect these two termini directly by a straight segment (right)

Full size image

Once we can assign knot types to open chains, we can also define geometric quantities that characterize such knots, in particular the knot core and knot tails. The knot core is the shortest subchain of a given chain, for which a given knot type is detected; it can be easily determined by cutting consecutive residues from both termini, and checking whether the remaining chain is still knotted (in the probabilistic sense described above). Knot tails, by definition, consist of all residues which do not form the knot core, i.e. these are parts of the backbone chain between either of its termini and the knot core. We also characterize protein knots as being deep or shallow; the latter ones are those which can be untied by thermal fluctuations, and typically their tails consist of not more than a few residues. Deep knots cannot be untied by thermal fluctuations and they have longer tails.

Fig. 8.5
figure 5

KMT algorithm. If a triangle defined by three consecutive residues (represented by C\(_{\alpha }\) atoms) is not pierced by any other segment of the backbone chain, then the middle atom in this triple is removed. This operation is repeated for all consecutive triples of residues as long as possible, resulting in a simplified chain with the same topology

Full size image

In the analysis of protein knots we also use the so called KMT algorithm [34], which simplifies a given chain without changing its topology. This algorithm works as follows. We analyze triangles determined by all triples of consecutive residues (represented by C\(_{\alpha }\) atoms). In case such a triangle is not pierced by any other segment of the protein chain, we remove the middle residue from a given triangle (and so reduce the triangle to the segment connecting remaining two residues), see Fig. 8.5. This operation simplifies the (closed) chain without changing its topological type. Such operations are performed as long as possible, leading ultimately to a simplified chain. In particular, if the chain is reduced to only three residues, this means that the original configuration represented the unknot – therefore the KMT algorithm is a simple method to check whether a given chain is not knotted (one should however be careful when interpreting the results of the KMT algorithm – there are certain peculiar unknotted configurations that cannot be reduced simply to three residues). It is also useful to use the KMT algorithm before calculation of knot polynomials – this may significantly reduce their computation time.

3.2 Proteins with Knots and Slipknots – KnotProt Server and Database

For a long time it was believed that knots cannot be formed in proteins, due to their complexity. A possibility of finding knots in proteins was discussed for the first time by Mansfield, who also found a shallow knot in human carbonic anhydrase [42]. The first example of a deeply knotted protein was found by Taylor in 2000 [71], and subsequently other examples of knotted proteins were identified [32, 39, 43, 76]. The most complicated protein knot is the Stevedore’s knot \(6_1\), identified in [5]. Proteins with slipknots were identified and analyzed e.g. in [32, 63].

These days the main source of data that facilitates detection of knots is the Protein Data Bank (PDB, or RCSB database), which stores geometric configurations of more than hundred thousands proteins. It is impossible to identify knots in such a large set of proteins without the use of mathematical and computer tools. In fact, detection of a knot even in a single protein is usually impossible just by a naked eye, due to the complicated entangled structure of the backbone chain. This is why various algorithms and mathematical techniques that we summarized above, involving in particular computation of knot polynomials, are indispensable in the search of knots in proteins. Several databases that store information about knotted proteins were constructed some years ago, for example [33, 35]. However, a modern database and server that stores up to date (and regularly updated), and much more extensive information about proteins with knots and slipknots, is the KnotProt [29], whose features we summarize in what follows.

The KnotProt database, http://knotprot.cent.uw.edu.pl, contains information about all proteins with knots or slipknots. This database contains not only the information about a type of a knot in a given protein and some of its geometric features (e.g. the length of loose ends and the size of the knotted core), but it also presents an internal geometric structure of a given protein in terms of a matrix diagram, which is called the knotting fingerprint. The form and properties of such diagrams will be introduced in the next section. Moreover, the database presents extensive information about the biological function of proteins with knots and slipknots, structural and homological similarity to other knotted or unknotted proteins, and various statistics. In addition, the KnotProt database enables users to upload protein or polymer structures, analyze whether they form knots or slipknots, and generate their knotting fingerprints.

As of today (spring 2017), there are 993 knotted chains identified in KnotProt, and 473 chains with slipknots. This is around 2% of all proteins deposited in the Protein Data Bank. Knotted proteins are found in all kingdoms of life [30]. Knots are found in globular proteins, including those from mitochondria or a ribosome, and in membrane proteins. Around 90% of knotted proteins act as enzymes, whose active site – responsible e.g. for binding ligands – is located in the knotted core. Some knotted proteins are responsible for DNA binding, and some still have an unknown function. The biggest family of proteins with a deep knot is the SPOUT family [72]. The smallest and rather deeply knotted protein, from methanocaldococcus jannaschii, consists of 92 amino acids and is known as MJ0366. The deepest knot is found in protein with unknown function from T. pallidum (PDB code: 5ijr chain A) – its tails have length of at least 100 amino acids. This protein consists of three domains and the middle one is knotted. A deep knot exists also in the family of membrane proteins, calcium exchanger protein (e.g. protein with PDB code 4k1c). A protein structure with an artificial (designed) knot is also known [31].

Table 8.1 A list of families of proteins with knots (following [30]). In the second column a representative structure of each family is given (PDB codes include the chain identificator as the last letter, in the subscript). In the third column the knot type is given, and in the last column the knot fingerprint is provided (whose meaning is explained in the text). A sign in the superscript of the knot type denotes its chirality
Full size table
Table 8.2 A list of families of proteins with slipknots. In the second column a representative structure of each family if given (PDB codes include the chain identificator as the last letter, in the subscript). In the last column the slipknot fingerprint is provided (whose meaning is explained in the text). A sign in the superscript of the knot type denotes its chirality
Full size table

We present a list of representative proteins with knots and slipknots, based on the KnotProt database, in Tables 8.1 and 8.2. In the first column of these tables representative entangled proteins are listed, grouped according to their function, and PDB codes of such representative structures are given in the second column. In Table 8.1 in the third column a type of a knot for the whole chain is provided. In the last column of both tables knotting fingerprints (whose meaning is explained below) of respective structures are given.

3.3 Knotting Fingerprint for Knots and Slipknots

As we discussed earlier, knots in proteins are formed in open chains, which is subtle from mathematical perspective and enables their identification only in a probabilistic manner. However, once a relevant definition of knots in open chains is provided, it can be used not only to determine a type of the knot for the whole chain under consideration, but also for all subchains of such a knot. Such an analysis provides much more accurate and detailed information about entangled proteins. It also enables rigorous detection of slipknots, which can be defined as chains which are unknotted as a whole, but which possess a subchain which is knotted. It is convenient to present an information about knotting of all subchains of a given chain in terms of a matrix diagram, called knotting fingerprint, see Fig. 8.6, which was introduced in [67] following [32].

Fig. 8.6
figure 6

An illustration of knotting fingerprints which shows how to interpret them (following [67]). Horizontal and vertical edges of each triangle represent the backbone chain (from N to C terminus). For each point (i, j) in the matrix diagram we verify whether a subchain stretched between ith and jth residue is knotted – if so, we color this point (in black in this example). If the whole protein chain forms a knot, then the neighborhood of the left bottom corner of the matrix diagram is black (left panel). If the whole chain is not knotted but contains a slipknot, then the left bottom corner is not black (middle and right panels). The location of the black rectangles enables to determine the knotted core (the largest subchain of the whole chain for which a knot is still detected), and remaining parts of the chain are referred to as knot tails (left panel). In case of slipknots, we can analogously determine the location of various parts of the chain, referred to as the slipknot loop, knotted core, and slipknot tails (middle and right panels)

Full size image

More precisely, the knotting fingerprint presents data about knotting of each subchain of a given chain in a lower-triangular part of matrix of the size \(N\times N\), where N is the length of the whole chain. The position (i, j) of this matrix represents a subchain spanned between ith and jth residue of the backbone chain, and it is colored according to the type of the (most probable) knot formed by this subchain. The intensity of the color corresponds to the probability of forming such a knot. Typically such a matrix diagram consists of several approximately rectangular regions, which represent various types of knots spanned by various subchains. Such a diagram is a source of various interesting information. First, it enables identification of the minimal length of the knotted region (i.e. the size of the knotted core), the depth of a knot (i.e. the number of amino acids that can be removed from either end of the protein chain before converting it from a knot to a different type of knot or an unknot), and other geometric data characterizing a knot. Second, the location of various knots along the chain indicates their biological and physical role, especially if it is correlated with the location of active sites.

It is also useful to encode the pattern of knots on subchains of a given chain in a simplified notation, which lists all those types of knots identified in the fingerprint matrix. For example by K\(4_1 3_1\) we denote a protein which forms \(4_1\) knot, and which possesses a subchain forming \(3_1\) knot; the initial letter K means that the whole chains forms \(4_1\) knot. In case the whole chain forms a slipknot the letter S is used; for example, S\(4_1 3_1\) means that the whole chain forms a slipknot, and some of its subchains form knots of type \(4_1\) and \(3_1\). Knotting patterns (including the orientation (or mirror image) of identified knots, denoted by ± in the superscript) of some representative proteins with knots and slipknots are provided in the last column in Tables 8.1 and 8.2.

In Fig. 8.7 we present examples of the most complicated fingerprints of a knot and a slipknot found to date. The knotted chain (left) with the fingerprint K\(6_1 6_1 4_1 3_1\) is the structure of DehI (PDB code 3bjx chain A). The chain with the slipknot (right) with the fingerprint S\(3_1 4_1 3_1 3_1 3_1\) is the crystal structure of uracil transporter–uraa (PDB code 3qe7A). Fingerprints for all protein structures with knots and slipknots identified to date can be found in the KnotProt database.

Fig. 8.7
figure 7

Most complicated knotting fingerprints identified in the KnotProt database. The knotted protein (PDB code 3bjx chain A, left) forms \(6_1\) knot, and its various subchains form also another \(6_1\) knot and \(4_1\) and \(3_1\) knots – such a configuration is denoted schematically as K\(6_1 6_1 4_1 3_1\). A protein with slipknot (PDB code 3qe7 chain A, right) is unknotted as a whole, however some of its subchains form \(4_1\) and various \(3_1\) knots. Each type of knot is denoted by different color (\(3_1\) – green, \(4_1\) – orange, \(6_1\) – blue), whose intensity corresponds to probability of detection of this type of knot. Cartoon representations of these two proteins are also shown in each case, with colors changing from red at the N-terminus to blue at the C-terminus

Full size image

3.4 Folding of Knotted Proteins

An important challenge in the study of entangled proteins is to understand and describe not only their geometric configurations which determine biological activity and function, but also folding mechanisms which lead to such configurations. Even though some experiments with knotted proteins have been conducted, in recent years their folding mechanisms have been studied mainly theoretically, using various coarse grained models. Knots identified in proteins to date are of twist type, and they can be made in one step, by threading of a tail through a twisted loop (the number of twists determines the type of the resulting knot). Current results suggest that knots are not made spontaneously along the protein backbone (and then slight to the final native location), but they are created in two main steps [64]: the first is formation of a twisted native loop, and the second is threading a shorter knot tail through this loop, as shown in Fig. 8.8. In case of proteins with more complex structure, twisted native loop flips over a core of the protein creating e.g. the \(6_1\) knot also just in one step [5]. Flipping mechanism was also observed for proteins with slipknots [64].

Fig. 8.8
figure 8

Twist knots (which are found in proteins) are created by forming a loop and twisting it several times, and then threading one terminus through this loop

Full size image

One of the most commonly analysed proteins are Yibk and YebA, members of SPOUT family, which possess a deep trefoil knot. Theoretical studies with an unbiased structure based model revealed that these proteins can self tie, via formation of a twisted loop and threading shorter C-terminal tail [64]. Detailed analysis showed that the tail threads through the twisted loop in the slipknot configuration and this threading is a rate limiting step. The same pathway is also observed when non-native contacts are introduced [79]. Even though these proteins have been very extensively studied, still only kinetics pathways are known [41, 54, 74].

The free energy landscape however has been uncovered theoretically for a few small knotted proteins with rather shallow knots. In particular reversible folding via a slipknot conformation was observed for the smallest knotted protein (known to date), MJ0366 [48], with a structure based model, and it was further extensively studied e.g. in [4, 44]. Furthermore, explicit all atom simulations showed that this protein can self-tie and electrostatic interactions facilitate tying of a knot [49]. The self-tying mechanism of MJ0366 was also suggested experimentally [80]. Reversible folding was also observed for artificially designed proteins [31], where both theoretical and experimental studies suggested that topological constrains are responsible for their slower folding [37, 66].

Theoretical studies of proteins with more complex knots, such as \(5_2\) and \(6_1\), also suggest that knotting happens just in one step, which in this case corresponds to flipping the twisted loop over the core of the protein [5, 83]. Moreover folding of those proteins consists of parallel pathways and intermediates steps. Experimental studies of these proteins suggest that their folding mechanism involves at least one intermediate state, see e.g. [2, 36], and proteins are prone to misfold at the final state of folding [38, 81]. Influence of knot type on folding pathway based on lattice models was also investigated, e.g. in [20, 56].

Since proteins in vivo are surrounded by crowded environment and their folding could be supported by chaperons, or they could fold cotranslationally, it was also analyzed how these aspects affect knotting mechanism [8, 40, 57]. For example, when a chaperon is approximated by a cylindrical box, it was found that knotting is still a rate limiting step, however a chaperon significantly smooths the free energy landscape for smallest knotted proteins MJ0366, VirC2 and DndE [47], as well as proteins with complex fingerprint \(5_23_13_1\) [83]. Experimental study on YibK, YebA shown that chaperon can significantly speed up the folding process [40]. Cotranslational knotting with theoretical methods was extensively studied e.g. in [8].

Even though in principle the folding pathways leading to knotted configurations have been proposed, the origin (type of interactions) of the driving force needed to overcome the topological barrier [12, 55], and the influence of chain stiffness [66], are still under investigation. Moreover it is important to mention that a certain exception in folding mechanism was observed based on a three domain protein from T. Pallidum (PDB code 5jir chain A) where the middle domain is knotted. This protein probably folds via a shallow knot formed at random position [30]. Other approach to understand free knotting mechanism and reviews discussing folding pathways of knotted proteins can be found e.g. in [19, 28, 68, 77].

3.5 Function of Knotted Proteins

Another crucial challenge, apart from characterizing folding and geometry of entangled proteins, is to understand what is the role and the function of entanglement. This question is currently actively studied. A review of all knotted proteins shows that the topological fingerprint is well conserved in proteins separated even by million years of evolution and very low sequence similarity [67]. Moreover, more than 90% of known knotted proteins are enzymes, whose active sites are located inside the knotted core. These observations suggest that knots provide some advantages for the hosting organism.

Analysis of analogous proteins having the same function – methylation of tRNA [27] – but different topology also reveals some information about the role of a knot. An example of such a pair of proteins involves a bacterial one with a trefoil \(3_1\) knot (TrmD), and an eukaryotic one which is unknotted (Trm5). As showed in [7], the knot responds to the motions of the whole protein, even though it belongs to the rigid part of the structure. The trefoil knot in the TrmD protein is capable of transferring the signal coming from the substrates further through the protein, by its internal moves. Mutations of key residues in the area of the knot suppress this motion and make the protein unable to conduce the methyl transfer. The fact that the knot plays a role in the enzymatic function suggests that knots play more profound role than just stabilizing the structure. Stabilizing role of knots however should not be neglected, and it is important e.g. in phytochromes, which are red/far-red light photoreceptors that direct photosensory responses across the bacterial, fungal and plant kingdoms [17, 78]. The binding pocket of those proteins is stabilized by a deep figure-eight knot. Some other suggestions about the role of knots are presented in [14, 53].

Additional information about knots in proteins was obtained based on mechanical manipulations, via single molecule experiment both in vitro and in silico (by computer analysis) [51, 58]. First, molecular dynamics simulations with structure based model [59, 60] showed that a knotted protein is more resistant than an unknotted one [61]. Second, it was found in [6, 62] that upon pulling proteins by their termini, knots tighten along the backbone at deterministic locations. Conditions to untie knotted proteins were established in [65] and tested experimentally in [84]. Furthermore, it was shown that knotted proteins can block or be pulled through narrow channels, depending on the applied force [69, 70, 82]. A surprising tying of a knot on the protein backbone was also observed in thermal and chemical denaturation [3, 41]. Furthermore, mechanical manipulations of proteins with slipknots showed that they form certain metastable conformations [25, 26, 63].

4 Links in Proteins

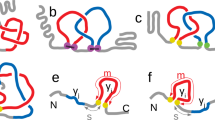
In knot theory, apart from knots, also another class of entangled structures is considered, which are called links. A link consists of several closed loops (called components of a link), such that each of those loops may be knotted, and moreover pairs, triples, etc. of loops can be simultaneously interlinked. Any knot may be regarded as a link with only one component. The simplest example of a non-trivial link is the Hopf link, formed by two loops linked in the simplest possible way. Another link that can be made out of two loops is the Solomon link. Hopf link and Solomon link are shown in Fig. 8.9 (in the middle).

Links in proteins have been identified only very recently, and they can be considered from two perspectives [11]. First, links can be identified in a single protein chain if it has additional linkages, for example disulfide bridges. Each such bridge defines a closed loop, and if several such loops are present in one protein chain, then the whole structure forms a link (which is nontrivial if those loops are interlinked). Importantly, links defined in such a way are properly defined from mathematical perspective and there is no need to consider probabilistic methods to identify them – we call such links deterministic. Once orientation of component loops is introduced – e.g. induced from the orientation of the backbone from N to C terminus – the notion of chirality of links can be defined, see Fig. 8.9.

Fig. 8.9
figure 9

Deterministic links identified in proteins (following [11]): the Hopf link and the Solomon link (whose mathematical structure is shown in the middle). In the left a cartoon representation of a protein forming a given link is shown. A schematic representation of protein backbone is shown in the right, with two link components in blue and red, the linkages in orange, and remaining parts of the protein chain in black. The orientation of each component loop can be induced from the orientation of the backbone from N to C terminus – once it is taken into account, two types of the Hopf link can be considered

Full size image
Table 8.3 Families of proteins (following [11]) with the Hopf link (with positive and negative orientation, respectively in the upper and lower part of the table, as indicated in the last column). For each family the function and a representative chain are given respectively in the second and the third column. L1 and L2 denote the size of the two loops of the Hopf link, P1 and P2 is the signed index of a residue piercing through each of those loops. “# of hom.” is the number of homologs for a given structure, “# of loops” is the number of disulfide-based covalent loops in the structure (e.g. if 4, there are 2 covalent loops forming the Hopf link and two trivial covalent loops), “Size” is the number of residues in the structure, “Loop sep.” is the sequential distance between the loops. The dashed line separates the humanly modified protein with PDB code 3T93. Proteins are ordered according to the size of the first pierced loop
Full size table
Table 8.4 Families of proteins (following [11]) with the Solomon link. For each family the function and a representative chain are given respectively in the second and the third column. L1 and L2 denote the size of the two loops of the Hopf link, P1 and P2 is the signed index of a residue piercing through each of those loops. “# of hom.” is the number of homologs for a given structure, “# of loops” is the number of disulfide-based covalent loops in the structure (e.g. if 4, there are 2 covalent loops forming the Solomon link and two trivial covalent loops), “Size” is the number of residues in the structure, “Loop sep.” is the sequential distance between the loops
Full size table

On the other hand, links can also be made of several separate chains, which form dimers, trimers, etc. [15]. To identify such links, each component chain must be closed (e.g. by connecting its termini on a large sphere, similarly as in the case of knots), and then the HOMFLY-PT polynomial is calculated. A type of such a link may depend on details how termini of all chains are connected, and so we call such links as probabilistic.

All proteins with links identified in the Protein Data Bank are presented in the LinkProt database [15], available at http://linkprot.cent.uw.edu.pl. As of spring 2017, 124 deterministic and 8456 probabilistic links (1071 linked proteins with 30% of sequence similarity) have been identified in this database. This database is also regularly updated, so that it always contains an up to date list of proteins with links. Deterministic links identified in proteins to date form one of two simplest links – Hopf link and Solomon link – as shown in examples in Fig. 8.9. Once the orientation of two component loops is introduced, one can consider two versions of the Hopf link, and both of them are found in proteins (in this case there is a natural orientation of each loop induced by the ordering of the protein from N to C terminus). In Fig. 8.9 in the left a cartoon representation of a given protein is shown, and in the right the protein backbone is shown in a simplified way, with link components colored in blue and red, linkages (closing the loops) shown in orange, and remaining parts of the protein chain in black. Furthermore, all non-redundant structures (found to date) that form deterministic Hopf link, together with their geometric properties and the function, are listed in Table 8.3. Analogous data for non-redundant proteins that form deterministic Solomon link is shown in Table 8.4.

Probabilistic chains identified in LinkProt database form more configurations, which involve two, three or four components. One of the most interesting configurations is \(6^3_3\) (probabilistic) link, which involves three symmetrically and mutually interlinked components (note that it should not be confused with the Borromean rings). As there are many more protein configurations forming probabilistic links, to learn about their properties we encourage a reader to browse the LinkProt database.

Currently the function of links in proteins is not well understood, however they definitely provide additional topological stability [11] (in addition to stabilizing role of disulfide bridges and closed loops). Link topology is also responsible for misfolding of a hosted protein [11].

5 Proteins with Lassos

The last class of entangled proteins that we discuss are proteins with lassos, introduced systematically in [45]. Lassos can be identified in structures with disulfide (or other types of) bridges. Similarly as in (deterministic) links, such a bridge defines a closed loop. By a lasso we mean a configurations which consists of such a loop, through which some other part (or parts) of the backbone chain is threaded. The pattern of such threading may be quite complicated: a protein chain may pierce the loop several times, it can wind around the backbone chain forming a loop, etc. Note that configurations similar to lassos were studied in [75]; we also stress that lassos should not be confused with cystein knots [9, 10, 16].

Fig. 8.10
figure 10

An oxidoreductase protein (PDB code 2oiz) forming a lasso (left), with the disulfide bridge shown in orange (following [45]). In the middle a schematic representation of the protein chain and the triangulated minimal surface spanned on the loop (closed by the disulfide bridge) are shown; the surface is pierced, respectively by 127th and 172nd chain segment, at two triangles (in green and blue color, which indicates the direction of piercing). A baricentric representation of the minimal surface is shown in the right

Full size image

In order to define lassos unambiguously, we propose to span an auxiliary surface of minimal area (analogous to a soap bubble), called the minimal surface, on the closed loop. To determine such a surface, or more precisely a triangulated approximation to such a surface, we use tools and algorithms from computer graphics [45]. The orientation of the loop (from N to C terminal) induces the orientation of the surface spanned on this loop, which enables to identify a direction of piercing of this surface by a protein terminus, as shown in Fig. 8.10.

Fig. 8.11
figure 11

Various types of lassos identified in proteins (following [45]). The orange segment denotes a bridge/linkage forming a closed loop. Top row: single lasso, double lasso, and triple lasso (denoted respectively \(L_1\), \(L_2\) and \(L_3\)). Bottom row: supercoiled lasso (denoted LS), and lasso involving two termini piercing the loop (denoted LL)

Full size image

Several lasso motifs identified so far in proteins are shown in Fig. 8.11. One class of motifs involves one protein terminus piercing the minimal surface once, or several times from opposite directions, as shown in the first row in this figure. Such configurations are called single lasso, double lasso, triple lasso, etc., and denoted respectively \(L_1\), \(L_2\), \(L_3\), etc. Another lasso motif involves one terminus winding several times around the closed loop and piercing the minimal surface each time from the same direction; we call such a configuration a supercoiling and denote it LS. Finally, a configuration where two termini pierce through the closed loop is denoted LL, or more precisely \(LL_{i,j}\), where i and j denote the number of times each terminus pierces the minimal surface. For each of those motifs an information about the direction of piercings and the piercing terminus can also be provided. More complicated lasso configurations, involving several loops, also exist, for example such as shown in Fig. 8.12.

Fig. 8.12
figure 12

More complicated lasso configurations, involving several loops (following [13])

Full size image

An example of a protein forming a lasso of type \(L_2\) – an oxidoreductase protein (PDB code 2oiz) – is shown in Fig. 8.10. Cartoon representation of the protein is shown in the left, with the disulfide bridge shown in orange. A simplified protein structure is shown in the middle, with the grey triangulated minimal surface spanned on the closed loop, pierced by one terminus at two triangles (green and blue color, indicating the direction of piercing). A baricentric planar representation of the minimal surface with pierced triangles is shown in the right. The numbers 127 and 172 indicate the numbers of segments connecting consecutive C\(_{\alpha }\) atoms that pierce the surface.

Table 8.5 Families of proteins with various types of lassos (following [45]). In the first bullet groups of enzymes are listed in order of decreasing number of occurrences; in the second bullet PDB classes of non-enzymatic proteins are listed in order of decreasing number of occurrences. In case of \(L_1\) lasso only groups with more than 9 elements are listed
Full size table

All proteins with lassos identified to date are collected in the LassoProt database [13], available at http://lassoprot.cent.uw.edu.pl. As of spring 2017, there are 6446 structures with lassos in this database, which have been identified in all kingdoms of life, in globular and membrane proteins. We list families of these proteins in Table 8.5, together with the number of lasso structures in each family, and grouped into enzymes and non-enzymes. It truns out that around 18%, i.e. 376 out of 2021 protein structures with disulfide bonds (data from the year 2015), form lassos in the nonredundant set (i.e. proteins with sequence similarity lower than 30%). Furthermore, geometric properties of lassos can be analyzed using the online PyLasso server [46], available at http://pylasso.cent.uw.edu.pl.

Apart from their geometry, also functions and other properties of proteins with lassos have been studied. In [1, 52] it was shown that the lasso motif is well preserved in antimicrobial proteins, where the lasso stabilizes the entire fold. Lassos also have a therapeutic potential, similarly as proteins with cystein knots [16]. Even though the influence of lassos on proteins’ stability and biological activity have been analyzed systematically only recently, it is already known that e.g. in leptin the presence of a lasso slows down folding, but facilitates receptor binding [22,23,24].

6 Conclusions

We have presented various types of entangled structures in proteins: knots, slipknots, links and lassos. Their crucial feature is the fact that the whole protein chain needs to be considered to identify its type of entanglement; in this sense entanglement is a global property of a protein chain. Some years ago it was believed that entangled proteins, in particular knots, cannot exist, due to the complexity of their structure. However more recently many such structures have been found, and it has become clear that their existence is not accidental and they must play certain biological and physical role.

We have also presented databases and servers that assemble and regularly update information about entangled structures, as well as a plugin that facilitates analysis of lassos:

Apart from geometric structure of all protein chains, also an information on their function, various classifications, a list of similar chains, etc., are provided in the above databases. In these websites one can also upload other polymer-like structures, not necessarily proteins, and analyze if they contain knots, slipknots, links or lassos.

In last few years the studies of entangled proteins have grown into a new, rapidly developing and interdisciplinary field, which involves methods and techniques from biophysics, biochemistry, computer science, branches of mathematics such as topology and knot theory, etc. There are plenty of opportunities and outstanding questions in studying entangled proteins, which involve understanding their function, evolution, folding mechanisms, and other features. We encourage a reader to try to answer some of these questions too.