Keywords

1.1 Introduction

It seems that so far a quite a few versions of lesson study are practicing in the world. Although the author would like to distinguish them from Japanese lesson study, he simply uses the term “lesson study” in this Chapter with consideration of consistency in the book. The history of lesson study in Japan spans more than a century (Makinae, 2010). For Japanese educators, lesson study is like the air they breathe. It came to the attention of educators outside of Japan primarily through The Teaching Gap (Stigler & Hiebert, 1999), which described findings from the Trends in International Mathematics and Science Study (TIMSS) video study on eighth grade mathematics lessons in several countries. One chapter, “Japan’s approach to the improvement of classroom teaching”Footnote 1, provoked enormous interest in lesson Study (Stigler & Hiebert, 1999). Independently, some educators such as Lewis also noticed the significance of Japanese lesson study and brought this to the attention of the international community (Lewis & Tsuchida, 1998). Since then, many mathematics teachers and teacher educators around the world have been involved in lesson study and many books and research papers have been written on its various aspects (Department for Children, Schools and Families, 2008; Doig & Groves, 2011; Hart, Alston, & Murata, 2011; Lewis, 2002; Lewis, Perry, & Hurd, 2009; Ono & Ferreira, 2010; White & Lim, 2008). However, some aspects of lesson study still seem to not be well understood outside Japan .

One crucial aspect of Japanese mathematics instruction is the method of teaching mathematics through problem solving. The international education community took a great interest in this when they were introduced to the typical structure of a Japanese mathematics lesson through watching a lesson in action in the TIMSS video study. Stigler and Hiebert (1999) refer to this method of instruction as “structured problem solving.” However, teaching mathematics through problem solving has been largely overshadowed by interest in incorporating lesson study as a model for professional development . I assert that lesson study and teaching mathematics through problem solving are two wheels of a cart: one cannot succeed without the success of the other. In this chapter, I will discuss the close relationship between lesson study and teaching mathematics through problem solving.

1.2 Lesson Study Components and Process

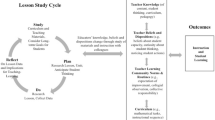
The lesson study process is illustrated in Fig. 1.1 as having five steps. This figure differs from other, similar diagrams in other publications that only have four steps (e.g. Lewis, 2002; Lewis & Hurd, 2011). The inclusion of a fifth step more accurately portrays how Japanese teachers progress through the lesson study cycle . Borrowing from Lewis’s (2002) and Lewis and Hurd’s (2011) descriptions, each step can be summarized as follows:

Fig. 1.1
figure 1

Steps of a lesson study cycle (Fujii, 2014a, p. 113)

Full size image
  1. 1.

    Goal Setting: Teachers consider long-term goals for student learning and development. They identify gaps between these long-term goals and current reality and decide the research theme.

  2. 2.

    Lesson Planning: Teachers collaboratively plan a research lesson designed to address the goals. They prepare a “lesson proposal,” a document that describes the research theme, content goals, connections between the current content and related content from previous and later grades, rationale for the chosen approach, a detailed plan for the research lesson , anticipated student thinking, data collection, etc.

  3. 3.

    Research Lesson: One team member teaches the research lesson while the other members of the planning team, staff members from across the school, and, usually, an external knowledgeable other observe and collect data.

  4. 4.

    Post-lesson Discussion: Observers share data from the lesson in a formal lesson colloquium, highlighting successes and issues concerning student learning, disciplinary content, lesson and unit design, and broader aspects of teaching and learning.

  5. 5.

    Reflection: Not only the instructor, but also other members in the school consolidate and document what was learned from the lesson study cycle so that it can be implemented in the future, and formulate new questions for the next cycle. They write a report or bulletin that includes the original research lesson proposal, student data from the research lesson , and reflections on what was learned.

Steps 3 and 4, the Research Lesson and Post-Lesson Discussion , are the most visible and, as such, are what has attracted the attention of the international education community . This leads to a typical misconception: that the Research Lesson and Post-lesson Discussion alone constitute lesson study. Lesson study is sometimes introduced as an open lesson by a veteran teacher “jumping in” to another teacher’s classroom (Takahashi, 2013, p. 84). But the whole picture is much larger. Each step in the lesson study cycle closely relates to the others and Steps 1 and 2 provide a crucial foundation for the success of the more visible Steps 3 and 4. Step 3, the Research Lesson , is a lesson in which students work on their own to solve a given task for which they have not been shown solution strategies and critically analyze and reflect on their own and other students’ solutions. This approach to mathematics instruction was described by Stigler and Hiebert (1999) as a “structured problem solving lesson.” I will refer to the teaching method in this step as “teaching mathematics through problem solving.”

1.3 Teaching Mathematics Through Problem Solving in Japan

1.3.1 The Structure of Teaching Mathematics Through Problem Solving

The meaning of “problem-solving” varies depending on the culture and historical time in which it is referred. We can see a clear progression of the changing meaning of “problem solving” in Japan after Word War II (Soma, 2000):

  1. (1)

    (1945–1954)—The term “problem solving” appears as it applies to “life experience lessons” (In elementary school this could be participating school festivals, exploring the town, learning how to make bread, etc.).

  2. (2)

    (1955–1964)—“Problem solving” appears as it applies to word problems.

  3. (3)

    (1965–1974)—“Problem solving” appears as it applies to methods of instruction.

Japanese mathematics lessons have their own clear style, which often fascinates foreign observers and is often regarded as unique. Becker et al. (1990) identified “students’ rising and bowing” as the first of eight components in a typical Japanese mathematics lesson. Stigler and Hiebert (1999) included “reviewing the previous lesson” as one of five major components. But these points of view are those of observers; Japanese teachers generally do not think about the structure of their lessons in these ways. What Japanese educators consciously strive to include in every problem-solving lesson are the following four activities, as seen in Table 1.1.

Table 1.1 The four phases of teaching mathematics through problem solving
Full size table

These four activities or components are the framework of the lesson. Each component is 5–20 min long as part of a 45–50 min lesson. I will now describe each phase in detail.

1.3.1.1 Present the Problem for the Day

Some people may misinterpret “present the problem” as providing a detailed explanation or demonstration of the procedures involved in solving the given problem. However, this is not actually the case. In The Teaching Gap, Stigler and Hiebert (1999, p. 77) write, “the (Japanese) teacher presents a problem to the students without first demonstrating how to solve the problem,” and, “we saw that a feature we hardly noticed before is perhaps one of the most important features of U.S. lessons—that the teacher almost always demonstrates a procedure for solving problems before assigning them to students.”

In Japan , “present the problem” means to make students understand the context of a given task and the corresponding mathematical conditions that would be used to solve that task . Japanese educators distinguish between “teaching how to solve the task ” and “problem solving based mathematics instruction,” in which students learn how to solve the problem by solving it themselves. Therefore, it is important to choose the task carefully. If chosen well, the task allows for the important new mathematical ideas to emerge in classroom discussion .

Doig, Groves, and Fujii (2011) explain that there are four types of tasks typically used in lesson study:

  1. (1)

    Tasks that directly address a concept

  2. (2)

    Tasks that develop mathematical processes

  3. (3)

    Tasks that are chosen based on a rigorous examination of scope and sequence

  4. (4)

    Tasks that address a common misconception.

Typically, only one task is given in a lesson. People unfamiliar with this approach may feel that it is strange to only give students one problem per mathematics lesson. However, Japanese educators have studied and seen the success of this approach. Much thought is given to the selection and presentation of a lesson’s task , so that the implementation of this single task can accomplish all the goals of the lesson.

Below are the following principles for an ideal task (Fujii, 2015):

  1. A.

    It is appropriate and mathematically valuable in terms of the aims of the lesson.

  2. B.

    It interests the students.

  3. C.

    It is at the appropriate level of difficulty.

  4. D.

    It can be solved in several ways.

  5. E.

    It has a potential to elicit valuable basic wisdom.

1.3.1.2 Students Work to Solve the Problem

If the task principle “interests the students,” is effective, students can start solving the task without any help from the teacher. While students work to solve the task on their own, the teacher in the classroom is extremely busy. The teacher must move among the students, practicing what we call in Japanese kikan-jyunshi, which means purposeful scanning or monitoring. Almost all teachers in other countries behave similarly, but what is consciously being done may differ from one country to another. To prove this point, Hino (2003) identified the result from the Learners Perspective Study to show how these conscious approaches were different between an Australian teacher and a Japanese teacher. An Australian math teacher was interviewed:

Ms. M: Well I have to make sure that everyone’s … involved and everyone’s… participating in the lesson I guess - that I’m not excluding anyone … that um … that I’m encouraging everyone to have a go …

It seems that she is trying to consult with every student individually. So what do Japanese teachers consciously do during kikan-jyunshi? In Japan , the teacher:

  1. A.

    Identifies how each student is solving the problem. Anticipated solutions, including typical incorrect solutions, are part of their prepared lesson plan .

  2. B.

    Takes notes of the general atmosphere and how most students are solving the problem.

  3. C.

    Gives hints to slower learners. If necessary, asks faster learners to come up with another way of solving the problem.

  4. D.

    Plans what they should do during the compare and discuss (neriage) phase.

One of the most difficult aspects of kikan-jyunshi is the necessity to anticipate potential student solutions during lesson planning . This is particularly difficult for novice teachers. However, I think this practice of trying to prepare all possible solutions improves Japanese teachers’ teaching abilities to see the mathematics through the eyes of the student and consider how best to facilitate their understanding of the underlying concepts or skills. Furthermore, it underscores how lesson planning , Step 2 of the lesson study cycle in Fig. 1.1, is a critical factor in determining the quality of mathematics teaching. Anticipating solutions enriches a teacher’s knowledge on the topic and deepens their understanding of their students’ cognitive nature and abilities. During kikan-jyunshi, if a teacher discovers an unexpected solution, they may ask the student about their thought process and record their answer. After the lesson, during the Post-Lesson Discussion , Step 4 of the lesson study cycle , teachers discuss how likely students actually were to attempt the anticipated student solutions listed in the lesson plan .

It is also important for the teacher to look beyond individual solutions and grasp how the class, as a whole, is approaching the task . While engaging in kikan-jyunshi, a teacher has to decide which student will present first and think about how to direct the class discussion . They must collect information and compose scenarios for the next phase of the lesson, compare and discuss (neriage). Usually, student-teachers or novice teachers, or even experienced teachers, find kikan-jyunshi extremely difficult. During the Post-Lesson Discussion , Step 4 of the lesson study cycle , teachers discuss the instructor’s kikan-jyunshi, supported by evidence or data collected by observers during the Research Lesson .

1.3.1.3 Compare and Discuss (Neriage)

The third phase of a lesson, called neriage in Japanese, assumes that students will arrive at different solution methods and therefore focuses on a comparison and discussion of those different solution methods. During the neriage phase o, students’ solutions are typically written in order from “naïve” to “sophisticated” on the blackboard. Therefore, the teacher should be careful as certain students may realize why they are always the first to present. Teachers must also carefully plan how everything will be written on the blackboard in order to best compare and contrast students’ solutions. The blackboard is used to organize both thought processes and results. Japanese teachers have been reluctant to use overhead projectors as they are small and therefore unsuitable for showing complete thought processes.

The neriage phase is difficult for novice teachers as it is closely connected to kikan-jyunshi. Novice teachers can typically give positive comments to each student, but struggle to elicit and clarify points that a student doesn’t understand. Sometimes, students cannot distinguish between two similar solutions. In this case, the teacher has to explain how these two solutions are significantly different from each other. Or sometimes it’s the opposite issue: two solutions appear to be different but are actually the same. Neriage provides an opportunity for teachers to foster mathematical ways of thinking in their students. In other words, it is a chance to focus on process. Mathematical ways of thinking cannot be demonstrated by simply reviewing the definition of concepts, they can only be truly experienced through problem solving activities. Therefore, Japanese teachers teach mathematics through problem solving. This kind of lesson encourages students to think mathematically and helps them become independent learners. This is one of the ultimate goals of school education.

Sometimes the neriage phase may appear to be implemented well, but is actually not. These cases typically are a result of a one-to-many correspondence between teacher and students describing their solutions during discussion . Takahashi (2008) described this phenomenon as “show-and-tell.” The heart of neriage is reflective discourse (Doig, Groves, & Fujii, 2011). Although rather a classic citation, neriage should be an actualization of Vygotsky’s zone of proximal development (Ohtani, 2014). Therefore, during neriage, teachers must see the students’ potential as high as possible and help them move toward their potential from what they came up on their own, i.e., what they can do without help.

1.3.1.4 Teacher Summarizes the Lesson (Matome)

Fujii, Kumagai, Shimizu, and Sugiyama (1998) identified that American teachers tend not to summarize the lesson at the end of a class. Without this phase, the lesson ends with students only being able to take satisfaction in their individual work. By including a summary at the end of the lesson, every student can also feel satisfaction regarding the mathematical concepts explored.

Matome, or “summarizing the lesson,” is brief, but critically important. It reflects the teacher’s value system and helps impart this to students. Students may listen carefully to the teacher’s final words. If the teacher concludes a lesson with a simply a review of mathematical procedure, students may feel that procedural knowledge is what matters most. However, if teachers sum up the lesson by reviewing how students constructed their ideas, it sends the message to students that how they think is also important. In other words, during matome, the teacher should review not only content but also process.

1.3.2 A Textbook Example Elucidating How to Teach Mathematics Through Problem Solving

Japanese teachers often say that they teach mathematics by using a textbook, but never teach a textbook. Therefore, it has been taboo for textbooks to explicate how to teach. Only one mathematics textbook out of six includes content showing how to implement the teaching mathematics through problem solving (Fujii & Iitaka, 2011). The textbook has been translated into English (Tokyo Shoseki Co., Ltd. 2011) and the first phase of a Japanese mathematics lesson, Present the problem for the day, can be seen in Fig. 1.2. The example problem asks students to find the area of an L-shaped figure. The page is on the right, so students cannot see the answer unless they turn to the next page. The next two pages, shown in Fig. 1.3, illustrate the third and fourth phases, Compare and discuss (neriage) and The teacher sums up the lesson (matome) (Tokyo Shoseki Co., Ltd. 2011). The textbook suggests three solutions to be shown on the blackboard for the neriage phase. However, in this case, a different student tries to understand their classmate’s solution by interpreting their proposed mathematical expression. Other solutions are also possible if, for example, students count the unit squares to find the area of the L shape as.

Fig. 1.2
figure 2

The first page (Tokyo Shoseki Co., Ltd. 2011)—Present the problem for the day

Full size image
Fig. 1.3
figure 3

The second and third pages (Tokyo Shoseki Co., Ltd. 2011)—Compare and discuss (neriage) and the teacher sums up the lesson (matome)

Full size image

Although the teacher’s comment “we need to use what we have learned so far, don’t we?” in Fig. 1.4 may seem rather general, it still clearly addresses the thought process needed for learning mathematics.

Fig. 1.4
figure 4

Enlarged section of the teacher sums up the lesson (matome)

Full size image

1.4 Unifying Lesson Study with Teaching Mathematics Through Problem Solving

1.4.1 Lesson Planning Is a Critical Step of Lesson Study

The Research Lesson is usually based on the “teaching mathematics through problem solving” structure, in which a whole lesson is taught on a single mathematical task . Choosing the correct task is critical, and is in part why Lesson Planning is so important to the lesson study cycle .

Watanabe, Takahashi, and Yoshida (2008) identified four core steps involved in constructing an instruction plan for a lesson from their case studies of Japanese teachers: (1) Understand the scope and sequence, (2) Understand children’s mathematics, (3) Understand the mathematics, (4) During Lesson Planning , teachers plan the flow of the research lesson , based on the structure of teaching mathematics through problem solving and this is an important part of the planning process. In research conducted by the author in three schools in Japan , the average proportion of time spent on planning the flow of the Research Lesson , omitting meetings that did not involve the lesson plan , was 72%; if all meetings are included, the proportion becomes 63% (Fujii, 2016). The discussions specific to the flow of the research lesson during the planning meetings at each the three schools align with the four phases of teaching mathematics through problem solving (Table 1.1). For example, at the second meeting at school S (Fujii, 2016), teachers talked about the aim of the lesson and the concrete methods needed to achieve the research theme for only 3 min. A 15-min discussion ensued on how students might grasp the given task , which relates to phase 1, Present the problem for the day. Then there was a 14-min discussion about likely student responses , which relates to phase 2, Students work to solve the problem. Following that, there was a 15-min discussion about how to organize the comparison and discussion period, which relates to phase 3, Compare and discuss (neriage). Finally, 5 min were spent discussing how to conclude the lesson, which relates to phase 4, The teacher sums up the lesson. Out of these 49 min of discussion about the flow of the Research Lesson , the proportions of time spent on these four phases were about 31, 29, 31 and 10%, respectively. The other two schools showed similar proportions (Fujii, 2016).

Discussions by teachers during the Lesson Planning step (Fig. 1.1) can also be classified from another perspective: appropriateness of the task , plausibility of the anticipated student solutions, and quality of the compare and discuss (neriage) phase, which are now considered in further detail.

1.4.2 Appropriateness of the Task

Discussions about a proposed task for a research lesson can be classified into two types. The first type is a discussion about the task and unit from an advanced mathematical perspective, in which teachers clarify the scope and sequence of relevant topics and expansion of the content. In research conducted by the author (Fujii, 2016), I found that when teachers talked about the position of the unit within the curriculum, they carefully referred to the National Course of Study (NCS) published by the Ministry of Education, Culture, Sports, Science and Technology (2008).Footnote 2 For example, teachers at school M used their own diagram as they discussed why the unit was important and traced the students’ learning path leading to the unit.

The second type of discussion involves the task itself. Teachers discuss how well the task suits the goal of the lesson, including detailed consideration of which numbers should appear in the task , the context of the task , etc.

This aspect of lesson study was also noted in The Teaching Gap (Stigler & Hiebert, 1999, p. 117), who reported that teachers would talk about the “problem with which the lesson would begin, including such details as the exact wording and numbers to be used.” The research lesson described in The Teaching Gap (Stigler & Hiebert, 1999) covers the topic of teaching to first graders how to subtract a single-digit number from a two-digit number (less than 20) with regrouping. There are 36 possible problems that could be used to introduce this topic (for example, 18 − 9, 17 − 9, 17 − 8…11 − 2). This is regarded as an important area of content and which of these 36 subtractions should be the first for children to learn is hotly contested (Fujii, 2015). What is used in textbooks is typically 12 − 9 or 13 − 9.

The reason these are chosen is because the subtrahend 9 is close to ten. It is easier for students to separate, for example, 12 into 10 and 2, subtract 9 from 10, and then add the difference to 2. This can be written as the mathematical expression 12 − 9 = (10 + 2) − 9 = (10 − 9) + 2. We call this approach the subtracting-adding strategy.

However for a task such as 12 − 3, we can see that 2 and 3 are close to each other. Therefore, 3 can be broken down into 2 and 1, which gives us 12 − (2 + 1) and then (12 − 2) − 1. 2 is subtracted from 12 which gives us 10, and then one is deducted from 10, giving us a final answer of 9. We call this approach the subtracting-subtracting strategy. The teachers in The Teaching Gap (Stigler & Hiebert, 1999) decided not to use 12 − 9 from the textbooks because “it’s not very interesting.” One teacher suggested using 15 − 8 or 15 − 7 instead; another suggested using 11 − 6, “Because kids can conceptualize in their heads about up to the number 6 at this age” (Stigler & Hiebert, 1999, p. 118). Another teacher proposed 12 − 7, because “one of her students, who was a low achiever, happened to have seven family members. Everyone agreed that this was a good idea (Stigler & Hiebert, 1999, p. 118). Finally, the teachers decided to use 12 − 7, which seemed likely to provoke the subtraction-addition and subtraction-subtraction strategies equally, allowing for a discussion that would compare the relative merits of these two methods (Stigler & Hiebert, 1999). Such careful scrutiny of the sequencing of tasks is unusual by Western norms. Researchers have noted that, “Western observers are often astonished by the order of presentation being the subject of so much study and debate. However, Japanese lesson study is frequently used to investigate sequences of tasks that are different from those traditionally used” (Doig, Groves, & Fujii, 2011, p. 194). Such close attention to the specific numbers does not mean that teachers are focused merely on a concrete level of thinking and encouraging students to think about particular numbers. On the contrary: teachers consider the general aspect of a number as quasi-variable—deliberately used in a general way so that it serves as a representative of many numbers, just as a variable would be used (Fujii & Stephens, 2001, 2008). Numbers are often chosen based on their quasi-variable power, or on how well they demonstrate a general truth.

For instance, the tasks 12 − 9 and 13 − 9 are likely to lead students to the discovery of the subtraction-addition strategy. They are not mere calculation problems, but serve to introduce a particular general procedure for subtracting with regrouping in the base-ten system. Appreciating the base-ten system, the place value notation system and its benefit for calculation is more important than simply getting an answer and gaining skill at calculating 12 − 9. Therefore, the Japanese method of instruction is called “teaching mathematics through problem solving,” and not “teaching how to solve the task .”

1.4.3 Anticipated Student Solutions

In all three schools in this author’s research (Fujii, 2016), teachers spent a significant amount of time discussing likely student responses to the task that would be given in the Research Lesson . These discussions usually began by considering what would be most likely response from the class as a whole. The discussion then moved on to consider likely responses from students who learned at a faster or slower pace. It is interesting to note that at each school teachers solved the task while role-playing as their students.

Teachers also discussed anticipated solutions in terms of the vertical curriculum and how students’ prior learning was expected to be a resource for students to solve the task . For example, in the second meeting in School S, there was the following exchange (Fujii, 2016, p. 418):

Teacher A::

Students learned how to arrange to get the same numbers for time or distance, didn’t they?

Teacher B::

Yes, I suppose. However, the idea of a common multiple was learned a long time ago from the students’ point of view.

Teacher C::

Probably they forgot the procedure to find the common multiple.

Teacher B::

When they learned division of decimal numbers, they learned the idea of per-unit. It’s the same thing here. However, the idea of per-unit was not learned in the context of comparing things.

Principal::

The idea of per-unit quantity was applicable for comparing crowdedness. That is a mathematical way of thinking that could be applicable for Speed.

This kind of detailed and concrete consideration of previously-learned content was observed in all three schools.

1.4.4 The Compare and Discuss (Neriage) Phase

In order to gain an appreciation for which method or solution is better or best to use for solving a given task , students need to see alternative strategies. Therefore, a lesson teaching mathematics through problem solving includes the compare and discuss (neriage) phase for students to compare and interpret their classmates’ methods and to discuss similarities and differences among strategies as a class. Each correct solution has equal value in terms of achieving an answer. However, the ideas involved may not have equal value. During the neriage phase, the teacher elicits these ideas and discusses the value of each solution. In Fujii (2016), a teacher at school S during the lesson planning meeting clearly stated, “Although each strategy is sure to get the correct answer, we should not end there…I want the students to know that getting the answer is not the final goal” (p. 419). It is important to note that the neriage phase is an opportunity to cultivate students’ ways of thinking or attitudes towards arriving at a mathematical solution. Unifying lesson study with teaching mathematics through problem solving will cultivate students’ habits of mind.

1.4.5 Tasks Designed During Lesson Planning Are Evaluated During Post-lesson Discussion

One of the critical features of teaching mathematics through problem solving in the context of lesson study, is the evaluation of the appropriateness of the task used in the research lesson during a Post-Lesson Discussion , Step 4 in the lesson study cycle (Fig. 1.1). The quality of a task is not judged based on an abstract determination about whether it is good or not for teaching a certain mathematical concept. Its quality is judged based on concrete evidence collected during the Research Lesson evidencing how students responded to it.

The evaluation of a task is also discussed by teachers in terms of how well it promotes educational values. In fact, Japanese teachers often say that the aim of problem solving lessons is not for students to merely get an answer to the problem, but rather to teach them mathematical ways of thinking. During the Post-Lesson Discussion , Step 4 in Fig. 1.1, final comments usually by the knowledgeable other typically address educational values. For example, a final commentator is quoted in The Teaching Gap (Stigler & Hiebert, 1999, p. 182) explicitly addressing broad educational values, “He urged teachers to think carefully about what were the most important ‘skills for living’ that students should be learning from their mathematics instruction.” Using, as an example, the formula for finding the area of a trapezoid, he says, “teachers should help students realize that moving from complicated to more simple forms is a convenient and a clever thing to do” (p. 183). This is an example of how Japanese teaching mathematics through problem solving lessons address both content and process, and how lesson study prioritizes such educational values. In this way, lesson study and teaching mathematics through problem solving are inseparable in terms of addressing educational values.

1.4.6 Why We Observe and Discuss Lessons in Lesson Study

When conducting “teaching mathematics through problem solving” during a Research Lesson , the aim is not only to develop or deepen students’ content knowledge, but to also foster their mathematical ways of thinking and perspectives. In other words, the aim of the lesson is to unify content and thought process. However, thought processes are invisible. We cannot explicitly teach students how to think and this makes teaching this very difficult. What a teacher can do is anticipate student responses when Lesson Planning , Step 2 of the lesson study cycle in Fig. 1.1. Then, during the Research Lesson , Step 3 of Fig. 1.1, the instructor and fellow observers can note students’ processes as they become visible in their work. Observers can also note how the instructor deals with students’ thought processes. Following the Research Lesson , the instructor and observers can then use these notes as concrete examples of how to teach particular solutions and teach mathematical thinking. This is why the Research Lesson works best as a public lesson with the participation of many observers. Later, during the Post-Lesson Discussion , Step 4 in Fig. 1.1, all participants in the Research Lesson can discuss and evaluate the activities within the lesson using the concrete evidence they have collected. After the Post-lesson Discussion , comes Reflection, Step 5 in Fig. 1.1. During Reflection, participating teachers’ reflections are written and later published as an annual school report.

Each step in the lesson study cycle is closely related. Lesson study is a system for teachers to learn how to teach students not only content but also thought processes to help them become independent thinkers. This is why it is essential for any school that wants to incorporate the lesson study system to follow all 5 steps, ensuring unification with the method of teaching mathematics through problem solving.

1.5 Unifying Lesson Study with Teaching Mathematics Through Problem Solving

1.5.1 The Japanese National Course of Study

The research conducted by this author (Fujii, 2015) found that during Lesson Planning meetings, Step 2 in Fig. 1.1, teachers frequently referred to the National Course of Study (NCS) when they needed to confirm the role of the unit or Research Lesson within the whole curriculum. Sometimes, teachers talked about the placement of the content to teach in the lesson in the previous NCS. This is a more difficult conversation to have in countries which lack a clear curriculum. Lewis and Tsuchida (1998) argued that having a frugal, shared curriculum was necessary for implementing lesson study. With a clear curriculum sequence, teachers could identify the value of the Research Lesson or the unit within the curriculum. More importantly, the NCS, clarifying teaching and learning over the course of a student’s experience in school, is a necessary component for implementing a teaching mathematics through problem solving lesson. Without the NCS, it would be difficult for teachers to anticipate students’ idea or solutions. In other words, the teacher needs clear information regarding their students’ learning history . By using the NCS to identify related content that students learned in previous grades, teachers can more accurately anticipate how students might solve a given task . The NCS makes it possible to clarify students’ learning trajectory. It plays an important role in designing lessons which teach mathematics through problem solving. This point has not yet been articulated in academic papers or practical reports on lesson study in Japan , but it is an important one.

1.5.2 Kyozaikenkyu: An Essential Component of Lesson Study

The five steps of lesson study, shown in Fig. 1.1, are the core essentials of lesson study. However, there is another essential component which connects to each of these components, kyozaikenkyu. Kyozaikenkyu is known in English as “the study of instructional materials.” When Japanese teachers begin their Lesson Planning they first engage in kyozaikenkyu. Watanabe et al. (2008) says “This practice is a central activity in teachers’ everyday practice, but it plays a particularly important role in lesson study. In fact, one way lesson study contributes to the improvement of everyday instruction is through kyozaikenkyu (p. 133).” During the Post-Lesson Discussion and Reflection, Japanese teachers will often remark, particularly when they are unsatisfied with the research lesson , that they should have done kyozaikenkyu more thoroughly.

I believe that teachers outside of Japan who want to implement lesson study need both to understand and successfully implement kyozaikenkyu. However the process of kyozaikenkyu is complex. Watanabe et al. (2008) list some essential questions which teachers need to ask in the process of kyozaikenkyu as follows:

  • What does this idea really mean?

  • How does this idea relate to other ideas?

  • What is/are the reason(s) for teaching this idea at this particular point in the curriculum?

  • What ideas do students already understand that can be used as a starting point for this new idea?

  • Why is this particular problem useful in helping students develop this new idea?

  • How can students solve this problem using what they already know, and how can their solution strategies be used to develop this new idea?

  • What are common mistakes? Why do students make such mistakes? How should teachers respond to those mistakes?

  • What new ideas are students expected to build using this idea in the future?

  • What manipulatives and other materials should be provided to students?

  • How do they influence students’ learning?

Watanabe et al. (2008) warn that teachers should not take these questions as simply a checklist, but rather that they must understand why these questions are important when planning a lesson.

A concrete example of this is school M from the research conducted by this author (Fujii, 2016). School M made a school report based on their research which was originally written in Japanese and then translated into English by Project IMPULS in 2011. In the report, the school clearly shows the process of lesson planning as outlined below.

Figure 1.5. shows that the process starts with the term Kyozaikenkyu No. 1 and No. 2. Kyozaikenkyu No. 1 is the actualization of the school’s research theme into the Research Lesson . Kyozaikenkyu No. 2 is the study of the NCS, teaching guides, textbooks published by other companies, and other reading resources. In Fig. 1.5, kyozaikenkyu seems to have a rather narrow meaning. However, this figure actually shows that kyozaikenkyu will continue into other activities such as developing teaching materials, improving classroom discussion , improvement of questioning, improving summarizing of the lesson, and improving blackboard organization. To sum up, kyozaikenkyu involves examining teaching materials and tasks from both mathematical and educational points of view as well as from the students’ perspectives. Although kyozaikenkyu is recognized as a critical practice of lesson study by Japanese educators, teachers outside Japan often neglect it. This may be because the effort involved is almost invisible, the same way that 90% of an iceberg is hidden underwater, with all of our attention going to its visible tip (Doig et al., 2011, p. 182).

Fig. 1.5
figure 5

The process of lesson planning at school M (Matsuzawa Elementary School, 2011)

Full size image

1.5.3 Lesson Study as an Organic System

The Post-lesson Discussion , Step 4 in Fig. 1.1, provides a context for revising the task used during the Research Lesson , Step 3 in Fig. 1.1. However, this does not mean to imply that there is any value in re-teaching . Some countries seem eager to re-teach the Research Lesson . However, the most serious misinterpretation of lesson study is the question, “Should a research lesson always be re-taught?” (Fujii, 2014b).

The possible roots of this misconception might come from the lesson study steps as described in The Teaching Gap (Stigler & Hiebert, 1999, pp. 112–113). Stigler and Hiebert (1999) describe 6 steps, the last of which is called “Teaching the revised lesson.” While it is true that, sometimes, Japanese teachers will perform trial lessons, this is different from simply re-teaching the whole lesson. Trial lessons are performed in Japan only in situations such as huge, nation-wide research lessons, in which observers come over from all over Japan . These trial lessons are taught just before the actual Research Lesson , because the instructor feels that it would be too risky to implement a lesson plan for the very first time in front of so many outside observers. The teacher will use this trial lesson to fine-tune their plan in light of students’ actual responses . However, the teacher still needs to assume that students’ responses during the actual Research Lesson will differ from those they encountered during the trial lesson. By misinterpreting this practice as plain re-teaching of the same lesson, student responses are de-emphasized, which goes against the core values of lesson study.

Re-teaching disrespects students’ right to the best education one can provide them. Having the thought of re-teaching at the back of one’s mind is like treating the first class as a pawn to be sacrificed in order to improve one’s own teaching skills. It benefits teachers and lesson plan creators at the expense of their students. An instructor leading a Research Lesson needs to feel that their lesson plan is the best one that they and their planning team could create. The lesson plan should be the result of extensive effort. In other words, Japanese teachers feel that the best lesson plan should be implanted during their Research Lesson , and the Research Lesson is the proving ground for teachers.

The misinterpretation of re-teaching suggests a practice of revising a faulty part and replacing it. An inorganic system is composed of parts that may be easily replaced. However, lessons and lesson study are organic systems, each part is systemic, not systematic. But what does it mean to state, “A lesson is an organic system” and “lesson study is an organic system?” Figure 1.6 shows a possible conceptual model for lesson study as an organic system in which the 5 steps of lesson study exist on a two-dimensional plane. Figure 1.6 differs from Fig. 1.1 in that these steps function as an organic system, each joined together by the additional component of Educational Values—the heart and most important factor of lesson study (Fujii, 2014a). This heart is shown in Fig. 1.6 as the third dimension of lesson study. When educational values are taken into account, lesson study can clearly be interpreted as an organic system, each component inseparable from the others.

Fig. 1.6
figure 6

An organic model of lesson study

Full size image

1.6 Final Remarks

The Japanese NCS mainly covers content for each grade, from kindergarten to high school levels. However, at the symposium held in Tokyo in 2015 hosted by Project IMPULS at Tokyo Gakugei University (IMPULS, 2017), participants argued that it is important for educators not only consider mathematical content, but also mathematical processes. They also discussed the relationship between content and processes. They described their dual nature as:

  • Content nests inside the processes.

  • Processes nest inside the content.

The NCS mainly covers content. How can we understand process from examining the NCS? In the 1958 NCS for mathematics, the term “mathematical ways of thinking” was listed for the first time as a goal of mathematical education. That was the first time not only content but also process was addressed in the NCS. Since then, “mathematical ways of thinking” has been one of the most important components of mathematics education in Japan .

On the other hand, at the symposium, we were pleased to recognize that the Japanese way of teaching mathematics, mondai-kaiketsu-gata-jyugyou, which is referred to here as “teaching mathematics through problem solving,” is highlighted as reflecting what Stigler and Hiebert (1999) described as “structured problem solving.” The Japanese style of teaching mathematics was considered as a reliable method of crystalizing the dual nature of content and processes. The results of the TIMSS 2002 support this view. The average percentages of TIMSS Mathematics Topics taught in Japanese schools, either prior to or during the year of the assessment, were 54% for grade 4, however, the achievement scores (average scale score) was 69% for these grade 4 students. These are remarkable findings; it shows that Japanese grade 4 students could solve tasks in the TIMSS which had not been taught to them in school. In other words, they could perform beyond what they have been taught. This fact supports the assertion that by “teaching mathematics through problem solving” we have been teaching not only content but also processes. We could say that Japanese educators have been implementing the “teaching mathematics through problem solving” approach to the curriculum without a defined theory or consciousness. However, this new insight demands that the concept of “teaching mathematics through problem solving” be fully described, along with lesson study, as the two concepts are two wheels of the same cart.