Abstract
Hartmut Ehrig and others in [EWT83] studied normal form results for complex generating constraints imposed on basic specifications. Since then this work has been followed by subsequent results concerning normal forms for structured specifications, typically built from basic specifications using union, translation and hiding. We consider generating constraints as additional specification-building operations and follow and extend the results concerning normal forms for the resulting specifications with various forms of generating constraints.
This work has been partially supported by the (Polish) National Science Centre, grant 2013/11/B/ST6/01381 (AT).
Access provided by CONRICYT-eBooks. Download chapter PDF
Similar content being viewed by others
Keywords
- Basic Constraint Propagation
- Normal Form Result
- Specification-building Operations
- Hartmut Ehrig
- Signature Morphism
These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.
1 Introduction
Hartmut Ehrig and others in [EWT83] studied normal form results for complex generating constraints imposed on basic specifications. Although from today’s point of view the results were somewhat restricted in their generality, they spurred a line of work on normal forms of structured specifications, notably in [BHK90] and in the current general version in [Bor02], which turned out to be crucial in the study of proof systems for consequences of structured specifications, and in the analysis of completeness properties of such proof systems. But the more recent normal form results largely disregarded generating (or reachability) properties as imposed by the constraints studied in [EWT83]. Our aim here is to fill this gap, by generalising the results of [EWT83] as follows.
First, as has been standard since the introduction of institutions [GB84, GB92] to free algebraic specifications from dependency on a specific logical system, we abstract away from the specifics of the underlying logical system and present our results in the framework of a rather arbitrary logical system formalised as an institution with minimal extra structure and assumed properties.
Then, we consider a normal form of specifications that is somewhat more restrictive than the canonical constraints in [EWT83], giving a normal form result that is a bit sharper than the corresponding result in [EWT83].
Finally, and most crucially, Ehrig et al. [EWT83] studied generating constraints that impose generation requirements within models of a “flat” basic specification (presentation) only. We study generating constraints imposed by a more general specification building operation, which may be mixed with other specification-building operations in an arbitrary way, so that generating requirements may be imposed in multiple “layers” within models of an arbitrarily complex specification. This makes the study more delicate, and in fact the normal form result one might expect does not carry over to this more general case.
Dedication: This study is dedicated to the memory of Hartmut Ehrig. We are grateful to Hartmut for his kindness and generosity over the years. We represented different “schools” of thought on algebraic specification, but Hartmut was always friendly and willing to explain his ideas and to try to understand our point of view.
2 Constraints in the Standard Algebraic Framework
We begin with a summary of [EWT83].
As was usual at the time, the investigation was carried out in the context of the standard algebraic framework [EM85]. Specifications are presentations \(\langle {\varSigma ,\varPhi }\rangle \) where \(\varSigma \) is a standard many-sorted signature and \(\varPhi \) is a set of \(\varSigma \)-axioms, usually equations. The category of \(\varSigma \)-algebras \(\mathbf{Alg}(\varSigma )\) is defined as usual, with the notion of satisfaction between algebras and axioms yielding the obvious semantics of presentations:  .
.
The category of algebraic signatures \(\mathbf{AlgSig}\) with standard signature morphisms \(\sigma :\varSigma \rightarrow \varSigma '\) is cocomplete. For each signature morphism \(\sigma :\varSigma \rightarrow \varSigma '\), we have a \(\sigma \)-reduct functor \(U_\sigma :\mathbf{Alg}(\varSigma ')\rightarrow \mathbf{Alg}(\varSigma )\). A signature morphism \(\sigma :\varSigma \rightarrow \varSigma '\) is a presentation morphism \(\sigma :\langle {\varSigma ,\varPhi }\rangle \rightarrow \langle {\varSigma ',\varPhi '}\rangle \) if  . Colimits lift from the category of signatures to the category of presentations. The crucial satisfaction condition and amalgamation properties hold as expected—see Sect. 3 for more general formulations, or check for instance [ST12].
. Colimits lift from the category of signatures to the category of presentations. The crucial satisfaction condition and amalgamation properties hold as expected—see Sect. 3 for more general formulations, or check for instance [ST12].
For each presentation \( PRES \), the authors of [EWT83] introduce constraints on \( PRES \), which are built from the empty constraint \(\emptyset \), with semantics  , using union, with
, using union, with  , and the following constructors, for any presentation morphisms \(\sigma : PRES '\rightarrow PRES \), \(\sigma ': PRES \rightarrow PRES '\) and constraint \(C'\) on \( PRES '\):
, and the following constructors, for any presentation morphisms \(\sigma : PRES '\rightarrow PRES \), \(\sigma ': PRES \rightarrow PRES '\) and constraint \(C'\) on \( PRES '\):
-
translation \(\mathrm { TRA }_\sigma \):

-
reflection \(\mathrm { REF }_{\sigma '}\):

-
generating constraint \(\mathrm { GEN }_\sigma \):
 , where
, where  is \(U_\sigma \)-generated in
is \(U_\sigma \)-generated in  if in
if in  there is no proper subalgebra of A with the same \(\sigma \)-reduct as A.
there is no proper subalgebra of A with the same \(\sigma \)-reduct as A.
A constraint on \( PRES \) of the form \(\mathrm { REF }_{\sigma _3}(\mathrm { TRA }_{\sigma _2}(\mathrm { GEN }_{\sigma _1}(\emptyset )))\) is called canonical. Such constraints might be easier to read in the diagrammatic notation of [EWT83]:
for presentations \( PRES _i\) and presentation morphisms \(\sigma _i\), \(i=1,2,3\).
The key result in [EWT83] is the following normal form theorem:
Theorem 2.1
([EWT83]). For each constraint on \( PRES \) an equivalent canonical constraint may be constructed. \(\square \)
We found the result very interesting and analysed it in detail already at the time [Tar83]. One observation was that the above form of canonical constraints is the only one possible for Theorem 2.1 to hold—that is, no other order of generating constraints, translation and reflection would work. Another was that some of the assumptions in [EWT83] are either misleading or unnecessary. For instance, the authors require reduct functors to lift isomorphisms, which in the standard algebraic framework excludes presentation morphisms that are not injective on sorts. Even if we could accept this as a reasonable restriction, it turns out that this property cannot be maintained under the constructions used in the proof of Theorem 2.1. Fortunately, such details did not prove to be crucial for the correctness of the proof, and the paper and the above theorem influenced subsequent developments, most notably the simpler normal form results for specifications without generating constraints in [BHK90, Bor02] and much work based in turn on those results.
3 Institutions with Model Inclusions
To capture in a very general way the concept of a submodel, we will require our model categories to come with inclusions.
A class of morphisms in a category is called a class of inclusions if it imposes a partial order on the objects of the category; to be precise, we require that
-
all identities are inclusions
-
inclusions are closed under composition
-
between any two objects there is at most one inclusion (in either direction, i.e., for objects A, B, either there is no inclusion between A and B, or there is a unique inclusion from A to B, or from B to A, but not both unless A and B coincide).
In other words, a category with inclusions is a pair \(\mathbb {C}=\langle {\mathcal {C},\mathcal {I}}\rangle \) such that \(\mathcal {C}\) is a category and \(\mathcal {I}\) is a wide thin skeletal subcategory of \(\mathcal {C}\); the morphisms of \(\mathcal {I}\) are called inclusions. If there is an inclusion \(\iota :A\rightarrow B\) then we say that A is a subobject of B and write \(A\subseteq B\).
When no confusion may arise, we use the standard categorical terminology and notation in \(\mathbb {C}\) to refer to the corresponding concepts in \(\mathcal {C}\). So, for instance, we write \(|\mathbb {C}|\) for the class \(|\mathcal {C}|\) of objects in \(\mathcal {C}\), by a diagram in \(\mathbb {C}\) we mean a diagram in \(\mathcal {C}\), by (co)limits in \(\mathbb {C}\) we mean (co)limits in \(\mathcal {C}\), etc.
A functor between categories with inclusions \(F:\langle {\mathcal {C},\mathcal {I}}\rangle \rightarrow \langle {\mathcal {C}',\mathcal {I}'}\rangle \) is a functor \(F:\mathcal {C}\rightarrow \mathcal {C}'\) that preserves inclusions, \(F(\mathcal {I})\subseteq \mathcal {I}'\). Clearly, such functors compose, and so this yields the (quasi-)category \(\mathbf{ICat}\) of categories with inclusions.
These are extremely mild requirements concerning the subcategory of inclusions. For instance, in contrast to some other work, e.g. [DGS93, CR97, GR04, CMST17], we have no need to assume that inclusions form part of a (strict) factorisation system for \(\mathcal {C}\), or that they admit intersections and unions, etc.
An institution with model inclusions \(\mathbf{INS}\) consists of:
-
a category \(\mathbf{Sign}_\mathbf{INS}\) of signatures;
-
a functor \(\mathbf{Sen}_\mathbf{INS}:\mathbf{Sign}_\mathbf{INS}\rightarrow \mathbf{Set}\), giving a set \(\mathbf{Sen}_\mathbf{INS}(\varSigma )\) of \(\varSigma \)-sentences for each signature \(\varSigma \in |\mathbf{Sign}_\mathbf{INS}|\); and a function \(\mathbf{Sen}_\mathbf{INS}(\sigma ) :\mathbf{Sen}_\mathbf{INS}(\varSigma ) \rightarrow \mathbf{Sen}_\mathbf{INS}(\varSigma ')\) which translates \(\varSigma \)-sentences to \(\varSigma '\)-sentences for each signature morphism \(\sigma :\varSigma \rightarrow \varSigma '\);
-
a functor
 , giving a category \(\mathbf{Mod}_\mathbf{INS}(\varSigma )\) of \(\varSigma \)-models with model inclusions for each signature \(\varSigma \in |\mathbf{Sign}_\mathbf{INS}|\); and a functor \(\mathbf{Mod}_\mathbf{INS}(\sigma ) :\mathbf{Mod}_\mathbf{INS}(\varSigma ') \rightarrow \mathbf{Mod}_\mathbf{INS}(\varSigma )\) which translates \(\varSigma '\)-models to \(\varSigma \)-models and \(\varSigma '\)-morphisms to \(\varSigma \)-morphisms, preserving model inclusions, for each signature morphism \(\sigma :\varSigma \rightarrow \varSigma '\); and
, giving a category \(\mathbf{Mod}_\mathbf{INS}(\varSigma )\) of \(\varSigma \)-models with model inclusions for each signature \(\varSigma \in |\mathbf{Sign}_\mathbf{INS}|\); and a functor \(\mathbf{Mod}_\mathbf{INS}(\sigma ) :\mathbf{Mod}_\mathbf{INS}(\varSigma ') \rightarrow \mathbf{Mod}_\mathbf{INS}(\varSigma )\) which translates \(\varSigma '\)-models to \(\varSigma \)-models and \(\varSigma '\)-morphisms to \(\varSigma \)-morphisms, preserving model inclusions, for each signature morphism \(\sigma :\varSigma \rightarrow \varSigma '\); and -
a family \(\langle {{\models _{\mathbf{INS},\varSigma }} \subseteq {|\mathbf{Mod}_\mathbf{INS}(\varSigma )| \times \mathbf{Sen}_\mathbf{INS}(\varSigma )}}\rangle _{\varSigma \in |\mathbf{Sign}_\mathbf{INS}|}\) of satisfaction relations
such that for any signature morphism \(\sigma :\varSigma \rightarrow \varSigma '\) the translations \(\mathbf{Mod}_\mathbf{INS}(\sigma )\) of models and \(\mathbf{Sen}_\mathbf{INS}(\sigma )\) of sentences preserve the satisfaction relation, that is, for any \(\varphi \in \mathbf{Sen}_\mathbf{INS}(\varSigma )\) and \(M' \in |\mathbf{Mod}_\mathbf{INS}(\varSigma ')|\) the following satisfaction condition holds:
Note that institutions with model inclusions are not “inclusive institutions” in the sense of [DGS93, GR04, CMST17]: we require inclusion structure on models, not on signatures.
Examples of institutions with model inclusions abound. The institution \(\mathbf{EQ}\) of equational logic has many-sorted algebraic signatures as signatures, many-sorted algebras as models with the usual notion of subalgebra determining the model inclusions and (explicitly quantified) equations as sentences. The institution \(\mathbf{FOPEQ}\) of first-order predicate logic with equality has signatures that add predicate names to many-sorted algebraic signatures, models that extend algebras by interpreting predicate names as relations with inclusions that are required to preserve these relations, and sentences that are all closed (no free variables) formulae of first-order logic with equality. See [ST12] for detailed definitions of these and many other institutions, which often can be enriched with the obvious concept of a submodel, to yield institutions with model inclusions.
We will freely use standard terminology, and say that a \(\varSigma \)-model M satisfies a \(\varSigma \)-sentence \(\varphi \), or that \(\varphi \) holds in M, whenever \(M \models _{\mathbf{INS}, \varSigma } \varphi \). We will omit the subscript INS, writing \(\mathbf{INS}= \langle {\mathbf{Sign}, \mathbf{Sen}, \mathbf{Mod}, \langle {{\models _\varSigma }}\rangle _{\varSigma \in |\mathbf{Sign}|}}\rangle \). Similarly, the subscript \(\varSigma \) on the satisfaction relations will often be omitted. For any signature morphism \(\sigma :\varSigma \rightarrow \varSigma '\), the translation function \(\mathbf{Sen}(\sigma ) :\mathbf{Sen}(\varSigma ) \rightarrow \mathbf{Sen}(\varSigma ')\) will be denoted by \(\sigma :\mathbf{Sen}(\varSigma ) \rightarrow \mathbf{Sen}(\varSigma ')\), the coimage function w.r.t. \(\mathbf{Sen}(\sigma )\) by \(\sigma ^{-1} :{\mathcal {P}}(\mathbf{Sen}(\varSigma ')) \rightarrow {\mathcal {P}}(\mathbf{Sen}(\varSigma ))\), and the reduct functor \(\mathbf{Mod}(\sigma ) :\mathbf{Mod}(\varSigma ') \rightarrow \mathbf{Mod}(\varSigma )\) by  . Thus, the satisfaction condition may be re-stated as: \(M'\models \sigma (\varphi )\) iff
. Thus, the satisfaction condition may be re-stated as: \(M'\models \sigma (\varphi )\) iff  .
.
An institution with inclusions \(\mathbf{INS}\) is (finitely) exact if its category \(\mathbf{Sign}\) of signatures is (finitely) cocomplete, and the functor  maps (finite) colimits of signatures to limits of model categories with inclusions in \(\mathbf{ICat}\). This adjusts the usual notion of exactness [ST12] to the framework where model inclusions are considered. In particular, the following stronger form of the amalgamation property [EM85] holds:
maps (finite) colimits of signatures to limits of model categories with inclusions in \(\mathbf{ICat}\). This adjusts the usual notion of exactness [ST12] to the framework where model inclusions are considered. In particular, the following stronger form of the amalgamation property [EM85] holds:
Lemma 3.1
Given a finitely exact institution with model inclusions \(\mathbf{INS}\), consider a pushout of signatures

Then, for any \(M_1 \in |\mathbf{Mod}(\varSigma _1)|\) and \(M_2 \in |\mathbf{Mod}(\varSigma _2)|\) such that  , there exists a unique \(M' \in |\mathbf{Mod}(\varSigma ')|\) such that
, there exists a unique \(M' \in |\mathbf{Mod}(\varSigma ')|\) such that  and
and  . Moreover, for any submodels \(N_1\subseteq M_1\) and \(N_2\subseteq M_2\) such that
. Moreover, for any submodels \(N_1\subseteq M_1\) and \(N_2\subseteq M_2\) such that  (hence
(hence  the unique \(N' \in |\mathbf{Mod}(\varSigma ')|\) such that
the unique \(N' \in |\mathbf{Mod}(\varSigma ')|\) such that  and
and  is a submodel of \(M'\), \(N'\subseteq M'\). \(\square \)
is a submodel of \(M'\), \(N'\subseteq M'\). \(\square \)
The standard institutions with model inclusions mentioned above (\(\mathbf{EQ}\), \(\mathbf{FOPEQ}\), etc.) are exact, hence enjoy the amalgamation property captured by Lemma 3.1.
Given a signature morphism \(\sigma :\!\varSigma \rightarrow \varSigma '\) and class \(\mathcal {M}'\!\subseteq \!|\mathbf{Mod}(\varSigma ')|\) of models, we say that a model \(M'\in |\mathbf{Mod}(\varSigma ')|\) is \(\sigma \)-generated in \(\mathcal {M}'\) if \(M'\in \mathcal {M}'\) and it has no proper submodels in \(\mathcal {M}'\) with the same \(\sigma \)-reduct: for any submodel \(M''\subseteq M'\) if \(M''\in \mathcal {M}'\) and  then \(M''=M'\). By taking \(\mathcal {M}'=|\mathbf{Alg}(\varSigma ')|\) we obtain the standard definition of \(\sigma \)-generated model, which requires \(M'\) to be generated by the set of all its elements in the carriers of
then \(M''=M'\). By taking \(\mathcal {M}'=|\mathbf{Alg}(\varSigma ')|\) we obtain the standard definition of \(\sigma \)-generated model, which requires \(M'\) to be generated by the set of all its elements in the carriers of  . But note that when \(\mathcal {M}'\varsubsetneq |\mathbf{Alg}(\varSigma ')|\)—in particular, when \(\mathcal {M}'\) is not closed under submodels—models that are generated in \(\mathcal {M}'\) need not be generated in the standard sense, exactly as in [EWT83]. For this reason a better terminology might be “minimal”, as in [ST88], but we retain the terminology of [EWT83] to avoid confusion.
. But note that when \(\mathcal {M}'\varsubsetneq |\mathbf{Alg}(\varSigma ')|\)—in particular, when \(\mathcal {M}'\) is not closed under submodels—models that are generated in \(\mathcal {M}'\) need not be generated in the standard sense, exactly as in [EWT83]. For this reason a better terminology might be “minimal”, as in [ST88], but we retain the terminology of [EWT83] to avoid confusion.
4 Structured Specifications in Institutions with Model Inclusions
Taking an institution as a starting point for talking about specifications, each signature \(\varSigma \) captures static information about the interface of a software system with each \(\varSigma \)-model representing a possible realisation of such a system, and with \(\varSigma \)-sentences used to describe properties that a realisation is required to satisfy. As a consequence, it is natural to regard the meaning of any specification \( SP \) built in an institution \(\mathbf{INS}=\langle {\mathbf{Sign}, \mathbf{Sen}, \mathbf{Mod}, \langle {{\models _\varSigma }}\rangle _{\varSigma \in |\mathbf{Sign}|}}\rangle \) as given by its signature \( Sig [ SP ]\in |\mathbf{Sign}|\) together with a class \( Mod [ SP ]\) of \( Sig [ SP ]\)-models. Specifications \( SP \) with \( Sig [ SP ]=\varSigma \) are referred to as \(\varSigma \)-specifications.
The semantics of specifications yields the obvious notion of specification equivalence: two specifications \( SP _1\) and \( SP _2\) are equivalent, written \(SP_1\equiv SP _2\), if \( Sig [ SP _1]= Sig [ SP _2]\) and \( Mod [ SP _1]= Mod [ SP _2]\).
Specifications we will consider are built from basic specifications (presentations in \(\mathbf{INS}\)) using specification-building operations [ST12]. Specification formalisms differ in the choice of these operations, but typically all share a kernel introduced in ASL [SW83, ST88], where specifications are built from basic specifications using union, translation, and hiding. Following [EWT83], we add generating constraints to this repertoire, to capture constraints as studied there via a more general specification-building operation. We use a syntax inspired by that of Casl [BM04].
- basic specifications::
-
For any signature \(\varSigma \in |\mathbf{Sign}|\) and set \(\varPhi \subseteq \mathbf{Sen}(\varSigma )\) of \(\varSigma \)-sentences, a basic specification \(\langle {\varSigma ,\varPhi }\rangle \) is a specification with:

- union::
-
For any signature \(\varSigma \in |\mathbf{Sign}|\), given \(\varSigma \)-specifications \( SP _1\) and \( SP _2\), their union \( SP _1 \cup SP _2\) is a specification with:

- translation::
-
For any signature morphism \(\sigma :\varSigma \rightarrow \varSigma '\) and \(\varSigma \)-specification \( SP \),
 is a specification with:
is a specification with: 
- hiding::
-
For any signature morphism \(\sigma :\varSigma \rightarrow \varSigma '\) and \(\varSigma '\)-specification \( SP '\), \( SP '~\mathbf {hide}~\mathbf {via}~\sigma \) is a specification with:

- generating constraints::
-
For any signature morphism \(\sigma :\varSigma \rightarrow \varSigma '\), \(\varSigma \)-specification \( SP \) and \(\varSigma '\)-specification \( SP '\), \(\mathbf {generate}~\mathbf {by}~\sigma ~\mathbf {from}~ SP ~\mathbf {in}~ SP '~\) is a specification with:
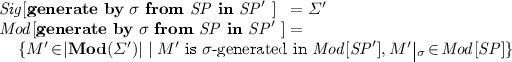
The above specification-building operations may be arbitrarily combined to derive additional specification-building operations that capture some common patterns of their use. For instance:
- enrichment::
-
For any specification \( SP \) and a set \(\varPhi \subseteq \mathbf{Sen}( Sig [ SP ])\) of sentences, \( SP ~ \mathbf {then}~\varPhi ~\) abbreviates \( SP \cup \langle { Sig [ SP ],\varPhi }\rangle \).
5 Algebraic Properties of Specification-Building Operations
We start by recalling some easy facts concerning the standard specification-building operations [ST12]:
Proposition 5.1
In any institution, under the obvious requirements on specification signatures, sentences and signature morphisms involved to ensure well-formedness of the specifications concerned:
-
1.
\(\langle {\varSigma ,\varPhi _1}\rangle \cup \langle {\varSigma ,\varPhi _2}\rangle \equiv \langle {\varSigma ,\varPhi _1\cup \varPhi _2}\rangle \)
-
2.

-
3.

-
4.

-
5.

-
6.
 \(\square \)
\(\square \)
The following easy fact follows directly from Proposition 5.1(4 and 6):
Proposition 5.2
In any institution \(\mathbf{INS}\), consider the following commuting diagram of signatures:

Then for any \(\varSigma _1\)-specification \( SP _1\) and \(\varSigma _2\)-specification \( SP _2\),

\(\square \)
Proposition 5.3
In any finitely exact institution \(\mathbf{INS}\), given a pushout of signatures

-
1.
 , for any \(\varSigma _1\)-specification \( SP _1\), and
, for any \(\varSigma _1\)-specification \( SP _1\), and -
2.

for any \(\varSigma _1\)-specification \( SP _1\) and \(\varSigma _2\)-specification \( SP _2\).
Proof
See Propositions 5.6.5 and 5.6.7 in [ST12]. \(\square \)
We can also derive algebraic properties for derived specification-building operations; for instance the following property follows directly from Proposition 5.1(6 and 2):
Proposition 5.4
For any specification \( SP \), set \(\varPhi \subseteq \mathbf{Sen}( Sig [ SP ])\) of sentences and signature morphism \(\sigma : Sig [ SP ]\rightarrow \varSigma '\),

\(\square \)
In \(\mathbf {generate}~\mathbf {by}~\sigma ~\mathbf {from}~ SP ~\mathbf {in}~ SP '~\), both the “source” specification \( SP \) and the “target” specification \( SP '\) may be arbitrarily complex, built using any combination of specification-building operations, including generating constraints. This is considerably more general than the constraints considered in [EWT83], where in particular the “target” specification, within which we select the generated models, was taken to be a basic specification.
To begin with, let us note that the complexity of the source specification in a generating constraint may easily be removed. The source specification does not affect the generation property of the models within the target specification, and so it may be moved out of the scope of the constraint and imposed separately:
Proposition 5.5
In any institution with model inclusions \(\mathbf{INS}\), for any signature morphism \(\sigma :\varSigma \rightarrow \varSigma '\), \(\varSigma \)-specification \( SP \) and \(\varSigma '\!\)-specification \( SP '\!\),
Proof
From the definition of the semantics of the specification-building operations involved. \(\square \)
The following property will be used to combine generating constraints:
Lemma 5.6
Consider two constraints \(\mathbf {generate}~\mathbf {by}~\sigma _1~\mathbf {from}~ SP _1~\mathbf {in}~ SP '_1~\) and \(\mathbf {generate}~\mathbf {by}~\sigma _2~\mathbf {from}~ SP _2~\mathbf {in}~ SP '_2~\), where \( Sig [ SP _1]=\varSigma _1\), \( Sig [ SP '_1]=\varSigma '_1\), \( Sig [ SP _2]=\varSigma _2\), \( Sig [ SP '_2]=\varSigma '_2\). Let \(\varSigma _0\) be a coproduct of \(\varSigma _1\) and \(\varSigma _2\) with injections \(i_1:\varSigma _1\rightarrow \varSigma _0\) and \(i_2:\varSigma _2\rightarrow \varSigma _0\), and \(\varSigma '_0\) be a coproduct of \(\varSigma '_1\) and \(\varSigma '_2\) with injections \(i'_1:\varSigma '_1\rightarrow \varSigma '_0\) and \(i'_2:\varSigma '_2\rightarrow \varSigma '_0\), and let \(\sigma _0:\varSigma _0\rightarrow \varSigma '_0\) be the unique signature morphism such that \(i_1\mathord {;}\sigma _0 = \sigma _1\mathord {;}i'_1\) and \(i_2\mathord {;}\sigma _0 = \sigma _2\mathord {;}i'_2\).

Then for any model \(M'\!\in \!|\mathbf{Mod}(\varSigma '_0)|\), \(M'\) is \(\sigma _0\)-generated in \( Mod [( SP '_1\!~\mathbf {with}~\!i'_1 ) \cup ( SP '_2~\mathbf {with}~i'_2 )]\) iff both  is \(\sigma _1\)-generated in \( Mod [ SP '_1]\) and
is \(\sigma _1\)-generated in \( Mod [ SP '_1]\) and  is \(\sigma _2\)-generated in \( Mod [ SP '_2]\).
is \(\sigma _2\)-generated in \( Mod [ SP '_2]\).
Proof
For the “only if” part, consider a model \(M'\in |\mathbf{Mod}(\varSigma '_0)|\) such that \(M'\) is \(\sigma _0\)-generated in \( Mod [( SP '_1~\mathbf {with}~i'_1 ) \cup ( SP '_2~\mathbf {with}~i'_2 )]\). Consider a submodel  such that \(N'_1\in Mod [ SP '_1]\) and
such that \(N'_1\in Mod [ SP '_1]\) and  . Let \(N'\in |\mathbf{Mod}(\varSigma '_0)|\) be (the unique model) such that
. Let \(N'\in |\mathbf{Mod}(\varSigma '_0)|\) be (the unique model) such that  and
and  . Then \(N'\subseteq M'\) (by Lemma 3.1), \(N'\in Mod [( SP '_1~\mathbf {with}~i'_1 ) \cup ( SP '_2~\mathbf {with}~i'_2 )]\) (from the definition of the semantics of structured specifications), and
. Then \(N'\subseteq M'\) (by Lemma 3.1), \(N'\in Mod [( SP '_1~\mathbf {with}~i'_1 ) \cup ( SP '_2~\mathbf {with}~i'_2 )]\) (from the definition of the semantics of structured specifications), and  (since
(since  , and
, and  . Hence \(N'=M'\), and so
. Hence \(N'=M'\), and so  , which shows that
, which shows that  is \(\sigma _1\)-generated in \( Mod [ SP '_1]\). By symmetry,
is \(\sigma _1\)-generated in \( Mod [ SP '_1]\). By symmetry,  is \(\sigma _2\)-generated in \( Mod [ SP '_2]\).
is \(\sigma _2\)-generated in \( Mod [ SP '_2]\).
For the opposite implication, suppose both  is \(\sigma _1\)-generated in \( Mod [ SP '_1]\) and
is \(\sigma _1\)-generated in \( Mod [ SP '_1]\) and  is \(\sigma _2\)-generated in \( Mod [ SP '_2]\). Consider a submodel \(N'\subseteq M'\) such that \(N'\in Mod [( SP '_1~\mathbf {with}~i'_1 ) \cup ( SP '_2~\mathbf {with}~i'_2 )]\) and
is \(\sigma _2\)-generated in \( Mod [ SP '_2]\). Consider a submodel \(N'\subseteq M'\) such that \(N'\in Mod [( SP '_1~\mathbf {with}~i'_1 ) \cup ( SP '_2~\mathbf {with}~i'_2 )]\) and  . Then
. Then  is a submodel of
is a submodel of  such that
such that  . Therefore
. Therefore  . By symmetry,
. By symmetry,  . Hence \(N'=M'\), which shows \(M'\) is indeed \(\sigma _0\)-generated in \( Mod [( SP '_1~\mathbf {with}~i'_1 ) \cup ( SP '_2~\mathbf {with}~i'_2 )]\). \(\square \)
. Hence \(N'=M'\), which shows \(M'\) is indeed \(\sigma _0\)-generated in \( Mod [( SP '_1~\mathbf {with}~i'_1 ) \cup ( SP '_2~\mathbf {with}~i'_2 )]\). \(\square \)
Corollary 5.7
Under the notation of Lemma 5.6:
Proof
Let \( SP _l\) be the specification on the left-hand side of the equivalence, and let \( SP _r\) be the specification on its right-hand side.
Consider \(M'_0\in Mod [ SP _l]\). Then  is \(\sigma _1\)-generated in \( Mod [ SP '_1]\) and
is \(\sigma _1\)-generated in \( Mod [ SP '_1]\) and  is \(\sigma _2\)-generated in \( Mod [ SP '_2]\). Hence, by Lemma 5.6, \(M'_0\) is \(\sigma _0\)-generated in \( Mod [( SP '_1~\mathbf {with}~i'_1 ) \cup ( SP '_2~\mathbf {with}~i'_2 )]\). Moreover,
is \(\sigma _2\)-generated in \( Mod [ SP '_2]\). Hence, by Lemma 5.6, \(M'_0\) is \(\sigma _0\)-generated in \( Mod [( SP '_1~\mathbf {with}~i'_1 ) \cup ( SP '_2~\mathbf {with}~i'_2 )]\). Moreover,  and
and  , hence we have
, hence we have  . Thus, \(M'_0\in Mod [ SP _r]\).
. Thus, \(M'_0\in Mod [ SP _r]\).
Consider now \(M'_0\in Mod [ SP _r]\). \(M'_0\) is \(\sigma _0\)-generated in \( Mod [( SP '_1~\mathbf {with}~i'_1 ) \cup ( SP '_2~\mathbf {with}~i'_2 )]\), hence by Lemma 5.6,  is \(\sigma _1\)-generated in \( Mod [ SP '_1]\) and
is \(\sigma _1\)-generated in \( Mod [ SP '_1]\) and  is \(\sigma _2\)-generated in \( Mod [ SP '_2]\). Moreover,
is \(\sigma _2\)-generated in \( Mod [ SP '_2]\). Moreover,  , hence
, hence  and
and  . Thus
. Thus  and
and  , which shows that \(M'_0\in Mod [ SP _l]\). \(\square \)
, which shows that \(M'_0\in Mod [ SP _l]\). \(\square \)
6 Normal Form Results
We now come to the presentation of so-called normal-form results for structured specifications, whereby we show that all specifications of a certain kind are equivalent to a specification in a certain simple “normal form”.
The first such result is easy:
Theorem 6.1
In any institution \(\mathbf{INS}\), for every specification \( SP \) built from basic specifications using union and translation, there is an equivalent (basic) specification of the form \(\langle {\varSigma ,\varPhi }\rangle \) (where \(\varPhi \) is finite provided the basic specifications involved in \( SP \) are finite).
Proof
By induction on the structure of specifications, using Proposition 5.1(1 and 2). \(\square \)
Then, using Propositions 5.1 and 5.3, one can show the following normal form result by an easy induction on the structure of specifications:
Theorem 6.2
Let \(\mathbf{INS}\) be a finitely exact institution. For every specification \( SP \) built from flat specifications using union, translation and hiding, there is an equivalent specification of the form \(\langle {\varSigma ,\varPhi }\rangle ~\mathbf {hide}~\mathbf {via}~\sigma \) (where \(\varPhi \) is finite provided the basic specifications involved in \( SP \) are finite).
Proof
See Theorem 5.6.10 in [ST12]. \(\square \)
The above key result may be derived from the normal form result for constraints in [EWT83] (see Theorem 2.1 above). It was given in a very similar form in [BHK90] for the standard institution of first-order logic, and then generalised in [Bor02] to an arbitrary exact institution. The result proved crucial for a number of further foundational developments, notably in the study of completeness of standard logical systems for proving consequences of structured specifications.
However, unlike the normal form result in [EWT83], Theorem 6.2 does not address specifications with generating constraints. The key problem is to reduce the complexity of the specifications involved in the generating constraints.
A generating constraint \(\mathbf {generate}~\mathbf {by}~\sigma ~\mathbf {from}~ SP ~\mathbf {in}~ SP '~\) is source-trivial if \( SP \) is a basic specification with no axioms, i.e., is of the form \(\langle { Sig [ SP ],\emptyset }\rangle \). A constraint \(\mathbf {generate}~\mathbf {by}~\sigma ~\mathbf {from}~ SP ~\mathbf {in}~ SP '~\) is basic if \( SP '\) is a basic specification.
As already mentioned, the complexity of the source specifications in generating constraints is not a problem:
Corollary 6.3
In any institution \(\mathbf{INS}\) with model inclusions, any structured specification built from basic specifications using union, translation, hiding and generating constraints is equivalent to a specification built from basic specifications using union, translation, hiding and source-trivial generating constraints.
Proof
Follows from Proposition 5.5 by induction on the structure of specifications. \(\square \)
We are now ready for a direct generalisation of Theorem 2.1, the main normal form result in [EWT83].
As recalled in Sect. 2, the canonical constraints of [EWT83] are of the form:
In terms of the specification-building operations introduced in Sect. 4, this may be written as follows:

with further requirements to ensure that the signature morphisms involved are in fact presentation morphisms. We will show below that the above form may be considerably simplified, by collecting all of the axioms involved in one place:
A specification is in basic normal form if it has the form:

where the signatures and signature morphisms are as in the following diagram:
This makes Theorem 6.4 below stronger, even in the standard algebraic framework, than Theorem 2.1.
Theorem 6.4
In any finitely exact institution \(\mathbf{INS}\) with model inclusions, any structured specification built from basic specifications using union, translation, hiding and basic generating constraints is equivalent to a specification in basic normal form.
Proof
First, by Corollary 6.3 (and Proposition 5.5) it is enough to consider structured specifications built from basic specifications using union, translation, hiding and source-trivial basic generating constraints. For those, we proceed by induction on the structure of specifications concerned, considering the last specification-building operation involved and assuming that its arguments, if any, are in basic normal form:
- basic specifications::
-

- union::
-
The following diagram in \(\mathbf{Sign}\) may help to follow the equivalences below:


- translation::
-
$$\begin{aligned} \begin{array}{l} (((\mathbf {generate}~\mathbf {by}~\sigma ~\mathbf {from}~\langle {\varSigma ,\emptyset }\rangle ~\mathbf {in}~\langle {\varSigma ',\varPhi '}\rangle ~)~\mathbf {with}~\sigma ' )~\mathbf {hide}~\mathbf {via}~\delta )~\mathbf {with}~\tau \\ \qquad {} \equiv {} (by \, Proposition~5.3(1), taking \, a \, pushout \, {\varSigma '}{\mathop {\longrightarrow }\limits ^{\tau '}}{\bullet }{\mathop {\longleftarrow }\limits ^{\delta '}}{\widehat{\varSigma '}} of\, the \,span\\ \qquad \qquad \qquad {\varSigma '}{\mathop {\longleftarrow }\limits ^{\delta }}{\widehat{\varSigma }}{\mathop {\longrightarrow }\limits ^{\tau }}{\widehat{\varSigma '}}) \\ (((\mathbf {generate}~\mathbf {by}~\sigma ~\mathbf {from}~\langle {\varSigma ,\emptyset }\rangle ~\mathbf {in}~\langle {\varSigma ',\varPhi '}\rangle ~)~\mathbf {with}~\sigma ' )~\mathbf {with}~\tau ' )~\mathbf {hide}~\mathbf {via}~\delta ' \\ \qquad {} \equiv {} (by\, Proposition~5.1(4)) \\ ((\mathbf {generate}~\mathbf {by}~\sigma ~\mathbf {from}~\langle {\varSigma ,\emptyset }\rangle ~\mathbf {in}~\langle {\varSigma ',\varPhi '}\rangle ~)~\mathbf {with}~\sigma '\mathord {;}\tau ' )~\mathbf {hide}~\mathbf {via}~\delta ' \end{array} \end{aligned}$$
- hiding::
-
$$ \begin{array}{l} (((\mathbf {generate}~\mathbf {by}~\sigma ~\mathbf {from}~\langle {\varSigma ,\emptyset }\rangle ~\mathbf {in}~\langle {\varSigma ',\varPhi '}\rangle ~)~\mathbf {with}~\sigma ' )~\mathbf {hide}~\mathbf {via}~\delta )\!~\mathbf {hide}~\mathbf {via}~\delta ' \\ \qquad {} \equiv {} (by\, Proposition~5.1(5)) \\ ((\mathbf {generate}~\mathbf {by}~\sigma ~\mathbf {from}~\langle {\varSigma ,\emptyset }\rangle ~\mathbf {in}~\langle {\varSigma ',\varPhi '}\rangle ~)~\mathbf {with}~\sigma ' )~\mathbf {hide}~\mathbf {via}~\delta '\mathord {;}\delta \end{array} $$
- source-trivial basic generating constraints::
-
$$ \begin{array}{l} \mathbf {generate}~\mathbf {by}~\sigma ~\mathbf {from}~\langle {\varSigma ,\emptyset }\rangle ~\mathbf {in}~\langle {\varSigma ',\varPhi '}\rangle ~ \\ \qquad {} \equiv {} (by\, Proposition~5.1(3)) \\ ((\mathbf {generate}~\mathbf {by}~\sigma ~\mathbf {from}~\langle {\varSigma ,\emptyset }\rangle ~\mathbf {in}~\langle {\varSigma ',\varPhi }\rangle ~)~\mathbf {with}~ id _{\varSigma '} )~\mathbf {hide}~\mathbf {via}~ id _{\varSigma '} \end{array} $$
\(\square \)
One might expect that Theorem 6.4 can be generalised to cover arbitrary specifications built from basic specifications using union, translation, hiding and (not necessarily basic) generating constraints. Unfortunately, in general this need not be the case, as the following counterexample shows.
Counterexample 6.5
Consider a very simple institution \(\mathbf{INS}_0\) with three signatures \(\varSigma _\emptyset \), \(\varSigma _1\) and \(\varSigma _2\), and signature morphisms \(\sigma :\varSigma _\emptyset \rightarrow \varSigma _1\), \(\delta :\varSigma _1\rightarrow \varSigma _2\) (and identities and the composition \(\sigma \mathord {;}\delta \)). This defines the signature category, which is finitely cocomplete. Let \(\mathbf{Mod}_0(\varSigma _\emptyset )\) be a singleton. Then let \(\mathbf{Mod}_0(\varSigma _1)\) contain three distinct models \(K_1\), \(N_1\) and \(M_1\) such that \(K_1\subseteq N_1\subseteq M_1\). Let \(\mathbf{Mod}_0(\varSigma _2)\) have two distinct models \(N_2\) and \(M_2\) with no inclusions other than identities. We also put  and
and  . Finally, let \(\mathbf{Sen}(\varSigma _\emptyset )=\mathbf{Sen}_0(\varSigma _1)=\mathbf{Sen}_0(\varSigma _2)=\emptyset \).
. Finally, let \(\mathbf{Sen}(\varSigma _\emptyset )=\mathbf{Sen}_0(\varSigma _1)=\mathbf{Sen}_0(\varSigma _2)=\emptyset \).
Consider
Clearly, \(N_1\) is the only model of the above specification. By a simple analysis of all possible cases, no \(\varSigma \)-specification in basic normal form has \(N_1\) as the only model: \(\{N_1\}\) cannot be the model class of a specification without generating constraints, since \(N_1\) and \(M_1\) cannot be distinguished in such a specification. All basic generating constraints here admit all models of their target specifications, except for the following one:
which does not have \(N_1\) as a model, since it has a proper submodel \(K_1\). Hence, no specification in basic normal form built on this constraint has \(N_1\) as a model.
Unfortunately, the above construction is not quite right: the institution we defined does not satisfy our assumptions, since the model functor is not continuous. For instance, the coproduct of \(\varSigma _1\) and \(\varSigma _2\) is \(\varSigma _2\), but the class of its models is not a product of the model classes of \(\varSigma _1\) and \(\varSigma _2\). The overall idea of the counterexample works, but the following more complex construction is needed.
Consider a category \(\mathcal {C}_0\) with two objects \(\varSigma _1\) and \(\varSigma _2\) and a morphism \(\delta :\varSigma _1\rightarrow \varSigma _2\), with model categories, reduct functor, and sets of sentences defined as above.
Let the category of signatures in \(\mathbf{INS}'_0\) be the category \(\mathbf{Set}^{\rightarrow }\) of morphisms in \(\mathbf{Set}\), i.e. signatures now consist of two sets and a function between them, written \(X_2{{\mathop {\rightarrow }\limits ^{f}}}X_1\), and signature morphisms \(\sigma :(X_2{{\mathop {\rightarrow }\limits ^{f}}}X_1)\rightarrow (X'_2{{\mathop {\rightarrow }\limits ^{f'}}}X'_1)\) are pairs of functions \(\sigma _1:X_1\rightarrow X'_1\) and \(\sigma _2:X_2\rightarrow X'_2\) such that \(f\mathord {;}\sigma _1=\sigma _2\mathord {;}f'\). It is well-known that \(\mathbf{Set}^{\rightarrow }\) is cocomplete. In fact, this is a special case of the construction of a free cocomplete category generated by any category \(\mathcal {C}\), given by the Yoneda embedding of \(\mathcal {C}\) into the category  of presheaves on \(\mathcal {C}\), see e.g. [Awo06] (Example 9.15 and Proposition 9.16). This also justifies the following choice of representation of the original signatures here: we identify \(\varSigma _1\) with \(\emptyset {\rightarrow }\{ id _{\varSigma _1}\}\) and \(\varSigma _2\) with \(\{ id _{\varSigma _2}\}{\rightarrow }\{\delta \}\), and \(\delta \) with the unique morphism between them. We may write \(\varSigma _\emptyset \) for the initial signature \(\emptyset {\rightarrow }\emptyset \).
of presheaves on \(\mathcal {C}\), see e.g. [Awo06] (Example 9.15 and Proposition 9.16). This also justifies the following choice of representation of the original signatures here: we identify \(\varSigma _1\) with \(\emptyset {\rightarrow }\{ id _{\varSigma _1}\}\) and \(\varSigma _2\) with \(\{ id _{\varSigma _2}\}{\rightarrow }\{\delta \}\), and \(\delta \) with the unique morphism between them. We may write \(\varSigma _\emptyset \) for the initial signature \(\emptyset {\rightarrow }\emptyset \).
In \(\mathbf{Set}^{\rightarrow }\), the signature \(X_2{{\mathop {\rightarrow }\limits ^{f}}}X_1\) is a colimit of a diagram with nodes \(X_2\uplus X_1\), where \(\varSigma _2\) is the object in each node in \(X_2\) and \(\varSigma _1\) is the object in each node in \(X_1\), with edges from f(s) to s labelled by \(\delta \) for each node \(s\in X_2\). Now, extend the model functor so that the category \(\mathbf{Mod}'_0(X_2{{\mathop {\rightarrow }\limits ^{f}}}X_1)\) is the limit in \(\mathbf{ICat}\) of the image of this diagram w.r.t. \(\mathbf{Mod}_0\) (as defined above on \(\varSigma _1\), \(\varSigma _2\) and \(\delta \)). This means in particular that a model P over a signature \(X_2{{\mathop {\rightarrow }\limits ^{f}}}X_1\) is a pair of functions \(P_1:X_1\rightarrow \{K_1,N_1,M_1\}\) and \(P_2:X_2\rightarrow \{N_2,M_2\}\) such that for \(x_2\in X_2\),  . Such a model P is a submodel of \(P'\) iff \(P_2(x_2)=P'_2(x_2)\) for \(x_2\in X_2\), and \(P_1(x_1)\subseteq P'_1(x_1)\) for \(x_1\in X_1\). Model reducts are given by (pre)composition with signature morphisms. Then for the sentence functor we set \(\mathbf{Sen}_0(X_2{{\mathop {\rightarrow }\limits ^{f}}}X_1)=\emptyset \).
. Such a model P is a submodel of \(P'\) iff \(P_2(x_2)=P'_2(x_2)\) for \(x_2\in X_2\), and \(P_1(x_1)\subseteq P'_1(x_1)\) for \(x_1\in X_1\). Model reducts are given by (pre)composition with signature morphisms. Then for the sentence functor we set \(\mathbf{Sen}_0(X_2{{\mathop {\rightarrow }\limits ^{f}}}X_1)=\emptyset \).
Now, the institution so sketched is exact, and the counterexample works: the specification
has no equivalent \(\varSigma _1\)-specification in basic normal form. To see this, just note that for any basic generating constraint C with \( Sig [C]=(X_2{{\mathop {\rightarrow }\limits ^{f}}}X_1)\), for any \(P\in Mod [C]\), if for \(x_1\in (X_1\setminus f(X_2))\), \(P(x_1)=N_1\) then there are \(P',P''\in Mod [C]\) such that \(P'(x_1)=K_1\) and \(P''(x_1)=M_1\), and if for \(x_2\in X_2\), \(P(x_2)=N_2\) then there is \(P'\in Mod [C]\) such that \(P'(x_2)=M_2\). Moreover, this property of specifications is preserved under translation w.r.t. any signature morphism. It follows then that no \(\varSigma _1\)-specification in basic normal form has \(N_1\) (or rather, P such that \(P_1( id _{\varSigma _1})=N_1\)) as its unique model. \(\square \)
The source of the trouble is the use of hiding within the target specifications for generating constraints. One might suppose that when hiding is forbidden, the normal form result holds even if other specification-building operations are permitted within the target specifications used in generating constraints. Unfortunately, this is not the case: nested generating constraints may yield a similar effect as captured by Counterexample 6.5.
Counterexample 6.6
Consider a very simple institution \(\mathbf{INS}_1\) with three signatures \(\varSigma \), \(\varSigma _1\) and \(\varSigma _2\) and non-identity morphisms \(\sigma _1:\varSigma _1\rightarrow \varSigma \) and \(\sigma _2:\varSigma _2\rightarrow \varSigma \). \(\mathbf{Mod}_1(\varSigma _1)\) has three distinct models \(K_1\), \( LN _1\) and \(M_1\) with \(K_1\subseteq LN _1\subseteq M_1\), \(\mathbf{Mod}(\varSigma _2)\) has two distinct models \( KL _2\) and \( NM _2\) with \( KL _2\subseteq NM _2\), and \(\mathbf{Mod}(\varSigma )\) has four distinct models K, L, N and M with \(K\subseteq L\subseteq N\subseteq M\). We put  ,
,  and
and  and
and  . Finally, we assume that there are no sentences in \(\mathbf{INS}_1\), i.e., \(\mathbf{Sen}_1(\varSigma )=\mathbf{Sen}_1(\varSigma _1)=\mathbf{Sen}_1(\varSigma _2)=\emptyset \).
. Finally, we assume that there are no sentences in \(\mathbf{INS}_1\), i.e., \(\mathbf{Sen}_1(\varSigma )=\mathbf{Sen}_1(\varSigma _1)=\mathbf{Sen}_1(\varSigma _2)=\emptyset \).
Then \( Mod [\mathbf {generate}~\mathbf {by}~\sigma _1~\mathbf {from}~\langle {\varSigma _1,\emptyset }\rangle ~\mathbf {in}~\langle {\varSigma ,\emptyset }\rangle ~]=\{K,L,M\}\), and so the constraint
has K and M as its only models. It is easy to check though that no basic generating constraint, and no specification in basic normal form, has \(\{K,M\}\) as its model class.
As in Counterexample 6.5, the above does not quite give a counterexample: the defined institution is not exact. Therefore, a construction of a new institution \(\mathbf{INS}'_1\) analogous to that in Counterexample 6.5 has to be carried out.
Let \(\mathcal {C}_1\) be the category with three signatures and morphisms as defined above. Take its free cocomplete closure via the Yoneda embedding into the category of presheaves over \(\mathcal {C}_1\),  . More explicitly, the resulting new category of signatures has objects of the form \(X_1{{\mathop {\leftarrow }\limits ^{f_1}}}X{{\mathop {\rightarrow }\limits ^{f_2}}}X_2\), where \(X_1\), X and \(X_2\) are sets and \(f_1:X\rightarrow X_1\) and \(f_2:X\rightarrow X_2\) are functions. A morphism \(h:(X_1{{\mathop {\leftarrow }\limits ^{f_1}}}X{{\mathop {\rightarrow }\limits ^{f_2}}}X_2)\rightarrow (X'_1{{\mathop {\leftarrow }\limits ^{f'_1}}}X'{{\mathop {\rightarrow }\limits ^{f'_2}}}X'_2)\) consists of three functions \(h_1:X_1\rightarrow X'_1\), \(h_0:X\rightarrow X'\) and \(h_2:X_2\rightarrow X'_2\) such that \(h_0\mathord {;}f'_1 = f_1\mathord {;}h_1\) and \(h_0\mathord {;}f'_2 = f_2\mathord {;}h_2\). We identify \(\varSigma _1\) with \(\{id_{\varSigma _1}\}{\leftarrow }\emptyset {\rightarrow }\emptyset \), \(\varSigma _2\) with \(\emptyset {\leftarrow }\emptyset {\rightarrow }\{id_{\varSigma _2}\}\), \(\varSigma \) with \(\{\sigma _1\}{\leftarrow }\{id_{\varSigma }\}{\rightarrow }\{\sigma _2\}\), and the morphisms \(\sigma _1:\varSigma _1\rightarrow \varSigma \) and \(\sigma _2:\varSigma _2\rightarrow \varSigma \) with unique morphisms between them. We do not add any sentences, so that the sentence functor \(\mathbf{Sen}'_1\) yields the empty set on every signature.
. More explicitly, the resulting new category of signatures has objects of the form \(X_1{{\mathop {\leftarrow }\limits ^{f_1}}}X{{\mathop {\rightarrow }\limits ^{f_2}}}X_2\), where \(X_1\), X and \(X_2\) are sets and \(f_1:X\rightarrow X_1\) and \(f_2:X\rightarrow X_2\) are functions. A morphism \(h:(X_1{{\mathop {\leftarrow }\limits ^{f_1}}}X{{\mathop {\rightarrow }\limits ^{f_2}}}X_2)\rightarrow (X'_1{{\mathop {\leftarrow }\limits ^{f'_1}}}X'{{\mathop {\rightarrow }\limits ^{f'_2}}}X'_2)\) consists of three functions \(h_1:X_1\rightarrow X'_1\), \(h_0:X\rightarrow X'\) and \(h_2:X_2\rightarrow X'_2\) such that \(h_0\mathord {;}f'_1 = f_1\mathord {;}h_1\) and \(h_0\mathord {;}f'_2 = f_2\mathord {;}h_2\). We identify \(\varSigma _1\) with \(\{id_{\varSigma _1}\}{\leftarrow }\emptyset {\rightarrow }\emptyset \), \(\varSigma _2\) with \(\emptyset {\leftarrow }\emptyset {\rightarrow }\{id_{\varSigma _2}\}\), \(\varSigma \) with \(\{\sigma _1\}{\leftarrow }\{id_{\varSigma }\}{\rightarrow }\{\sigma _2\}\), and the morphisms \(\sigma _1:\varSigma _1\rightarrow \varSigma \) and \(\sigma _2:\varSigma _2\rightarrow \varSigma \) with unique morphisms between them. We do not add any sentences, so that the sentence functor \(\mathbf{Sen}'_1\) yields the empty set on every signature.
A signature \(X_1{{\mathop {\leftarrow }\limits ^{f_1}}}X{{\mathop {\rightarrow }\limits ^{f_2}}}X_2\) is a colimit of a diagram with nodes \(X_1\uplus X\uplus X_2\), where nodes in \(X_1\) carry \(\varSigma _1\), nodes in X carry \(\varSigma \) and nodes in \(X_2\) carry \(\varSigma _2\), and edges from \(f_1(x)\) to x are labelled by \(\sigma _1\) and from \(f_2(x)\) to x are labelled by \(\sigma _2\), for all \(x\in X\). We define the model functor \(\mathbf{Mod}'_1\) so that \(\mathbf{Mod}'_1(X_1{{\mathop {\leftarrow }\limits ^{f_1}}}X{{\mathop {\rightarrow }\limits ^{f_2}}}X_2)\) is the limit in \(\mathbf{ICat}\) of the image of this diagram under \(\mathbf{Mod}_1\) (as defined above for \(\mathcal {C}_1\)). That is, any model \(P\in |\mathbf{Mod}'_1(X_1{{\mathop {\leftarrow }\limits ^{f_1}}}X{{\mathop {\rightarrow }\limits ^{f_2}}}X_2)|\) consist of three functions \(P_1:X_1\rightarrow \{K_1, LN _1,M_1\}\), \(P_0:X\rightarrow \{K,L,N,M\}\) and \(P_2:X_2\rightarrow \{ KL _2, NM _2\}\) such that for \(x \in X\),  and
and  . Such a model is a submodel of \(P'\in |\mathbf{Mod}(X_1{{\mathop {\leftarrow }\limits ^{f_1}}}X{{\mathop {\rightarrow }\limits ^{f_2}}}X_2)|\) if for all \(x_1\in X_1\), \(P_1(x_1)\subseteq P'_1(x_1)\), and similarly for X and \(X_2\). Model reducts are given by (pre)composition with signature morphisms. For a class of models \(\mathcal {P}\subseteq |\mathbf{Mod}'_1(X_1{{\mathop {\leftarrow }\limits ^{f_1}}}X{{\mathop {\rightarrow }\limits ^{f_2}}}X_2)|\) and \(x\in X\), we write \(\mathcal {P}(x) = \{ P_0(x) \mid P\in \mathcal {P}\}\).
. Such a model is a submodel of \(P'\in |\mathbf{Mod}(X_1{{\mathop {\leftarrow }\limits ^{f_1}}}X{{\mathop {\rightarrow }\limits ^{f_2}}}X_2)|\) if for all \(x_1\in X_1\), \(P_1(x_1)\subseteq P'_1(x_1)\), and similarly for X and \(X_2\). Model reducts are given by (pre)composition with signature morphisms. For a class of models \(\mathcal {P}\subseteq |\mathbf{Mod}'_1(X_1{{\mathop {\leftarrow }\limits ^{f_1}}}X{{\mathop {\rightarrow }\limits ^{f_2}}}X_2)|\) and \(x\in X\), we write \(\mathcal {P}(x) = \{ P_0(x) \mid P\in \mathcal {P}\}\).
Consider now a signature morphism \(h:(X_1{{\mathop {\leftarrow }\limits ^{f_1}}}X{{\mathop {\rightarrow }\limits ^{f_2}}}X_2)\rightarrow (X'_1{{\mathop {\leftarrow }\limits ^{f'_1}}}X'{{\mathop {\rightarrow }\limits ^{f'_2}}}X'_2)\) and constraint \(C'=\mathbf {generate}~\mathbf {by}~h~\mathbf {from}~\langle {X_1{{\mathop {\leftarrow }\limits ^{f_1}}}X{{\mathop {\rightarrow }\limits ^{f_2}}}X_2,\emptyset }\rangle ~\mathbf {in}~\langle {X'_1{{\mathop {\leftarrow }\limits ^{f'_1}}}X'{{\mathop {\rightarrow }\limits ^{f'_2}}}X'_2,\emptyset }\rangle ~\). We analyse the class of the models of \(C'\). Let \(x'\in X'\).
-
For some \(x\in X\), \(x'=h_0(x)\) (and so \(f'_1(x')=h_1(f_1(x))\) and \(f'_2(x')=h_2(f_2(x))\)). Then \( Mod [C'](x')=\{K,L,N,M\}\), since informally, the corresponding component of the signature morphism is the identity on this “occurrence” of \(\varSigma \).
-
\(x'\) is not in the image of \(h_0\); then we have the following subcases.
-
For some \(x_1\in X_1\) and \(x_2\in X_2\), \(h_1(x_1)=f'_1(x')\) and \(h_2(x_2)=f'_2(x')\). Then \( Mod [C'](x')=\{K,L,N,M\}\), since informally, the corresponding component of the signature morphism is the map from the coproduct of \(\varSigma _1\) and \(\varSigma _2\) to this “occurrence” of \(\varSigma \) given by \(\sigma _1\) and \(\sigma _2\), and the reducts w.r.t. \(\sigma _1\) and \(\sigma _2\) do not jointly identify any models from \(\{K,L,N,M\}\).
-
For some \(x_1\in X_1\), \(h_1(x_1)=f'_1(x')\) but \(f'_2(x')\) is not in the image of \(h_2\). Then \( Mod [C'](x')=\{K,L,M\}\), since informally, the corresponding component of the signature morphism is \(\sigma _1\), and the reduct w.r.t. \(\sigma _1\) glues L and N together.
-
For some \(x_2\in X_2\), \(h_2(x_2)=f'_2(x')\) but \(f'_1(x')\) is not in the image of \(h_1\). Then \( Mod [C'](x')=\{K,N\}\), since informally, the corresponding component of the signature morphism is \(\sigma _2\), and the reduct w.r.t. \(\sigma _2\) glues K and L as well as N and M together.
-
Neither is \(f'_1(x')\) in the image of \(h_1\) nor is \(f'_2(x')\) in the image of \(h_2\). Then \( Mod [C'](x')=\{K\}\), since informally, the corresponding component of the signature morphism is the unique morphism from the initial signature to \(\varSigma \), and the reduct w.r.t. this morphism glues all models together.
Consequently, for any basic generation constraint \(C'\) as above, for \(x'\in X'\), the class \( Mod [C](x')\) is in the family \(\mathcal {F}= \{ \{K,L,N,M\}\), \(\{K,L,M\}\), \(\{K,N\}\), \(\{K\} \}\). Moreover, this property is preserved under translation of specifications, since the family \(\mathcal {F}\) is closed under intersection, and under hiding (reducts w.r.t. signature morphisms). Therefore, no specification in basic normal form may have \(\{K,M\}\) is its class of models. \(\square \)
The above counterexamples show that in general we cannot avoid nesting of structured specifications within generation constraints. We say that a specification is in nested normal form if either it is a basic specification, or it is built as follows:
where \( SP '\) is a specification in nested normal form.
Corollary 6.7
In any finitely exact institution \(\mathbf{INS}\) with model inclusions, any structured specification built from basic specifications using union, translation, hiding and generating constraints is equivalent to a specification in nested normal form.
Proof
As in the proof of Theorem 6.4, we first use Corollary 6.3 to allow us to deal with source-trivial generating constraints only. Then the proof proceeds by double induction, on the maximal depth of nesting of generating constraints in the specifications, and then on the structure of specifications. When the depth of nesting is at most 1, the result follows by Theorem 6.4. Otherwise, we proceed by induction on the structure of specification, assuming the thesis for all specifications with a smaller depth of nesting of generating constraints. The case of basic specifications is trivial. The cases for translation and hiding follow much as in the proof of Theorem 6.4. For generating constraints, the thesis follows by the inductive assumption, since the specification used within the generating constraint has a smaller depth of nesting of generating constraints. For the case of union, we get by an argument analogous to that in the proof of Theorem 6.4 for the case of union:

Now, the thesis follows by the inductive assumption, since the depth of nesting of generating constraints in  is lower than in the original specification. \(\square \)
is lower than in the original specification. \(\square \)
7 Final Remarks
We started with the normal form result for constraints as studied in [EWT83] in the standard algebraic framework. We have shown that this result carries over to the more general setting of an arbitrary institution with some minimal extra structure: the notion of a submodel needed to capture the definition of generated model used in [EWT83]. Moreover, we sharpened the result somewhat via the use of a more restrictive definition of normal form.
We then considered the more general problem of normalising specifications where generating constraints are imposed in a class of models of an arbitrary specification, not just a presentation as in [EWT83]. Unfortunately, two counterexamples show that the normal form result does not carry over to this more general situation. Some nesting of generating constraints must be allowed, leading to a considerably weaker normal form result for this more general case.
The difficulties we encountered are linked to the definition of generated model in [EWT83], which we retained here. A standard alternative would be to free the concept of generated model from its dependency on the class of models of the specification at hand, and consider generation in the class of all models over the given signature. In the standard algebraic framework this leads to the usual notion of generated algebra, where all elements are values of terms with variables taking values in the indicated carriers, with the usual connection to structural induction, as in Casl [BCH+04]. For specifications with generating constraints of this special form, by easy adaptation of Theorem 6.4 and its proof one can build an equivalent normal form of the following shape:

Restricting to this special case would considerably limit the power of generating constraints as considered here. For instance, in AI applications, McCarthy’s notion of circumscription [McC80] used to impose a “closed world assumption” could not be captured in general, since no predicate ever holds in generated models over a first-order signature without any axioms or constraints imposed on the class of models considered. It is worth mentioning that a similarly general construct was introduced in DOL, the Distributed Ontology, Modeling and Specification Language [MCNK15].
One issue we did not touch on here at all is the development of proof systems for structured specifications. This is well-studied in the context of specifications built from basic specifications using union, translation and hiding, with a standard compositional proof system for consequences of specifications given in the framework of an arbitrary institution already in [ST88]. Completeness results follow under additional assumptions about the institution (most notably, interpolation is needed) where the proof of completeness heavily relies on the normal form result [Bor02]. It is well-known that once generating constraints are added, there is no hope for completeness [MS85]. However, in [ST14] we showed that the compositional proof system for structured specification built from basic specifications using union, translation and hiding is the best sound compositional proof system possible. It would be interesting to see how to carry this over to specifications with generating constraints, with some sound approximate techniques for proving consequences of generating constraints. Perhaps the normal form results studied here could be used to “concentrate” the necessary incompleteness at specific points in the structure of specifications, linked to the use of generating constraints in the normal forms.
References
Awodey, S.: Category Theory. Oxford University Press, New York (2006)
Baumeister, H., Cerioli, M., Haxthausen, A., Mossakowski, T., Mosses, P.D., Sannella, D., Tarlecki, A.: Casl semantics. In: [Mos04] (2004)
Bergstra, J.A., Heering, J., Klint, P.: Module algebra. J. Assoc. Comput. Mach. 37(2), 335–372 (1990)
Bidoit, M., Mosses, P.D. (eds.): CASL User Manual. LNCS, vol. 2900. Springer, Heidelberg (2004). https://doi.org/10.1007/b11968. http://www.informatik.uni-bremen.de/cofi/index.php/CASL
Borzyszkowski, T.: Logical systems for structured specifications. Theor. Comput. Sci. 286(2), 197–245 (2002)
Codescu, M., Mossakowski, T., Sannella, D., Tarlecki, A.: Specification refinements: calculi, tools, and applications. Sci. Comput. Program. 144, 1–49 (2017)
Căzănescu, V.E., Roşu, G.: Weak inclusion systems. Math. Struct. Comput. Sci. 7(2), 195–206 (1997)
Diaconescu, R., Goguen, J.A., Stefaneas, P.: Logical support for modularisation. In: Huet, G., Plotkin, G. (eds.) Logical Environments, pp. 83–130. Cambridge University Press, Cambridge (1993)
Ehrig, H., Mahr, B.: Fundamentals of Algebraic Specification 1. EATCS Monographs on Theoretical Computer Science, vol. 6. Springer, Heidelberg (1985). https://doi.org/10.1007/978-3-642-69962-7
Ehrig, H., Wagner, E.G., Thatcher, J.W.: Algebraic specifications with generating constraints. In: Diaz, J. (ed.) ICALP 1983. LNCS, vol. 154, pp. 188–202. Springer, Heidelberg (1983). https://doi.org/10.1007/BFb0036909
Goguen, J.A., Burstall, R.M.: Introducing institutions. In: Clarke, E., Kozen, D. (eds.) Logic of Programs 1983. LNCS, vol. 164, pp. 221–256. Springer, Heidelberg (1984). https://doi.org/10.1007/3-540-12896-4_366. Many revised versions were widely circulated, with [GB92] as the endpoint
Goguen, J.A., Burstall, R.M.: Institutions: abstract model theory for specification and programming. J. Assoc. Comput. Mach. 39(1), 95–146 (1992)
Goguen, J.A., Roşu, G.: Composing hidden information modules over inclusive institutions. In: Owe, O., Krogdahl, S., Lyche, T. (eds.) From Object-Orientation to Formal Methods. LNCS, vol. 2635, pp. 96–123. Springer, Heidelberg (2004). https://doi.org/10.1007/978-3-540-39993-3_7
McCarthy, J.: Circumscription – a form of non-monotonic reasoning. Artif. Intell. 13(1–2), 27–39 (1980)
Mossakowski, T., Codescu, M., Neuhaus, F., Kutz, O.: The distributed ontology, modeling and specification language – DOL. In: Koslow, A., Buchsbaum, A. (eds.) The Road to Universal Logic. SUL, pp. 489–520. Springer, Cham (2015). https://doi.org/10.1007/978-3-319-15368-1_21
Mosses, P.D. (ed.): Casl Reference Manual. LNCS, vol. 2960. Springer, Heidelberg (2004). https://doi.org/10.1007/b96103
MacQueen, D., Sannella, D.: Completeness of proof systems for equational specifications. IEEE Trans. Softw. Eng. SE–11(5), 454–461 (1985)
Sannella, D., Tarlecki, A.: Specifications in an arbitrary institution. Inf. Comput. 76(2–3), 165–210 (1988)
Sannella, D., Tarlecki, A.: Foundations of Algebraic Specification and Formal Software Development. Monographs in Theoretical Computer Science. An EATCS Series. Springer, Heidelberg (2012)
Sannella, D., Tarlecki, A.: Property-oriented semantics of structured specifications. Math. Struct. Comput. Sci. 24(2), e240205 (2014)
Sannella, D., Wirsing, M.: A kernel language for algebraic specification and implementation: extended abstract. In: Karpinski, M. (ed.) FCT 1983. LNCS, vol. 158, pp. 413–427. Springer, Heidelberg (1983). https://doi.org/10.1007/3-540-12689-9_122
Tarlecki, A.: Remarks on [EWT83]. Unpublished note, Department of Computer Science, University of Edinburgh (1983)
Acknowledgements
Thanks to the anonymous referees for their constructive comments.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2018 Springer International Publishing AG, part of Springer Nature
About this chapter
Cite this chapter
Sannella, D., Tarlecki, A. (2018). On Normal Forms for Structured Specifications with Generating Constraints. In: Heckel, R., Taentzer, G. (eds) Graph Transformation, Specifications, and Nets. Lecture Notes in Computer Science(), vol 10800. Springer, Cham. https://doi.org/10.1007/978-3-319-75396-6_15
Download citation
DOI: https://doi.org/10.1007/978-3-319-75396-6_15
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-75395-9
Online ISBN: 978-3-319-75396-6
eBook Packages: Computer ScienceComputer Science (R0)







 , where
, where  is
is  if in
if in  there is no proper subalgebra of A with the same
there is no proper subalgebra of A with the same  , giving a category
, giving a category 

 is a specification with:
is a specification with: 

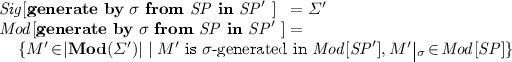





 , for any
, for any 


