New Findings on the Shock Reflection from Wedges with Small Concave Tips

Abstract

Planar shock reflection from straight wedges and wedges with small concave tips is considered. It is demonstrated that, in shock tube experiments for a certain wedge angle and incident shock Mach number, the resulting reflection is of irregular type in the presence of a small concave tip with an arc radius as small as 4 mm while a straight wedge with the same wedge angle produces a regular reflection. In the numerical experiments, corner signal tracking is used to demonstrate that in the case of a concave tip wedge the corner signal is always merged with the Mach stem and never detaches. It is concluded that for the prediction of the Mach-to-regular reflection transition angle for wedges with concave tips, it is essential to predict as accurately as possible the strength of the Mach stem. An initial development of an analytical method to predict the transition angle is then provided.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

The present paper continues previous studies on unsteady shock wave reflections from wedges with straight and concave tips [1, 2]. Lau-Chapdelaine and Radulescu [2] numerically demonstrated that the resulting reflection pattern (regular or Mach reflection) established far away from the wedge tip may differ depending on whether the reflecting wedge has a straight or concave tip. Parametric studies by Alzamora Previtali et al. [1] showed that the effect is observed for shock Mach numbers corresponding to the dual solution domain (where both Mach and regular reflection are physically admissible) and wedge angles ranging from the transition angle predicted by the sonic criterion to a value slightly lower than predicted by von Neumann’s criterion, i.e., within the most part of the dual solution domain. The first experimental demonstration of the effect for a concave tip wedge with the radius of curvature $R=12$ mm and a straight wedge with the same angle (52$^\circ$) is also provided in [1].

Fig. 1

Schematic sketch of the experimental model in the test section

It is obviously of interest to investigate whether or not even smaller, minute, radii of curvature would also alter the resulting reflection pattern as compared to the one observed with a straight wedge of the same angle. As a step in this direction, Sect. 2 of the present paper presents experimental results obtained with the radius of curvature R as small as 4 mm.

The subsequent Sect. 3 contains some preliminary developments aiming at an analytical treatment to predict the Mach-to-regular reflection transition angle for wedges with concave tips. The final section of this paper summarizes the current findings and outlines the directions of future studies.

2 Experimental Studies

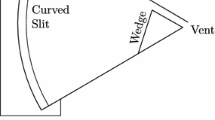
The experimental shock tube setup and diagnostics used in the present paper are similar to the ones described in [1, 3]. As shown in Fig. 1, the experiments are conducted in a conventional diaphragm-operated shock tube with rectangular 150 mm $\times$ 75 mm cross section. The test section windows of 215 mm in diameter allow for optical access. The wedge plate of 170 mm in length attached to the wedge base has two tips: straight and concave. Therefore, by simply turning the plate by 180$^\circ$, the desired tip is facing the incoming shock wave.

The test gas is air. Different initial pressures in the test section, ranging from 3.7 to 16 kPa, are used to obtain the desirable shock Mach numbers for given driver gas pressure and diaphragm thickness. The tests are conducted at ambient temperature, which is in the range of 290–293 K. The driver gas is helium. The shock Mach number is determined from time-of-arrival data obtained by means of three KISTLER pressure transducers mounted flush with the shock tube wall ahead of and within the test section. Each Mach number obtained from such a measurement has an uncertainty of $\pm 0.006$.

High-speed video cameras (Shimadzu HPV-1 and HPV-X) are used for time-resolved shadowgraph or schlieren visualization at frame rates of $10^6$ (HPV-1) and $10^7$ (HPV-X) frames per second with an exposure time of 250 ns (HPV-1) and 55 ns (HPV-X). The spatial resolution of the cameras is $312\times 260$ pixels for the HPV-1 and $400\times 250$ pixels for the HPV-X. The pixels of the HPV-X are about half the size of those of the HPV-1, which leads to an improved spatial resolution. Both cameras have an in-situ image storage sensor (ISIS) and record 100 (HPV-1) and 128 (HPV-X) frames, respectively.

2.1 Results

The experimental results for a nominal incident shock Mach number 3, a wedge angle of 52$^\circ$, and a wedge tip radius of 4 mm are shown in Figs. 2 and 3.

With the goal of improving resolution, different portions of the test model were visualized in different experiments with correspondingly increased image magnification. The first three images in Fig. 2a–c are from a single test giving a magnified view near the rounded tip of the wedge while the fourth image, Fig. 2d, shows the area near the wedge’s trailing edge in a second test (the Mach numbers for the two experiments are essentially identical within measurement uncertainty: $3.017 \pm 0.006$ and $3.020 \pm 0.006$). Figure 3 corresponds to an experiment (shock Mach number $2.986 \pm 0.006$) with an even higher magnification near the concave tip. It is clear from these images that even with such a small concave tip the resulting reflection (Fig. 2) is and remains of irregular type.

Fig. 2

Shadowgraph movie frames for the wedge angle $\theta _\mathrm{w}=52^\circ$ and the concave tip radius $R=4$ mm: a–c the shock Mach number $M_\mathrm{s}=3.017$; d $M_\mathrm{s}=3.020$. The scale on the wedge indicates length in millimeters

Fig. 3

Shadowgraph movie frames for the wedge angle $\theta _\mathrm{w}=52^\circ$, the concave tip radius $R=4$ mm, and the shock Mach number $M_\mathrm{s}=2.986$. The scale on the wedge is not visible due to the absence of front lighting; however, the scale can be judged from the radius of wall curvature equal to 4 mm. The experiment corresponds to the highest magnification possible with the present setup

Fig. 4

Schlieren movie frame for the straight wedge with the angle of $\theta _\mathrm{w}=52^\circ$, and the shock Mach number $M_\mathrm{s}=2.872$. The scale on the wedge indicates length in millimeters

The characteristic shape of the reflected wave corresponding to a DMR (double Mach reflection) is not only clearly visible near the trailing edge of the wedge but can also be traced back to very early moments, such as the right image of Fig. 3.

As shown in Fig. 4, a straight wedge of the same angle, for a close shock Mach number of $2.872 \pm 0.006$, produces a regular reflection. As is typical for a regular reflection off a wedge with an angle exceeding the angle corresponding to the sonic transition criterion, the reflected shock is initially straight and begins to bend smoothly only when affected by the corner signal.

3 Preliminary Theoretical Analysis

The theoretical analysis suggested below is partly based on the findings from numerical modeling. Therefore, in the next subsection, a brief summary of the CFD tools used in the present study is given.

3.1 CFD Tools

The numerical results presented below are obtained with the Euler (inviscid, non-heat-conducting) flow model. The gas is assumed to be ideal with constant specific heats ($\gamma = 1.4$). An adaptive unstructured finite-volume flow solver [4] is used. The solver employs a node-centered, second order in space and time (for smooth solutions and uniform grids), MUSCL-Hancock TVD finite-volume scheme [5].

To shed some light on the disturbance propagation in the flow under consideration, the signal tracking technique proposed in [6] is used to study the propagation of the corner signal front. In this technique, signals are considered as infinitesimally weak sound waves propagating with the local speed of sound relative to the flow and being carried by the flow itself as well. The tracking is done at the end of each time step as a post-processing procedure. Since no actual disturbance is introduced to the flow, the technique is as accurate as the numerical flowfield itself. Information about the velocity of the corner signal and its path can therefore be obtained from numerical experiments.

3.2 Analytical Considerations

There are at least three ways to be followed if one desires to develop an analytical treatment to predict the Mach-to-regular reflection transition angle for wedges with concave tips. It is to be emphasized that the transition considered here is between the resulting Mach or regular reflection established asymptotically, far away from the concave tip. In other words, for wedges with concave tips, the initial reflection is always of irregular type which eventually (when the incident shock has covered a distance considerably exceeding the tip radius of curvature) either remains a Mach reflection or, if the wedge angle exceeds a certain critical angle called “transition angle,” turns into a regular reflection. It is the transition angle between these two final outcomes that are of interest.

The first possible approach is to generalize the treatment suggested by Itoh et al. [7] for the transition on a fully concave (cylindrical) surface. Their idea is to consider the trajectory of the triple point and find its intersection with the wall surface, which is, by definition, the transition point. Since this task appears to be intractable using the full conservation laws (the Euler equations) without any simplifying assumptions, Itoh et al. [7] use the geometrical shock dynamics approach based on the CCW (Chester–Chisnell–Whitham) theory. Along the lines proposed by Milton [8], they derive a correction accounting for the presence of the reflected shock wave and the tangential discontinuity for an incident shock of arbitrary strength.

The second way is to follow the ideas of Ben-Dor and Takayama [9, 10], see also a summary in [11], for the transition on concave cylindrical surfaces. Their approach is based on the length-scale concept and involves the consideration of corner signal propagation behind the incident shock and the induced Mach stem. According to this concept, the moment just before transition represents the last time the corner-generated signal can catch up with the triple point.

Fig. 5

Inviscid CFD simulations of shock wave ($M_\mathrm{s} = 3.0$) reflection from wedges with corner signal tracking. The corner signal front at the displayed time moment is shown with a thin solid line. The wedge angle is $\theta _\mathrm{w}=52^\circ$ in both cases shown: a the case of a straight wedge; the corner signal front runs along the reflected shock and then comes to the surface well behind the reflected point, i.e., the signal is not catching up with the reflection point. This corresponds to the regular nature of the observed shock reflection; b the case of a concave tip wedge; it is seen that the Mach stem and the respective portion of the corner signal front coincide

Finally, another approach is advocated for concave cylindrical surfaces in the companion paper of these Proceedings [12]. It is based on the examination of the propagation of weak disturbances (“corner signals”) in the flow. Such an examination, carried out via numerical modeling, reveals that the speed of corner signals (generated by the leading edge of the reflecting surface as well as by all subsequent wall segments) always exceeds that of the foot of the Mach stem, and, therefore, the signal fronts stay merged with the Mach stem at all times. From this point of view, the speed of corner signals does not appear to be the deciding factor in transition. In [12], it is shown that the prediction of the Mach stem velocity along the reflecting surface is a key for accurate prediction of transition.

In the present paper, a similar examination of corner signal propagation is conducted for wedges with concave tips. Figure 5a shows an instant Mach number flowfield (the Mach number is given in the laboratory frame of reference) generated when a planar shock wave with shock Mach number 3.0 reflects from a straight wedge of $52^\circ$ (the same angle as in the experiments shown in the previous section). This simulation tracks the corner signal, which is induced when the incident shock has just reached the wedge leading edge. The instant corner signal front is shown in Fig. 5a as a thin black line. As expected for a wedge angle exceeding the sonic angle (50.81$^\circ$), the corner signal is clearly behind the reflection point. There is a straight portion of the reflected shock, not affected by the corner signal. Figure 5b shows the instant corner signal front for a concave tip wedge with the wedge angle of $52^\circ$. It is seen that the portion of the front propagating along the wedge coincides with the Mach stem, from the wedge wall to the triple point. The analysis of the reflection process as a whole confirms that the corner signal is always merged with the Mach stem and never detaches. This should be expected because the flow downstream from the Mach steam is always subsonic relatively to the Mach stem and, therefore, the corner signal velocity $V+c$ behind the Mach stem in the laboratory frame of reference is greater than the velocity of the Mach stem in the same reference frame (V is the local flow velocity, and c is the local speed of sound). Hence, the corner signal catches up with the Mach stem at the same instant as it is generated and stays merged with it (obviously, it cannot go ahead of the Mach stem).

From this point of view, as already mentioned above, similarly to the case of a fully concave reflecting surface, the corner signal speed does not appear to be the deciding factor in transition: the speed of the foot of the Mach stem will determine when (and if) the Mach stem vanishes.

Fig. 6

Schematics of InMR–TRR (inverse Mach reflection–transitioned regular reflection) transition on a wedge with a concave tip, illustrating the analytical treatment of the present paper

The subsequent derivations are assisted by the schematics shown in Fig. 6. The transition takes place at the time moment $t^\mathrm{tr}$ when the Mach stem vanishes at $x=x^\mathrm{tr}$ or $x_\mathrm{w}=x_\mathrm{w}^\mathrm{tr}$. In Fig. 6, the coordinate x is along the horizontal x-axis while the curvilinear coordinate $x_\mathrm{w}$ is along the reflecting surface; the origin of both coordinates is at the leading edge of the wedge. The incident shock moves with a constant velocity $V_\mathrm{s}$ so that $t^\mathrm{tr}=x^\mathrm{tr}/V_\mathrm{s}$. The foot of the Mach stem moves with a velocity $V_\mathrm{w}^\mathrm{st}$ which is changing in time during the course of wave propagation. Therefore, the time $t^\mathrm{tr}$ can be also determined via integration along the reflecting surface. This would then lead to the following general relation for the determination of the transition point:

$$\begin{aligned} \frac{x^\mathrm{tr}}{V_\mathrm{s}}=\int \limits _0^{x_\mathrm{w}^\mathrm{tr}} \frac{\mathrm{d}x_\mathrm{w}}{V_\mathrm{w}^\mathrm{st}} \end{aligned}$$

(1)

The integral can be split into two parts corresponding to the circular arc of the concave tip and the straight portion of the wedge:

$$\begin{aligned} \frac{x^\mathrm{tr}}{V_\mathrm{s}}=\int \limits _0^{x_\mathrm{w}^A} \frac{\mathrm{d}x_\mathrm{w}}{V_\mathrm{w}^\mathrm{st}}+\int \limits _{x_\mathrm{w}^A}^{x_\mathrm{w}^\mathrm{tr}} \frac{\mathrm{d}x_\mathrm{w}}{V_\mathrm{w}^\mathrm{st}}, \end{aligned}$$

(2)

where $x_\mathrm{w}^A$ (or $x^A$) is the coordinate of the point where the circular and straight segments of the wedge meet.

It would be more convenient to operate with the wall angle $\theta _\mathrm{w}$ (which is also the polar angle of the arc, see Fig. 6) and the respective transition angle $\theta _\mathrm{w}^\mathrm{tr}$. Furthermore, let us express the distance between point A and the transition point as $\lambda R$ where $\lambda$ is a nondimensional factor and R is the radius of the concave cylindrical portion of the wedge. This leads to the following relation:

$$\begin{aligned} \frac{R\sin \theta _\mathrm{w}^\mathrm{tr}+\lambda R\cos \theta _\mathrm{w}^\mathrm{tr}}{V_\mathrm{s}}=\int \limits _0^{\theta _\mathrm{w}^\mathrm{tr}} \frac{{R\mathrm d}\theta _\mathrm{w}}{V_\mathrm{w}^\mathrm{st}}+\int \limits _{x_\mathrm{w}^A}^{x_\mathrm{w}^{A}+\lambda R} \frac{\mathrm{d}x_\mathrm{w}}{V_\mathrm{w}^\mathrm{st}}. \end{aligned}$$

(3)

After dividing both sides by R and making a simple variable transformation, $\tilde{x}_\mathrm{w}=(x_\mathrm{w}-x_\mathrm{w}^A)/R$, in the second integral, we arrive at

$$\begin{aligned} \frac{\sin \theta _\mathrm{w}^\mathrm{tr}+\lambda \cos \theta _\mathrm{w}^\mathrm{tr}}{V_\mathrm{s}}=\int \limits _0^{\theta _\mathrm{w}^\mathrm{tr}} \frac{\mathrm{d}\theta _w}{V_\mathrm{w}^\mathrm{st}}+\int \limits _{0}^{\lambda } \frac{\mathrm{d}\tilde{x}_\mathrm{w}}{V_\mathrm{w}^\mathrm{st}}. \end{aligned}$$

(4)

It is to be noted that assuming $\lambda = 0$, i.e., considering a fully concave cylindrical surface, without a straight wedge, Eq. (4) reduces to the relation obtained in [12] for the concave cylindrical surface:

$$\begin{aligned} \frac{\sin \theta _\mathrm{w}^\mathrm{tr}}{\theta _\mathrm{w}^\mathrm{tr}}=V_\mathrm{s}\times \frac{1}{\theta _\mathrm{w}^\mathrm{tr}}\int \limits _0^{\theta _\mathrm{w}^\mathrm{tr}} \frac{\mathrm{d}\theta _w}{V_\mathrm{w}^\mathrm{st}}. \end{aligned}$$

(5)

Numerical experiments show, see the data presented in [1], that the asymptotic angle $\chi$ between the triple point trajectory and the wedge surface approaches zero at transition, and therefore, it can be safely assumed that $\lambda \gg 1$, which means that the transition takes place far away from the wedge tip—it may be conjectured that this happens “at infinity.” This is also consistent with the goal of obtaining the transition angle between the resulting, asymptotic ($x_\mathrm{w}\rightarrow \infty$) reflection patterns. By considering that $\lambda \gg 1$, Eq. (4) can therefore be simplified to

$$\begin{aligned} \frac{\cos \theta _\mathrm{w}^\mathrm{tr}}{V_\mathrm{s}}=\frac{1}{\lambda }\int \limits _{0}^{\lambda } \frac{\mathrm{d}\tilde{x}_\mathrm{w}}{V_\mathrm{w}^\mathrm{st}}= {\bigg \langle \frac{1}{V_\mathrm{w}^\mathrm{st}}\bigg \rangle } \end{aligned}$$

(6)

or

$$\begin{aligned} \cos \theta _\mathrm{w}^\mathrm{tr}=V_\mathrm{s}\times \bigg \langle \frac{1}{V_\mathrm{w}^\mathrm{st}}\bigg \rangle \, \end{aligned}$$

(7)

where $\langle \frac{1}{V_\mathrm{w}^\mathrm{st}}\rangle$ denotes an averaged value of the inverse velocity of the Mach stem foot along the straight portion of the wedge.

Fig. 7

Mach number history of the Mach stem on the reflecting surface of a wedge with a concave tip ($M_\mathrm{s} = 3.0$ and $\theta _\mathrm{w} = 52^\circ$). The vertical solid line corresponds to the point where the concave tip and the straight portion of the wedge meet

Numerical experiments indicate that the strength of the Mach stem does not vary significantly when it propagates along the wedge away from the tip, see Fig. 7. Then, the Mach stem velocity ${V_\mathrm{w}^\mathrm{st}}$ can be assumed to have a constant value of $\langle {V_\mathrm{w}^\mathrm{st}}\rangle$, resulting in

$$\begin{aligned} \cos \theta _\mathrm{w}^\mathrm{tr}=\frac{V_\mathrm{s}}{\langle V_\mathrm{w}^\mathrm{st}\rangle }\ . \end{aligned}$$

(8)

The relation can be also rewritten in terms of Mach numbers as follows:

$$\begin{aligned} \cos \theta _\mathrm{w}^\mathrm{tr}=\frac{M_\mathrm{s}}{\langle M_\mathrm{w}^\mathrm{st}\rangle }\ . \end{aligned}$$

(9)

Thus, to predict the transition angle, it is necessary to predict the Mach stem strength when it propagates along the wedge. The correctness of this principle can be verified via numerical experiments. For example, for the incident shock Mach number $M_s = 3.0$ and the wedge angle $\theta _\mathrm{w} = 59.5^\circ$ (the value is chosen to be close to the transition angle), numerical experiments give the value of 5.852 for $\langle M_\mathrm{w}^\mathrm{st}\rangle$ at the end of the wedge. Then, Eq. (9) results in $\theta _\mathrm{w}^\mathrm{tr} = 59.2^\circ$, which is very close to the transition angle value of $59.79^\circ$ for $M_s = 3.0$ determined via numerical experiments in [1]. Thus, it is to be concluded that if one succeeded in predicting the Mach stem strength along the wedge, this would automatically lead to a correct prediction of transition.

As demonstrated in Fig. 7, the CCW theory results in a significantly lower value of the Mach stem Mach number as compared to the numerical prediction. It is also seen that the use of $V+c$ value behind the incident shock as the velocity of the Mach stem, as in [9, 10], is completely unacceptable. The issue remains open for investigation.

4 Conclusions

In the shock tube experiments of the present paper, it is demonstrated that, for a certain wedge angle and incident shock Mach number, the resulting reflection is of irregular type in the presence of a small concave tip with the arc radius as small as 4 mm while a straight wedge with the same wedge angle produces a regular reflection. The result is of obvious practical significance: it clearly points to the possibility, under certain conditions, of having an unexpected reflection pattern (and pressure and temperature values associated with it) due to corner roundings which might be erroneously perceived as insignificant.

The present paper provides a basis for the subsequent development of an analytical method to predict the MR–RR transition angle for wedges with concave tips. It is shown that it is essential to predict as accurately as possible the strength of the Mach stem. Further developments aiming at such predictions are presently under way.

Numerical simulations using the Navier–Stokes equations are also to be carried out. The study of the influence of viscous effects is essential because in most shock tube experiments, high Mach numbers (>2) can only be achieved at low pressures in the test section. As a result, the Reynolds number based on the tip radius R can be as low as 15,000 for $R = 4$ mm, and, therefore, viscous effects may significantly shift the transition boundaries.