Abstract
Function Secret Sharing (FSS) and Homomorphic Secret Sharing (HSS) are two extensions of standard secret sharing, which support rich forms of homomorphism on secret shared values.
-
An m-party FSS scheme for a given function family \({\mathcal {F}}\) enables splitting a function \(f: \{0,1\}^n \rightarrow \mathbb {G}\) from \({\mathcal {F}}\) (for Abelian group \(\mathbb {G}\)) into m succinctly described functions \(f_1,\dots ,f_m\) such that strict subsets of the \(f_i\) hide f, and \(f(x) = f_1(x) + \cdots + f_m(x)\) for every input x.
-
An m-party HSS is a dual notion, where an input x is split into shares \(x^1,\dots ,x^m\), such that strict subsets of \(x^i\) hide x, and one can recover the evaluation P(x) of a program P on x given homomorphically evaluated share values \(\mathsf{Eval}(x^1,P),\dots ,\mathsf{Eval}(x^m,P)\).
In the last few years, many new constructions and applications of FSS and HSS have been discovered, yielding implications ranging from efficient private database manipulation and secure computation protocols, to worst-case to average-case reductions.
In this treatise, we introduce the reader to the background required to understand these developments, and give a roadmap of recent advances (up to October 2017).
Supported in part by ISF grant 1861/16, AFOSR Award FA9550-17-1-0069, and ERC Grant no. 307952.
Access provided by CONRICYT-eBooks. Download conference paper PDF
Similar content being viewed by others
Keywords
- Secret Sharing Homomorphisms (HSS)
- Evaluation Homomorphism
- Average-case Reductions
- Secure Computation
- Non-interactive Key Exchange (NIKE)
These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.
1 Introduction
A secret sharing scheme [38] enables a dealer holding a secret s to randomly split s into m shares, such that certain subsets of the shares can be used to reconstruct the secret and others reveal nothing about it. The simplest type of secret sharing is additive secret sharing, where the secret is an element of an Abelian group \(\mathbb {G}\), it can be reconstructed by adding all m shares, and every subset of \(m-1\) shares reveals nothing about the secret. A useful feature of this secret sharing scheme is that it is (linearly) homomorphic, in the sense that if m parties hold shares of many secrets, they can locally compute shares of the sum of all secrets. This feature of additive secret sharing (more generally, linear secret sharing) is useful for many cryptographic applications.
A line of recent works [6,7,8,9,10,11, 28] has investigated secret sharing schemes which support richer classes of homomorphism. In this survey, we present recent developments in the following (closely related) natural extensions of additive secret sharing:
-
Function Secret Sharing (FSS) [6]. Suppose we are given a class \(\mathcal F\) of efficiently computable and succinctly described functions \(f:\{0,1\}^n\rightarrow \mathbb {G}\). Is it possible to split an arbitrary function \(f\in \mathcal F\) into m functions \(f_1,\ldots ,f_m\) such that: (1) each \(f_i\) is described by a short key \(k_i\) that enables its efficient evaluation, (2) strict subsets of the keys completely hide f, and (3) \(f(x)=\sum _{i=1}^m f_i(x)\) (on every input x)? We refer to a solution to this problem as a function secret sharing (FSS) scheme for \(\mathcal F\).
-
Homomorphic Secret Sharing (HSS) [8]. A (m-party) HSS scheme for class of programsFootnote 1 \(\mathcal {P}\) randomly splits an input x into sharesFootnote 2 \((x^1,\dots ,x^m)\) such that: (1) each \(x^i\) is polynomially larger than x, (2) subsets of shares \(x^i\) hide x, and (3) there exists a polynomial-time local evaluation algorithm \(\mathsf{Eval}\) such that for any “program” \(P \in \mathcal {P}\) (e.g., a boolean circuit, formula or branching program), the output P(x) can be efficiently reconstructed from \(\mathsf{Eval}(x^1,P),\dots ,\mathsf{Eval}(x^m,P)\).
FSS can be thought of as a dual notion of HSS, where the roles of the function and input are reversed: FSS considers the goal of secret sharing a function f (represented by a program) in a way that enables compact evaluation on any given input x via local computation on the shares of f, and HSS considers the goal of secret sharing an input x in a way that enables compact evaluation of any given function f via local computation on the shares of x.
While any FSS scheme can be viewed as an HSS scheme for a suitable class of programs and vice versa, the notions of “FSS for \(\mathcal {P}\)” and “HSS for \(\mathcal {P}\)” for a given program class \(\mathcal {P}\) are not identical, in that FSS allows the share size to grow with the size of the programs \(P \in \mathcal {P}\), whereas HSS restricts share size to grow with the size of the input to P.
In addition, HSS admits a natural multi-input variant (where secrets originating from different parties can be homomorphically evaluated on together), whereas in FSS the secret function always originates from a single source.
In different applications and examples, FSS or HSS perspective is more natural.
Computational security. Unlike secret sharing with basic linear homomorphism, it can be shown that most nontrivial FSS and HSS cannot provide information theoretic hiding [6, 11, 28]. For example, even for simple classes \({\mathcal {F}}\) (such as the class of point functions), the best possible solution is to additively share the truth-table representation of f, whose shares consist of \(2^n\) group elements. But if one considers a computational notion of hiding, then there are no apparent limitations to what can be done for polynomial-time computable f. This is what we refer to when we speak of FSS/HSS.
Homomorphic secret sharing vs. fully homomorphic encryption. HSS can be viewed as a relaxed version of fully homomorphic encryption (FHE) [26, 37], where instead of a single party homomorphically evaluating on encrypted data, we allow homomorphic evaluation to be distributed among two parties who do not interact with each other. As in the case of FHE, we require that the output of \(\mathsf{Eval}\) be compact in the sense that its length depends only on the output length |P(x)| but not on the size of P. But in fact, a unique feature of HSS that distinguishes it from traditional FHE is that the output representation can be additive. E.g., we can achieve \(\mathsf{Eval}(x^0,P)+\mathsf{Eval}(x^1,P)=P(x)\ {\mathrm {mod}}\, \beta \) for some positive integer \(\beta \ge 2\) that can be chosen arbitrarily. This enables an ultimate level of compactness and efficiency of reconstruction that is impossible to achieve via standard FHE. For instance, if P outputs a single bit and \(\beta =2\), then the output P(x) is reconstructed by taking the exclusive-or of two bits.
Other related notions. We note that other forms of secret sharing of functions and homomorphic secret sharing have been considered in the literature. An initial study of secret sharing homomorphisms is due to Benaloh [4], who presented constructions and applications of additively homomorphic secret sharing schemes. Further exploration of computing on secret shared data took place in [1]. Secret sharing of functions has appeared in the context of threshold cryptography (cf. [19, 20]). However, these other notions either apply only to very specific function classes that enjoy homomorphism properties compatible with the secret sharing, or alternatively they do not require a simple (e.g., additive) representation of the output which is essential for the applications we consider.
1.1 This Survey
The aim of this document is to serve as a centralized resource for FSS and HSS, providing sufficient background to approach existing papers, and appropriate references of where to look for further details. In what follows, we present:
-
Formal definitions. This includes a discussion on different choices of reconstruction procedures (and why we focus on linear reconstruction), an application-targeted definition of FSS, and a broader theory-oriented definition of HSS.
-
Constructions. A guide to existing constructions within the literature, and an overview of two specific constructions: FSS for point functions from one-way functions [9], and HSS for branching programs (with 1/poly error) from the Decisional Diffie-Hellman assumption [8].
-
Applications. Discussion on implications and applications of FSS and HSS and appropriate pointers.
Low-end vs. high-end. A recurring theme throughout the survey is that constructions and applications fall predominantly into two categories:
-
“Low-end” lightweight constructions for simple function classes.
-
“High-end” powerful constructions for broad function classes.
The former refers to constructions from symmetric-key primitives (in particular, one-way functions), sits closer to current practical applications, and is most frequently associated with the FSS formulation. The latter includes constructions from public-key primitives, yields powerful feasibility implications, and is most frequently associated with the HSS formulation. We will present results from this perspective.
2 Definitions
At their core, FSS/HSS are secret sharing schemes, and as such demand two central properties: (1) Correctness, dictating the appropriate homomorphic evaluation guarantees, and (2) Privacy, requiring that subsets of shares do not reveal the original secret.
When defining FSS/HSS, there are a handful of different choices to be made that result in slightly shifted notions of varying generality. We choose two such definitions to present:
-
1.
FSS targeted definition, most directly in line with practical applications.
-
2.
HSS general definition, which can be instantiated to capture different notions from the literature, including those of theoretical works such as [8, 10, 11] as well as the FSS definition from above.
Before jumping to these definitions, we begin with some basic notation and a discussion on different choices of output decoding structure.
2.1 Basic Notation
We denote the security parameter by \(\lambda \).
Modeling function families. A function family is defined by a pair \({\mathcal {F}}=(P_{\mathcal {F}},E_{\mathcal {F}})\), where \(P_{\mathcal {F}}\subseteq \{0,1\}^*\) is an infinite collection of function descriptions \({\hat{f}}\), and \(E_{\mathcal {F}}:P_{\mathcal {F}}\times \{0,1\}^*\rightarrow \{0,1\}^*\) is a polynomial-time algorithm defining the function described by \({\hat{f}}\). Concretely, each \({\hat{f}}\in P_{\mathcal {F}}\) describes a corresponding function \(f:D_f\rightarrow R_f\) defined by \(f(x)=E_{\mathcal {F}}({\hat{f}},x)\). We assume by default that \(D_f=\{0,1\}^n\) for a positive integer n (though will sometimes consider inputs over non-binary alphabets) and always require \(R_f\) to be a finite Abelian group, denoted by \(\mathbb {G}\). When there is no risk of confusion, we will sometimes write f instead of \({\hat{f}}\) and \(f\in {\mathcal {F}}\) instead of \({\hat{f}}\in P_{\mathcal {F}}\). We assume that \({\hat{f}}\) includes an explicit description of both \(D_f\) and \(R_f\) as well as a size parameter \(S_{{\hat{f}}}\).
2.2 Discussion on Output Decoding Structure
One can consider FSS/HSS with respect to many choices of output decoding structure: that is, the procedure used to combine homomorphically evaluated shares into the desired output. Based on the structure of the chosen decoding process, the corresponding scheme will have very different properties: more complex decoding procedures open the possibility of achieving FSS/HSS for more general classes of functions, but place limits on the applicability of the resulting scheme. Many choices for the structure of the output decoding function yield uninteresting notions, as we now discuss (following [6]). For convenience, we adopt the language of FSS.
Arbitrary reconstruction. Consider, for example, FSS with no restriction on the reconstruction procedure for parties’ output shares. Such wide freedom renders the notion non-meaningfully trivial. Indeed, for any efficient function family \({\mathcal {F}}\), one could generate FSS keys for a secret function \(f \in {\mathcal {F}}\) simply by sharing a description of f interpreted as a string, using a standard secret sharing scheme. The evaluation procedure on any input x will simply output x together with the party’s share of f, and the decoding procedure will first reconstruct the description of f, and then compute and output the value f(x).
This construction satisfies correctness and security as described informally above (indeed, each party’s key individually reveals no information on f). But, the scheme clearly leaves much to be desired in terms of utility: From just one evaluation, the entire function f is revealed to whichever party receives and reconstructs these output shares. At such point, the whole notion of function secret sharing becomes moot.
“Function-private” output shares. Instead, from a function secret sharing scheme, one would hope that parties’ output shares \(f_i(x)\) for input x do not reveal more about the secret function f than is necessary to determine f(x). That is, we may impose a “function privacy” requirement on the reconstruction scheme, requiring that pairs of parties’ output shares for each input x can be simulated given just the corresponding outputs f(x).
This requirement is both natural and beneficial, but by itself still allows for undesired constructions. For example, given a secret function f, take one FSS key to be a garbled circuit of f, and the second key as the information that enables translating inputs x to garbled input labels. This provides a straightforward function-private solution for one output evaluation, and can easily be extended to the many-output case by adding shared secret randomness to the parties’ keys.Footnote 3 Yet this construction (and thus definition) is unsatisfying: although the evaluate output shares \(f_i(x)\) now hide f, their size is massive—for every output, comparable to a copy of f itself. (Further, this notion does not give any cryptographic power beyond garbled circuits.)
Succinct, function-private output shares. We thus further restrict the scheme, demanding additionally that output shares be succinct: i.e., comparable in size to the function output.
This definition already captures a strong, interesting primitive. For example, as described in Sect. 4, achieving such an FSS scheme for general functions implies a form of communication-efficient secure multi-party computation. Additional lower bounds on this notion are shown in [11]. However, there is one final property that enables an important class of applications, but which is not yet guaranteed: a notion of share compressibility.
More specifically: One of the central application regimes of FSS [6, 9, 28] is enabling communication-efficient secure (m-server) Private Information Retrieval (PIR). Intuitively, to privately recover an item \(x_i\) from a database held by both servers, one can generate and distribute a pair of FSS keys encoding a point function \(f_i\) whose only nonzero output is at secret location i. Each server then responds with a single element, computed as the weighted sum of each data item \(x_j\) with the server’s output share of the evaluation \(f_i(x_j)\). Correctness of the DPF scheme implies that the xor of the two servers’ replies is precisely the desired data item \(x_i\), while security guarantees the servers learn nothing about the index i. But most importantly, the linear structure of the DPF reconstruction enabled the output shares pertaining to all the different elements of the database to be compressed into a single short response.
On the other hand, consider, for example, the PIR scenario but where the servers instead hold shares of the function \(f_i\) with respect to a bitwise AND reconstruction of output shares in the place of xor/addition. Recovery of the requested data item \(x_i\) now implies computing set intersection—and thus requires communication complexity equal to the size of the database [34]! We thus maintain the crucial property that output shares can be combined and compressed in a meaningful way. To do so, we remain in stride with the linearity of output share decoding.
Primary focus: linear share decoding. We focus predominantly on the setting of FSS where the output decoder is a linear function of parties’ shares. That is, we assume the output shares \(f_i(x)\) lie within an Abelian group \(\mathbb {G}\) and consider a decoding function \(\mathsf{Dec}: \mathbb {G}^m \rightarrow \mathbb {G}\) linear in \(\mathbb {G}\). This clean, intuitive structure in fact provides the desired properties discussed above: Linearity of reconstruction provides convenient share compressibility. Output shares must themselves be elements of the function output space, immediately guaranteeing share succinctness. And as shown in [6], the linear reconstruction in conjunction with basic key security directly implies function privacy. Unless otherwise specified we will implicitly take an “FSS scheme” (or HSS) to be one with a linear reconstruction procedure.
2.3 Function Secret Sharing: Targeting Applications
We next present a targeted definition of FSS, which lies most in line with the use of FSS within current practical applications. The definition follows [9], extending the original definition from [6] by allowing a general specification of allowable leakage: i.e., partial information about the function that can be revealed.
Recall in the language of FSS, we consider a client holding a secret function \(f \in {\mathcal {F}}\) who splits f into shares \(f_i\) supporting homomorphic evaluation on inputs x in the domain of f. We use notation of the shares \(f_i\) described by keys \(k_i\).
Modeling leakage. We capture the allowable leakage by a function \(\mathsf{Leak}:\{0,1\}^*\rightarrow \{0,1\}^*\), where \(\mathsf{Leak}(f)\) is interpreted as the partial information about f that can be leaked. When \(\mathsf{Leak}\) is omitted it is understood to output the input domain \(D_f\) and the output domain \(R_f\). This will be sufficient for most classes considered; for some classes, one also needs to leak the size \(S_{f}\). But, one can consider more general choices of \(\mathsf{Leak}\), which allow a tradeoff between efficiency/feasibility and revealed information. (E.g., the construction of FSS for decision trees in [9] leaks the topology of the tree but hides the labels; see Sect. 3.)
Definition 1 (FSS: Syntax)
An m-party function secret sharing (FSS) scheme is a pair of algorithms \((\mathsf{Gen},\mathsf{Eval})\) with the following syntax:
-
\(\mathsf{Gen}(1^\lambda , \hat{f})\) is a PPT key generation algorithm, which on input \(1^\lambda \) (security parameter) and \(\hat{f} \in \{0,1\}^*\) (description of a function f) outputs an m-tuple of keys \((k_1,\ldots ,k_m)\). We assume that \({\hat{f}}\) explicitly contains an input length \(1^n\), group description \(\mathbb {G}\), and size parameter.
-
\(\mathsf{Eval}(i, k_i, x)\) is a polynomial-time evaluation algorithm, which on input \(i\in [m]\) (party index), \(k_i\) (key defining \(f_i:\{0,1\}^n\rightarrow \mathbb {G}\)) and \(x \in \{0,1\}^n\) (input for \(f_i\)) outputs a group element \(y_i \in \mathbb {G}\) (the value of \(f_i(x)\), the i-th share of f(x)).
When m is omitted, it is understood to be 2.
Definition 2 (FSS: Requirements)
Let \({\mathcal {F}}=(P_{\mathcal {F}},E_{\mathcal {F}})\) be a function family and \(\mathsf{Leak}:\{0,1\}^*\rightarrow \{0,1\}^*\) be a function specifying the allowable leakage. Let m (number of parties) and t (secrecy threshold) be positive integers. An m-party t-secure FSS for \({\mathcal {F}}\) with leakage \(\mathsf{Leak}\) is a pair \((\mathsf{Gen},\mathsf{Eval})\) as in Definition 1, satisfying the following requirements.
-
Correctness: For all \({\hat{f}}\in P_{\mathcal {F}}\) describing \(f:\{0,1\}^n\rightarrow \mathbb {G}\), and every \(x \in \{0,1\}^n\), if \((k_1,\ldots ,k_m) \leftarrow \mathsf{Gen}(1^\lambda ,{\hat{f}})\) then \(\Pr \left[ \sum _{i=1}^m \mathsf{Eval}(i,k_i,x) = f(x) \right] = 1\).
-
Secrecy: For every set of corrupted parties \(S \subset [m]\) of size t, there exists a PPT algorithm \(\mathsf{Sim}\) (simulator), such that for every sequence \({\hat{f}}_1,{\hat{f}}_2,\ldots \) of polynomial-size function descriptions from \(P_{\mathcal {F}}\), the outputs of the following experiments \(\mathsf{Real}\) and \(\mathsf{Ideal}\) are computationally indistinguishable:
-
\(\mathsf{Real}(1^\lambda )\): \((k_1,\ldots ,k_m) \leftarrow \mathsf{Gen}(1^\lambda , {\hat{f}}_\lambda )\); Output \((k_i)_{i \in S}\).
-
\(\mathsf{Ideal}(1^\lambda )\): Output \(\mathsf{Sim}(1^\lambda , \mathsf{Leak}({\hat{f}}_\lambda ))\).
-
When \(\mathsf{Leak}\) is omitted, it is understood to be the function \(\mathsf{Leak}({\hat{f}})=(1^n,S_{{\hat{f}}},\mathbb {G})\) where \(1^n\), \(S_{{\hat{f}}}\), and \(\mathbb {G}\) are the input length, size, and group description contained in \({\hat{f}}\). When t is omitted it is understood to be \(m-1\).
A useful instance of FSS, introduced by Gilboa and Ishai [28], is a distributed point function (DPF). A DPF can be viewed as a 2-party FSS for the function class \(\mathcal F\) consisting of all point functions, namely all functions \(f:\{0,1\}^n\rightarrow \mathbb {G}\) that evaluate to 0 on all but at most one input.
Definition 3 (Distributed Point Function)
A point function \(f_{\alpha ,\beta }\), for \(\alpha \in \{0,1\}^{n}\) and \(\beta \in \mathbb {G}\), is defined to be the function \(f:\{0,1\}^n\rightarrow \mathbb {G}\) such that \(f(\alpha )=\beta \) and \(f(x)=0\) for \(x\ne \alpha \). We will sometimes refer to a point function with \(|\beta |=1\) (resp., \(|\beta |>1\)) as a single-bit (resp., multi-bit) point function. A Distributed Point Function (DPF) is an FSS for the family of all point functions, with the leakage \(\mathsf{Leak}({\hat{f}})=(1^n,\mathbb {G})\).
A concrete security variant. For the purpose of describing and analyzing some FSS constructions, it is sometimes convenient (e.g., in [9]) to consider a finite family \({\mathcal {F}}\) of functions \(f:D_f\rightarrow R_f\) sharing the same (fixed) input domain and output domain, as well as a fixed value of the security parameter \(\lambda \). We say that such a finite FSS scheme is \((T,\epsilon )\) -secure if the computational indistinguishability requirement in Definition 2 is replaced by \((T,\epsilon )\)-indistinguishability, namely any size-T circuit has at most an \(\epsilon \) advantage in distinguishing between \(\mathsf{Real}\) and \(\mathsf{Ideal}\). When considering an infinite collection of such finite \({\mathcal {F}}\), parameterized by the input length n and security parameter \(\lambda \), we require that \(\mathsf{Eval}\) and \(\mathsf{Sim}\) be each implemented by a (uniform) PPT algorithm, which is given \(1^n\) and \(1^\lambda \) as inputs.
2.4 Homomorphic Secret Sharing: A General Definition
Recall that HSS is a dual form of FSS. We now consider more general multi-input HSS schemes that support a compact evaluation of a function F on shares of inputs \(x_1,\ldots ,x_n\) that originate from different clients. More concretely, each client i randomly splits its input \(x_i\) between m servers using the algorithm \(\mathsf{Share}\), so that \(x_i\) is hidden from any t colluding servers (we assume \(t=m\,-\,1\) by default). Each server j applies a local evaluation algorithm \(\mathsf{Eval}\) to its share of the n inputs, and obtains an output share \(y^j\). The output \(F(x_1,\ldots ,x_n)\) is reconstructed by applying a decoding algorithm \(\mathsf{Dec}\) to the output shares \((y^1,\ldots ,y^m)\). To avoid triviality, we consider various restrictions on \(\mathsf{Dec}\) that force it to be “simpler” than direct computation of F.
Finally, for some applications it is useful to let F and \(\mathsf{Eval}\) take an additional input \(x_0\) that is known to all servers. This is necessary for a meaningful notion of single-input HSS (with \(n=1\)) [8], and function secret sharing [6, 9]. Typically, the extra input \(x_0\) will be a description of a function f applied to the input of a single client, e.g., a description of a circuit, branching program, or low-degree polynomial. For the case of FSS, the (single) client’s input is a description of a program and the additional input \(x_0\) corresponds to a domain element.
We now give our formal definition of general HSS. We give a definition in the plain model; this definition can be extended in a natural fashion to settings with various forms of setup (e.g., common public randomness or a public-key infrastructure, as considered in [10]). We follow the exposition of [11]. Recall subscripts denote input (client) id and superscripts denote share (server) id.
Definition 4 (HSS)
An n-client, m-server, t-secure homomorphic secret sharing scheme for a function \(F: (\{0,1\}^*)^{n+1} \rightarrow \{0,1\}^*\), or (n, m, t)-HSS for short, is a triple of PPT algorithms \((\mathsf{Share},\mathsf{Eval},\mathsf{Dec})\) with the following syntax:
-
\(\mathsf{Share}(1^\lambda , i, x)\): On input \(1^\lambda \) (security parameter), \(i \in [n]\) (client index), and \(x \in \{0,1\}^*\) (client input), the sharing algorithm \(\mathsf{Share}\) outputs m input shares, \((x^1,\ldots ,x^m)\).
-
\(\mathsf{Eval}\big (j, x_0, (x_1^j,\dots ,x_n^j)\big )\): On input \(j \in [m]\) (server index), \(x_0\in \{0,1\}^*\) (common server input), and \(x_1^j,\dots ,x_n^j\) (jth share of each client input), the evaluation algorithm \(\mathsf{Eval}\) outputs \(y^j\in \{0,1\}^*\), corresponding to server j’s share of \(F(x_0;x_1,\dots ,x_n)\).
-
\(\mathsf{Dec}(y^1,\dots ,y^m)\): On input \((y^1,\dots ,y^m)\) (list of output shares), the decoding algorithm \(\mathsf{Dec}\) computes a final output \(y\in \{0,1\}^*\).
The algorithms \((\mathsf{Share},\mathsf{Eval},\mathsf{Dec})\) should satisfy the following correctness and security requirements:
-
Correctness: For any \(n+1\) inputs \(x_0,\dots , x_n \in \{0,1\}^*\),
$$ \Pr \left[ \begin{array}{c} \forall i \in [n]~ (x_i^1,\ldots ,x_i^m) \leftarrow \mathsf{Share}(1^\lambda ,i,x_i) \\ \forall j \in [m]~ y^j \leftarrow \mathsf{Eval}\big (j, x_0, (x_1^j,\dots ,x_n^j)\big ) \end{array} : \mathsf{Dec}(y^1,\dots ,y^m) = F(x_0;x_1,\dots ,x_n) \right] = 1. $$Alternatively, in a statistically correct HSS the above probability is at least \(1-\mu (\lambda )\) for some negligible \(\mu \) and in a \(\delta \)-correct HSS (or \(\delta \)-HSS for short) it is at least \(1-\delta -\mu (\lambda )\), where the error parameter \(\delta \) is given as an additional input to \(\mathsf{Eval}\) and the running time of \(\mathsf{Eval}\) is allowed to grow polynomially with \(1/\delta \).
-
Security: Consider the following semantic security challenge experiment for corrupted set of servers \(T \subset [m]\):

Denote by \(\mathsf{Adv}(1^\lambda , \mathcal {A}, T) := \Pr [b = b'] - 1/2\) the advantage of \(\mathcal {A}\) in guessing b in the above experiment, where probability is taken over the randomness of the challenger and of \(\mathcal {A}\).
For circuit size bound \(S=S(\lambda )\) and advantage bound \(\alpha =\alpha (\lambda )\), we say that an (n, m, t)-HSS scheme \(\varPi =(\mathsf{Share},\mathsf{Eval},\mathsf{Dec})\) is \((S,\alpha )\)-secure if for all \(T \subset [m]\) of size \(|T| \le t\), and all non-uniform adversaries \(\mathcal {A}\) of size \(S(\lambda )\), we have \(\mathsf{Adv}(1^\lambda ,\mathcal {A},T) \le \alpha (\lambda )\). We say that \(\varPi \) is:
-
computationally secure if it is (S, 1 / S)-secure for all polynomials S;
-
statistically \(\alpha \)-secure if it is \((S,\alpha )\)-secure for all S;
-
statistically secure if it statistically \(\alpha \)-secure for some negligible \(\alpha (\lambda )\);
-
perfectly secure if it is statistically 0-secure.
-
Remark 1 (Unbounded HSS)
Definition 4 treats the number of inputs n as being fixed. We can naturally consider an unbounded multi-input variant of HSS where F is defined over arbitrary sequences of inputs \(x_i\), and the correctness requirement is extended accordingly. We denote this flavor of multi-input HSS by \((*,m,t)\)-HSS. More generally, one can allow all three parameters n, m, t to be flexible, treating them as inputs of the three algorithms \(\mathsf{Share},\mathsf{Eval},\mathsf{Dec}\).
Remark 2 (Comparing to FSS Definition)
Function secret sharing (FSS) as per Definition 2 can be cast in the definition above as (1, m)-HSS for the universal function \(F(x;P)=P(x)\), where \(P\in \mathcal P\) is a program given as input to the client and x is the common server input.
Note the security requirement for HSS in Definition 4 is expressed as an indistinguishability guarantee, whereas the FSS definition from the previous section (Definition 2) referred instead to efficient simulation given leakage on the secret data. However, the two flavors are equivalent for every function family \({\mathcal {F}}\) and leakage function \(\mathsf{Leak}\) for which \(\mathsf{Leak}\) can be efficiently inverted; that is, given \(\mathsf{Leak}({\hat{f}})\) one can efficiently find \({\hat{f}}'\) such that \(\mathsf{Leak}({\hat{f}}')=\mathsf{Leak}({\hat{f}})\). Such an inversion algorithm exists for all instances of \({\mathcal {F}}\) and \(\mathsf{Leak}\) considered in existing works.
As discussed, Definition 4 can be trivially realized by \(\mathsf{Eval}\) that computes the identity function. To make HSS useful, we impose two types of requirements on the decoding algorithm.
Definition 5 (Additive and compact HSS)
We say that an (n, m, t)-HSS scheme \(\varPi =(\mathsf{Share},\mathsf{Eval}, \mathsf{Dec})\) is:
-
Additive if \(\mathsf{Dec}\) outputs the exclusive-or of the m output shares. Alternatively, if \(\mathsf{Dec}\) interprets its m arguments as elements of an Abelian group \(\mathbb {G}\) (instead of bit strings), and outputs their sum in \(\mathbb {G}\).Footnote 4
-
Compact if the length of the output shares is sublinear in the input length when the inputs are sufficiently longer than the security parameter. Concretely:
-
We say that \(\varPi \) is \(g(\lambda ,\ell )\)-compact if for every \(\lambda ,\ell \), and inputs \(x_0,x_1,\ldots ,x_n\in \{0,1\}^\ell \), the length of each output share obtained by applying \(\mathsf{Share}\) with security parameter \(\lambda \) and then \(\mathsf{Eval}\) is at most \(g(\lambda ,\ell )\).
-
We say that \(\varPi \) is compact if it is \(g(\lambda ,\ell )\)-compact for g that satisfies the following requirement: There exists a polynomial \(p(\cdot )\) and sublinear function \(g'(\ell )=o(\ell )\) such that for any \(\lambda \) and \(\ell \ge p(\lambda )\) we have \(g(\lambda ,\ell )\le g'(\ell )\).
In the case of perfect security or statistical \(\alpha \)-security with constant \(\alpha \), we eliminate the parameter \(\lambda \) and refer to \(\varPi \) as being \(g(\ell )\)-compact.
-
Remark 3 (Other notions of compactness)
One could alternatively consider a stronger notion of compactness, requiring that the length of each output share is of the order of the output length (whereas Definition 5 requires merely for it to be sublinear in the input size). Every additive HSS scheme satisfies this notion. HSS schemes that satisfy this notion but are not additive were used in the context of private information retrieval and locally decodable codes in [2]. A different way of strengthening the compactness requirement is by restricting the computational complexity of \(\mathsf{Dec}\), e.g., by requiring it to be quasi-linear in the length of the output. See Sect. 4.1 (worst-case to average-case reductions) for motiving applications.
Remark 4 (Special HSS Cases)
-
We will sometimes be interested in additive HSS for a finite function F, such as the AND of two bits; this can be cast into Definition 4 by just considering an extension \(\hat{F}\) of F that outputs 0 on all invalid inputs. (Note that our notion of compactness is not meaningful for a finite F.)
-
As noted above, the common server input \(x_0\) is often interpreted as a “program” P from a class of programs \(\mathcal P\) (e.g., circuits or branching programs), and F is the universal function defined by \(F(P;x_1,\ldots ,x_n)=P(x_1,\ldots ,x_n)\). We refer to this type of HSS as HSS for the class \(\mathcal P\).
3 Constructions of FSS and HSS
FSS/HSS constructions as of the writing of this survey (October 2017) are as follows. Given complexity measures are with respect to n-bit inputs.
“Low End”: FSS from One-Way Functions
Here \(\lambda \) corresponds to a pseudorandom generator seed length, taken to be 128 bits in an AES-based implementation. Unless otherwise specified, for \(m=2\) servers.
-
Point functions (“Distributed Point Functions”).
The class of point functions consists of those functions \(f_{\alpha ,\beta }\) which evaluate to \(\beta \) on input \(\alpha \) and to 0 otherwise.
-
Implicitly constructed in [15] with key size \(O(2^{\epsilon n})\) bits for constant \(\epsilon > 0\). Formally defined and constructed recursively with key size \(O(n^{\log _2(3)} \lambda )\) bits, in [28]. Improved to \(O(n \lambda )\) bits via tree-based solution in [6].
-
Current best: Key size \(\lambda + n(\lambda +2) - \lfloor \log \lambda / |\beta | \rfloor \) bits, in [9].Footnote 5
For \(m>2\) servers: nontrivial (but poor) key size \(O(2^m 2^{n/2} \lambda )\) bits, in [6].
-
-
Comparison and Intervals [6, 9].
The class of comparison functions consists of those functions \(f_a\) which output 1 on inputs x with \(a < x\). Interval functions \(f_{(a,b)}\) output 1 precisely for inputs x that lie within the interval \(a< x < b\), and 0 otherwise.
Constructions follow a similar structure as DPFs. Best key size for comparison functions \(n(\lambda +3)\) bits, for interval functions \(2n(\lambda +3)\) bits [9].
-
\(NC^0\) predicates (i.e., functions with constant locality) [6].
For locality d, the key size grows as \(O(\lambda \cdot n^d)\). For example, this includes bit-matching predicates that check a constant number of bits d.
-
Decision trees [9].
A decision tree is defined by: (1) a tree topology, (2) variable labels on each node v (where the set of possible values of each variable is known), (3) value labels on each edge (the possible values of the originating variable), and (4) output labels on each leaf node.
In the construction of [9], the key size is roughly \(\lambda \cdot |V|\) bits, where V is the set of nodes, and evaluation on a given input requires |V| executions of a pseudorandom generator, and a comparable number of additions. The FSS is guaranteed to hide the secret edge value labels and leaf output labels, but (in order to achieve this efficiency) reveals the base tree topology and the identity of which variable is associated to each node.
Constant-dimensional intervals. A sample application of FSS for decision trees is constant d-dimensional interval queries: that is, functions \(f(x_1,\dots ,x_d)\) which evaluate to a selected nonzero value precisely when \(a_i \le x_i \le b_i\) for some secret interval ranges \((a_i,b_i)_{i \in [d]}\). For n-bit inputs \(x_i\), FSS for d-dimensional intervals can be obtained with key size and computation time \(O(\lambda \cdot n^d)\). For small values of d, such as \(d = 2\) for supporting a conjunction of intervals, this yields solutions with reasonably good concrete efficiency.
We observe that FSS constructions for the function classes above can be combined with server-side database operations, to emulate private database operations of richer function classes, such as Max/Min and top-k [40]. (See Sect. 4.2.)
“High End”: HSS from Public-Key Cryptography
-
Branching programs (capturing logspace, \({\mathsf{NC}^1}\)), for 2-servers, with inverse-polynomial \(\delta \)-correctness, from Decisional Diffie-Hellman (DDH) [8]. Evaluation runtime grows as \(1/\delta \).
Heavily optimized versions of this construction are given in [7, 10].
-
General circuits, from Learning With Errors (LWE) [6, 23].
More specifically, in the language of Definition 4: Additive (n, m)-HSS for arbitrary n, m and polynomial-size circuits can be obtained from the Learning With Errors (LWE) assumption, by a simple variation of the FSS construction from spooky encryption of [23] (more specifically, their techniques for obtaining 2-round MPC). See [11] for details.
(It was also previously shown how to achieve FSS for general circuits from subexponentially secure indistinguishability obfuscation in [6].)
Intuition of Constructions. In the following two subsections, we present high-level intuition behind two specific constructions: (1) the optimized OWF-based DPF of [9], and (2) the DDH-based \(\delta \)-HSS for branching programs of [8].
3.1 Overview: Distributed Point Function from OWF
We give an intuitive description of the (2-party) distributed point function (DPF) \((\mathsf{Gen}^\bullet ,\mathsf{Eval}^\bullet )\) construction from [9] (following the text therein). Recall a DPF is an FSS scheme for the class of point functions \(f_{\alpha ,\beta } : \{0,1\}^n \rightarrow \mathbb {G}\) whose only nonzero evaluation is \(f_{\alpha ,\beta }(\alpha ) = \beta \). For simplicity, consider the case of a DPF with a single-bit output \(\mathbb {G}=\{0,1\}\) and \(\beta =1\).
Basic key structure. At a high level, each of the two DPF keys \(k_0,k_1\) defines a GGM-style binary tree [29] with \(2^n\) leaves, where the leaves are labeled by inputs \(x\in \{0,1\}^n\). We will refer to a path from the root to a leaf labeled by x as the evaluation path of x, and to the evaluation path of the special input \(\alpha \) as the special evaluation path. Each node v in a tree will be labeled by a string of length \(\lambda +1\), consisting of a control bit t and a \(\lambda \)-bit seed s, where the label of each node is fully determined by the label of its parent. The function \(\mathsf{Eval}^\bullet \) will compute the labels of all nodes on the evaluation path to the input x, using the root label as the key, and output the control bit of the leaf.
Generating the keys. We would like to maintain the invariant that for each node outside the special path, the two labels (on the two trees) are identical, and for each node on the special path the two control bits are different and the two seeds are indistinguishable from being random and independent. Note that since the label of a node is determined by that of its parent, if this invariant is met for a node outside the special path then it is automatically maintained by its children. Also, we can easily meet the invariant for the root (which is always on the special path) by just explicitly including the labels in the keys. The challenge is to ensure that the invariant is maintained also when leaving the special path.
Towards describing the construction, it is convenient to view the two labels of a node as a mod-2 additive secret sharing of its label, consisting of shares \([t]=(t_0,t_1)\) of the control bit t and shares \([s]=(s_0,s_1)\) of the \(\lambda \)-bit seed s. That is, \(t=t_0\oplus t_1\) and \(s=s_0\oplus s_1\). The construction employs two simple ideas.
-
1.
In the 2-party case, additive secret sharing satisfies the following weak homomorphism: If G is a PRG, then \(G([s])=(G(s_0),G(s_1))\) extends shares of the 0-string \(s=0\) into shares of a longer 0-string \(S=0\), and shares of a random seed s into shares of a longer (pseudo-)random string S, where S is pseudo-random even given one share of s.
-
2.
Additive secret sharing is additively homomorphic: given shares [s], [t] of a string s and a bit t, and a public correction word CW, one can locally compute shares of \([s\oplus (t\cdot CW)]\). We view this as a conditional correction of the secret s by CW conditioned on \(t=1\).
To maintain the above invariant along the evaluation path, we use the two types of homomorphism as follows. Suppose that the labels of the i-th node \(v_i\) on the evaluation path are [s], [t]. To compute the labels of the \((i\,+\,1)\)-th node, the parties start by locally computing \([S]=G([s])\) for a PRG \(G:\{0,1\}^\lambda \rightarrow \{0,1\}^{2\lambda +2}\), parsing [S] as \([s^L, t^L, s^R, t^R]\). The first two values correspond to labels of the left child and the last two values correspond to labels of the right child.
To maintain the invariant, the keys will include a correction word CW for each level i. As discussed above, we only need to consider the case where \(v_i\) is on the special path. By the invariant we have \(t=1\), in which case the correction will be applied. Suppose without loss of generality that \(\alpha _i=1\). This means that the left child of \(v_i\) is off the special path whereas the right child is on the special path. To ensure that the invariant is maintained, we can include in both keys the correction \(CW^{(i)}=(s^L, t^L, s^R\oplus s', t^R\oplus 1)\) for a random seed \(s'\). Indeed, this ensures that after the correction is applied, the labels of the left and right child are [0], [0] and \([s'],[1]\) as required. But since we do not need to control the value of \(s'\), except for making it pseudo-random, we can instead use the correction \(CW^{(i)}=(s^L, t^L, s^L, t^R\oplus 1)\) that can be described using \(\lambda +2\) bits. This corresponds to \(s'=s^L\oplus s^R\). The n correction values \(CW^{(i)}\) are computed by \(\mathsf{Gen}^\bullet \) from the root labels by applying the above iterative computation along the special path, and are included in both keys.
Finally, assuming that \(\beta =1\), the output of \(\mathsf{Eval}^\bullet \) is just the shares [t] of the leaf corresponding to x. A different value of \(\beta \) (from an arbitrary Abelian group) can be handled via an additional correction \(CW^{(n+1)}\).
3.2 Overview: \(\delta \)-HSS for Branching Programs from DDH
We next give a simplified overview of the HSS construction from [8], following exposition from [7]. Cast into the framework of Definition 4, this yields an additive public-key \((*,2)\)-\(\delta \)-HSS for the class of branching programs under the DDH assumption.
For simplicity of notation (and for greater efficiency), we assume circular security of ElGamal encryption. This assumption can be replaced by standard DDH by replacing ElGamal encryption with the circular secure public-key encryption scheme of Boneh, Halevi, Hamburg, and Ostrovsky [5], as shown in [8].
RMS Programs
The construction of [8] supports homomorphic evaluation of straight-line programs of the following form over inputs \(w_i \in \mathbb {Z}\), provided that all intermediate computation values in \(\mathbb {Z}\) remain “small,” bounded by a parameter M (where the required runtime grows with this size bound).
Definition 6 (RMS programs)
The class of Restricted Multiplication Straight-line (RMS) programs consists of a magnitude bound \(1^M\) and an arbitrary sequence of the four following instructions, each with a unique identifier \(\mathsf{id}\):
-
Load an input into memory: \((\mathsf{id}, \hat{y}_j\leftarrow \hat{w}_i)\).
-
Add values in memory: \((\mathsf{id}, \hat{y}_k \leftarrow \hat{y}_i + \hat{y}_j)\).
-
Multiply value in memory by an input value: \((\mathsf{id}, \hat{y}_k \leftarrow \hat{w}_i \cdot \hat{y}_j)\).
-
Output value from memory, as element of \(\mathbb {Z}_\beta \): \((\mathsf{id},\beta , \hat{O}_j \leftarrow \hat{y}_i)\).
If at any step of execution the size of a memory value exceeds the bound M, the output of the program on the corresponding input is defined to be \(\bot \). We define the size of an RMS program P as the number of its instructions.
In particular, RMS programs allow only multiplication of a memory value with an input (not another memory value). RMS programs with \(M=2\) are powerful enough to efficiently simulate boolean formulas, logarithmic-depth boolean circuits, and deterministic branching programs (capturing logarithmic-space computations). For concrete efficiency purposes, their ability to perform arithmetic computations on larger inputs can also be useful.
Encoding \(\mathbb {Z}_q\) Elements. Let \(\mathbb {H}\) be a prime-order group, with a subgroup \(\mathbb {G}\) of prime order q (the DDH group). Let g denote a generator of \(\mathbb {G}\). For any \(x \in \mathbb {Z}_q\), consider the following 3 types of two-party encodings:
Level 1: “Encryption.” For \(x\in \mathbb {Z}_q\), we let \(\left[ {x} \right] \) denote \(g^x\), and  denote \((\left[ {r} \right] , \left[ {r\cdot c + x} \right] )\) for a uniformly random \(r \in \mathbb {Z}_q\), which corresponds to an ElGamal encryption of x with a secret key \(c\in \mathbb {Z}_q\). (With short-exponent ElGamal, c is a 160-bit integer.) We assume that c is represented in base B (\(B=2\) by default) as a sequence of s digits \((c_i)_{1\le i \le s}\) We let \({\left[ \left[ \left[ x \right] \right] \right] }_{c}\) denote
denote \((\left[ {r} \right] , \left[ {r\cdot c + x} \right] )\) for a uniformly random \(r \in \mathbb {Z}_q\), which corresponds to an ElGamal encryption of x with a secret key \(c\in \mathbb {Z}_q\). (With short-exponent ElGamal, c is a 160-bit integer.) We assume that c is represented in base B (\(B=2\) by default) as a sequence of s digits \((c_i)_{1\le i \le s}\) We let \({\left[ \left[ \left[ x \right] \right] \right] }_{c}\) denote  . All level-1 encodings are known to both parties.
. All level-1 encodings are known to both parties.
Level 2: “Additive shares.” Let \(\left\langle {x} \right\rangle \) denote a pair of shares \(x_0,x_1\in \mathbb {Z}_q\) such that \(x_0= x_1+x\), where each share is held by a different party. We let \(\langle \!\langle {x}\rangle \!\rangle _c\) denote \((\left\langle {x} \right\rangle , \left\langle {x\cdot c} \right\rangle ) \in (\mathbb {Z}_q^2)^2\), namely each party holds one share of \(\left\langle {x} \right\rangle \) and one share of \(\left\langle {x\cdot c} \right\rangle \). Note that both types of encodings are additively homomorphic over \(\mathbb {Z}_q\), namely given encodings of x and \(x'\) the parties can locally compute a valid encoding of \(x+x'\).
Level 3: “Multiplicative shares.” Let \(\left\{ {x}\right\} \) denote a pair of shares \(x_0,x_1\in \mathbb {G}\) such that the difference between their discrete logarithms is x. That is, \(x_0=x_1\cdot g^x\).
Operations on Encodings
We manipulate the above encodings via the following two types of operations, performed locally by the two parties:
-
1.
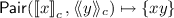 . This pairing operation exploits the fact that \(\left[ {a} \right] \) and \(\left\langle {b} \right\rangle \) can be locally converted to \(\left\{ {ab}\right\} \) via exponentiation.
. This pairing operation exploits the fact that \(\left[ {a} \right] \) and \(\left\langle {b} \right\rangle \) can be locally converted to \(\left\{ {ab}\right\} \) via exponentiation. -
2.
\(\mathsf {Convert} (\left\{ {z}\right\} , \delta ) \mapsto \left\langle {z} \right\rangle \), with failure bound \(\delta \). The implementation of \(\mathsf {Convert} \) is also given an upper bound M on the “payload” z (\(M=1\) by default), and its expected running time grows linearly with \(M/\delta \). We omit M from the following notation.
The \(\mathsf {Convert} \) algorithm works as follows. Each party, on input \(h\in \mathbb {G}\), outputs the minimal integer \(i\ge 0\) such that \(h\cdot g^i\) is “distinguished,” where roughly a \(\delta \)-fraction of the group elements are distinguished. Distinguished elements were picked in [8] by applying a pseudo-random function to the description of the group element. An optimized conversion procedure from [10] (using special “conversion-friendly” choices of \(\mathbb {G}\subset \mathbb {Z}^*_p\) and \(g=2\)) applies the heuristic of defining a group element to be distinguished if its bit-representation starts with \(d\approx \log _2 (M/\delta )\) leading 0’s; this was further optimized by considering instead the \((d\,+\,1)\)-bit string \(1||0^d\) in [7]. Note that this heuristic only affects the running time and not security, and thus it can be validated empirically. Correctness of \(\mathsf {Convert} \) holds if no group element between the two shares \(\{z\} \in \mathbb {G}^2\) is distinguished.
Finally, \(\mathsf {Convert} \) can signal that there is a potential failure if there is a distinguished point in the “danger zone.” Namely, Party \(b=0\) (resp., \(b=1\)) raises a potential error flag \(\bot \) if \(h\cdot g^{-i}\) (resp., \(h\cdot g^{i-1}\)) is distinguished for some \(i=1,\ldots ,M\).
Note that we used the notation M both for the payload upper bound in \(\mathsf {Convert}\) and for the bound on the memory values in the definition of RMS programs (Definition 6). In the default case of RMS program evaluation using base 2 for the secret key c in level 1 encodings, both values are indeed the same. (However, when using larger basis, they can differ in parts of the computation, and a more careful analysis can improve error bound guarantees.)
Let \(\mathsf {PairConv} \) be an algorithm that sequentially executes the two operations \(\mathsf {Pair} \) and \(\mathsf {Convert} \) above:  , with error \(\delta \). We denote by \(\mathsf {Mult} \) the following algorithm:
, with error \(\delta \). We denote by \(\mathsf {Mult} \) the following algorithm:
-
Functionality: \(\mathsf {Mult} ({\left[ \left[ \left[ x \right] \right] \right] }_{c}, \langle \!\langle {y}\rangle \!\rangle _c, \delta ) \mapsto \langle \!\langle {xy}\rangle \!\rangle _c\)
-
Parse \({\left[ \left[ \left[ x \right] \right] \right] }_{c}\) as
 .
. -
Let
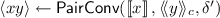 for \(\delta '=\delta /(s+1)\).
for \(\delta '=\delta /(s+1)\). -
For \(i=1\) to s, let
 .
. -
Let \(\left\langle {xy \cdot c} \right\rangle = \sum _{i=1}^s B^{i-1}\left\langle {xy\cdot c_i} \right\rangle \).
-
Return \((\left\langle {xy} \right\rangle , \left\langle {xy \cdot c} \right\rangle )\).
-
HSS for RMS Programs
Given the above operations, an additive \(\delta \)-HSS for RMS programs is obtained as follows. This can be cast as HSS in Definition 4 with a key generation setup.
-
Key generation: \(\mathsf{Gen}(1^\lambda )\) picks a group \(\mathbb {G}\) of order q with \(\lambda \) bits of security, generator g, and secret ElGamal key \(c\in \mathbb {Z}_q\). It output
 , where \(h = g^c\), and \((\mathsf{ek}_0,\mathsf{ek}_1)\leftarrow \left\langle {c} \right\rangle \), a random additive sharing of c.
, where \(h = g^c\), and \((\mathsf{ek}_0,\mathsf{ek}_1)\leftarrow \left\langle {c} \right\rangle \), a random additive sharing of c. -
Share: \(\mathsf{Share}(\mathsf{pk},x)\) uses the homomorphism of ElGamal to compute and output \({\left[ \left[ \left[ x \right] \right] \right] }_{c}\).
-
RMS program evaluation: For an RMS program P of multiplicative size S, the algorithm \(\mathsf{Eval}(b,\mathsf{ek}_b, (\mathsf{ct}_1,\ldots ,\mathsf{ct}_n), P,\) \(\delta , \beta )\) processes the instructions of P, sorted according to \(\mathsf{id}\), as follows. We describe the algorithm for both parties b jointly, maintaining the invariant that whenever a memory variable \(\hat{y}\) is assigned a value y, the parties hold level-2 shares \(Y=\langle \!\langle {y}\rangle \!\rangle _c\).
-
\(\hat{y}_j\leftarrow \hat{x}_i\): Let \(Y_j \leftarrow \mathsf {Mult} ({\left[ \left[ \left[ x_i \right] \right] \right] }_c,\langle \!\langle {1}\rangle \!\rangle _c, \delta /S)\), where \(\langle \!\langle {1}\rangle \!\rangle _c\) is locally computed from \((\mathsf{ek}_0,\mathsf{ek}_1)\) using \(\left\langle {1} \right\rangle =(1,0)\).
-
\(\hat{y}_k \leftarrow \hat{y}_i + \hat{y}_j\): Let \(Y_k \leftarrow Y_i + Y_j\).
-
\(\hat{y}_k \leftarrow \hat{x}_i \cdot \hat{y}_j\): Let \(Y_k \leftarrow \mathsf {Mult} ({\left[ \left[ \left[ x_i \right] \right] \right] }_c,Y_j, \delta /S)\).
-
\((\beta , \hat{O}_j \leftarrow \hat{y}_i)\): Parse \(Y_i\) as \((\left\langle {y_i} \right\rangle , \left\langle {y_i\cdot c} \right\rangle )\) and output \(O_j=\left\langle {y_i} \right\rangle +(r,r)\mod \beta \) for a fresh (pseudo-)random \(r\in \mathbb {Z}_q\).
The confidence flag is \(\bot \) if any of the invocations of \(\mathsf {Convert} \) raises a potential error flag, otherwise it is \({\top }\).
-
The pseudorandomness required for generating the outputs and for \(\mathsf {Convert} \) is obtained by using a common pseudorandom function key that is (implicitly) given as part of each \(\mathsf{ek}_b\), and using a unique nonce as an input to ensure that different invocations of \(\mathsf{Eval}\) are indistinguishable from being independent.
A single-input (“secret-key”) HSS variant is simpler in two ways. First, \(\mathsf{Share}\) can directly run \(\mathsf{Gen}\) and generate \({\left[ \left[ \left[ x \right] \right] \right] }_{c}\) from the secret key c. Second, an input loading instruction \(\hat{y}_j\leftarrow \hat{x}_i\) can be processed directly, without invoking \(\mathsf {Mult} \), by letting \(\mathsf{Share}\) compute \(Y_j \leftarrow \langle \!\langle {x_i}\rangle \!\rangle _c\) and distribute \(Y_j\) as shares to the two parties.
Performance. The cost of each RMS multiplication or input loading is dominated by \(s+1\) invocations of \(\mathsf {PairConv} \), where each invocation consists of \(\mathsf {Pair} \) and \(\mathsf {Convert} \). The cost of \(\mathsf {Pair} \) is dominated by one group exponentiation (with roughly 200-bit exponent in [7]). The basis of the exponent depends only on the key and the input, which allows for optimized fixed-basis exponentiations when the same input is involved in many RMS multiplications. When the RMS multiplications apply to 0/1 values (this is the case when evaluating branching programs), the cost of \(\mathsf {Convert} \) is linear in \(BS/\delta \), where the B factor comes from the fact that the payload z of \(\mathsf {Convert} \) is bounded by the size of the basis. When \(\delta \) is sufficiently small, the overall cost is dominated by the \(O(BS^2s/\delta )\) “conversion” steps, where each step consists of multiplying by g and testing whether the result is a distinguished group element.
4 Applications and Implications
In this section, we turn to implications of FSS and HSS constructions. We begin by describing what is known about the relation of FSS/HSS to other primitives, and then address applications of both “low-end” and “high-end” construction regimes.
4.1 Relation to Other Primitives
Below are the primary known theoretical implications of FSS/HSS primitives.
One-way functions. FSS for any “sufficiently rich” function class \({\mathcal {F}}\) (e.g., point functions) necessitates the existence of OWF [28]. Further, in such an FSS, each output share \(f_i\) viewed as a function on its own must define a pseudorandom function [6]. Note that this is not a-priori clear from the security definition, which only requires that the shares hide f.
(Amortized) Low-communication secure computation. It was shown in [6] that FSS for a function class \({\mathcal {F}}\) strictly containing the decryption circuit for a secure symmetric-key encryption scheme implies amortized low-communication protocols for secure two-party computation of a related function class, relying on a reusable source of correlated randomness (that can be realized via one-time offline preprocessing). Given HSS for \({\mathcal {F}}\), the same result holds without needing to amortize over the preprocessing.Footnote 6
At the time of this result, all known approaches for obtaining such protocols relied on fully homomorphic encryption or related primitives, and as such this was viewed as a “barrier” against achieving such FSS without FHE. In an interesting twist, this was reversed by the work of [8], which succeeded in constructing a form of HSS for \({\mathsf{NC}^1}\) (and thus succinct secure computation) from DDH.
However, the “barrier” still seems legitimate as evidence against the possibility of constructing general FSS/HSS (or even classes such as \({\mathsf{NC}^1}\) or possibly \(\mathsf {AC}^0\)) from weak cryptographic assumptions such as the existence of one-way functions or oblivious transfer.
Non-interactive key exchange (NIKE) & 2-message oblivious transfer (OT). The power of additive multi-input HSS (where inputs from different parties can be homomorphically computed on together; c.f. Definition 4) seems to be much greater than its single-input counterpart. Whereas constructions for single-input HSS exist for some function classes from OWF, to date all constructions of multi-input HSS rely on a select list of heavily structured assumptions: DDH, LWE, and obfuscation [8, 23].
It appears this is in some sense inherent: As shown in [11], even a minimal version of 2-party, 2-server additive HSS for the AND of two input bits implies the existence of non-interactive key exchange (NIKE) [21], a well-studied cryptographic notion whose known constructions are similarly limited to select structured assumptions. NIKE is black-box separated from one-way functions and highly unlikely to be implied by generic public-key encryption or oblivious transfer.
On the other hand, this same type of (2, 2)-additive-HSS for AND is unlikely to be implied by NIKE, as the primitive additionally implies the existence of 2-message oblivious transfer (OT) [8], unknown to follow from NIKE alone. Further connections from HSS to 2-round secure computation have been demonstrated in [10, 11].
Worst-case to average-case reductions. A different type of implication of HSS is in obtaining worst-case to average-case reductions in P. Roughly speaking, the HSS evaluation function \(\mathsf{Eval}\) for homomorphically evaluating a function F defines a new function \(F'\) such that computing F on any given input x can be reduced to computing \(F'\) on two or more inputs that are individually pseudorandom (corresponding to the HSS secret shares of x). A similar application was pointed out in [17] using fully homomorphic encryption (FHE) (and a significantly weaker version in [28] using DPF). Compared to the FHE-based reductions, the use of HSS has the advantages of making only a constant number of queries to a Boolean function \(F'\) (as small as 2), and minimizing the complexity of recovering the output from the answers to the queries. The latter can lead to efficiency advantages in the context of applications (including the settings of fine-grained average-case hardness and verifiable computation; see [11]). It also gives rise to worst-case to average-case reductions under assumptions that are not known to imply FHE, such as the DDH assumption.
4.2 Applications in the One-Way Function Regime
FSS in the “low-end” regime has interesting applications to efficient private manipulation of remotely held databases, extending the notions of Private Information Retrieval (PIR) [16] and Private Information Storage (PIS) [35] to more expressive instruction sets. Recently, FSS has also been shown to yield concrete efficiency improvements in secure 2-party computation protocols for programs with data-dependent memory accesses. We describe these in greater detail below.
Multi-server PIR and secure keyword search. Suppose that each of m servers holds a database D of keywords \(w_j\in \{0,1\}^n\). A client wants to count the number of occurrences of a given keyword w without revealing w to any strict subset of the servers. Letting \(\mathbb {G}=\mathbb Z_{m+1}\) and \(f=f_{w,1}\) (the point function evaluating to 1 on target value w), the client can split f into m additive shares and send to server i the key \(k_i\) describing \(f_i\). Server i computes and sends back to the client \(\sum _{w_j\in D} f_i(w_j)\). The client can then find the number of matches by adding the m group elements received from the servers. Standard PIR corresponds to the same framework with point function \(f_{i,1}\) for target data index i. In this application, FSS for other classes \(\mathcal F\) can be used to accommodate richer types of search queries, such as counting the number of keywords that lie in an interval, satisfy a fuzzy match criterion, etc. We note that by using standard randomized sketching techniques, one can obtain similar solutions that do not only count the number of matches but also return the payloads associated with a bounded number of matches (see, e.g., [36]).
Splinter [40]. In this fashion, FSS for point functions and intervals are the core of the system Splinter [40] of Wang et al., serving private search queries on a Yelp clone of restaurant reviews, airline ticket search, and map routing. On top of the functionalities offered directly by the FSS, the system supports more expressive queries, such as MAX/MIN and TOP-k, by manipulating the database on the server side such that a point function/interval search on the modified database answers the desired query. (Here the type of query is revealed, but the search parameters are hidden.) Splinter reports end-to-end latencies below 1.6 s for realistic workloads, including search within a Yelp-like database comparable to 40 cities, and routing within real traffic-map data for New York City.
Incremental secret sharing. Suppose that we want to collect statistics about web usage of mobile devices without compromising the privacy of individual users, and while allowing fast collection of real-time aggregate usage data. A natural solution is to maintain a large secret-shared array of group elements between m servers, where each entry in the array is initialized to 0 and is incremented whenever the corresponding web site is visited. A client who visits URL u can now secret-share the point function \(f=f_{u,1}\), and each server i updates its shared entry of each URL \(u_j\) by locally adding \(f_i(u_j)\) to this share. The end result is that only position \(u_j\) in the shared array is incremented, while no collusions involving strict subsets of servers learn which entry was incremented. Here too, applying general FSS can allow for more general “attribute-based” writing patterns, such as secretly incrementing all entries whose public attributes satisfy some secret predicate. The above incremental secret sharing primitive can be used to obtain low-communication solutions to the problem of private information storage [35], the “writing” analogue of PIR.
Riposte [18]. FSS for point functions on a \(2^{20}\)-entry database are used in this way in the anonymous broadcast system Riposte of Corrigan-Gibbs et al. [18]. Roughly, in the system each user splits his message \(\mathsf{msg}\) as a point function \(f_{r,\mathsf{msg}}\) for a random position index \(r \in [2^{20}]\). Shares of such functions across many users are combined additively by each server, and ultimately the aggregate is revealed. FSS security guarantees that the link from each individual user to his contributed message remains hidden.
Protecting against malicious clients. In some applications, malicious clients may have incentive to submit bogus FSS shares to the servers, corresponding to illegal manipulations of the database. This can have particularly adverse effects in writing applications, e.g., casting a “heavy” vote in a private poll, or destroying the current set of anonymous broadcast messages. Because of this, it is desirable to have efficient targeted protocols that enable a client to prove the validity of his request before it is implemented, via minimal interaction between the client and servers. Such protocols have been designed for certain forms of DPFs and related settings in [9, 18].
Secure 2-party computation (2PC) of RAM programs. A standard challenge in designing secure computation protocols is efficiently supporting data-dependent memory accesses, without leaking information on which items were accessed (and in turn on secret input values). Since the work of [35], this is typically addressed using techniques of Oblivious RAM (ORAM) [31] to transform a memory access to a secret index i from data size N into a sequence of \(\mathsf{polylog}(N)\) memory accesses whose indices appear independent of i. Indeed, a line of works in the past years have implemented and optimized systems for ORAM in secure computation.
Floram [39]. In a surprising recent development, Doerner and shelat [39] demonstrated an FSS-based 2PC system that—despite its inherent poor O(N) asymptotic computation per private access of each secret index i (instead of \(\mathsf{polylog}(N))\)—concretely outperforms current ORAM-based solutions.
In their construction, similar to use of ORAM in 2PC, the two parties in the secure computation act as the two servers in the FSS scheme, and an underlying (circuit-based) secure computation between the parties emulates the role of the client. The core savings of their approach is that, while overall computation is high, the emulation of “client” operations in the FSS requires a very small secure computation in comparison to prior ORAM designs (up to one hundred times smaller for the memory sizes they explore). Their implemented 2PC system Floram [39] (“FSS Linear ORAM”) outperforms the fastest previously known ORAM implementations, Circuit ORAM [41] and Square-root ORAM [43], for datasets that are 32 KiB or larger, and outperforms prior work on applications such as secure stable matching [24] or binary search [32] by factors of two to ten.
4.3 Applications in the Public-Key Regime
In the “high-end” regime, HSS can serve as a competitive alternative to FHE in certain application settings. Fully homomorphic encryption (FHE) [26, 37] is commonly viewed as a “dream tool” in cryptography, enabling one to perform arbitrary computations on encrypted inputs. For example, in the context of secure multiparty computation (MPC) [3, 13, 30, 42], FHE can be used to minimize the communication complexity and the round complexity, and shift the bulk of the computational work to any subset of the participants. However, despite exciting progress in the past years, even the most recent implementations of FHE [14, 25, 33] are still quite slow and require large ciphertexts and keys. This is due in part to the limited set of assumptions on which FHE constructions can be based [12, 22, 27], which are all related to lattices and are therefore susceptible to lattice reduction attacks. As a result, it is arguably hard to find realistic application scenarios in which current FHE implementations outperform optimized versions of classical secure computation techniques (such as garbled circuits) when taking both communication and computation costs into account.
A main motivating observation is that unlike standard FHE, HSS can be useful even for small computations that involve short inputs, and even in application scenarios in which competing approaches based on traditional secure computation techniques do not apply at all.
Advantages of HSS. As with FHE, HSS enables secure computation protocols that simultaneously offer a minimal amount of interaction and collusion resistance. However, the optimal output compactness of HSS makes it the only available option for applications that involve computing long outputs (or many short outputs) from short secret inputs (possibly along with public inputs). More generally, this feature enables applications in which the communication and computation costs of output reconstruction need to be minimized, e.g., for the purpose of reducing power consumption. For instance, a mobile client may wish to get quickly notified about live news items that satisfy certain secret search criteria, receiving a fast real-time feed that reveals only pointers to matching items. Further advantages of group-based HSS over existing FHE implementations include smaller keys and ciphertexts and a lower startup cost.
HSS Applications
Applications of HSS include small instances of general secure multiparty computation, as well as distributed variants of private information retrieval, functional encryption, and broadcast encryption. Exploring concrete such applications (and optimizing the DDH-based \(\delta \)-HSS construction) is the primary focus of [7].
Secure MPC with minimal interaction. Using multi-input HSS, a set of clients can outsource a secure computation to two non-colluding servers by using the following minimal interaction pattern: each client independently sends a single message to the servers (based on its own input and the public key), and then each server sends a single message to each client. Alternatively, servers can just publish shares of the output if the output is to be made public. The resulting protocol is resilient to any (semi-honest) collusion between one server and a subset of the clients, and minimizes the amount of work performed by the clients. It is particularly attractive in the case where many “simple” computations are performed on the same inputs. In this case, each additional instance of secure computation involves just local computation by the servers, followed by a minimal amount of communication and work by the clients.
Secure data access. HSS yields several different applications in the context of secure access to distributed data. For example, HSS can be used to construct a 2-server variant of attribute based encryption, in which each client can access an encrypted file only if its (public or encrypted) attributes satisfy an encrypted policy set up by the data owner. Other sample applications include 2-server private RSS feeds, in which clients can receive succinct notifications about new data that satisfies their encrypted matching criteria, and 2-server PIR schemes with general boolean queries. These applications benefit from the optimal output compactness feature of HSS discussed above, minimizing the communication from servers to clients and the computation required for reconstructing the output.
Unlike competing solutions based on classical secure computation techniques, HSS-based solutions only involve minimal interaction between clients and servers and no direct interaction between servers. In fact, for the RSS feed and PIR applications, the client is free to choose an arbitrary pair of servers who have access to the data being privately searched. These servers do not need to be aware of each other’s identity, and do not even need to know they are participating in an HSS-based cryptographic protocol: each server can simply run the code provided by the client on the (relevant portion of) the data, and return the output directly to the client.
Correlated randomness generation. An interesting application scenario is where the target output itself is an additive secret sharing. HSS provides a method for non-interactively generating sources of correlated randomness that can be used to speed up classical protocols for secure two-party computation. Concretely, following a setup phase, in which the parties exchange HSS shares of random inputs, the parties can locally expand these shares (without any communication) into useful forms of correlated randomness. The non-interactive nature of the correlated randomness generation is useful for hiding the identities of the parties who intend to perform secure computation (e.g., against network traffic analysis), as well as the time and the size of the computation being performed.
Useful correlations considered in [7] include bilinear correlations (which capture “Beaver triples” as a special case) and truth-table correlations. The work of [7] also proposes further compression of communication in the setup phase by using homomorphic evaluation of local PRGs, and present different approaches for improving its asymptotic computational complexity. However, this PRG-based compression is still in the theoretical regime (too slow to be realized with good concrete running time using the current implementation of group-based HSS).
5 Future Directions
The study of FSS/HSS is a rapidly expanding new field of research, which continues to surprise and reveal even further layers of mystery. This survey is by no means a comprehensive coverage of all that is known, but rather seeks to facilitate future study by providing a semi-centralized resource with helpful pointers.
We close with a selection of open problems, as well as an excitement (on behalf of the author) for what is yet to come.
5.1 Open Problems
-
Improved FSS from OWF
-
Improved DPF efficiency and/or lower bounds?
-
OWF-based FSS for CNF/DNF formulas? Better FSS for decision trees?
-
3-server DPF with better than \(2^{n/2}\) key size?
-
Separations between OWF and FSS for new function classes \({\mathcal {F}}\)?
-
-
Improved HSS from DDH
-
Better error-to-computation tradeoff (in share conversion step of \(\mathsf{Eval}\))?
-
DDH-based error-free HSS for branching programs?
-
DDH-based \(\delta \)-HSS for circuits (or anything beyond branching programs)?
-
DDH-based HSS for \({>}2\) servers?
-
-
New types of constructions
-
FSS/HSS from new assumptions?
-
HSS from LWE without going through FHE?
-
-
Applications & Implementations
-
Better optimizations for implementation?
-
Implementation of “high-end” HSS-based applications?
-
New application settings of FSS & HSS?
-
Notes
- 1.
Function vs. program: Note that in FSS we will consider simple classes of functions where each function has a unique description, whereas in HSS we consider functions with many programs computing it. For this reason we refer to “function” for FSS and “program” for HSS.
- 2.
- 3.
Namely, for each new x, the parties will first use their shared randomness to coordinately rerandomize the garbled circuit of f and input labels, respectively.
- 4.
In this case, we think of the function F and all HSS algorithms \(\mathsf{Share},\mathsf{Eval},\mathsf{Dec}\) as implicitly receiving a description of \(\mathbb {G}\) as an additional input.
- 5.
In particular: \(\lambda + n(\lambda + 2)\) for \(\lambda \)-bit outputs, and \(\lambda + n(\lambda +2) - \lfloor \log \lambda \rfloor \) for 1-bit outputs.
- 6.
Recall in HSS the secret share size scales with input size and not function description size.
References
Beimel, A., Burmester, M., Desmedt, Y., Kushilevitz, E.: Computing functions of a shared secret. SIAM J. Discrete Math. 13(3), 324–345 (2000)
Beimel, A., Ishai, Y., Kushilevitz, E., Orlov, I.: Share conversion and private information retrieval. In: CCC 2012, pp. 258–268 (2012)
Ben-Or, M., Goldwasser, S., Wigderson, A.: Completeness theorems for non-cryptographic fault-tolerant distributed computation (extended abstract). In: STOC, pp. 1–10 (1988)
Benaloh, J.C.: Secret sharing homomorphisms: keeping shares of a secret secret (extended abstract). In: Odlyzko, A.M. (ed.) CRYPTO 1986. LNCS, vol. 263, pp. 251–260. Springer, Heidelberg (1987). https://doi.org/10.1007/3-540-47721-7_19
Boneh, D., Halevi, S., Hamburg, M., Ostrovsky, R.: Circular-secure encryption from decision Diffie-Hellman. In: Wagner, D. (ed.) CRYPTO 2008. LNCS, vol. 5157, pp. 108–125. Springer, Heidelberg (2008). https://doi.org/10.1007/978-3-540-85174-5_7
Boyle, E., Gilboa, N., Ishai, Y.: Function secret sharing. In: Oswald, E., Fischlin, M. (eds.) EUROCRYPT 2015. LNCS, vol. 9057, pp. 337–367. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-46803-6_12
Boyle, E., Couteau, G., Gilboa, N., Ishai, Y., Orrù, M.: Homomorphic secret sharing: optimizations and applications. In: ACM SIGSAC CCS, pp. 2105–2122 (2017)
Boyle, E., Gilboa, N., Ishai, Y.: Breaking the circuit size barrier for secure computation under DDH. In: Robshaw, M., Katz, J. (eds.) CRYPTO 2016. LNCS, vol. 9814, pp. 509–539. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-53018-4_19
Boyle, E., Gilboa, N., Ishai, Y.: Function secret sharing: improvements and extensions. In: ACM SIGSAC CCS, pp. 1292–1303 (2016)
Boyle, E., Gilboa, N., Ishai, Y.: Group-based secure computation: optimizing rounds, communication, and computation. In: Coron, J.-S., Nielsen, J.B. (eds.) EUROCRYPT 2017. LNCS, vol. 10211, pp. 163–193. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-56614-6_6
Boyle, E., Gilboa, N., Ishai, Y., Lin, H., Tessaro, S.: Foundations of homomorphic secret sharing. In: ITCS (2017)
Brakerski, Z., Vaikuntanathan, V.: Efficient fully homomorphic encryption from (standard) LWE. SIAM J. Comput. 43(2), 831–871 (2014)
Chaum, D., Crépeau, C., Damgård, I.: Multiparty unconditionally secure protocols (extended abstract). In: STOC, pp. 11–19 (1988)
Chillotti, I., Gama, N., Georgieva, M., Izabachène, M.: Faster fully homomorphic encryption: bootstrapping in less than 0.1 seconds. In: Cheon, J.H., Takagi, T. (eds.) ASIACRYPT 2016. LNCS, vol. 10031, pp. 3–33. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-53887-6_1
Chor, B., Gilboa, N.: Computationally private information retrieval (extended abstract). In: Proceedings of 29th Annual ACM Symposium on the Theory of Computing, pp. 304–313 (1997)
Chor, B., Goldreich, O., Kushilevitz, E., Sudan, M.: Private information retrieval. J. ACM 45(6), 965–981 (1998)
Chung, K.-M., Kalai, Y., Vadhan, S.: Improved delegation of computation using fully homomorphic encryption. In: Rabin, T. (ed.) CRYPTO 2010. LNCS, vol. 6223, pp. 483–501. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-14623-7_26
Corrigan-Gibbs, H., Boneh, D., Mazières, D.: Riposte: An anonymous messaging system handling millions of users. In: IEEE Symposium on Security and Privacy, SP, pp. 321–338 (2015)
De Santis, A., Desmedt, Y., Frankel, Y., Yung, M.: How to share a function securely. In: Proceedings of 26th Annual ACM Symposium on Theory of Computing, pp. 522–533 (1994)
Desmedt, Y., Frankel, Y.: Threshold cryptosystems. In: Brassard, G. (ed.) CRYPTO 1989. LNCS, vol. 435, pp. 307–315. Springer, New York (1990). https://doi.org/10.1007/0-387-34805-0_28
Diffie, W., Hellman, M.: New directions in cryptography. IEEE Trans. Inf. Theor. 22(6), 644–654 (1976)
van Dijk, M., Gentry, C., Halevi, S., Vaikuntanathan, V.: Fully homomorphic encryption over the integers. In: Gilbert, H. (ed.) EUROCRYPT 2010. LNCS, vol. 6110, pp. 24–43. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-13190-5_2
Dodis, Y., Halevi, S., Rothblum, R.D., Wichs, D.: Spooky encryption and its applications. In: Robshaw, M., Katz, J. (eds.) CRYPTO 2016. LNCS, vol. 9816, pp. 93–122. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-53015-3_4
Doerner, J., Evans, D., Shelat, A.: Secure stable matching at scale. In: ACM SIGSAC CCS, pp. 1602–1613 (2016)
Ducas, L., Micciancio, D.: FHEW: bootstrapping homomorphic encryption in less than a second. In: Oswald, E., Fischlin, M. (eds.) EUROCRYPT 2015. LNCS, vol. 9056, pp. 617–640. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-46800-5_24
Gentry, C.: Fully homomorphic encryption using ideal lattices. In: STOC, pp. 169–178 (2009)
Gentry, C., Sahai, A., Waters, B.: Homomorphic encryption from learning with errors: conceptually-simpler, asymptotically-faster, attribute-based. In: Canetti, R., Garay, J.A. (eds.) CRYPTO 2013. LNCS, vol. 8042, pp. 75–92. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-40041-4_5
Gilboa, N., Ishai, Y.: Distributed point functions and their applications. In: Nguyen, P.Q., Oswald, E. (eds.) EUROCRYPT 2014. LNCS, vol. 8441, pp. 640–658. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-642-55220-5_35
Goldreich, O., Goldwasser, S., Micali, S.: How to construct random functions. J. ACM 33(4), 792–807 (1986)
Goldreich, O., Micali, S., Wigderson, A.: How to play any mental game or a completeness theorem for protocols with honest majority. In: STOC, pp. 218–229 (1987)
Goldreich, O., Ostrovsky, R.: Software protection and simulation on oblivious RAMs. J. ACM 43(3), 431–473 (1996)
Gordon, S.D., Katz, J., Kolesnikov, V., Krell, F., Malkin, T., Raykova, M., Vahlis, Y.: Secure two-party computation in sublinear (amortized) time. In: ACM CCS, pp. 513–524 (2012)
Halevi, S., Shoup, V.: Bootstrapping for HElib. In: Oswald, E., Fischlin, M. (eds.) EUROCRYPT 2015. LNCS, vol. 9056, pp. 641–670. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-46800-5_25
Kalyanasundaram, B., Schnitger, G.: The probabilistic communication complexity of set intersection. SIAM J. Discrete Math. 5(4), 545–557 (1992)
Ostrovsky, R., Shoup, V.: Private information storage (extended abstract). In: ACM Symposium on the Theory of Computing, pp. 294–303 (1997)
Ostrovsky, R., Skeith III, W.E.: Private searching on streaming data. In: Shoup, V. (ed.) CRYPTO 2005. LNCS, vol. 3621, pp. 223–240. Springer, Heidelberg (2005). https://doi.org/10.1007/11535218_14
Rivest, R.L., Adleman, L., Dertouzos, M.L.: On data banks and privacy homomorphisms. In: Workshop on Foundations of Secure Computation, Georgia Institute of Technology, Atlanta, GA, pp. 169–179. Academic, New York (1978)
Shamir, A.: How to share a secret. Commun. ACM 22(11), 612–613 (1979)
Doerner, J., Shelat, A.: Scaling ORAM for secure computation. In: ACM SIGSAC CCS, pp. 523–535 (2017)
Wang, F., Yun, C., Goldwasser, S., Vaikuntanathan, V., Zaharia, M.: Splinter: practical private queries on public data. In: 14th USENIX Symposium on Networked Systems Design and Implementation, NSDI, pp. 299–313 (2017)
Wang, X., Chan, T.H., Shi, E.: Circuit ORAM: on tightness of the Goldreich-Ostrovsky lower bound. In: ACM SIGSAC CCS, pp. 850–861 (2015)
Yao, A.C.C.: How to generate and exchange secrets (extended abstract). In: FOCS, pp. 162–167 (1986)
Zahur, S., Wang, X.S., Raykova, M., Gascón, A., Doerner, J., Evans, D., Katz, J.: Revisiting square-root ORAM: efficient random access in multi-party computation. In: IEEE Symposium on Security and Privacy, SP, pp. 218–234 (2016)
Acknowledgements
Tremendous thanks to my FSS/HSS partners in crime, Niv Gilboa and Yuval Ishai, and to additional coauthors on the presented works: Geoffroy Couteau, Huijia Rachel Lin, Michele Orrù, and Stefano Tessaro.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2017 Springer International Publishing AG
About this paper
Cite this paper
Boyle, E. (2017). Recent Advances in Function and Homomorphic Secret Sharing. In: Patra, A., Smart, N. (eds) Progress in Cryptology – INDOCRYPT 2017. INDOCRYPT 2017. Lecture Notes in Computer Science(), vol 10698. Springer, Cham. https://doi.org/10.1007/978-3-319-71667-1_1
Download citation
DOI: https://doi.org/10.1007/978-3-319-71667-1_1
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-71666-4
Online ISBN: 978-3-319-71667-1
eBook Packages: Computer ScienceComputer Science (R0)






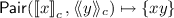 . This pairing operation exploits the fact that
. This pairing operation exploits the fact that  .
.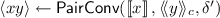 for
for  .
. , where
, where