Synchronization in Kuramoto Oscillators Under Single External Oscillator

Abstract

In this chapter we study the influence of a single strongly attractively coupled external oscillator on a system of coupled Kuramoto oscillators. First we go through the original method used by Kuramoto to solve this system of coupled oscillators. Then we use a later approach developed by Ott and Antonsen. We will use this approach first to solve the original system and show that the results match. Next we will solve a variations of the this system using Ott-Antonsen method, after which we will use it to solve our particular system. We consider a variation of the Kuramoto system which shows multiple regions of synchronization. First we observe the effects of attractive and repulsive couplings. Next we qualitatively study the effect of the initial frequency distribution of the internal oscillators, both the mean and the standard deviation of different distributions like the Gaussian and Lorentzian distributions, on these synchronization regions.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

Synchronization has always been an interesting topic of study since its discovery by Huygen’s (1673) in coupled pendulum. In a field as diverse and encompassing as non-linear dynamics, coupled systems and their synchronization behaviour has been used to model a wide variety of systems from those in Biology and Physics to Economics. Many studies on the mathematical aspects of collective synchronization have been done in the past decades. These systems have a lot of applications in physical systems like Josephson junction, electrochemical array, etc. (Yamaguchi et al. 2003; Kiss et al. 2002; Wiesenfeld and Swift 1995; Pantaleone 1998; Hubler et al. 1997).

Many types of synchronization have been observed. Two types of synchronization are of immediate interest in our case. They are spontaneaous synchronization and froced synchronization. In many coupled systems, there can be spontaneous synchronization (Pikovsky et al. 2001; Strogatz 2004; Boccaletti et al. 2002). That is, for a critical value of a parameter, the system shows some collective behavior without any external influence. In case of forced synchronization, the system shows collective behavior due to an external forcing term. There are many more different types of synchronization that may be induced due to many factors, including noise (Flandoli et al. 2017).

One interesting coupled system that shows a variety of different synchronization behaviour was proposed by Kuramoto (1975). The Kuramoto system is a system of N-coupled phase oscillators. These can be thought of as a collection of limit cycles. Under certain conditions, these coupled phase oscillators were seen to undergo the phenomenon of synchronization. Many different variations of the system, including even second-order differential forms were studied (Bountis et al. 2014; Olmi et al. 2014; Jaros et al. 2015), many of whom showed partial synchronizations, chimera (Maistrenko et al. 2017) and even solitary states (Jaros et al. 2017).

A system similar to the one that will be studied in this chapter was analyzed by Childs and Strogatz in 2008 (Strogatz 2008). These systems show different types of synchronization. An interesting fact about this specific system is that even repulsive coupling of oscillators lead to synchronization. Not only that, they show behavior very similar to that shown when the oscillators have attractive coupling. This is true for different distributions of the initial frequencies making it a very general phenomenon.

To understand the system better, we can consider the Kuramoto system to be a set of points moving around in a unit circle with $\theta$ position and angular velocity $\omega$. We can see that some transformations, like $\theta \longrightarrow \theta +c$, where c is a constant does not change the system. A commonly used transformation of the system during calculations is $\omega \longrightarrow \omega +c$. This is called the rotating frame transformation. This can be seen as the unit circle with all the point oscillators itself rotating at a frequency. Also, now addition of external force could be seen as the unit circle itself experiencing the force rather than the same force being applied to every single oscillator, since both scenarios give the same equation.

There are many ways of solving the basic system. First we will see the method that was used by Kuramoto (1975, 1984) to solve this system, after which we will use a method suggested by Ott and Antonsen (2008).

2 Solving Kuramoto System

First we will see the method used by Kuramoto to solve this system (Kuramoto 1975, 1984). The Kuramoto model is a simple model of N-coupled oscillators with different frequencies. The simple Kuramoto system is given by

$$\begin{aligned} \dfrac{d\theta _{i}}{dt}=\omega _{i}+\dfrac{K}{N}\sum _{j=1}^{N}sin(\theta _{j}-\theta _{i}) \end{aligned}$$

(1)

where $i=1,\ldots ,N$ denote the N oscillators. Here $\omega _{i}$ gives the frequencies of the ith oscillator. That is the frequency at which the oscillator would move had it not been coupled to other oscillators. $\theta _{i}$ denotes the phase of the ith oscillator. The parameter K gives the coupling strength. We have taken the coupling to be a sine function as was done in the original Kuramoto article, although there have been many generalizations done in later years.

We can see from the system equations that in the case of $K>0$, which is the one we are working with, the coupling is making the system come closer. That is, if the phase of an individual oscillator is smaller than the average phase, then the coupling will increase it, while if the individual oscillator has a larger than average phase, then it will be decreased by the coupling. The system has a natural tendency to synchronize towards the average phase.

It should also be noted that $N^{-1}$ is also an important term in the coupling. If not for this term, the coupling would not be N-independent in the thermodynamic limit of $N\longrightarrow \infty$, which is the case we consider for analysis.

We define $\psi$ as $R=re^{i\psi }=\dfrac{1}{N}\sum _{i=1}^{n}e^{i\theta _{i}}$ where R is called an order parameter. It can be seen from this expression, that $\psi$ gives the average phase, and is hence called the ‘mean field’, while r gives the variation of the individual oscillators phase from $\psi$. This will be used as the measure for synchronization as when all sysntems are synchronized, $r=1$.

We now write the system equations as a function of r and $\psi$

$$\begin{aligned} \dfrac{d\theta _{i}}{dt}&=\omega _{i}+\dfrac{K}{N}Im\left[ \sum _{i=1}^{n}e^{i(\theta _{j}-\theta _{i})}\right] \\[10pt]&=\omega _{i}+\dfrac{K}{N}Im \left[ e^{-i\theta _{i}}\sum _{i=1}^{n}e^{i\theta _{j}}\right] \\[10pt]&=\omega _{i}+Im[Ke^{-i\theta _{i}}re^{i\psi }]\\[10pt]&=\omega _{i}+Krsin(\psi -\theta _{i}) \end{aligned}$$

From this form of the system equations we see that Kuramoto system can be thought of as a system of oscillators being forced by a mean field. This also explains neatly the tendency of the system to synchronize into the mean field.

Now we do the transformation $\theta \longrightarrow \theta -\psi$ and $\varOmega$ is assumed to be the steady state frequency of the oscillators. One thing to be noted is that, for solving his system, Kuramoto used a few assumption, like the existence of a steady state. To understand this, we can think of it as the system of N-oscillators being thought of as a single oscillator moving in the unit circle at $\psi$ angle and $\varOmega$ frequency. This assumption was later verified by the self-consistency condition. Coming back to the calculation, we do one more transformation in which we go to a rotating frame with $\varOmega$ frequency. This eliminated the $\psi$ and $\varOmega$ terms leaving us with the equation

$$\begin{aligned} \Rightarrow \dfrac{d\theta _{i}}{dt}=\omega _{i}-Krsin(\theta _{i}) \end{aligned}$$

Since we are taking steady state solutions, we have $r=constant$.

There are two types of solutions for the oscillators described above depending on the two terms on the right-hand side.

If $|\omega _{i}| \leqslant Kr$, then the oscillators converge to a steady state and reach synchronization. This implies that at steady state $\mid \omega _{i}\mid =Krsin\theta _{i}$

$$\begin{aligned} \Rightarrow \theta _{i}=sin^{-1}(\frac{Kr}{\omega _{i}}) \leqslant \frac{pi}{2} \end{aligned}$$

This set of oscillators are called phase locked, as undoing the transformations would mean that these are moving at the same frequency $\varOmega$.

Now let us consider the other case where $|\omega _{i}|\ge Kr$. These oscillators do not synchronize but move freely around the unit circle.

Now the problem which arises is: Is r and $\psi$ constant? This was solved by Kuramoto by assuming that the mean of the drifting oscillators form a stationary distribution on the circle. If $\rho (\theta ,\omega )d\theta$ denote the fraction of oscillators with frequency $\omega$ that lie between $\theta$ and $\theta +d\theta$, then this $\rho$, to satisfy the stationary distribution condition, should be inversely proportional to the speed.

$$\begin{aligned} \Rightarrow \rho (\theta ,\omega )=\frac{C}{\omega -Krsin\theta } \end{aligned}$$

Here $C=\frac{1}{2\pi }\sqrt{\omega ^{2}-(kr)^{2}}$ is the normalization constant.

Now to solve the system and to justify our assumptions, we will invoke the self-consistency condition. Since the order parameter has to be a constant as assumed,

$$\begin{aligned}<e^{i\theta }>=<e^{i\theta }>_{lock}+<e^{i\theta }>_{drift} \end{aligned}$$

where $<>$ denote the population averages. Continuing from here, since $\psi =0$, $<e^{i\theta }>=r$.

$$\begin{aligned} \Rightarrow r=<e^{i\theta }>_{lock}+<e^{i\theta }>_{drift} \end{aligned}$$

Due to symmetry of the system as $N\longrightarrow \infty$,

$$\begin{aligned}<e^{i\theta }>_{lock}=<cos\theta >_{lock}=\int _{-Kr}^{Kr}cos\theta (\omega )g(\omega )d\omega \end{aligned}$$

For the drifting oscillators

$$\begin{aligned} <e^{i\theta }>_{drift}=\int _{-\pi }^{\pi }\int _{|\omega |>Kr}e^{i\theta }\rho (\theta ,\omega )g(\omega )d\omega d\theta \end{aligned}$$

This integral vanishes due to the symmetry of $\rho$. Therefore now the whole self-consistency is given just by the locked terms, which is written in terms of $\theta$ as

$$\begin{aligned} r=Kr\int _{-\pi /2}^{\pi /2}cos^{2}\theta g(Krsin\theta )d\theta \end{aligned}$$

which has two solutions, the trivial $r=0$ and the other given by

$$\begin{aligned} 1=K\int _{-\pi /2}^{\pi /2}cos^{2}\theta g(Krsin\theta )d\theta \end{aligned}$$

This shows the increase in r beyond a critical $K_{c}$ given by

$$\begin{aligned} K_{c}=\dfrac{2}{\pi g(0)} \end{aligned}$$

For Lorentzian distribution, the integral can be calculated exactly and gives $r=\sqrt{1-\dfrac{K_{c}}{K}}$.

3 Ott-Antonsen Method for Solving Kuramoto-Like Systems

3.1 Original Kuramoto System

As of now, we have defined and solved the simple Kuramoto system. We have shown the existence of a synchronous state in the $N\longrightarrow \infty$ limit and derived the expression for the the order parameter r. But as intuitive as the proof and calculations for the system have been, it is not a general method. As in, even though this works for a simple Kuramoto system, the same method cannot be used for systems derived from it, like the Kuramoto system with an external forcing term.

There are many methods used to solve this system, most of which are similar to the method shown above. This process is done by separating the system into different sub-populations and then using self-consistency to arrive at a solution for r. We will be using a different approach proposed by Ott and Antonsen (2008). The crux of this method is the use of an anzatz given by them. The reason and proof for the use of this anzatz is given in has been studied in their publication and further used in many others. Here we will just be showing the process involved with the solving.

The simple Kuramoto system is again given by

$$\begin{aligned} \dfrac{d\theta _{i}}{dt}=\omega _{i}+\dfrac{K}{N}\sum _{j=1}^{N}sin\left( \theta _{j}-\theta _{i}\right) \end{aligned}$$

(2)

where $i=1 \ldots N$ denote the N oscillators.

We define $\psi$ and r the same way as before

$$\begin{aligned} re^{i\psi }=\dfrac{1}{N}\sum _{i=1}^{n}e^{i\theta _{i}} \end{aligned}$$

Re-writing the equation again in terms of $\psi$ and r

$$\begin{aligned} \dfrac{d\theta _{i}}{dt}&=\omega _{i}+\dfrac{K}{N}Im\left[ \sum _{i=1}^{n}e^{i(\theta _{j}-\theta _{i})}\right] \\[10pt]&=\omega _{i}+\dfrac{K}{N}Im\left[ e^{-i\theta _{i}}\sum _{i=1}^{n}e^{i\theta _{j}}\right] \\[10pt]&=\omega _{i}+Im\left[ Ke^{-i\theta _{i}}re^{i\psi }\right] \end{aligned}$$

$$\begin{aligned} \dfrac{d\theta _{i}}{dt} =\omega _{i}+Krsin\left( \psi -\theta _{i}\right) \end{aligned}$$

(3)

It is easier to use Eq. (3) for simulations since as is shown, it is the same system in a different form.

For our calculations

$$\begin{aligned} \dfrac{d\theta _{i}}{dt}&=\omega _{i}+\dfrac{K}{N}\left( \sum _{i=1}^{n}\dfrac{e^{i(\theta _{j}-\theta _{i})}-e^{-i(\theta _{j}-\theta _{i})}}{2i}\right) \\[10pt]&=\omega _{i}+\dfrac{K}{2i}\left( Re^{-i\theta _{i}}-R^{*}e^{i\theta _{i}}\right) \end{aligned}$$

In the continuous limit of $N\rightarrow \infty$, let f be the probability distribution of $\theta$ and

$$\begin{aligned} g(\omega )=\int _{0}^{2\pi }f\left( \omega ,\theta ,t\right) d\theta \end{aligned}$$

(4)

be the time-independent oscillator frequency distribution.

The continuity equation is given by

$$\begin{aligned} \dfrac{\partial f}{\partial t}+\dfrac{\partial }{\partial \theta }(\,f\dot{\theta })=0 \end{aligned}$$

$$\begin{aligned} \Rightarrow \dfrac{\partial f}{\partial t}+\dfrac{\partial }{\partial \theta }\left[ (\omega _{i}+\dfrac{K}{2i}(Re^{-i\theta }-R^{*}e^{i\theta }))f\right] \end{aligned}$$

(5)

where

$$\begin{aligned} R=\int _{0}^{2\pi }d\theta \int _{-\infty }^{\infty }d\omega fe^{i\theta } \end{aligned}$$

(6)

Expanding f using Fourier series gives us

$$\begin{aligned} f=\frac{g(\omega )}{2\pi }\left[ 1+\left[ \sum _{n=1}^{\infty }f_{n}(\omega ,t)e^{in\theta }+f_{n}^{*}(\omega ,t)e^{-in\theta }\right] \right] \end{aligned}$$

We will now use the anzatz provided by Ott and Antonsen

$$\begin{aligned} f_{n}(\omega ,t)=\left[ \alpha (\omega ,t)\right] ^{n} \end{aligned}$$

where $|\alpha (\omega ,t)|\leqslant 1$ so that the system is convergent.

Putting this back in Eq. (5) and taking only the coefficients of $e^{i\theta }$, we get

$$\begin{aligned} \frac{\partial \alpha }{\partial t}+\left[ \alpha \omega i+\frac{k}{2i}(R\alpha ^{2}-R^{*})i\right] =0 \end{aligned}$$

$$\begin{aligned} \Rightarrow \frac{\partial \alpha }{\partial t}+\frac{k}{2}\left( R\alpha ^{2}-R^{*}\right) +i\omega \alpha =0 \end{aligned}$$

(7)

and into Eq. (6)

$$\begin{aligned} R^{*}=\int _{\infty }^{\infty }d\omega \alpha (\omega ,t)g(\omega ) \end{aligned}$$

(8)

As of now, this converted an infinite dimensional system in $\theta$ to an infinite dimensional system in $\omega$. To solve the system, we need to make this into a finite dimensional set of differential equations, which is what this method will do in the following steps.

Now we will solve the equation for an example of $\omega$—distribution. Here we take it to be Lorentzian.

$$\begin{aligned} g(\omega )&=\frac{\varDelta }{\pi }\frac{1}{\left[ (\omega -\omega _{0})^{2}+\varDelta ^{2}\right] }\\[10pt]&=\frac{1}{2\pi i}\left[ \frac{1}{\omega -\omega _{0}-i\varDelta }-\frac{1}{\omega -\omega _{0}+i\varDelta }\right] \end{aligned}$$

By going into a rotating frame using the transformation $\omega \longrightarrow \frac{\omega -\omega _{0}}{\varDelta }$ and $\theta \longrightarrow \theta -\omega _{0}t$, we can see that it is possible to put $\omega _{0}=0$ and $\varDelta =1$.

Putting this in Eq. (8) and solving using the residue method, we get

$$\begin{aligned} R=\alpha ^{*}(-i,t) \end{aligned}$$

(9)

Using this and $R=re^{i\psi }$ into Eq. (7), we get

$$\begin{aligned} \frac{\partial }{\partial t}\left( re^{-i\psi }\right) +\frac{k}{2}\left( r^{3}e^{-i\psi }-re^{-i\psi }\right) +re^{-i\psi }=0 \end{aligned}$$

$$\begin{aligned} \Rightarrow \frac{\partial r}{\partial t}e^{-i\psi }-ire^{-i\psi }\frac{\partial \psi }{\partial t}+\frac{k}{2}(r^{3}e^{-i\psi }-re^{-i\psi })+re^{-i\psi }=0 \end{aligned}$$

Separating the real and imaginary parts, we have

$$\begin{aligned} \dfrac{\partial r}{\partial t}+\frac{k}{2}\left( r^{3}-r\right) +r =0 \end{aligned}$$

(10)

$$\begin{aligned} \dfrac{\partial \psi }{\partial t} =0 \end{aligned}$$

(11)

On solving Eqs. (10) and (11), we get

$$\begin{aligned} r(t)=\sqrt{\frac{(1-\frac{2}{K})}{|1+[\frac{1-\frac{2}{K}}{r(0)^{2}}-1]e^{(1-\frac{K}{2})t}|}} \end{aligned}$$

From this we can see that for $K<2$, which is the critical k value, the order parameter r goes to zero, signifying that the system is not synchronized. For $K>2$, the order parameter is non-zero asymptotically. This is the same as was seen in the previous section, with $K_{c}=2$.

3.2 Kuramoto System with External Force

The Kuramoto system with an external driving force (Sakaguchi 1988) is given by

$$\begin{aligned} \dfrac{d\theta _{i}}{dt}=\omega _{i}+\dfrac{K}{N}\sum _{j=1}^{N}sin(\theta _{j}-\theta _{i})+Fsin(\varOmega t-\theta _{i}) \end{aligned}$$

(12)

where $i=1 \ldots N$ denote the N oscillators.

R and $\psi$ are defined exactly the same as in the last section. $R=re^{i\psi }=\dfrac{1}{N}\sum _{i=1}^{n}e^{i\theta _{i}}$.

Following the same method (Antonsen et al. 2008; Ott and Antonsen 2008; Childs and Strogatz 2008), we can get a different form of the same equation which is easier to work with in simulations. Therefore Eq. (12) is rewritten as

$$\begin{aligned} \dfrac{d\theta _{i}}{dt}&=\omega _{i}+Krsin\left( \psi -\theta _{i}\right) +Fsin\left( \varOmega t-\theta _{i}\right) \end{aligned}$$

Now to reduce this infinite dimensional equation, we follow the same procedure as in the previous section.

For our calculations

$$\begin{aligned} \dfrac{d\theta _{i}}{dt}&=\omega _{i}+\dfrac{K}{N}\left( \sum _{i=1}^{n}\dfrac{e^{i(\theta _{j}-\theta _{i})}-e^{-i(\theta _{j}-\theta _{i})}}{2i}\right) +F\frac{e^{i(\varOmega t-\theta _{i})}-e^{-i(\varOmega t-\theta _{i})}}{2i} \end{aligned}$$

Now we put $\theta _{i}\longrightarrow \theta _{i}+\varOmega t$

$$\begin{aligned} \dfrac{d\theta _{i}}{dt}&=\omega _{i}-\varOmega +\dfrac{K}{N}\left( \sum _{i=1}^{n}\dfrac{e^{i(\theta _{j}-\theta _{i})}-e^{-i(\theta _{j}-\theta _{i})}}{2i}\right) +F\frac{e^{-i\theta _{i}}-e^{i\theta _{i}}}{2i}\\[10pt]&=\omega _{i}-\varOmega +\dfrac{1}{2i}[(KR+F)e^{-i\theta _{i}}-(KR^{*}+F)e^{i\theta _{i}}] \end{aligned}$$

Since K and R are real

$$\begin{aligned} \dfrac{d\theta _{i}}{dt}=\omega _{i}-\varOmega +\dfrac{1}{2i}\left[ (KR+F)e^{-i\theta _{i}}-(KR+F)^{*}e^{i\theta _{i}}\right] \end{aligned}$$

For the continuous system as $N\longrightarrow \infty$, first we write the continuity equation which gives us

$$\begin{aligned} \Rightarrow \dfrac{\partial f}{\partial t}+\dfrac{\partial }{\partial \theta }\left[ \omega -\varOmega +\dfrac{1}{2i}\left[ (KR+F)e^{-i\theta }-(KR+F)^{*}e^{i\theta }\right] f\right] \end{aligned}$$

(13)

and R being the same as before. Now we do the Fourier expansion, take the same ansatz and check for the coefficients of $e^{i\theta }$, which gives us

$$\begin{aligned} \frac{\partial \alpha }{\partial t}+\frac{1}{2}\left[ (KR+F)^{*}\alpha ^{2}-(KR+F)\right] +\left[ 1+i(\varOmega -\omega )\right] \alpha =0 \end{aligned}$$

We again consider the Lorentzian distribution for $\omega$ where we put $\varDelta =1$ and $\omega =\omega _{0}$ and repeat the same process, after which we get

$$\begin{aligned} \frac{\partial R}{\partial t}+\frac{1}{2}\left[ (KR+F)^{*}R^{2}-(KR+F)\right] +\left[ 1+i(\varOmega -\omega _{0})\right] R=0 \end{aligned}$$

Considering $R=re^{i\psi }$, we can simplify this into two equations

$$\begin{aligned} \dot{r}=-\varDelta r+\frac{(1-r^{2})}{2}\left( F\cos (\psi )+Kr\right) \end{aligned}$$

(14)

$$\begin{aligned} \dot{\psi }=-(\varOmega -\omega _{0})-\frac{F}{2r}(1+r^{2})\sin (\psi ) \end{aligned}$$

(15)

This can be solved with the system being depended on the parameters $K,F,(\varOmega -\omega _{0})$ (Childs and Strogatz 2008).

4 Model of the System

In this section we study a synchronization of Kuramoto-like phase oscillators with a time-dependent external force. The equations of motion are as follows:

$$\begin{aligned} \left. \begin{array}{c} \dot{\theta }_{i}=\omega _{i}+\frac{K}{N}\sum \nolimits _{j=1}^{N}\sin (\theta _{i}-\theta _{j})-F\sin (\theta _{i}-\xi )\\ \dot{\dot{\xi }}=\sigma -\frac{F}{N}\sum \nolimits _{j=1}^{N}\sin (\xi -\theta _{j}) \end{array}\right\} \end{aligned}$$

(16)

where $i=1\dots N$ and N is number of single Kuramoto-like oscillators. Parameter K refers to strength of internal oscillators, $\omega _{i}$ is frequency of single node, F is external force and $\sigma$ refers to external frequency. The phase of each Kuramoto-like system is given by $\theta _{i}$ and phase of external oscillator is $\xi$. In our study we vary parameters F, K and $\omega _{i}$ while external frequency is always fixed to $\sigma =1.5$. The frequencies $\omega _{i}$ are given by mean frequency $\omega _{0}$, standard derivation and distribution (Gaussian, uniform or Lorenzian).

There are two ways to visualize this system. One way is to consider this as a set of Kuramoto oscillators experiencing a force. But unlike the normal force, in our system the force is dependent to an extent on the internal oscillators. That is this force is influence by the oscillators themselves.

The other way is to think of this system as a set of kuramoto oscillators being influence by a lone strongly coupled external kuramoto oscillator. We have mainly used this approach in explaining the results that we observed.

5 Numerical Study

Fig. 1 shows how the order parameter r changes with the strength of the external oscillator for both repulsive and attractive coupling (Figs. 1a and 1b respectively). The synchronization state appears for both type of coupling, however for a repulsive coupling, it occurs for smaller values of F then for the attractively coupled oscillators. Additionally, we observe two ranges of synchronous motion with desynchronization between them.

Fig. 1

Order parameter in repulsive and attractive coupling. The parameters are $\omega _{0}=0.5$, standard deviation = 0.01, $\sigma =1.5$: a $K=1.5$ for repulsive and b $K=-1.5$ for attractive coupling

To see if these two regions are the same or distinct we calculate the ratio of mean frequency $\overline{\omega }$ of the oscillators to the frequency of the external oscillator $\sigma$ (see Fig. 2) was plotted as shown in Fig. 2a. As can be seen here, these regions are qualitatively different. This implies that the first synchronization region refers to phase locked solution with ratio 2:1 between synchronized Kuramoto-like oscillators and external frequency. The second region is typical 1:1 locked state.

To study this phenomenon in detail, we increased the external frequency to 30 times higher then internal frequency. The ratios are plotted in Fig. 2b. Transition to synchronization state occurs every time the internal frequency reaches an integer multiple value of the external frequency. That is to say that the repulsively coupled oscillators synchronize separately into natural frequencies which are integer multiples of the external frequency and that this is a more general phenomenon with not two but many different internal synchronizations depending on the initial difference between the external and internal frequencies. Nevertheless it is clear that for higher ratios the plateau of synchronous motion becomes narrower.

Fig. 2

Plot of the change in the ratio of mean frequency $\overline{\omega }$ of the oscillators to frequency of the the external oscillator $\sigma$ with respect to the parameter F for repulsive coupling for three values of $\sigma =1.5$ (panel (a)), $\sigma =2.5$ (panel (b)) and $\sigma =15$ (panel (c)). The other parameters are $\omega _{0}=0.5$, standard deviation $= 0.01$ and $K=1.5$

Fig. 3

Panels (a), (b) and (c) show the variation of order parameter r with increasing external oscillator interaction(F) for an initial $\omega _{i}$ distribution as Lorentzian with varying standard deviation of 0.1, 0.01, 0.001 respectively

Fig. 4

Panels (a), (b) and (c) show the variation of order parameter r with increasing external oscillator interaction(F) for an initial $\omega _{i}$ distribution as Gaussian with varying standard deviation of 0.1, 0.01, 0.001 respectively

Fig. 5

Panels (a), (b) and (c) show the variation of order parameter r with increasing external oscillator interaction (F) for an initial $\omega _{i}$ distribution as Uniform with varying standard deviation of 0.1, 0.01, 0.001 respectively

Fig. 6

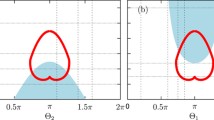
a Shows the variation of the order parameter (in color) with respect to external oscillator interaction (F) and the strength of internal coupling (K) for a given $\varOmega =-(\sigma -\omega _{0})$, where $\omega _{0}=0.5, \sigma =1.5$, for Lorentzian distribution as the initial oscillator frequency distribution. b Shows the variation of the order parameter (in false color) with respect to the external force/oscillator interaction (F) and $\varOmega =-(\sigma -\omega _{0})$, where $\omega _{0}=0.5, \sigma$ increases from −1 to 1, for Lorentzian distribution as the initial oscillator frequency distribution for a fixed strength of internal coupling $(K) = 1.5$

Aforementioned results are for Lorentzian internal frequency distribution. To see how general this phenomenon is, we repeat the process with different initial frequency distribution for the internal oscillators, each time varying the standard deviation. Figure 3 shows the plot of the change of order parameter for varying strength of external oscillator for the Lorentzian distribution for varying standard deviation, that is 0.1, 0.01, 0.001. Figure 4 shows the same plot but with the internal oscillators now in an initial distribution that is Gaussian and Fig. 5 shows again the same plot, but now for a Uniform initial internal frequency distribution. As it is easy to see, the observed phenomenon is independent of the frequency distribution, although we observe that it is sensitive to the standard deviation. The region of the transition is changing with the standard deviation whereas the regions themselves are independent of the distribution. Also the smaller the standard deviation, the more pronounced the effect. That is, for more identical oscillator, we see that the different regions and their boundaries become more distinct. This could mean that the transition region depends on how nearly identical the initial frequencies are.

Now we base the initial $\omega -distribution$ as Lorentzian distribution again. As can be noted, there are three main parameters of consideration in the system equations. They are, the strength of the external oscillators (F), the coupling strength of the internal oscillators (K) and the difference between the mean internal frequency ($\omega _{0}$) and the frequency of the external oscillator ($\sigma$). To see how theses parameters affect the order parameter, we plot Fig. 6. This plot shows that the observed phenomenon is robust and exists for wide range of system parameters. In both panels we vary external force F in range $F\in [0,2]$, however vertical axis is different, i.e., in panel (a) we change strength of external oscillators K from 0 to 2.0 and in panel (b) the difference $\varOmega =-(\sigma -\omega _{0})$ between the external frequency and the mean internal frequency. In color we show the order parameter r. In Fig. 6a synchronous range (yellow color) appears for $K>0.6$ nearly independ of the external oscillator strength F. It is present till $K\approx 1.1$ (with some variations with where the oscillators desynchronize a change in the ratio between frequencies from 2:1 to 1:1 occurs. Above $K\approx 1.3$ the synchronous state persists and is stable. In Fig. 6b the structure is more complex due to change of ratio between the frequencies. For most of $\varOmega$ values two or more ranges of synchronization appear.

6 Analysis

The system we are dealing with is

$$\begin{aligned} \left. \begin{array}{c} \dot{\theta }_{i}=\omega _{i}+\frac{K}{N}\sum \nolimits _{j=1}^{N}\sin (\theta _{i}-\theta _{j})-F\sin (\theta _{i}-\xi )\\ \dot{\dot{\xi }}=\sigma -\frac{F}{N}\sum \nolimits _{j=1}^{N}\sin (\xi -\theta _{j}) \end{array}\right\} \end{aligned}$$

(17)

which consists of N coupled oscillators which are acting under a force, whose frequency is coupled with the system using an attractive coupling. It is easier to see this by writing Eq. (17) using the mean field $\psi$ and the order parameter R defined as

$$\begin{aligned} Re^{i\psi }=\frac{1}{N}\sum _{j=1}^{N}e^{i\theta _{j}} \end{aligned}$$

(18)

using (18), we can rewrite (17) as

$$\begin{aligned} \left. \begin{array}{c} \dot{\theta }_{i}=\omega _{i}+KR\sin (\theta _{i}-\psi )-F\sin (\theta _{i}-\xi )\\ \dot{\dot{\xi }}=\sigma -FR\sin (\xi - \psi ) \end{array}\right\} \end{aligned}$$

(19)

This is an easier form to understand. This system has atleast two different ways of attaining synchronisation: with either the mean field $\psi$ or the forcing field $\phi$. In fact both these types of synchronisation has been oberved in this system as can be seen from the Fig. 1.

Now to analyze this system we go into a rotating frame. That is we do the transformation $\theta _{i}\rightarrow \theta _{i}-\xi$. After which we follow the procedure given by Ott and Antonsen and taking the $\omega -distribution$ to be Lorentzian to finally arrive at

$$\begin{aligned} \dot{R}=\frac{1}{2}\left[ (KR+F)^{*}R^{2}-(KR+F)\right] -\frac{F}{2}(R-R^{*})-\left[ \varDelta +i(\sigma -\omega _{0})\right] R \end{aligned}$$

where $\omega _{0}$ is the mean and $\varDelta$ the width of the $\omega -distribution$.

Now by putting $R=re^{i\psi }$, we can simplify the whole system into the following two equations:

$$\begin{aligned} \dot{r}=-\varDelta r+\frac{(1-r^{2})}{2}(F\cos (\psi )-Kr) \end{aligned}$$

(20)

$$\begin{aligned} \dot{\psi }=\varOmega -\frac{F}{2r}(1+3r^{2})\sin (\psi ) \end{aligned}$$

(21)

where $\varOmega =-(\sigma -\omega _{0})$, $\psi$ is the mean field of the full system.

Fig. 7

Analytical and numerical plots for order parameter with F for different $\varDelta$ values

Figure 7 shows the order parameter as calculated from the equation with increasing value of F for different $\varDelta$ values along with the respective numerical result.

7 Conclusion

We observed that in the presence of a strong attractively coupled oscillator, a system of repulsively coupled kuramoto oscillators reach synchronization faster than a system of attractively coupled oscillators. There are different regions of synchronization of the internal oscillators, characterized by their frequencies. They are such that the mean of the internal oscillators are integer multiples of the external oscillator frequency.

Next found out that this phenomenon is independent of the initial frequency distribution by repeating the numerical simulations for a total of three different initial internal frequency distributions: namely the Lorentzian, Gaussian and uniform distributions.

We also observed that even though this phenomenon occurs independent of the initial internal frequency distribution, they are dependent on the width of the distribution, which characterizes how close these initial values are and the smaller the width, the more clearer these separate regions became. In other words the more identical the initial distribution, the more clear the observed phenomenon.

Finally, we solved this system of equations using the method given by Ott-Antonsen. After having done the analysis, it was discovered that this phenomenon was not seen analytically.