Keywords

Introduction

The University of Paderborn requires the course “Introduction into the culture of mathematics” for all first-year pre-service teachers (lower track secondary school) to help them to accomplish the transition to higher mathematics . This course has been developed and taught by Biehler and Kempen (2013). Refining and evaluating the course is a main focus of the author’s dissertation. In this course, four different kinds of proofs are used to foster students’ proof skills: the generic proof with numbers, the generic proof in the context of figurate numbers , the formal proof and the proof in the context of figurate numbers using “geometric variables” (Kempen and Biehler 2016). The course’s three main objectives are: (1) to enhance students’ transition to the mathematical formal proof, (2) to promote the mathematical symbolic language in a meaningful way and (3) to equip students with “intellectual-honest” (Stylianides 2007) ways of proving, that can be used in school mathematics later on. The course is evaluated and refined in a design based research scenario (Gravemeijer and Cobb 2006). In this chapter I will outline the part of the project in which students rated the conviction , verification and explanatory power of the different kinds of proofs in the beginning of the course.

Theoretical Background

In the teaching of mathematical proof , different kinds of proofs have been introduced and discussed by mathematics educators (Dreyfus et al. 2012). In various domains of education much attention has been paid to the concept of generic proof (e.g., Rowland 2002; Karunakaran et al. 2014; Stylianides 2010); “A generic proof aims to exhibit a complete chain of reasoning from assumptions to conclusion, just as in a general proof; however, […] a generic proof makes the chain of reasoning accessible to students by reducing its level of abstraction; it achieves this by examining an example that makes it possible to exhibit the complete chain of reasoning without the need to use a symbolism that the student might find incomprehensible” (Dreyfus et al. 2012, p. 204). From a pedagogical point of view, several important questions arise when using a generic proof: How can one expose the generality of an argumentation given in a concrete context to a reader of the proof? How can a reader of a ‘generic proof’ know what part of the concrete examples presented are meant to be generic? (cf. Biehler and Kempen 2013; Mason and Pimm 1984; Reid and Vallejo Vargas 2017, this volume). Building on this discussion, Biehler and Kempen (2013) developed a pedagogical concept of generic proofs : In a generic proof the generic argument is illustrated in concrete examples and its validity and generality is explicitly expressed in words. In the following, I will refer to this concept. (Examples of generic proofs will be given below.)

In contrast to the suggestions in the literature for the use of the generic proofs , their benefits and usefulness for the learning of mathematical proof has not been investigated in detail yet. With this research study, I want to contribute to the ongoing discussion on the usefulness of different kinds of proofs with respect to conviction , verification and explanation.

In mathematics proofs are said to cover different functions. The most prominent ones are verification/conviction , explanation, systematization, discovery and communication (e.g., de Villiers 1990). Referring to the work of Hersh (1993) I argue that there are two important aspects of proofs: conviction and explanatory power. In dealing with the function conviction, the distinction between relative and absolute conviction made by Weber and Mejia-Ramos (2015) seems to be fruitful to clarify two different functions a proof might fulfill. Absolute conviction is about the mathematical ‘objective’ truth of a statement, verified by a mathematical proof . In the following, this function of establishing objective truth will be called verification. Relative conviction is meant as a personal subjective conviction that a statement is or might be true: a reader of a proof “has a relative conviction in a claim if the subjective level of probability that one attribute to that claim being true exceeds a certain” (ibid., p. 16). This relative conviction will be meant when using the term conviction in the following. An important distinction in the teaching of proofs has been given by Hanna (1989) who distinguishes between proofs that (only) prove that a theorem is true and proofs that (also) explain why it is true. From an educational point of view she highlights the function of explanation. In the following part, I will give a brief theoretical outline on these, as I consider three different functions of proofs: verification, conviction and explanation.

Verification

Verification is concerned with the ‘truth’ of a statement. A proof verifies a statement by showing that it is a necessary conclusion from axioms or previous proved theorems. Everyone who agrees with the arguments and logic inferences has to agree with the concluding results. It is this view on mathematical proof that lends the finding to be timeless (Weber 2014): The proven theorem will be ‘true’ forever.

Conviction

Mathematical proof is said to be a convincing argument (e.g., Hanna 1989; Hersh 1993). Here, conviction is considered a personal and subjective category (see above). A proof may convince us that a statement is true, i.e., the reader is persuaded without any doubt that the statement holds in every possible case and that no counterexample may exist. This view on conviction is related to the concept of “epistemic value” of Duval (1990, 2007). As Reid and Knipping (2010, p. 74) mention: “it is important to recognize that while logically a statement can only be true or false, psychologically it can take on one of many values, which Duval (1990, 2007) calls its “epistemic value””. Accordingly, the epistemic value highlights the individual perception of conviction as a personal judgement of whether a proposition is believed (cf. ibid., p. 74).

Explanation

Hanna (1989) stresses that a proof can give insight as to why a statement is true. She further states: “I will say that proof explains when it shows what “characteristic property” entails the theorem it purports to prove” (Hanna 1989, p. 47). Explanatory proofs often make use of geometric descriptions to reach the conclusion. These kinds of representations are said to be more comprehensible or accessible for learners and ease the transition to algebra (compare Flores 2002). As explicated by Hanna (2017, in this book), explanation can have different meanings. In the philosophy of mathematics an intra-mathematical focus on explanation is emphasized, stressing the connections between mathematical statements and their mutual relationships (compare the quotation by Hanna above). From a pedagogical point of view, explanation can be understood as conveying some kind of insight, why a mathematical statement is true. In this sense, explanation is closely related to the aim of personal understanding. However, for this study, one has to stress that ‘to explain’ is defined implicitly by what is meant individually by the students.

Following the theoretical considerations above, verification can be considered a concept that stands for its own. A reader of a proof might perceive the necessity of a conclusion in a proof or not. However, one might identify a link between explanation and (relative) conviction . Conviction is linked to a personal judgement based on one’s knowledge and understanding. The initial point of an explanation is a deficit in someone’s knowledge. Accordingly, an explanation aims at increasing someone’s knowledge and thus may change his epistemic situation (compare Kiel 1999, p. 72 f.) and therefore may lead to conviction .

Findings from the Literature

Results from different studies suggest that some students do not accept deductive proofs as verification (e.g., Fischbein and Kedem 1982; Healy and Hoyles 2000; for an overview, see Reid and Knipping 2010). In these studies, after having seen a correct deductive proof, some learners did not accept the immanent general verification of the proof to cover all possible cases. This non-acceptance of a correct proof gets even more important when looking at generic proofs . In the study of Tabach et al. (2010) about half of the secondary school teachers rejected correct generic proofs due to a perceived lack of generality. In the study of Martin and Harel (1989) between 42 and 46% of the 101 pre-service teachers gave only low ratings to the generic proofs (‘particular proof’) concerning verification. Also Dreyfus (2000) and Knuth (2002) showed that teachers might underestimate proofs making use of concrete examples and narratives. Kempen and Biehler (2016) identified different perceptions of generic proofs (with numbers) and found that few students were convinced by the generic proofs both from a logical and psychological perspective.

In the study of Healy and Hoyles (2000), students were asked to rate different types of arguments (empirical, algebraic and narrative) with regard to explanatory power (the answer “…is an easy way to explain to someone in your class who is unsure”; ibid., p. 403). There, the algebraic arguments had the lowest ratings concerning explanatory power, whereas the narrative arguments obtained the highest. Concerning students’ preference for their own approach to prove a theorem, the authors conclude: “students preferred arguments that they could evaluate and that they found convincing and explanatory, preferences that excluded algebra ” (ibid., p. 426).

Research Questions

This chapter focuses on the degree of conviction , verification and explanatory power perceived by pre-service teachers when reading different kinds of proofs. The research question is: How do pre-service teachers (lower track secondary school) rate the conviction , verification and explanatory power of four different kinds or proofs (the generic proof with numbers, the generic proof in the context of figurate numbers , the proof in the context of figurate numbers using “geometric variables”, and the formal proof) at the beginning of a course for first-year students?

This research question is a part of a wider research project, where the impact of the course “Introduction into the culture of mathematics ” was evaluated with a pre- and a post-test. The focus of this chapter is on the results of the pre-test that took place in the first session of the course. The results also give insight into students’ understanding of mathematical proof when entering university.

Methodology

In the first session of the course, the participants were asked to complete a proof questionnaire (paper and pencil). These students’ had passed the German Abitur (final secondary school examination) when graduating at the ‘Gymnasium’ (higher track secondary school). The questionnaire included each type of concrete proof mentioned above, one type for each statement (see below). The students had to rate different aspects of the proofs on a six-level Likert scale ([1] totally disagree … [6] totally agree). The aspects to be rated were verification, generality, conviction , explanatory power, and acceptance as correct and valid proof. It was then possible to construct a high reliable scale of “proof acceptance”. In this contribution, the focus is on the questionnaire’s following three statements: (i) “The reasoning convinces me that the statement is true” [conviction]; (ii) “The reasoning shows that the statement is true for every time and 100%” [verification]; (iii) “The reasoning explains to me why the statement is true” [explanatory power]. In addition to the following proofs, no further information was given to the students. The items to be answered (see above) did not contain the annotations “conviction ”, “verification” and “explanation”.

I chose a different statement for each proof being rated. When using four different proofs to one statement in a previous pilot study, I identified influences between the different proofs that weakened the results. So I made the choice for using four different statements, even though in this case the ratings of one proof might be influenced by the correspondent statement. The proofs to be rated in this study were selected after piloting different kinds of proofs to different statements twice.

The students answered the questionnaire by using an anonymous code. Their answers had no impact on students’ grades in the course in any way. The proofs to be rated are shown below.

  • Statement (1): The sum of an odd natural number and its double is always odd.

Generic proof with numbers:

$$ 1 + 2 \cdot 1 = 3 \cdot 1 = 3,\quad 5 + 2 \cdot 5 = 3 \cdot 5 = 15,\quad 13 + 2 \cdot 13 = 3 \cdot 13 = 39 $$

The sum of an odd natural number and its double equals three times the initial number. Since the initial number is an odd number, one obtains the product of two odd numbers. Since the product of any two odd numbers is always odd, the result will always be an odd number.

  • Statement (2): The sum of five consecutive natural numbers is always divisible by five.

Generic proof in the context of figurate numbers:

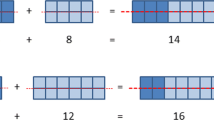
In the representation of the sum of five consecutive natural numbers by figurate numbers , one always obtains the same shape of stairs on the right side. By transforming these stairs—taking the edge at the bottom right and putting it above—one always obtains five equal rows. So the result will always be divisible by five (Fig. 16.1).

Fig. 16.1
figure 1

The sum of five consecutive numbers represented by figurate numbers

Full size image

  • Statement (3): The square of an even natural number is always divisible by four.

Proof with geometric variables:

(This proof was given without any verbal explanation. Here, the geometric variables are used to express the generality that has to be explained in the case of the generic proofs above.) (Fig. 16.2).

Fig. 16.2
figure 2

A proof with “geometric variables” and figurate numbers

Full size image

  • Statement (4): For all natural numbers \( \varvec{a},\varvec{b},\varvec{c} \) : If \( \varvec{b} \) is a multiple of \( \varvec{a} \) and \( \varvec{c} \) is a multiple of \( \varvec{a} \) , then \( \left( {\varvec{b} + \varvec{c}} \right) \) is a multiple of \( \varvec{a} \).

Formal Proof:

Let \( a, b, c \) be natural numbers. Since \( b \) is a multiple of \( a \) , there exists a natural number \( n \) with: \( n \cdot a = b \) . Since \( c \) is a multiple of \( a \) , there exists a natural number \( m \) with: \( m \cdot a = c \) . We get: \( b + c = n \cdot a + m \cdot a = \left( {n + m} \right) \cdot a \) . Since \( \left( {n + m} \right) \) is a natural number, \( \left( {b + c} \right) \) is a multiple of a. □

Results

In our study 149 pre-service teachers (94 female and 55 male; age: \( {\bar{\text{a}}} = 21.14 \)) were asked to rate four different kinds of proofs: the generic proof with numbers (“GenN”), the generic proof in the context of figurate numbers (“GenFig”), the formal proof (“FP”), and the proof in the context of figurate numbers using “geometric variables” (“GV”). Here, I am examining on the proofs’ conviction , verification and explanatory power. Each aspect was rated on a six-level Likert scale ([1] totally disagree … [6] totally agree). The results of students’ ratings are shown below. (Since not all students have answered every question, some results refer to a sample size less than 149.)

  • Conviction (ratings of the item “The reasoning convinces me that the statement is true.”)

Students rated the proof using geometric variables as the proof that was the least convincing with a median of 3. The generic proof with numbers had a median of 4, which means “just a little agreement”, but the responses show a higher variation (first quartile: 2, third quartile 5). The generic proof with figurate numbers (median: 5) and the formal proof (median: 6) were rated the highest (see Fig. 16.3). The differences concerning the medians are pairwise highly statistically significant (p < 0.001), the difference between the medians of “GenN” (4) and “GV” (3) is significant with ‘only’ p = 0.036 (Wilcoxon-test).

Fig. 16.3
figure 3

Boxplots and statistical data concerning the item “conviction ” ([1] totally disagree … [6] totally agree)

Full size image

  • Verification (ratings of the item “The reasoning shows that the statement is true for every time and 100%.”)

Concerning verification, the generic proof with numbers had the median of 1, which means “totally disagree”. Having a look at the boxplot (see Fig. 16.4), the position of the box seems to be considerable (first quartile: 1, third quartile: 2). The generic proof with figurate numbers and the proof with geometric variables had a median of 2, but the responses show a high variation. The formal proof (median: 6) was rated the highest (first quartile: 4, third quartile: 6). All differences concerning the medians are pairwise highly statistically significant (p < 0.001; Wilcoxon-test).

Fig. 16.4
figure 4

Boxplots and statistical data concerning the item “verification” ([1] totally disagree … [6] totally agree)

Full size image

  • Explanatory power (ratings of the item “The reasoning explains why the statement is true.”)

With regard to explanatory power, the proof with geometric variables had the lowest median. In this case, the high variation of ratings is remarkable (first quartile: 1, third quartile: 4). The generic proof with numbers was rated with a median of four and the generic proof with figurate numbers with a median of five. Concerning the explanatory power, the formal proof is considered the best (see Fig. 16.5). All differences concerning the median are pairwise highly statistically significant (p < 0.001; Wilcoxon-test).

Fig. 16.5
figure 5

Boxplots and statistical data concerning the item “explanatory power” ([1] totally disagree [6] totally agree)

Full size image

Discussion

In this study, 149 pre-service teachers were asked to rate four different kinds of proofs (a generic proof with numbers, a generic proof in the context of figurate numbers , a proof in the context of figurate numbers using “geometric variables”, and the formal proof) concerning the aspects conviction , verification and explanation. The study took place in the first session of a mathematics course for first-year students.

At the beginning of the course, the formal proof achieved the highest ratings in all the three categories: “conviction ”, “verification” and “explanatory power”. Concerning conviction , the generic proofs got the medians of 4 and 5, whereas the proof with geometric variables was rated the lowest with a median of 3. With regard to verification, the generic proofs were rejected by most of the students (median of 1 and 2), as was the proof with geometric variables (median of 2). These results also show that conviction and verification can be distinguished in this study. Most of the students stated little agreement to the explanatory power of the generic proofs (medians of 4 and 5). And the proof with geometric variables was only considered slightly explanatory (median of 3) with high variation.

Comparing the generic proofs, the generic proof in the context of figurate numbers is rated higher in all three cases (conviction , verification and explanation). Accordingly, the notational system of figurate numbers seems to be more convincing and explanatory for the students and seems to imply a higher form of verification for them.

The fact that the formal proof is always rated higher than the generic proofs is a little surprising, because in the generic proofs the argument is explicitly written down, in addition to the concrete examples that illustrate the argument. These results conflict with the assumption that generic proofs are more explanatory by themselves (compare Hemmi 2006; Rowland 1998). But one can conclude that in this study, the mathematical symbolic language is perceived as both convincing and explanatory by the students and that the pre-service teachers accept the verification fulfilled in the formal proof.

Concerning the proof with geometric variables, one might assume that this kind of representation might not be known to all students. In addition, this proof was the only one that was not accompanied by any narrative or algebraic-symbolic expression. This fact might also explain the high variation of ratings.

It seems obvious that students’ ratings of the proofs also rely on their former mathematics classes at school. Here, the concept of the didactical contract of Brousseau (1997) and the theory of socio-mathematical norms of Yackel and Cobb (1996) can be taken into account to give explanations for students’ choices. Students learned explicitly and implicitly what kind of argument they might consider as a proof or not during their former mathematics classes at school. In addition, the content of an argument and its appearance has to be considered. Also Healy and Hoyles (2000) and Stylianides and Stylianides (2009) stress that the appearance of an argument influences learners’ evaluation.

Following these considerations, the results do not only depend on the different kinds of proofs (the appearance) and on the different statements being proved, but also on the different educational background of the participants. However, as has been shown above, a geometrical representation does not guarantee that the proof will be considered explanatory. On the contrary, when the students are not familiar with this kind of representation, they may not understand the argument. These findings stress the awareness that a representation is neither self-evident nor self-explanatory and that its use does not necessarily lead to understanding (cf. Jahnke 1984). These results can be supported by taking a semiotic perspective. I.e., Peirce introduces the term ‘collateral knowledge’ to subsume all the knowledge one needs to read and to work in a notational system with some kind of representations he calls diagrams (Hoffmann 2005; Stjernfelt 2000). This collateral knowledge has to be developed by learners to do mathematics in general and to perform and to understand mathematical reasoning in particular. Following these considerations, learners must spent some time to acquire representations and symbols as mathematical tools. Working in and reading a notational system has to be learned explicitly (as proposed in the context of diagram literacy in Diezmann and English 2001). But as was shown above, when the mathematical symbolic language has been acquired by a learner, it becomes a convincing and explanatory tool to fulfill verification. More research is needed to investigate the role of students’ former mathematics classes, the content of an argument and its representation when dealing with mathematical proof .

Having in mind that generic proofs and figurate numbers are said to be useful and adequate tools to perform reasoning and proving even in school mathematics , several questions arise: How can school students develop an adequate understanding of mathematical proof when they might not understand or accept the general verification fulfilled by a given (generic) proof either? Do school students or students at university have enough time to acquire collateral knowledge about all the representations and symbols the teachers want them to use? How might students at school and at university learn about the different functions of mathematical proof when not perceiving them? Following these considerations, it seems valuable to highlight the meaning of proof acceptance when discussing forms of proofs and proving in the classroom.

As Hanna (1995) points out, explanatory proof can have different forms depending on the classroom context and the experience of the learners. According to the results of this study, one has to consider the explanatory power of the mathematic symbolic language and to rethink the concept of proofs that prove and proofs that explain.