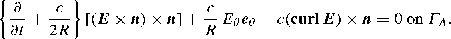Abstract
The aim of this first chapter is to present the physics framework of electromagnetism, in relation to the main sets of equations, that is, Maxwell’s equations and some related approximations. In that sense, it is neither a purely physical nor a purely mathematical point of view. The term model might be more appropriate: sometimes, it will be necessary to refer to specific applications in order to clarify our purpose, presented in a selective and biased way, as it leans on the authors’ personal view. This being stated, this chapter remains a fairly general introduction, including the foremost models in electromagnetics. Although the choice of such applications is guided by our own experience, the presentation follows a natural structure.
Access provided by CONRICYT-eBooks. Download chapter PDF
The aim of this first chapter is to present the physics framework of electromagnetism, in relation to the main sets of equations, that is, Maxwell’s equations and some related approximations. In that sense, it is neither a purely physical nor a purely mathematical point of view. The term model might be more appropriate: sometimes, it will be necessary to refer to specific applications in order to clarify our purpose, presented in a selective and biased way, as it leans on the authors’ personal view. This being stated, this chapter remains a fairly general introduction, including the foremost models in electromagnetics. Although the choice of such applications is guided by our own experience, the presentation follows a natural structure.
Consequently, in the first section, we introduce the electromagnetic fields and the set of equations that governs them, namely Maxwell’s equations. Among others, we present their integral and differential forms. Next, we define a class of constitutive relations, which provide additional relations between electromagnetic fields and are needed to close Maxwell’s equations. Then, we briefly review the solvability of Maxwell’s equations, that is, the existence of electromagnetic fields, in the presence of source terms. We then investigate how they can be reformulated as potential problems. Finally, we relate some notions on conducting media.
In Sect. 1.2, we address the special case of stationary equations, which have time-periodic solutions, the so-called time-harmonic fields. The useful notion of plane waves is also introduced, as a particular case of the time-harmonic solutions.
Maxwell’s equations are related to electrically charged particles. Hence, there exists a strong correlation between Maxwell’s equations and models that describe the motion of particles. This correlation is at the core of most models in which Maxwell’s equations are coupled with other sets of equations: two of them—the Vlasov–Maxwell model and an example of a magnetohydrodynamics model (or MHD)—will be detailed in Sect. 1.3.
We introduce in the next section approximate models of Maxwell’s equations, ranging from the static to the time-dependent ones, in which one or all time derivatives are neglected. We also consider a general way of deriving such approximate models.
In Sect. 1.5, we recall the classification of partial differential equations, and check that Maxwell’s equations are hyperbolic partial differential equations.
At an interface between two media, the electromagnetic fields fulfill some conditions. In a similar way, when one of the media is considered as being exterior to the domain of interest,Footnote 1 interface conditions are then formulated as boundary conditions on the boundary of the domain. Also, to reduce the overall computation cost, one usually truncates the domain by introducing an artificial boundary, on which (absorbing) boundary conditions are prescribed. Another possibility is to introduce a thin, dissipative layer, in which the fields are damped. This constitutes the first topic of Sect. 1.6. The second topic is the radiation condition, which is required for problems set in unbounded domains to discriminate between outgoing and incoming waves.
The aim of the last section is to recall the basic notions of energy in the context of Maxwell’s equations. In particular, notions such as electromagnetic energy flow, Poynting vector and energy conservation are defined.
We conclude this introductory chapter by providing a set of bibliographical references.
1.1 Electromagnetic Fields and Maxwell’s Equations
We present the electromagnetic fields in their time-dependent form, as the solutions to Maxwell’s equations. The various components of the electric and of the magnetic fields are related to source terms by either a set of integral equations or a set of first-order partial differential equations. Then, we study the constitutive relations, which provide additional relations for the electromagnetic fields. With this set of equations—differential Maxwell equations and constitutive relations—we can state that, starting from a given configuration, the electromagnetic fields (exist and) evolve in a unique way. We also expose another formulation, called the potential formulation, with a reduced number of unknowns, which can be interpreted as primitives of the electromagnetic fields. Finally, we conclude with a brief study of conducting/insulating media.
1.1.1 Integral Maxwell Equations
The propagation of the electromagnetic fields in continuum media is described using four space- and time-dependent functions. If we respectively denote by x = (x 1, x 2, x 3) and t the space and time variables, these four \(\mathbb {R}^3\)-valued, or vector-valued, functions defined in time-space \(\mathbb {R}\times \mathbb {R}^3\) are
-
1.
the electric field E ,
-
2.
the magnetic induction B ,
-
3.
the magnetic field Footnote 2 H ,
-
4.
the electric displacement D .
These vector functions are governed by the integral Maxwell equations below. These four equations are respectively called Ampère’s law, Faraday’s law, Gauss’s law and the absence of magnetic monopoles. They read as (system of units SI)
Above, S, S′ are any surface of \(\mathbb {R}^3\), and V , V ′ are any volume of \(\mathbb {R}^3\). One can write elements dS and dl as dS = n dS and dl = τ dl, where n and τ are, respectively, the unit outward normal vector to S and the unit tangent vector to the curve ∂S. When S is the closed surface bounding a volume, then n is pointing outward from the enclosed volume. Similarly, the unit tangent vector to ∂S is pointing in the direction given by the right-hand rule.
There are two source terms, respectively, ϱ and J. ϱ is an \(\mathbb {R}\)-valued, or scalar-valued, function called the electrostatic charge density . It is a non-vanishing function in the presence of electric charges. J is an \(\mathbb {R}^3\)-valued function called the current density . It is a non-vanishing function as soon as there exists a charge displacement, or in other words, an electric current. Now, take the time-derivative of Eq. (1.3) and consider S = ∂V in Eq. (1.1): by construction, S is a closed surface (∂S = ∅), so that these data satisfy the integral charge conservation equation
Again, V is any volume of \(\mathbb {R}^3\).
1.1.2 Equivalent Reformulation of Maxwell’s Equations
Starting from the integral form of Maxwell’s equations (1.1–1.4), one can reformulate them in a differential form,Footnote 3 with the help of Stokes and Ostrogradsky formulas

One easily derives the differential Maxwell equations (system of units SI):


The differential charge conservation equation can be expressed as
However, the above set of equations is not equivalent to the integral set of equations. As a matter of fact, two notions are missing.
The first one is related to the behavior of the fields across an interface between two different media. Let Σ be such an interface.
Starting from the volumic integral equations (1.3)–(1.4), we consider thin volumes V 𝜖 crossing the interface. As 𝜖 goes to zero, their height goes to zero, and so does the area of their top and bottom faces (parallel to the interface), with proper scaling. The top and bottom faces are disks whose radius is proportional to 𝜖, while the height is proportional to 𝜖 2. As a consequence, the area of the lateral surface is proportional to 𝜖 3 and its contribution is negligible as 𝜖 goes to zero. Passing to the limit in Eqs. (1.3) and (1.4) then provides some information on the jump of the normal (with respect to Σ) components of D and B:
Above, [f] Σ denotes the jump across the interface f top − f bottom , and n Σ is the unit normal vector to Σ going from bottom to top. The right-hand side σ Σ corresponds to the idealized surface charge density on Σ: formally, ϱ = σ Σ δ Σ .Footnote 4
Starting from Eqs. (1.1)–(1.2), the reasoning is similar. For the tangential components, one gets
with j Σ the (idealized) surface current density on Σ (j Σ is tangential to Σ).
Finally, if div Σ denotes the surface divergence, or tangential divergence, operator, integral charge conservation equation (1.5) yields
The second notion is topological. For instance, one can consider that the domain of interest is the exterior of a thick (resistiveFootnote 5) wire, or the exterior of a finite set of (perfectly conducting5) spheres. In the first case, the domain is not topologically trivial, and in the second one, its boundary is not connected. In both instances, a finite number of relations—derived from homology theory—have to be added to the differential equations (1.6)–(1.9) and the interface relations (1.11)–(1.12) (see Chap. 3 for details). We assume that, by doing so, we obtain a framework that is equivalent to the integral Maxwell equations (1.1)–(1.4).
1.1.3 Constitutive Relations
Maxwell’s equations are insufficient to characterize the electromagnetic fields completely. The system has to be closed by adding relations that describe the properties of the medium in which the electromagnetic fields propagate. These are the so-called constitutive relations , relating, for instance, D and B to E and H, namely
(We could also choose a priori to use such a relation as D = D(E, B), etc.)
These constitutive relations can be very complex. For this reason, we will make a number of assumptions on the medium (listed below), which lead to generic expressions of the constitutive relations. This will yield three main categories of medium, which are, from the more general to the more specific:
-
1.
the chiral medium , a linear and bi-anisotropic medium ;
-
2.
the perfect medium , a chiral, non-dispersive and anisotropic medium ;
-
3.
the inhomogeneous medium , a perfect and isotropic medium, and its sub-category, the homogeneous medium, which is, in addition, spatially homogeneous.
In what follows, E(t) (or B(t), etc.) denotes the value of the electric field on \(\mathbb {R}^3\) at time t: x↦E(t, x). Let us now list the assumptions about the medium.
-
The medium is linear . This means that its response is linear with respect to electromagnetic inputs (also called excitations later on). In addition, it is expected that when the inputs are small, the response of the medium is also small.
-
The medium satisfies a causality principle . In other words, the value of (D(t), B(t)) depends only on the values of (E(s), H(s)) for s ≤ t.
-
The medium satisfies a time-invariance principle . Let τ > 0 be given. If the response to t↦(E(t), H(t)) is t↦(D(t), B(t)), then the response to t↦(E(t − τ), H(t − τ)) is t↦(D(t − τ), B(t − τ)).
Note that the first assumption corresponds to a linear approximation of D = D(E, H): for electromagnetic fields, whose amplitude is not too large, a first-order Taylor expansion is justified. Furthermore, the smallness requirement can be viewed as a stability condition (with respect to the inputs). An immediate consequence of the second assumption is that, if (E(s), H(s)) = 0 for all s ≤ t 0, then (D(t 0), B(t 0)) = 0. Taking all those assumptions into account leads to the constitutive relations

Let us comment on expression (1.13).
The constitutive parameters  ,
,  ,
,  and
and  are 3 × 3 tensor real-valued functions or distributions of the space variable x. Indeed, according to the time-invariance principle, these quantities must be independent of t. Among them,
are 3 × 3 tensor real-valued functions or distributions of the space variable x. Indeed, according to the time-invariance principle, these quantities must be independent of t. Among them,  is called the dielectric tensor, while
is called the dielectric tensor, while  is called the tensor of magnetic permeability.
is called the tensor of magnetic permeability.
The constitutive parameters  ,
,  ,
,  and
and  are 3 × 3 tensor real-valued functions of the time and space variables (t, x). The notation ⋆ denotes the convolution product, a priori with respect to the four variables (t, x):
are 3 × 3 tensor real-valued functions of the time and space variables (t, x). The notation ⋆ denotes the convolution product, a priori with respect to the four variables (t, x):

The causality principle implies  , for all s < 0. As a consequence, the convolution product reduces to
, for all s < 0. As a consequence, the convolution product reduces to

Often, the response depends very locally (in space) on the behavior of the input. So, one assumes locality in space in the convolution product, or, in other words, that the integral in y is taken over a “small” volume around the origin. Here, we further restrict this dependence, as we consider that one can (formally) writeFootnote 6  , etc. We finally reach the expression of the convolution product ⋆
, etc. We finally reach the expression of the convolution product ⋆

To summarize the above considerations, the constitutive parameters  ,
,  ,
,  and
and  are 3 × 3 tensor real-valued functions of the time variable t which vanish uniformly for strictly negative values of t, and as a consequence, the convolution product ⋆ is performed with respect to positive times only (cf. (1.14)).
are 3 × 3 tensor real-valued functions of the time variable t which vanish uniformly for strictly negative values of t, and as a consequence, the convolution product ⋆ is performed with respect to positive times only (cf. (1.14)).
To carry on with the comments on (1.13), we note that the right-hand side can be divided into two parts:

is called the optical response . It is instantaneous, since the values of the input are considered only at the current time. The other part,

is called the dispersive response , hence a notation with an index d . It is dispersive in time, and as such, it models the memory of the medium.
The relations (1.13) with the convolution products as in (1.14) are linear and bi-anisotropic; they model a linear and bi-anisotropic medium , also called a chiral medium . Several simplifying assumptions can be made:
-
The medium is non-dispersive when the dispersive response (1.16) vanishes. In other words, the response of the medium is purely optical (1.15).
-
The medium is anisotropic provided that
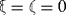 .
. -
An anisotropic medium is isotropic when, additionally, the 3 × 3 tensors
 and
and 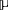 are proportional to the identity matrix:
are proportional to the identity matrix: 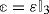 and
and 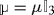 .
.
For an anisotropic medium, the constitutive parameters ε and μ are scalar real-valued functions of x: ε and μ are respectively called the electric permittivity and the magnetic permeability of the medium.
In this monograph, apart from the “general” case of a chiral medium, we shall assume most of the time that the medium is perfect , that is, non-dispersive and anisotropic, or inhomogeneous , that is, perfect and isotropic. In a perfect medium, the constitutive relations read as

In this case, the differential Maxwell equations (1.6–1.9) can be written with the unknowns E and H. They read as




To write down Eqs. (1.6–1.9) with the unknowns E and B, one has to note that  is necessarily invertible on \(\mathbb {R}^3\), since we assumed at the beginning that the constitutive relations could also have been written as H = H(E, B)…So, Eqs. (1.18–1.21) can be equivalently recast as
is necessarily invertible on \(\mathbb {R}^3\), since we assumed at the beginning that the constitutive relations could also have been written as H = H(E, B)…So, Eqs. (1.18–1.21) can be equivalently recast as



In an inhomogeneous medium, one simply replaces the tensor fields  and
and  with the scalar fields ε and μ in Eqs. (1.18–1.21) or in Eqs. (1.22–1.25).
with the scalar fields ε and μ in Eqs. (1.18–1.21) or in Eqs. (1.22–1.25).
Finally, if the perfect medium is also isotropic and spatially homogeneous, we say (for short) that it is a homogeneous medium . In a homogeneous medium, the constitutive relations can finally be expressed as
Above, ε and μ are constant numbers. Remark that vacuum is a particular case of a homogeneous medium, which will be often considered in this monograph. The electric permittivity and the magnetic permeability are, in that case, denoted as ε 0 (ε 0 = (36π.109)−1F m−1) and μ 0 (μ 0 = 4π.10−7H m−1), and we have the relation c 2ε 0μ 0 = 1, where c = 3.108m s−1 is the speed of light . The differential Maxwell equations become, in this case,


1.1.4 Solvability of Maxwell’s Equations
What about the proof of the existence of electromagnetic fields on \(\mathbb {R}^3\)?
To begin with, there exist many “experimental proofs” of the existence of electromagnetic fields! These experiments actually led to the definition of the equations that govern electromagnetic phenomena, and of the related electromagnetic fields, by Maxwell and many others during the nineteenth and twentieth centuries. So, it is safe to assume that these fields exist, the challenge being mathematical and computational nowadays…
Where does the theory originate? Let us give a brief account of one of the more elementary (mathematically speaking!) results on charged particles at rest (results have also been obtained for circuits, involving currents).
The fundamental experimental results we report here were obtained by Charles Augustin de Coulomb in 1785, when he studied repulsive or attractive forces between charged bodies, small elder balls. In the air—a homogeneous medium (ε = ε a )—let us consider two charged particles, part 1 and part, at rest. Their respective positions are x 1 and x, whereas their respective electric charges are q 1 and q. In short, Coulomb’s results (now known as Coulomb’s law ) state that the two particles interact electricallyFootnote 7 with one another, in the following way. The force F acting on particle part and originating from particle part 1 is such that:
-
it is repulsive if q 1q > 0, and attractive if q 1q < 0 ;
-
its direction is parallel to the line joining the two particles ;
-
its modulus is proportional to |x −x 1|−2 ;
-
its modulus is also proportional to q 1 and q .
If one sets the proportionality coefficient to (the modern) 1∕4πε a , one finds that
Now, define the electric field as the force per unit charge. One infers that
Interestingly, it turns out, after some elementary computations, that one has
In particular, one gets that  , which bears a striking resemblance to Faraday’s law (1.27) for a system at rest. Moreover, after another series of simple computations, one finds that div E = ϱ
1∕ε
a
, where ϱ
1 is equal to \(\varrho _1({\boldsymbol {x}})=q_1\delta _{{\boldsymbol {x}}_1}({\boldsymbol {x}})\): in other words, the charge density is created by the particle part
1, so Gauss’s law (1.28) is satisfied too…
, which bears a striking resemblance to Faraday’s law (1.27) for a system at rest. Moreover, after another series of simple computations, one finds that div E = ϱ
1∕ε
a
, where ϱ
1 is equal to \(\varrho _1({\boldsymbol {x}})=q_1\delta _{{\boldsymbol {x}}_1}({\boldsymbol {x}})\): in other words, the charge density is created by the particle part
1, so Gauss’s law (1.28) is satisfied too…
Furthermore, Coulomb proved that the total force produced by N charged particles on an (N + 1)-th particle (all particles being at rest) is equal to the sum of the individual two-particle forces, so the same conclusions can actually be drawn for any discrete system of charged particles at rest! The formula for the charge density is then \(\varrho _N({\boldsymbol {x}})=\sum _{1\le i\le N}q_i\delta _{{\boldsymbol {x}}_i}({\boldsymbol {x}})\), while
See Sects. 1.3 and 1.7 for continuations.
Now, we focus on the mathematical existence of electromagnetic fields. Evidently, we note that one can devise by hand some solutions to Maxwell’s equations for well-chosen right-hand sides (using, for instance, Fourier Transform or Green functions, cf. Chapter 6 of [141]). However, one can also solve this set of equations in more general and more systematic ways. We give two examples below.
The first one deals with the mathematical existence of the electromagnetic fields, assuming a homogeneous medium in \(\mathbb {R}^3\). More precisely, one adds initial conditions to Eqs. (1.26–1.29), which read as
(Above, we assume that the problem begins at time t = 0.)
The couple (E 0, B 0) constitutes part of the data, the other part being t↦(J(t), ϱ(t)), for t ≥ 0. The set of equations (1.26–1.29) together with the initial conditions (1.31) is called a Cauchy problem. Based on the semi-group theory, one can prove that there exists one, and only one, solution t↦(E(t), B(t)), for t ≥ 0, to this Cauchy problem. Moreover, it depends continuously on the data (the so-called stability condition ). In a more compact way, whenever an existence, uniqueness and continuous dependence with respect to the data result is achieved, one says that the related problem is well-posed : in our case, the Cauchy problem set in all space \(\mathbb {R}^3\) made of a homogeneous medium is well-posed. Obviously, once the existence and uniqueness of (E, B) is achieved, the same conclusion follows for \((\boldsymbol {D},\boldsymbol {H})=(\varepsilon _0\,\boldsymbol {E},\mu _0^{-1}\,\boldsymbol {B})\) (see Chap. 5 for more details).
Here, one has to be very careful, since the uniqueness and continuous dependence of the solution require a (mathematical) measure of the electromagnetic fields and of the data. To achieve these results, one uses the quantity W vac (see below) as the measure for the fields. In this case, it reads as
It turns out that W vac defines the electromagnetic energy in this kind of medium. For more details on energy-related matters, we refer the reader to the upcoming Sect. 1.7.
The second result deals with the existence of the electromagnetic fields, assuming now a general chiral medium in \(\mathbb {R}^3\). By using the same mathematical tools (in a more involved way, see [140]), one can also derive a well-posedness result. To measure the fields, one resorts to an integral similar to (1.32), namely
Note that this measure is used to define the stability condition, which has been previously mentioned. Once the existence and uniqueness of (E, H) is achieved, the same conclusion follows for (D, B), according to the constitutive relations (1.13).
Remark 1.1.1
In a bounded domain, one can derive similar results, with a variety of mathematical tools. We refer the reader again to Chap. 5.
1.1.5 Potential Formulation of Maxwell’s Equations
Let us introduce another formulation of Maxwell’s equations. For the sake of simplicity, we assume that we are in vacuum (in all space, \(\mathbb {R}^3\)), with Maxwell’s equations written in differential form as Eqs. (1.26–1.29). According to the divergence-free property of the magnetic induction B, there exists a vector potential A such that

Plugging this into Faraday’s law (1.27), we obtain

Then, there exists a scalar potential ϕ such that
This allows us to introduce a formulation in the variables (A, ϕ) - the vector potential and the scalar potential, respectively - since it holds there that

This formulation requires only the four unknowns A and ϕ, instead of the six unknowns for the E and B-field formulation. Moreover, any couple (E, B) defined by Eqs. (1.34–1.35) automatically satisfies Faraday’s law and the absence of free magnetic monopoles. From this (restrictive) point of view, the potentials A and ϕ are independent of one another. Now, if one takes into account Ampère’s and Gauss’s laws, constraints appear in the choice of A and ϕ (see Eqs (1.37–1.38) below). Also, the vector potential A governed by Eq. (1.35) is determined up to a gradient of a scalar function: there lies an indetermination that has to be removed. On the other hand, for the scalar potential, the indetermination is up to a constant: it can be removed simply by imposing a vanishing limit at infinity. Several approaches can be used to overcome this difficulty. In what follows, two commonly used methods are exposed. If one recalls the identity

then Eqs. (1.26) and (1.28), with the electromagnetic fields expressed as in (1.34–1.35), yield
These equations suggest that one considers either one of the following two conditions , each one of them helpful in its own way for removing the indetermination.
1.1.5.1 Lorentz Gauge
Let us take (A, ϕ) such that the gradient-term in Eq. (1.37) vanishes:
Hence, Eqs. (1.37–1.38) are written within the Lorentz gauge framework as
This gauge is often used for theoretical matters, since it amounts to solving two wave equations, a vector one for A and a scalar one for ϕ . Remark as well that these equations are independent of the coordinate system. This property is useful for many instances, such as, for example, those originating from the theory of relativity.
1.1.5.2 Coulomb Gauge
This consists in setting the first term in Eq. (1.38) to zero. We thus consider A such that
Equations (1.37–1.38) are now written as
Choosing such a gauge yields a potential ϕ, which is related to ϱ by a static equation (however, ϕ and ϱ can be time-dependent). This model is often used when A is irrelevant, because electrostatic phenomena dominate. This is usually the case in plasma models (see, for instance, Sect. 1.4.5).
Remark 1.1.2
The calculations formally performed here are justified for problems posed in all space. Actually, difficulties appear for the same problems posed in a bounded domain. The first ones are due to the topological nature of the domain. The other ones revolve around the definition of compatible boundary conditions on the potentials (A, ϕ), with respect to those of the electromagnetic fields (E, B). For an extended discussion, we refer the reader to Chap. 3.
1.1.6 Conducting and Insulating Media
For a medium that is also a conductor , we have to describe the property of the medium in terms of conductivity. This leads to expression of the current density J as a function of the electric field E
Assuming that the medium is linear, the current density J and the electric field E are governed by Ohm’s law

where  is a 3 × 3 tensor real-valued function of the space variable x, which is called the tensor of conductivity. The quantity
is a 3 × 3 tensor real-valued function of the space variable x, which is called the tensor of conductivity. The quantity  is also a 3 × 3 tensor real-valued function, but of the time variable t. The convolution product is similar to (1.14): it is realized in time, enforcing the causality principle. Similarly to the constitutive relations, we shall usually restrict our studies to a perfect medium. In this case, Ohm’s law is expressed as
is also a 3 × 3 tensor real-valued function, but of the time variable t. The convolution product is similar to (1.14): it is realized in time, enforcing the causality principle. Similarly to the constitutive relations, we shall usually restrict our studies to a perfect medium. In this case, Ohm’s law is expressed as

If, in addition, the medium is inhomogeneous,  and σ is called the conductivity
. In the particular case of a homogeneous medium, the conductivity is independent of x. Alternatively, one could introduce the resistivity
σ
−1 of the medium, together with the notion of a resistive medium
.
and σ is called the conductivity
. In the particular case of a homogeneous medium, the conductivity is independent of x. Alternatively, one could introduce the resistivity
σ
−1 of the medium, together with the notion of a resistive medium
.
In most cases, the current density can be divided into two parts,
where J
ext
denotes an externally imposed current density, and J
σ
is the current density related to the conductivity  of the medium by the relation (1.39). As a consequence, one has to modify Ampère’s law (1.6), which can be read as
of the medium by the relation (1.39). As a consequence, one has to modify Ampère’s law (1.6), which can be read as

On the one hand, if the medium
is an insulator ( ) there is no electrically generated current in this medium. An insulator is also called a dielectric
. So, one has, in the absence of an externally imposed current, J = 0.
) there is no electrically generated current in this medium. An insulator is also called a dielectric
. So, one has, in the absence of an externally imposed current, J = 0.
On the other hand, we will often deal with a perfectly conducting medium, that is, a perfect conductor , in which the conductivity is assumed to be “infinite”: all electromagnetic fields (and in particular, E and B) are uniformly equal to zero in such a medium. This ideal situation is often used to model metals. Let us discuss the validity of this statement, which is related to the skin depth δ inside a conducting medium. This length is the characteristic scale on which the electromagnetic fields vanish inside the conductor, provided its thickness is locally much larger than δ. The fields decay exponentially relative to the depth (distance from the surface), and so one can consider that they vanish uniformly at a depth larger than a few δ. Note that this behavior is not contradictory to the accumulation of charges and/or currents at the surface of the conductor, the so-called skin effect . The skin depth depends on the frequency ν of the inputs and on the conductivity of the medium: δ is proportional to (σ ν)−1∕2 (see Sect. 1.2.3 for details). For radio signals in the 1–100 MHz frequency range, δ varies from 7 to 70 10−6 m for copper. In the case of a perfect conductor, we simply assume that the skin depth is equal to zero for all inputs. As we noted above, one can have non-zero charge and/or current densities at the surface of a perfect conductor: this is the infinite skin effect .
1.2 Stationary Equations
It can happen that one studies fields and sources for which the behavior in time is explicitly known. For instance, time-periodic solutions to Maxwell’s equations, respectively called time-harmonic electromagnetic fields and time-harmonic Maxwell equations. We first study the basic properties related to these fields and equations. Next, we address the topic of electromagnetic plane waves, which are a class of particular solutions, widely used in theoretical physics and in applications, for instance, to assess numerical methods for the time-harmonic Maxwell equations, or to build radiation conditions.
1.2.1 Time-Harmonic Maxwell Equations
We deal with time-periodic, or time-harmonic, solutions to Maxwell’s equations in a perfect medium (here, \(\mathbb {R}^3\)), with a known time dependence \(\exp (-\imath \omega t)\), \(\omega \in \mathbb {R}\). Basically, it is assumed that the time Fourier Transform of the complex-valued fields, for instance,
is of the form \(\hat {\boldsymbol {E}}(\omega ',{\boldsymbol {x}})=\delta (\omega '-\omega )\otimes \boldsymbol {e}({\boldsymbol {x}})\), so that taking the reverse time Fourier Transform yields
The real-valued (physical) solutions are then written as
Equivalently, one has \(\boldsymbol {E}(t,{\boldsymbol {x}})=\frac {1}{2}\{\boldsymbol {e}({\boldsymbol {x}})\exp (-\imath \omega t)+\overline {\boldsymbol {e}}({\boldsymbol {x}})\exp (\imath \omega t))\}\), etc. As a consequence, one can restrict the study of time-harmonic fields to positive values of ω, which is called the pulsation . It is related to the frequency ν by the formula ω = 2πν.
Remark 1.2.1
Formally, for a pulsation ω equal to zero, one gets static fields, in the sense that they are independent of time. In this way, static fields are a “special instance” among stationary fields.
The data ϱ(t, x) and J(t, x) are also time-harmonic:
Evidently, the time dependence is identical between the data and the solution. Here, we just used straightforward computations!
On the other hand, what happens when one only knows that the data are time-harmonic (without any information on the fields)? In other words, how do the fields, seen as the solution to Maxwell’s equations, behave? The answer, which is much more subtle than the above-mentioned computations, is known as the limiting amplitude principle . It is important to note that this principle can be rigorously/mathematically justified, cf. [104]. It turns out that, provided the data is compactly supported in space, the solution adopts a time-harmonic behavior as t goes to infinity, in bounded regions (of \(\mathbb {R}^3\)). So, common sense proves true in this case. Provided that ϱ and J behave as in Eqs. (1.45–1.46), then the electromagnetic fields behave as in Eqs. (1.41–1.44) when t → +∞, with the same pulsation ω.
The time-harmonic Maxwell equations are


where the charge conservation equation (1.10) becomes
Since the medium is perfect, we have

so that we can express the time-harmonic Maxwell equations in the electromagnetic fields e and b, as



Clearly, one of the fields can be removed in (1.52) and (1.53) to give us


On the one hand, the set of equations (1.56–1.57) is often called a fixed frequency problem . GivenFootnote 8 ω ≠ 0 and non-vanishing data (j, r), find the solution (e, b). The conditions (1.54) and (1.55) on the divergence of the electromagnetic fields are contained in Eqs. (1.56–1.57): simply take their respective divergence, and use the charge conservation equation (1.51) for the electric field, bearing in mind that ω ≠ 0.
On the other hand, one can assume that the current and charge densities vanish. The equations read as



As noted earlier, the condition on the divergence of the electromagnetic fields would be implicit in Eqs. (1.58–1.59) under the condition ω ≠ 0. However, one does not make this assumption here. The set of equations (1.58–1.61) is usually called an unknown frequency problem : find the triples (ω, e, b) with (e, b) ≠ (0, 0) governed by (1.58–1.61). The same set of equations can be considered as an eigenvalue problem, also called an eigenproblem . Here, the pulsation ω is not the eigenvalue. More precisely, its square ω 2 is related to the eigenvalue. For that, it is useful (but not mandatory, see Chap. 8) to assume that the medium is homogeneous, so that ε and μ are constants, as, for instance, in vacuum.
Remark 1.2.2
The unknown frequency problem models free vibrations of the electromagnetic fields. On the other hand, the fixed frequency problem models sustained vibrations (via a periodic input) of the fields.
In a homogeneous medium, eliminating, as previously, the e-field or the b-field from one of the above Eqs. (1.52–1.53) yields, with f
e
= ıωμ
j and  as the (possibly vanishing) right-hand sides,
as the (possibly vanishing) right-hand sides,

where
Using the identity (1.36) leads to, with \(\boldsymbol {f}_e^{\prime }=-\boldsymbol {f}_e+\varepsilon ^{-1} \operatorname {\mathrm {\mathbf {grad}}} r\), \(\boldsymbol {f}_b^{\prime }=-\boldsymbol {f}_b\),
From the point of view of the fixed frequency problem (\((\boldsymbol {f}_e^{\prime },\boldsymbol {f}_b^{\prime })\neq (0,0))\), this means that each component of the vector fields e or b (here called ψ) is governed by the scalar Helmholtz equation
From the point of view of the eigenvalue problem, (λ, ψ) is simply a couple eigenvalue–eigenvector of the Laplace operator: the pulsation ω is related to the eigenvalue λ by the relation (1.62).
Remark 1.2.3
It is important to remark that the components are not independent of one another. Indeed, the components are linked by the divergence-free conditions div e = 0 and div b = 0. As we will see in Sect. 1.6, Eq. (1.63) plays an important role in establishing the radiation condition, which is widely used in diffraction problems.
1.2.2 Electromagnetic Plane Waves
Let us study a particular class of periodic solutions to Maxwell’s equations, the plane waves solutions , in a homogeneous medium (again, \(\mathbb {R}^3\)).
Introduce the time-space Fourier Transform of complex-valued fields, for instance,
The plane waves can be viewed as the reverse time-space Fourier transform of fields, which possess the following form in the phase space (ω′, k ′):
(E 0 and B 0 both belong to \(\mathbb {C}^3\), and k is a vector of \(\mathbb {R}^3\), called the wave vector).
From the above, we deduce that the complex-valued plane waves consist of solutions of the form
We keep the convention, according to which the physical electromagnetic fields are obtained by taking the real part of (1.64–1.65): for instance,
Again, the pulsation ω takes only positive values.
Remark 1.2.4
We will examine how the plane waves are involved in obtaining the absorbing boundary conditions (cf. Sect. 1.6).
A plane wave propagates. To measure its velocity of propagation, one usually considers the velocity at which a constant phase (a phase is the value of (E c, B c) at a given time and position) travels. It is called the phase velocity and, according to expressions (1.64–1.65), it is equal to
So, k≠0. The quantity |k| is called the wave number , and λ = 2π∕|k| is the associated wavelength . If we let \(\boldsymbol {d}\in \mathbb {S}^2\) be the direction of k, i.e., k = |k|d, we can further define the vector velocity of propagation, v p = v p d.
Let us consider that the medium is without sources (charge and current density), so that the fields and pulsation solve the problem (1.52–1.55) with zero right-hand sides, due to the explicit time-dependence of the plane waves. In addition, they have a special form with respect to the space variable x, so one has  and div E = ı
k ⋅E. The equations become, since ε, μ are constant numbers,
and div E = ı
k ⋅E. The equations become, since ε, μ are constant numbers,
One can remove B 0 from the first two equations to obtain
This equation requires the vector k × (k ×E 0) to be parallel to E 0, which is possible if and only if k ⋅E 0 = 0, i.e., Eq. (1.69) precisely. This yields |k|2 = εμω 2, and then k × (k ×E 0) = −|k|2E 0. Finally, this allows one to characterize a plane wave as a solution to the following system of equations:
Expression (1.71), relating k to ω, is called the dispersion relation (see, for instance, [151]). Additionally, the relations (1.72–1.73) prove that E 0 and B 0 are transverse to the propagation direction of the plane waves, and orthogonal to one another.
From (1.66) and (1.71), one infers that v p = c, with \(c=1/\sqrt {\varepsilon \mu }\). Denoting k = |k|, one may compute the group velocity defined by
which usually measures the velocity at which energy is conveyed by a wave. In a homogeneous medium (see (1.71)), k↦ω(k) is linear. Hence, the group velocity is the same for all electromagnetic plane waves, and equal to the phase velocity: v g = v p . These waves are non-dispersive, and in this sense, a homogeneous medium itself is non-dispersive.
To conclude this series of elementary computations, we have established that, for any wave vector \(\boldsymbol {k}\in \mathbb {R}^3\setminus \{0\}\), there exists an electromagnetic complex-valued plane wave, which reads as
with E 0 verifying (1.72) and related to B 0 as in (1.73).
More generally, the electromagnetic fields in \(\mathbb {R}^3\) can be considered as a superposition of plane waves (plus constant fields), so that E 0 and B 0 depend on the wave vector, and one ultimately has
The physical electromagnetic fields can be expressed in two forms. First, as
Second (and the expressions are equivalent), as
Remark 1.2.5
Everywhere in space, any couple (k, ω) such that c |k| = ω yields a plane wave governed by Maxwell’s equations (with all possible choices of propagation directions in \(\mathbb {S}^2\)). In particular, any strictly positive ω is admissible, which yields all values λ > 0 (cf. (1.62)). If one thinks in terms of the eigenvalue problem (1.58–1.61), the corresponding “eigenvector” is not measurable in the sense of (1.32), so it is called a generalized eigenvector. Adding the constant vectors (generalized eigenvectors related to λ = 0), the set of values λ is {λ ≥ 0}, which is the continuous spectrum. In a bounded domain, however, the situation is completely different: a quantisation phenomenon occurs, i.e., only certain definite values of ω are possible. What is more, classical eigenvectors exist, and the set of eigenvalues is discrete and countable. Most examples studied in this book will fall into the latter category of a countable spectrum.
1.2.3 Electromagnetic Plane Waves Inside a Conductor
Let us focus on the time-harmonic Maxwell equations inside an inhomogeneous conductor. In this case, it holds that j(x) = σ(x)e(x), in the absence of an externally imposed current. The time-harmonic Maxwell equations (1.52–1.55) become

with the complex-valued ε σ = ε + ıσω −1. From now on, the medium is assumed to be spatially homogeneous. Consider an electromagnetic plane wave as in (1.64–1.65), that is, \(\boldsymbol {e}({\boldsymbol {x}})=\boldsymbol {E}_0\exp (\imath \boldsymbol {k}\cdot {\boldsymbol {x}})\) and \(\boldsymbol {b}({\boldsymbol {x}})=\boldsymbol {B}_0\exp (\imath \boldsymbol {k}\cdot {\boldsymbol {x}})\), with \(\boldsymbol {k}\in \mathbb {C}^3\) of the form k = k d, where d is a real unit vector and \(k=k_++\imath k_-\in \mathbb {C}\). Note that one can write
so d can be considered as the actual direction of propagation, if k + > 0. This is the convention we adopt below.
One reaches Eqs. (1.67–1.70), with ε replaced by ε σ . Eliminating B 0, one finds the relation k × (k ×E 0) = −ε σ μω 2E 0. It follows that k 2 = ε σ μω 2, and one finds that
with s = ±1. According to the convention we adopted, one necessarily has s = +1. In particular, it holds that k − > 0, so one can write
with an attenuation factor \(\exp (-k_-\boldsymbol {d}\cdot {\boldsymbol {x}})\). The electromagnetic plane wave is absorbed by the conductor as it propagates. In other words, the conductor is a dissipative medium . To conclude, note that the notion of skin depth follows from this discussion, if one considers an approximation of the attenuation factor when η = σ(ωε)−1 ≫ 1. More precisely, the skin depth δ is the distance parallel to d such that the attenuation factor decreases by a factor \(\exp (1)\), i.e., k −δ = 1. Since η ≫ 1,
which is the result stated in Sect. 1.1.6.
As ε σ depends on ω, electromagnetic waves inside a conductor are dispersive, in the sense that they do not travel at the same velocity for different ω (see also Sect. 1.2.4 next). To characterize their behavior, one can study their group velocity , now equal to \(v_g(k_+^0) = \omega '(k_+^0)\), which measures the velocity at which energy is transported, for values of k + close to \(k_+^0\).
1.2.4 Dispersive Media
Applying the (time) Fourier transform to a convolution product results in the product of the (time) Fourier transforms, times 2π. One infers that the constitutive relations (1.13) can be equivalently recast in the ω variable asFootnote 9

It follows that a medium is non-dispersive as soon as the Fourier transforms of the constitutive parameters are independent of ω. We outline the discussion below on some properties of the constitutive parameters for “physically reasonable” media, cf. [169, §1] for details. Assuming that the causality principle holds, it follows that

This expression has two simple, but important, consequences. First, because  is a real-valued tensor, it holds that
is a real-valued tensor, it holds that  for all \(\omega \in \mathbb {R}\). Also, one notices that
for all \(\omega \in \mathbb {R}\). Also, one notices that  has a regular analytic continuation in the upper half-plane ℑ(ω) > 0. In addition, assume, for instance, that
has a regular analytic continuation in the upper half-plane ℑ(ω) > 0. In addition, assume, for instance, that  is square integrable over \(\mathbb {R}\). Then, one can build dispersion relations, also called the Kramers-Kronig relations
, that respectively relate the real part
is square integrable over \(\mathbb {R}\). Then, one can build dispersion relations, also called the Kramers-Kronig relations
, that respectively relate the real part  to all imaginary parts
to all imaginary parts  and the imaginary part
and the imaginary part  to all real parts
to all real parts  :
:

where pv denotes Cauchy’s principal value. On the other hand, if  is square integrable over \(\mathbb {R}\) and if one of the two Kramers-Kronig relations holds,Footnote 10 one finds by applying the (time) inverse Fourier transform that
is square integrable over \(\mathbb {R}\) and if one of the two Kramers-Kronig relations holds,Footnote 10 one finds by applying the (time) inverse Fourier transform that  for s < 0. Hence, the causality principle holds.
for s < 0. Hence, the causality principle holds.
Among dispersive media, one model, which describes the optical (and thermal) properties of some metals, has received renewed attention in recent years. This is the Lorentz model
, with  , where \(\hat \varepsilon _L = \varepsilon _0\) is the optical response and the dispersive response is given by
, where \(\hat \varepsilon _L = \varepsilon _0\) is the optical response and the dispersive response is given by
Above, ω
p
is the plasma frequency, γ
L
≥ 0 is a damping coefficient that accounts for the dissipation, and ω
L
≠0 is the resonance pulsation. The case ω
L
= 0 is usually called the Drude model. One may also add a parameter that acts on the optical response: \(\hat \varepsilon _L\) is modified to \(\hat \varepsilon _L=\varepsilon _\infty \varepsilon _0\) with ε
∞
≥ 1. Note that in the absence of damping, there exist pulsation ranges in which \(\hat \varepsilon _L+\hat \varepsilon _d(\omega )<0\). One may generalize the Lorentz model by defining  with different values of the resonance pulsation ω
L
for 1 ≤ L ≤ N
G
, and where f
L
are strength factors. By construction, the one-pulsation Lorentz model with γ
L
> 0 is square integrable, and it fulfills the Kramers-Kronig relations. As a consequence, the causality principle holds for this model. Thanks to the results of footnote 10, the causality principle is also verified in the absence of damping.
with different values of the resonance pulsation ω
L
for 1 ≤ L ≤ N
G
, and where f
L
are strength factors. By construction, the one-pulsation Lorentz model with γ
L
> 0 is square integrable, and it fulfills the Kramers-Kronig relations. As a consequence, the causality principle holds for this model. Thanks to the results of footnote 10, the causality principle is also verified in the absence of damping.
Finally, the real and imaginary parts of \(\hat \varepsilon _{d}\) have been measured experimentally for a number of metals. In general, \(\hat \varepsilon _d\) is approximately real, i.e., \(|\Re (\hat \varepsilon _d(\omega ))|\) is usually much larger than \(|\Im (\hat \varepsilon _d(\omega ))|\). In given pulsation ranges, these experiments can be matched by either the one-resonance Lorentz model, or the generalized model, with appropriately chosen coefficients.
As seen previously, an inhomogeneous conductor is dispersive. Indeed, in Ampère’s law (1.40), ∂ t D is replaced by ε∂ t E + σ E. So, after the time Fourier transform, one finds that \(-\imath \omega \hat {\boldsymbol {D}}(\omega ) = -\imath \omega \varepsilon \hat {\boldsymbol {E}}(\omega ) + \sigma \hat {\boldsymbol {E}}(\omega )\). In (1.74), \(\hat \varepsilon _{d,cond}\) is equal to
As expected, \(\hat \varepsilon _{cond}=\varepsilon +2\pi \hat \varepsilon _{d,cond}\) is equal to ε σ as defined in Sect. 1.2.3.
1.3 Coupling with Other Models
Maxwell’s equations are related to electrically charged particles. For instance, Gauss’s law (1.3) can be viewed as a (proportionality) relation between the flux of the electric displacement D through a surface and the amount of charges contained inside. In the same way, Coulomb’s law allows one to express the electromagnetic interaction force between particles, from which one can deduce the static equations for the electric field E. In a more general way, the motion of charged particles generates electromagnetic fields. Conversely, for a population of charged particles with a mass m and a charge q (for simplicity reasons, we consider particles that belong to a single species), the main force field is the electromagnetic force field, called the Lorentz force . This force describes the way in which the electromagnetic fields E(t, x) and B(t, x) act on a particle with a velocity v(t):
Hence, there exists a strong correlation between Maxwell’s equations and models that describe the motion of (charged) particles. This correlation is at the core of most coupled models, where Maxwell’s equations appear jointly with other sets of equations, which usually govern the motion of charged particles.
To describe the motion of a set of N particles, one can consider the molecular level, namely by looking simultaneously at the positions (x i )1≤i≤N and the velocities (v i )1≤i≤N of these particles. Assuming that the particles follow Newton’s law, the equations of motion are written as
Above, F is the external force acting on the particles and F int denotes the interaction force that occurs between the particles. These equations are complemented with initial conditions, for instance, at time t = 0,
Note that the system (1.76–1.77) is uniquely solvable, in the sense that it allows one to determine the motion of the N particles. This corresponds to a mechanical description of the set of particles.
Another approach—the statistical description —relies on
π N is the N-particle distribution function: π N (t, X, V ) d X d V denotes the probability that the N particles are respectively located at positions (x 1, ⋯, x N ), with velocities (v 1, ⋯, v N ), at time t. Then, if one considers the actual trajectory of the particles in the 6N-dimensional space t↦(X(t), V (t)), it holds that
Indeed, along the trajectory actually followed by the particles, no particle is created, and no particle vanishes.
With the help of the chain rule, one can rewrite the previous equation as
(This is the Liouville equation.)
One can prove that the mechanical and statistical descriptions are equivalent, via the method of characteristics (see, for instance, [98]).
The charge and current densities induced by the motion of these particles can be written as
where \(\delta _{{\boldsymbol {x}}_i(t)}\) is the Dirac mass in x i (t).
In the following, we will consider more tractable approaches, namely the kinetic model and the fluid model . Note that the kinetic description can be viewed as an intermediate stage between the molecular and the fluid descriptions: it contains information on the distribution of the particle velocities, which is lost in a fluid description. Indeed, the fluid model consists in looking at macroscopic averages of the quantities associated with the particles. The next two subsections are devoted to the models resulting from the coupling of Maxwell’s equations with either the kinetic or the fluid approach.
1.3.1 Vlasov–Maxwell Model
In this kinetic approach , we consider a population of charged particles, subject to a given external force field F(t, x, v) such thatFootnote 11 div v F = 0. Each particle is characterized by its position x and its velocity v in the so-called phase space \(({\boldsymbol {x}},{\boldsymbol {v}})\in \mathbb {R}_{\boldsymbol {x}}^3\times \mathbb {R}_{\boldsymbol {v}}^3\). Instead of considering each particle individually, we introduce the distribution function f(t, x, v), which can be defined as the average number of particles in a volume d x d v of the phase space. So, we have
How can this approach be related to the mechanical description (1.76–1.77), or to the statistical description (1.78–1.79)? Simply, if we denote by X − and V − the variables (x 2, ⋯, x N ) and (v 2, ⋯, v N ), we remark that
is an admissible distribution function. Let it be called f.
Now, we recall that Eq. (1.76) writes
Here, we assume that F int does not depend on (v k ) k . More generally, it would be enough that \(\mathrm {div}_{{\boldsymbol {v}}_k}\boldsymbol {F}_{int}=0\), for all k.
To determine the equations that govern f, we integrate Eq. (1.79) with respect to X −, V −. This leads to
We note that the first two terms are directly expressed in terms of f, since the differentiation is performed in t, or in x = x 1, both of which are absent in (X −, V −). Let us perform the integration by parts of the penultimate integrals with respect to the variable x k (the same index as in the summation). If there is no particle flux at infinity, when |x k |→ +∞, we find that, since it holds that \(\mathrm {div}_{{\boldsymbol {x}}_k}{\boldsymbol {v}}_k=0\) (v k is another variable), one has
Similarly, integrating the last integrals with respect to the variable v k , we find that they vanish too (\(\mathrm {div}_{{\boldsymbol {v}}_k}{\boldsymbol {v}}_k=3\) is independent of t). Next, we have to deal with the middle term, which can be split as
Then, summing up, we reach the relation
The right-hand side is called the collision integral. To model collisions, one usually rewrites this right-hand side as a collision kernel Q(f), which is the rate of change of f per unit time. There are different expressions of Q(f) (linear, quadratic, etc.) depending on the physics involved, which can be very intricate. This yields the relation
Finally, substituting the expression of the Lorentz force (1.75) in this equation, we obtain that the distribution function f(t, x, v) is governed by the following transport equation, called the Boltzmann equation :
In the kinetic description, the expressions (1.80) of the charge and the current densities are respectively given by
When there are several species of particle (respectively, with masses (m α ) α and charges (q α ) α ), one introduces one distribution function per species (f α ) α . Each function is governed by Eq. (1.81). Then, the contributions of all species add up to define ϱ and J,
When several species coexist, the collision integrals include intra-species interactions and inter-species interactions. The inter-species interactions here model transferred quantities (such as the momentum or the energy) between different species. If the collision kernels (Q α (f)) α model elastic collisions between neighboring particles, then conservation laws apply. One finds that
To simplifyFootnote 12 the presentation, we neglect collisions, so the distribution function is governed by the so-called Vlasov equation
when only a single species of particles is concerned. To be able to couple the Vlasov equation with Maxwell’s ones, one has to check that ϱ and J, defined as above, satisfy the differential charge conservation equation (1.10). First, one has div x v = 0 in the phase space, so that v ⋅∇ x f = div x (f v). In the same way, one has F ⋅∇ v f = div v (f F). So, the integration of q times Eq. (1.87) in v over \(\mathbb {R}^3_{v}\) yields
Assuming that f|F| goes to zero sufficiently rapidly when |v| goes to infinity, we obtain, by integration by parts, that the last term vanishes. Indeed,
So, we conclude that ϱ and J given by Eqs. (1.82–1.83) satisfy the differential charge conservation equation as expected.
The relations (1.22–1.25) and (1.82–1.87) clearly express the coupling of Maxwell’s and Vlasov’s equations, since ϱ(t, x) and J(t, x) are the right-hand sidesFootnote 13 of Maxwell’s equations. Moreover, the electromagnetic fields E and B play a crucial role in the force F acting on the particles, cf. Eq. (1.75). Hence, even if Vlasov’s equation and Maxwell’s equations are linear, their coupling yields a problem that is globally quadratic. Indeed, the term \(\frac {q}{m}(\boldsymbol {E}+{\boldsymbol {v}}\times \boldsymbol {B})\cdot \nabla _{{\boldsymbol {v}}} f\) is a quadratic term in f, since E and B depend linearly13 on f through ϱ and J. Thus, the Vlasov–Maxwell model is a non-linear, strongly coupled problem to solve. See Chap. 10 for mathematical studies on this topic.
For the sake of completeness, we conclude this section with a review of several variants of the Vlasov–Maxwell model, which are used in certain applications according to the relative importance of electromagnetic phenomena. For instance, when rapid electromagnetic phenomena occur, it is more consistent to assume a priori that particles obey the relativistic laws of motion. In this framework, phase space is described in terms of positions and momenta \(({\boldsymbol {x}},\boldsymbol {p})\in \mathbb {R}^3_{{\boldsymbol {x}}}\times \mathbb {R}^3_{\boldsymbol {p}}\) rather than velocities. The distribution function is written as f(t, x, p); and velocity becomes a function of momentum:
The distribution function is governed by a modified version of (1.87), namely
The charge and current densities are now defined as
These satisfy the differential charge conservation equation (1.10).
1.3.2 Magnetohydrodynamics
Magnetohydrodynamics (MHD) is the study of the flow of a conducting fluid under the action of applied electromagnetic fields, e.g., a plasma . Usually, one considers the plasma as a solution of electrons and ions (a compressible, conducting, two-fluid). Roughly speaking, it consists in coupling the classical hydrodynamical equations for the fluid with an approximation of Maxwell’s equations, in which the displacement current ∂ t D is neglected.
In a first step, we recall how one can build a fluid model from the Vlasov equation (1.87). Then, we derive usable expressions for the magnetic induction. Finally, the hydrodynamical equations are coupled to Maxwell’s, to finally yield the magnetohydrodynamics model.
As recalled in the introduction to this section, hydrodynamical models are based on a set of conservation equations derived from the Vlasov equation. A simple way to derive these equations is to take the moments of the Vlasov equation. Indeed, fluid descriptions consist in looking at macroscopic averages (with respect to the velocities) of the particle quantities over volumes that are large enough to cancel the statistical fluctuations, but that are small compared to the scales of interest. Hence, fluid unknowns are moments of the distribution function f, such as the particle density n(t, x), the mass density ρ(t, x), the mean velocity u(t, x), the mean energy W(t, x) or the 3 × 3 pressure tensor \(\mathbb {P}(t,{\boldsymbol {x}})\). The first four can be respectively defined as
For the sake of completeness, we have included the moment of order 2 that corresponds to the mean energy. Note that the preceding equations, together with Eqs. (1.82–1.83), immediately yield
Before proceeding, we introduce a variable that allows us to describe the random motion of the fluid:
Then, the pressure tensor \(\mathbb {P}(t,{\boldsymbol {x}})\) is defined as
(Above, w ⊗w is a symmetric tensor of order 3.)
We split this tensor as
The field p is the scalar pressure of the fluid. From the above, one easily infers the relation 2nW = mn|u|2 + 3p, which corresponds to a splitting of the energy (kinetic and internal). Usually, ρ, u and p are called the hydrodynamical variables .
To obtain the evolution equations, we multiply Eq. (1.87) by a test function ϕ(v) and integrate with respect to v to get
Using an integration-by-parts formula (for the last term), and assuming that fϕ|F| goes to zero sufficiently rapidly at infinity, we find
Now, choosing ϕ(v) respectively equal to 1, (v k )k=1,2,3 and |v|2, in other words, by taking moments of order 0, 1 and 2, we obtain a sequence of hydrodynamical evolution equations.
First, taking ϕ(v) = 1 leads to the integral equation

or, with the above definitions of the mass density and mean velocity,
To write simple expressions for the moments of order 1 and 2, let us consider the special case of a laminar (or monokinetic) beam that is a gas in which all the particles move at the same velocity u(t, x). In this case, the distribution function becomes simply
As a consequence, for the moment of order 1, we find the equivalent scalar or vector formulas
(The definition of the vector operator div is clear from the equivalence between the scalar and vector formulas.)
For the moment of order 2, we note that in this special case of a laminar beam, one has \(\mathbb {P}=0\). The fluid is without pressure (in particular, p = 0). Equations (1.88–1.89) are, respectively, the mass and momentum conservation equations for a fluid without pressure.
On the other hand, what happens when such a construction is used to establish fluid equations in general? For instance, for a simple fluid with pressure, or for a fluid including several species of particle. If there are two or more species (labeled by the index α), then one builds one Eq. (1.88) and one Eq. (1.89) per species. Equation (1.88) remains unchanged. For the moments of order 1, Eq. (1.89) retains the same structure, with the following modifications (on the vector formula):
-
The pressure tensor appears on the left-hand side. More precisely, the second term is changed to \(\mathbf {div\,}(\rho \,\boldsymbol {u}\otimes \boldsymbol {u}+\mathbb {P}) = \mathbf { div}(\rho \,\boldsymbol {u}\otimes \boldsymbol {u}) + \operatorname {\mathrm {\mathbf {grad}}} p + \mathbf {div\,}\mathbb {Q}\).
-
For a fluid including several species of particles, a term is added on the right-hand side, to take into account the transferred mean momentum Tr α between different species.
To summarize, one obtains the system of equations


According to Eq. (1.86), it holds that ∑ α Tr α = 0.
Furthermore, the evolution of the mean energy (moment of order 2) is governed by an equation that involves \(\mathbb {Q}_\alpha \), the flux of kinetic energy K α , which is a moment of order 3, and finally, the heat H α , generated by the collisions between particles of different species (on the right-hand side). So, one needs to choose ϕ(v) of degree 3 to derive the equation governing the flux of kinetic energy K α . But this would yield a term of order 4, and so on… In other words, one gets a series of equations that is exact, but not closed!
To avoid this problem, one has to add a “closure relation” to the system of equations at some point. For instance, one chooses to keep the hydrodynamical variables (ρ α ) α , (u α ) α , (p α ) α , whereas the other terms \(\mathbb {Q}_\alpha \), Tr α , K α and H α are approximated or, in other words, expressed as functions of the hydrodynamical variables. To that aim, one usually assumes (see [151, 155]) that the distribution function f α is close to a Maxwellian distribution.Footnote 14 In this situation, one can determine the higher-order terms approximately, and after some simplifications, one finally derives a modified momentum conservation equation together with a “closure relation”, that involves only (ρ α ) α , (u α ) α , (p α ) α .
Let us follow Lifschitz [155], to see how one can write a closed system in the particular case of a plasma. More precisely, we consider a two-fluid, made of electrons (q e = −e) and a single species of ions, so the hydrodynamical variables are (ρ α )α=e,i, (u α )α=e,i, (p α )α=e,i. The aim is to model slow, large-scale plasma evolution. The assumptions originating from the physics involved can be listed as follows:
-
The plasma is electrically neutral: q e n e + q i n i = 0 ;
-
The pressure is scalar: \(\mathbb {Q}_e = \mathbb {Q}_i = 0\) ;
-
The electron inertia can be neglected: ∂ t (ρ e u e ) + div (ρ e u e ⊗u e ) = 0.
First, we remark that since q e n e + q i n i = 0, ρ e is proportional to ρ i . Equation (1.90) writes (for α = i)
Then, Eq. (1.91) writes (for α = i, e)

Adding up these two equations (recall that Tr i + Tr e = 0), we find
Moreover, we know from the definition of the current density that one has J = n e q e u e + n i q i u i = n i q i (u i −u e ), so the right-hand side can finally be expressed in terms of J and B only:
One could carry out the same analysis for the evolution of the mean energy. In the same spirit as Eq. (1.86), the energy conservation law writes H i + H e = −Tr i ⋅u i −Tr e ⋅u e , where the sum H i + H e corresponds to the Joule effect. It is omitted here (see Eq. (1.98) below for the final result).
In particular, a relevant set of hydrodynamical variables is ρ = ρ i , u = u i , and p = p i + p e . Based on this observation, it turns out that one can consider the electrically neutral plasma as a one-fluid.
Let us return now to Maxwell’s equations. In the MHD model, the displacement current ∂ t D is always neglected with respect to the induced current J. This corresponds to the magnetic quasi-static model (see the upcoming Sect. 1.4). Moreover, we know that ϱ = n e q e + n i q i = 0. The electric field E is thus divergence-free (more precisely, div ε E = 0). In terms of the Helmholtz decomposition (1.120) (see Sect. 1.4 again), this means that E is transverse: E = E T. So, Maxwell’s equations write


We note that Eq. (1.93) allows us to express the right-hand side of Eq. (1.92) in terms of B only, since one has

Now, the equation governing the evolution of B, namely Faraday’s law (1.94) requires knowledge of E T. It appears that (see, for instance, [155], Eq. (7.12)), to take the motion of the fluid into account, Ohm’s law (1.39) can be generalized to
(σ S is sometimes called the Spitzer conductivity. )
With this relation, we can remove the electric field from Faraday’s law:

The main conclusion is that, for the magnetohydrodynamics model (MHD) that governs the evolution of the plasma, a relevant set of variables is ρ, u, p, and B. Let us recall them here. For the sake of completeness, we have added Eq. (1.98), which governs the evolution of the mean energy, with the parameter γ set to 5∕3:



Briefly commenting on Eqs. (1.96–1.100), we note first that Eq. (1.100) is implied by Eq. (1.99). Also, E T and J are respectively determined by Eqs. (1.94) and (1.93). Thus, all fields can be inferred from these equations. For some applications, one can consider that \(\sigma _S^{-1}=0\), thus leading to the ideal set of MHD equations. In other words, the plasma is perfectly conducting. Contrastingly, when the plasma is resistive, one cannot set \(\sigma _S^{-1}\) to zero, and one has to solve the resistive set of MHD equations.
Another variant of the above model is given by the incompressible, viscous, resistive MHD equations, which come up when the conducting fluid is a liquid (such as molten metal or an electrolyte, e.g., salt water) rather than an ionised gas. Compared to gases, liquids are typically nearly incompressible, but much more viscous and dense; this requires different scalings and approximations. Namely, the system (1.96)–(1.100) is modified as follows:
-
1.
The mass density ρ, or equivalently the particle density n, of the fluid is assumed to be constant: this is the incompressibility condition. The conservation equation (1.96) reduces to div u = 0; this equality serves as the “closure relation”, replacing the adiabatic closure (1.98).
-
2.
The momentum conservation equation (1.97) is modified by introducing a viscosity term − νΔ u. Under certain scaling assumptions, such a term appears [58, §2.2] when the system of hydrodynamic equations is derived from the Boltzmann equation (1.81), rather than the Vlasov equation (1.87).
-
3.
We allow for some external, non-electromagnetic force f (such as gravity) acting on the fluid, in addition to the Lorentz and pressure forces.
Thus, we arrive at the system:


The notation (a ⋅∇)b stands for \(\sum _{i=1}^3 a_i\, \partial _{x_i} \boldsymbol {b}\); the replacement of div(u ⊗u) with (u ⋅∇)u is possible thanks to div u = 0. See Chap. 10 for mathematical studies on how to solve the MHD equations.
1.4 Approximate Models
We have already introduced the time-dependent Maxwell equations formulated as problems with field or potential unknowns. Let us now adopt a different point of view. As a matter of fact, many problems in computational electromagnetics can be efficiently solved at a much lower cost by using approximate models of Maxwell’s equations. As a particular case, the static models are straightforward approximations corresponding to problems with “very slow” time variations or “zero frequency” phenomena (with a pulsation ω “equal to zero”), so that one can neglect all time derivatives. We also present a fairly comprehensive study on how to derive approximate models, as in [96, 176]. These models are studied mathematically in Chap. 6.
1.4.1 The Static Models
Let us consider problems (and solutions) that are time-independent, namely static equations, in a perfect medium. In other words, we assume that ∂ t ⋅ = 0 in Maxwell’s equations (1.22–1.25). This assumption leads to (with non-vanishing charge and current densities)

where the superscript stat indicates that we are dealing with static unknowns. In the following two subsubsections, we will consider the electric and the magnetic cases separately. Again, they are set in all space, \(\mathbb {R}^3\).
Remark 1.4.1
Within the framework of the time-harmonic Maxwell equations (see Sect. 1.2), we looked for solutions to Maxwell’s equations with an explicit time-dependence. In this setting, the static equations can be viewed as time-harmonic Maxwell equations with a pulsation ω “equal to zero”. This interpretation can be useful, for instance, for performing an asymptotic analysis.
1.4.1.1 Electrostatics
Equation  yields \(\boldsymbol {E}^{stat}=- \operatorname {\mathrm {\mathbf {grad}}} \phi ^{stat}\), where ϕ
stat denotes the electrostatic potential
; see the connection to (1.33) when ∂
t
⋅ = 0. As
yields \(\boldsymbol {E}^{stat}=- \operatorname {\mathrm {\mathbf {grad}}} \phi ^{stat}\), where ϕ
stat denotes the electrostatic potential
; see the connection to (1.33) when ∂
t
⋅ = 0. As  , the potential ϕ
stat solves the ellipticFootnote 15 problem
, the potential ϕ
stat solves the ellipticFootnote 15 problem

Moreover, in a homogeneous medium (for instance, in vacuum  ), we obtain the electrostatic problem with unknown ϕ
stat
), we obtain the electrostatic problem with unknown ϕ
stat
This is the Poisson equation in variable ϕ stat (see, for instance, Chapter 3 of [103, Volume II]), which is an elliptic partial differential equation (PDE), and by definition, a static problem, much cheaper to solve computationally than the complete set of Maxwell’s equations. Then, one sets \(\boldsymbol {E}^{stat}=- \operatorname {\mathrm {\mathbf {grad}}} \phi ^{stat}\) to recover the electrostatic field.
1.4.1.2 Magnetostatics
In a similar manner, a static formulation can be written for the magnetic induction B
stat. By applying the curl operator to equation  , we obtain
, we obtain

In a homogeneous medium (for instance, in vacuum  ), and using the identity (1.36) again, we obtain the magnetostatic problem
), and using the identity (1.36) again, we obtain the magnetostatic problem

whose solution, B stat , is called the magnetostatic field. This is a vector Poisson equation, i.e., an elliptic PDE (left Eq.), with a constraint (right Eq.). Again, this formulation leads to problems that are easier to solve than the complete set of Maxwell’s equations.
Note also that one has  (see (1.35)). If, moreover, the Coulomb gauge is chosen to remove the indetermination on the vector potential A
stat, one finds the alternate magnetostatic problem
(see (1.35)). If, moreover, the Coulomb gauge is chosen to remove the indetermination on the vector potential A
stat, one finds the alternate magnetostatic problem
with A
stat as the unknown. Then, one sets  to recover the magnetostatic field.
to recover the magnetostatic field.
1.4.2 A Scaling of Maxwell’s Equations
In order to define an approximate model, one has to neglect one or several terms in Maxwell’s equations. The underlying idea is to identify parameters, whose value can be small (and thus, possibly negligible). To derive a hierarchy of approximate models , one can perform an asymptotic analysis of those equations with respect to the parameters. This series of models is called a hierarchy, since considering a supplementary term in the asymptotic expansion leads to a new approximate model. An analogous principle is used, for instance, to build approximate (paraxial) models when simulating data migration in geophysics modelling (cf. among others [41, 85]). From a numerical point of view, the approximate models are useful, first and foremost, if they coincide with a physical framework, and second, because in general, they efficiently solve the problem at a lower computational cost.
In the sequel, let us show how to build such approximate models formally (i.e., without mathematical justifications), recovering, in the process, static models, but also other intermediate ones.
Let us consider Maxwell’s equations in vacuum (1.26–1.29). As a first step, we introduce a scaling of these equations based on the following characteristic values:
In order to build dimensionless Maxwell equations, we set
We thus obtain for Maxwell’s equations in vacuum


As far as the charge conservation equation (1.10) is concerned, we find
Now, given \(\overline {l}, \overline {t}\), \(\overline {\varrho }\), we choose \(\overline {E},\overline {B},\overline {J}\) such that
We define the parameter η with
Maxwell’s equations in the dimensionless variables E ′, B ′ can be written as

while the charge conservation equation writes
Assuming now that the characteristic velocity \(\overline {v}\) is small with respect to the speed of light c, we have
This assumption is usually called the low frequency approximation , since it assumes “slow” time variations, which correspond after a time Fourier Transform to small pulsations/frequencies.
Obviously, the static models are obtained by setting η = 0 in these equations. Thus, they appear as a zero-order approximation of Maxwell’s equations. Next, we derive more accurate approximate models.
1.4.3 Quasi-Static Models
More general approximate models can be obtained by discriminating the time variations, respectively, of the electric field and the magnetic induction. Hence, after the scaling step in Maxwell’s equations in vacuum, that is, in Eqs. (1.107–1.110), if we suppose that
we easily obtain that we may neglect the time derivative ∂ t B in Faraday’s law, whereas the coefficient of the time derivative ∂ t E in Ampère’s law is comparable to one. We then obtain the electric quasi-static model , which can be written in the physical variables E, B as


It can be proven (see Sect. 6.4) that this model is a first-order approximation of Maxwell’s equations. As mentioned, it is formally built by assuming that the time variations of the magnetic induction are negligible.
In a similar way, let us suppose, contrastingly, that
thus we may neglect the time derivative ∂ t E in Ampère’s law, whereas the coefficient of the time derivative ∂ t B in Faraday’s law is comparable to one. We thus obtain the magnetic quasi-static model , which can also be written in the physical variables E, B as


This set of equations constitutes another first-order approximation of Maxwell’s equations, which is derived formally by assuming that the time variations of the electric field, namely the displacement current, are negligible.
At first glance, there is no difference between the quasi-static electric equations (1.112–1.113) plus the quasi-static magnetic equations (1.116–1.117) and the static ones (1.104). However, we observe that the right-hand sides are time-dependent in the case of the quasi-static equations, whereas they are static in the other case. Let us consider, for instance, the electric quasi-static model (i.e., ∂ t B is negligible). The right-hand side ϱ of the Poisson equation (1.113) is (explicitly) time-dependent, since it is related to the electric field E that is a priori time-dependent. Now, with the supplementary assumption that ∂ t E is also negligible, ϱ becomes a static right-hand side and the twice quasi-static model is actually static.
From now on, it is important to note that the “quasi-static/static” difference is not only a terminological subtlety. Indeed, from a numerical point of view, solving a quasi-static problem with a time-dependent right-hand side, amounts to solving a series of static problems after the time-discretization is performed [22].
1.4.4 Darwin Model
Let us introduce another approximate model, also known as the Darwin model [90]. It consists in introducing a Helmholtz decomposition of the electric field as
where E
L, called the longitudinal part, is characterized by  , and E
T, the transverse part, is characterized by div E
T = 0. Starting from Maxwell’s equations in vacuum, one then assumes that ε
0∂
t
E
T can be neglected in Ampère’s law: one neglects only the transverse part of the displacement current, whereas, in the quasi-static model, the total displacement current ε
0∂
t
E is neglected. In this sense, it is a more sophisticated model than the quasi-static one. Moreover, it can be proven (see Sect. 6.4), by using the low frequency approximation (1.111) and the resulting dimensionless form of Maxwell’s equations, that this model yields a second-order approximation of the electric field and a first-order approximation of the magnetic induction.
, and E
T, the transverse part, is characterized by div E
T = 0. Starting from Maxwell’s equations in vacuum, one then assumes that ε
0∂
t
E
T can be neglected in Ampère’s law: one neglects only the transverse part of the displacement current, whereas, in the quasi-static model, the total displacement current ε
0∂
t
E is neglected. In this sense, it is a more sophisticated model than the quasi-static one. Moreover, it can be proven (see Sect. 6.4), by using the low frequency approximation (1.111) and the resulting dimensionless form of Maxwell’s equations, that this model yields a second-order approximation of the electric field and a first-order approximation of the magnetic induction.
The Darwin model in vacuum is written in the physical variables E, B as

Then, if one uses the Helmholtz decomposition (1.120) with div E T = 0 and \(\boldsymbol {E}^L=- \operatorname {\mathrm {\mathbf {grad}}}\phi \), we see that the three fields B, E T and ϕ solve three elliptic PDEs, namely (1.121) and

Compared with the original time-dependent problem, these problems are easier to solve. As a matter of fact, only the data are time-dependent, while the operators are time-independent.
To conclude, we emphasize that the main difficulty, when using the Darwin model in a bounded domain, is how to define suitable boundary conditions for each part of the electric field: more precisely, how one should “split” the boundary condition on E into two boundary conditions on E L and E T. We refer the reader to [83, 96] for more details (see also Sect. 6.4).
1.4.5 Coupled Approximate Models
When considering the Vlasov-Maxwell model, in many cases, the interactions between particles are mainly electrostatic; the self-consistent magnetic field is negligible. Furthermore, particles have velocities that are much smaller than c: they obey the non-relativistic dynamic. So, one reverts to the position-velocity description of phase space \(({\boldsymbol {x}},{\boldsymbol {v}})\in \mathbb {R}^3_{{\boldsymbol {x}}}\times \mathbb {R}^3_{{\boldsymbol {v}}}\); in addition, in the Lorentz force, the term v ×B is negligible before E, unless there is a strong external magnetic field (as in tokamaks, for instance). One replaces the Maxwell’s equations with an electric quasi-static model; and the magnetic part (1.114)–(1.115) is irrelevant. The electric part (1.112)–(1.113) is rephrased as \(\boldsymbol {E} = - \operatorname {\mathrm {\mathbf {grad}}}\phi \) and − Δϕ = ϱ∕ε 0. Thus, we arrive at the Vlasov–Poisson system:
with ϱ given by (1.82). Also, there exist intermediate models such as Vlasov–Darwin, which couples Eq. (1.87) with the model of Sect. 1.4.4 (see, for instance, [7, 36]).
1.5 Elements of Mathematical Classifications
In this section, we first recall the definition of some standard operators, together with a classification of the partial differential equations (PDE) and their physical counterparts. In a second part, we reformulate and classify Maxwell’s equations. In the last part, we present well-known computations that establish a correspondence between the time-harmonic dependence with the notion of resonance. The material presented here is very classical: the well-informed reader may skip this section.
1.5.1 Standard Differential Operators
Let us begin by recalling the definitions of the four operators \( \operatorname {\mathrm {\mathbf {grad}}}\), div, Δ and  , which we use throughout this book.
, which we use throughout this book.
Let E n be a finite-dimensional Euclidean space of dimension n, endowed with the scalar product ⋅, and let A n be an affine space over E n . Furthermore, let U be an open subset of A n . Respectively introduce a scalar field on U, \(f\ :\ U \rightarrow \mathbb {R}\) , and a vector field on U, f : U → E n .
Assume that f is differentiable at M ∈ U, and let Df(M) be its differential at M. Then, the gradient of f at M is defined by
Provided that f is differentiable on U, the vector field \(M\mapsto \operatorname {\mathrm {\mathbf {grad}}} f(M)\) is called the gradient of f on U. The operator, \( \operatorname {\mathrm {\mathbf {grad}}}\), is called the gradient operator.
Assume that f is differentiable at M ∈ U, then the divergence of f at M is defined by
where tr denotes the trace of a linear operator. Provided that f is differentiable on U, the scalar field M↦div f(M) is called the divergence of f on U. The operator, div, is called the divergence operator.
Assume that f is twice differentiable at M ∈ U, then the Laplacian of f at M is defined by
Provided that f is twice differentiable on U, the scalar field M↦Δf(M) is called the Laplacian of f on U. The operator, Δ, is called the Laplace operator.
Consider that n = 3, and assume that f is differentiable at M ∈ U. Then, for any given v 0 ∈ E 3, the mapping f ×v 0 : U → E 3 is differentiable at M. The curl of f at M is defined by

Provided that f is differentiable on U, the vector field  is called the curl of f on U. The operator,
is called the curl of f on U. The operator,  , is called the curl operator.
, is called the curl operator.
In physics, one is mainly interested in three-dimensional Euclidean and affine spaces E 3 and A 3. Moreover, to obtain expressions that involve partial derivatives, let us introduce (e 1, e 2, e 3) as an orthonormal basis of E 3, (O, e 1, e 2, e 3) as an affine (or cartesian) coordinate system of A 3, and finally, (x 1, x 2, x 3) as the associated coordinates, that is, M = O +∑i=1,2,3x i e i . We can write f =∑i=1,2,3f i e i . Then, with respect to the affine coordinate system, the four operators defined above can be respectively expressed as

1.5.2 Partial Differential Equations
We begin with the simple case of a linear second-order two-dimensional partial differential equation
where the solution u, the coefficients A, B, …, F and the data G are functions of (x, y). It is well known that, following the sign of the discriminant
one can build a classification of partial differential equations that write as in Eq. (1.122) in a domain Dom of \(\mathbb {R}^2\). We have the classes:
-
1.
if B 2 − AC < 0 on the domain Dom, the PDE (1.122) is of the elliptic type. It corresponds to equilibrium problems, such as, for instance, the static problems, and it can be written in a canonical form, the prototype being the Poisson equation (cf. Sect. 1.4.1).
-
2.
if B 2 − AC = 0 on the domain Dom, the PDE (1.122) is of the parabolic type. It can also be transformed into a canonical form, a typical example being the heat transfer equation. From a physical point of view, this corresponds to diffusion problems.
-
3.
if B 2 − AC > 0 on the domain Dom, the PDE (1.122) is of the hyperbolic type. After rewriting the equation under its canonical form, one can easily identify the wave equation as the prototype of the hyperbolic equation. An important property of the hyperbolicity is that it corresponds to propagation of solutions with a finite velocity.
If we consider now the more general second-order linear partial differential equation set in a domain of \(\mathbb {R}^n\), that is, in n variables, it can be written as
where the solution u, the coefficients a ij , b i , c, and the data d are functions of the n variables (x i )1≤i≤n. In order to classify the PDEs (1.123) into different types, we consider the so-called principal part, that is, the highest-order terms in (1.123), which we express as
Above, \({\boldsymbol {\partial }}=(\frac {\partial }{\partial x_1},\ldots,\frac {\partial }{\partial x_n})^T \in \mathbb {R}^n\), and \(\mathbb {A}\) denotes the n × n matrix of the coefficients a ij , and l.o.t. (or lower-order terms) stands for first or zero-order terms that vanish if the a ij s are constant. Now, using Schwarz’s theorem \(\partial ^2_{ij} =\partial ^2_{ji}\), one can rewrite the coefficients a ij so as to obtain a symmetric matrix \(\mathbb {A}\), which we assume to belong to \(\mathbb {R}^{n \times n}\) (i.e., it is a real-valued matrix). Classically, all eigenvalues of the symmetric real-valued matrix \(\mathbb {A}\) are real. We denote them by λ 1, λ 2, …, λ n , counted with their multiplicity. Furthermore, we introduce a corresponding orthonormal set of eigenvectors u 1, …, u n , such that \(\mathbb {A}\) can be diagonalized as
where \(\mathbb {U}\) is an orthogonal matrix (\(\mathbb {U}^T=\mathbb {U}^{-1}\)) with the eigenvectors u i as its n columns. Introducing now the directional derivative operator
we define the vector differential operator
Plugging this expression into the first term of the right-hand side of (1.124) and using the orthogonal character of the matrix \(\mathbb {U}\) gives us
In this way, one gets that (1.124) can be rewritten equivalently
where the l.o.t. here again represents the lower-order terms. This expression provides an obvious way to extend the previous classification to the general case, which appears to be strongly related to the sign of the eigenvalues λ i . Hence, we define, by analogy to the two-dimensional case, several classes of partial differential equation:
-
1.
if either λ i > 0, ∀i or λ i < 0, ∀i, the equation is said to be elliptic ;
-
2.
if exactly one of the λ i > 0 or λ i < 0 and all other (λ j )j ≠ i exhibit an opposite sign, the equation is said to be hyperbolic ;
-
3.
if one of the λ i = 0, the equation can be parabolic . For that, all other (λ j )j ≠ i must exhibit a fixed sign ;
-
4.
other instances are possible:
-
if Card{λ i = 0}≥ 2, the equation is said to be semi-parabolic ;
-
if λ i ≠0, ∀i, and Card{λ i > 0}≥ 2, Card{λ i < 0}≥ 2, the equation is said to be semi-hyperbolic.
-
When we are dealing with a system of equations that can be reformulated as one or several PDEs acting on vector unknowns, we refer to it as a vector PDEs . As we shall see in the next subsection, the time-dependent Maxwell equations are an example of hyperbolic vector PDEs.
To end this subsection, we remark that there exist other ways to define the elliptic, parabolic and hyperbolic types of equation. In particular, when we deal with systems of equations, one can relate the classification to the inversibility of the principal symbol of the operator, namely the Fourier transform of the highest-order terms. We refer the interested reader, for instance, to [92, 93].
1.5.3 Maxwell’s Equations Classified
Though it is often alluded to in this chapter, we have not so far explicitly classified Maxwell’s equations. It turns out to be quite easy. Assume we are considering a homogeneous medium (vacuum):
let us build ∂
t
(Eq. (1.26)) (Eq. (1.27))\(-c^2 \operatorname {\mathrm {\mathbf {grad}}}\)(Eq. (1.28)) formally, to find
(Eq. (1.27))\(-c^2 \operatorname {\mathrm {\mathbf {grad}}}\)(Eq. (1.28)) formally, to find
Then, build ∂
t
(Eq. (1.27) Eq. (1.26)\()-c^2 \operatorname {\mathrm {\mathbf {grad}}}(\)Eq. (1.29)) to find
Eq. (1.26)\()-c^2 \operatorname {\mathrm {\mathbf {grad}}}(\)Eq. (1.29)) to find

Both vector PDEs, respectively governing the behavior of E and B, are vector wave equations and, as such, they are hyperbolic . In particular, the electromagnetic fields propagate with finite speed (equal to c, see Sect. 1.2.2). They have to be supplemented with some first-order initial conditions . Indeed, to obtain Eqs. (1.125–1.126), one differentiates in time both Ampère’s and Faraday’s laws. If one keeps only these equations, constant values (w.r.t. the time variable) of those laws—considered as mathematical expressions—are neglected. Hence, one adds the relations

which equivalently write, with the help of the zero-order initial condition (1.31),

Also, one must keep Gauss’s law (1.28) and the absence of magnetic monopoles (1.29), which appear here as constraints on the solutions to Eqs. (1.125–1.126).
Remark 1.5.1
One can choose not to add contributions resulting from the divergence part of the fields, to reach


Let us examine briefly—and formally—how the set of second-order equations (1.125–1.126), supplemented with the initial conditions (1.31) and (1.127) and constraints (1.28–1.29), allow us to recover the original set of Maxwell’s equations (1.26–1.29), supplemented with the initial condition (1.31). Gauss’s law and the absence of magnetic monopoles are contained in both sets of equations, and so is the zero-order initial condition. To recover Ampère’s and Faraday’s laws, introduce the quantities

According to the initial conditions (1.31) and (1.127), one has U(0) = V (0) = 0. Then, after some elementary manipulations, one finds that

(Above, one uses the charge conservation equation (1.10) to prove that U is divergence-free.)
In other words, we showed that the couple (V, c −2U) solves the set of Eqs. (1.26–1.29) with zero right-hand sides, and with zero initial condition (1.31). So, it is equal to zero, according to the results on the solvability of Maxwell’s equations. We thus conclude that it holds that

as announced.
The calculations performed here formally can be mathematically justified to prove the equivalence between the first-order and the second-order Maxwell equations. We refer the reader to Chap. 7.
1.5.4 Resonance vs. Time-Harmonic Phenomena
We consider the time-dependent Maxwell equations in a homogeneous medium (for instance, vacuum), set in a bounded domain Dom, written as two second-order wave equations (see Eqs. (1.128)–(1.129)). Assuming that there is no charge, both electromagnetic fields are divergence-free. The wave equations for each of the fields being of the same nature, we will consider only one of them, for instance,

with the initial conditions
Since the domain Dom is bounded, one has to add a boundary condition, such as the perfect conductor boundary condition (1.135). The problem to solve can be expressed as
where:
-
U(t) is the unknown, here the electric field ;
-
A is the operator acting on the solution, here
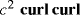 ;
; -
F(t) is the right-hand side, here \(-\varepsilon _0^{-1}\partial _t\boldsymbol {J}\) ;
-
U 0, U 1 is the initial data.
The problem is set in the vector space of divergence-free solutions with vanishing tangential components on the boundary, the so-called domain of the operator A. It can be proven that the operator A is compact, self-adjoint and positive-definite, and that there exists an orthonormal basis of eigenmodes (μ k )k≥1 and a set of corresponding non-negative eigenvalues (λ k )k≥1 (counted with their multiplicity) such that A μ k = λ k μ k for all k ≥ 1 (we refer the reader to Chap. 8 for details). Moreover, the multiplicities of all eigenvalues are finite, and furthermore, limk→+∞λ k = +∞. The set {λ k , k ≥ 1} is the spectrum of the operator A. Such modes correspond to the so-called free vibrations of the electric field. One can expand the solution U and the initial data on the basis:
Solving the problem (1.130) mode by mode yields, thanks to the superposition principle,
with \(\omega _k=\sqrt {\lambda _k}\) for all k. As pointed out by the expression (1.131), the values ω k play a particular role in the physical interpretation. Assume that the energy input to the system can be expressed by a right-hand side F(t) such as
with a prescribed positive ω. This corresponds to the so-called sustained vibrations of the electric field, expressed here in the time-dependent case. Computing the mode-by-mode solution with this right-hand side, one finds that u k (t) is equal to
-
1.
\(\displaystyle \frac {f_k}{2 \omega _k}\{\frac {1}{\omega - \omega _k} + \frac {1}{\omega + \omega _k}\}(\cos {}(\omega _k t)-\cos {}(\omega t))\) if ω ≠ ω k ;
-
2.
respectively \(\displaystyle \frac {f_k}{2 \omega }t \sin {}(\omega t)\) if ω = ω k ,.
Incase 1, all terms in (1.131) appear with a bounded amplitude, the leading term being proportional to \(f_k(\omega - \omega _k)^{-1}\omega _k^{-1}\) when ω ≈ ω k . If case 2 occurs, there exist one or several terms in (1.131), i.e., those that write \((2\omega )^{-1}f_kt \sin {}(\omega t)\) for k such that ω k = ω, which have an unbounded amplitude, equal to (2ω)−1f k t. This is called a resonance. It can occur only when the excitation frequency ω is equal to one of the ω k ’s. For this reason, the quantities (ω k ) k are called resonance frequenciesFootnote 16 of the system.
This result can also be interpreted in terms of energy. Indeed, taking the dot product of (1.130-left) by U ′ and integrating over the domain Dom yields
It can be written as
Above,
The first term between brackets represents a kinetic energy, the second one represents a potential energy and the right-hand side represents the power brought to the system at a given time t. Integrating this equation over time leads to the energy conservation equation
in which the energy brought to the system is \(\displaystyle \int _0^t (\boldsymbol {F}(s) | {\boldsymbol {U}}'(s)) ds\). Assuming again that F is of the form (1.132), the energy has a bounded amplitude as soon as ω∉{ω k , k ≥ 1}. Contrastingly, this amplitude is unbounded if ω = ω k . Physically, the resonance corresponds to the excitation of one eigenmode of the system, creating an unbounded increase of its internal energy.
Let us now build a solution to the time-harmonic problem, cf. Sect. 1.2.1. We introduce a right-hand side F with harmonic time-dependence \(\exp (-\imath \omega t)\ (\omega >0\)), that is, \(\boldsymbol {F}(t,{\boldsymbol {x}})={\Re }(\boldsymbol {f}({\boldsymbol {x}})\exp (-\imath \omega t))\), with a complex-valued f. Let us consider that the solution U to Eq. (1.130-left) adopts the same time-harmonic dependence for t large enough, so that \({\boldsymbol {U}}(t,{\boldsymbol {x}})={\Re }(\boldsymbol {u}({\boldsymbol {x}})\exp (-\imath \omega t))\), with a complex-valued u. Plugging the expression of U into Eq. (1.130-left) and using, as above, expansions of u and f yields, with obvious notations,
Now, Eq. (1.133) is equivalent to \((\omega _k^2-\omega ^{2})\,u_k = f_k\) for all k. Assume that ω is equal to some ω k . In order for a solution to exist, one must have f k = 0 for all the corresponding indices k (such that ω = ω k ). It follows that no resonance can occur in the time-harmonic case. From a mathematical point of view, one can use the Fredholm alternative (cf. Chap. 4 for a more detailed discussion).
1.6 Boundary Conditions and Radiation Conditions
In order to close Maxwell’s equations when the domain is a strict subset of \(\mathbb {R}^3\), one must provide conditions, in addition to the differential Maxwell equations (1.6–1.9). These conditions are usually imposed on the boundary of the domain, and they are called the boundary conditions . Also, when the domain is unbounded in at least one direction, it is interesting, from a computational point of view, to bound it. The computational domain thus corresponds to a truncation of the original domain. This can be achieved via the introduction of an artificial boundary, and an ad hoc absorbing boundary condition is imposed on this boundary, so that the electromagnetic waves can leave the computational domain without (significant) reflections. Another possibility is to introduce—not a boundary plus a boundary condition—but a thin, dissipative layer, in which the waves can propagate while being damped at the same time. This technique is called the perfectly matched layers . In other respects, when one focuses on the time-harmonic Maxwell equations (1.47–1.50), one must add a condition at infinity, which permits us to discriminate incoming and outgoing waves: this condition is called a radiation condition . Physically, it prevents energy inputs from infinity. Mathematically, it allows one to prove uniqueness results.
1.6.1 Boundary Conditions
As we remarked at the beginning of this section, the differential Maxwell equations are insufficient to characterize the fields in a strict subset of \(\mathbb {R}^3\). On the other hand, the integral Maxwell equations yield four interface conditions, respectively described by Eqs. (1.11) and (1.12). How can these conditions be used? Let us call \(\mathcal {O}\) the domain of interest, and \(\partial \mathcal {O}\) its boundary. Note that \(\partial \mathcal {O}\) can alternatively be seen as the interface between \(\mathcal {O}\) and \(\mathbb {R}^3\setminus \overline {\mathcal {O}}\), so the electromagnetic fields fulfill conditions (1.11–1.12) on \(\partial \mathcal {O}\). In addition, the behavior of the electromagnetic fields is known in \(\mathbb {R}^3\setminus \overline {\mathcal {O}}\) (otherwise, we would have to compute them!) or, more realistically, in an exterior domain \(\mathcal {O}'\) included in \(\mathbb {R}^3\setminus \overline {\mathcal {O}}\), such that \(\overline {\mathcal {O}}\cap \overline {\mathcal {O}}'=\partial \mathcal {O}\). As a consequence, one can gather some useful information as to the behavior of the fields in \(\mathcal {O}\), on the boundary \(\partial \mathcal {O}\).
For instance, let us assume now that the domain \(\mathcal {O}\) is bounded, or partially bounded (i.e., along one direction, like the “pipe” in Fig. 1.1), and that it is encased (at least locally) in a perfect conductor. Then, as we saw in Sect. 1.1, the fields vanish outside \(\mathcal {O}\) (cf. our discussion on skin depth and on the notion of perfect conductor). From condition (1.11 right), we infer that
with n the unit outward normal vector to \(\partial \mathcal {O}\), with the convention that outward goes from \(\mathcal {O}\) to \(\mathcal {O}'\). Likewise, from condition (1.12 left), we get
The conclusion is that the normal component \(B_n=\boldsymbol {B}\cdot \boldsymbol {n}_{|\partial \mathcal {O}}\) (respectively tangential components \(\boldsymbol {E}_{\top }=\boldsymbol {n}\times (\boldsymbol {E}\times \boldsymbol {n})_{|\partial \mathcal {O}}\)) of B (respectively E) uniformly vanish on \(\partial \mathcal {O}\): we call these conditionsFootnote 17 the perfect conductor boundary conditions .
From the physical point of view, these conditions are macroscopic, since they result from the idealization of quantities defined on surfaces. On the other hand, from a mathematical point of view, these conditions are sufficient to ensure the uniqueness of the solution, in the absence of topological considerations. As we shall see in Chap. 5, condition (1.134) can be rigorously inferred from condition (1.135), whereas the reciprocal assertion is not valid.
From the point of view of wave propagation, the perfect conductor boundary condition can be viewed as a reflection condition. Indeed, since the electromagnetic fields uniformly vanish inside the perfect conductor, one can say that the boundary completely reflects any impinging plane wave. As a consequence, the reflection coefficient, which is equal to the ratio of amplitudes between the reflected and incident waves, has a unit value. Also, in terms of energy, no energy is transmitted to the exterior domain \(\mathcal {O}'\). In other words, the energy flux through the boundary is equal to zero, and the energy remains constant in the domain \(\mathcal {O}\) (in the absence of sources).
However, there also exist media that are more or less dissipative. This occurs, for instance, when the exterior medium \(\mathcal {O}'\) is a conductor (but not a perfect one). The fields do not vanish inside \(\mathcal {O}'\), so a wave originating from the domain \(\mathcal {O}\) penetrates into the exterior domain \(\mathcal {O}'\). More precisely, if we consider an impinging plane wave, it should penetrate—at least partially—into \(\mathcal {O}'\), where it is damped. In the special case when \(\partial \mathcal {O}\) is a plane and if the velocity of propagation of the plane wave is equal to \(\boldsymbol {c}=1/\sqrt {\varepsilon \mu }\,\boldsymbol {n}\), one finds by direct computations that it holds that
So, to allow a plane wave to penetrate into \(\mathcal {O}'\), one usually introduces a boundary condition, called the impedance boundary condition , which is written as
In its simplest form, the impedance Z is a positive number, which is characteristic of the medium. The obvious example is \(Z=\sqrt {\mu /\varepsilon }\), which allows the plane wave with velocity \(\boldsymbol {c}=1/\sqrt {\varepsilon \mu }\,\boldsymbol {n}\) to leave the domain \(\mathcal {O}\) without being reflected (when \(\partial \mathcal {O}\) is a plane). More generally, Z is an operator (local in space), and the generalized impedance boundary condition is understood as \(\boldsymbol {E}\times \boldsymbol {n}_{|\partial \mathcal {O}} + Z(\boldsymbol {n}\times (\boldsymbol {H}\times \boldsymbol {n})_{|\partial \mathcal {O}})=0\). In terms of energy, this condition allows the electromagnetic energy to decrease in the domain. Note that condition (1.136) is usually considered for time-harmonic fields (see [26] for an example of time-dependent fields), and in this instance, Z can be a function of the pulsation ω.
In most cases, these boundary conditions are not sufficient to model problems originating from physical situations efficiently. Let us consider more specifically the time-dependent Maxwell equations in a domain \(\mathcal {O}\). Obviously, if the domain \(\mathcal {O}\) is not bounded, it has to be “numerically adjusted” to perform numerical computations. Note that this difficulty occurs for exterior problems (diffraction, etc.) as well as for interior problems (waveguides, etc.) (see Figs. 1.2 (left) and 1.3 (left)). Let the computational domain Ω be equal, for instance, toFootnote 18 \(\mathcal {O}\cap B(O,R)\), with a suitable radius R. Then, the boundary of the computational domain ∂Ω can be split into two parts:
-
a “physical” part, which is included in \(\partial \mathcal {O}\): \(\varGamma =\partial \varOmega \cap \partial \mathcal {O}\).
-
the remainder, Γ A , which is purely “artificial”.
For a diffraction problem on a bounded object , the radius R is chosen so that Γ A does not intersect the “physical” boundary \(\partial \mathcal {O}\) (see Fig. 1.2 (right)). In other words, there holds ∂Γ ∩ ∂Γ A = ∅, with \(\varGamma =\partial \mathcal {O}\), Γ A = ∂B(O, R). So, for numerical purposes, one handles a truncated exterior problem .
Contrastingly, for an interior problem, R is usually chosen in such a way that Γ A intersects the “physical” boundary: ∂Γ ∩ ∂Γ A ≠ ∅ (see Fig. 1.3 (right)). In the latter case and as a rule of thumb, one must be careful to avoid artificial boundaries Γ A that intersect \(\partial \mathcal {O}\) at positions where the electromagnetic fields can be locally “intense”, such as the neighborhood of reentrant corners and/or edges of \(\partial \mathcal {O}\). For numerical purposes, one handles a truncated interior problem .
On Γ, one imposes the boundary conditions that model the behavior of the exterior medium, as previously. On the artificial boundary Γ A , a boundary condition is also required. Let us go back to a plane wave with a velocity of propagation c = c d: when d ⋅n > 0, one says that the wave is outgoing , whereas it is said to be incoming when d ⋅n < 0. Physically, one has to model the following behavior: outgoing electromagnetic waves should leave the computational domain Ω freely without being reflected at this boundary. Or, equivalently, outgoing waves are absorbed at the artificial boundary, and the corresponding condition is called an absorbing boundary condition .
Let (E ex, B ex) denote the (exact) solution to the problem set in \(\mathcal {O}\), and let (E, B) be the (possibly approximate) solution to the problem set in Ω. Here, the term “problem” refers to Maxwell’s equations in the domain, plus the boundary conditions on the boundary of the aforementioned domain.
It is possible to construct an exact absorbing boundary condition, which is usually called the transparent boundary condition . It can be written as \(\boldsymbol {E}^{ex}\times \boldsymbol {n}_{|\varGamma _A} + T(\boldsymbol {n}\times (\boldsymbol {B}^{ex}\times \boldsymbol {n})_{|\varGamma _A})=0\), where T is a pseudo-differential operator (note the similarities with the generalized impedance boundary condition). The action of the operator T can be expressed in two equivalent ways. Either T is considered as a transfer operator that relates the trace of the tangential trace of the magnetic induction to its electric counterpart, and its action is written as an (infinite) expansion in spherical harmonics. Or, an integral representation of the fields can be used (in Ω and in \(\mathbb {R}^3\setminus B(O,R)\)), which is determined by the values of the tangential traces of both fields on Γ A .
Mathematically, if one imposes the transparent boundary condition on Γ A , it can be proven that the restriction of the exact fields (E ex, B ex) to Ω is equal to (E, B). Or, the other way around, one can build an extension of the fields (E, B) to \(\mathcal {O}\) that coincides with the exact solution (see, for instance, [128]).
However, the transparent condition is non-local both in space and time: for practical implementations, it is impossible to use the operator Texactly as it is… So, for numerical purposes, one can choose, for instance, truncated (finite) expansions, when the action of T is expressed via a transfer operator (see below); or Boundary Element Methods that allow one to approximate integral representations.
Alternatively, one can choose to devise approximate conditions: the absorbing boundary conditions (referred to as ABC or ABCs from now on). Within the same framework, it is often required to model incoming waves from infinity. The incoming waves should be able to enter the domain Ω. The parameters describing these incoming waves can be prescribed by given functions (denoted e ⋆ and b ⋆ in the following), defined on the artificial boundary Γ A . A set of ABCs for Maxwell’s equations can be written as
These conditions are obtained by locally approximating the boundary Γ A by its tangent plane. Moreover, an outgoing plane wave, which propagates normally to the boundary, is not reflected. In that case, we have to choose e ⋆ = 0 or b ⋆ = 0. On the other hand, when e ⋆ ≠ 0 or b ⋆ ≠ 0, conditions (1.137–1.138) enable an incoming plane wave that propagates normally to the boundary to enter the domain freely. The conditions (1.137–1.138) are known as the Silver–Müller ABCs [165]. When e ⋆ = 0 or b ⋆ = 0, they are said to be homogeneous.
Note that since we are considering boundary conditions that are an approximation of the exact transparent boundary condition, it follows that (E, B) is different from the restriction of the exact fields (E ex, B ex) to Ω.
If one differentiates Eq. (1.138) with respect to time and uses the trace of Faraday’s law on Γ A , one finds another expression of the Silver–Müller boundary condition that involves the electric field alone

Or, as we already mentioned, one can choose to approximate the transparent boundary condition directly. This can be achieved when the artificial boundary is “smooth”, by performing either a Taylor expansion or a rational (Padé) expansion of the operator T, in terms of a small parameter: in the high-frequency limit, the (small) parameter is equal to the angle of incidence \(\widehat {(\boldsymbol {d},\boldsymbol {n})}\) of the waves on Γ A . Keeping only the zero-order term, one recovers Eq. (1.138) with b ⋆ = 0. Keeping the zero- and first-order terms, one tailors a priori a new ABC.Footnote 19 However, in the special case when the artificial boundary is a sphere Γ A = ∂B(O, R), the “new” condition still coincides with (1.138). Hence, the initial Silver–Müller ABCs, obtained by merging Γ A with its tangent plane, are still satisfactory up to the first order in this special geometry.
The precision of an ABC can be measured with the help of plane wave analysis: any plane wave impinging on Γ A is partially reflected (and partially refracted). The reflection coefficient (the ratio of amplitudes between the reflected and incident waves) depends on the angle of incidence \(\theta =\widehat {(\boldsymbol {d},\boldsymbol {n})}\in ]-\pi /2,\pi /2[\). When the reflection coefficient behaves like
one says that the ABC is of order α. Using this scale and assuming that Γ A is a plane, one finds that the Silver–Müller condition (1.139) is of order 1, whereas the perfect conductor condition is, by construction, of order zero. One can also build ABCs of higher order. The following condition has been proposed in [147]:

or, alternatively,

where \( \operatorname {\mathrm {\mathbf {grad}}}_\varGamma \) is the surface gradient, or tangential gradient, operator,
and  is the surface curl, or tangential curl, operator
. Assuming that Γ
A
is a plane, it is proven that the condition (1.140) or (1.141) is of order 2.
is the surface curl, or tangential curl, operator
. Assuming that Γ
A
is a plane, it is proven that the condition (1.140) or (1.141) is of order 2.
Note that the ABCs are not equivalent to one another. In other words, two different conditions yield two different sets of electromagnetic fields.
As we remarked earlier, approximate conditions such as the Silver–Müller ABCs have been developed as an alternate choice to the numerical approximation of the transparent boundary conditions. In particular, condition (1.139), used in conjunction with the differential Maxwell equations (and another condition on Γ), leads to a well-posed problem [187]. In addition, the Silver–Müller boundary condition is sufficiently accurate for most interior problems, and it is straightforward to implement numerically [21]. Contrastingly, for exterior problems, the use of higher-order approximations is recommended [108]. A possible drawback of the higher-order ABCs is that they can lead to problems that are not well-posed. Finally, we note that these instances of ABCs can be used in the time-harmonic regime.
The last technique we review is credited to Bérenger [39, 40]. To adjust the domain, one adds not an artificial boundary, but one, or a set of, artificial layers, made of artificial media. These artificial layers, and the media they are made of, exhibit special features:
-
(i)
Interfaces between the computational domain and an artificial layer or between two artificial layers are plane.
-
(ii)
Electromagnetic plane waves that propagate in the artificial media are attenuated: these media are dissipative.
-
(iii)
At the interface between the layers and the computational domain, plane waves are not reflected (whatever the angle of incidence).
-
(iv)
At the interface between two layers, plane waves are not reflected (whatever the angle of incidence).
Basically, one first designs several types of layer. They are labeled L
x
, L
y
, L
z
, depending on the chosen—constant (cf. (i))—direction of the normal vector (n
I
= e
x
, e
y
, e
z
) to the interface between the computational domain and each of the surrounding layers (see Fig. 1.4 (left)). To fulfill (ii-iii), the conductivities in the artificial media have to be adjusted carefully. Indeed, in addition to the conductivity σ, one also needs to introduce a magnetic conductivity σ
⋆ such that in the artificial medium, Faraday’s law reads as  . Furthermore, one has to split the magnetic induction into two parts, and then, one has to duplicate Faraday’s law on those two parts. By doing so,Footnote 20 one introduces additional degrees of freedom, so that the problem at hand is solvable.
. Furthermore, one has to split the magnetic induction into two parts, and then, one has to duplicate Faraday’s law on those two parts. By doing so,Footnote 20 one introduces additional degrees of freedom, so that the problem at hand is solvable.
Second, to reconnect two different layers, for instance, L x and L y , one introduces another artificial layer L xy , so that (iv) is fulfilled at the interfaces ∂L x ∩ ∂L xy and ∂L y ∩ ∂L xy (see Fig. 1.4 (center)) through the use of similar techniques.
Note that there always exists a solution to the previous problems: in other words, one can always choose the conductivities in the various artificial media so that (ii-iv) hold.
Finally, this set of artificial layers is surrounded by a boundary on which one imposes perfect conductor boundary conditions (see Fig. 1.4 (right)). The various artificial layers are called perfectly matched layers (or PMLs, for short) . Unsplit versions of the PMLs (based on stretched coordinates in the artificial media, see [75, 174]) have been developed. In other words, the magnetic induction is not split anymore in the artificial media, which reduces the total number of unknowns there. The same result can be achieved by the use of anisotropic artificial media (as proposed in [181]), resulting in the so-called uniaxial PML (UPML).
From an algorithmic or computational point of view, outgoing plane waves can leave the computational domain freely. Then, they are damped in the PMLs, before being reflected by the perfect conductor boundary conditions. On their way back, they are damped once more before entering the computational domain freely. However, because of the dissipation in the artificial media, the energy of the plane waves that enter the computational domain after traveling in the PMLs is negligible. This process leads to numerical implementations that are extremely efficient in practice. From a mathematical point of view, the use of either the set of original PMLs of Bérenger or of unsplit versions leads to problems that are (conditionally) well-posed mathematically (see [34, 35, 146]).
1.6.2 Radiation Conditions
So far, we have focused mostly on the time-dependent Maxwell equations. Here, we deal with the time-harmonic case as in Sect. 1.2, in a homogeneous medium. Let ω > 0 be the pulsation.
Let us assume for simplicity that the charge density ϱ is equal to 0, so that the current density is divergence-free. Under these conditions, each field is solving a fixed frequency problem, which can be written in the manner of the Helmholtz-like equations (1.56–1.57),

As we already pointed out, this equation is strongly connected to the scalar Helmholtz equation (1.63), for which it is well known that the uniqueness of the solution requires a so-called radiation condition at infinity.
Now, as far as radiation conditions are concerned, they are generally associated with diffraction problems (see Fig. 1.2). In others words, we are concerned with waves coming from infinity that are impinging on an obstacle K: we are interested in solving the problem in \(\mathcal {O}=\mathbb {R}^3\setminus \overline K\). As we saw before, there may be (partial) absorption, as well as scattering by the obstacle, which leads to different kinds of boundary condition on this obstacle.
In practice, the computational problem is usually set within a bounded domain, for instance, \(B(O,R)\setminus \overline K\). An ad hoc boundary condition is chosen on ∂B(O, R), together with the companion numerical approximation of this boundary condition (see the previous discussion on transparent boundary conditions and/or ABCs).
Then, supplementary conditions, which characterize the behavior of the solution at infinity, are required. Denoting by (r, θ, ϕ) the spherical coordinates with associated vector basis (e r , e θ , e ϕ ), we seek a condition that depends on r only, so that it can be applied on the exterior boundary ∂B(O, R). At first glance, it seems that imposing that the solution decrease like r −1 at infinity is sufficient. Indeed, this condition is similar to the one that is required for the well-posedness of the scalar Poisson equation Δw = f in an exterior domain: it can be easily understood as a requirement for avoiding a situation in which the total energy \(\int _{\mathcal {O}}|w|{ }^2\,d{\boldsymbol {x}}\) would be unbounded. However, unlike the case of the Poisson equation, this condition is not sufficient to ensure uniqueness of the solution to the Helmholtz equation. To illustrate this point, let us introduce radial solutions to the scalar Helmholtz equation Δw + λw = 0 set in \(\mathbb {R}^3\). In other words, since we are studying uniqueness, Eq. (1.63) is solved in \(\mathbb {R}^3\) with a zero right-hand side. Namely, we look for solutions of the form w(x) = ζ(r). Under this assumption, Eq. (1.63) becomes, for r > 0,
with \(k=\sqrt {\lambda }=\omega /c\). The general solution to the previous equation is
Two families of solutions coexist. One with the + sign in the exponent, corresponding to an outgoing wave, the second with the − sign, associated with an incoming wave.Footnote 21 Hence, the uniqueness of the solution (up to a multiplicative constant) can be recovered by imposing a radiation condition, that is, a condition that describes the behavior of the solution at infinity, depending on whether one wants to select an outgoing wave or an incoming wave. As a matter of fact, from Eq. (1.143), we find
This leads to the following radiation conditions, whose names correspond to those given for the scalar Helmholtz equation:
-
1.
The outgoing Sommerfeld condition (imposes C − = 0 in Eq. (1.143))
$$\displaystyle \begin{aligned} \frac{\partial w}{\partial r}-\imath k w=O(\frac{1}{r^2})\,. \end{aligned}$$ -
2.
The incoming Sommerfeld condition (imposes C + = 0 in Eq. (1.143))
$$\displaystyle \begin{aligned} \frac{\partial w}{\partial r}+\imath k w=O(\frac{1}{r^2})\,. \end{aligned}$$
Both instances are necessary and sufficient conditions to ensure uniqueness of the solution to the scalar Helmholtz equation.
Remark 1.6.1
To express the general solution to the scalar Helmholtz equation, one uses expansions expressed in spherical coordinates as
This expansion is due to [23, 205] (see also [167]).
Let us consider the scalar, time-dependent, wave equation (in time-space \(\mathbb {R}\times \mathbb {R}^3\))
One finds, assuming that the solution is radial in space, i.e., w(t, x) = φ(t, r):
This can be written equivalently as
Now, solutions to (∂ t ± c∂ r )(rφ) = 0 write rφ = f(r ∓ ct), so that rφ = f out (r − ct) + f inc (r + ct).
To see that f out (r − ct) (respectively f inc (r + ct)) actually corresponds to an outgoing wave (respectively an incoming wave), let us go back to the time-harmonic regime.
Assuming, in addition, a time-harmonic dependence of these solutions like \(\varphi (t,r)= {\Re }(\zeta (r)\exp (-\imath \omega t))\), we have
This is equivalent in turn to ∂ r (rζ) = +ıkrζ or ∂ r (rζ) = −ıkrζ for r > 0, so that according to Eq. (1.143), ζ coincides with the solution obtained there. Moreover, we observe that (∂ t + c∂ r )(rφ) = 0 in the time-dependent regime corresponds to ∂ r (rζ) = +ıkrζ in the time-harmonic regime. We conclude by identification that
corresponds to an outgoing wave. In the same manner,
corresponds to an incoming wave, as advertised above.
Denoting by u a radial solution to the time-harmonic Maxwell equations (1.142) with a zero right-hand side, one finds that two families of solutions coexist, in the form of an incoming part (denoted by u −) and an outgoing part (denoted by u +). Again, one may select the outgoing or the incoming parts, via radiation conditions for the solution:
-
1.
The outgoing Silver–Müller radiation condition (imposes u − = 0)
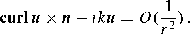 (1.144)
(1.144) -
2.
The incoming Silver–Müller radiation condition (imposes u + = 0)
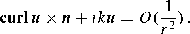 (1.145)
(1.145)
Often in the literature (see [86, 167]), the Silver–Müller radiation conditions appear in another form, derived from the first-order time-harmonic Maxwell equations (1.52–1.55), with a zero right-hand side. In this instance, both electric field e and magnetic induction b are involved in the outgoing or incoming expressions that read, respectively, as:
-
1.
First-order outgoing expression
$$\displaystyle \begin{aligned} \boldsymbol{e} - c\boldsymbol{b}\times\boldsymbol{n} = O(\frac{1}{r^2}), \text{ or } c\boldsymbol{b} + \boldsymbol{e}\times\boldsymbol{n} = O(\frac{1}{r^2}), \end{aligned} $$(1.146) -
2.
First-order incoming expression
$$\displaystyle \begin{aligned} \boldsymbol{e} + c\boldsymbol{b}\times\boldsymbol{n} = O(\frac{1}{r^2}), \text{ or } c\boldsymbol{b} - \boldsymbol{e}\times\boldsymbol{n} = O(\frac{1}{r^2})\,. \end{aligned} $$(1.147)
How can these conditions be used mathematically? For instance, let us go back to a diffraction problem, as pictured in Fig. 1.2. The total electric field e can be split into two parts: the incident wave e inc , the known impinging wave that propagates in the medium, and would not be affected in the absence of a scatterer ; and the scattered wave e sca , our unknown. By definition, the scattered wave is supposed to be outgoing, i.e., fulfill condition (1.144). Mathematically, this is expressed as

According to [134], this outgoing Silver–Müller radiation condition on e sca , together with the differential Maxwell equations (and a perfect conductor boundary condition on Γ) on the total field e = e inc + e sca , leads to a well-posed problem.
To emphasize the differences between the time-harmonic Maxwell equations (1.142) and the vector Helmholtz one, note that the solutions to (1.142) satisfy a constraint on the divergence: they are divergence-free (see remark 1.2.3). This is not the case of the plain radial solutions v(r) to the vector Helmholtz equation. Nevertheless, these computations being essentially based on the asymptotic behavior of ζ ±(r), the Silver–Müller radiation conditions—considered componentwise for the time-harmonic Maxwell equations—are expected to be equivalent to the Sommerfeld radiation conditions. Indeed, it was proven that each component of any solution to Maxwell’s equations satisfying the Silver–Müller radiation conditions also satisfies the corresponding Sommerfeld radiation conditions for the scalar Helmholtz equation, and vice versa (see [86] for a proof).
Let us conclude this section by briefly exposing the relation between the Silver–Müller radiation condition (1.146) and the Silver–Müller ABCs (1.137–1.138) in its homogeneous form, that is, with (e ⋆, b ⋆) = (0, 0). Note first that the similarity appears in the time-harmonic case, when comparing (1.137–1.138) with relations (1.146). Second, for the time-dependent case, recall that the ABCs were obtained by assuming that an outgoing plane wave, which propagates normally to the boundary, is not reflected. According to the previous discussion, the ABCs can also be viewed as a way of selecting a direction of propagation, by removing the incoming wave, the outgoing wave leaving the domain freely.
1.7 Energy Matters
The aim of this section is to recall the basic notions related to the energy in the context of Maxwell’s equations.
Let us consider first the case of a homogeneous medium (vacuum). Our starting point is Faraday’s law (1.27) and the absence of magnetic monopoles (1.29). We have seen that there exist two independent potentials, A and ϕ, that can be used to take into account these two relations, and define the electromagnetic fields as in Eqs. (1.34–1.35). For our purpose here, we say that (A(t, x))t,x and (ϕ(t, x))t,x are the generalized coordinates of our system. Then, let us introduce the Lagrangian density
together with the Lagrangian on a frozen (w.r.t. time) volume \(V\subset \mathbb {R}^3\)
Then, the idea is to use the least action principle, which amounts to finding extrema of the action (with t 1 < t 2 given)
over trajectories t↦(A(t), ϕ(t)) with fixed initial and final states. In other words, one chooses infinitesimal variations δ A and δϕ such that (δ A, δϕ)(t 1) = (δ A, δϕ)(t 2) = 0 in the volume V . A necessary condition for an extremum of S to exist is that δS = 0, with
for all admissible variations (δ A, δϕ). In a first step, one adds a new constraint on the variations, namely that (δ A, δϕ)(t) = 0 for all t ∈ ]t 1, t 2[, on the surface ∂V . One finds that the electromagnetic fields necessarily satisfy Ampère’s and Gauss’s laws, which appear within this framework as equations of motion of the electromagnetic fields. In a second step, one removes all constraints on the variations, to focus on the relation that defines δS, which now takes into account Ampère’s and Gauss’s laws, and holds for all variations (this is not the least action principle anymore). One finds that another necessary condition appears, which can be written as
This is an integral electromagnetic energy conservation relation . Indeed, let
be the density of electromagnetic energy , and let
be the vector flux of the electromagnetic energy , called the Poynting vector . The conservation relation (1.149) writes
From a physical point of view, the third term can be seen as the power dissipated by the Joule effect, and the second as the flux of the electromagnetic energy entering or leaving the domain V .
It can be written in differential form as
Note that one can define the total electromagnetic energy by
As originally expressed by Feynman [110], no doubt better than by us, we cannot be sure that these definitions are the “correct definitions”. However, if one has a look at other possibilities in the definition of the Lagrangian density (1.148), one always comes up with non-linear terms in the equations of motion of the electromagnetic fields. Thus, it is “natural” to keep the simplest expressions, that is, (1.149–1.150). Nevertheless, these definitions have to be considered as modelling assumptions , which are used extensively in the mathematical analyses (see Chap. 5).
Let us consider next the case of a perfect medium, in which the constitutive relations read as in (1.17), with symmetric tensors  and
and  . By analogy, we first introduce the density of electromagnetic energy
:
. By analogy, we first introduce the density of electromagnetic energy
:
Since  and
and  are both independent of t, one gets ∂
t
w = ∂
t
D ⋅E + ∂
t
B ⋅H.
are both independent of t, one gets ∂
t
w = ∂
t
D ⋅E + ∂
t
B ⋅H.
We also introduce the Poynting vector S, defined as
Taking the divergence of S, we obtain

By using Faraday’s and Ampère’s laws, we can substitute in this expression  by − ∂
t
B and
by − ∂
t
B and  by ∂
t
D + J to reach
by ∂
t
D + J to reach
This equation is the differential electromagnetic energy conservation in the case of a perfect medium, and it can also be expressed in integral form, in any frozen volume V , as
In the more general case of a chiral medium, the previous notions (density, conservation of energy) are much more complex to build.
Let us examine now the case of static electromagnetic fields (cf. Sect. 1.4, Eqs. (1.104)), in vacuum.
Let us focus first on the total electrostatic energy: recall that \(\boldsymbol {E}^{stat}=- \operatorname {\mathrm {\mathbf {grad}}} \phi ^{stat}\), with a potential ϕ stat governed by the Poisson equation (1.105). Then, one has, with the help of Ostrogradsky’s formula,
It remains to explain why the rightmost term vanishes when R goes to infinity. For that, let us return to formula (1.30), which expresses the (static) electric field created by N charged particles. This formula can be further generalized to a volume distribution of charged particles, with density ϱ. One reaches
The above expression can be rewritten as a convolution product in space:
Introducing G(y) = |y|−1, which satisfies \(\boldsymbol {G} = - \operatorname {\mathrm {\mathbf {grad}}} G\), one gets
with ϕ stat the corresponding electrostatic potential.
Provided that the support of ϱ is a bounded subset of \(\mathbb {R}^3\)—physically, provided that there are no charged particles at infinity—one finds that
with C ϱ a constant that depends on ϱ. Therefore, one has
So, the conclusion follows. For a volumic distribution of charges—without charges at infinity—the total electrostatic energy is equal to
Remark 1.7.1
Expression (1.153) involves the potential ϕ stat and the charge density ϱ, which are related by the Poisson equation (1.105). Thus, it can also be viewed as the potential energy of the system of charges.
Interestingly, and for volume distribution of charged particles, Expression (1.153) includes the self-energy of the distribution. In other words, if V 0 denotes the support of the charge density, the expression
has a meaning. This can be proven mathematically, due to the properties of the Green kernel G.
Contrastingly, the potential ϕ stat is meaningless for discrete systems of charged particles (see Eq. (1.30), right) at the positions (x i )1≤i≤N of the charges, and the charge density ϱ writes as a sum of Dirac masses located, respectively, at (x i )1≤i≤N. So, one cannot define the self-energy for discrete sets of charged particles. This is consistent with the fact that, in this situation, E stat is not square integrable in volumes enclosing one or several charges.
So far, we have considered 3D- and 0D-supported charge distributions. In-between these two configurations, there exist 1D- and 2D-supported charge distributions, such as idealized wires and surface charges on perfect conductors (cf. the infinite skin effect for the latter). On the one hand, it turns out that one can define the self-energy of surface charge distributions as
But on the other hand, one cannot define the self-energy for linear charge distributions.
The discussion of the total magnetostatic energy
follows the same lines, since one has  , with A
stat governed by the vector Poisson equation (1.106), with a constraint on the divergence. As previously, using Stokes’ formula and provided there are no currents at infinity, one then finds the identity
, with A
stat governed by the vector Poisson equation (1.106), with a constraint on the divergence. As previously, using Stokes’ formula and provided there are no currents at infinity, one then finds the identity
Provided the time-dependent electromagnetic fields behave similarly at infinity, i.e., |E(t, x)|≤ C ϱ (t) |x|−2 and |H(t, x)|≤ C J (t) |x|−2, one finds that
To conclude this section, we write down the electromagnetic energy flow in the case of a time-harmonic dependent field. The electromagnetic fields are expressed as in (1.41–1.42), and we substitute these expressions in the Poynting vector (1.151), which characterizes the energy flow, to obtain the complex-valued Poynting vector S c
This complex-valued Poynting vector is generally used to measure the energy flow for complex-valued electromagnetic fields (\(\boldsymbol {S}={\Re }(\boldsymbol {S}^c))\).
Finally, we consider the electromagnetic fields, expressed as a superposition of plane waves (in a homogeneous medium). Using Parseval’s formula, we remark that the total electromagnetic energy also writes
1.8 Bibliographical Notes
Concerning the form of Maxwell’s equations, we relied on the physical approach of Jackson [141, Chapter 1] and on the topological approach of Gross and Kotiuga [127]. See also the book by Jones [148]. As far as the constitutive relations are concerned, References [141, 149, 152, 156] have been helpful. The experimental results acquired a historical status a long time ago, cf. Coulomb’s experiments in 1785. The “existence” results of electromagnetic fields in all space \(\mathbb {R}^3\) can be found in many places: we chose [140] for the general case of a chiral medium and Chapter 6 in the monograph by Cessenat [72] for the particular case of a homogeneous medium. In regard to conducting media, we used the numerical results from [127, Chapter 1]. Regarding the issue of vanishing electromagnetic fields inside perfect conductors, we mention [167, Chapter 5], where illuminating comments and (partial) mathematical justification can be found. Let us mention [94, 141, 142, 161, 195] for the definition of skin depth in different models ; see also [191] for the notion of magnetic skin depth.
On the vast topic of the stationary Maxwell equations, we refer the reader (for instance) to the introductory book by Laval [153], and to the monograph by Krall and Trivelpiece [151]. See also the book by Van Bladel [201]. The limiting amplitude principle is rigorously proven in the monograph by Sanchez and Sanchez [183].
As far as the approximate models are concerned, we refer the reader to the works of Raviart and co-workers [96, 176], where the general methodology on how to build those models is described. In geophysics, approximate models are considered, for instance, in [41, 85]. The static models have been scrutinized extensively by Durand in his three-volume series [103]: in particular, an impressive number of computations carried out by hand (before the era of personal computers) are available. The Darwin model is named after C. G. Darwin, who studied the motion of charged particles in the 1920s [90]. In bounded domains, References [83, 96] provide some insight as to how one can define suitable boundary conditions for the transverse and longitudinal parts of the electric field.
The derivation of the Boltzmann and Vlasov equations can be found, for instance, in the monographs by Krall and Trivelpiece [151] or by Lifschitz [155] (physical point of view), or in the classnotes by Desvillettes [98] (mathematical point of view). Regarding plasma physics, we refer to [73].
To our knowledge, the first theoretical works on the Vlasov equation are those of Arseneev [11, 12]. For the coupled Vlasov–Maxwell system of equations, local existence and uniqueness results of classical solutions can be found in [95, 200] or in [122, 206]. Global existence results of weak solutions appeared in [101, 129]. See also a survey in [58].
For the study of the transparent boundary conditions, including their representations and their approximations, we recommend reading the monograph by Nédélec [167].
The Sommerfeld ABC that we recalled for the Helmholtz equation is named after A. Sommerfeld [193]. The Silver–Müller ABCs that we described are named after C. Müller [165] and S. Silver [189]. In their time-dependent form, they have been designed (cf. [21]) in the same spirit as the ones given in [45, pp. 370–371]. There exists a wide literature on the topic of ABCs: see, for instance, [105] for the scalar wave equation and [38, 118, 147, 187] for Maxwell’s equations. In the time-harmonic regime, there also exist many noticeable research works, such as [10, 37, 187]. As far as Bérenger’s PMLs are concerned, we refer the reader to the seminal papers [39, 40], and to variants, for instance [2, 51, 75, 115, 116, 174, 181].
For radiation conditions, we refer the reader to the monographs [86, 165, 167] and to [134].
The notion of electromagnetic energy is studied in-depth in many monographs. Many aspects have been scrutinized: physical, computational, mathematical, etc. We refer, respectively, to the book by Laval [153], and the monographs by Jackson [141], Durand [103, Volume I] and Cessenat [72, Chapter 1].
Notes
- 1.
Unless otherwise specified, in this chapter, a domain is an open region of space. Another meaning is given for the mathematical studies, starting in Chap. 2.
- 2.
H is sometimes called the magnetizing field.
- 3.
The standard differential operators
 , div, \( \operatorname {\mathrm {\mathbf {grad}}}\), and Δ are mathematically defined in Sect. 1.5.1.
, div, \( \operatorname {\mathrm {\mathbf {grad}}}\), and Δ are mathematically defined in Sect. 1.5.1. - 4.
By definition, δ Σ is the surface Dirac mass on Σ, so one has \(\int \varrho v = \int _\varSigma \sigma _\varSigma v_{|\varSigma } \,dS\) for ad hoc functions v.
- 5.
See the end of the section.
- 6.
By definition, \(\delta _{{\boldsymbol {x}}_0}\) is the Dirac mass in x 0, so one has \(\int \varrho _0 v = q_0 v({\boldsymbol {x}}_0)\) for ad hoc functions v.
- 7.
Or: electrostatically.
- 8.
To deserve the label fixed frequency problem, one assumes a non-vanishing value of the pulsation. Otherwise, one solves a static problem, cf. Sect. 1.4.1.
- 9.
The fields
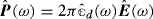 and
and 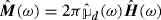 are respectively called electric and magnetic polarizations
.
are respectively called electric and magnetic polarizations
. - 10.
Other conditions on
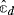 lead to the same conclusion. For instance, if
lead to the same conclusion. For instance, if 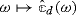 is a real-valued, even function of ω that can be expressed as a rational fraction, with decaying condition
is a real-valued, even function of ω that can be expressed as a rational fraction, with decaying condition  for large |ω|.
for large |ω|. - 11.
In particular, this is the case for the Lorentz force (1.75). As a matter of fact, div v F(t, x, v) = q (div v E + div v (v ×B)) = 0, since the electromagnetic fields are independent of v in the phase space.
- 12.
- 13.
It can happen that, in Maxwell’s equations, parts of ϱ and J are due to external charge and current sources. In this case, E and B depend in an affine way on f.
- 14.
Id est, consider \(f_\alpha ({\boldsymbol {v}})\approx A_\alpha \exp (-B_\alpha |{\boldsymbol {v}}-\boldsymbol {u}_\alpha |{ }^2)\), with A α , B α > 0.
- 15.
See the upcoming Sect. 1.5 for a precise definition.
- 16.
More precisely, ω is a pulsation and the corresponding frequency is ω∕(2π).
- 17.
One may also use the interface conditions to describe electromagnetic fields globally in \(\mathbb {R}^3\): this is an integral representation. More precisely [167, §5.5], consider that \(\mathbb {R}^3\) is split into two media M + and M −, one of them being bounded, and let Σ be the interface between the two media. If one is interested in the electromagnetic fields that are governed by the homogeneous time-harmonic equations in M + and M −, then, assuming that the jump j Σ = −[H ×n Σ ] Σ (condition (1.12 right)) is known, one can use integral representation formulas for the values of E(x) and H(x), for all \({\boldsymbol {x}}\in \mathbb {R}^3\setminus \varSigma \). The integrals are taken over Σ and depend only on j Σ . In the same spirit, one can represent the (different) values of E ±(x Σ ) and H ±(x Σ ) for all x Σ ∈ Σ. Within this framework, one may generalize these results in the presence of magnetic polarization by assuming that the magnetic current on Σ, m Σ = [E ×n Σ ] Σ , is also different from 0. In this case, one ends up with integral representation formulas of E and H, with integrals over Σ that depend on j Σ and m Σ . In the same manner, one may use the jump relation σ Σ = [D ⋅n Σ ] Σ (1.11 left) to solve a diffraction problem expressed as a scalar Helmholtz equation, assuming σ Σ is known, where the unknown is the scalar electric potential.
- 18.
Instead of B(O, R), one can choose any reasonable volume in which the computations ought to be performed: a cube, as in Fig. 1.3 (right, rightmost Γ A ), etc.
- 19.
For instance (see [187]), if the artificial boundary Γ A is a cylinder of radius R and axis Oz, one gets
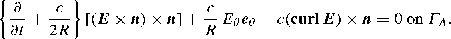
with E = E r e r + E θ e θ + E z e z in cylindrical coordinates.
- 20.
Manipulating Maxwell’s equations thusly is certainly admissible, since one is dealing with artificial media, in which the electromagnetic fields are artifacts…
- 21.
Indeed, the unit outward normal vector to ∂B(O, R) is n = e r . Moreover, since x = r e r on ∂B(O, R), for an outgoing plane wave that propagates normally to ∂B(O, R) (k out = k e r ), one finds k out ⋅x = kr. Respectively, for an incoming plane wave that propagates normally to ∂B(O, R) (k in = −k e r ), k in ⋅x = −kr.
References
S. Abarbanel, D. Gottlieb, J.S. Hestaven, Non-linear PML equations for time-dependent electromagnetics in three dimensions. J. Sci. Comput. 28, 125–137 (2006)
J.J. Ambrosiano, S.T. Brandon, E. Sonnendrücker, A finite element formulation of the Darwin PIC model for use on unstructured grids. J. Comput. Phys. 121, 281–297 (1995)
X. Antoine, H. Barucq, A. Bendali, Bayliss-Turkell-like radiation conditions on surfaces of arbitrary shape. J. Math. Anal. Appl. 229, 184–211 (1999)
A.A. Arseneev, Local uniqueness and existence of classical solution of Vlasov’s system of equations. Sov. Math. Dokl. 15, 1223–1225 (1974)
A.A. Arseneev, Global existence of a weak solution of Vlasov’s system of equations. U.S.S.R. Comput. Math. Math. Phys. 15, 131–143 (1975)
F. Assous, P. Degond, E. Heintzé, P.-A. Raviart, J. Segré, On a finite element method for solving the three-dimensional Maxwell equations. J. Comput. Phys. 109, 222–237 (1993)
F. Assous, F. Tsipis, A PIC method for solving a paraxial model of highly relativistic beams. J. Comput. Appl. Math. 227, 136–146 (2008)
F.V. Atkinson, On Sommerfeld’s radiation condition. Philos. Mag. 40, 645–651 (1949)
A. Bachelot, V. Lange, Time dependent integral method for Maxwell’s equations with impedance boundary condition, in Boundary Element Technology, vol. 10, ed. by C.A. Brebbia, M.H. Aliabadah (Wessex Institute of Technology, Southampton, 1995), pp. 137–144
E. Bécache, S. Fauqueux, P. Joly, Stability of perfectly matched layers, group velocities and anisotropic waves. J. Comput. Phys. 188, 399–433 (2003)
E. Bécache, P. Joly, On the analysis of Bérenger’s perfectly matched layers for Maxwell’s equations. Math. Model. Numer. Anal. 36, 87–119 (2002)
S. Benachour, F. Filbet, P. Laurençot, E. Sonnendrücker, Global existence for the Vlasov-Darwin system in \(\mathbb {R}^3\) for small initial data. Math. Methods Appl. Sci. 26, 297–319 (2003)
A. Bendali, P. Guillaume, Non-reflecting boundary conditions for waveguides. Math. Comput. 68, 123–144 (1999)
A. Bendali, L. Halpern, Conditions aux limites absorbantes pour le système de Maxwell dans le vide en dimension 3. C. R. Acad. Sci. Paris Ser. I 307, 1011–1013 (1988)
J.-P. Bérenger, A perfectly matched layer for the absorption of electromagnetic waves. J. Comput. Phys. 114, 185–200 (1994)
J.-P. Bérenger, Three-dimensional perfectly matched layer for the absorption of electromagnetic waves. J. Comput. Phys. 127, 363–379 (1996)
A.J. Berkhout, Seismic Migration (Elsevier, Amsterdam, Oxford, New York, Tokyo, 1984)
C.K. Birdsall, A.B. Langdon, Plasmas Physics via Computer Cimulation (McGraw-Hill, New York, 1985)
V.A. Bokil, M.W. Buksas, Comparison of finite difference and mixed finite element methods for perfectly matched layer models. Commun. Comput. Phys. 2, 806–826 (2007)
F. Bouchut, F. Golse, M. Pulvirenti, Kinetic Equations and Asymptotic Theory. Series in Applied Mathematics (Gauthier-Villars, 2000)
M. Cessenat, Mathematical Methods in Electromagnetism. Linear Theory and Applications. Advances in Mathematics for Applied Sciences, vol. n41 (World Scientific, Singapore, 1996)
F.F. Chen, Introduction to Plasma Physics (Plenum Press, New York, London, 1974)
W.C. Chew, W.H. Weedon, A 3D perfectly matched medium from modified Maxwell’s equations with stretched coordinates. Microw. Opt. Technol. Lett. 7, 599–604 (1994)
P. Ciarlet, Jr., E. Sonnendrücker, A decomposition of the electric field. Application to the Darwin model. Math. Methods Appl. Sci. 7(8), 1085–1120 (1997)
J.F. Claerbout, Imaging the Earth’s Interior (Blackwell Scientific Publications, Oxford, 1985)
D. Colton, R. Kress, Inverse Acoustic and Electromagnetic Theory (Springer, Berlin, 1998)
C.G. Darwin, The dynamical motion of particles. Philos. Mag. 39, 537–551 (1920)
R. Dautray, J.-L. Lions, Analyse mathématique et calcul numérique pour les sciences et les techniques (Masson, Paris, 1987)
R. Dautray, J.-L. Lions, Mathematical Analysis and Numerical Methods for Science and Technology (Springer, Berlin, 1990)
P.A. Davidson, An Introduction to Magnetohydrodynamics (Cambridge University Press, Cambridge, 2001)
P. Degond, Local existence of the solutions of the Vlasov-Maxwell equations and convergence to the Vlasov-Poisson equations for infinite light velocity. Math. Methods Appl. Sci. 8, 533–558 (1986)
P. Degond, P.-A. Raviart, An analysis of the Darwin model of approximation to Maxwell’s equations. Forum Math. 4, 13–44 (1992)
L. Desvillettes, Quelques outils d’analyse pour les équations de Vlasov et de Landau, in Ecole CEA-EDF-INRIA, Equations cinétiques et applications à la physique (2005)
R.J. DiPerna, P.-L. Lions, Global weak solutions of Vlasov-Maxwell systems. Commun. Pure Appl. Math. 42, 729–757 (1989)
E. Durand, Electrostatique (Masson, Paris, 1964)
D.M. Eidus, The principle of limiting absorption. Russ. Math. Surv. 24, 97–167 (1969)
B. Engquist, A. Majda, Absorbing boundary conditions for acoustic and elastic wave equations. Math. Comput. 31, 629–651 (1977)
X. Feng, Absorbing boundary conditions for electromagnetic wave propagation. Math. Comput. 68, 145–168 (1999)
R. Feynman, Leighton, Sands, The Feynman Lectures on Physics: Electromagnetism (Addison-Wesley, Reading, 1964)
S.D. Gedney, An anisotropic perfectly-matched layer absorbing medium for the truncation of FT-TD lattices. IEEE Trans. Antennas Propag. 44, 1630–1639 (1996)
S.D. Gedney, The perfectly matched layer absorbing medium, in Advances in Computational Electrodynamics, ed. by A. Taflove (Artech House, 1998), pp. 263–344
D. Givoli, A spatially exact non-reflecting boundary condition for time dependent problems. Comput. Methods Appl. Mech. Eng. 95, 97–113 (1992)
R.T. Glassey, W. Strauss, Singularity formation in a colisionless plasma could only occur at high velocities. Arch. Ration. Mech. Anal. 92, 56–90 (1986)
P.W. Gross, P.R. Kotiuga, Electromagnetic Theory and Computation: A Topological Approach. MSRI Publications Series (Cambridge University Press, Cambridge, 2004)
M.J. Grote, J.B. Keller, On nonreflecting boundary conditions. J. Comput. Phys. 122, 231–243 (1995)
Y. Guo, Global weak solutions of the Vlasov-Maxwell system with boundary conditions. Commun. Math. Phys. 154, 245–263 (1993)
C. Hazard, M. Lenoir, On the solution of time-harmonic scattering problems for Maxwell’s equations. SIAM J. Math. Anal. 27, 1597–1630 (1996)
A.D. Ioannidis, I.G. Stratis, A. Yannacopoulos, Electromagnetic wave propagation in dispersive bianisotropic media, in Proc. of the 6th Int. Workshop on Advances in Scattering and Biomedical Engineering, ed. by D. Fotiadis et al. (World Scientific, 2003), pp. 295–304
J.D. Jackson, Classical Electrodynamics, 3rd edn. (Wiley, New York, 1999)
B. Jensen, The quantum extension of the Drude-Zener theory in polar semiconductors, in Handbook of Optical Constants of Solids, ed. by E.D. Palik (Academic Press, New York, 1998), pp. 169–188
P. Joly, An elementary introduction to the construction and the analysis of perfectly matched layers for time domain wave propagation. SeMA J. 57, 5–48 (2012)
P. Joly, B. Mercier, Une nouvelle condition transparente d’ordre 2 pour les équations de Maxwell en dimension 3. Technical Report INRIA, vol. 1047 (1989)
D.S. Jones, Methods in Electromagnetic Wave Propagation (Clarendon Press, Oxford, 1998)
A. Karlsson, G. Kristensson, Constitutive relations, dissipation and reciprocity for the Maxwell equations in the time domain. Technical Report (Revision No. 2: August 1999) Lund Institute of Technology, CODEN:LUTEDX/(TEAT-7005)/1-36/(1989), Lund (1999)
N.A. Krall, A.W. Trivelpiece, Principles of Plasma Physics (McGraw-Hill, New York, 1973)
A. Lakhtakia, V.K. Varadan, V.V. Varadan, Time-Harmonic Electromagnetic Fields in Chiral Media. Lecture Notes in Physics (Springer, Berlin, 1989)
G. Laval, Matière et rayonnement (Ecole Polytechnique, Palaiseau, 1986)
A.E. Lifschitz, Magnetohydrodynamics and Spectral Theory (Kluwer Academic, 1989)
I. Lindell, A. Shivola, S. Tertyakov, A. Viitanen, Electromagnetic Waves in Chiral and Bi-isotropic Media (Artech House, Boston, 1994)
S.A. Maier, Plasmonics: Fundamentals and Applications (Springer, 2007)
C. Müller, Foundations of the Mathematical Theory of Electromagnetic Waves (Springer, Berlin, 1969)
J.-C. Nédélec, Acoustic and Electromagnetic Equations. Applied Mathematical Sciences, vol. 144 (Springer, New York, 2001)
H.M. Nussenzveig, Causality and Dispersion Relations (Academic Press, New York, 1972)
C. Rappaport, Perfectly matched absorbing boundary conditions based on anisotropic lossy mapping of space. IEEE Microw. Guid. Wave Lett. 5, 90–92 (1995)
P.-A. Raviart, E. Sonnendrücker, A hierarchy of approximate models for the Maxwell equations. Numer. Math. 73, 329–372 (1996)
Z. Sacks, D. Kinsland, R. Lee, J.F. Lee, A perfectly matched anisotropic absorber for use as an absorbing boundary condition. IEEE Trans. Antennas Propag. 43, 1460–1463 (1995)
J. Sanchez Hubert, E. Sanchez Palencia, Vibration and Coupling of Continuous Systems (Springer, 1989)
M. Sesques, Conditions aux limites artificielles pour le système de Maxwell, PhD Thesis, Bordeaux I University, France, 1990 (in French)
S. Silver, Microwave Antenna Theory and Design. M.I.T. Radiation Laboratory Series, vol. 12 (McGraw-Hill, New York, 1949)
F. Simpson, K. Bahr, Practical Magnetotellurics (Cambridge University Press, Cambridge, 2005)
A. Sommerfeld, Die Greensche Funktion der Schwingungsgleichung. Jber. Deutsch. Math. Verein. 21, 309–353 (1912)
T.H. Stix, Waves in Plasmas (American Institute of Physics, New York, 1992)
S. Ukai, T. Okabe, On classical solution in the large in time of two dimensional Vlasov’s equation. Osaka J. Math. 15, 245–261 (1978)
J. Van Bladel, Electromagnetic Fields (McGraw-Hill, New York, 1985)
C.H. Wilcox, An expansion theorem for electromagnetic fields. Commun. Pure Appl. Math. 9, 115–134 (1956)
S. Wollman, An existence and uniqueness theorem for the Vlasov-Maxwell system. Commun. Pure Appl. Math. 37, 457–462 (1984)
Author information
Authors and Affiliations
Rights and permissions
Copyright information
© 2018 Springer International Publishing AG, part of Springer Nature
About this chapter
Cite this chapter
Assous, F., Ciarlet, P., Labrunie, S. (2018). Physical Framework and Models. In: Mathematical Foundations of Computational Electromagnetism. Applied Mathematical Sciences, vol 198. Springer, Cham. https://doi.org/10.1007/978-3-319-70842-3_1
Download citation
DOI: https://doi.org/10.1007/978-3-319-70842-3_1
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-70841-6
Online ISBN: 978-3-319-70842-3
eBook Packages: Mathematics and StatisticsMathematics and Statistics (R0)


 .
. and
and  are proportional to the identity matrix:
are proportional to the identity matrix:  and
and 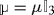 .
.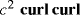 ;
;



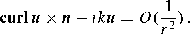
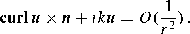
 , div,
, div, 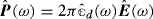 and
and 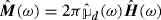 are respectively called electric and magnetic polarizations
.
are respectively called electric and magnetic polarizations
.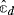 lead to the same conclusion. For instance, if
lead to the same conclusion. For instance, if 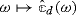 is a real-valued, even function of ω that can be expressed as a rational fraction, with decaying condition
is a real-valued, even function of ω that can be expressed as a rational fraction, with decaying condition  for large |ω|.
for large |ω|.