A J-Interaction Integral to Compute Force Stress and Couple Stress Intensity Factors for Cracks in Functionally Graded Micropolar Materials

Abstract

In contrast to classical elasticity, the micropolar continuum theory allows to describe materials with significant microstructural effects, such as particulate, granular and porous composites. Such materials show a size effect and have often a spatially varying distribution of mechanical properties. This contribution focuses on the establishment of the interaction integral (I-integral) for decoupling the force stress intensity factors (FSIFs) and couple stress intensity factors (CSIFs) of a crack in functionally graded micropolar material (FGMM). The I-integral is derived from the J-integral by superimposing an auxiliary field on the actual field. The auxiliary field is examined using three different definitions including the constant-constitutive-tensor (CCT) formulation, the non-equilibrium (NE) formulation and the incompatibility (IC) formulation. The NE and IC formulations are more appropriate than the CCT formulation because the I-integral using the CCT formulation involves strain gradients and curvature gradients, which may cause loss of accuracy in numerical calculations. Furthermore, we introduce the patched extended finite element method (patched-XFEM), which replaces crack-tip enrichment functions from the XFEM by a local refined mesh to improve the numerical precision. The I-integral in combination with the patched-XFEM is employed to examine numerically the influence of material parameters on the FSIFs and CSIFs.

1 Introduction

The micropolar continuum theory is preferable to describe materials where microstructural effects are significant, such as particulate, granular and porous composites, whereas the classical continuum theory does not enable it. A current overview about micropolar continuum theory can be found in [1,2,3]. The micropolar continuum concept was first proposed by Cosserat and Cosserat [4], who introduced three rotational degrees of freedom, in addition to translational degrees of freedom. The micropolar continuum did not receive much attention until the elaborate studies of Eringen [5, 6], who introduced a general theory of a microelastic continuum. Cowin [7] used an internal length to describe the size effect and the coupling number N to characterize a continuous transition from classical elasticity to micropolar elasticity. The size effect was first observed by researchers [8,9,10,11,12] in foam and porous materials. The experiments [11, 12] showed that the porous specimens behaved much stiffer than expected from classical elasticity under torsion of slender cylinders and under bending of plates and beams, but size effects were not observed in tension. In particular, the micropolar elastic theory accurately fits the experimental data for the effective stiffness of bone samples from the osteon to the whole bone [12, 13]. Moreover, many natural porous materials show a spatially gradation of the mechanical properties to match an optimal design. Nevertheless, issues of fracture and fatigue have to be considered to maintain high strength and durability.

Through analyzing a crack in an infinite two-dimensional (2D) micropolar medium, researchers [14, 15] found that both force stresses and couple stresses near a crack tip have an $r^{-1/2}$ singularity. They proposed to use the force stress intensity factors (FSIFs) and couple stress intensity factors (CSIFs) to characterize the crack-tip fields. Paul and Sridharan [16, 17] analyzed the influence of the micropolar constitutive material parameters on the FSIFs and CSIFs for penny-shaped and Griffith cracks in a micropolar medium. They found that both the mode-I FSIF and the CSIF depend on the internal length parameter as well as the coupling number N. Sridharan [18] analyzed an insulated penny-shaped crack in micropolar media under uniform heat-flow loading. He found that the mode-II FSIF depends on the intrinsic length parameter and the coupling number N, and that its value remains higher than those obtained from the classical continuum theory. Diegele et al. [19] provided the near-tip asymptotic field solutions for a mixed-mode crack in a 2D isotropic micropolar solid. They showed that aside from two FSIFs and one CSIF characterizing the singular terms, two constant force stresses and one constant couple stress are involved in the expressions of force stresses and couple stresses, respectively. Recently, a number of research works on fracture of micropolar materials have been carried out in theoretical [20,21,22,23,24,25] and numerical approaches including the finite element method (FEM) [26, 27] the boundary element method (BEM) [28, 29] and the extended finite element method (XFEM) [30, 31].

In practical numerical calculations, only few methods are effective to extract the crack-tip fracture parameters for micropolar elasticity. Jaric [32] proposed a path-independent J-integral that equals the crack-tip energy release rate. However, the mixed-mode FSIFs and CSIFs cannot be decoupled from the J-integral. An effective approach to decouple the mode-I FSIF, the mode-II FSIF and the in-plane CSIF is the I-integral [33], which is derived from the J-integral based on the superposition of the actual field and an auxiliary field. The I-integral was first proposed by Stern et al. [34] for classical elastic media. As the auxiliary field can be designed freely, the I-integral allows not only to decouple the mixed-mode SIFs, but also to extract the crack-tip T-stress [35]. The I-integral was developed for functionally graded materials (FGMs) [36, 37] which is a category of nonhomogeneous materials with properties varying continuously with location. Compared to the analytical models for FGMs [38, 39], the I-integral is easily implemented in practical fracture analyses. The merit of the I-integral is demonstrated in crack analyses of FGMs, bi-materials, and fiber-reinforced composites [40,41,42,43,44,45]. Recently, Yu et al. [33] developed the I-integral for extracting the FSIFs and CSIFs of micropolar materials and proved that the I-integral is domain-independent for interfaces.

The present contribution aims to discuss the validity of the I-integral for functionally graded micropolar materials (FGMMs) through the selection of different applicable auxiliary fields. The outline is as follows. Section 2 briefly introduces the micropolar elastic theory and the linear elastic fracture theory for FGMMs. Section 3 discusses three applicable auxiliary fields and derives the domain forms of the I-integral. Section 4 introduces briefly the patched XFEM. Several examples are provided in Sect. 5 to verify the validity of the auxiliary fields. Finally, a summary is given in Sect. 6.

2 Fracture Mechanics of FGMMs

2.1 Governing Equations for Micropolar Elasticity

In the micropolar continuum theory, each material point has six degrees of freedom, including three displacement components and three micro-rotation components. For a centrosymmetric isotropic micropolar solid without body forces and body couples, the governing equations are as follows [46]:

• Kinematic equations:

  $$\begin{aligned}&{{\varepsilon }_{ij}}={{u}_{j,i}}-{{e}_{ijk}}{{\phi }_{k}} \\&{{\chi }_{ij}}={{\phi }_{j,i}} \nonumber \end{aligned}$$

  (1)

  where ${{u}_{j}}$ and ${{\phi }_{k}}$ are the components of displacement and micro-rotation vectors, respectively, ${{\varepsilon }_{ij}}$ and ${{\chi }_{ij}}$ are the components of microstrain and curvature tensors, respectively, and ${e_{ijk}}$ is the permutation tensor. The subscripts $i, \, j,\, k$ and l range from (1) to (3), and the repetition of a subscript in a term denotes a summation with respect to that index over its range. A comma denotes a partial derivative.

• Equilibrium equations (without body forces and body couples):

  $$\begin{aligned}&{{\sigma }_{ji,j}}=0 \\&{{m}_{ji,j}}+{{e}_{ijk}}{{\sigma }_{jk}}=0 \nonumber \end{aligned}$$

  (2)

• Constitutive equations:

  $$\begin{aligned}&{{\sigma }_{ij}}={{A}_{ijkl}}{{\varepsilon }_{kl}}=\lambda {{\varepsilon }_{kk}}{{\delta }_{ij}}+(\mu +\kappa ){{\varepsilon }_{ij}}+\mu {{\varepsilon }_{ji}} \\&{{m}_{ij}}={{B}_{ijkl}}{{\chi }_{kl}}=\alpha {{\chi }_{kk}}{{\delta }_{ij}}+\gamma {{\chi }_{ij}}+\beta {{\chi }_{ji}} \nonumber \end{aligned}$$

  (3)

  where ${{\sigma }_{ij}}$ and ${{m}_{ij}}$ are the force stress and couple stress tensors, respectively, $\lambda$ and $\mu$ are Lamé’s constants, and $\kappa$, $\alpha$, $\beta$ and $\gamma$ are the micropolar material parameters. The stress is also expressed by the macrostrain tensor ${{e}_{ij}}={({{u}_{i,j}}+{{u}_{j,i}})}/{2}\;$ and the macrorotation vector ${{r}_{k}}={{{e}_{klm}}{{u}_{m,l}}}/{2}\;$ as ${{\sigma }_{ij}}=\lambda {{e}_{kk}}{{\delta }_{ij}}+(2\mu +\kappa ){{e}_{ij}}+\kappa {{e}_{ijk}}({{r}_{k}}-{{\phi }_{k}})$. For micropolar elasticity, the shear modulus G, Young’s modulus E and Poisson’s ratio $\nu$ are given by [20]:

  $$\begin{aligned} G=\mu +\frac{\kappa }{2}, \quad \nu =\frac{\lambda }{2\lambda +2G}, \quad E=2G(1+\nu ) \end{aligned}$$

  (4)

  In addition, the characteristic length in torsion ${{l}_{t}}$, and the characteristic length in bending, ${{l}_{b}}$ and the coupling number N given by [20]

  $$\begin{aligned} {{l}_{t}}=\sqrt{\frac{\beta +\gamma }{2G}}, \quad {{l}_{b}}=\sqrt{\frac{\gamma }{4G}}, \quad N=\sqrt{\frac{\kappa }{2G+\kappa }} \end{aligned}$$

  (5)

  are used to describe the micropolar materials. Due to the existence of two internal characteristic lengths, the micropolar theory is capable to predict size effects. The coupling number N satisfies the relation $0\le N\le 1$, where $N=0$ corresponds to the classical elastic theory and $N=1$ the couple stress theory. The micropolar constants satisfy the following inequalities [1, 46,47,48]:

  $$\begin{aligned}&3\lambda +2G\ge 0,&G\ge 0,\qquad&\kappa \ge 0 \\&3\alpha +\beta +\gamma \ge 0,&-\gamma \le \beta \le \gamma&\quad \nonumber \end{aligned}$$

  (6)

Fig. 1

A two-dimensional functionally graded micropolar solid with an inclined crack

2.2 Crack-Tip Asymptotic Fields in FGMMs

Let’s consider a 2D functionally graded micropolar body occupying the space R with a crack as shown in Fig. 1. Only in-plane displacement components ${{u}_{1}}$, ${{u}_{2}}$ and micro-rotation component ${{\phi }_{3}}$ are non-zero, and thus the governing equations are simplified to:

$$\begin{aligned}&{{\varepsilon }_{ij}}={{u}_{j,i}}-{{e}_{ij3}}{{\phi }_{3}},&{{\chi }_{i3}}={{\phi }_{3,i}} \end{aligned}$$

(7)

$$\begin{aligned}&{{\sigma }_{ji,j}}=0,&{{m}_{i3,i}}+{{e}_{ij3}}{{\sigma }_{ij}}=0 \end{aligned}$$

(8)

$$\begin{aligned}&{{\sigma }_{ij}}={{A}_{ijkl}}(\mathbf {x}){{\varepsilon }_{kl}},&{{m}_{i3}}=\gamma (\mathbf {x}){{\chi }_{i3}} \end{aligned}$$

(9)

The material parameters ${{A}_{ijkl}}(\mathbf {x})$ ($i,j,k,l=1,2$) and $\gamma (\mathbf {x})$ are spatially continuous and piecewise differentiable in domain R. The boundary conditions are given by

$$\begin{aligned}&{{u}_{i}}={{{\bar{u}}}_{i}}\text { on }\partial {{R}^{u}},&{{\sigma }_{ij}}{{n}_{i}}={{{\bar{t}}}_{j}}\text { on }\partial {{R}^{\sigma }} \\ \nonumber&{{\phi }_{3}}={{{\bar{\phi }}}_{3}}\text { on }\partial {{R}^{\phi }},&{{m}_{i3}}{{n}_{i}}={{{\bar{m}}}_{3}}\text { on }\partial {{R}^{m}} \end{aligned}$$

(10)

where $\partial R=\partial {{R}^{u}}+\partial {{R}^{\sigma }}=\partial {{R}^{\phi }}+\partial {{R}^{m}}$ is the boundary of R, ${{\bar{t}}_{i}}$ and ${{\bar{m}}_{3}}$ are the force traction and the couple traction, respectively, on the boundary, ${{\bar{u}}_{i}}$ and ${{\bar{\phi }}_{3}}$ are the displacement and the micro-rotation, respectively, prescribed on the boundary, and ${{n}_{i}}$ is the unit outward normal vector to the boundary.

In a small circular region ${{R}_{\varepsilon }}$ around the crack tip, the dependence of material parameters on coordinates $\mathbf {x}={{x}_{i}}\,{{\mathbf {e}}_{i}}$ in FGMMs ${{A}_{ijkl}}(\mathbf {x})$ and $\gamma (\mathbf {x})$ can be expressed in a Taylor series expansion as

$$\begin{aligned}&{{A}_{ijkl}}(r,\theta )=A_{ijkl}^{0}+rA_{ijkl}^{(1)}(\theta )+\frac{{{r}^{2}}}{2}A_{ijkl}^{(2)}(\theta )+\ldots \equiv A_{ijkl}^{0}+{{{\tilde{A}}}_{ijkl}} \\&\gamma (r,\theta )={{\gamma }_{0}}+r{{\gamma }^{(1)}}(\theta )+\frac{{{r}^{2}}}{2}{{\gamma }^{(2)}}(\theta )+\ldots \equiv {{\gamma }_{0}}+\tilde{\gamma } \nonumber \end{aligned}$$

(11)

where $A_{ijkl}^{0}$ and ${{\gamma }_{0}}$ are the local material constants evaluated at the crack tip, $A_{ijkl}^{(n)}(\theta )$ and ${{\gamma }^{(n)}}(\theta )$ are angular functions with $n=1,2,\ldots$. ${{\tilde{A}}_{ijkl}}\sim {\ }O(r)$ and $\tilde{\gamma }\sim {\ }O(r)$ are higher order terms of material parameters. Substituting Eq. (11) into Eqs. (7)–(9) yields

$$\begin{aligned}&(A_{ijkl}^{0}+{{{\tilde{A}}}_{ijkl}})({{u}_{l,kj}}-{{e}_{kl3}}{{\phi }_{3,j}})+{{{\tilde{A}}}_{ijkl,j}}({{u}_{l,k}}-{{e}_{kl3}}{{\phi }_{3}})=0, \\&({{\gamma }_{0}}+\tilde{\gamma }){{\phi }_{3,ii}}+{{{\tilde{\gamma }}}_{,i}}{{\phi }_{3,i}}+{{e}_{ij3}}(A_{ijkl}^{0}+{{{\tilde{A}}}_{ijkl}})({{u}_{l,k}}-{{e}_{kl3}}{{\phi }_{3}})=0 \nonumber \end{aligned}$$

(12)

Following Ref. [19], we assume that

$$\begin{aligned}&{{u}_{i}}(r,\theta )=u_{i}^{(0)}(\theta ){{r}^{s}}+u_{i}^{(1)}(\theta ){{r}^{s+1/2}}+u_{i}^{(2)}(\theta ){{r}^{s+1}}+\ldots , \\&{{\phi }_{3}}(r,\theta )=\phi _{3}^{(0)}(\theta ){{r}^{s}}+\phi _{3}^{(1)}(\theta ){{r}^{s+1/2}}+\phi _{3}^{(2)}(\theta ){{r}^{s+1}}+\ldots \nonumber \end{aligned}$$

(13)

where the superscript s is an unspecified positive number. If the region ${{R}_{\varepsilon }}$ is sufficiently small, the influence of higher-order terms of material constants can be ignored. Keeping the singular terms of $O({{r}^{s-2}})$ and $O({{r}^{s-3/2}})$ and ignoring higher-order terms, one can simplify (12) as

$$\begin{aligned} A_{ijkl}^{0}{{u}_{l,kj}}=0, \qquad {{\gamma }_{0}}{{\phi }_{3,ii}}=0 \end{aligned}$$

(14)

The expressions in Eq. (14) are identical to those for a homogeneous micropolar solid with material constants evaluated at the crack tip in FGMMs. Adopting the solution process given in Ref. [19], one obtains the result that in the vicinity of the crack tip, both the displacement and micro-rotation have a ${{r}^{1/2}}$-singularity. The terms $u_{i}^{(0)}$, $u_{i}^{(1)}$, $\phi _{3}^{(0)}$ and $\phi _{3}^{(1)}$ are identical to those given by Diegele et al. [19] for homogeneous micropolar materials, while the terms $u_{i}^{(n)}$ and $\phi _{3}^{(n)}$ ($n\ge 2$) for FGMMs are different from those in [19] due to the nonhomogeneity of material property. Therefore, for the generalized plane strain condition, the expressions of ${{u}_{i}}$ and ${{\phi }_{3}}$ are given by

$$\begin{aligned}&{{u}_{1}}=\left[ {{K}_{I}}f_{1}^{I}(\theta )+{{K}_{II}}f_{1}^{II}(\theta ) \right] \sqrt{\frac{r}{2\pi }} \\&+\left( {{k}_{I}}\frac{1-{{\nu }_{0}}}{2{{G}_{0}}}\cos \theta +{{k}_{II}}\frac{2{{G}_{0}}+{{\kappa }_{0}}}{4{{G}_{0}}{{\kappa }_{0}}}\sin \theta \right) r+O({{r}^{{3}/{2}\;}})+\ldots \nonumber \\&{{u}_{2}}=\left[ {{K}_{I}}f_{2}^{I}(\theta )+{{K}_{II}}f_{2}^{II}(\theta ) \right] \sqrt{\frac{r}{2\pi }} \nonumber \\&-\left( {{k}_{I}}\frac{{{\nu }_{0}}}{2{{G}_{0}}}\sin \theta +{{k}_{II}}\frac{2{{G}_{0}}-{{\kappa }_{0}}}{4{{G}_{0}}{{\kappa }_{0}}}\cos \theta \right) r+O({{r}^{{3}/{2}\;}})+\ldots \nonumber \end{aligned}$$

(15)

$$\begin{aligned} {{\phi }_{3}}=\frac{{{L}_{3}}}{{{\gamma }_{0}}}\sqrt{\frac{2r}{\pi }}\sin \frac{\theta }{2}+\frac{{{l}_{3}}}{{{\gamma }_{0}}}r\cos \theta +O({{r}^{{3}/{2}\;}})+\ldots \end{aligned}$$

(16)

The crack-tip force stresses and couple stresses are expressed as

$$\begin{aligned}&{{\sigma }_{ij}}=\frac{1}{\sqrt{2\pi r}}\left[ {{K}_{I}}g_{ij}^{I}(\theta )+{{K}_{II}}g_{ij}^{II}(\theta ) \right] \\&+\left( {{k}_{I}}{{\delta }_{i1}}{{\delta }_{j1}}+{{k}_{II}}{{\delta }_{i1}}{{\delta }_{j2}} \right) +O({{r}^{{1}/{2}\;}})+\ldots \nonumber \end{aligned}$$

(17)

$$\begin{aligned} {{m}_{i3}}=\frac{{{L}_{3}}}{\sqrt{2\pi r}}\left( -{{\delta }_{i1}}\sin \frac{\theta }{2}+{{\delta }_{i2}}\cos \frac{\theta }{2} \right) +{{l}_{3}}{{\delta }_{i1}}+O({{r}^{{1}/{2}\;}})+\ldots \end{aligned}$$

(18)

where ${{K}_{I}}=\underset{r\rightarrow 0}{\mathop {\lim }}\,\{\sqrt{2\pi r}{{\left. {{\sigma }_{22}} \right| }_{\theta =0}}\}$, ${{K}_{II}}=\underset{r\rightarrow 0}{\mathop {\lim }}\,\{\sqrt{2\pi r}{{\left. {{\sigma }_{21}} \right| }_{\theta =0}}\}$ and ${{L}_{3}}=\underset{r\rightarrow 0}{\mathop {\lim }}\,\{\sqrt{2\pi r}{{\left. {{m}_{23}} \right| }_{\theta =0}}\}$ are the mode-I FSIF, mode-II FSIF and in-plane CSIF, respectively. The coefficients ${{k}_{I}}$, ${{k}_{II}}$, and ${{l}_{3}}$ represent constant stress terms due to crack opening, crack sliding and in-plane micro-rotation, respectively. It can be observed that both the normal stress ${{\sigma }_{11}}$ and the shear stress ${{\sigma }_{12}}$ have a constant term. This is different from the classical fracture mechanics, where only the normal stress ${{\sigma }_{11}}=T$ has a constant term. The angular functions $f_{i}^{I}$, $f_{i}^{II}$, $g_{i}^{I}$, and $g_{i}^{II}$ for the generalized plane strain condition are given by [33]:

$$\begin{aligned}&f_{1}^{I}=\frac{{{S}_{0}}}{4{{G}_{0}}}\left[ \left( 5-4{{\nu }_{0}} \right) \cos \frac{\theta }{2}-\cos \frac{3\theta }{2} \right] -\frac{{{\nu }_{0}}}{{{G}_{0}}}\cos \frac{\theta }{2} \\&f_{2}^{I}=\frac{{{S}_{0}}}{4{{G}_{0}}}\left[ \left( 3-4{{\nu }_{0}} \right) \sin \frac{\theta }{2}-\sin \frac{3\theta }{2} \right] +\frac{1-{{\nu }_{0}}}{{{G}_{0}}}\sin \frac{\theta }{2} \nonumber \end{aligned}$$

(19)

$$\begin{aligned}&f_{1}^{II}=\frac{{{S}_{0}}}{4{{G}_{0}}}\left[ \left( 5-4{{\nu }_{0}} \right) \sin \frac{\theta }{2}+\sin \frac{3\theta }{2} \right] +\frac{1-{{\nu }_{0}}}{{{G}_{0}}}\sin \frac{\theta }{2} \\&f_{2}^{II}=\frac{{{S}_{0}}}{4{{G}_{0}}}\left[ \left( 4{{\nu }_{0}}-3 \right) \cos \frac{\theta }{2}-\cos \frac{3\theta }{2} \right] +\frac{{{\nu }_{0}}}{{{G}_{0}}}\cos \frac{\theta }{2} \nonumber \end{aligned}$$

(20)

$$\begin{aligned}&g_{11}^{I}=\frac{{{S}_{0}}}{4}\left( 3\cos \frac{\theta }{2}+\cos \frac{5\theta }{2} \right) ,&g_{12}^{I}=\frac{{{S}_{0}}}{4}\left( 3\sin \frac{\theta }{2}+\sin \frac{5\theta }{2} \right) -\sin \frac{\theta }{2} \\&g_{21}^{I}=\frac{{{S}_{0}}}{4}\left( -\sin \frac{\theta }{2}+\sin \frac{5\theta }{2} \right) ,&g_{22}^{I}=\frac{{{S}_{0}}}{4}\left( \cos \frac{\theta }{2}-\cos \frac{5\theta }{2} \right) +\cos \frac{\theta }{2} \nonumber \end{aligned}$$

(21)

$$\begin{aligned}&g_{11}^{II}=\frac{{{S}_{0}}}{4}\left( -3\sin \frac{\theta }{2}-\sin \frac{5\theta }{2} \right) -\sin \frac{\theta }{2},&g_{12}^{II}=\frac{{{S}_{0}}}{4}\left( 3\cos \frac{\theta }{2}+\cos \frac{5\theta }{2} \right) \\&g_{21}^{II}=\frac{{{S}_{0}}}{4}\left( -\cos \frac{\theta }{2}+\cos \frac{5\theta }{2} \right) +\cos \frac{\theta }{2},&g_{22}^{II}=\frac{{{S}_{0}}}{4}\left( -\sin \frac{\theta }{2}+\sin \frac{5\theta }{2} \right) \nonumber \end{aligned}$$

(22)

The micropolar constant ${{S}_{0}}$ is defined by

$$\begin{aligned} {{S}_{0}}=\frac{1-2(1-{{\nu }_{0}})N_{0}^{2}}{1+2(1-{{\nu }_{0}})N_{0}^{2}} \end{aligned}$$

(23)

where ${{N}_{0}}=\sqrt{{{{\kappa }_{0}}}/{(2{{G}_{0}}+{{\kappa }_{0}})}\;}$ is the coupling number evaluated at the crack tip. The constant ${{S}_{0}}$ satisfies the relation $\tfrac{1}{1.5-{{\nu }_{0}}}-1\le {{S}_{0}}\le 1$ due to $0\le {{N}_{0}}\le 1$. It can be observed that the above angular functions $f_{i}^{I}$, $f_{i}^{II}$, $g_{i}^{I}$, and $g_{i}^{II}$ degenerate to the corresponding functions of classical elastic theory for ${{N}_{0}}=0$ and to the couple stress theory for ${{N}_{0}}=1$ [20]. For the generalized plane stress condition, Poisson’s ratio in the above expressions must be replaced with ${{{\nu }_{0}}}/{(1+{{\nu }_{0}})}$. Researchers [49, 50] found that the nature of the near tip displacement for FGMs is precisely the same as for homogeneous materials (the form of the terms proportional to ${{r}^{1/2}}$ and r in the displacement expression for FGMs is identical to that for homogeneous materials). It is also the case for the near tip displacement and micro-rotation of FGMMs.

Fig. 2

Integral paths around the crack tip

3 Interaction Integral (I-integral)

The J-integral for a micropolar material is given by [51]

$$\begin{aligned} J=\underset{{{\varGamma }_{\varepsilon }}\rightarrow 0}{\mathop {\lim }}\,\int _{{{\varGamma }_{\varepsilon }}}{\left[ \frac{1}{2}({{\sigma }_{jk}}{{\varepsilon }_{jk}}+{{m}_{j3}}{{\chi }_{j3}}){{\delta }_{i1}}-{{\sigma }_{ij}}{{u}_{j,1}}-{{m}_{i3}}{{\phi }_{3,1}} \right] {{n}_{i}}d\varGamma }\, , \end{aligned}$$

(24)

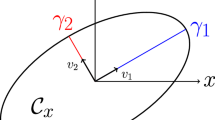
where ${{\varGamma }_{\varepsilon }}$ is an integral contour around the crack tip, as shown in Fig. 2. Superimposing an auxiliary field ($u_{i}^{aux}$, $\phi _{3}^{aux}$) on the actual field (${{u}_{i}}$, ${{\phi }_{3}}$) of the considered crack problem leads to a new state for which the J-integral is given by

$$\begin{aligned} J^{(S)}=\lim _{\varGamma _\varepsilon \rightarrow 0}\,\int _{\varGamma _\varepsilon } \left\{ \begin{array}{cc} &{}\frac{1}{2}[(\sigma _{jk}+\sigma _{jk}^{aux})({\varepsilon }_{jk}+\varepsilon _{jk}^{aux})+({m}_{j3} + m_{j3}^{aux})({\chi _{j3}}+\chi _{j3}^{aux})]{{\delta }_{i1}} \\ &{} -({{\sigma }_{ij}}+\sigma _{ij}^{aux})(u_{j,1}+u_{j,1}^{aux})-({{m}_{i3}}+m_{i3}^{aux})({\phi }_{3,1}+\phi _{3,1}^{aux}) \end{array} \right\} n_i d \varGamma \end{aligned}$$

(25)

Expanding the J-integral and extracting the cross terms, one obtains the I-integral [33]

$$\begin{aligned} I=\underset{{{\varGamma }_{\varepsilon }}\rightarrow 0}{\mathop {\lim }}\,\int _{{{\varGamma }_{\varepsilon }}} {\left[ \begin{matrix} &{} \frac{1}{2}(\sigma _{jk}^{aux}{{\varepsilon }_{jk}}+{{\sigma }_{jk}}\varepsilon _{jk}^{aux}+m_{j3}^{aux}{{\chi }_{j3}}+{{m}_{j3}}\chi _{j3}^{aux}){{\delta }_{i1}} \\ \\ &{} -\sigma _{ij}^{aux}{{u}_{j,1}}-{{\sigma }_{ij}}u_{j,1}^{aux}-m_{i3}^{aux}{{\phi }_{3,1}}-{{m}_{i3}}\phi _{3,1}^{aux} \end{matrix} \right] {{n}_{i}}d\varGamma } \end{aligned}$$

(26)

The auxiliary field must be defined prior to the computation of the I-integral.

3.1 Three Formulations of the Auxiliary Field

Kim and Paulino [37] proposed three formulations of the auxiliary field for functionally graded materials, i.e. a constant-constitutive-tensor (CCT) formulation, a nonequilibrium (NE) formulation and an incompatibility (IC) formulation. Rao and Kuna [52, 53] showed the validity of these three definitions for functionally graded piezoelectric and magnetoelectroelastic materials. Similarly, three formulations are defined for FGMMs here. All of these three formulations adopt the same definitions for the auxiliary displacement and micro-rotation, i.e.

$$\begin{aligned}&u_{i}^{aux}=\left[ K_{I}^{aux}f_{i}^{I}(\theta )+K_{II}^{aux}f_{i}^{II}(\theta ) \right] \sqrt{\frac{r}{2\pi }} \nonumber \\&\phi _{3}^{aux}=\frac{L_{3}^{aux}}{{{\gamma }_{\text {0}}}}\sqrt{\frac{2r}{\pi }}\sin \frac{\theta }{2} , \end{aligned}$$

(27)

where $K_{I}^{aux}$, $K_{II}^{aux}$ and $L_{3}^{aux}$ are the auxiliary mode-I FSIF, mode-II FSIF and in-plane CSIF, respectively. The angular functions $f_{i}^{I}$ and $f_{i}^{II}$ are identical to those in Eqs. (19) and (20). However, different formulations are used to define the auxiliary force stress, couple stress, microstrain and curvature, i.e.

• CCT formulation

  $$\begin{aligned}&\varepsilon _{ij}^{aux}=u_{j,i}^{aux},&\chi _{i3}^{aux}=\phi _{3,i}^{aux} \end{aligned}$$

  (28)
  $$\begin{aligned}&\sigma _{ij}^{aux}=A_{ijkl}^{\text {0}}\varepsilon _{kl}^{aux},&m_{i3}^{aux}={{\gamma }_{0}}\chi _{i3}^{aux} \end{aligned}$$

  (29)

  In the CCT formulation, all auxiliary variables are the asymptotic analytical solutions of a crack in an infinite homogeneous micropolar plate. Here, the material constants in the auxiliary constitutive Eq. (29) are different from those in the actual constitutive Eq. (3). As a result, the auxiliary field satisfies the equilibrium equations $\sigma _{ij,i}^{aux}=0$ and $m_{i3,i}^{aux}=0$, but violates the relations $\sigma _{ij}^{aux}\ne {{A}_{ijkl}}(\mathbf {x})\varepsilon _{kl}^{aux}$ and $m_{i3}^{aux}\ne \gamma (\mathbf {x})\chi _{i3}^{aux}$ for any coordinate apart from the crack tip.

• NE formulation

  $$\begin{aligned}&\varepsilon _{ij}^{aux}=u_{j,i}^{aux},&\chi _{i3}^{aux}=\phi _{3,i}^{aux} \end{aligned}$$

  (30)
  $$\begin{aligned}&\sigma _{ij}^{aux}={{A}_{ijkl}}\varepsilon _{kl}^{aux},&m_{i3}^{aux}=\gamma \chi _{i3}^{aux} \end{aligned}$$

  (31)

  In the NE formulation, the auxiliary force stress and couple stress are not the asymptotic analytical solutions of a crack in a homogeneous micropolar plate, but defined using the actual material properties of FGMMs. As a result, the auxiliary field does not satisfy the equilibrium equations, i.e. $\sigma _{ij,i}^{aux}\ne 0$ and $m_{i3,i}^{aux}\ne 0$.

• IC formulation

  $$\begin{aligned}&\sigma _{ij}^{aux}=A_{ijkl}^{\text {0}}u_{l,k}^{aux},&m_{i3}^{aux}={{\gamma }_{0}}\phi _{3,i}^{aux} \end{aligned}$$

  (32)
  $$\begin{aligned}&\varepsilon _{ij}^{aux}=A_{ijkl}^{-1}\sigma _{kl}^{aux},&\chi _{i3}^{aux}={{\gamma }^{-1}}m_{i3}^{aux} \end{aligned}$$

  (33)

  In the IC formulation, the auxiliary force stress and couple stress are the asymptotic analytical solutions of a crack in a homogeneous micropolar plate so that $\sigma _{ij,i}^{aux}=0$ and $m_{i3,i}^{aux}=0$, whereas the auxiliary strain and curvature are defined using the actual material properties which results in $\varepsilon _{ij}^{aux}\ne u_{j,i}^{aux}$ and $\chi _{i3}^{aux}\ne \phi _{3,i}^{aux}$.

For homogeneous materials, all of the above three formulations coincide with each other, whereas none of the above three formulations satisfies all three governing relations for FGMMs, i.e. the constitutive, equilibrium and compatibility equations.

3.2 Numerical Calculation of the I-Integral

For practical calculations, the infinitesimal contour integral Eq. (26) must be converted into an equivalent domain integral. A traction-free crack is considered for which the crack-face boundary conditions are

$$\begin{aligned}&{{n}_{i}}{{\sigma }_{ij}}=0, \quad {{n}_{i}}{{m}_{ij}}=0, \quad \text {on }\varGamma _{C}^{+}\text { and }\varGamma _{C}^{-} \end{aligned}$$

(34)

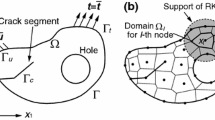
where $\varGamma _{C}^{+}$ and $\varGamma _{C}^{-}$ represent the top and bottom faces of a crack, respectively. As shown in Fig. 2, we convert the I-integral into an equivalent domain integral by Gauss’ theorem as

$$\begin{aligned} I=\int _{A}{\frac{\partial }{\partial {{x}_{i}}}\left\{ \left[ \begin{matrix} &{} \sigma _{ij}^{aux}{{u}_{j,1}}+{{\sigma }_{ij}}u_{j,1}^{aux}+m_{i3}^{aux}{{\phi }_{3,1}}+{{m}_{i3}}\phi _{3,1}^{aux} \\ \\ &{} -\frac{1}{2}(\sigma _{jk}^{aux}{{\varepsilon }_{jk}}+{{\sigma }_{jk}}\varepsilon _{jk}^{aux}+m_{j3}^{aux}{{\chi }_{j3}}+{{m}_{j3}}\chi _{j3}^{aux}){{\delta }_{i1}} \end{matrix} \right] w \right\} dA} \end{aligned}$$

(35)

where a smooth weighting function w is introduced with values varying from 1 on ${{\varGamma }_{\varepsilon }}$ to 0 on ${{\varGamma }_{B}}$. Applying the auxiliary fields defined above, one can simplify the I-integral as follows:

• I-integral using the CCT formulation

  $$\begin{aligned} I=\int _{A}{\left[ \begin{matrix} &{} \sigma _{ij}^{aux}{{u}_{j,1}}+{{\sigma }_{ij}}u_{j,1}^{aux}-\frac{1}{2}(\sigma _{jk}^{aux}{{\varepsilon }_{jk}}+{{\sigma }_{jk}}\varepsilon _{jk}^{aux}){{\delta }_{i1}} \\ \\ \nonumber &{} +m_{i3}^{aux}{{\phi }_{3,1}}+{{m}_{i3}}\phi _{3,1}^{aux}-\frac{1}{2}(m_{j3}^{aux}{{\chi }_{j3}}+{{m}_{j3}}\chi _{j3}^{aux}){{\delta }_{i1}} \end{matrix} \right] {{w}_{,i}} \,dA} \nonumber \end{aligned}$$
  $$\begin{aligned} \nonumber&+\int _{A}{\left[ (\sigma _{12}^{aux}-\sigma _{21}^{aux}){{\phi }_{3,1}}-({{\sigma }_{12}}-{{\sigma }_{21}})\phi _{3,1}^{aux} \right] wdA} \\&+\frac{1}{2}\int _{A}{\left[ \begin{matrix} &{} ({{A}_{ijkl}}-A_{ijkl}^{0})({{\varepsilon }_{ij}}\varepsilon _{kl,1}^{aux}-\varepsilon _{ij}^{aux}{{\varepsilon }_{kl,1}})-{{A}_{ijkl,1}}{{\varepsilon }_{ij}}\varepsilon _{kl}^{aux} \\ \\ &{} +(\gamma -{{\gamma }_{0}})({{\chi }_{i3}}\chi _{i3,1}^{aux}-\chi _{i3}^{aux}{{\chi }_{i3,1}})-{{\gamma }_{,1}}{{\chi }_{i3}}\chi _{i3}^{aux} \end{matrix} \right] w\,dA} \end{aligned}$$

  (36)

• I-integral using the NE formulation

  $$\begin{aligned} \nonumber&I=\int _{A}{\left( \begin{matrix} &{} \sigma _{ij}^{aux}{{u}_{j,1}}+{{\sigma }_{ij}}u_{j,1}^{aux}-{{\sigma }_{jk}}\varepsilon _{jk}^{aux}{{\delta }_{i1}} \\ \\ &{} +m_{i3}^{aux}{{\phi }_{3,1}}+{{m}_{i3}}\phi _{3,1}^{aux}-{{m}_{j3}}\chi _{j3}^{aux}{{\delta }_{i1}} \end{matrix} \right) {{w}_{,i}}\,dA} \\ \nonumber&+\int _{A}{\left[ (\sigma _{12}^{aux}-\sigma _{21}^{aux}){{\phi }_{3,1}}-({{\sigma }_{12}}-{{\sigma }_{21}})\phi _{3,1}^{aux} \right] wdA} \\&+\int _{A}{\left( \sigma _{ij,i}^{aux}{{u}_{j,1}}-{{A}_{ijkl,1}}{{\varepsilon }_{ij}}\varepsilon _{kl}^{aux}+m_{i3,i}^{aux}{{\phi }_{3,1}}-{{\gamma }_{,1}}{{\chi }_{i3}}\chi _{i3}^{aux} \right) w\,dA} \end{aligned}$$

  (37)

• I-integral using the IC formulation

  $$\begin{aligned} \nonumber&I=\int _{A}{\left( \begin{matrix} &{} \sigma _{ij}^{aux}{{u}_{j,1}}+{{\sigma }_{ij}}u_{j,1}^{aux}-\sigma _{jk}^{aux}{{\varepsilon }_{jk}}{{\delta }_{i1}} \\ \\ &{} +m_{i3}^{aux}{{\phi }_{3,1}}+{{m}_{i3}}\phi _{3,1}^{aux}-m_{j3}^{aux}{{\chi }_{j3}}{{\delta }_{i1}} \\ \end{matrix} \right) {{w}_{,i}}\,dA} \\ \nonumber&+\int _{A}{\left[ (\sigma _{12}^{aux}-\sigma _{21}^{aux}){{\phi }_{3,1}}-({{\sigma }_{12}}-{{\sigma }_{21}})\phi _{3,1}^{aux} \right] wdA} \\&+\int _{A}{\left\{ [{{(A_{ijkl}^{0})}^{-1}}-A_{ijkl}^{-1}]{{\sigma }_{ij}}\sigma _{kl,1}^{aux}+(\gamma _{0}^{-1}-{{\gamma }^{-1}}){{m}_{i3}}m_{i3,1}^{aux} \right\} w\,dA} \end{aligned}$$

  (38)

It can be observed that each of the above three domain forms of the I-integral contains three parts, whereby the third integral caused by material nonhomogeneity vanishes for homogeneous micropolar materials. The I-integral using the CCT formulation Eq. (36) contains strain gradient (${{\varepsilon }_{kl,1}}$), curvature gradient (${{\chi }_{i3,1}}$) and material property gradient (${{A}_{ijkl,1}}$ and ${{\gamma }_{,1}}$). The I-integral using the NE formulation Eq. (37) contains neither strain gradient nor curvature gradient, but contains material property gradient. The I-integral using the IC formulation Eq. (38) contains none of them. Since the I-integral using the CCT formulation contains strain and curvature gradients, its numerical computation will lose accuracy. Therefore, the NE and IC formulations are more appropriate than the CCT formulations for FGMMs. In addition, the I-integral using the IC formulation is effective for micropolar composites due to its domain-independence for interfaces [19].

3.3 Extraction of the FSIFs and CSIFs

In order to derive the relations between the I-integral and the intensity factors, we take the integral path ${{\varGamma }_{\varepsilon }}$ along a circle of radius r. Substituting $d\varGamma =rd\theta$ into Eq. (26) yields

$$\begin{aligned} I=\underset{r\rightarrow 0}{\mathop {\lim }}\,\int _{-\pi }^{\pi }{\left[ \begin{matrix} &{} \frac{1}{2}(\sigma _{jk}^{aux}{{\varepsilon }_{jk}}+{{\sigma }_{jk}}\varepsilon _{jk}^{aux}+m_{j3}^{aux}{{\chi }_{j3}}+{{m}_{j3}}\chi _{j3}^{aux}){{\delta }_{i1}} \\ \\ &{} -\sigma _{ij}^{aux}{{u}_{j,1}}-{{\sigma }_{ij}}u_{j,1}^{aux}-m_{i3}^{aux}{{\phi }_{3,1}}-{{m}_{i3}}\phi _{3,1}^{aux} \end{matrix} \right] {{n}_{i}}rd\theta }\, . \end{aligned}$$

(39)

In a small region ${{R}_{\varepsilon }}$ around the crack tip, the material constants $A_{ijkl}^{-1}$ and ${{\gamma }^{-1}}$ can be expressed using a Taylor series expansion as

$$\begin{aligned} \begin{array}{cc} &{} A_{ijkl}^{-1}(r,\theta )={{(A_{ijkl}^{0})}^{-1}}+r\frac{\partial A_{ijkl}^{-1}}{\partial r}(\theta )+\frac{{{r}^{2}}}{2}\frac{{{\partial }^{2}}A_{ijkl}^{-1}}{\partial {{r}^{2}}}(\theta )+\ldots . \\ \\ &{} {{\gamma }^{-1}}(r,\theta )=\gamma _{0}^{-1}+r\frac{\partial {{\gamma }^{-1}}}{\partial r}(\theta )+\frac{{{r}^{2}}}{2}\frac{{{\partial }^{2}}{{\gamma }^{-1}}}{\partial {{r}^{2}}}(\theta )+\ldots . \\ \end{array} \end{aligned}$$

(40)

As $r\rightarrow 0$, only the singular terms in the expansions of ${{\sigma }_{ij}}$, ${{m}_{i3}}$, ${{u}_{j,i}}$, ${{\phi }_{3,i}}$, $\varepsilon _{ij}^{aux}$ and $\chi _{i3}^{aux}$ contribute to the I-integral. Substituting Eq. (40), the actual and auxiliary fields into Eq. (39) yields

$$\begin{aligned} I=\frac{1+{{S}_{0}}}{{{{{E}'}}_{0}}}({{K}_{I}}K_{I}^{aux}+{{K}_{II}}K_{II}^{aux})+\frac{{{L}_{3}}L_{3}^{aux}}{{{\gamma }_{0}}} \end{aligned}$$

(41)

where

$$\begin{aligned} {{{E}'}_{0}}=\left\{ \begin{array}{cc} {{E}_{0}} &{} \text {(plane stress)} \\ \frac{{{E}_{0}}}{1-\nu _{0}^{2}} &{} \text {(plane strain)} \\ \end{array} \right. \end{aligned}$$

(42)

Taking the vector $[K_{I}^{aux},\text { }K_{II}^{aux},\text { }L_{3}^{aux}]$ sequentially to be $[1,\text { }0,\text { }0]$, $[0,\text { }1,\text { }0]$ and $[0,\text { }0,\text { }1]$, one can compute the corresponding I-integrals ${{I}^{({{K}_{I}})}}$, ${{I}^{({{K}_{II}})}}$ and ${{I}^{({{L}_{3}})}}$, so that the FSIFs and CSIFs can be solved according to the relations

$$\begin{aligned} {{K}_{I}}=\frac{{{{{E}'}}_{0}}}{1+{{S}_{0}}}{{I}^{({{K}_{I}})}}, \quad {{K}_{II}}=\frac{{{{{E}'}}_{0}}}{1+{{S}_{0}}}{{I}^{({{K}_{II}})}}, \quad {{L}_{I}}={{\gamma }_{0}}{{I}^{({{L}_{3}})}}. \end{aligned}$$

(43)

4 Patched XFEM for Micropolar Materials

Through embedding local solutions of boundary-value problems into the finite element approximation, the extended finite element method (XFEM) [54] allows cracks and material interfaces to be tackled independently of the mesh. The XFEM can greatly facilitate the modeling process, especially for crack propagation problems. Recently, the XFEM has been developed for micropolar elasticity [30, 31], too. The displacement approximation in the XFEM usually contains the standard finite element shape functions, the enrichment for crack faces and the enrichment for crack tips. The enrichment for crack faces is only a function of position, whereas the enrichment for crack tips is dependent on material constitutive equation. The use of the crack-tip enrichment is mainly used to improve the numerical accuracy. If the finite element mesh is sufficiently fine and the I-integrals are applied, it is not necessary to use the crack-tip enrichment functions. For FGMMs, we herein adopt the displacement and micro-rotation approximations as

$$\begin{aligned} \left\{ \begin{matrix} u_{1}^{h}(\mathbf {x}) \\ u_{2}^{h}(\mathbf {x}) \\ \phi _{3}^{h}(\mathbf {x}) \\ \end{matrix} \right\} =\sum \limits _{p\in {{S}_{N}}}{{{N}_{p}}(\mathbf {x})\left\{ \begin{matrix} u_{1}^{p} \\ u_{2}^{p} \\ \phi _{3}^{p} \\ \end{matrix} \right\} }+\sum \limits _{p\in {{S}_{H}}}{{{N}_{p}}(\mathbf {x}){{{\bar{H}}}_{p}}(\mathbf {x})\left\{ \begin{matrix} b_{1}^{p} \\ b_{2}^{p} \\ b_{3}^{p} \\ \end{matrix} \right\} } \end{aligned}$$

(44)

Here, $u_{i}^{p}$, $\phi _{3}^{p}$ and $b_{i}^{p}$ are the nodal displacements, nodal micro-rotation, and the additional degrees of freedom, respectively. ${{N}_{p}}(\mathbf {x})$ is the standard finite element shape function, ${{\bar{H}}_{p}}(\mathbf {x})=H(\mathbf {x}-\bar{\mathbf {x}})-H({{\mathbf {x}}_{p}}-\bar{\mathbf {x}})$ is the shifted enrichment function for a crack face, where $\mathbf {x}$, ${{\mathbf {x}}_{p}}$ and $\bar{\mathbf {x}}$ denote an arbitrary point, the nodal point and the point on a crack face, respectively. ${{S}_{N}}$ and ${{S}_{H}}$ are the set of standard nodes and the set of enriched nodes, respectively. For a n-node element cut by a crack, the nodal degrees-of-freedom are expressed as

$$\begin{aligned}&\{\mathbf {a}\}={{\left[ \begin{array}{*{35}{l}} u_{1}^{(1)} &{} u_{2}^{(1)} &{} \phi _{3}^{(1)} &{} ... &{} u_{1}^{(n)} &{} u_{2}^{(n)} &{} \phi _{3}^{(n)} \\ \end{array} \right] }^{\mathrm {T}}} \\ \nonumber&\{\mathbf {b}\}={{\left[ \begin{array}{*{35}{l}} b_{1}^{(1)} &{} b_{2}^{(1)} &{} b_{3}^{(1)} &{} ... &{} b_{1}^{(n)} &{} b_{2}^{(n)} &{} b_{3}^{(n)} \\ \end{array} \right] }^{\mathrm {T}}} \end{aligned}$$

(45)

The displacement and micro-rotation are expressed in matrix form as

$$\begin{aligned} \left\{ \begin{array}{c} {{\mathbf {u}}^{h}} \\ \phi _{3}^{h} \\ \end{array} \right\} =\left[ \begin{array}{cc} {{\mathbf {N}}^{a}} &{} {{\mathbf {N}}^{b}} \\ \end{array} \right] \left\{ \begin{array}{c} \mathbf {a} \\ \mathbf {b} \\ \end{array} \right\} \end{aligned}$$

(46)

Here, $[{{\mathbf {N}}^{a}}]=\left[ \begin{array}{cccc} {{N}_{(1)}}\mathbf {I} &{} {{N}_{(2)}}\mathbf {I} &{} ... &{} {{N}_{(n)}}\mathbf {I} \\ \end{array} \right]$, $[{{\mathbf {N}}^{b}}]=\left[ \begin{array}{cccc} {{{\bar{H}}}_{(1)}}{{N}_{(1)}}\mathbf {I} &{} {{{\bar{H}}}_{(2)}}{{N}_{(2)}}\mathbf {I} &{} ... &{} {{{\bar{H}}}_{(n)}}{{N}_{(n)}}\mathbf {I} \\ \end{array} \right]$, and $\mathbf {u}={{\left[ \begin{array}{cc} {{u}_{1}} &{} {{u}_{2}} \\ \end{array} \right] }^{\mathrm {T}}}$, where $\mathbf {I}$ is an identity matrix of order 3. The strain and curvature are expressed in matrix form as

$$\begin{aligned} \left\{ \begin{array}{c} \mathbf {\varepsilon } \\ \mathbf {\chi } \\ \end{array} \right\} =\left[ \begin{array}{cc} {{\mathbf {B}}^{a}} &{} {{\mathbf {B}}^{b}} \\ \end{array} \right] \left\{ \begin{array}{c} \mathbf {a} \\ \mathbf {b} \\ \end{array} \right\} \end{aligned}$$

(47)

Here, $\{\mathbf {\varepsilon }\}={{[\begin{matrix} {{\varepsilon }_{11}} &{} {{\varepsilon }_{12}} &{} {{\varepsilon }_{21}} &{} {{\varepsilon }_{22}} \\ \end{matrix}]}^{\mathrm {T}}}$, $\{\mathbf {\chi }\}={{[\begin{matrix} {{\chi }_{13}} &{} {{\chi }_{23}} \\ \end{matrix}]}^{\mathrm {T}}}$, $[{{\mathbf {B}}^{a}}]=\left[ \begin{matrix} {{\mathbf {B}}_{(1)}} &{} {{\mathbf {B}}_{(2)}} &{} ... &{} {{\mathbf {B}}_{(n)}} \\ \end{matrix} \right]$ and $[{{\mathbf {B}}^{b}}]=\left[ \begin{matrix} {{{\bar{H}}}_{(1)}}{{\mathbf {B}}_{(1)}} &{} {{{\bar{H}}}_{(2)}}{{\mathbf {B}}_{(2)}} &{} ... &{} {{{\bar{H}}}_{(n)}}{{\mathbf {B}}_{(n)}} \\ \end{matrix} \right]$, where

$$\begin{aligned} \nonumber \begin{matrix} [{{\mathbf {B}}_{p}}]=\left[ \begin{matrix} {{N}_{p,1}} &{} 0 &{} 0 \\ 0 &{} {{N}_{p,1}} &{} -{{N}_{p}} \\ {{N}_{p,2}} &{} 0 &{} {{N}_{p}} \\ 0 &{} {{N}_{p,2}} &{} 0 \\ 0 &{} 0 &{} {{N}_{p,1}} \\ 0 &{} 0 &{} {{N}_{p,2}} \\ \end{matrix} \right] ,&p=(1),\text { }\ldots \text { }(n) \end{matrix} \end{aligned}$$

Substituting Eq. (47) into the weak forms of the governing equations

$$\begin{aligned} \int _{R}{\left\{ \begin{array}{cc} \delta {{\mathbf {\varepsilon }}^{\mathrm {T}}} &{} \delta {{\mathbf {\chi }}^{\mathrm {T}}} \\ \end{array} \right\} [\mathbf {C}(\mathbf {x})]\left\{ \begin{array}{c} \mathbf {\varepsilon } \\ \mathbf {\chi } \\ \end{array} \right\} dV}=\int _{\partial {{R}^{\sigma }}}{\left\{ \begin{array}{cc} \delta {{\mathbf {u}}^{\mathrm {T}}} &{} \delta {{\phi }_{3}} \\ \end{array} \right\} \left\{ \begin{array}{c} \mathbf {t} \\ {{m}_{3}} \\ \end{array} \right\} dS}\, , \end{aligned}$$

(48)

one obtains the linear equations

$$\begin{aligned} \left[ \begin{array}{cc} \mathbf {K}_{aa}^{e} &{} \mathbf {K}_{ab}^{e} \\ \mathbf {K}_{ba}^{e} &{} \mathbf {K}_{bb}^{e} \\ \end{array} \right] \left\{ \begin{array}{c} \mathbf {a} \\ \mathbf {b} \\ \end{array} \right\} =\left\{ \begin{array}{c} {{\mathbf {F}}^{e}} \\ \mathbf {0} \\ \end{array} \right\} \, . \end{aligned}$$

(49)

Here, $\mathbf {C}(\mathbf {x})$ is material matrix of FGMMs, $\mathbf {t}={{\left[ \begin{matrix} {{t}_{1}} &{} {{t}_{2}} \\ \end{matrix} \right] }^{\mathrm {T}}}$ is the traction vector. The element stiffness matrices and the nodal force vector for one element e are

$$\begin{aligned}&[\mathbf {K}_{aa}^{e}]=\int _{{{V}^{e}}}{{{[{{\mathbf {B}}^{a}}]}^{\mathrm {T}}}[\mathbf {C}(\mathbf {x})][{{\mathbf {B}}^{a}}]dV} \nonumber \\&[\mathbf {K}_{bb}^{e}]=\int _{{{V}^{e}}}{{{[{{\mathbf {B}}^{b}}]}^{\mathrm {T}}}[\mathbf {C}(\mathbf {x})][{{\mathbf {B}}^{b}}]dV} \\&[\mathbf {K}_{ab}^{e}]=\int _{{{V}^{e}}}{{{[{{\mathbf {B}}^{a}}]}^{\mathrm {T}}}[\mathbf {C}(\mathbf {x})][{{\mathbf {B}}^{b}}]dV}={{[\mathbf {K}_{ba}^{e}]}^{\mathrm {T}}} \nonumber \end{aligned}$$

(50)

.

$$\begin{aligned} \{{{\mathbf {F}}^{e}}\}=\int _{S}{{{[{{\mathbf {N}}^{a}}]}^{\mathrm {T}}}\left\{ \begin{array}{c} \mathbf {t} \\ {{m}_{3}} \end{array} \right\} dS} \end{aligned}$$

(51)

For plane strain condition, the material matrix $\mathbf {C}$ is expressed as

$$\begin{aligned}{}[\mathbf {C}]=\left[ \begin{array}{cc} \begin{array}{cccc} \lambda +2G &{} 0 &{} 0 &{} \lambda \\ 0 &{} G+{\kappa }/{2}\; &{} G-{\kappa }/{2}\; &{} 0 \\ 0 &{} G-{\kappa }/{2}\; &{} G+{\kappa }/{2}\; &{} 0 \\ \lambda &{} 0 &{} 0 &{} \lambda +2G \\ \end{array} &{} \mathbf {0} \\ \mathbf {0} &{} \begin{array}{cc} \gamma &{} 0 \\ 0 &{} \gamma \\ \end{array} \\ \end{array} \right] \end{aligned}$$

while for plane stress condition, the parameter $\lambda$ in the material matrix $\mathbf {C}$ should be replaced with ${2G\lambda }/{(2G+\lambda )}\;$.

In order to achieve satisfactory precision in the region around the crack tip, Yu et al. [45] proposed to patch a refined mesh on the main mesh. The technique was referred to as the patched XFEM. When the crack propagates, the patched mesh goes together with the crack tip. For FGMMs, the nonhomogeneous $>>$graded$<<$ element technique [40] is adopted, namely, the material properties at each integration point are used in the calculation of the above element stiffness matrices.

5 Numerical Examples

In this section, internal and edge cracks are studied sequentially to verify the validity of different auxiliary fields and to examine the influence of material parameters on the FSIFs and CSIFs.

5.1 Internal Cracks

Figure 3(a) shows an inclined crack of length 2a and angle $\omega$ located in a square plate of length 2W subjected to tensile load ${{\sigma }_{app}}={{\sigma }_{o}}{{e}^{\eta {{x}_{1}}}}$. Young’s modulus varies with ${{x}_{1}}$ according to $E={{E}_{o}}{{e}^{\eta {{x}_{1}}}}$, whereas Poisson’s ratio $\nu$, the coupling number N, and the characteristic length ${{l}_{b}}$ remain constant in the entire plate. The data used in numerical analysis are as follows: ${{\sigma }_{o}}=1$ MPa, ${{E}_{o}}=1$ GPa, $\nu =0.3$ and ${{l}_{b}}=0.01$ mm.

Example 1: An Infinite Square Plate with an Inclined Crack

First, the geometric parameters $a=1$ mm and $W=20$ mm, the material gradient parameter $\eta =0$ and the coupling number $N=0.01$ are used to model an infinite homogeneous classical elastic plate, for which the analytical solution of the FSIFs is given by

$$\begin{aligned}&{{K}_{I}}={{\sigma }_{o}}\sqrt{\pi a}\,{{\cos }^{2}}\omega \\&{{K}_{II}}={{\sigma }_{o}}\sqrt{\pi a}\,\sin \omega \cos \omega \nonumber \end{aligned}$$

(52)

Then, the geometric and material parameters are set to $a=1$ mm, $W=10$ mm, $\beta =0.5$ and $N=0.01$ to model a functionally graded classical elastic plate. The classical elastic plate with such a configuration was investigated by Dolbow and Gosz [36]. As shown in Fig. 3b, the finite element mesh consists of 1945 eight-node quadrilateral (Q8) and 24 six-node quarter-point (T6qp) singular elements around the crack tips, with a total of 1969 elements and 6026 nodes.

Fig. 3

A cracked micropolar plate under tension

As shown in Fig. 3c, the region being comprised of elements totally and partially enclosed by a circle ${{C}_{I}}$ of radius ${{R}_{I}}$ is selected to be the integration domain. In this example, ${{R}_{I}}=6{{h}_{e}}$, where ${{h}_{e}}=0.012$ is the radial edge length of an element at the crack tip. A right-hand Cartesian coordinate frame $({{x}_{1}},{{x}_{2}},{{x}_{3}})$ is used, which leads to negative CSIF values for this example. The negative sign in the CSIFs just denotes the direction and thus, the normalized CSIFs ${-{{L}_{3}}}/{{{L}_{0}}}\;$ are given in the tables. Tables 1 and 2 list the normalized intensity factors ${{{K}_{I}}}/{{{K}_{0}}}\;$, ${{{K}_{II}}}/{{{K}_{0}}}\;$ and ${-{{L}_{3}}}/{{{L}_{0}}}\;$ for a homogeneous plate ($\eta =0$) and for a functionally graded plate ($\eta =0.5$), respectively, where the reference factors ${{K}_{0}}={{\sigma }_{o}}\sqrt{\pi a}$ and ${{L}_{0}}={{l}_{b}}{{K}_{0}}$ are used for the internal crack. The results show that all three formulations of I-integral generate the same results for the homogeneous plate. For the functionally graded plate, the IC formulation and the NE formulation deliver the same results, which have a difference of less than 1.0% with the results computed using the CCT formulation. All CSIF values approach zero, which indicates that it is reasonable to use the coupling number $N=0.01$ to simulate a classical elastic plate. The present FSIFs are compared with the analytical results of Eq. (52) (see Table 1) and those published in Ref. [36] (see Table 2). An agreement within 1.0% is shown for all three formulations.

Table 1 Normalized FSIFs and CSIFs at the right tip of a crack in an infinite homogeneous plate (Example 1: $a/W=0.05,~\eta =0,~N=0.01,~R_I/h_e=6$)

Table 2 Normalized FSIFs and CSIFs of a crack in a functionally graded plate (Example 1: $a/W=0.1,~\eta =0.5,~N=0.01,~R_I/h_e=6$)

Example 2: A Functionally Graded Plate with an Inclined Crack

The geometric and material parameters are set to $a=1$ mm, $W=10$ mm, $\eta =0.5$ and $N=0.01$ and $N=0.5$ to model a functionally graded micropolar plate. As shown in Fig. 3c, six integration domains of ${{{R}_{I}}}/{{{h}_{e}}}$ = 3, 6, 12, 24, 48 and 96 are used to compute the FSIFs and CSIFs in order to verify the domain-independence of the I-integrals. The relative deviation ${{D}_{r}}=\left| {({{K}_{\max }}-{{K}_{\min }})}/{{{K}_{\text {mean}}}}\; \right| \times 100\%$ is used to estimate the difference of the intensity factors computed using different integration domains, where ${{K}_{\max }}$, ${{K}_{\min }}$ and ${{K}_{\text {mean} }}$ denote the maximum, minimum and average values of the intensity factors, respectively.

Tables 3 and 4 list the normalized intensity factors for $N=0.01$ and $N=0.5$, respectively. The relative deviation ${{D}_{r}}$ for both the NE formulation and the IC formulation does not exceed 1.0%, whereas ${{D}_{r}}$ for the CCT formulation is about 3.0%. It indicates that the computation of the strain gradient probably causes numerical inaccuracy in finite element analysis. In addition, a relatively weaker convergence is observed for the CCT formulation when the size of integration domain increases, which is in accordance with the discussion for classical FGMs, see [37]. Therefore, the NE and IC formulations are more appropriate than the CCT formulation for FGMMs.

Table 3 Normalized FSIFs and CSIFs of a crack in a functionally graded plate (Example 2: $a/W=0.1,~\eta =0.5,~N=0.01,~\omega =18^\circ$)

Table 4 Normalized FSIFs and CSIFs of a crack in a functionally graded micropolar plate (Example 2: $a/W=0.1,~\eta =0.5,~N=0.5,~\omega =18^\circ$)

Example 3: Influence of Coupling and Gradation

First, the geometric parameters are set fixed to $a=1$ mm, $W=10$ mm and $\omega =18{}^\circ$. We take the coupling number $N=0.01\sim 0.99$ and gradation factor $\eta =0\sim 0.5$ in order to study their influence on the FSIFs and CSIFs. The IC formulation is used to compute the FSIFs and CSIFs, which are shown in Fig. 4a, b. Irrespective of whether the material is homogenous ($\eta =0$) or nonhomogeneous ($\eta =0.5$), all FSIFs and CSIFs at both crack tips increase monotonically as the coupling number N increases. As shown in Fig. 5a, b, for both $N=0.01$ and $N=0.5$, all FSIFs and CSIFs at the right (left) crack tip increase (decrease) monotonically as the gradient parameter $\eta$ increases.

Fig. 4

Normalized FSIFs and CSIFs versus the coupling number N in a a homogeneous plate of $\eta =0$ and b a functionally graded plate of $\eta =0.5$ (Example 3)

Fig. 5

Normalized FSIFs and CSIFs versus the gradient parameter $\eta$ for the coupling number a $N=0.01$ and b $N=0.5$ (Example 3)

Next, the geometric and material parameters are set fixed to $W=10$ mm, $\omega =18{}^\circ$, $N=0.5$, and $\eta =0$ and 0.5, and the crack length is taken to be $a=1\sim 6$ mm in order to verify its influence on the normalized intensity factors. For a homogeneous micropolar plate, as shown in Fig. 6a, all FSIFs and CSIFs at both crack tips increase as the crack length a increases. Contrary, for a functionally graded micropolar plate ($\eta =0.5$), as shown in Fig. 6b, all FSIFs and CSIFs at the right (left) crack tip increase (decrease) monotonically with growing crack length a. This example indicates that the material property gradient substantially affects the varying trend of the FSIFs and CSIFs.

Fig. 6

Normalized FSIFs and CSIFs versus crack length a / W in a a homogeneous plate of $\eta =0$ and b a functionally graded plate of $\eta =0.5$ (Example 3)

5.2 Edge Cracks

As shown in Fig. 7, the second model is a rectangular plate of length $2H=20$ mm and width $W=11$ mm subjected to tension loading ${{\sigma }_{app}}=100$ MPa, which contains an edge crack of length a and angle $\omega$. The finite element mesh consists of 1293 elements and 3997 nodes.

Fig. 7

A rectangular plate with an edge crack under tension

Example 4: A Homogeneous Rectangular Plate with a Horizontal Edge Crack

The geometric and material parameters are set as $a=1$ mm, $\omega =0$, $E=100$ GPa and $\nu =0.3$ to model a horizontal edge crack in a homogeneous plate. A classical elastic plate for which the coupling number is set as $N=0.01$ and a micropolar plate of $N=0.85$ are investigated. For a classical elastic plate with such a configuration, the solution of the FSIFs is given in [55] by

$$\begin{aligned}&\begin{matrix} K_{I}^{cl}=k \, {{\sigma }_{app}}\sqrt{\pi a}, \quad &{} K_{II}^{cl}=0 \\ \end{matrix} \\&k=1.12-0.23\frac{a}{W}+10.55{{\left( \frac{a}{W} \right) }^{2}}-21.72{{\left( \frac{a}{W} \right) }^{3}}+30.39{{\left( \frac{a}{W} \right) }^{4}} \nonumber \end{aligned}$$

(53)

The micropolar plate with such a configuration was investigated by Atroshchenko and Bordas [29]. For both plates, the material parameter ${{l}_{b}}$ is taken to be $0.01, 2.55\times 10^{-2}, 2.55\times 10^{-1}, 2.55\times 10^{-1/2}$ and 2.55, sequentially. The FSIFs and CSIFs are normalized by $K_{I}^{cl}=208\text { MPa m}{{\text {m}}^{1/2}}$ and ${{L}_{0}}={{\sigma }_{app}}a\sqrt{\pi a}=177\text { MPa m}{{\text {m}}^{3/2}}$, respectively.

Table 5 lists the normalized mode-I FSIFs and in-plane CSIFs for a classical elastic plate ($N=0.01$). All three formulations generate the same results for a homogeneous plate and thus, the normalized intensity factors are only listed once. When comparing the present results with the reference solution, an agreement within 0.5% is shown. Table 6 lists the normalized mode-I FSIFs and in-plane CSIFs for a micropolar plate ($N=0.85$). The present results agree within 1.0% with those in Ref. [29]. In addition, the value of ${{l}_{b}}$ affects neither the FSIFs nor the CSIFs when the coupling number N approaches to zero (see Table 5), but affects both the FSIFs and the CSIFs evidently (see Table 6).

Example 5: A Functionally Graded Plate with an Edge Crack

Here, the crack length is taken to be $a=3$ mm, while the crack inclination angle varies from $\omega =0{}^\circ$ to $\omega =72{}^\circ$. The material parameters are set to $E=E_{o}(1+x_1/W)$, $\nu =0.3$, ${{l}_{b}}=0.8$ mm and $N=0.01$, 0.8 and 0.99, where ${{E}_{o}}=100$ GPa. Table 7 lists the FSIFs and CSIFs normalized by ${{K}_{0}}={{\sigma }_{app}}\sqrt{\pi a}$ and ${{L}_{0}}={{l}_{b}}{{K}_{0}}$, respectively. The results show that the normalized FSIFs and CSIFs obtained using all three I-integral formulations agree within 0.1% with each other.

Table 5 Normalized FSIFs and CSIFs of an edge crack in a homogeneous plate (Example 4: $\omega =0^\circ ,~E=100\,GPa,~\nu =0.3,~R_I/h_e=6$)

Table 6 Normalized FSIFs and CSIFs of an edge crack in a homogeneous micropolar plate (Example 4: $\omega =0^\circ ,~E=100\,GPa,~\nu =0.3,~R_I/h_e=6$)

Table 7 Normalized FSIFs and CSIFs of a crack in a functionally graded plate (Example 5: $E=E_0(1+x_1/W),~E_0=100\,GPa,~\nu =0.3,~l_b=0.8,~R_I/h_e=6$)

Example 6: A Functionally Graded Plate with a Horizontal Edge Crack

Next, the crack inclination angle is taken to be $\omega =0{^\circ }$ and the crack length varies from $a=1$ mm to $a=8$ mm. In order to study the influence of the variation of material stiffness on the FSIFs and CSIFs, the following three functions are chosen to define Young’s modulus:

• Function 1: $E={{E}_{o}}(1+4{{{x}_{1}}}/{W}\;)$

• Function 2: $E={{E}_{o}}[1+4{{({{{x}_{1}}}/{W}\;)}^{2}}]$

• Function 3: $E={{E}_{o}}[1+8{{{x}_{1}}}/{W}\;-4{{({{{x}_{1}}}/{W}\;)}^{2}}]$

Fig. 8

Young’s modulus $E/E_0$ versus $x_1/W$ (Example 6)

Fig. 9

Normalized FSIFs and CSIFs versus crack length a for the coupling number a $N=0.01$, b $N=0.4$ and c $N=0.99$ (Example 6)

Fig. 10

Normalized FSIFs and CSIFs versus the coupling number N for an edge crack of length a $a=3$ mm and b $a=7$ mm (Example 6)

As shown in Fig. 8, Young’s modulus of all three functions increases from ${{E}_{o}}$ at ${{x}_{1}}=0$ to $5{{E}_{o}}$ at ${{x}_{1}}=W$, but these slopes are ascending (Function 2) or descending (Function 3) or constant (Function 1). The other material parameters are set as ${{E}_{o}}=100$ GPa, $\nu =0.3$ and ${{l}_{b}}=0.8$ mm. The NE formulation is used to solve the FSIFs and CSIFs. Figure 9a–c show the normalized intensity factors ${{{K}_{I}}}/{{{K}_{0}}}\;$ and ${{{L}_{3}}}/{{{L}_{0}}}\;$ varying with the crack length for $N=0.01$, 0.4 and 0.99, respectively, where ${{K}_{0}}={{\sigma }_{app}}\sqrt{\pi a}$ and ${{L}_{0}}={{l}_{b}}{{K}_{0}}$. For all of the above three functions, both the mode-I FSIFs and the CSIFs increase significantly with the increase of the crack length a. The FSIFs and CSIFs in descending order are ${{K}_{I}}{{|}_{\text {Function 2}}}>{{K}_{I}}{{|}_{\text {Function 1}}}>{{K}_{I}}{{|}_{\text {Function 3}}}$ and ${{L}_{3}}{{|}_{\text {Function 2}}}>{{L}_{3}}{{|}_{\text {Function 1}}}>{{L}_{3}}{{|}_{\text {Function 3}}}$ for $a\le 3$ mm, and the inverse order can be observed for $a \ge 3$ mm. In other words, Function 3 is better for weakening the crack-tip force stress and couple stress concentration for a small edge crack, while Function 2 is better for a large edge crack. The reason is a different gradient of Young’s modulus. The higher the gradient in front of the crack, the more is the crack loading released.

Figure 10a, b show the normalized intensity factors ${{{K}_{I}}}/{{{K}_{0}}}\;$ and ${{{L}_{3}}}/{{{L}_{0}}}\;$ varying with the coupling number N for $a=3$ mm and $a=7$ mm, respectively. The normalized FSIFs and CSIFs have the same trends for all of the above three functions as the coupling number N increases. With increasing coupling number N, the normalized FSIFs ${{{K}_{I}}}/{{{K}_{0}}}\;$ first decreases and then increases a little for $a=3$ mm, while ${{{K}_{I}}}/{{{K}_{0}}}\;$ first decreases quickly and then varies slightly for $a=7$ mm, and the normalized CSIF ${{{L}_{3}}}/{{{L}_{0}}}\;$ increases monotonically for both $a=3$ mm and $a=7$ mm.

6 Summary and Conclusions

In order to calculate the crack-tip intensity factors for a crack in nonhomogeneous micropolar materials by the I-integral, three applicable formulations are proposed to define the auxiliary field, i.e.,

• CCT formulation (violation of the constitutive equations),

• NE formulation (violation of the equilibrium equations),

• IC formulation (violation of the compatibility equations).

Each of these formulations results in a consistent domain form of the I-integral, in which extra terms naturally appear to compensate for the difference between homogeneous and nonhomogeneous materials. In details,

• The I-integral using the CCT formulation contains strain gradient, curvature gradient and material property gradient. It is not appropriate for nonhomogeneous micropolar materials because the strain gradient and curvature gradient may cause inaccuracy in numerical calculations.

• The I-integral using the NE formulation does not involve any strain gradient or curvature gradient. Therefore, it is reliable for nonhomogeneous micropolar materials with differentiable properties.

• The I-integral using the IC formulation does not involve any material property gradient. It is effective for micropolar material with arbitrary continuous or discontinuous properties.

In order to compute the various I-integrals numerically for arbitrary two-dimensional cracked bodies, the patched-XFEM is applied. The patched-XFEM preserves crack face enrichment functions but renounces crack-tip enrichment functions from the displacement and micro-rotation approximations. Instead, a refined mesh is patched on the main mesh around the crack tip to improve the precision of numerical solution. The I-integral combined with the patched-XFEM is employed to extract the FSIFs and CSIFs for various internal and edge crack configurations in functionally graded micropolar plates. Numerical results show that the NE formulation and the IC formulation give best accuracy for nonhomogeneous micropolar materials, while the CCT formulation generates larger relative errors for nonhomogeneous micropolar materials. For an internal crack, all FSIFs and CSIFs at both crack tips increase monotonically when the coupling number increases, and the differences between the two crack tips are enlarged with increasing gradient parameter. For an edge crack, the increase of coupling number causes a monotonic growth of CSIF, while the mode-I FSIF first decreases and then varies slightly. All these examples demonstrate that material property functions affect the FSIFs and CSIFs substantially.