Keywords

1 Introduction

This research is based on an issue that remained open in the investigation done by Salazar (2009), in which the need to configure the dynamic figural register is explicitly stated in the context of solving tasks involving geometry content in which one interacts with dynamic representation environments (DREs).

To pick up this issue, I present research related to semiotics, specifically the semiotics of Peirce, with Duval’s theory of Registers of Semiotic Representation. I concentrate on geometry teaching, due to the importance of the use of figures, and on research in which there is evidence of the pertinence of DREs in geometry teaching and learning.

The research by Dionizio and Bandt (2012) aims at identifying the journey taken by semiotics in order to position the theory of Registers of Semiotic Representation. They present the relation between Duval’s theory and aspects of Peirce’s semiotics, and they point out that, for Duval, Peirce’s model classifying all types of representations is essential in terms of a triadic process of interpretation that leads to distinguishing several hierarchical levels of signs.

In that sense, the research by Silva (2013) is important because it also relates the theory of Registers of Semiotic Representation to Peirce’s semiotics, and it shows the link between their concepts; that is to say, based on the hierarchical model of signs, she shows that the three cognitive operations essential to configure every register of semiotic representation—formation, treatment and conversion of an identifiable representation—are related to three out of the ten classifications of sign according to Peirce: qualisign, a quality that is a sign; sinsign, a real thing or event that is a sign; and legisign, a law that is a sign. Regarding mathematics teaching and learning, she identifies a comparative semiotic model, in which qualisign relates to the recognition of the characteristics of the given mathematical object in the formation of a representation, sinsign to the treatments in the representations of the mathematical object, and legisign to the changes made in the representations of the mathematical object through deductive reasoning.

The use of figures is fundamental in geometry teaching because it allows us to have access to the represented mathematical objects, infer properties, and solve problems. Further, as Duval (1995) states, the cognitive activity required in geometry demands more than other areas of mathematics considering that operations on figures, and their corresponding discourses, have to be simultaneous.

For these reasons, I looked for research such as that by Pavanello (2004), Marmolejo and Vega (2005), and Fortuny et al. (2010), which points out the importance of the use of figures in geometry, considering that they favor the development of the ability to abstract and generalize, because, from a level in which the represented geometric figures are recognized (by perception) despite perceiving them all as indivisible, a level is reached in which the properties of these figures are distinguished so as to establish relations between them with regard to their properties.

Also, on the one hand, researchers specify that the importance of geometric figures lies in the fact that they form an essential intuitive support for the development of geometric problems, because they allow students to see much more than what the formulations say; they allow the formulation of propositions and the heuristic exploration of complex situations. Therefore, it is necessary to differentiate the ways a figure may be seen, and to select those ways that are pertinent and powerful to solve the posed geometric problem.

On the other hand, the research by Miskulin et al. (2003) shows, from a semiotic perspective, the main characteristics and didactic-pedagogical potentialities of different technological environments used in mathematics teaching in a public university. They analyzed these environments through the syntheses done by students who used them in their classes, and they identified those potentialities. Another research study I consider important is the one by Mendes (2006), which presents a semiotic analysis of the game application called Simcity. The way of playing is subject to the interaction and/or interpretation each player attributes to the game in a given instant, for which he or she uses different representations. It is worth mentioning that, in both studies, it was perceived that the process of semiosis occurred at every instant during the interactions with the software.

Regarding DREs, the work of Veloso (2000) and Gravina (2001, 2008) points out that the DRE interactive interface allows the exploration and experimentation of the represented objects, and the immediate feedback helps students question the results of their actions/operations and verify the validity of their conjectures. In the same line of thought, Laborde (2001), Olivero and Robutti (2001), Restrepo (2008) and Grinkraut (2009) confirm that DREs possess a visual language that stimulates communication, and their interactivity stimulates students to be interested in the mathematical content that can be worked on with these environments.

Additionally, Artigue (2002) and Laborde (2005) maintain that, when DREs are used strategically, they can be really useful for students to justify the results of a given task, or they can use them as a tool to validate constructions, elaborate conjectures and inferences related to the properties of the represented mathematical objects. Further, in the construction of mathematical knowledge with the use of technology—with dynamic representation software in our case—DREs can facilitate the visualization of properties of different represented mathematical objects that could not be discovered with other resources.

Regarding the dragging function that facilitates the heuristic exploration of the figures because it allows the simulation of movement that facilitates the change of position, shape, and measure, Olivero (2003) states that it possesses three essential functions:

Feedback: Since the student is in control of the constructions he or she performs, dragging offers a powerful means of feedback that helps the development of strategies to solve a problem situation […]

Mediator between figure and design: It is given that it allows the invalidation of mistaken constructions […]

Analysis or search mode: Dragging allows the student to examine his or her construction and search its invariable properties by exploring the figure. (pp. 56–59)

Likewise, researchers such as Salazar et al. (2012), da Silva and Salazar (2012), García-Cuéllar (2014), Salazar (2015), Gómez (2015) and Peñaloza (2016) show that the use of DREs in the processes of geometry teaching favors the interpretation of the properties that characterize represented geometric figures. This focus on the interpretation of properties happens because, in the sense of Duval, DREs accelerate their treatments and articulate their apprehensions. In addition, they invigorate conversions among different registers of semiotic representation, which confirms the need to characterize the dynamic figural register.

As a consequence, given the importance of the geometric figures in geometry teaching and the current benefit provided by the interaction with DREs, it is considered necessary to research how the figural register is configured when interacting with these environments.

Based on the aforementioned issues, in this chapter I aim to answer the following question: How is the dynamic figural register constituted when interacting with DREs? Therefore, I first present aspects from the theory of Registers of Semiotic Representation.

2 Registers of Semiotic Representation

Duval (1995) explains that semiotic complexity is behind the difficulties in mathematics learning and that the analysis of mathematical productions demands tools for semiotic analysis adapted to cognitive processes mobilized in every mathematical activity.

Regarding the mathematical activity, this is done necessarily in a context of representation, since there is no other way to have access to the object but by its representation. Semiotic representations are generally considered as a means to externalize mental representations for communication purposes, but they are also essential for the cognitive activity, since they play a fundamental role in the development of mental representations, the execution of different cognitive functions, and the production of knowledge.

In addition, all learning is related to the semiosis and noesis processes, where semiosis is the apprehension or production of a semiotic representation and noesis is the conceptual apprehension of an object; thus, noesis is inseparable from semiosis. According to Duval (1993), “they are productions constituted by the use of signs belonging to a system of representation, which have their own difficulties in meaning and functioning” (p. 39). Regarding mathematics, semiotic representations are the ones that allow conceptualization, reasoning and problem solving.

Duval explains that natural language, algebraic, graphic and figural representations are external, conscious semiotic representations; that is, they are representations produced by students, which can be executed when doing operations in a given semiotic system. Duval defines these systems as registers of semiotic representation since they allow the three cognitive activities that are essential in every register: formation, treatment and conversion.

The formation of a representation is constituted by a group of noticeable marks that can be identified as the representation of something in a given system, such as the design of a geometric figure, the elaborations of a diagram, etc. that have to respect certain rules, such as the rules of construction for figures, etc., which play two roles: on the one hand, these rules ensure the conditions of identification and recognition of the representation and, on the other hand, they ensure the possibility of using it for the treatments.

Regarding the treatment, it is “to transform representations according to the only rules typical of the system so as to obtain other representations that can constitute knowledge earning in comparison with the initial representations” (Duval 2004, p. 30). The nature and number of these rules may vary from one system to another; for example, reconfiguration is a typical treatment of geometric figures, which, depending on the problem, requires a specific number of configurations. The conversion of a representation is the external transformation of a representation into another representation in another semiotic system. Treatments and conversions are independent sources of incomprehension or mental block in students. However, Duval states that conversion is the most decisive transformation for comprehension in mathematics.

Regarding mathematics, and geometry especially, I know it demands a cognitive activity more complex than other domains of mathematics because it is necessary to construct, reason and see figures at the same time, since treatments in the figural register are simultaneous as there must be coordination between figural treatments and those of theoretical discourse in natural language. In that sense, figures can be seen and analyzed based on perception, which allows the distinguishing of their shape and the recognition of their geometric properties, not only of visually distinguished shapes, but also based on reproducing or constructing them with tools.

In that sense, Duval (2005) explains that, to be able to do a cognitive analysis of a figure, figural units must be considered. These figural units are the most basic shapes into which every figure can be analyzed. For example, they can be 3D (polyhedra), 2D (polygons), 1D (lines or curves) and 0D (points).

Regarding the construction or reproduction of a figure, Duval states that manipulative material (pieces of a puzzle, Tangram folding paper, etc.) can be used, allowing material objects to be manipulated, such as a ruler (calibrated or not), a compass, a mold, etc., since they allow the construction operation, and software, as shown in Fig. 12.1.

Fig. 12.1
figure 1

Source Adapted from Duval (2005, p. 14)

Classification of tools to construct figures.

Full size image

In addition, heuristically using figures in geometry to solve problems, explain properties, elaborate conjectures, etc., depends on two operations, namely, the division of the figure into figural units of the same dimension that rely on perception (operation of reconfiguration), and the dimensional deconstruction of figures. The significance of the latter resides in the fact that the mathematical way of seeing figures consists in decomposing them as nD/2D shapes, that is into figural units of inferior dimension in comparison with the given figure. For example, the figure of a cube (3D) is decomposed into a configuration of squares (2D figural units) and the squares are decomposed into lines or line segments (1D figural units). The lines or segments can be decomposed into points (0D figural units); in relation to the points, they are visible when they appear as the intersection of 1D figural units (secant lines or lines that form a corner: vertices, angles, etc.).

In relation to the figural register, Duval (2011) indicates that, from a cognitive point of view, in mathematics education it should be assumed that geometric figures form a register of semiotic representations. Likewise, based on the way one ‘sees’ a figure, Duval explains that it is possible to analyze it cognitively according to its shape, to the geometric knowledge it activates, and to the tools used for its construction. There are three aspects he considers to be important in analyzing a figure:

  • Shape of the figure: based on the perception of the figure, whose contours are closed and where the figure can be seen as a group by juxtaposition, in which there are as many shapes as closed contours; or by superposition, in which there are less shapes than closed contours.

  • Knowledge of the geometric properties of the figure, which must be activated for their analysis and whose figural units must be considered, or visual variables which are related to the number of dimensions: 0D (a point), 1D (a line), 2D (a surface), and qualitative variations of shape, contour, orientation, etc.

  • Tools used to represent the figure or to construct it, which may include the following: manipulative material (pieces of puzzles, Tangram folding paper, etc.) that allow the manipulation of objects, ruler (calibrated or not), compass, mold, etc. that allow construction operations, as seen in Fig. 12.1.

Regarding the classification of tools to construct geometric figures, I observe that Duval does not explore the use of DREs. In that sense, DREs must be considered because, as we know, they are useful tools for geometry teaching and learning since they allow the representation of geometric objects and they have been rekindling interest in studying geometry in the last few decades. Another reason is because, unlike tools, DREs allow the carrying out of operations of figure construction, whether by juxtaposition or superposition, which can only be done separately with the aforementioned tools.

Also, DREs facilitate seeing the figure geometrically as an assembly of 0D, 1D or 2D figural units; in other words, an analysis of the figure’s dimensional deconstruction can be done. In that sense, Mithalal (2011) explains:

Dimensional deconstruction consists in seeing the representation of an object as a set of figural units linked by geometric properties. This last point is fundamental because it designates the role of those properties in this process: it is not enough to isolate figural units; it is also necessary to organize them geometrically. (p. 115)

Therefore, dimensional deconstruction allows the studying of the transformation of a figure into a different one of the same dimension, and it allows the identification of its figural units. Then, it is conjectured that, when DREs are used, the dimensional deconstruction is accelerated because the student may quickly identify the figural units of which the figure is composed when using the tools in the software as well as the dragging function. Likewise, changing the position of the observer also allows him to identify the figural units of a given figure.

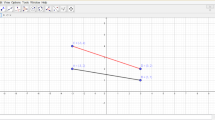
For example, the task I present, adapted from the research by Gómez (2015), consists in relating the measurement of the area of the \({\text{FGHE}}\) quadrilateral to the measurement of the area of the new \({\text{FGG}}^{\prime}{\text{F}}^{\prime}\) figure.

To solve it, auxiliary lines are constructed (to deconstruct the figure); that is, figural units of a smaller dimension are used, namely 1D (lines, circumference networks) and 0D (points). In addition, the geometric properties used include the dragging function of DREs, so it is possible to analyze the transformation of the ABCD quadrilateral (see the left side of Fig. 12.2) into a different figure of the same dimension (see the right side of Fig. 12.2). Also, when doing these operations, it is validated that, since \({\text{F}}^{\prime } {\text{F}} = 2{\text{EF}}\) and \({\text{F}}^{\prime } {\text{G}}^{\prime } = {\text{FG}}\) and since \({\text{F}}^{\prime } {\text{F}}\parallel {\text{G}}^{\prime } {\text{G}}\) and \({\text{F}}^{\prime } {\text{G}}\parallel {\text{EH}}\parallel {\text{FG}}\), the new figure formed is a parallelogram \({\text{FGG}}^{\prime } {\text{F}}^{\prime }\) of the 2:1 ratio, by relating the two measurements of the area.

Fig. 12.2
figure 2

Dimensional deconstruction

Full size image

When figures are constructed in DREs, it is likely that they are cognitively different than when it is done in a non-dynamic environment, because treatments are accelerated and the coordination between the figure treatments and the discourse is different, as the discourse is in the figure.

For these reasons, I point out that these environments make it viable to elaborate conjectures about the properties of the mathematical objects represented in them, whether by juxtaposition or superposition.

3 Dynamic Figural Register

Since the aim of the research is to identify how the three cognitive activities, namely, formation, treatment and conversion, occur when working with geometry content and interacting with DREs, each one of them is presented next with examples, taking the work of Gómez and Salazar (2016) as reference.

3.1 Dynamic Formation

According to Duval (1995), the formation of a semiotic representation consists in representing a given object in a certain semiotic system; it is essential for this formation to respect the rules of conformity of the semiotic system used. It is worth mentioning that these rules of conformity define a system of semiotic representation and the types of constitutive units of all possible representations. In addition, they allow the recognition of the representations as representations in a given register. Regarding the formation in the figural register, it occurs by identifying the figural units and their combination based on the geometric properties of the figure.

In that sense, Duval (2011) explains that there are several ways to recognize the shapes or figural units of a figure, though recognizing a shape excludes the possibility of recognizing others.

That is why, in DREs, forming a semiotic representation, which I call dynamic formation, at least three different ways to recognize a figure are identified. In the first one, to identify a geometric object in DREs, a given tool is activated, allowing the creation of the desired figure. In this case, the student recognizes the characteristics of the object he or she wishes to represent through its figural units.

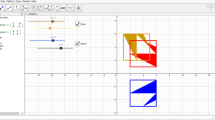
For example, given the task to create any ABC triangle, it is necessary to recognize the characteristics of a triangle in order to perform the task. In this section, the student must activate geometry knowledge. Thus, in Fig. 12.3, I observe that the polygon tool makes it possible to create the requested figure since it shows the representation of the object associated with a “key” that allows the student to directly recognize in the tool the figure requested, which in this case is a triangle.

Fig. 12.3
figure 3

Dynamic formation–shape 1

Full size image

In the second way of dynamic formation (see Fig. 12.4), the rules of formation of semiotic representation also depend on the choice of elemental figural units and their combination. This sequence occurs because of the conditions of GeoGebra DRE (advantages and/or limitation of the same environment). In the case of the previous task, at the perceptive level, variations related to the number of dimensions stand out, such as 0 (point), 1 (line/segment) or 2 (surface), and qualitative variations in shape, orientation, color, etc.

Fig. 12.4
figure 4

Dynamic formation–shape 2

Full size image

The third means of dynamic formation is the one that refers to a geometric construction in which properties stay invariant; that is, the variation of the parameters in Geogebra allows the discovery of invariants and the generalization of particular cases. For example, in the task to construct an ABCD square, the formation of the square is presented on the left of the DRE and, on the right, the protocol of construction that allows the showing of 0D and 1D (points and points of intersection, lines, segments) figural units and 2D units (circumference and polygon) in the construction, as shown in Fig. 12.5.

Fig. 12.5
figure 5

Formation of a square

Full size image

By using the dragging function, the constructed figure keeps its properties invariant. In addition, this type of formation allows the observation of the dimensional deconstruction of the figure since lines, segments and points are identified. Picking up aspects from Peirce’s semiotics and from the theory of Registers of Semiotic Representation, I observe that the formation of a dynamic semiotic representation is related to the qualisign, which is the first classification of signs and which, in mathematics teaching, is related to the recognition of the characteristics of the mathematical object.

3.2 Dynamic Treatments

According to Duval (2005), treatments are executed in the figure when modifications are done, for instance: changing its position while preserving the same configuration (change of orientation, translation, figure rotation, length of the sides, etc.), and decomposing the figure into its figural units, combining these to form another figure or dividing it into other subfigures that might or might not be regrouped to form other figures.

I highlight that the treatments are accelerated when two fundamental functions of DREs are used, which are as follows: direct manipulation, which allows the changing of position of the figure or the position of the work area; and dragging, which allows the rapid carrying out of operations related to figure reconfiguration. This way, the types of figure treatment that I identified in this study are changing the position of the figure without modifying it by using the function of direct manipulation; changing the length of the sides of the figure by using the dragging function as well as the homothecy tool, which multiples every distance by the same factor from a fixed point; and reconfiguring the figure, in which the dragging function is used as well as other specific tools that depend on the constructed figure.

But I must also point out that these treatments are not necessarily done separately or in sequence because they can be done simultaneously in DREs. These treatments possess specific features; in this part, I focus on figure reconfiguration.

Reconfiguring a figure: to do this type of treatment (dividing a figure into other subfigures), the tools needed are used from DREs, depending on the figure and the problem to be solved in order to separate, regroup or form another figure from an initial configuration. In addition, with the dragging function, the heuristic function of the figure is improved since configurations can be done rapidly and dynamically. To explain this type of treatment when using DREs, a task is presented (see Fig. 12.6), which was adapted from the research by Gómez (2015), Salazar and Almouloud (2015), Gómez and Salazar (2016), where GeoGebra DRE was used.

Fig. 12.6
figure 6

Task 1

Full size image

Figure 12.7 shows the file that has to be opened to do the requested activity.

Fig. 12.7
figure 7

Source Salazar and Almouloud (2015, p. 933)

Figure of the task.

Full size image

I observe that, when using DREs, the discourse about the activity is different from that when the same activity is presented without the use of these environments. In addition, a file is presented in the activity, which is ready for the student to move the S point and change the position of the EFSH square, through direct manipulation and dragging, to configure the requested figures.

The following are three possible configurations that can occur when solving the task with dynamic treatments:

The intersection of the figures represents a square: to get this configuration and be able to establish the configuration and the requested relation, the student could use the tools and draw perpendicular lines L1 and L2, which intersect in the E point (see Fig. 12.8), and then move (drag) the S vertex until getting the requested configuration.

Fig. 12.8
figure 8

Source Salazar and Almouloud (2015, p. 934)

EKCJ square.

Full size image

In the previous figure, the \({\overline{EH}}\;and\;{\overline{EF}}\) sides of the EFSH square overlap in L1 and L2, and the square figure is created by overlapping the two 2D figures (two squares), which creates another figure of equal dimension (EKCJ square). The student can easily perceive and state that the intersection of the figures represents a square that coincides with the fourth part of the ABCD square.

On the other hand, in Fig. 12.9, another solution to the configuration of the square is shown. In this case, the student drew perpendicular lines that cut in the E center, then he projected the lines on the sides of the ABCD square, and marked the M and N points of the \({\overline{AB}}\; and\; {\overline{BC}}\) sides respectively (middle points of these sides). Afterwards, he dragged the S point to the position and verified with the middle point tool that the intersection of the \({\overline{EF}}\) side with the \({\overline{ AB}}\) side is the M point, and the intersection of the \(\normalsize {\overline{EH}}\) side with the \({\overline{BC}}\) side is the N point.

Fig. 12.9
figure 9

Source Salazar and Almouloud (2015, p. 935)

The square–other solutions.

Full size image

I consider that the student did the dimensional deconstructions of the figure because he explored the relations between the 0D units (points, points of intersection), 1D (lines) and 2D (squares), the group being by superposition.

The intersection of the figures represents a triangle: in this case, the student may draw the \({\overline{AC}}\;and\;{\overline{BD}}\) diagonals of the ABCD square and, using direct manipulation, drag the S point until the requested figure is configured.

The position can change then until forming a BEC triangle over the ABCD square, for example (see Fig. 12.10). In this case, also by grouping and superposition, it is perceived that the intersection of the figures coincides with the fourth part of the ABCD square.

Fig. 12.10
figure 10

Source Salazar and Almouloud (2015, p. 936)

Another configuration.

Full size image

The intersection of the figures represents any quadrilateral: when dividing the ABCD quadrilateral into four congruent regions by the L1 and L2 perpendicular lines (Fig. 12.11) of the ABCD quadrilateral, with the use of the tools in the software it is possible to establish a relation between the subfigures that form due to the sequence of subfigures (triangles and squares); that is, the figure is deconstructed dimensionally since the following examples are identified: 1D figural units (points of intersection between the L1 and L2 perpendicular lines and the sides of the ABCD square), and 2D figural units such as triangles in the EKCJ and EKCP quadrilaterals.

In Fig. 12.11, it can be observed that, when the S vertex is dragged, the regions formed are easily distinguished, and the relation is identified between the surface of the ABCD square and the quadrilateral formed with the intersection of the EFSH square (activation of geometry knowledge, such as the congruence of triangles). In addition, with the dragging function, the heuristic function of the geometric figure is improved when using DRE since the student can do reconfigurations dynamically. Regarding the treatment of a dynamic representation based on the semiotic model for mathematics teaching and learning, this coincides with sinsign, which is the third type of Peirce’s signs.

Fig. 12.11
figure 11

Source Salazar and Almouloud (2015, p. 937)

Another configuration of any quadrilateral.

Full size image

3.3 Dynamic Conversion

According to Duval (2011), a conversion constitutes an external transformation of a representation into another, preserving all of or part of the content of the initial representation. It demands that the student coordinate representations. In that sense, conversion requires us to perceive the difference between the content of the representation (noesis) and the signifier that represents it (semiosis), and it explains that if the connection between noesis and semiosis is not established, the conversion becomes incomprehensible or impossible to do.

After the treatments in the DRE are done, the following question is answered: What is the relation between the surface formed by the intersection of the squares and the surface of the ABCD square? In natural language, the surface formed by the intersection of the squares is the fourth part of the surface of the ABCD square.

The register of the figures is finally configured in DREs, which I call: dynamic figural register since the three cognitive activities that allow the configuration of a register of semiotic representation are developed.

I highlight that the DRE functions of direct manipulation and dragging facilitate the development of these cognitive activities. Moreover, they facilitate the processes of visualization, in the sense of Duval, of mathematical objects because they allow the student to treat the figure differently than in other non-dynamic environments. Thus they are powerful tools that must be used well in mathematics classes and when teaching geometry notions in particular.

4 Conclusions

The operations that are possible to do in the figure, such as modifying the position and reconfiguring when using DREs, are countless since the functions of direct manipulation and dragging allow the acceleration of figural treatments. This acceleration prompts the student to use geometric properties to construct a given figure, besides invalidating mistaken constructions and favoring the assimilation of the invariants related to the represented geometric objects.

The three fundamental cognitive activities required to construct the dynamic figural register in DREs are done differently than when working in non-dynamic environments because the functions of direct manipulation and dragging allow the building of relations between the figural and discursive treatments. In addition, treatments are accelerated in the dynamic figural register; and figure variations, such as changing the position of the length of the side of a figure and reconfiguring it, can be done economically.

Regarding the way to see a figure, in the sense of Duval, DREs allow the perception of the figure by juxtaposition or superposition, which allow figural operations (reconfiguration and dimensional deconstruction) to be done by students differently than when working with other tools.

Moreover, the dragging function, which allows the carrying out of treatments when using DREs, also serves as a feedback function because, since the student is ‘in control’ of the constructions he does, he can carry out strategies to solve a problem. It is important to highlight that, when using DREs, the dragging function allows the position and length of the sides of a figure to be changed simultaneously. This feature of these environments permits the student to explore the figure interactively and dynamically.

Regarding geometry teaching, I agree with Duval when he states that it is necessary to pose tasks that allow figure variation, other figures that help ‘see’ the solution and those that, on the contrary, make it difficult or impossible to see it. Afterwards, organize tasks in which dimensional deconstruction is unpredictable, since this is contrary to perception and immediate recognition of the figural units.