Abstract
In this note we extend integral weight harmonic Maass forms to functions defined on the upper and lower half-planes using the method of Poincaré series. This relates to Rademacher’s “expansion of zero” principle, which was recently employed by Rhoades to link mock theta functions and partial theta functions.
Access provided by CONRICYT-eBooks. Download conference paper PDF
Similar content being viewed by others
1 Introduction and Statement of Results
In [12], Rhoades found a method to uniformly describe partial theta functions and mock theta functions as manifestations of a single function. He showed that Ramanujan’s mock theta function f(q) (defined below), with q := e 2πiτ and τ in the upper half-plane \(\mathbb {H}\), in some sense “leaks” through the real line to a partial theta function ψ(q −1) (given below) on the lower half-plane \(-\mathbb {H}\). His construction follows the “expansion of zero” principle of Rademacher (see [4], [6], [7, Chapter IX], and [10]). Rademacher showed, using his exact formula for the partition function, that the partition generating function can be extended to the lower half-plane, and he later proved [11] that this extension is identically zero in the lower half plane. We note that there are other relations of partial theta functions and mock theta functions. For example one, which is due to Zagier and Zwegers, passes through asymptotic expansions (see for example [5]).
Let us now say a few more words concerning mock theta functions. Originally introduced by Ramanujan in his last letter to Hardy, mock theta functions have since found applications in many areas of mathematics. We now understand that they fit into the larger framework of harmonic Maass forms, as shown by Zwegers [14] (see also [9, 13]). That is, the mock theta functions are examples of mock modular forms, which are the holomorphic parts of harmonic Maass forms (see Sect. 2 for definitions). Thus, it is natural to ask whether Rhoades’ construction applies to the non-holomorphic completion of f(q) and, if so, what is the image of that function in the lower half-plane? One hope, which has not yet been realized, is that this might shed some light on the problem of finding a completion of the partial theta functions to non-holomorphic modular forms. General partial theta functions have the shape
with ψ a primitive Dirichlet character and \(\nu \in \mathbb {Z}\) such that ψ(−1) = (−1)ν+1. In particular these functions are not modular forms.
We begin by more closely recalling Rhoades’ results. The partial theta function which Rhoades studied is given by
and the associated mock theta function is Ramanujan’s third order function
Now set
and (with \(\zeta _a^b:=e^{\frac {2\pi ib}{a}}\))
where r is taken sufficiently small such that \(|\operatorname {Log}\left (\zeta _{2c}^dq\right )|\gg r\) and such that the integral converges. Moreover let ω h,c be the multiplier of the Dedekind η-function (which can be given explicitly in terms of Dedekind sums, see [11]). Then define the function
where d (mod 2c)∗ indicates that the sum ranges over those d modulo 2c with \(\gcd (d,2c)=1\). This function converges in both the upper and lower half-planes, i.e., for \(\tau \in \mathbb {H}\cup (-\mathbb {H})\). Moreover, Rhoades’ main result states that
As discussed above, we describe a similar phenomenon for both the holomorphic and non-holomorphic parts of Maass–Poincaré series. To state our results, we first require some notation. Throughout, let \(k\in 2\mathbb {Z}\), and let \(M_k^!(\Gamma _0(N))\) denote the space of weakly holomorphic modular forms of weight k on Γ0(N). Let \(S_k^!(\Gamma _0(N))\) denote the subspace of \(M_k^!(\Gamma _0(N))\) consisting of forms whose Fourier expansion at i∞ has constant term equal to zero. For \(f(\tau )=:\sum _n c_f(n) q^n \in S_k^!(\Gamma _0(N))\), we define the (holomorphic) Eichler integral
and the non-holomorphic Eichler integral (τ = u + iv)
Here Γ(s, y) denotes the incomplete gamma function defined in (2.1). Note that with
we have
For even k > 2 and \(m\in \mathbb {Z}\), let P k,m denote the holomorphic Poincaré series (defined in Sect. 2 below). If m < 0, these functions are weakly holomorphic forms, while for m > 0, they are cusp forms. For \(k\in -2\mathbb {N}\) and m > 0, let F k,−m be the Maass-Poincaré series of Sect. 2. They are harmonic Maass forms with exponential growth in their holomorphic part.
Theorem 1.1
Let \(k\in -2\mathbb {N}\) and \(m\in \mathbb {N}\) . Then the function \(H_{k,m}:= H_{k,m}^+ + H_{k,m}^-\) (defined in (3.3) and (3.6) below) converges for all \(\tau \in \mathbb {H}\cup (-\mathbb {H})\) . Furthermore, if \(\tau \in \mathbb {H}\) we have
and if \(\tau \in -\mathbb {H}\) we have
To prove Theorem 1.1, we determine the extension of the holomorphic and non-holomorphic parts of F k,−m separately, in Sects. 3.1 and 3.2, respectively. The computation involving the holomorphic part closely follows [12], and the extension is provided by the simple fact that
For the non-holomorphic part, the situation is similar, but somewhat more complicated, and the extension is provided by the functional equation of the polylogarithm Li1−k (q) (defined in (3.5) below), namely
Remark
If one tries to mimic the computations of Sect. 3.2 in the case of half-integral weight, the situation is complicated by the analogue of (1.1) for \(k\notin \mathbb {Z}\), namely
where ζ(2 − k, u) denotes the Hurwitz zeta function. It is unclear whether the resulting function in the lower-half plane has any relation to a known modular-type object.
The paper is organized as follows. In Sect. 2 we recall the definitions and some basic properties of harmonic Maass forms and Poincaré series. In Sect. 3 we prove Theorem 1.1.
2 Preliminaries
2.1 Harmonic Maass Forms
In this section we recall basic facts of harmonic Maass forms, first introduced by Bruinier and Funke in [2]. We begin with their definition.
Definition
For \(k\in 2\mathbb {N}\), a weight k harmonic Maass form for Γ0(N) is any smooth function \(f:\mathbb {H}\rightarrow \mathbb {C}\) satisfying the following conditions:
-
(1)
For all
 we have $$\displaystyle \begin{aligned} f\left(\frac{a\tau+b}{c\tau+d}\right)=(c\tau+d)^kf(\tau). \end{aligned}$$
we have $$\displaystyle \begin{aligned} f\left(\frac{a\tau+b}{c\tau+d}\right)=(c\tau+d)^kf(\tau). \end{aligned}$$ -
(2)
We have Δ k (f) = 0 where Δ k is the weight k hyperbolic Laplacian
$$\displaystyle \begin{aligned} \Delta_k:=-v^2\left(\frac{\partial^2}{\partial u^2}+\frac{\partial^2}{\partial v^2}\right)+ikv\left(\frac{\partial}{\partial u}+i\frac{\partial}{\partial v}\right). \end{aligned}$$ -
(3)
There exists a polynomial \(P_f(\tau )\in \mathbb {C} [q^{-1}]\) such that
$$\displaystyle \begin{aligned} f(\tau)-P_f(\tau)=O(e^{\varepsilon v}) \end{aligned}$$as v →∞ for some ε > 0. Analogous conditions are required at all cusps.
Denote the space of such harmonic Maass forms by \(H_k\left (\Gamma _0(N)\right )\). Every \(f\in H_k\left (\Gamma _0(N)\right )\) has an expansion of the form
with the holomorphic part having a q-expansion
and the non-holomorphic part having an expansion of the form
Here Γ(s, v) is the incomplete gamma function defined, for v > 0, as the integral
2.2 Poincaré Series
In this section, we recall the definitions and properties of various Poincaré series. The general construction is as follows. Let φ be any translation-invariant function, which we call the seed of the Poincaré series in question. Then, in the case of absolute convergence, we can define a function satisfying weight k modularity by forming the sum
where  is the group of translations. Convergence is, in particular, satisfied by functions φ satisfying φ(τ) = O(v
2−k+ε) as v → 0.
is the group of translations. Convergence is, in particular, satisfied by functions φ satisfying φ(τ) = O(v
2−k+ε) as v → 0.
A natural choice for φ is a typical Fourier coefficient in the space of automorphic functions one is interested in. For example, in the case of weakly holomorphic modular forms one may choose, for \(m \in \mathbb {Z}\),
Define for \(k\in 2\mathbb {N}\) with k > 2 and \(m\in \mathbb {Z}\) the Poincaré series of exponential type by
To give their Fourier expansion, we require the Kloosterman sums
where e(x) := e 2πix. A direct calculation yields the following duality:
A very useful property of the Poincaré series is that they have explicit Fourier expansions, as given in the following theorem.
Theorem 2.1
Suppose that k > 2 is even.
-
i)
If \(m\in \mathbb {N}\) , the Poincaré series P k,m are in S k ( Γ0(N)). We have the Fourier expansion \(P_{k,m} (\tau ) =\sum _{n=1}^\infty b_{k,m}(n)q^n,\) where
$$\displaystyle \begin{aligned} b_{k,m}(n) = \left(\frac{n}{m} \right)^{\frac{k-1}{2}} \left( \delta_{m,n} + 2 \pi (-1)^{\frac{k}{2}} \sum_{ \substack{c>0 \\ N\mid c}} \frac{K(m,n;c)}{c} J_{k-1} \left( \frac{4 \pi \sqrt{mn}}{c}\right)\right). \end{aligned}$$Here δ m,n is the Kronecker delta-function and J s denotes the usual J-Bessel function.
-
ii)
For \(m\in -\mathbb {N}\) , the Poincaré series P k,m are elements of \(M_k^!(\Gamma _0(N))\) . We have the Fourier expansion \( {P}_{k,m} (\tau ) =q^{m} +\sum _{n=1}^{\infty } b_{k,m}(n)q^n,\) where
$$\displaystyle \begin{aligned} b_{k,m}(n) = 2 \pi (-1)^{\frac{k}{2}}\left|\frac{n}{m} \right|^{\frac{k-1}{2}} \sum_{ \substack{c>0 \\ N\mid c}} \frac{K(m,n;c)}{c} I_{k-1} \left( \frac{4 \pi \sqrt{|mn|}}{c} \right). \end{aligned}$$Here I s denotes the usual I-Bessel function. Moreover, P k,m is holomorphic at the cusps of Γ0(N) other than i∞.
We next turn to the construction of harmonic Maass forms via Poincaré series. Such series have appeared in many places in the literature, indeed in the works of Niebur [8] and Fay [3] in the 1970’s, long before the recent advent of harmonic Maass forms. Define
where the seed ϕ k,m is given by
Here Γ∗ is the normalized incomplete gamma function
The analogous exact formula for coefficients of these Poincaré series is then given in the following theorem (see, e.g., [3] or [1] for a proof).
Theorem 2.2
If k < 0 is even and \(m\in -\mathbb {N}\) , then F k,m ∈ H k ( Γ0(N)). We have
and
We have the Fourier expansion
with
Moreover, for n ≥ 1 and ε ∈{+, −}, we have
3 Proof of Theorem 1.1
To prove Theorem 1.1, we consider the holomorphic and non-holomorphic parts of F k,−m separately.
3.1 The Holomorphic Part
We first extend the holomorphic part \(F_{k,-m}^+\) of F k,−m to a function defined for |q|≠ 1, closely following [12]. Using Theorem 2.2, we have, for |q| < 1,
where
Using the series expansion of the I-Bessel function
we obtain
where
We insert the integral representation (for r > 0)
and we conclude that
where \(\alpha ^+_{m,c}(s)\) is the series
which is absolutely convergent for all s. Equation (3.1) then becomes
Here we take r sufficiently small so that \(|e^s \zeta _c^d q|<1\). Define
We can now define the function which exists away from the real line. To be more precise, since \(\phi ^+_{k,m}\) is regular for all v ≠ 0, the function
is defined for \(\tau \in \mathbb {H} \cup (-\mathbb {H})\).
We now consider the Fourier expansion of the function \(H_{k,m}^+(\tau )\) for τ in the lower half-plane, so suppose for the remainder of the proof that v < 0. In this case, we have
where r is chosen so that |e −s q −1| < 1. By reversing the calculation which led to (3.3), making the change of variables s↦ − s, and using that I 1−k (−ix) = i 1−k J 1−k (x), we find that
Thus we have
Note that the second and the third terms on the right-hand side of (3.4) cancel, since
By (2.2), we conclude that
if τ is in the lower half-plane.
3.2 The Non-holomorphic Part
Next we extend the non-holomorphic part \(F_{k,-m}^-(\tau )\) to a function \(H_{k,m}^-(\tau )\), which is defined for |q|≠ 1. We have, by Theorem 2.2,
where
Using the integral representation of the incomplete Gamma function and making a change of variables, we find that
thus
As above, we use the series expansion of the J-Bessel function
to obtain
where
Thus we have, again using (3.2),
where
Here r is chosen so that r < 2πv. Thus
Here Li s (w) is the polylogarithm, defined for \(s\in \mathbb {C}\) and |w| < 1 by
We now again introduce a function defined away from the real line. Define
and
Using the functional equation
we obtain, for v < 0, and using that k is even,
Since v < 0 we can now use the series representation of Li k−1. This yields

The innermost integral is (inserting the definition of \(\alpha _{m,c}^-(s)\), making the change of variables s↦ − s, and using (3.2))
Thus
Therefore, using that K(m, n;c) is real, we conclude that
References
Bringmann, K., Folsom, A., Ono, K., Rolen, L.: Harmonic Maass forms and mock modular forms: theory and applications, AMS Colloquium Series (to appear)
Bruinier, J.H., Funke, J.: On two geometric theta lifts. Duke Math. J. 125(1), 45–90 (2004)
Fay, J.D.: Fourier coefficients of the resolvent for a Fuchsian group. J. Reine Angew. Math. 293/294, 143–203 (1977)
Knopp, M.I.: Construction of automorphic forms on H-groups and supplementary Fourier series. Trans. Am. Math. Soc. 103, 168–188 (1962)
Lawrence, R., Zagier, D.: Modular forms and quantum invariants of 3-manifolds. Asian J. Math. 3, 93–108 (1999)
Lehner, J.: Partial fraction decompositions and expansions of zero. Trans. Am. Math. Soc. 87, 130–143 (1958)
Lehner, J.: Discontinuous Groups and Automorphic Functions. Mathematical Surveys, vol. VIII. American Mathematical Society, Providence, RI (1964)
Niebur, D.: A class of nonanalytic automorphic functions. Nagoya Math. J. 52, 133–145 (1973)
Ono, K.: Unearthing the Visions of a Master: Harmonic Maass Forms and Number Theory. Current Developments in Mathematics, vol. 2008, pp. 347–454. International Press, Somerville, MA (2009)
Rademacher, H.: A convergent series for the partition function p(n). Proc. Natl. Acad. Sci. U. S. A. 23(2), 78–84 (1937)
Rademacher, H.: Topics in Analytic Number Theory. Springer, New York/Heidelberg (1973). Edited by E. Grosswald, J. Lehner and M. Newman, Die Grundlehren der mathemathischen Wissenschaften, Band 169
Rhoades, R.C.: A unified approach to partial and mock theta functions. Math. Res. Lett. (to appear)
Zagier, D.: Ramanujan’s mock theta functions an their applications (d’après Zwegers and Bringmann-Ono). Ásterique 326: Exp. No. 986, vii–viii, 143–164 (2010). 2009. Séminaire Bourbaki. Vol. 2007/2008
Zwegers, S.P.: Mock theta functions, Ph.D. thesis, Universiteit Utrecht (2002)
Acknowledgements
The research of the second author is supported by the Alfried Krupp Prize for Young University Teachers of the Krupp foundation and the research leading to these results receives funding from the European Research Council under the European Union’s Seventh Framework Programme (FP/2007–2013)/ERC Grant agreement n. 335220—AQSER.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2017 Springer International Publishing AG
About this paper
Cite this paper
Andersen, N., Bringmann, K., Rolen, L. (2017). Images of Maass-Poincaré Series in the Lower Half-Plane. In: Bruinier, J., Kohnen, W. (eds) L-Functions and Automorphic Forms. Contributions in Mathematical and Computational Sciences, vol 10. Springer, Cham. https://doi.org/10.1007/978-3-319-69712-3_2
Download citation
DOI: https://doi.org/10.1007/978-3-319-69712-3_2
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-69711-6
Online ISBN: 978-3-319-69712-3
eBook Packages: Mathematics and StatisticsMathematics and Statistics (R0)



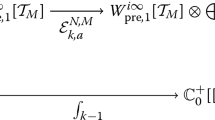
 we have
we have