Abstract
We show that certain paramodular cuspidal automorphic irreducible representations of \({\mathrm {GSp}}(4,\mathbb {A}_{\mathbb {Q}})\), which are not CAP, are globally generic. This implies a multiplicity one theorem for paramodular cuspidal automorphic representations. Our proof relies on a reasonable hypothesis concerning the non-vanishing of central values of automorphic L-series.
Access provided by CONRICYT-eBooks. Download conference paper PDF
Similar content being viewed by others
1 Introduction
Atkin-Lehner theory defines a one-to-one correspondence between cuspidal automorphic irreducible representations of \({\mathrm {GL}}(2,\mathbb {A}_{\mathbb {Q}})\) with archimedean factor in the discrete series and normalized holomorphic elliptic cuspidal newforms on the upper half plane, that are eigenforms for the Hecke algebra. As an analogue for the symplectic group \({\mathrm {GSp}}(4,\mathbb {A}_{\mathbb {Q}})\), a local theory of newforms has been developed by Roberts and Schmidt [19] with respect to paramodular groups.
However, still lacking for this theory is the information whether paramodular cuspidal automorphic irreducible representations of \({\mathrm {GSp}}(4,\mathbb {A}_{\mathbb {Q}})\) occur in the cuspidal spectrum with multiplicity one. Furthermore, holomorphic paramodular cusp forms, i.e. those invariant under some paramodular subgroup of \({\mathrm {Sp}}(4,\mathbb {Q})\), do not describe all holomorphic Siegel modular cusp forms. Indeed, at least if the weight of the modular forms is high enough, one is lead to conjecture that the paramodular holomorphic cusp forms exactly correspond to those holomorphic modular cusp forms for which their local non-archimedean representations, considered from an automorphic point of view, are generic representations. Under certain technical restrictions, we show that this is indeed the case.
To be more precise, suppose Π = ⊗ v Π v is a paramodular cuspidal automorphic irreducible representation of \({\mathrm {GSp}}(4,\mathbb {A}_{\mathbb {Q}})\), which is not CAP and whose archimedean factor Π ∞ is in the discrete series. Under the assumption of the hypothesis below we prove that the local representations Π v are generic at all non-archimedean places. Furthermore, we show that the hypothesis implies that Π occurs in the cuspidal spectrum with multiplicity one and is uniquely determined by almost all of its local factors Π v . The hypothesis imposed concerns the non-vanishing of central L-values and is crucial for our approach.
Hypothesis 1.1
Suppose Π is a globally generic unitary cuspidal automorphic irreducible representation of
\({\mathrm {GSp}}(4,\mathbb {A}_{\mathbb {Q}})\)
and α and β > 0 are real numbers. Then there is a unitary idele class character
 , locally trivial at a prescribed non-archimedean place of
\(\mathbb {Q}\)
, such that the twisted Novodvorsky L-function
, locally trivial at a prescribed non-archimedean place of
\(\mathbb {Q}\)
, such that the twisted Novodvorsky L-function
does not vanish at s = 1/2 + i(α + kβ) for some integer k.
The analogous hypothesis for the group GL(4) would imply our hypothesis, see Proposition 4.4. The corresponding statement for GL(2) is well-known [28, Thm. 4]. For GL(r), r = 1, 2, 3, compare [7, 10]. An approximative result for GL(4) has been shown by Barthel and Ramakrishnan [2], later improved by Luo [13]: Given a unitary globally generic cuspidal automorphic irreducible representation Π of \({\mathrm {GL}}(4,\mathbb {A}_{\mathbb {Q}})\), a finite set S of \(\mathbb {Q}\)-places and a complex number s 0 with Re(s 0) ≠ 1/2 there are infinitely many Dirichlet characters μ such that μ v is unramified for v ∈ S and the completed L-function \(\Lambda ((\mu \circ \det )\otimes \Pi ,s)\) does not vanish at s = s 0.
We remark, there is good evidence for our result (Theorem 4.5) on genericity of paramodular representations. In fact, the generalized strong Ramanujan conjecture for cuspidal automorphic irreducible representations \(\Pi =\otimes ^{\prime }_v\Pi _v\) of \({\mathrm {GSp}}(4,\mathbb {A}_{\mathbb {Q}})\) (not CAP) predicts that every local representation Π v should be tempered. But paramodular tempered local representations Π v at non-archimedean places are always generic by Lemma 3.2.
2 Preliminaries
The group G = GSp(4) (symplectic similitudes of genus two) is defined over \(\mathbb {Z}\) by the equation
for (g, λ) ∈GL(4) ×GL(1) and  with
with  . Since λ is uniquely determined by g, we write g for (g, λ) and obtain the similitude character
. Since λ is uniquely determined by g, we write g for (g, λ) and obtain the similitude character
Fix a totally real number field \(F/\mathbb {Q}\) with integers \(\mathfrak {o}\) and adele ring \(\mathbb {A}_F=\mathbb {A}_\infty \times \mathbb {A}_{\mathrm {fin}}\). For the profinite completion of \(\mathfrak {o}\) we write \(\mathfrak {o}_{\mathrm {fin}}\subseteq \mathbb {A}_{\mathrm {fin}}\). The paramodular group \(K^{\mathrm {para}}(\mathfrak {a})\subseteq \mathbf {G}(\mathbb {A}_{\mathrm {fin}})\) attached to a non-zero ideal \(\mathfrak {a}\subseteq \mathfrak {o}\) is the group of all
An irreducible smooth representation Π = Π ∞ ⊗ Πfin of \(\mathbf {G}(\mathbb {A}_F)\) is called paramodular if Πfin admits non-zero invariants under \(K^{\mathrm {para}}(\mathfrak {a})\) for some non-zero ideal \(\mathfrak {a}\).
Two irreducible automorphic representations are said to be weakly equivalent if they are locally isomorphic at almost every place. A cuspidal automorphic irreducible representation of GSp(4) is CAP if it is weakly equivalent to a constituent of a globally parabolically induced representation from a cuspidal automorphic irreducible representation of the Levi quotient of a proper parabolic subgroup. In that case we say that Π is strongly associated to this parabolic. The three standard proper parabolic subgroups of G are the Borel B, Siegel parabolic P and Klingen parabolic Q:

3 Poles of Local Spinor Factors
Fix a local nonarchimedean place v of F with completion F
v
, valuation character  for x ∈ F
v
, residue field \(\mathfrak {o}_v/\mathfrak {p}_v\) of order q and uniformizer \(\varpi \in \mathfrak {p}_v\). In this section we consider preunitary irreducible admissible representations Π
v
of
for x ∈ F
v
, residue field \(\mathfrak {o}_v/\mathfrak {p}_v\) of order q and uniformizer \(\varpi \in \mathfrak {p}_v\). In this section we consider preunitary irreducible admissible representations Π
v
of  . The non-supercuspidal Π
v
have been classified by Sally and Tadic [22] and we use their notation. Roberts and Schmidt [19] have designated them with roman numerals. Π
v
is called paramodular if it admits non-zero invariants under the local factor at v of some paramodular group.
. The non-supercuspidal Π
v
have been classified by Sally and Tadic [22] and we use their notation. Roberts and Schmidt [19] have designated them with roman numerals. Π
v
is called paramodular if it admits non-zero invariants under the local factor at v of some paramodular group.
Remark 3.1
Every paramodular Π v has unramified central character.
Indeed, the intersection of \(K_v^{\mathrm {para}}(\mathfrak {a})\) with the center of G is isomorphic to \(\mathfrak {o}_v^\times \).
Lemma 3.2
For tempered preunitary irreducible admissible representations Π v the following assertions are equivalent:
-
i)
Π v is generic and has unramified central character,
-
ii)
Π v is paramodular.
Proof
By Remark 3.1, we can assume that Π v has trivial central character. Then this is a result of Roberts and Schmidt [19, 7.5.8]. □
Recall that for every smooth character  the local Tate L-factor is
the local Tate L-factor is
For a generic irreducible admissible representation Π v of G and a smooth complex character μ of \(F_v^\times \), Novodvorsky [15] has defined a local degree four spinor L-factor L Nvd( Π v , μ, s). Piatetskii-Shapiro and Soudry [17, 18] have given a construction of a local degree four spinor L-factor L ( Λ,ψ)( Π v , μ, s) for infinite-dimensional irreducible admissible representations of G.Footnote 1 This L-factor depends on the choice of a Bessel model ( Λ, ψ). The Bessel models have been classified by Roberts and Schmidt [20]. Poles of L ( Λ,ψ)( Π v , μ, s) are called regular if they occur as poles of certain zeta integrals [18, §2]; the other poles are exceptional. For generic Π v every pole is regular [17, Thm. 4.3].
Lemma 3.3
For every generic irreducible admissible representation Π v of G, the quotient L ( Λ,ψ)( Π v , μ, s)/L Nvd( Π v , μ, s) is holomorphic. If Π v is also preunitary and irreducible Borel induced and if Λ is unitary, then L ( Λ,ψ)( Π v , μ, s) = L Nvd( Π v , μ, s).
Proof
L ( Λ,ψ)( Π v , μ, s) has only regular poles [17, Thm. 4.4]. For the case of non-split Bessel models, the regular poles have been determined explicitly by DanismanFootnote 2 [3,4,5]. For split Bessel models, see [21]. The poles of L Nvd( Π v , μ, s) have been determined by Takloo-Bighash [27] and cancel each pole of L ( Λ,ψ)( Π v , μ, s). Irreducible fully Borel induced Π v are theta lifts from GSO(2, 2), see [8, Thm. 8.2vi)], so the second statement holds by Piatetskii-Shapiro and Soudry [18, Thm. 2.4]. This also follows from [21] and [5]. □
Lemma 3.4
Let Π v be a preunitary non-generic irreducible admissible representations of G, that is not one-dimensional, and μ a unitary character. Then L ( Λ,ψ)( Π v , μ, s) has a regular pole on the line Re(s) = 1/2 exactly in the following cases:
-
IIb
 for a pair of characters χ, σ that are either both unitary or satisfy χ
2 = ν
2β
for
\(0<\beta <\tfrac {1}{2}\)
with unitary χσ. The regular poles with Re(s) = 1/2 come from the Tate factor L(ν
−1/2
χσ, s), so they occur if and only if χσ is unramified.
for a pair of characters χ, σ that are either both unitary or satisfy χ
2 = ν
2β
for
\(0<\beta <\tfrac {1}{2}\)
with unitary χσ. The regular poles with Re(s) = 1/2 come from the Tate factor L(ν
−1/2
χσ, s), so they occur if and only if χσ is unramified.
-
IIIb
 for unitary characters σ and χ with χ ≠ 1. The regular poles with Re(s) = 1/2 come from the Tate factors L(ν
−1/2
σ, s) and L(ν
−1/2
σχ, s), so they occur for unramified σ or σχ, respectively.
for unitary characters σ and χ with χ ≠ 1. The regular poles with Re(s) = 1/2 come from the Tate factors L(ν
−1/2
σ, s) and L(ν
−1/2
σχ, s), so they occur for unramified σ or σχ, respectively.
-
Vb,c
Π v ≅L(ν 1/2 ξStGL(2), ν −1/2 σ) for unitary characters σ and ξ with ξ 2 = 1 ≠ ξ. The regular poles with Re(s) = 1/2 come from the Tate factor L(ν −1/2 σ, s) and appear for unramified σ.
-
Vd
 for unitary characters σ and ξ with ξ
2 = 1 ≠ ξ. The regular poles with Re(s) = 1/2 come from the Tate factors L(ν
−1/2
σ, s) and L(ν
−1/2
ξσ, s), and occur for unramified σ or ξσ, respectively.
for unitary characters σ and ξ with ξ
2 = 1 ≠ ξ. The regular poles with Re(s) = 1/2 come from the Tate factors L(ν
−1/2
σ, s) and L(ν
−1/2
ξσ, s), and occur for unramified σ or ξσ, respectively.
-
VIc
Π v ≅L(ν 1/2StGL(2), ν −1/2 σ) for unitary σ. The Tate factor L(ν −1/2 σ, s) gives rise to regular poles with Re(s) = 1/2 when σ is unramified.
-
VId
 for unitary σ. The Tate factor L(ν
−1/2
σ, s)2
gives rise to double regular poles with Re(s) = 1/2 when σ is unramified.
for unitary σ. The Tate factor L(ν
−1/2
σ, s)2
gives rise to double regular poles with Re(s) = 1/2 when σ is unramified.
-
XIb
Π v ≅L(ν 1/2 π, ν −1/2 σ), where π is a preunitary supercuspidal irreducible admissible representation of GL(2, F v ) with trivial central character and σ is a unitary character. The regular poles with Re(s) = 1/2 occur with the Tate factor L(ν −1/2 σ, s) when σ is unramified.
Proof
For non-split Bessel models, see Danisman [3,4,5]. For split Bessel models, see [21]. □
Lemma 3.5
Up to isomorphism, the paramodular non-generic preunitary irreducible admissible representations Π v of G are exactly the following:
-
IIb
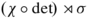 , for characters χ, σ such that χσ is unramified and either both are unitary or
, for characters χ, σ such that χσ is unramified and either both are unitary or
 for
\(0<\beta <\tfrac {1}{2}\)
with unitary characters χσ,
for
\(0<\beta <\tfrac {1}{2}\)
with unitary characters χσ,
-
IIIb
 , for unramified unitary characters χ, σ with χ ≠ 1,
, for unramified unitary characters χ, σ with χ ≠ 1,
-
IVd
σ ∘sim, for unramified unitary characters σ,
-
Vb,c
L(ν 1/2 ξStGL(2), ν −1/2 σ), for ξ with
 and unramified unitary σ,
and unramified unitary σ,
-
Vd
 , for unramified unitary characters σ, ξ with
, for unramified unitary characters σ, ξ with
 ,
,
-
VIc
L(ν 1/2St, ν −1/2 σ), for unramified unitary characters σ,
-
VId
 , for unramified unitary characters σ,
, for unramified unitary characters σ,
-
XIb
L(ν 1/2 π, ν −1/2 σ), for a supercuspidal preunitary irreducible admissible representation π of GL(2, F v ) with trivial central character and an unramified unitary character σ.
Proof
By Remark 3.1, we can assume that the central character is trivial. For non-supercuspidal Π v , see Tables A.2 and A.12 of Roberts and Schmidt [19]. Supercuspidal non-generic Π v are not paramodular by Lemma 3.2. □
Proposition 3.6
Let Π v be a paramodular preunitary irreducible admissible representation of G, that is not one-dimensional and μ a unitary character. The following assertions are equivalent:
-
i)
Π v is non-generic,
-
ii)
the spinor L-factor L ( Λ,ψ)( Π v , μ, s) has a pole on the line
 .
.
Proof
By the previous two lemmas, for non-generic Π v there is a regular pole on the line Re(s) = 1/2. If Π v is generic, poles do not occur on the line Re(s) = 1/2 by Lemma 3.3 and [27]. □
The proposition fails without the paramodularity assumption. For example, type Vd is always non-generic, but has a pole in  if and only if σ or ξσ are unramified.
if and only if σ or ξσ are unramified.
4 Global Genericity
Let \(F=\mathbb {Q}\) with adele ring \(\mathbb {A}=\mathbb {R}\times \mathbb {A}_{\mathrm {fin}}\). In the following,  is a cuspidal automorphic irreducible representation of \(\mathbf {G}(\mathbb {A})\), not CAP, with central character ω
Π, such that Π
∞
belongs to the discrete series. Global Bessel models ( Λ, ψ) of Π are always unitary. We want to show that if Π is paramodular, then Π
v
is locally generic at every nonarchimedean place v.
is a cuspidal automorphic irreducible representation of \(\mathbf {G}(\mathbb {A})\), not CAP, with central character ω
Π, such that Π
∞
belongs to the discrete series. Global Bessel models ( Λ, ψ) of Π are always unitary. We want to show that if Π is paramodular, then Π
v
is locally generic at every nonarchimedean place v.
The Euler product  converges for s in a right half plane and admits a meromorphic continuation to \(\mathbb {C}\) [17, Thm. 5.3]. This is the global degree four spinor L-series of Piatetskii-Shapiro and Soudry.
converges for s in a right half plane and admits a meromorphic continuation to \(\mathbb {C}\) [17, Thm. 5.3]. This is the global degree four spinor L-series of Piatetskii-Shapiro and Soudry.
Proposition 4.1 (Generalized Ramanujan)
The spherical local factors Π
v
of Πfin
are isomorphic to irreducible tempered principal series representations
 for unramified unitary complex characters χ
1, χ
2, σ of
\(\mathbb {Q}_v^\times \).
for unramified unitary complex characters χ
1, χ
2, σ of
\(\mathbb {Q}_v^\times \).
Proof
See [31, Thm. 3.3]. □
Proposition 4.2
Π is weakly equivalent to a unique globally generic cuspidal automorphic irreducible representation Πgen of \(\mathbf {G}(\mathbb {A})\) whose archimedean local component Πgen,∞ is the generic constituent in the local archimedean L-packet of Π ∞ . The lift Π↦ Πgen commutes with character twists by unitary idele class characters. The central characters of Πgen and Π coincide.
Proof
See [29, Thm. 1]; the proof relies on certain Hypotheses A and B shown in [31]. The lift commutes with twists because Πgen is unique. The central characters are weakly equivalent, so they coincide globally by strong multiplicity one for \({\mathrm {GL}}(1,\mathbb {A})\). □
Proposition 4.3
If Π is not CAP and not a weak endoscopic lift, then the discrete series representation Π ∞ is contained in an archimedean local L-packet \(\{ \Pi _\infty ^W , \Pi _\infty ^H \}\) such that the multiplicities of \(\Pi _\infty ^W \otimes \Pi _{\mathrm {fin}}\) and \(\Pi _\infty ^H \otimes \Pi _{\mathrm {fin}}\) in the cuspidal spectrum coincide. Here \(\Pi _\infty ^H\) denotes the holomorphic constituent and \(\Pi _\infty ^W\) the generic constituent.
Proof
By Proposition 4.2, Π is weakly equivalent to a globally generic representation Π′ of \(\mathbf {G}(\mathbb {A})\), which satisfies multiplicity one [12]. Now [30, Prop. 1.5] implies the statement. □
Proposition 4.4
Suppose Π is globally generic. Then there is a unique globally generic automorphic irreducible representation \(\tilde {\Pi }\) of \({\mathrm {GL}}(4,\mathbb {A})\) with partial Rankin-Selberg L-function
for a sufficiently large set S of places. This lift is local in the sense that \(\tilde {\Pi }_v\) only depends on Π v . It commutes with character twists by unitary idele class characters.
Proof
For the existence and locality of the lift, see Asgari and Shahidi [1]; uniqueness follows from strong multiplicity one for GL(4). It remains to be shown that \(\Pi \mapsto \tilde {\Pi }\) commutes with character twists. Indeed, by Proposition 4.1, almost every local factor is of the form  with unitary unramified characters χ
1, χ
2, σ. Its local lift \(\tilde {\Pi }_v\) is the parabolically induced \({\mathrm {GL}}(4,\mathbb {A})\)-representation
with unitary unramified characters χ
1, χ
2, σ. Its local lift \(\tilde {\Pi }_v\) is the parabolically induced \({\mathrm {GL}}(4,\mathbb {A})\)-representation
[1, Prop. 2.5]. Therefore, the lift \(\Pi _v\mapsto \tilde {\Pi }_v\) commutes with local character twists at the unramified Π v . Strong multiplicity one for GL(4) implies the statement. □
Theorem 4.5
Suppose Π = ⊗ v Π v is a paramodular unitary cuspidal irreducible automorphic representation of \(\mathbf {G}(\mathbb {A}_{\mathbb {Q}})\) that is not CAP nor weak endoscopic. We assume that Π ∞ is in the discrete series and that Hypothesis 1.1 holds. Then Π v is locally generic at all nonarchimedean places v.
Proof
By Proposition 4.3 we may assume without loss of generality that Π ∞ is a holomorphic discrete series representation. By Propositions 4.2 and 4.3 there exists a cuspidal automorphic irreducible representation Ξ, weakly equivalent to Π with archimedean factor Ξ ∞ ≅ Π ∞ , such that Ξ v is locally generic at every non-archimedean place v < ∞. There exist global Bessel models ( Λ, ψ) and ( ΛΞ, ψ Ξ) for Π and Ξ, respectively. By assumption Π is paramodular, so by a twist we can assume that the central character is trivial. The central characters of Π and Ξ coincide, so Ξ is also paramodular [19, Thm. 7.5.4].
Let S be the finite set of places, including ∞, such that Ξ v ≅ Π v is spherical for every place v∉S. For these v∉S, the local L-factors coincide by Proposition 4.1 and Lemma 3.3. For every idele class character μ this implies
Now assume there is at least one non-archimedean place w ∈ S where Π w is not generic. By Proposition 3.6, the right hand side of (2) must have an arithmetic progression \((s_k)_{k\in \mathbb {Z}}\) of poles s k = 1/2 + i(α + kβ) with \(\beta =2\pi /\ln (p_w)\) and some real α depending only on Π w and μ w . Indeed, we show below that the L-factors of Π ∞ ≅ Ξ ∞ do not have poles on the line ℜ(s) = 1/2 for any Bessel model.
Π is not CAP, so L ( Λ,ψ)( Π, μ, s) is holomorphic. Hence \(L_{(\Lambda _{\Xi },\psi _{\Xi })}(\Xi ,\mu ,s_k)=0\) for every k by (2). Especially, the partial L-function \(L_{(\Lambda _{\Xi },\psi _{\Xi })}^S(\Xi ,\mu ,s)\) vanishes at s = s k for every k and every finite set S.
If Hypothesis 1.1 is true, there is \(k\in \mathbb {Z}\) and a unitary idele class character μ of \(\mathbb {Q}^\times \backslash \mathbb {A}^\times \) with μ w = 1 such that for a sufficiently large finite set S, including all the archimedean and ramified places, the partial L-function \(L_{\mathrm {Nov}}^S(\Xi ,\mu ,s_k)\neq 0\) does not vanish. For v∉S the local L-factors of Novodvorsky and Piatetskii-Shapiro coincide by Proposition 4.1 and Lemma 3.3, so the same non-vanishing assertion holds for \(L_{(\Lambda _{\Xi },\psi _{\Xi })}^S(\Xi ,\mu ,s_k)\). This is a contradiction, so the place w does not exist.
It remains to be shown that the archimedean L-factor of Π ∞ in the holomorphic discrete series of lowest weight l ≥ l′≥ 3 does not admit poles on the line Re(s) = 1/2. Regular and exceptional poles can be defined analogous to the non-archimedean case. By [17, Thm. 4.2], exceptional poles only occur on the line ℜ(s) = −1/2 because the central character is unitary. By the archimedean analogue of [3, Prop. 2.5], the regular poles are the poles of the archimedean regular zeta integrals
attached to the Bessel functions φ v (λ) = ℓ( Π ∞ (diag(λ, λ, 1, 1)v) for v ∈ Π ∞ and the Bessel functional ℓ. In fact these zeta integrals are holomorphic for Re(s) > −3/2 and to show this it suffices to estimate the growth of φ v (λ) as λ → 0.
The holomorphic lowest weight vector v hol ∈ Π ∞ satisfies \(\vert \varphi _{v_{hol}}(\lambda )\vert \leq C \lambda ^{(l+l')/2}\exp (- c\lambda )\) with positive real constants C and c [26, (1-26)]. Since (l + l′)/2 ≥ 3, the zeta integral ζ reg (v hol , μ, s) converges for ℜ(s) > −3/2. The other K ∞ -types τ of Π ∞ are obtained from v hol by repeatedly applying the differential operator (Maaß operator)
see [14, §5.1]. It is easy to see that this can only improve convergence. □
Corollary 4.6
In the situation of the theorem, if Π ∞ is generic, then Π is globally generic.
Proof
Π is locally generic at every place. By Proposition 4.2, there is a globally generic automorphic representation Πgen, weakly equivalent to Π. By a result of Jiang and Soudry [12], Π = Πgen in the cuspidal spectrum. □
A cuspidal automorphic irreducible representation Π of \(\mathbf {G}(\mathbb {A})\), not CAP, is a weak endoscopic lift if there is a pair of cuspidal automorphic irreducible representations σ 1, σ 2 of \({\mathrm {GL}}(2,\mathbb {A})\) with the same central character, and local spinor L-factor
at almost every place [31, §5.2]. This condition does not depend on the global Bessel model ( Λ, ψ) by Proposition 4.1 and Lemma 3.3.
Proposition 4.7
Suppose a paramodular cuspidal irreducible automorphic representation Π ≅ ⊗ v Π v of \(\mathbf {G}(\mathbb {A}_{\mathbb {Q}})\) is a weak endoscopic lift with local archimedean factor Π ∞ in the discrete series. Then Π is globally generic.
Proof
σ 1 and σ 2 are attached to holomorphic elliptic modular forms [31, Cor. 4.2]. They are locally tempered at every place v by the Ramanujan conjecture (Deligne). The local endoscopic lifts Π v are also tempered [31, §4.11]. At the non-archimedean places Π v is then generic by Lemma 3.2. Then the archimedean factor Π ∞ is generic [31, Thm. 5.2]. Hence Π is globally generic [31, Thm. 4.1], [12]. □
5 Multiplicity One and Strong Multiplicity One
We show the multiplicity one theorem and the strong multiplicity one theorem for paramodular cuspidal automorphic representations of \(\mathbf {G}(\mathbb {A}_{\mathbb {Q}})\) under certain restrictions. It is well-known that strong multiplicity one fails without the paramodularity assumption [6, 11].
Lemma 5.1
A cuspidal automorphic irreducible representation Π of \(\mathbf {G}(\mathbb {A}_{\mathbb {Q}})\) , that is strongly associated to the Borel or Klingen parabolic subgroup, is never paramodular.
Proof
Every such representation is a theta lift Π = θ(σ) of an automorphic representation σ of \({\mathrm {GO}}_T(\mathbb {A}_{\mathbb {Q}})\) for an anisotropic binary quadratic space T over \(\mathbb {Q}\), see Soudry [24]. Let d
T
be the discriminant of T, then T is rationally equivalent to (K, t ⋅N
K
) for the norm N
K
of the quadratic field  and a squarefree integer t. Fix a non-archimedean place v of \(\mathbb {Q}\) that ramifies in K. The norm form on
and a squarefree integer t. Fix a non-archimedean place v of \(\mathbb {Q}\) that ramifies in K. The norm form on  remains anisotropic. By Lemma A.1, the local Weil representation of \(\mathbf {G}(\mathbb {Q}_v)\times {\mathrm {GO}}_T(\mathbb {Q}_v)\) is not paramodular. Thus the global Weil representation is not paramodular either. Since paramodular groups are compact, the functor of passing to invariants is exact and therefore the paramodular invariant subspace of Π = θ(σ) is zero. □
remains anisotropic. By Lemma A.1, the local Weil representation of \(\mathbf {G}(\mathbb {Q}_v)\times {\mathrm {GO}}_T(\mathbb {Q}_v)\) is not paramodular. Thus the global Weil representation is not paramodular either. Since paramodular groups are compact, the functor of passing to invariants is exact and therefore the paramodular invariant subspace of Π = θ(σ) is zero. □
Theorem 5.2 (Multiplicity One)
Suppose Π is a paramodular cuspidal automorphic irreducible representation of \(\mathbf {G}(\mathbb {A})\) with archimedean factor Π ∞ in the discrete series. If Hypothesis 1.1 holds, Π occurs in the cuspidal spectrum with multiplicity one.
Proof
A weak endoscopic lift occurs in the cuspidal spectrum with multiplicity at most one [31, Thm. 5.2]. If Π is CAP, it is strongly associated to the Siegel parabolic by Lemma 5.1. Then it is a Saito-Kurokawa lift in the sense of Piatetskii-Shapiro [16] and occurs with multiplicity one [9, (5.10)]. If Π is neither CAP nor weak endocopic, we can assume that Π ∞ is generic by Proposition 4.3. By Corollary 4.6, Π is globally generic and the assertion holds by a result of Jiang and Soudry [12]. □
Theorem 5.3 (Strong Multiplicity One)
Suppose two paramodular automorphic cuspidal irreducible representations Π1 , Π2 of \(\mathbf {G}(\mathbb {A}_{\mathbb {Q}})\) are locally isomorphic at almost every place. Assume that the archimedean local factors are either both in the generic discrete series or both in the holomorphic discrete series of \(\mathbf {G}(\mathbb {R})\) . If Hypothesis 1.1 holds, Π1 = Π2 coincide in the cuspidal spectrum.
Proof
Suppose Π1 and Π2 are not CAP. After possibly replacing the archimedean factor by the generic constituent in its local L-packet, we can assume that both Π1 and Π2 are globally generic by Corollary 4.6 and Proposition 4.7. Strong multiplicity one holds for globally generic representations [12, 25].
If Π1 and Π2 are CAP, they are strongly associated to the Siegel parabolic by Lemma 5.1 and occur as Saito-Kurokawa lifts in the sense of Piatetskii-Shapiro [16]. For each non-archimedean place v, the local factors Π1,v and Π2,v are non-generic and belong to the same Arthur packet. Exactly one constituent of this Arthur packet is non-tempered [23, §7]. Both local factors Π1,v and Π2,v are non-tempered by Lemma 3.2 and therefore isomorphic. The local factors Π1,∞ , Π2,∞ at the archimedean place are in the discrete series, so they are isomorphic to the unique discrete series constituent of the archimedean Arthur packet [23, §4]. Thus Π1 and Π2 are locally isomorphic at every place. They coincide in the cuspidal spectrum by Theorem 5.2. □
Notes
- 1.
Unfortunately, detailed proofs of their results are not available.
- 2.
Danisman assumes odd characteristic. This is used in the proof of [3, Prop. 4.3], but not necessary.
References
Asgari, M., Shahidi, F.: Generic transfer from GSp(4) to GL(4). Comput. Math. 142, 541–550 (2006)
Barthel, L., Ramakrishnan, D.: A nonvanishing result for twists of L-functions of GL(n). Duke Math. J. 74(3), 681–700 (1994)
Danisman, Y.: Regular poles for the p-adic group GSp4. Turk. J. Math. 38, 587–613 (2014)
Danisman, Y.: Regular poles for the p-adic group GSp4 II. Turk. J. Math. 39, 369–394 (2015)
Danisman, Y.: L-factor of irreducible
 . Chin. Ann. Math. 38B(4), 1019–1036 (2017)
. Chin. Ann. Math. 38B(4), 1019–1036 (2017)File, D., Takloo-Bighash, R.: A remark on the failure of strong multiplicity one for GSp(4). Manuscripta Math. 140, 263–272 (2013). https://doi.org/10.1007/s00229-012-0545-2
Friedberg, S., Hoffstein, J.: Nonvanishing theorems for automorphic L-functions on GL(2). Ann. Math. 142(2), 385–423 (1995)
Gan, W.T., Takeda, S.: Theta correspondences for GSp(4). Represent. Theory 15, 670–718 (2011)
Gan, W.T.: The Saito-Kurokawa space for PGSp 4 and its transfer to inner forms. In: Tschinkel, Y., Gan, W.T., Kudla, S. (eds.) Eisenstein Series and Applications. Progress in Mathematics, vol. 258, pp. 87–124. Birkhäuser, Boston (2008)
Hoffstein, J., Kantorovich, A.: The first non-vanishing quadratic twist of an automorphic L-series. Preprint (2010). arXiv 1008.0839
Howe, R., Piatetski-Shapiro, I.I.: Some examples of automorphic forms on Sp4. Duke Math. J. 50(1), 55–106 (1983)
Jiang, D., Soudry, D.: The multiplicity-one theorem for generic automorphic forms on GSp(4). Pac. J. Math. 229(2), 381–389 (2007)
Luo, W.: Non-vanishing of L-functions for GL(n, A Q ). Duke Math. J. 128(2), 199–207 (2005)
Maurischat, K., Weissauer, R.: Phantom holomorphic projections arising from Sturm’s formula. Preprint (2016). arXiv:1605.01868
Novodvorsky, M.E.: Automorphic L-functions for GSp(4). In: Automorphic Forms, Representations, and L-functions. Proceedings of Symposia in Pure Mathematics, vol. 33(2), pp. 87–95. AMS, Providence (1979)
Piatetskii-Shapiro, I.: On the Saito-Kurokawa lifting. Inv. Math. 71, 309–338 (1983)
Piatetskii-Shapiro, I.: L-functions for GSp4. Pac. J. 181(3), 259–275 (1997)
Piatetskii-Shapiro, I., Soudry, D.: The L and 𝜖 factors for GSp(4). J. Fac. Sci. Univ. Tokyo 28, 505–530 (1981)
Roberts, B., Schmidt, R.: Local Newforms for GSp(4). Lecture Notes in Mathematics, vol. 1918. Springer (2007)
Roberts, B., Schmidt, R.: Some results on Bessel functionals for GSp(4). Doc. Math. 21, 467–553 (2016)
Rösner, M., Weissauer, R.: Regular poles for L-series attached to split Bessel models of GSp(4). Preprint (2017)
Sally, P., Tadić, M.: Induced representations and classifications for GSp(2, F) and Sp(2, F). Mém. Soc. Math. Fr. 52, 75–133 (1994)
Schmidt, R.: The Saito-Kurokawa lifting and functoriality. Am. J. Math. 127(1), 209–240 (2005)
Soudry, D.: The CAP representations of GSp(4). J. Reine Angew. Math. 383, 97–108 (1988)
Soudry, D.: A uniqueness theorem for representations of GSO(6) and the strong multiplicity one for generic representations of GSp(4). Isr. J. Math. 58(3), 257–287 (1988)
Sugano, T.: Holomorphic cusp forms on quaternion unitary groups. J. Fac. Sci. Univ. Tokyo Sect. 1A 31, 521–568 (1984)
Takloo-Bighash, R.: L-functions for the p-adic group GSp(4). Am. J. Math. 122(6), 1085–1120 (2000)
Waldspurger, J.-L.: Correspondence de Shimura et quaternions. Forum Math. 3, 219–307 (1991)
Weissauer, R.: Existence of Whittaker models related to four dimensional symplectic Galois representations. In: Modular Forms on Schiermonnikoog, pp. 67–149. Cambridge University Press, Cambridge (2008)
Weissauer, R.: Four dimensional Galois representations. In: Tilouine, J., Carayol, H., Harris, M., Vignéras, M.-F. (eds.) Formes automorphes (II), Le cas du groupe GSp(4). Asterisque, vol. 302, pp. 67–149. Société Mathématique de France, Paris (2005)
Weissauer, R.: Endoscopy for GSp(4) and the Cohomology of Siegel Modular Threefolds. Lecture Notes in Mathematics, vol. 1968. Springer, Berlin (2009)
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Appendices
Appendix 1: The Weil Representation
Let K/F be a ramified quadratic field extension of a local nonarchimedean number field F with principal ideals \(\mathfrak {p}_{K}\) and \(\mathfrak {p}\). The anisotropic binary quadratic form T = (K, N K/F ) defines the F-bilinear form \((x,y)_T=(x\bar {y}+\bar {x}y)/2\) for x, y ∈ K where \(\bar {\ }\) is the Galois conjugation on K/F. Fix a non-trivial additive character ψ of F with conductor \(\mathfrak {p}^c\), the largest broken ideal in the kernel of ψ. The Schrödinger model of the smooth Weil representation ω of G(F) ×GO T (F) is given by the space of Schwarz-Bruhat functions \(\phi \in \mathcal {S}(K^2\times F^\times )\) with the action of G(F) given on generators by

Here γ(ψ ∘ T) is the Weil index. The Haar measure is normalized, depending on t, such that ω preserves the L 2-scalar product in \(\mathcal {S}(K^2\times F^\times )\). The action of h ∈GO(T) is by
Lemma A.1
The Weil representation ω of G(F) ×GO T (F) is not paramodular.
Proof
Suppose \(\phi \in \mathcal {S}(K^2\times F^\times )\) is invariant under \(K^{\mathrm {para}}(\mathfrak {p}^n)\) for some n. For (x, t) in the support of ϕ we must have ψ(t∑
i,j
s
ij
(x
i
, x
j
)
T
) = 1 for every  . This implies \(t \varpi _F^{-n}(x_1,x_1)_T\in \mathfrak {p}^c\) and \(t(x_2,x_2)_T\in \mathfrak {p}^c\), so ϕ(⋅ , t) has support in
. This implies \(t \varpi _F^{-n}(x_1,x_1)_T\in \mathfrak {p}^c\) and \(t(x_2,x_2)_T\in \mathfrak {p}^c\), so ϕ(⋅ , t) has support in
By the same argument,  has support in \(\mathfrak {p}_K^{c-v_F(t)-n}\times \mathfrak {p}_K^{c-v_F(t)}\). By Fourier theory, ϕ(⋅ , t) is constant on cosets modulo
has support in \(\mathfrak {p}_K^{c-v_F(t)-n}\times \mathfrak {p}_K^{c-v_F(t)}\). By Fourier theory, ϕ(⋅ , t) is constant on cosets modulo
with the relative different ideal \(\mathfrak {d}_{K/F}=\mathfrak {p}_K\). This implies ϕ = 0. □
Appendix 2: On Regular Poles Attached to Split Bessel Models for GSp(4)
For infinite-dimensional representations Π of G = GSp(4, F) with central character ω Π, where F is a local non-Archimedean field, Piatetskii-Shapiro [17] has constructed a local L-factor
attached to a choice of a Bessel model ( Λ, ψ). To be precise, fix the standard Siegel parabolic subgroup P = MN in G with Levi M and unipotent radical N as above. For a non-degenerate linear form ψ of N, the connected component \(\tilde {T}\) of the stabilizer of ψ in M is isomorphic to the unit group L × for a quadratic extension L/F. A Bessel character is a pair ( Λ, ψ) where Λ is a character of \(\widetilde {T}\). The coinvariant space Π( Λ,ψ) with respect to the action of \(\widetilde {T}N\) by ( Λ, ψ) is at most one-dimensional [17, Thm. 3.1], [20, Thm. 6.3.2]. If it is non-zero, we say Π has a Bessel model. Such a Bessel model is called anisotropic or split, depending on whether L is a field or not. The Bessel models have been classified by Roberts and Schmidt [20].
The local factor L ( Λ,ψ)( Π, s) has a regular part \(L^{\mathrm {reg}}_{(\Lambda ,\psi )}(\Pi ,s)\) and an exceptional part \(L^{\mathrm {ex}}_{(\Lambda ,\psi )}(\Pi ,s)\). For generic Π it coincides with its regular part [17, Thm. 4.3]. Danisman [3,4,5] has shown that the regular part does not depend on the choice of an anisotropic Bessel model. Especially, for generic Π and anisotropic Bessel models the L-factor L ( Λ,ψ) coincides with the L-factor that was constructed by Novodvorsky [15] in a completely different way. One may therefore expect that the L-factor does not depend on the choice of any Bessel model. This expectation was formulated by Piatetski-Shapiro and Soudry [18, p.1] and proven for the case of Borel induced Π [18, Thm. 2.4]. Further motivation originated from the results of Danisman.
In [21] we determine the regular part of L ( Λ,ψ)( Π, s) for split Bessel models. For non-generic Π there are finitely many split Bessel models. The regular part of the L-factors attached to arbitrary Bessel models is the product of Tate L-factors given in Table 1, as shown in [21]. Hence the expectation holds true for non-generic Π, i.e. \(L^{\mathrm {reg}}_{(\Lambda ,\psi )}(\Pi ,s)\) is independent of any Bessel model.
In general, however, this is false. For generic Π there are infinitely many split Bessel models and for certain cases the attached L-factor is a divisor of Novodvorsky’s L-factor. For the precise results we refer to [21].
Let us briefly recall the notation. Up to equivalence, we can assume the split Bessel model is given by  for a non-trivial additive character ψ of F and some character Λ of \(\tilde {T}=\{diag(t_1,t_2,t_1,t_2)\,|\, t_1,t_2\in {F}^\times \}\). For fixed central character ω
Π, every Λ is uniquely determined by its restriction to ρ(t
1) = Λ(t
1, 1, t
1, 1). We have a decomposition \(N=\tilde {N}\times S\) where \(\tilde {N}\) is in the kernel of ψ and S commutes with \(\widetilde {T}\). Let T = {diag(1, 1, t, t) | t ∈ F
×}⊆ G. For every TS-module E of finite length it can be shown that the canonical morphism E
S → E
S
from S-invariants to S-coinvariants is injective and we consider the finite-dimensional quotient as a T-module
for a non-trivial additive character ψ of F and some character Λ of \(\tilde {T}=\{diag(t_1,t_2,t_1,t_2)\,|\, t_1,t_2\in {F}^\times \}\). For fixed central character ω
Π, every Λ is uniquely determined by its restriction to ρ(t
1) = Λ(t
1, 1, t
1, 1). We have a decomposition \(N=\tilde {N}\times S\) where \(\tilde {N}\) is in the kernel of ψ and S commutes with \(\widetilde {T}\). Let T = {diag(1, 1, t, t) | t ∈ F
×}⊆ G. For every TS-module E of finite length it can be shown that the canonical morphism E
S → E
S
from S-invariants to S-coinvariants is injective and we consider the finite-dimensional quotient as a T-module
For an irreducible representation Π of G, the space of coinvariants with respect to the action of \(\widetilde {T}\widetilde {N}\) by ρ defines a TS-module \(\widetilde {\Pi }=\Pi _{\rho }\) of finite length. It turns out that the quotient \(\mathcal {L}(\widetilde \Pi )\) completely determines the regular part of the L-function: For T-characters χ let a(χ) be the multiplicity of χ in the semisimplification of the T-module \(\mathcal {L}(\widetilde {\Pi })\). The regular part of the L-factor is the product of Tate L-factors
Notice a(χ) ≠ 0 implies that χ occurs as a T-character in the unnormalized Siegel Jacquet module Π N because \(\widetilde {\Pi }_S={(\Pi _N)}_{\tilde {T},\Lambda }\). For unitary generic Π this connection with the Siegel-Jacquet module easily implies that L ( Λ,ψ)(s, Π) does not have a pole on the critical line ℜ(s) = 1/2. Indeed, these poles come from characters χ with |χ| = ν −1. For generic unitary Π it follows from the list of constituents in the Siegel-Jacquet module [19, A.3], that they do not occur. For our application in Lemma 3.3, this is crucial.
To calculate the factor a(χ), we study the T-module \(\mathcal {L}(\widetilde {\Pi })\). For semisimple \(\widetilde \Pi \) we would have \(\mathcal {L}(\widetilde \Pi )=0\), so the non-trivial L-factors come from indecomposable extensions of TS-modules. We observe that the L-factor is the expected one if and only if \(\widetilde {\Pi }^S\) vanishes. The analogous assertion in the anisotropic case holds true by Proposition 4.7 of Danisman [3]. In the split case the necessary information is provided by a combination of various techniques, as for instance P 3-theory in the sense of Roberts and Schmidt [19], a detailed study of the Siegel-Jacquet module and the analysis of induced representations for which Π is an irreducible quotient.
Rights and permissions
Copyright information
© 2017 Springer International Publishing AG
About this paper
Cite this paper
Rösner, M., Weissauer, R. (2017). Multiplicity One for Certain Paramodular Forms of Genus Two. In: Bruinier, J., Kohnen, W. (eds) L-Functions and Automorphic Forms. Contributions in Mathematical and Computational Sciences, vol 10. Springer, Cham. https://doi.org/10.1007/978-3-319-69712-3_14
Download citation
DOI: https://doi.org/10.1007/978-3-319-69712-3_14
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-69711-6
Online ISBN: 978-3-319-69712-3
eBook Packages: Mathematics and StatisticsMathematics and Statistics (R0)




 for a pair of characters χ, σ that are either both unitary or satisfy χ
2 = ν
2β
for
for a pair of characters χ, σ that are either both unitary or satisfy χ
2 = ν
2β
for
 for unitary characters σ and χ with χ ≠ 1. The regular poles with Re(s) = 1/2 come from the Tate factors L(ν
−1/2
σ, s) and L(ν
−1/2
σχ, s), so they occur for unramified σ or σχ, respectively.
for unitary characters σ and χ with χ ≠ 1. The regular poles with Re(s) = 1/2 come from the Tate factors L(ν
−1/2
σ, s) and L(ν
−1/2
σχ, s), so they occur for unramified σ or σχ, respectively.
 for unitary characters σ and ξ with ξ
2 = 1 ≠ ξ. The regular poles with Re(s) = 1/2 come from the Tate factors L(ν
−1/2
σ, s) and L(ν
−1/2
ξσ, s), and occur for unramified σ or ξσ, respectively.
for unitary characters σ and ξ with ξ
2 = 1 ≠ ξ. The regular poles with Re(s) = 1/2 come from the Tate factors L(ν
−1/2
σ, s) and L(ν
−1/2
ξσ, s), and occur for unramified σ or ξσ, respectively.
 for unitary σ. The Tate factor L(ν
−1/2
σ, s)2
gives rise to double regular poles with Re(s) = 1/2 when σ is unramified.
for unitary σ. The Tate factor L(ν
−1/2
σ, s)2
gives rise to double regular poles with Re(s) = 1/2 when σ is unramified.
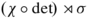 , for characters χ, σ such that χσ is unramified and either both are unitary or
, for characters χ, σ such that χσ is unramified and either both are unitary or
 for
for
 , for unramified unitary characters χ, σ with χ ≠ 1,
, for unramified unitary characters χ, σ with χ ≠ 1,
 and unramified unitary σ,
and unramified unitary σ,
 , for unramified unitary characters σ, ξ with
, for unramified unitary characters σ, ξ with
 ,
,
 , for unramified unitary characters σ,
, for unramified unitary characters σ,
 .
. . Chin. Ann. Math. 38B(4), 1019–1036 (2017)
. Chin. Ann. Math. 38B(4), 1019–1036 (2017)