Keywords

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction and Main Results

We are interested in covering a graph with (overlapping) pieces in such a way that (1) the number of pieces is small, (2) each piece is simple, and (3) every small subgraph is fully contained in at least one piece. Despite the graph theoretic interest in such coverings, it also has nice algorithmic applications. Consider e.g. the subgraph isomorphism problem. Here, we are given two graphs G and H as input, and we are asked to determine whether G contains a subgraph isomorphic to H. In many natural settings the pattern graph H we are looking for is small and in such case a covering as described above is most useful. By the first property, we can then iterate through the small number of pieces, by the third property, one of the pieces will contain our pattern graph. By the second property, we can test each piece for containment of H.

We can formulate the covering problem in an equivalent way from the point of view of graph coloring as follows. How many colors are required to color the vertices of a graph G such that the union of any p color classes induce a simple subgraph (understanding any p color classes as a piece in the above formulation)? It remains to specify what we mean by simple subgraphs.

From an algorithmic point of view, trees, or more generally, graphs of bounded tree-width are very well behaved graphs. Many NP-complete problems, in fact, all problems that can be formulated in monadic second order logic, are solvable in linear time on graphs of bounded tree-width [5, 6]. In particular, the subgraph isomorphism problem for every fixed pattern graph H is solvable in polynomial time on any graph of bounded tree-width.

Taking graphs of small tree-width as our simple building blocks, we can define a p -tree-width coloring of a graph G as a vertex coloring of G such that the union of any \(i\le p\) color classes induces a subgraph of tree-width at most \(i-1\). Using the structure theorem of Robertson and Seymour [33] for graphs excluding a fixed graph as a minor, DeVos et al. [11] proved that for every graph H and every integer \(p\ge 1\), there is an integer \(N=N(H,p)\), such that every H-minor-free graph admits a p-tree-width coloring with N colors.

Tree-depth is another important and useful graph invariant. It was introduced under this name in [25], but equivalent notions were known before, including the notion of rank [28], vertex ranking number and minimum height of an elimination tree [1, 10, 34], etc. In [25], Nešetřil and Ossona de Mendez introduced the notion of p-tree-depth colorings as vertex colorings of a graph such that the union of any \(i\le p\) color classes induces a subgraph of tree-depth at most i. Note that the tree-depth of a graph is always larger (at least by 1) than its tree-width, hence a low tree-depth coloring is a stronger requirement than a low tree-width coloring. Also based on the structure theorem, Nešetřil and Ossona de Mendez [25] proved that proper minor closed classes admit even low tree-depth colorings.

Not much later, Nešetřil and Ossona de Mendez [26] proved that proper minor closed classes are unnecessarily restrictive for the existence of low tree-depth colorings. They introduced the notion of bounded expansion classes of graphs, a concept that generalizes the concept of classes with excluded minors and with excluded topological minors. While the original definition of bounded expansion is in terms of density of shallow minors, it turns out low tree-depth colorings give an alternative characterisation: a class \(\mathcal {C}\) of graphs has bounded expansion if and only if for all \(p\in \mathbb {N}\) there exists a number \(N=N(\mathcal {C}, p)\) such that every graph \(G\in \mathcal {C}\) admits a p-tree-depth coloring with N(p) colors [26]. For the even more general notion of nowhere dense classes of graphs [27], it turns out that a class \(\mathcal {C}\) of graphs closed under taking subgraphs is nowhere dense if and only if for all \(p\in \mathbb {N}\) and all \(\varepsilon >0\) there exists \(n_0\) such that every n-vertex graph \(G\in \mathcal {C}\) with \(n\ge n_0\) admits a p-tree-depth coloring with \(n^\varepsilon \) colors.

Furthermore, there is a simple algorithm to compute such a decomposition in time \(\mathcal {O}(n)\) in case \(\mathcal {C}\) has bounded expansion and in time \(\mathcal {O}(n^{1+\varepsilon })\) for any \(\varepsilon >0\) in case \(\mathcal {C}\) is nowhere dense. As a result, the subgraph isomorphism problem for every fixed pattern H can be solved in linear time on any class of bounded expansion and in almost linear time on any nowhere dense class. More generally, it was shown in [13, 17] that every fixed first order property can be tested in linear time on graphs of bounded expansion, implicitly using the notion of low tree-depth colorings, and in almost linear time on nowhere dense classes [18].

Note that bounded expansion and nowhere dense classes of graphs are uniformly sparse graphs. In fact, bounded expansion classes of graphs can have at most a linear number of edges and nowhere dense classes can have no more than \(\mathcal {O}(n^{1+\varepsilon })\) many edges. This motivates our new definition of low rank-width colorings which extends the coloring technique to dense classes of graphs which are closed under taking induced subgraphs.

Rank-width was introduced by Oum and Seymour [32] and aims to extend tree-width by allowing well behaved dense graphs to have small rank-width. Also for graphs of bounded rank-width there are many efficient algorithms based on dynamic programming. Here, we have the important meta-theorem of Courcelle, Makowsky, and Rotics [8], stating that for every monadic second-order formula (with set quantifiers ranging over sets of vertices) and every positive integer k, there is an \(\mathcal {O}(n^3)-\)time algorithm to determine whether an input graph of rank-width at most k satisfies the formula. There are several parameters which are equivalent to rank-width in the sense that one is bounded if and only if the other is bounded. These include clique-width [7], NLC-width [36], and Boolean-width [3].

Low rank-width colorings. We now introduce our main object of study.

Definition 1

A class \(\mathcal {C}\) of graphs admits low rank-width colorings if there exist functions \(N:\mathbb {N}\rightarrow \mathbb {N}\) and \(Q:\mathbb {N}\rightarrow \mathbb {N}\) such that for all \(p\in \mathbb {N}\), every graph \(G\in \mathcal {C}\) can be vertex colored with at most N(p) colors such that the union of any \(i\le p\) color classes induces a subgraph of rank-width at most Q(i).

As proved by Oum [29], every graph G with tree-width k has rank-width at most \(k+1\), hence every graph class which admits low tree-depth colorings also admits low rank-width colorings. On the other hand, graphs admitting a low rank-width coloring can be very dense. We also remark that graph classes admitting low rank-width colorings are monotone under taking induced subgraphs, as rank-width does not increase by removing vertices.

Let us remark that due to the model-checking algorithm of Courcelle et al. [8], the (induced) subgraph isomorphism problem is solvable in cubic time for every fixed pattern H whenever the input graph is given together with a low rank-width coloring for \(p=|V(H)|\), using N(p) colors. Indeed, it suffices to iterate through all p-tuples of color classes and look for the pattern H in the subgraph induced by these color classes; this can be done efficiently since this subgraph has rank-width at most Q(p). The caveat is that the graph has to be supplied with an appropriate coloring. In this work we do not investigate the algorithmic aspects of low rank-width colorings, and rather concentrate on the combinatorial question of which classes admit such colorings, and which do not.

Our contribution. We prove that for every class \(\mathcal {C}\) of bounded expansion and every integer \(r\ge 2\), the class \(\{G^r:G\in \mathcal {C}\}\) of rth powers of graphs from \(\mathcal {C}\) admits low rank-width colorings. It is easy to see that there are classes of bounded expansion such that \(\{G^r:G\in \mathcal {C}\}\) has both unbounded rank-width and does not admit low tree-depth colorings. We furthermore prove that the class of unit interval graphs and the class of bipartite permutation graphs admit low rank-width colorings. On the negative side, we show that the classes of interval graphs and of permutation graphs do not admit low rank-width colorings. Finally, we also prove that every graph class admitting low rank-width colorings has the Erdős-Hajnal property [15] and is \(\chi \)-bounded [20].

2 Preliminaries

All graphs in this paper are finite, undirected and simple, that is, they do not have loops or parallel edges. Our notation is standard, we refer to [12] for more background on graph theory. We write V(G) for the vertex set of a graph G and E(G) for its edge set. A vertex coloring of a graph G with colors from S is a mapping \(c :V(G)\rightarrow S\). For each \(v\in V(G)\), we call c(v) the color of v. The distance between vertices u and v in G, denoted \(\mathrm {dist}_G(u,v)\), is the length of a shortest path between u and v in G. The rth power of a graph G is the graph \(G^r\) with vertex set V(G), where there is an edge between two vertices u and v if and only if their distance in G is at most r.

Rank-width was introduced by Oum and Seymour [32]. We refer to the surveys [21, 30] for more background. For a graph G, we denote the adjacency matrix of G by \(A_G\), where for \(x,y\in V(G)\), \(A_G[x,y]=1\) if and only if x is adjacent to y. Let G be a graph. We define the cut-rank function \(\mathrm {cutrk}_{G} :2^{V} \rightarrow \mathbb {N}\) such that \(\mathrm {cutrk}_G(X)\) is the rank of the matrix \(A_G[X, V(G)\setminus X]\) over the binary field (if \(X=\emptyset \) or \(X=V(G)\), then we let \(\mathrm {cutrk}_G(X)=0\)).

A rank-decomposition of G is a pair (T, L), where T is a subcubic tree (i.e. a tree where every node has degree 1 or 3) with at least 2 nodes and L is a bijection from V(G) to the set of leaves of T. The width of e is define as \(\mathrm {cutrk}_G(A^e_1)\) where \((A^e_1, A^e_2)\) is the vertex bipartition of G each \(A^e_i\) is the set of all vertices in G mapped to leaves contained in one of components of \(T-e\). The width of (T, L) is the maximum width over all edges in T, and the rank-width of G, denoted by \(\mathrm {rw}(G)\), is the minimum width over all rank-decompositions of G. If \(\left|V(G)\right|\le 1\), then G has no rank-decompositions, and the rank-width of G is defined to be 0.

The exact definitions of tree-decompositions, tree-width, and tree-depth are not needed in our reasoning. We include them in the appendix for completeness.

A graph is an interval graph if it is the intersection graph of a family \(\mathcal {I}\) of intervals on the real line, an interval graph is a unit interval graph if all intervals in \(\mathcal {I}\) have the same length. A graph is a permutation graph if it is the intersection graph of line segments whose endpoints lie on two parallel lines.

3 Powers of Sparse Graphs

In this section we show that the class of rth powers of graphs from a bounded expansion class admit low rank-width colorings. The original definition of bounded expansion classes by Nešetřil and Ossona de Mendez [26] is in terms of bounds on the density of bounded depth minors. We will work with the characterisation by the existence of low tree-depth colorings as well as by a characterisation in terms of bounds on generalized coloring numbers.

Theorem 2

(Nešetřil and Ossona de Mendez [26]). A class \(\mathcal {C}\) of graphs has bounded expansion if and only if for all \(p\in \mathbb {N}\) there exists a number \(N=N(\mathcal {C}, p)\) such that every graph \(G\in \mathcal {C}\) admits a p-tree-depth coloring with N colors.

Our main result in this section is the following.

Theorem 3

Let \(\mathcal {C}\) be a class of bounded expansion and \(r\ge 2\) be an integer. Then the class \(\{G^r:G\in \mathcal {C}\}\) of rth powers of graphs from \(\mathcal {C}\) admits low rank-width colorings.

For a graph G, we denote by \(\varPi (G)\) the set of all linear orders of V(G). For \(u,v\in V(G)\) and a non-negative integer r, we say that u is weakly r-reachable from v with respect to L, if there is a path P of length at most r between u and v such that u is the smallest among the vertices of P with respect to L. We denote by \(\mathrm {WReach}_r[G,L,v]\) the set of vertices that are weakly r-reachable from v with respect to L. The weak r -coloring number \(\mathrm {wcol}_r(G)\) of G is defined as

$$\begin{aligned} \mathrm {wcol}_r(G):= & {} \min _{L\in \varPi (G)}\,\max _{v\in V(G)}\, \bigl |\mathrm {WReach}_r[G,L,v]\bigr |. \end{aligned}$$

The weak coloring numbers were introduced by Kierstead and Yang [22] in the context of coloring and marking games on graphs. As shown by Zhu [37], classes of bounded expansion can be characterised by the weak coloring numbers.

Theorem 4

(Zhu [37]). A class \(\mathcal {C}\) has bounded expansion if and only if for all \(r\ge 1\) there is a number f(r) such that for all \(G\in \mathcal {C}\) it holds that \(\mathrm {wcol}_r(G)\le f(r)\).

In order to prove Theorem 3, we will first compute a low tree-depth coloring. We would like to apply the following theorem, relating the tree-width (and hence in particular the tree-depth) of a graph and the rank-width of its rth power.

Theorem 5

(Gurski and Wanke [19]). Let \(r\ge 2\) be an integer. If a graph H has tree-width at most p, then \(H^r\) has rank-width at most \(2(r+1)^{p+1}-2\).

We remark that Gurski and Wanke [19] proved this bound for clique-width instead of rank-width, but clique-width is never smaller than the rank-width [32].

The natural idea would be just to combine the bound of Theorem 5 with low tree-depth coloring given by Theorem 2. Note however, that when we consider any subgraph H induced by \(i\le p\) color classes, the graph \(H^r\) may be completely different from the graph \(G^r[V(H)]\), due to paths that are present in G but disappear in H. Hence we cannot directly apply Theorem 5. Instead, we will prove the existence of a refined coloring of G such that for any subgraph H induced by \(i\le p\) color classes, in the refined coloring there is a subgraph \(H'\) such that \(G^r[V(H)]\subseteq H'^r\) and such that \(H'\) gets only g(i) colors in the original coloring, for some fixed function g. We can now apply Theorem 5 to \(H'\) and use fact that rank-width is monotone under taking induced subgraphs.

In the following, we will say that a vertex subset X receives a color i under a coloring c if \(i\in c^{-1}(X)\). We first need the following definitions.

Definition 6

Let G be a graph, \(X\subseteq V(G)\) and \(r\ge 2\). A superset \(X'\supseteq X\) is called an r-shortest path hitter for X if for all \(u,v\in X\) with \(1<\mathrm {dist}_G(u,v)\le r\), \(X'\) contains an internal vertex of some shortest path between u and v.

Definition 7

Let G be a graph, let c be a coloring of G, and \(r\ge 2\) and \(d\ge 1\). A coloring \(c'\) is a (d, r)-good refinement of c if for every vertex set X that receives at most p colors under \(c'\), there exists an r-shortest path hitter \(X'\) of X that receives at most \(d\cdot p\) colors under c.

We use the weak coloring numbers to prove the existence of a good refinement.

Lemma 8

Let G be a graph and \(r\ge 2\) be an integer. Then every coloring c of G using k colors has a \((2\mathrm {wcol}_r(G), r)\)-good refinement using \(k^{2\mathrm {wcol}_r(G)}\) colors.

Proof

Let \(\varGamma \) be the set of colors used by c, and let \(d:=2\mathrm {wcol}_r(G)\). The (d, r)-good refinement \(c'\) that we are going to construct will use subsets of \(\varGamma \) of size at most d as the color set; the number of such subsets is at most \(k^{2\mathrm {wcol}_r(G)}\). Let L be a linear order of V(G) with \(\max _{v\in V(G)}\, \bigl |\mathrm {WReach}_r[G,L,v]\bigr |=\mathrm {wcol}_r(G)\). We construct a new coloring \(c'\) as follows:

  1. (1)

    Start by setting \(c'(v):=\emptyset \) for each \(v\in V(G)\).

  2. (2)

    For each pair of vertices u and v such that \(u\in \mathrm {WReach}_r[G, L, v]\), we add the color c(u) to \(c'(v)\).

  3. (3)

    For each pair u and v of non-adjacent vertices such that \(u<_L v\) and \(u\in \mathrm {WReach}_r[G,L,v]\), we do the following. Check whether there is a path P of length at most r connecting u and v such that all the internal vertices of P are larger than both u and v in L. If there is no such path, we do nothing for the pair u, v. Otherwise, fix one such path P, chosen to be the shortest possible, and let z be the vertex traversed by P that is the largest in L. Then we add the color c(z) to \(c'(v)\).

Thus, every vertex v receives in total at most \(2\mathrm {wcol}_{r}(G)\) colors of \(\varGamma \) to its final color \(c'(v)\): at most \(\mathrm {wcol}_{r}(G)\) in step (2), and at most \(\mathrm {wcol}_{r}(G)\) in step (3), because we add at most one color per each \(u\in \mathrm {WReach}_r[G,L,v]\). It follows that each final color \(c'(v)\) is a subset of \(\varGamma \) of size at most \(2\mathrm {wcol}_{r}(G)\).

We claim that \(c'\) is a (d, r)-good refinement of c. Let \(X\subseteq V(G)\) be a set that receives at most p colors under \(c'\), say colors \(A_1, \ldots , A_p\subseteq \varGamma \). Let \(X'\) be the set of vertices of G that are colored by colors in \(A_1\cup \cdots \cup A_p\) under c. Since \(|A_i|\le d\) for each \(i\in \{1,\ldots ,p\}\), we have that \(X'\) receives at most \(d\cdot p\) colors under c.

To show that \(X'\) is an r-shortest path hitter of X, let us choose any two vertices u and v in X with \(u<_L v\) and \(1<\mathrm {dist}_G(u,v)\le r\). If there is a shortest path from u to v whose all internal vertices are larger than u and v in L, by step (3), \(X'\) contains a vertex that is contained in one such path. Otherwise, a shortest path from u to v contains a vertex z with \(L(z)<L(v)\) other than u and v. This implies that there exists \(z'\in \mathrm {WReach}_r[G,L,v]\setminus \{u\}\) on the path such that \(c(z')\in c'(v)\), and hence \(z'\in X'\) by step (2). Therefore, \(X'\) is an r-shortest path hitter of X, as required.    \(\square \)

Definition 9

Let G be a graph, let \(X\subseteq V(G)\), and let \(r\ge 1\) be an integer. A superset \(X'\supseteq X\) is called an r-shortest path closure of X if for each \(u,v\in X\) with \(\mathrm {dist}_G(u,v)=\ell \le r\), \(G[X']\) contains a path of length \(\ell \) between u and v.

Definition 10

Let G be a graph, let c be a coloring of G, and let \(r\ge 2\) and \(d\ge 1\). A coloring \(c'\) is a (d, r)-excellent refinement of c if for every vertex set \(X\subseteq V(G)\) there exists an r-shortest path closure \(X'\) of X such that if X receives p colors in \(c'\), then \(X'\) receives at most \(d\cdot p\) colors in c.

We inductively define excellent refinements from good refinements.

Lemma 11

Let G be a graph, \(r\,\ge \,2\) an integer, and let \(d_r\,:=\,\prod _{2\le \ell \le r}2\mathrm {wcol}_\ell (G)\). Then every coloring c of G using at most k colors has a \((d_r, r)\)-excellent refinement using at most \(k^{d_r}\) colors.

Proof

We prove the lemma by induction on r. For \(r=2\), an r-shortest path hitter of a set X is an r-shortest path closure, and vice versa. Therefore, the statement immediately follows from Lemma 8. Now assume \(r\ge 3\). By induction hypothesis, there is a \((d_{r-1}, r-1)\)-excellent refinement \(c_1\) of c with at most \(k^{d_{r-1}}\) colors. By applying Lemma 8 to \(c_1\), we obtain a \((2\mathrm {wcol}_r(G),r)\)-good refinement \(c'\) of \(c_1\) with at most \((k^{d_{r-1}})^{2\mathrm {wcol}_r(G)}=k^{d_r}\) colors. We claim that \(c'\) is a \((d_r,r)\)-excellent refinement of c. Any set X which gets at most p colors from \(c'\) can be first extended to an r-shortest path hitter \(X'\) for X which receives at most \(2\mathrm {wcol}_r(G)\cdot p\) colors. Then \(X'\) can be extended by induction hypothesis to an \((r-1)\)-shortest path closure \(X''\) of \(X'\) which receives at most \(d_{r-1}\cdot 2\mathrm {wcol}_r(G)\cdot p=d_r\cdot p\) colors.

It remains to show that \(X''\) is an r-shortest path closure of X. Take any \(u,v\in X\) with \(\mathrm {dist}_G(u,v)=\ell \le r\). If \(\ell \le 1\), then u, v are already adjacent in G[X]. Otherwise, since \(X'\) is an r-shortest path hitter for X, there is a vertex \(z\in X'\) that lies on some shortest path connecting u and v in G. In particular, \(\mathrm {dist}_G(u,z)=\ell _1\) and \(\mathrm {dist}_G(z,v)=\ell _2\) for \(\ell _1,\ell _2\) satisfying \(\ell _1,\ell _2<\ell \) and \(\ell _1+\ell _2=\ell \). Since \(X''\) is an \((r-1)\)-shortest path closure of \(X'\), we infer that \(\mathrm {dist}_{G[X'']}(u,z)=\ell _1\) and \(\mathrm {dist}_{G[X'']}(z,v)=\ell _2\). Hence \(\mathrm {dist}_{G[X'']}(u,v)=\ell \) by the triangle inequality.    \(\square \)

Proof

(of Theorem 3 ). Let G be a graph in \(\mathcal {C}\) and let \(d_r:=\prod _{2\le \ell \le r}2\mathrm {wcol}_\ell (G)\). Since \(\mathcal {C}\) has bounded expansion, by Theorem 4, for each r, \(\mathrm {wcol}_r(G)\) is bounded by a constant only depending on \(\mathcal {C}\). We start by taking c to be a \((d_r\cdot p)\)-tree-depth coloring with \(N(d_r\cdot p)\) colors, where N is the function from Theorem 2. Then its \((d_r,r)\)-excellent refinement \(c'\) has the property that \(c'\) uses at most \(N(d_r\cdot p)^{d_r}\) colors, and every subset X which receives at most p colors in \(c'\) has an r-shortest path closure \(X'\) that receives at most \(d_r\cdot p\) colors in c. Thus, the graph induced on X in the rth power \(G^r\) is the same at the graph induced on X in the rth power \(G[X']^r\). Since \(G[X']\) has tree-depth at most \(d_r\cdot p\), by Theorem 5, \(G[X']^r\) has rank-width at most \(2(r+1)^{d_r\cdot p+1}-2\). Therefore, \(G^r[X]\) has rank-width at most \(2(r+1)^{d_r\cdot p+1}-2\) as well.    \(\square \)

We now give two example applications of Theorem 3. A map graph is a graph that can be obtained from a plane graph by making a vertex for each face, and adding an edge between two vertices, if the corresponding faces share a vertex. One can observe (\(\star \))Footnote 1 that every map graph is an induced subgraph of the second power of another planar graph, namely the radial graph of the original graph. Thus, map graphs have low rank-width colorings. A similar reasoning can be performed for line graphs of graphs from any bounded expansion graph class (\(\star \)). Thus, both map graphs and line graphs of graphs from any fixed bounded expansion graph class admit low rank-width colorings.

4 Other Positive Results

We now prove that unit interval graphs and bipartite permutation graphs admit low rank-width colorings.

Theorem 12

The class of unit interval graphs and the class of bipartite permutation graphs admit low rank-width colorings.

Our results follow from characterizations of these classes obtained by Lozin [23]. Let \(n,m\ge 1\). We denote by \(H_{n,m}\) the graph with \(n\cdot m\) vertices which can be partitioned into n independents sets \(V_1=\{v_{1,1},\ldots , v_{1,m}\}, \ldots , V_n=\{v_{n,1},\ldots , v_{n,m}\}\) so that for each \(i\in \{1,\ldots , n-1\}\) and for each \(j, j'\in \{1,\ldots , m\}\), vertex \(v_{i,j}\) is adjacent to \(v_{i+1,j'}\) if and only if \(j'\in \{1, \ldots , j\}\), and there are no edges between \(V_i\) and \(V_j\) if \(\left|i-j\right|\ge 2\). The graph \(\widetilde{H}_{n,m}\) is the graph obtained from \(H_{n,m}\) by replacing each independent set \(V_i\) by a clique.

Lemma 13

The following statements hold:

  1. 1.

    (Lozin [23]) The rank-width of \(H_{n,m}\) and of \(\widetilde{H}_{n,m}\) is at most 3n.

  2. 2.

    (Lozin [23]) Every bipartite permutation graph on n vertices is isomorphic to an induced subgraph of \(H_{n,n}\).

  3. 3.

    (Lozin [24]) Every unit interval graph on n vertices is isomorphic to an induced subgraph of \(\widetilde{H}_{n,n}\).

Hence, in order to prove Theorem 12, it suffices to prove that the graphs \(H_{n,m}\) and \(\widetilde{H}_{n,m}\) admit low rank-width colorings.

Proof

(of Theorem 12 ). For every positive integer p, let \(N(p):=p+1\) and \(Q(i):=3i\) for each \(i\in \{1, \ldots , p\}\). We prove that for all \(n,m\ge 1\), the graphs \(H_{n,m}\) and \(\widetilde{H}_{n,m}\) can be vertex colored using N(p) colors so that each of the connected components of the subgraph induced by any \(i\le p\) color classes has rank-width at most R(i). As rank-width and rank-width colorings are monotone under taking induced subgraphs, the statement of the theorem follows from Lemma 13.

Assume that the vertices of \(H_{n,m}\) (and \(\widetilde{H}_{n,m}\), respectively) are named \(v_{1,1},\ldots , v_{1,m}, \ldots \), \(v_{n,1},\ldots , v_{n,m}\), as in the definition. We color the vertices in the ith row, \(v_{i,1},\ldots , v_{i,m}\), with color \(j+1\) where \(j \in \{ 0, 1, \ldots , p\}\) and \(i\equiv j {\pmod {p+1}}\). Then any connected component H of a subgraph induced by \(i\le p\) colors is isomorphic to \(H_{i',m}\) (\(\widetilde{H}_{i',m}\), respectively) for some \(i'\le i\). Hence, according to Lemma 13, H has rank-width at most \(3i=Q(i)\), as claimed.    \(\square \)

5 Negative Results

In contrast to the result in Sect. 4, we prove that interval graphs and permutation graphs do not admit low rank-width colorings. For this, we introduce twisted chain graphs. Briefly, a twisted chain graph G consists of three vertex sets A, B, C where each of \(G[A\cup C]\) and \(G[B\cup C]\) is a chain graph, but the ordering of C with respect to the chain graphs \(G[A\cup C]\) and \(G[B\cup C]\) are distinct.

Definition 14

For a positive integer n, a graph on the set of \(3n^2\) vertices \(A\cup B\cup C\), where \(A=\{v_1, \ldots , v_{n^2}\}\), \(B=\{w_1, \ldots , w_{n^2}\}\), and \(C=\{z_{(i,j)}:1\le i,j\le n\}\), is called a twisted chain graph of order n if

  • for integers \(x,y, i, j\in \{1, \ldots , n\}\) and \(k=n(x-1)+y\), \(v_k\) is adjacent to \(z_{(i,j)}\) if and only if either (\(x<i\)) or (\(x=i\) and \(y\le j\));

  • for integers \(x,y, i, j\in \{1, \ldots , n\}\) and \(k=n(x-1)+y\), \(w_k\) is adjacent to \(z_{(i,j)}\) if and only if either (\(x<j\)) or (\(x=j\) and \(y\le i\));

  • the edge relation within \(A\cup B\) and within C is arbitrary.

We first show that a large twisted chain graph has large rank-width. We remark that a similar construction based on merging two chain graphs in a mixed order can be found in Brandstädt et al. [2]. Also, a slightly general construction was given by Dabrowski and Paulusma [9]. Obtaining any lower bound seems to follow from a careful examination and modification of the constructions given in [2] or [9]; however, we prefer to give our own direct proof for the sake of completeness. Also, in those papers, authors provided a lower bound of clique-width, and its direct application to rank-width does not provide a linear lower bound.

Lemma 15

( \(\star \) ). For every positive integer n, a twisted chain graph of order 12n has rank-width at least n.

Proof

(sketch). Let \(m:=12n\) and let G be a twisted chain graph of order m. Adopt the notation from the Definition 14 for G, and assume for the sake of contradiction that the rank-width of G is less than n. By a well-known fact about graphs of bounded rank-width, there exists a vertex bipartition (S, T) of G such that \(\mathrm {cutrk}_G(S)<n\) and at least one third of vertices of C belong to S, and at least one third belong to T.

Suppose now there are vertices \(v_{a_1},\ldots ,v_{a_k}\in A\cap S\) and \(z_{(b_1,c_1)},\ldots ,z_{(b_k,c_k)}\in C\cap T\) with the following property satisfied:

$$a_1\le (b_1-1)m+c_1< a_2\le (b_2-1)m+c_2< \cdots <a_k\le (b_k-1)m+c_k.$$

Then it can be easily seen that the submatrix of \(A_G[S,T]\) induced by rows corresponding to vertices \(v_{a_i}\) and columns corresponding to vertices \(z_{(b_i,c_i)}\) has ones in the upper triangle and on the diagonal, and zeroes in the lower triangle. The rank of this submatrix is k, so finding such a structure, called ordered (S, T)-matching, for \(k=n\) would contradict the assumption that \(\mathrm {cutrk}_G(S)<n\). Similarly if all vertices of \(v_{a_i}\) were contained in T instead of S, and all vertices \(z_{(b_i,c_i)}\) were contained in S instead of T. Also, a similar notion can be defined for B and C, but observe that there the vertices \(z_{(b_i,c_i)}\) need to be ordered lexicographically with the second coordinate being the leading one, instead of the first. This difference is the key to the proof.

Consider now all elements \((b,c)\in \{1,\ldots ,m\}\times \{1,\ldots ,m\}\), ordered lexicographically with the first coordinate leading. For each such (b, c), record whether \(z_{(b,c)}\) belongs to S or to T, and examine the obtained sequence of length \(m^2\), consisting of symbols S and T. If this sequence had alternation at least 4n, that is, we could see at least 4n times a T after an S, then it is not hard to convince oneself that there would be an ordered (S, T)-matching between A and C of order n, a contradiction. The same analysis can be performed between B and C, but now we order pairs from \(\{1,\ldots ,m\}\times \{1,\ldots ,m\}\) lexicographically with the second coordinate leading. It can be now easily seen that since at least a third of vertices of C belong to S and at least a third belong to T, one of these sequences has alternation at least \(\frac{m}{3}=4n\), which gives the desired contradiction.    \(\square \)

We now observe that if a graph class contains arbitrarily large twisted chain graphs, then it does not admit low rank-width colorings.

Theorem 16

Let \(\mathcal {C}\) be a hereditary graph class, and suppose for each positive integer n some twisted chain graph of order n belongs to \(\mathcal {C}\). Then \(\mathcal {C}\) does not admit low rank-width colorings.

Proof

We show that for every pair of integers \(m\ge 3\) and \(n\ge 1\), there is an graph \(G\in \mathcal {C}\) such that for every coloring of G with m colors, there is an induced subgraph H that receives at most 3 colors and has rank-width at least n. This implies that \(\mathcal {C}\) does not admit low rank-width colorings. We will need the following simple Ramsey-type argument.

Claim 1

( \(\star \) ). For all positive integers k, d, there exists an integer \(M=M(k,d)\) such that for all sets X, Y with \(|X|=|Y|=M\) and all functions \(f:X\times Y\rightarrow \{1,\ldots ,d\}\), there exist subsets \(X'\subseteq X\) and \(Y'\subseteq Y\) with \(|X'|=|Y'|=k\) such that f sends all elements of \(X'\times Y'\) to the same value.

Claim 1 follows, e.g., from [35, Theorem 11.5], but in the appendix we give a simple proof for the sake of completeness.

Let \(M_1:=M(12n, m)\), \(M_2:=M(M_1,m)\), and \(M_3:=M(M_2,m)\). Let \(G\in \mathcal C\) be a twisted chain graph of order \(M_3\); adopt the notation from Definition 14 for G. Suppose G is colored by m colors by a coloring c. By Claim 1, there exist \(X_1, Y_1\subseteq \{1, \ldots , M_3\}\) with \(|X_1|=|Y_1|=M_2\) such that \(\{z_{(x,y)}:(x,y)\in X_1\times Y_1\}\) is monochromatic under c.

Fig. 1.
figure 1

An interval intersection model of a twisted chain graph of order 2.

Full size image
Fig. 2.
figure 2

A permutation intersection model of a twisted chain graph of order 2.

Full size image

Now, for an index \(k\in \{1,\ldots ,M_3^2\}\), let \((i_1(k),j_1(k))\in \{1,\ldots ,m\}\times \{1,\ldots ,m\}\) be the unique pair such that \(k=(i_1(k)-1)M_3+j_1(k)\), and let \((i_2(k),j_2(k))\in \{1,\ldots ,m\}\times \{1,\ldots ,m\}\) be the unique pair such that \(k=(j_2(k)-1)M_3+i_2(k)\). By reindexing vertices A and C using pairs \((i_1(k),j_1(k))\) and \((i_2(k),j_2(k))\), we may view coloring c on A and C as a coloring on \(\{1,\ldots ,M_3\}\times \{1,\ldots ,M_3\}\). By applying Claim 1 to the vertices from A indexed by \(X_1\times Y_1\), we obtain subsets \(X_2\subseteq X_1\) and \(Y_2\subseteq Y_1\) such that \(|X_2|=|Y_2|=M_1\) and the set \(\{v_{(x-1)M_3+y}:x\in X_2, y\in Y_2\}\) is monochromatic. Finally, by applying Claim 1 to the vertices from B indexed by \(X_2\times Y_2\), we obtain subsets \(X_3\subseteq X_2\) and \(Y_3\subseteq Y_2\) such that \(|X_3|=|Y_3|=12n\) and the set \(\{w_{(y-1)M_3+x}:(x,y)\in X_3\times Y_3\}\) is monochromatic. Now observe that the subgraph \(G[\{v_{(x-1)M_3+y}, w_{(y-1)M_3+x}, z_{(x,y)}:(x,y)\in X_3\times Y_3\}]\) receives at most 3 colors, and is a twisted chain graph of order 12n. By Lemma 15 it has rank-width at least n, so this proves the claim.    \(\square \)

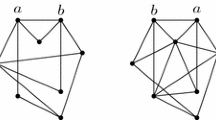
We now observe (\(\star \)) that a twisted chain graph of order n is an interval graph, provided each of A, B, and C is a clique, and there are no edges between A and B. Similarly, for each n there is a twisted chain graph of order n that is a permutation graph (\(\star \)). See Figs. 1 and 2 for examples of intersection models. By Theorem 16, we obtain the following.

Theorem 17

The classes of interval graphs and permutation graphs do not admit low rank-width colorings.

6 Erdős-Hajnal property and \(\chi \)-boundedness

A graph class \(\mathcal {C}\) has the Erdős-Hajnal property if there is \(\varepsilon >0\), depending only on \(\mathcal {C}\), such that every n-vertex graph in \(\mathcal {C}\) has either an independent set or a clique of size \(n^{\varepsilon }\). The conjecture of Erdős and Hajnal [15] states that for every fixed graph H, the class of graphs not having H as an induced subgraph has the Erdős-Hajnal property; cf. [4]. We prove that every class admitting low rank-width colorings has the Erdős-Hajnal property. For this we use the fact that graphs of bounded rank-width have the property, shown by Oum and Seymour [31].

Proposition 18

( \(\star \) ). Let \(\mathcal {C}\) be a class of graphs admitting low rank-width colorings. Then \(\mathcal {C}\) has the Erdős-Hajnal property.

A class \(\mathcal {C}\) of graphs is \(\chi \) -bounded if there exists a function \(f:\mathbb N\rightarrow \mathbb N\) such that for every \(G\in \mathcal {C}\) and an induced subgraph H of G, we have \(\chi (H)\le f(\omega (H))\), where \(\chi (H)\) is the chromatic number of H and \(\omega (H)\) is the size of a maximum clique in H. It was proved by Dvořák and Král’ [14] that for every p, the class of graphs of rank-width at most p is \(\chi \)-bounded. We observe that this fact directly generalizes to classes admitting low rank-width colorings.

Proposition 19

( \(\star \) ). Let \(\mathcal {C}\) be a class of graphs admitting low rank-width colorings. Then \(\mathcal {C}\) is \(\chi \)-bounded.

7 Conclusions

We introduced the concept of low rank-width colorings, and showed that such colorings exist on rth powers of graphs from any bounded expansion class, for any fixed r, as well as on unit interval and bipartite permutation graphs. These classes are non-sparse and have unbounded rank-width. On the negative side, the classes of interval and permutation graphs do not admit low rank-width colorings.

The obvious open problem is to characterise hereditary graph classes which admit low rank-width colorings in the spirit of the characterisation theorem for graph classes admitting low tree-depth colorings. We believe that Theorem 16 may provide some insight into this question, as it shows that containing arbitrarily large twisted chain graphs is an obstacle for admitting low rank-width colorings. Is it true that every hereditary graph class that does not admit low rank-width colorings has to contain arbitrarily large twisted chain graphs?

In this work we did not investigate the question of computing low rank-width colorings, and this question is of course crucial for any algorithmic applications. Our proof for the powers of sparse graphs can be turned into a polynomial-time algorithm that, given a graph G from a graph class of bounded expansion \(\mathcal {C}\), first computes a low tree-depth coloring, and then turns it into a low rank-width coloring of \(G^r\), for a fixed constant r. However, we do not know how to efficiently compute a low rank-width coloring given the graph \(G^r\) alone, without the knowledge of G. The even more general problem of efficiently constructing an approximate low rank-width coloring of any given graph remains wide open.

Finally, we remark that our proof for the existence of low rank-width colorings on powers of graphs from a class of bounded expansion actually yields a slightly stronger result. Precisely, Ganian et al. [16] introduced a parameter shrub-depth (or SC-depth), which is a depth analogue of rank-width, in the same way as tree-depth is a depth analogue of tree-width. It can be shown that for constant r, the rth power of a graph of constant tree-depth belongs to a class of constant shrub-depth, and hence our colorings for powers of graphs from a class of bounded expansion are actually low shrub-depth colorings. We omit the details.