Semi-discrete Optimal Transport in Patch Space for Enriching Gaussian Textures

Abstract

A bilevel texture model is proposed, based on a local transform of a Gaussian random field. The core of this method relies on the optimal transport of a continuous Gaussian distribution towards the discrete exemplar patch distribution. The synthesis then simply consists in a fast post-processing of a Gaussian texture sample, boiling down to an improved nearest-neighbor patch matching, while offering theoretical guarantees on statistical compliancy.

1 Introduction

Designing models for realistic and fast rendering of structured textures is a challenging research topic. In the past, many models have been proposed for exemplar-based synthesis, which consists in synthesizing a piece of texture having the same perceptual characteristics as an observed texture sample with still some innovative content. Several authors [2, 24] have proposed non-parametric methods based on progressive sampling of the texture using a copy-paste principle. This paved the way to many other successful synthesis methods relying on patch-based sampling [3, 11,12,13, 16, 19] (see [23] for a detailed review). Even if these methods can be applied very efficiently [13], they do not offer much mathematical guarantees (except asymptotic results [14]) which reflects for example in the growing garbage effect described in [2].

In contrast Gaussian texture models [4] are stationary and inherently respect the frequency content of the input texture. They can be efficiently simulated on the discrete plane $\mathbb {Z}^2$ [6] and even generalized to the framework of procedural noises defined in the continuous domain $\mathbb {R}^2$ (see e.g. [7] and references therein). They also allow for dynamic texture synthesis and mixing [25] and inpainting [5]. However the Gaussian model is intrinsically limited since the color distribution of the output is always symmetric around the mean color and the local texture patterns cannot contain salient features such as contrasted contours.

The main purpose of this work is to propose a theoretically sound post-processing of the Gaussian model to cope with some of these limitations. Since the color and local pattern information is a part of the patch distribution, we propose to apply a local operation that will transform the patch distribution of the Gaussian texture into the patch distribution of the input image. This can naturally be addressed using a semi-discrete optimal transport plan.

Several tools from optimal transport (OT) have already been applied to texture synthesis: Rabin et al. [20] and Xia et al. [25] formulate texture mixing via Wasserstein barycenters, Tartavel et al. [21] use Wasserstein distances in a variational formulation of texture synthesis, and Gutierrez et al. [9] apply discrete OT in order to specify a global patch distribution. Here, we suggest to locally apply a semi-discrete transport plan which can be seen as a tweaked nearest-neighbor projection.

Indeed, semi-discrete OT corresponds to assign the centers of Laguerre cells to each point of a well-designed Laguerre partition [1, 17]. So far, deterministic methods for solving semi-discrete methods have been limited to dimensions ${D=2}$ [17] and ${D=3}$ [15] using explicit geometric construction of the Laguerre tessellation. Recently, Genevay et al. [8] proposed several stochastic optimization schemes for solving entropy-regularized OT problems.

In Sect. 2 we summarize the non-regularized semi-discrete OT framework and the numerical solution given in [8]. In Sect. 3 we show how to use this algorithm to transport patch distributions (in dimensions $D=27$ or higher) thus enriching the Gaussian texture model. The resulting bilevel algorithm, can be seen as a non-iterative version of [11] with a global statistical constraint, which is confirmed by the experiments of Sect. 4.

2 Semi-discrete Optimal Transport

In this section, we recall the framework for semi-discrete optimal transport and the numerical solution given by Genevay et al. [8].

2.1 The Optimal Transport Problem and Its Dual Formulation

Let $\mu$, $\nu$ be two probability measures on $\mathbb {R}^D$. We assume that $\mu$ has a bounded probability density function $\rho$ and that $\nu$ is a discrete measure $\nu = \sum _{y \in S} \nu _y \delta _y$ with finite support S. Let us denote by $\varPi (\mu ,\nu )$ the set of probability measures on $\mathbb {R}^{D}\times \mathbb {R}^{D}$ having marginal distributions $\mu ,\nu$. If T is a measurable map, we denote by $T_\sharp \mu$ the push-forward measure defined as $T_\sharp \mu (A) = \mu (T^{-1}(A))$. If $v \in \mathbb {R}^S$, we define the c-transform of v with respect to the cost $c(x,y) = \Vert x-y\Vert ^2$ as $v^c(x) = \min _{y \in S} \Vert x-y\Vert ^2 - v(y)$, and $T_v$ the corresponding assignment uniquely defined almost everywhere by

$$\begin{aligned} T_v(x) = \mathop {\text {argmin}}\limits _{y \in S} \Vert x-y\Vert ^2 - v(y). \end{aligned}$$

(1)

When $v=0$, we get the nearest neighbor (NN) projection which assigns to x the closest point in S (unique for almost all x).

The preimages of $T_v$ define a partition of $\mathbb {R}^D$ (up to a negligible set), called the power diagram or Laguerre tessellation, the cells of which are defined as

$$\begin{aligned} {{\text {Pow}}}_v(y) = \{x \in \mathbb {R}^D \ | \ \forall z \in S \setminus \{y\} ,\ \Vert x-y\Vert ^2 - v(y) < \Vert x-z\Vert ^2 - v(z)\}. \end{aligned}$$

(2)

The Kantorovich formulation of optimal transport consists in solving

$$\begin{aligned} \min _{\pi \in \varPi (\mu ,\nu )} \int _{\mathbb {R}^D \times \mathbb {R}^D} \Vert x-y\Vert ^2 d\pi (x,y) . \end{aligned}$$

(3)

It has been shown [1, 10, 15, 22] that this problem admits solutions of the form $({\text {Id}}\times T_v)_\sharp \mu$ where v solves the dual problem

$$\begin{aligned} \mathop {\text {argmax}}\limits _{v \in \mathbb {R}^S} \ H(v) \quad \text {where} \quad H(v) = \int _{\mathbb {R}^D} v^c(x) \rho (x) dx + \sum _{y \in S} v(y)\nu _y . \end{aligned}$$

(4)

The same authors have shown that the function H is concave, $\mathcal {C}^1$-smooth, and that its gradient is given by $\frac{\partial H}{\partial v(y)}= - \mu ({{\text {Pow}}}_v(y)) + \nu _y$. Thus, v is a critical point of H if and only if $\mu ({{\text {Pow}}}_v(y)) = \nu _y$ for all y, which means that $(T_v)_\sharp \mu = \nu$.

2.2 Stochastic Optimization

Genevay et al. [8] have suggested to address the maximization of (4) by using a stochastic gradient ascent, which is made possible by writing

$$\begin{aligned} H(v) = \mathbb {E}[h(X,v)] \quad \text {where} \quad h(x,v) = v^c(x) + \sum _{y \in S} v(y) \nu _y \end{aligned}$$

(5)

and where X is a random variable with distribution $\mu$. Notice that for ${x \in {{\text {Pow}}}_v(y)}$, $v \mapsto v^c(x)$ is smooth with gradient $-e_y$ (where $\{e_y\}_{y \in S}$ is the canonical basis of $\mathbb {R}^S$). Therefore, for any $w \in \mathbb {R}^S$, for almost all $x \in \mathbb {R}^D$, $v \mapsto h(x,v)$ is differentiable at w and $\nabla _v h(x,w) = - e_{T_w(x)} + \nu .$ (abusing notation $(\nu _y) \in \mathbb {R}^S$).

In order to minimize $-H$, Genevay et al. propose the following averaged stochastic gradient descent (ASGD) initialized with $\tilde{v}_1 = 0$

$$\begin{aligned} \left\{ \begin{array}{l} \tilde{v}_k = \tilde{v}_{k-1} + \frac{C}{\sqrt{k}} \nabla _v h(x_k,\tilde{v}_{k-1}) \quad \text {where} \ x_k \sim \mu \\ v_k = \frac{1}{k} (\tilde{v}_1 + \ldots + \tilde{v}_k ) . \end{array}\right. \end{aligned}$$

(6)

Since $\nabla _v h(x,\tilde{v}_{k-1})$ exists x-a.s. and is bounded, the convergence of this algorithm is ensured by [18, Theorem 7], in the sense $\max (H) - \mathbb {E}[H(v_k)] = \mathcal {O}(\frac{\log k}{\sqrt{k}})$. The authors of [8] also proposed to address a regularized transport problem with a similar method but we do not discuss it here due to lack of space.

3 A Bilevel Model for Texture Synthesis

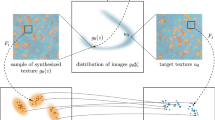
In this section, we introduce a bilevel model for texture synthesis that consists in first synthesizing a Gaussian version of the texture (with long range correlations but no geometric structures) and next transforming each patch of the synthesis with an optimal assignment (in order to enforce the patch distribution of the exemplar texture).

To be more precise, let us denote by $u : \varOmega \rightarrow \mathbb {R}^d$ the exemplar texture defined on a discrete domain $\varOmega \subset \mathbb {Z}^2$. Let $U : \mathbb {Z}^2 \rightarrow \mathbb {R}^d$ be the asymptotic discrete spot noise (ADSN) [4, 6] associated with u, which is defined as

$$\begin{aligned} \forall x \in \mathbb {Z}^2, \ U(x) = \bar{u} + \sum _{y \in \mathbb {Z}^2} t_u(y) W(x-y) \quad \text {where} \ {\left\{ \begin{array}{ll} \bar{u} = \frac{1}{|\varOmega |} \sum _{x \in \varOmega } u(x), \\ t_u = \frac{1}{\sqrt{|\varOmega |}} (u-\bar{u}) \mathbf {1}_{\varOmega } \end{array}\right. } \end{aligned}$$

(7)

where $\mathbf {1}_{\varOmega }$ is the indicator function, and where W is a normalized Gaussian white noise on $\mathbb {Z}^2$ (the convolution between $t_u$ and W is computed in Fourier domain). U is a stationary Gaussian random field whose first and second order moments are the empirical mean and covariance of the exemplar texture. In particular

$$\begin{aligned} \mathbb {E}[(U(x)-\bar{u})(U(y)-\bar{u})] = a_u(y-x) \quad \text {where} \quad a_u(z) = \sum _{x \in \mathbb {Z}^2} t_u(z)t_u(x+z)^T . \end{aligned}$$

(8)

Thus, U can be considered as a “Gaussianized” version of u, that has the correct correlations but no salient structures.

The second step consists in a patchwise operation. Let $\omega = \{-r,\ldots ,r\}^2$ be the patch domain with $r \in \mathbb {N}$. Let us denote by $\mu$ the distribution of patches of U, that is $\mu = \mathcal {N}(\bar{u},C)$ with $C(x,y) = a_u(y-x), \ x,y \in \omega$. Let us denote by $\nu$ the empirical distribution of patches of the exemplar texture u, that is $\nu = \frac{1}{|S|} \sum _{p \in S} \delta _p$, where $S = \{u_{|x + \omega } \ | \ x + \omega \subset \varOmega \} .$ Actually, in practice we approximate it with $\nu = \frac{1}{J} \sum _{j=1}^J \delta _{p_j}$ where $p_1, \ldots , p_J$ are $J=1000$ patches randomly drawn from the exemplar texture. Thus, $\mu$ and $\nu$ are two probability measures on $\mathbb {R}^D$ with $D = d(2r+1)^2$. Besides, $\mu$ is a Gaussian distribution that, except in degenerate cases, admits a probability density function $\rho$ with respect to the Lebesgue measure. Using the algorithm explained in Sect. 2.2, we compute the optimal assignment $T_v$ that realizes the semi-discrete OT from $\mu$ to $\nu$. We then apply this mapping $T_v$ to each patch of the Gaussian synthesis U, and we recompose an image V by averaging the “transported” patches: the value at pixel x is the average of values of x in all overlapping patches. More formally,

$$\begin{aligned} \forall x \in \mathbb {Z}^2, \quad&P_x = T_v(U_{|x+\omega }) , \end{aligned}$$

(9)

$$\begin{aligned} \forall x \in \mathbb {Z}^2, \quad&V(x) = \frac{1}{|\omega |} \sum _{h \in \omega } P_{x-h}(h) . \end{aligned}$$

(10)

Proposition 1

V is a stationary random field on $\mathbb {Z}^2$ and satisfies the following long-range independence property: if $\varGamma$ denotes the finite support of the auto-correlation function $a_u$ defined in (8), then for every $A,B \subset \mathbb {Z}^2$ such that ${(A-B) \cap (\varGamma + 4\omega ) = \varnothing }$ the restrictions $V_{|A}, V_{|B}$ are independent.

Proof

Since U is Gaussian, as soon as $x-y \notin \varGamma$. Therefore, if $x-y \notin \varGamma + 2\omega$, then and thus . After averaging we get as soon as $x-y \notin \varGamma + 4\omega$. The generalization to subsets A, B is straightforward.

This property is a guarantee of spatial stability for synthesis, meaning that the synthesis algorithm will not start to “grow garbage” as may do the method of [2]. We also have a guarantee on the patch distribution. Indeed, if $T_v$ is the true solution to the semi-discrete optimal-transport problem, then any patch $P_x$ is exactly distributed according to $\nu$. After recomposition, the distribution of $V_{|\omega }$ may not be exactly $\nu$ but is expected to be not too far away (as will be confirmed in Fig. 4). In this sense, V still respects the long range correlations (inherited from U) while better preserving the local structures.

Fig. 1.

Bilevel synthesis. Each row displays an exemplar texture, a sample of the associated ADSN model, and samples of the bilevel models obtained with $3 \times 3$ patch optimal assignment (OT) or patch nearest neighbor projection (NN), and the one with white noise initialization (WN). The OT assignment better preserves patch statistics than the NN projection. Besides, the last column illustrates the importance to start from a spatially correlated Gaussian model at the first level.

Fig. 2.

Influence of the patch size. On the middle column we display two original textures and on the other columns we display samples of the bilevel models with varying patch size using the patch optimal assignment (OT, first row) and the patch nearest neighbor projection (NN, second row). The OT performs in general better than a NN (it better preserves the color/patch statistics) but fails to reproduce complex geometry (like in the right example). (Color figure online)

Fig. 3.

Illustration of the semi-discrete OT and the convergence of ASGD (6) in 1D. (a) Semi-discrete Transport of a Gaussian distribution $\mu$ (red curve) towards a set of points $\nu$ (blue dots with $J=12$). The corresponding power diagram $\text {Pow}_v$ (in red lines) is compared to the Voronoi diagram $\text {Pow}_0$ (blue lines). The optimal transport plan $T_v$ (black lines) is compared to the nearest-neighbor matching $T_0$ (grey dotted lines). (b) ASGD in 1D. Evolution of the relative error, defined as $E(k) = \frac{{||v_{k} - v^\star ||}}{{||v^\star ||}}$ where $v^\star$ is the (closed-form) optimal solution and k the number of iterations. The curves are shown for $J = 10$, $10^2$, and $10^3$ points, using the same random sequence. (Color figure online)

Fig. 4.

Patch distribution (three first principal components). For the first image of Fig. 1 we plot the estimated distribution of patches in the three first principal components (columns) for different patch sizes (rows). The PCA transform is obtained on the exemplar patch distribution. We compare the patch distributions of the exemplar image (legend “ref”), of the synthesized image before patch recomposition (legend “OT”) and after (legend “OT recomp”), and of the transformed patch with nearest-neighbor projection (legend “NN”). Even if we only approximate the optimal transport mapping, it suffices to reproduce the reference patch distribution better than the NN projection.

4 Results and Discussion

In this section, we discuss experimental results of texture synthesis obtained with the proposed bilevel model. Figure 1 compares the synthesis results obtained with the Gaussian model before and after local transformation. One clearly observes the benefit of applying the optimal transport in the patch domain: it restores the color distribution of the exemplar and also creates salient features from the Gaussian content. In particular (Rows 1 and 3), it is able to break the symmetry of the color distribution which is a strong restriction of the Gaussian model.

Figures 1 and 2 demonstrate that the optimal assignment (OT) is better suited than the simple NN projection, as illustrated in Fig. 3(a). While these two operators project on the exemplar patches, the assignment is optimized to globally respect a statistical constraint. On Fig. 2 we also question the use of different patch sizes. The simple $1 \times 1$ case (which only amounts to apply a color map to the Gaussian field) is already interesting because it precisely respects the color distribution of the exemplar. Thus the bilevel model with $1\times 1$ patch can be seen as an extension of the ADSN model with prescribed marginal distributions. For a larger patch size, we observe only minor improvements of the model with slightly cleaner geometric structures.

One possible explanation could be the slow convergence speed in very high dimensions of the stochastic gradient descent scheme. In this non-smooth setting ($\nabla v(x,\cdot )$ is not Lipschitz continuous), the convergence rate given in [18] is only $\mathcal {O}(\tfrac{\log k}{\sqrt{k}})$. Besides, in our setting, we apply this algorithm for $10^6$ iterations with gradient step parameter $C=1$ in a very high-dimensional space $\mathbb {R}^D$ ($D=27$ for $3 \times 3$ RGB patches), and with discrete target distributions $\nu$ having large support ($J=|S \vert =10^3$). Updating all coordinates of v during the gradient descent requires to visit enough all the power cells. As a consequence, even in the 1D case, practical convergence can be very slow (see on Fig. 3(b) for $C=10$).

This means that in our experiments for texture synthesis, the convergence is not reached, and yet the OT solution provides better synthesis results than a simple NN approach, which is confirmed by examining the output patch distribution (Fig. 4). Interestingly, it is also true after patch recomposition (which remains to be properly justified).

The results obtained with this bilevel model raise several questions. First, one may very well question the use of the $\ell ^2$-distance for patch comparison, both in the transport problem and the recomposition step. It is already well known [11] that using other distances for recomposition may improve the visual quality of the results (less blur than with the $\ell ^2$ average). Also, it would be interesting to analyze more precisely the effect of the recomposition step on the patch distribution.