1 Introduction to Ionic Liquids

Ionic fluids consist entirely of ions. Within this category of materials, a new class of fluids has emerged in the last few decades under the term “Ionic Liquids” (ILs) [1, 2]. ILs differ from molten salts due to the fact that they are usually composed of one large asymmetric cation and one organic or inorganic anion and the combination of this type of ionic chemical structures leads to salts with lower melting temperatures. Following the description of Paul Walden who was one of the first [3, 4] to observe organic salts in 1914, ILs are considered as the salts that are in the liquid state at room temperature and by convention below \({100^\circ }\) C. In Fig. 14.1, some typical anions and cations are shown. There is a vast number of anions and cations that can be combined to form millions of potential ILs [5], revealing an enormous territory that despite having attracted great scientific interest in recent years, still remains largerly unexplored.

ILs are identified as novel designer solvents and advanced materials that can be utilized in a wide range of processes and applications. This fact is predominantly attributed to their great chemical tunability due to the diverse chemical structure of the anions and cations involved that enables the design of task specific ILs (TSILs) with controlled macroscopic properties. Apart from this important characteristic, ILs also combine a number of other exceptional properties [6,7,8,9] such as negligible vapour pressure, non-flammability, good thermal and electrochemical stability, wide range of temperatures over which they remain in the liquid state as well as very good solvation properties and in many cases high CO\(_2\) absorption and separation capacity [10, 11]. Their range of application constantly grows and extends from green chemistry and electrochemistry to biotechnology, environmental engineering and novel separation processes (Fig. 14.2).

Fig. 14.1
figure 1

Chemical structure of commonly used cations and anions

Full size image
Fig. 14.2
figure 2

Important properties of ILs and indicative range of applications

Full size image

2 Molecular Simulation

The plethora of ILs and the multitude of technologies in which ILs can be used, necessitates the unraveling of the underlying mechanisms [12] that are responsible for their macroscopic behaviour. Molecular simulation [13, 14] is based on the fundamental principles of statistical mechanics and provides a unique systematic way in this direction, enabling at the same time the prediction of a number of materials properties. Among the properties that can be calculated from molecular simulations are: (i) thermodynamic properties such as density, isothermal and isobaric compressibility, heat capacities, Gibbs free energy, Helmholtz free energy, activity coefficients, (ii) structural properties, (iii) dynamical and transport properties including local dynamics, diffusion coefficients, viscosities and ionic conductivities, (iv) surface and interfacial properties such as surface tension, (v) phase equilibria, (vi) mechanical properties and (vi) selectivity and permeability properties.

Various molecular simulation methods can be implemented depending on the materials under study and the time- and length-scales involved in the specific problem at hand, ranging from ab initio quantum mechanical methods, atomistic simulations (Monte Carlo, Molecular Dynamics, Transitions State Theory of Infrequent Events) to mesoscopic methods (Coarse-grained simulations, Kinetic Monte Carlo etc.). This chapter involves the computational study of ILs at the atomistic level using molecular dynamics (MD) simulation [15, 16].

The accuracy in the predictions of molecular simulation relies to a large extend on the force field used for the representation of the inter- and intramolecular interactions in the system. The interaction potential is typically of the form:

$$\begin{aligned} U=\sum _{bonds}k_b{\left( l-l_0\right) }^2+\sum _{angles}k_{\theta {}}{\left( \theta {}-{\theta {}}_0\right) }^2+\sum _{dihedrals}\sum _{n=1}^4k_{\chi {}}\left[ 1+\cos {\left( n\chi {}-\delta {}\right) }\right] + \nonumber \\ \sum _{impropers}k_{\psi {}}{\left( \psi {}-{\psi {}}_0\right) }^2+\sum _{\iota {}=1}^{n-1}\sum _{j>1}^n\left\{ 4\varepsilon _{ij}\left[ {\left( \frac{{\sigma {}}_{ij}}{r_{ij}}\right) }^{12}-{\left( \frac{{\sigma {}}_{ij}}{r_{ij}}\right) }^6\right] +\frac{q_iq_i}{4\pi {}{\varepsilon {}}_0r_{ij}}\right\} \end{aligned}$$
(14.1)

where l, \(\theta \), \(\chi \) and \(\psi \) denote bond length, bond angle, dihedral and improper angle, respectively, and the subscript “0” refers to the equilibrium values. In the dihedral potential term, parameter n is the multiplicity of the dihedral angle and \(\delta \) is the phase shift of the dihedral potential over the full range of rotation. Partial charges are denoted by \(q_{i}\), \({\varepsilon }_{0}\) is the vacuum permittivity and \(\varepsilon \), \(\sigma \) are the Lennard-Jones (LJ) parameters.

There are several difficulties and challenges in the molecular simulation of ILs [17,18,19]. The intense chemical diversity that characterizes the ions in ILs, prohibits the use of general force fields and necessitates the development and optimization of system specific interaction potentials. At the same time, complex inter-ionic and strong electrostatic interactions are present in these systems, hence polarizability and charge transfer effects have to be taken into account in order to simulate accurately their behaviour.

3 IL Structure and Dynamics

ILs exhibit a wide range of time scales in the relaxation of their various modes of motion. They retain their structural organization at much longer distances compared to ordinary liquids and are characterized by a sluggish dynamical behavior. ILs are glass-forming materials and therefore the prediction of their transport properties, especially at low temperatures, is a very demanding task. The discussion that follows focuses on molecular simulation results on ILs with imidazolium-based cations, specifically the 1-alkyl-3-methylimidazolium ([C\(_{n}\)mim\(^{+}\)]) cations, varying the cations alkyl tail, coupled with bis(trifluoromethylsulfonyl)imide ([TF\(_{2}\)N\(^{-}\)]) or tricyanomethanide ([TCM\(^{-}\)]) anions. MD simulations of several tens of nanoseconds were performed in a wide temperature range, and at atmospheric pressure using classical force fields that have been optimized and extensively validated for these two imidazolium-based IL families [20, 21].

3.1 Spatial Organization

ILs are heterogeneous fluids that due to the ionic interactions, form polar and non-polar domains [22]. Structural order is retained at long distances and is clearly depicted by intense oscillations in the radial distribution functions (RDF) [21, 23] of the ions center of mass. The anion-cation RDF reveals the strong ionic coupling of the counterions (Figs. 14.3 and 14.4) and exhibits multiple coordination shells (not in phase with the anion-anion RDF) while cation-cation RDFs show a much broader distribution. The spatial distribution function of the central carbon in [TCM\(^-\)] around [C\(_4\)mim\(^+\)] at 298K (using an iso-surface value equal to 8.1 nm\(^{-3}\)) is shown in Fig. 14.5.

Fig. 14.3
figure 3

Radial discribution functions (RDF) between the ions centers-of-mass of [C\(_{8}\)mim\(^{+}\)][TCM\(^{-}\)] IL at 298 K [21]

Full size image
Fig. 14.4
figure 4

Radial discribution functions (RDF) between the ions centers-of-mass of [C\(_{8}\)mim\(^{+}\)][TF\(_{2}\)N\(^{-}\)] IL at 398 K [23]

Full size image

The effect of the alkyl tail length on these properties was also investigated and tail aggregation phenomena (Fig. 14.6), which become more evident for the longer alkyl chain lengths, were detected by calculating radial distribution functions between different sites on the ions [20, 21, 23]. The microscopic local structure reflects a spatially heterogeneous environment that evolves from the interplay between short-range collective interactions (non-polar tail groups) and long-range electrostatic interactions (cation’s head groups). For a larger number of carbon atoms in the cation’s alkyl tail, liquid crystalline-like structures emerge [24].

Fig. 14.5
figure 5

Spatial distribution function of the central carbon in [TCM\(^-\)] around [C\(_{4}\)mim\(^+\)] (iso-surface value equal to 8.1 nm\(^{-3}\))

Full size image
Fig. 14.6
figure 6

Radial distribution function (RDF) between the terminal carbon atoms in the cation alkyl chain of [C\(_2\)mim\(^+\)][TCM\(^-\)] (black), [C\(_4\)mim\(^+\)][TCM\(^-\)] (red), [C\(_6\)mim\(^+\)][TCM\(^-\)] (blue) and [C\(_8\)mim\(^+\)][TCM\(^-\)] (green) at 298 K [21]

Full size image

3.2 Dynamical Heterogeneity

ILs are viscous liquids and their dynamics often resembles the one of the supercooled liquids. Cooperative motion and caging effects are present in these systems leading to heterogeneity phenomena [25,26,27,28,29,30] and to a non-Arrhenius behaviour. In glass-forming materials, at short times the particles are trapped in “cages” of adjacent particles, while the escape from the cage takes place at longer time scales as the temperature decreases. Complex and heterogeneous dynamics has been detected in ILs both experimentally [31,32,33,34,35] and computationally [20, 21, 35,36,37,38,39,40,41,42,43]

Fig. 14.7
figure 7

Non-Gaussian parameter \(\alpha _2(t)\) at 298, 348 and 398 K for a cation and b anion of [C\(_{8}\)mim\(^{+}\)][TF\(_{2}\)N\(^{-}\)] IL [20]

Full size image

An estimation of the time scales at which dynamic heterogeneity appears can be obtained from the non-Gaussian parameters \(\alpha _n(t), n=2,3, \ldots \) [44], with \(\alpha _2(t)\) defined as:

$$\begin{aligned} \alpha _2\left( t\right) =\dfrac{3\langle {\left| \mathbf {r}_i\left( t\right) -\mathbf {r}_i\left( t_0\right) \right| }^4 \rangle }{5 {\langle {\left| \mathbf {r}_i\left( t\right) -\mathbf {r}_i\left( t_0\right) \right| }^2\rangle }^2}-1 \end{aligned}$$
(14.2)

where \({\left| \mathbf {r}_i\left( t\right) -\mathbf {r}_i\left( t_0\right) \right| }\) represents the displacement of a particle (or an ion’s center of mass) at a time interval \(t-t{_0}\) and the brackets denote the mean over all particles. Non-zero values in \(\alpha _2(t)\) signify dynamical heterogeneity phenomena with the maximum being only indicative of the time of maximum heterogeneity, as the non-Gaussian behaviour may be preserved at much longer times [45, 46]. The ballistic motion is characterised by zero \(\alpha _2\left( t\right) \) values and \(\alpha _2\left( t\right) \) begins to increase at time scales associated with \(\beta \) relaxation, dropping again at the long time limit to zero (\(\alpha \) relaxation) [47].

The non-Gaussian parameter is plotted in Fig. 14.7 for the cation and the anion in [C\(_{8}\)mim\(^{+}\)][TF\(_{2}\)N\(^{-}\)] IL at three temperatures [20]. These plots clearly depict a non-Gaussian nature in both ions that is preserved at longer times, with the cation exhibiting a higher \(a_2\) peak than the anion. This is also true for the ILs with the shorter alkyl tails [20] and is indicative of a more pronounced heterogeneous behaviour for the cation. The maxima obtain a higher value as the temperature decreases and at longer times. In case of [C\(_{n}\)mim\(^{+}\)][TCM\(^{-}\)], the anion is the one with the more intense maximum [21, 48] as shown in Fig. 14.8 for [C\(_{8}\)mim\(^{+}\)][TCM\(^{-}\)] cation and anion at 298 K.

Fig. 14.8
figure 8

Non-Gaussian parameter \(\alpha _2(t)\) for the cation (red) and the anion (black) of [C\(_{8}\)mim\(^{+}\)] [TCM\(^{-}\)] IL at 298K [21]

Full size image

A quantification of the dynamic heterogeneity can be achieved by measuring a time-space correlation function corresponding to a classical expression of van Hove function [49]:

$$\begin{aligned} G\left( {\mathbf {r}},t\right) =\dfrac{1}{N}\left\langle \sum _{i=1}^{N}\sum _{j=1}^{N} \delta \left( \mathbf {r} - \mathbf {r}_i\left( t \right) + \mathbf {r}_j\left( 0 \right) \right) \right\rangle \end{aligned}$$
(14.3)

where \(\delta \) is Dirac delta and the brackets denote time average from an equilibrium trajectory in phase space. Therefore, although \(G\left( {\mathbf {r}},t\right) \) is a dynamic function, it is simultaneously a measure of an equilibrium property. The function \(G\left( {\mathbf {r}},t\right) \) is proportional to the probability that a particle is located at position \(\mathbf r\) at time t given that a particle was located at \(\mathbf r(0)\) at \(t=0\) and can be separated in a self (\(G_s\)) for \(i=j\) and a distinct part (\(G_d\)) for \(i \ne j\):

$$\begin{aligned} G\left( {\mathbf {r}},t\right) =G_s\left( {\mathbf {r}},t\right) +G_d\left( {\mathbf {r}},t\right) \end{aligned}$$
(14.4)

Single-ion dynamics can be quantified by the self-part of the van Hove correlation function [50] that provides the distribution of particle dispacements for different times:

$$\begin{aligned} G_s\left( {\mathbf {r}},t\right) =\dfrac{1}{N}\left\langle \sum _{i=1}^{N}\sum _{j=1}^{N} \delta \left( \mathbf {r} - \mathbf {r}_i\left( t \right) + \mathbf {r}_i\left( 0 \right) \right) \right\rangle \end{aligned}$$
(14.5)

At time \(t=0\), \(G_s\left( {\mathbf {r}},0\right) =\delta \) and for all times, it is normalized by:

$$\begin{aligned} \int G_s\left( {\mathbf {r}},t\right) d\mathbf {r}=1 \end{aligned}$$
(14.6)

At the long time limit, the particle is independent of its initial position:

$$\begin{aligned} \lim _{r\rightarrow \infty }G_s\left( {\mathbf {r}},t\right) = \lim _{t\rightarrow \infty }G_s\left( {\mathbf {r}},t\right) =\frac{1}{V}\approx 0 \end{aligned}$$
(14.7)

where V is the system volume. The probability density that a particle displaces by distance r [51] is given by:

$$\begin{aligned} g_s(r,t)=\int _{\theta =0}^{\pi } \int _{\phi =0}^{2\pi } G_s\left( {\mathbf {r}},t\right) r^2\sin \theta d\phi d\theta \end{aligned}$$
(14.8)

and for an isotropic medium \(G_s\left( {\mathbf {r}},t\right) =G_s\left( r,t\right) \) and \(g_s(r,t)=4 \pi r^2 G_s\left( {r},t\right) \).

In the case of Fickian diffusion, the self-part of the Van Hove function follows the Gaussian approximation [52]:

$$\begin{aligned} G{_s}{^g}\left( r,t\right) =\left[ \dfrac{3}{2\pi \left\langle \varDelta r^2(t) \right\rangle }\right] ^{\frac{3}{2}} \exp \left[ \frac{-3r^2}{2\left\langle \varDelta r^2(t) \right\rangle } \right] \end{aligned}$$
(14.9)

with \(\left\langle \varDelta r^2(t) \right\rangle \) being the mean square displacement (MSD) at a time interval t.

Fig. 14.9
figure 9

Self-part of the Van Hove function \(G_s\left( r,t\right) \) as a function of distance at 298 K plotted against the expected Gaussian distribution for a the cation and b the anion of [C\(_6\)mim\(^+\)][TCM\(^-\)]

Full size image

In Fig. 14.9, the self-part of the Van Hove function \(G_s\left( r,t\right) \) for (a) the cation and (b) the anion of [C\(_6\)mim\(^+\)][TCM\(^-\)] [21] is plotted against the expected Gaussian distribution at 298 K and for t \(=\) 100, 500, 1000, 3000 ps. Deviations of the \(G_s\left( r,t\right) \) from the expected Gaussian are evidence of dynamic heterogeneity, which for the systems under study is present at time intervals typically ranging from a few ps up to several ns. For the longer alkyl tail IL, the non-Gaussian behavior persists at longer times, while these deviations are diminished as the temperature is increased. A multifractal character has been also reported [42] in relation to the heterogeneous nature of ILs.

Fig. 14.10
figure 10

Radial distribution functions (RDF) between the centers of mass of slow anions slow cations (magenta), fast anions fast cations (blue) and fast slow anions and cations (black) plotted against the total RDF (red) calculated for a [C\(_6\)mim\(^+\)][TCM\(^-\)] [21] and b [C\(_6\)mim\(^+\)][TCM\(^-\)] at 298 K for t \(=\) 500 ps. The red line corresponds to the radial distribution functions between the anion-cation centers of mass as calculated from all ions

Full size image

The divergence between the \(G_s\left( r,t\right) \) and \(G{_s}{^g}\left( r,t\right) \) curves depicts the existence at intermediate times of ions with “faster” or “slower” mobility than expected based on that distance that each ion has travelled at time t. The crossing points of the two curves at short and long distances are used to identify dynamically distinguishable ions at a specific time interval [47].

The spatial correlation of these subsets of fast and slow ions manifests the occurrence of clustering phenomena between mobile and immobile ions. This is clearly shown in Fig. 14.10, in which the RDFs between the centers of mass of slow anions – slow cations, fast anions – fast cations and fast – slow anions and cations are shown for (a) [C\(_4\)mim\(^+\)][TCM\(^-\)] [21] and (b) [C\(_6\)mim\(^+\)][TCM\(^-\)] at 298 K for t \(=\) 500 ps. These RDFs are plotted against the RDF that corresponds to the anion-cation centers of mass as calculated from all ions, exhibiting maxima at the same distances with much higher peaks, though, in the case of ions of same mobility. The evolution of the clustering tendency in time is shown in Fig. 14.11 as calculated for fast cations and fast anions of [C\(_8\)mim\(^+\)][TF\(_2\)N\(^-\)] at 298 K and t = 10, 50, 100, 300 and 1000 ps [20].

Fig. 14.11
figure 11

Radial distribution functions between the centers of mass of fast cations and fast anions calculated at 298 K for t \(=\) 10, 50, 100, 300 and 1000 ps of [C\(_8\)mim\(^+\)][TF\(_2\)N\(^-\)] [20]

Full size image

3.3 Diffusional Anisotropy

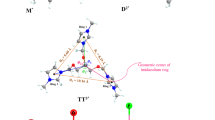
Anisotropy in the ions translational motion is present in some ionic species in ILs [20, 21, 40, 53]. Such phenomena can be traced by examining the ions diffusional motion along specific axes dictated by the geometry of the ions. In Fig. 14.12, four axes are defined for the case of imidazolium-based cations: the vector NN that connects the two nitrogen atoms in the imidazolium ring, the normal vector to the imidazolium ring, the vector NNp that is perpendicular to the former two vectors and the end-to-end vector N3-Ct of the alkyl tail.

Fig. 14.12
figure 12

The vectors defined on the imidazolium-based cation along which the translational motion of the center of mass was analyzed

Full size image
Fig. 14.13
figure 13

Mean square displacement (MSD) at 298 K calculated along the direction of the vector that is normal to the imidazolium plane (black), the vectors NN (red) and NNp (green), and along the the end-to-end vector N3-Ct of the alkyl tail (blue) of the cation compared to the 1/3 of the total MSD of the center of mass (magenta dashed line) for a [C\(_2\)mim\({}^{+}\)][TCM\({}^{-}\)], b [C\({}_4\)mim\({}^+\)][TCM\({}^-\)], c [C\({}_6\)mim\({}^+\)][TCM\({}^-\)] and d [C\({}_8\)mim\({}^+\)][TCM\({}^-\)] [21]

Full size image

Diffusional anisotropy can be extracted by comparing the MSD along each axis to the one third of the total MSD, as shown in Fig. 14.13 for the cations in [C\(_2\)mim\(^+\)][TCM\(^-\)], [C\(_4\)mim\(^+\)][TCM\(^-\)], [C\(_6\)mim\(^+\)][TCM\(^-\)] and [C\(_8\)mim\(^+\)][TCM\(^-\)] ILs at 298K. In case of an isotropic diffusional motion the MSD along any axis would coincide with the total MSD/3. For all systems presented, there is a more facile movement along the NN and N3-Ct vectors, which becomes more intense for the cations with the longer alkyl tails. For [C\(_8\)mim\(^+\)][TCM\(^-\)] IL in particular, the movement along the N3-Ct vector deviates from the one of NN vector, exhibiting at 1.5ns an MSD almost by a factor of two higher than the 1/3 of the total MSD. The movement along the NNp vector and the vector that is normal to the imidazolium plane appears to be rather hindered compared to the other two directions. At 298K, diffusional anisotropy is maintained over long timescales that extend even to the Einstein regime. Similar behaviour is observed for the [C\(_n\)mim\(^+\)][TF\(_2\)N\(^-\)] ILs in which, apart from the cation, there is also a preferential movement along the direction of the vector that connects the two sulfurs of the [TF\(_2\)N\(^-\)] anion [20].

3.4 Transport Properties

Long MD simulations in the order of several tens of nanoseconds have been performed for the determination of the transport properties of the ILs under study. The self-diffusion coefficients of the ions were calculated using the Einstein relation [54]:

$$\begin{aligned} D=\frac{1}{2d}\lim _{t\rightarrow \infty }\frac{d}{dt}\left\langle \left| \mathbf {r}_i(t) -\mathbf {r}_i(0) \right| ^2 \right\rangle \end{aligned}$$
(14.10)

where the brackets indicate the mean square displacement (MSD) over all ions’ centers of mass and d is the dimensionality of the conducted diffusivity.

Fig. 14.14
figure 14

Self-diffusion coefficients [21, 48] of the anion (squares) and the cation (circles) versus temperature for [C\(_8\)mim\(^+\)][TCM\(^-\)] IL. The open points correspond to NMR experimental measurements for the cation [55]

Full size image

The determination of the diffusion coefficients from an MD simulation presupposes that the system is simulated long enough, so that it has reached the Fickian regime. Normal diffusivity can be identified by a slope equal to unity in the log(MSD) versus log(t) plot. Self-diffusion coefficients were calculated for imidazolium-based ILs under study [20, 21, 48]. The self-diffusion coefficients for the ions in [C\(_8\)mim\(^+\)][TCM\(^-\)] IL are shown in Fig. 14.14 at various temperatures and at atmospheric pressure. The calculated diffusivities for the cation are in excellent agreement with NMR experimental measurements [55] of the same IL system, confirming the ability of the recently optimized force field [21] to reproduce the properties of the [C\(_n\)mim\(^+\)][TCM\(^-\)] IL family with great accuracy. No experimental results are currently available for the [TCM\(^-\)] anion.

Fig. 14.15
figure 15

Viscosity calculations from MD simulations (full points) [21, 48] as a function of temperature plotted against experimental data (lines with open points) [48, 56] for [C\(_8\)mim\(^+\)][TCM\(^-\)]

Full size image

Shear viscosity was extracted from the autocorrelation function of the pressure tensor using the Green-Kubo relation:

$$\begin{aligned} \eta =\frac{V}{k_BT} \int _{0}^{\infty }{dt}\left\langle P_{\alpha \beta }(t) P_{\alpha \beta }(0)\right\rangle \end{aligned}$$
(14.11)

where \(P_{\alpha \beta }(t)\) is the \(\alpha \beta \)-element of the pressure tensor at time t (\(\alpha \ne \beta \)). The temperature dependence of the viscosity is captured very well [20, 21, 48] for all ILs with good agreement with available experimental data. In Fig. 14.15, viscosities calculated from MD in a wide temperature range for [C\(_8\)mim\(^+\)][TCM\(^-\)] are plotted against experimental measurements exhibiting a very good agreement.

4 Conclusions

Ionic fluids inherently carry a higher degree of complexity than systems comprised of neutral species. ILs, in particular, exhibit an exceptional combination of properties that originate significantly from their dual organic and ionic nature. A fundamental understanding of the diverse interactions and the microscopic mechanisms that give rise to the non-trivial spatial and dynamical behaviour in ILs is required, especially considering more complex IL systems such as multi-compound IL fluids, ILs as gas separation media [10, 57] and under confinement in solid substrates [58, 59] or IL-IL mixtures [60, 61]. Theoretical and computational studies combined in a synergistic manner with high-resolution experimental techniques should target in elucidating the underlying complex phenomena, extending the fundamental knowledge and revealing the chemical structure – property relations in this class of advanced materials with enormous applicability in a wide range of state-of-the art technologies.