Keywords

1 Introduction

Service time of demands in classical models of Inventory Systems (IS) is usually assumed to be equal to zero (or inconsiderable). However, in real systems this assumption does not always hold. Therefore, IS models where demand service time is a positive quantity were introduced. These models with positive demand service time are called Queueing-Inventory Systems (QIS) and were first studied in [1, 2]. Detailed review of QIS models is given in [3].

In QIS model, usually, it is assumed that after service completion the inventory level decreases. However, in works [4, 5] are given the real systems where this condition does not hold and the models of such QIS are studied.

In this paper, studied QIS models are different from the models in [4, 5] in following moments. Firstly, unlike in [4, 5], the QIS models with perishable inventory are studied (Perishable QIS, PQIS). Secondly, we assume that the arrived demands enter the queue even when the inventory level is zero, while they become impatient in the queue. Thirdly, the mean service time for demands that acquire the item is different than for the demands do not acquiring the item. Finally, it is assumed that the replenishment orders are placed according to \((S-1, S)\) policy.

PQIS models have been extensively studied and developed in a peer-reviewed scientific literature. Numerous literature references on this subject are given in the review works [6,7,8,9], as well as, in monography [10]. The results of analysis of PQIS models with positive service time performed in [11,12,13,14,15,16,17] could be found in [18]. It should be noted that, the order replenishment policies (ORP) used in the most works belong to a (s, S) policy class.

At the same time, studying PQIS models with positive service time using different ORP in order to find the most optimal policy is a popular research subject. In this paper, \((S-1,S)\) policy is used. According to this policy, when inventory level decreases (after demand service completion or inventory perishing) an order of unit size is placed.

Some serious results of PQIS analysis with \((S-1,S)\) policy could be found in [19,20,21]. In these works, service time is assumed to be equal to zero, moreover in [19] the inventory level is right continuous. Analysis of available literature shows that the PQIS models with positive service time and \((S-1,S)\) policy are not studied. Therefore, methods of exact and asymptotic analysis of PQIS model with finite queue length are given in this paper.

The paper is organized as follows. In Sect. 2, the description of the investigated PQIS model is presented and main performance measures are introduced. Exact and approximate methods to calculate the steady-state probabilities as well as performance measures are developed in Sect. 3. High accuracy of the developed approximate formulas by using numerical experiments are demonstrated in Sect. 4. The results of solution of the problem for choosing optimal server rate to minimize the total cost are shown as well. Conclusion remarks are given in Sect. 5.

2 Model Description and Problem Statement

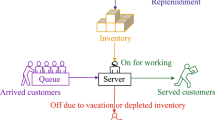
The studied system has a finite storage warehouse of size S and continuous inventory level monitoring. Each inventory item independently perishes after a random time with exponential distribution function with parameter \(\gamma \), \(\gamma > 0\). At the same time, the item reserved for the demand service is not perishable. In other words, inventory level decreases not only after the demand service, but also because of the item perishing.

Demands are arriving into the system according to Poisson arrival process with the intensity \(\lambda \) for acquiring the inventory items. For the simplicity, we assume that the demands acquiring the item requires unit resource, that is, after service completion of such demands inventory level decreases for a single unit.

If the inventory level is positive upon arrival moment the demand is taken for the service with probability 1 if the server is idle by that time; otherwise, demand joins the queue. Demands are assumed to join the queue even if the inventory level is zero. If upon arrival moment of the demand the inventory level is zero, then according to Bernoulli trial with the parameter \(\phi _1\) it joins the queue and waits for inventory replenishment for a certain time, while with the probability \(\phi _2\) demand leaves the system being unserved, \( \phi _1+\phi _2 = 1 \). In that cases, demands in queue are impatient, that is, if inventory level is zero every demand independently waits in the queue for an exponentially distributed random time with mean \(\tau ^{-1}\).

Queues with finite length is studied in this paper. In the model with finite queue, it is assumed that if at the moment of demand arrival there are N demands in the system (including the one that is being served) then it is lost with probability 1.

After service completion according to Bernoulli trial with parameter \(\sigma _1\) demand refuses to acquire the item, while with probability \(\sigma _2\) acquires, where, \(\sigma _1+\sigma _1=1\). If the demand refuses to acquire the item its service time has exponential distribution with mean \(\mu _1^{-1}\); otherwise its service time is exponentially distributed with mean \(\mu _2^{-1}\), \(\mu _2<\mu _1\).

Inventory replenishment is performed according to \((S-1,S)\) policy with delay, that is, the order lead time is a positive random quantity that has an exponential distribution with mean \(\nu ^{-1}\). So, if the number of pending orders at the moment is n, then the replenishment rate is \(n\nu \).

Problem is to find the joint distributions of inventory level and number of demands in the system. Solution of this problem will allow to calculate the performance measures of PQIS model, as well as, to perform its cost analysis. The main performance measures are the average values of the following quantities: inventory level \(S_{av}\), inventory perishing rate \(\varGamma _{av}\), average reorder rate RR, loss rate of the customers due to balking \(RL_b\), loss rate of the demands due to reneging \(RL_r\), average queue length \(L_{av}\).

3 Methods for Calculation of the System Performance Measures

System is modeled by 2-D MC with the states (m, n), where m - is inventory level, n - is number of demands in the system. State Space (SS) of the system is defined as follows:

$$\begin{aligned} E=\{ (m,n): m=0,1,\dots ,S, n=0,1,\dots ,N \} \end{aligned}$$
(1)

Transition rate from the state \((m_1,n_1) \in E\) to \((m_2,n_2) \in E\) is denoted by \(q((m_1,n_1),(m_2,n_2))\). All of these rates form generator matrix (Q-Matrix) of the given 2-D MC. Let’s consider the problem of their calculation.

Transition between the states of the system are related to the following events: (i) demand arrival, (ii) service completion, (iii) product perishing, (iv) leaving the queue due to impatience and (v) inventory replenishment.

Taking into account assumed replenishment policy, following cases are considered while determining the initial state \((m_1,n_1) \in E\) of the system: (1) \(m_1>0\); (2) \(m_1=0\).

When \(m_1>0\) transition from the state \((m_1,n_1)\) because of the events (iv) is impossible, as in that case, demands in the queue are patient. Other transitions are defined as follows.

If the number of demands in system is less than N at the moment of demand arrival (event (i)) then the number of demands increases by one unit, that is, transition to the state \((m_1,n_1+1) \in E\) occurs; intensity of that transition is equal to \(\lambda \). If after service completion the demand refuses to acquire the item (event of type (ii)), number of demands in the system is decreased by one, while inventory level remains unchanged, i.e. transition to the state \((m_1,n_1-1) \in E\) occurs and intensity of such transition is \(\mu _1\sigma _1\). If after service completion demand acquires the item (event of type (ii)), then both number of demands and inventory level decreases by one, that is, transition to the state \((m_1-1,n_1-1) \in E\) occurs; intensity of such transition is \(\mu _2(1-\sigma _1)\). After inventory item perishes (event of type (iii)) transition to the state \((m_1-1,n_1) \in E\) occurs, the intensity of such transition is equal to \(m_1\gamma \) for case \(n_1=0\) and to \((m_1-1)\gamma \) for case \(n_1>0\). At the moment of order replenishment (event of type (v)) transition to the state \((m_1+1,n_1) \in E\) occurs; intensity of such transition is equal to \((S-m_1)\nu \).

Consequently, for the case \(m_1>0\), non-negative elements of Q-matrix are defined as follows:

$$\begin{aligned} q((m_1,n_1),(m_2,n_2)) = {\left\{ \begin{array}{ll} \lambda , &{} \text{ if } m_2=m_1, \, n_2=n_1+1 \\ \mu _1\sigma _1, &{} \text{ if } m_2=m_1, \, n_2=n_1-1 \\ \mu _2\sigma _2, &{} \text{ if } m_2=m_1-1, \, n_2=n_1-1 \\ m_1\gamma , &{} \text{ if } m_2=m_1-1, \, n_2=n_1=0 \\ (m_1-1)\gamma , &{} \text{ if } m_2=m_1-1, \, n_1>0, \, n_2=n_1 \\ (S-m_1)\nu , &{} \text{ if } m_2=m_1+1, \, n_2=n_1 \\ 0, &{} \text{ otherwise } \end{array}\right. } \end{aligned}$$
(2)

Now, let at the initial state \((m_1,n_1) \in E\) holds the condition \(m_1=0\). In this case transition from the current state because of the events (ii) and (iii) is impossible, as in these states demand service could not be performed because of zero inventory level. In these states transitions for the events (i) and (v) are defined analogously as in (2) and the arrived demand joins the queue with the probability \(\phi _1\). Transition intensities because of demand impatience (event of type (iv)) are defined as follows: after the demand leaves the system because of impatience demand count decreases by one unit, while, inventory level remains unchanged, that is, transition to the state \((0,n_1-1) \in E\) occurs; intensity of such transition is equal to \(n_1\tau \). At the moment of the order replenishment transition to the state \((1,n_1)\) occurs; intensity of such transition is equal to \(S\nu \). So, for the case \(m_1=0\) non-negative elements of Q-matrix are defined as follows:

$$\begin{aligned} q((0,n_1),(m_2,n_2)) = {\left\{ \begin{array}{ll} \lambda \phi _1, &{} \text{ if } m_2=0, \, n_2=n_1+1 \\ n_1\tau , &{} \text{ if } m_2=0, \, n_2=n_1-1 \\ S\nu , &{} \text{ if } m_2=1, \, n_2=n_1 \\ 0, &{} \text{ otherwise } \end{array}\right. } \end{aligned}$$
(3)

It is clear from the formulas (2)−(3) that 2-D MC is irreducible and there exists stationary mode. Consequently, the steady-state probabilities p(m, n), \((m,n) \in E\) are the only solution of the system of balance equations (SBE), that are constructed based on the formulas (2) and (3). This SBE represents the set of linear equations of dimension \((S+1) \times (N+1)\). Due to its large dimension and obviousness the explicit form of SBE is not given in this work.

Required performance measures of the given PQIS are calculated through the steady state probabilities. So, the mean inventory level and the average number of demands in the system are calculated as the mathematical expectation of the corresponding random variables:

$$\begin{aligned} S_{av}=\sum \limits _{m\,=\,1}^S{ m \sum \limits _{n\,=\,0}^N {p(m,n);} } \end{aligned}$$
(4)
$$\begin{aligned} L_{av}=\sum \limits _{n\,=\,1}^N{ n \sum \limits _{m\,=\,0}^S {p(m,n);} } \end{aligned}$$
(5)

As the inventory item reserved for the servicing demand could not perish the average perishing intensity is calculated as follows:

$$\begin{aligned} \varGamma _{av} = \gamma \left( \sum \limits _{m\,=\,1}^S { (mp(m,0) + \sum \limits _{n\,=\,1}^N {(m\,-\,1)p(m,n)} ) } \right) \end{aligned}$$
(6)

Replenishment order is placed either every time after servicing the demands that require the inventory item or after the item perishing. Consequently, the average reorder rate is calculated as follows:

$$\begin{aligned} RR = \sum \limits _{m\,=\,1}^S ( m\gamma p(m,0) + ( (m-1)\gamma + \mu _2 \sigma _2 )( 1 - p(m,0) ) ) \end{aligned}$$
(7)

As it is noted above, the balking occurs if at the moment of demand arrival the waiting hall (queue) is full. Therefore, the average loss rate of demands due to balking \(RL_b\) is given by:

$$\begin{aligned} RL_b = \lambda \left( \sum \limits _{m\,=\,0}^S p(m,N) + \phi _2 \sum \limits _{n\,=\,0}^{N\,-\,1} p(0,n) \right) \end{aligned}$$
(8)

The reneging occurs only in the case of zero inventory level. Therefore, the average loss rate of the demands due to reneging \(RL_r\) is given by:

$$\begin{aligned} RL_r = \tau \sum \limits _{n\,=\,1}^{N} p(0,n) \end{aligned}$$
(9)

Analytic solution for the system could not be found due to the complexity of Q-matrix. The known numerical methods of linear algebra are only applicable for the Markov Chains of the moderate dimensions and become useless for the chains of larger dimension.

Therefore, approximate method [18] is used in this work that allows to perform asymptotic analysis of the performance measures of the given system for the large sizes of the inventory level and waiting hall for demands.

This method could be effectively applied for the models that work under large load; in other words, it is assumed that demand arrival intensity is far larger than the product perishing and replenishment rate, that is, \(\lambda \gg max\{ \gamma , \nu \}\). It should be noted that, this assumption is hold in many real PQIS. Moreover, as it was stated above, \(\mu _1 \gg \mu _2\).

Taking into account the above conditions, let’s consider the following split of the initial state space (1):

$$\begin{aligned} E = \bigcup \limits _{m\,=\,0}^S {E_m}, \, E_{m_1} \bigcap E_{m_2} = 0, \, m_1 \ne m_2 \end{aligned}$$
(10)

where \(E_m=\{ (m,n): n=0,1,\dots ,N \}, \, m=0,1,\dots ,S\).

Additionally, we conclude that the transition intensities inside a row are far larger than the transition intensities between the rows. Further, based on the split (10) of the initial state space (1), the following merge function is defined:

$$U((m,n))=\langle m \rangle $$

where \(\langle m \rangle \) is merged state that consists of all the states \(E_m, \, m=0,1,\dots ,S\). Let’s denote \(\mathrm {\varOmega } = \{ \langle m \rangle : m=0,1,\dots ,S \}\).

Approximate values of steady state probabilities \(\tilde{p}(m,n), \, (m,n) \in E\) of the current model are defined as follows (see [18]):

$$\begin{aligned} \tilde{p}(m,n)=\rho _m(n)\pi (\langle m \rangle ) \end{aligned}$$
(11)

where \(\rho _m(n)\) - is the probability of state (m, n) inside the merged model with the state space \(E_m\) and \(\pi (\langle m \rangle )\) - is the probability of a merged state \(\langle m \rangle \in \varOmega \).

Steady-state probabilities of the split and merged models are calculated as follows.

In the all states (m, n) within the split model with the state space \(E_m\) the first component is a constant, therefore, all the states of such class is determined only by the second component. Consequently, in the analysis of the split models with the state space \(E_m\) the state \((m,n) \in E_m\) could only be specified with the second component, so for the convenience, while studying the split models with the state space \(E_m\) its states (m, n) are simply denoted by \(n, \, n=0,1,\dots ,N\).

It is concluded from the formulas (2) that the state probabilities within all the split models with the state space \(E_m, \, m=1,2,\dots ,S\) are the same as in classical model M / M / 1 / N with load \(a=\lambda / \mu _1\sigma _1\), i.e.:

$$\begin{aligned} \rho _m(n)=a^n \frac{1-a}{1-a^{N+1}}, \, m=1,2,\dots ,S \end{aligned}$$
(12)

Remark 1

As the quantities \(\rho _m(n)\) do not depend on the index \(m, \, m=1,2,\dots ,S\) below these indexes are omitted.

It is concluded from the formula (3) that the state probabilities within the merged model with the state space \(E_0\) are the same as in Erlang model M / M / N / 0 with load \(b=\lambda \phi _1 / \tau \), that is:

$$\begin{aligned} \rho _0(n) = \frac{\theta (n)}{\sum \limits _{n\,=\,0}^N {\theta (j)}}, \, n=0,1, \dots ,N \end{aligned}$$
(13)

Further, the following notation is accepted: \(\theta (j) = \displaystyle \frac{b_j}{j!}\)

Let’s denote the transition intensity from the merged state \(\langle m_1 \rangle \) to another merged state \(\langle m_2 \rangle \) with \(q(\langle m_1 \rangle ,\langle m_2 \rangle ), \, \langle m_1 \rangle ,\langle m_2 \rangle \in \varOmega \). According to [18] these parameters are defined as follows:

$$\begin{aligned} q(\langle m_1 \rangle ,\langle m_2 \rangle ) = \sum _{\begin{array}{c} (m_1,n_1) \in E_{m_1},\\ (m_2,n_2) \in E_{m_2} \end{array}} { q((m_1,n_1),(m_2,n_2))p(m_1,n_1) } \end{aligned}$$
(14)

Taking into account (2), (3) and (12), (13), (14) after some transformations we found that the given intensities are calculated as follows:

$$\begin{aligned} q(\langle m_1 \rangle , \langle m_2 \rangle ) = {\left\{ \begin{array}{ll} \varLambda (m_1), &{} \text{ if } m_2=m_1-1 \\ (S-m_1)\nu , &{} \text{ if } m_2=m_1+1 \\ 0, &{} \text{ otherwise } \end{array}\right. } \end{aligned}$$
(15)

where \(\varLambda (m_1)=m_1\gamma \rho _0 + (1-\rho (0))(\mu _2\sigma _2 + (m_1-1)\gamma ), \, m_1=1,2, \dots , S\)

Then from (15) we get:

$$\begin{aligned} \pi (\langle m \rangle ) = \frac{S!\nu ^m}{(S-m)!} \frac{\pi (0)}{ \prod \limits _{i\,=\,1}^m \varLambda (i) }, \, m=1,2, \dots , S \end{aligned}$$
(16)

where \( \displaystyle { \pi (0) = \left( \sum \limits _{m\,=\,0}^S \frac{S!\nu ^m}{(S-m)!} \frac{1}{ \prod \limits _{i\,=\,1}^m \varLambda (i) } \right) ^{-1} }\)

Remark 2

We assume that \( \displaystyle { \prod \limits _{i\,=\,m}^n x_i = 1, \, \text{ if } m > n }\)

Afterwards, taking into account (12), (13), (14), (15), (16) from (11) approximate joint distributions \(\tilde{p}(m,n), \, (m,n) \in E\) of inventory level and number of demands in the system are found. Using these probabilities after some transformations from (4), (5), (6), (7), (8), (9) following formulas are obtained for the calculation of performance measures:

$$\begin{aligned} S_{av}\approx & {} \sum \limits _{m\,=\,1}^S {m \pi (\langle m \rangle )}\\ \varGamma _{av}\approx & {} \gamma \sum \limits _{m\,=\,1}^S {\pi (\langle m \rangle ) (m\rho (0) + (m-1)(1-\rho (0))) }\\ RR\approx & {} \sum \limits _{m\,=\,1}^S { ( m\gamma \rho (0) \pi (m) + (1-\rho (0)\pi (\langle m \rangle )) ( (m-1)\gamma + \mu _2\sigma _2 ) ) }\\ RL_b\approx & {} \lambda ( \rho (N)(1-\pi (\langle 0 \rangle )) + \pi (\langle 0 \rangle ) ( \rho _0(N)+ \phi _2(1-\rho _0(N)) ) )\\ RL_r\approx & {} \tau \pi (\langle 0 \rangle ) \sum \limits _{n\,=\,1}^N {n \rho _0(n)}\\ L_{av}\approx & {} \pi (\langle 0 \rangle ) \sum \limits _{n\,=\,1}^N {n\rho _0(n)} + (1-\pi (0))\sum \limits _{n\,=\,1}^N {n\rho (n)} \end{aligned}$$

4 Numerical Results

Due to the limitations to the volume of the work, only accuracy of the steady-state probabilities of the initial 2-D MC and performance measures is considered. It should be noted that, the evaluation of the accuracy of given formulas analytically is impossible. Therefore, comparative analysis of the obtained numerical results is used. The accuracy of the approximate values are evaluated by using following norms:

Maximum absolute value of differences:

$$\begin{aligned} \left\| N\right\| _1 = \max _{\begin{array}{c} n \in E \end{array}} |p(n) - \tilde{p}(n)| \end{aligned}$$
(17)

Cosine similarity:

$$\begin{aligned} \left\| N\right\| _2 = \frac{\sum \limits _{n \in E} {p(n) \tilde{p}(n)} }{ \sqrt{ \sum \limits _{n \in E} {(p(n))^2} } \sqrt{ \sum \limits _{n \in E} {(\tilde{p}(n))^2} } } \end{aligned}$$
(18)

Jaccard coefficient [22]:

$$\begin{aligned} \left\| N\right\| _3 = \frac{ \sum \limits _{n \in E} { \min \{p(n),\tilde{p}(n)\} } }{ \sum \limits _{n \in E} { \max \{p(n),\tilde{p}(n)\} } } \end{aligned}$$
(19)
Table 1. Estimation of accuracy of the steady-state probabilities versus various norms
Full size table

Results of the comparative analysis of the steady-state probabilities for the exact and approximate methods are given in Table 1. The initial parameters of the system are assumed as follows: \(\mu _1=15,\mu _2=3,\gamma =2,\nu =1,\tau =0.5,\sigma _1=0.3,\phi _1=0.6\)

The exact values of steady-state probabilities are calculated from corresponding balance equations using MATLAB package. Solving time of balance equations depends on its dimension and takes several hours for \(S \times N>5000\) (e.g.: for \(S=50\) and \(N=100\) with quad core CPU Core i7 2.40 Ghz and 8 GB RAM at least 3–4 h are required). It should be noted that, in the same PC approximately 3–4 s are needed for the calculation of performance measures for \(S=100\) and \(N=500\) while using the approximate method.

It is obvious from the Table 1 that the higher the arrival intensity is, the better accuracy of the calculated steady state probabilities of the model with respect to all norms is acquired, that is, with the increase of the arrival intensity the norm (17) is approaching 0, while the norms (18) and (19) are approaching 1. It is clear from split scheme (10) that with the increase of arrival intensity, the transition intensities between the state classes \(E_m, m=1,2,\dots ,S\) decrease; the smaller intensities between the classes of states of split model we have, the more accurate state probabilities of initial model we get. For the above initial data the analysis of accuracy of the system performance measures was performed as well (see Tables 2 and 3). It should be noted that, the performance measures (4), (6), (7), (8), (9) are almost the same when using exact and approximate approaches (see Table 2). Only the small errors (less than 5%) are observed while calculating measure (5) and this is acceptable in engineering calculations (see Table 3).

Table 2. Estimation of accuracy of accuracy of the performance measures (4), (6) and (7) for \(N \in [20,120], \lambda \in [20,60]\) ; EV - Exact Value, AV - Approximate Value
Full size table
Table 3. Estimation of accuracy of performance measures (5), (8) and (9)
Full size table

Remark 3

Zero values in Table 3 are not exactly equal to zero and are obtained after rounding the numbers to the 6th order precision.

Now let’s consider the problem of choosing the most optimal server. Let it is possible to choose the server from the predefined collection, where with the increase of the service rate the cost associated with the corresponding server increases as well. It is required to choose such server that will minimize the long-run expected total cost (TC).

$$\begin{aligned} TC = c_h S_{av} + c_r RR + c_b RL_b + c_g RL_r + c_p \varGamma _{av} + c_w L_{av} + c_s P_b \end{aligned}$$
(20)

where \(P_b\) is probability that server is busy, i.e. \(P_b = \sum \limits _{m\,=\,1}^S \sum \limits _{n\,=\,1}^N p(m,n)\). Here \(c_h\) is inventory carrying cost per unit item, \(c_r\) is setup cost per order, \(c_b\) is balking cost per customer, \(c_g\) is reneging cost per customer per unit time, \(c_p\) is the perishing cost per item per unit time, \(c_w\) is waiting time cost of a customer per unit time.

We assume that there are four possible options to choose the server: (1) \(\mu _1=5,\mu _2=1\); (2) \(\mu _1=8,\mu _2=2\); (3) \(\mu _1=10,\mu _2=4\); (4) \(\mu _1=15,\mu _2=5\). The values of the coefficients \(c_s\) when choosing the option \(k,k=1,2,3,4\) are designated as \(c_s^{(k)}\) and defined as: \(c_s^{(1)}=1,c_s^{(2)}=2,c_s^{(3)}=3,c_s^{(4)}=4\). The values of other parameters in the (20) are constants: \(c_h=1,c_r=0.1,c_b=3,c_g=2,c_p=2,c_w=1\).

Table 4. Results of solution of the problem (20) for \(N=150\)
Full size table

Some results of the problem solution for the above data are given in Table 4., where the numbers 1, 2 and 4 indicate the index of the optimal server selection option. It is obvious from the Table 4. that if the inventory level is increasing the optimal option is to choose the server with the lesser service rate, and, vice versa, for the smaller values of the inventory level the optimal option will be the servers with the greater service rates.

5 Conclusion

PQIS model with perishable inventory and positive service time is studied in this paper. It is assumed that some demands do not acquire the item after service completion. When inventory level is zero, demands join or leave the system according to Bernoulli trial. Demands are impatient in the queue when the inventory level is zero. Order lead time, as well as, item perishing time are random variables with the exponential distributions and finite mean. Inventory replenishment policy belongs to \((S-1,S)\) class. Exact and approximate formulas are given for calculation of steady-state probabilities of the given 2-D MC being the mathematical model of the studied system. Exact method is based on the solving of balance equations and is suitable for the moderate values of inventory level and length of the waiting hall for queuing the demands. Approximate approach is based on the state phase merging algorithms of 2-D Markov Chains and it is applicable for the systems of any dimension. High accuracy of the given formulas are shown using numerical experiments. Finally, the optimization problem of choosing optimal server for cost minimization is solved.