State Reduction in Analysis of a Tandem Queueing System with Correlated Arrivals

Abstract

Tandem queueing systems often arise in wireless networks modeling. Queueing models are very suitable for network performance evaluation but the system complexity exponential growth (or state space explosion) could make the analysis barely feasible. The paper presents a comparative study of various methods of a state space reduction for markovian arrival processes (MAP) and phase-type distributions (PH) applied to tandem queueing systems. The applied methods include nonlinear optimization, EM-algorithm and linear minimization. While most of the described algorithms are well-studied, a number of issues arises when applying them to a tandem system of a real wireless network. Particularly, it is shown that while all the algorithms could be applied to tandems with a small number of queues, bigger tandems require additional effort to get the appropriable results. Nevertheless, the results presented show that the departure MAPs reduction may help to solve the state space explosion problem.

1 Introduction

Wireless backbone networks play essential role in modern communication systems. One of the crucial applications of wireless networks are backhauls along the long objects like roads, railways or pipes. Such networks could be used for data transmission from surveillance cameras or sensors to data centers, as well as for providing Internet connection. IEEE 802.11 is a frequently used technology for such networks implementation due to a reasonable data transfer rate and a wide range of the available inexpensive equipment. While IEEE 802.11-based networks have many advantages, the performance of multi-hop networks could be insufficient, thus performance estimation and analysis are required.

A prospective approach for wireless networks performance analysis involves queueing systems with correlated arrivals. Such models become especially attractive when Markov random processes are used for both arrivals and service time distribution modeling. One of the perspective models are tandem queueing networks $MAP/PH/1/N \rightarrow \dots \rightarrow \bullet /PH/1/N$ with cross-traffic [20]. In this queueing system data transmission time is modelled with phase-type (PH) distributions and user traffic is modelled with Markovian arrival processes (MAP) [15]. Representing the user data with Markovian arrival processes allows to take into account correlated nature of real network traffic [5, 13] and PH-distributions provide sufficient approximation for a complex random process describing data transmission. The application of the tandem queueing systems described above for networks with linear topology was studied in general in the previous work [20].

The tandem queueing system analysis is affected by the exponential state space growth with the number of hops increasing. State space reduction techniques could be applied to solve this problem but their usage may lead to the precision loss and needs to be analysed carefully. Another issue to solve is to find a PH-distribution approximating the specific medium access scheme precisely enough.

While a plenty of MAP fitting approaches exists, their application to the wireless networks models analysis faces several difficulties. The data transmission over wireless channels involves a number of constant intervals for channel listening or scheduling which makes service time distribution more deterministic and causes additional correlation in departure processes. Another issue relates to very small values of distributions moments and large values of MAP generator entries (to be noted, the generator itself may contain hundreds or thousands of states), leading to the relative errors growth when applying the fitting algorithms to real data and it further requires an additional effort to improve accuracy. Last but not least is the performance issue since some algorithms could take hours of processor time to converge.

The paper presents a comparative study of various methods of state space reduction for markovian arrival processes and phase-type distributions applied to tandem queueing systems. We study the application of different methods and compare their performance and accuracy. We also provide the results of applying the state reduction techniques to a wireless tandem network containing up to ten stations and show that the departure process state space reduction methods could be applied for a real network analysis.

2 Tandem Queueing System

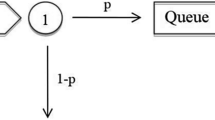
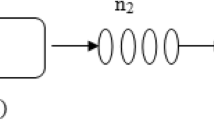
Let us consider $MAP/PH/1/N \rightarrow \dots \rightarrow \bullet /PH/1/N$ system as a wireless network model. This system consists of a chain of servers with PH-distributed service time and a buffer size N. Each server receives the output flow from a previous station and a cross-traffic modelling the data flow from the external users as a Markovian arrival process (MAP), see Fig. 1.

A Markovian arrival process is defined by an irreducible continuous-time Markov chain $\nu _t, t \ge 0$ with a finite state space $\{0,\dots ,W\}$. The process $\nu _t, t \ge 0$ is in state $\nu$ during exponentially distributed time with parameter $\lambda _\nu , \nu \in \overline{0,W}$. After the time expires the chain jumps from state $\nu$ to state $\tilde{\nu }$ with probability $p_{0}(\nu ,\tilde{\nu })$ if the transmission is unobserved and $p_{1}(\nu ,\tilde{\nu })$ otherwise. An observed transmission generates a message. It is also assumed that the process can not stay in the same state $\tilde{\nu }=\nu$ without message generation. Matrices $D_0, D_1$ are used to define the MAP:

$$\begin{aligned} (D_{0})_{\nu ,\nu '}&= {\left\{ \begin{array}{ll} -\lambda _{\nu }, &{} \text {if}~\nu =\nu ' \\ \lambda _{\nu }p_{0}(\nu ,\nu '), &{} \text {otherwise} \end{array}\right. } \\ (D_{1})_{\nu ,\nu '}&=\lambda _{\nu }p_{1}(\nu ,\nu '). \end{aligned}$$

The matrix $D=D_0 + D_1$ defines an infinitesimal generator of the random process $\nu _t, t \ge 0$. Its stationary probability vector $\varvec{\theta }$ is obtained from the system

$$\begin{aligned} \varvec{\theta } D=\mathbf {0},\qquad \varvec{\theta } \mathbf {1} = 1, \end{aligned}$$

where $\mathbf {0}$ is a row vector of zeros and $\mathbf {1}$ is a column vector of ones. The steady-state probability vector $\varvec{\pi }$ of a discrete time Markov chain embedded at arrival instants with a generator $P=(-D_0)^{-1} D_1$ can be obtained as the solution of the following linear system:

$$\begin{aligned} \varvec{\pi } P = \varvec{\pi },\qquad \varvec{\pi } \mathbf {1} = 1. \end{aligned}$$

Fig. 1.

A tandem network model

The average arrival intensity of a MAP is $\lambda =1/\varvec{\pi } (-D_0)^{-1}\mathbf {1}$. The k-th moment and lag-k correlation can be expressed as

$$\begin{aligned} m_k = k!\, \varvec{\pi } (-D_0)^{-k} \mathbf {1}, \quad k \ge 1, \end{aligned}$$

(1)

$$\begin{aligned} l_k = \frac{\lambda ^2 \varvec{\pi } (-D_0)^{-1} P^k (-D_0)^{-1} \mathbf {1} - 1}{\lambda ^2 \varvec{\pi } (-D_0)^{-2} \mathbf {1} - 1}, \quad k \ge 1. \end{aligned}$$

(2)

A phase-type (PH) distribution is defined as a hitting time of the absorbing state in a continuous-time Markov chain with a single absorbing state. Formally, a random variable X is said to have PH-distribution $X \sim PH(S, \varvec{\tau })$ if $\varvec{\tau } \in \mathbb {R}^V$ is a probability distribution and $S \in \mathbb {R}^{V \times V}$ is a subinfinitesimal matrix defining initial states probabilities and transition rates between non-absorbing states respectively. The background Markov chain has the following generator matrix:

$$\begin{aligned} \begin{pmatrix} S &{} -S\mathbf {1} \\ 0 &{} 1 \end{pmatrix} \end{aligned}$$

The k-th moment $\mathbb {E}[X^{k}]$, $X \sim PH(S, \varvec{\tau })$ can be found via the expression

$$\begin{aligned} m_k = k!\, \varvec{\tau } (-S)^{-k} \mathbf {1}, \quad k \ge 1. \end{aligned}$$

(3)

Markovian arrival processes and MAP/PH/1/N queues satisfy the following properties [20,21,22]:

• 1. The result of sifting a MAP with constant probability is also a MAP;

• 2. The composition of a finite number of MAPs is a MAP;

• 3. The departure process of MAP/PH/1/N system is also a MAP.

Note that MAP/PH/1/N queue can lose packets due to the queue overflow and the flow of lost packets is also a MAP. Taking into account these properties it can be shown that a departure process form the first server is a MAP and consequently the arrival processes to all succeeding servers are also MAPs as well as the departure processes. Thus an iterative procedure can be built to compute parameters of a queueing network [20].

However a state space of departure process is expressed as a cartesian product of the state spaces of MAP-input, PH-distribution and the queue length (the number of messages being queued and served). This fact results into an exponential state space growth also referred to as a state space explosion, making a precise analysis barely feasible for an arbitrary number of servers. To solve the state space explosion problem, the departure process of each queue can be approximated with a lower order MAP. Alternative approach is to approximate a process arriving at the queue, i.e. after the composition with cross-traffic.

Another problem considered is to find a PH-distribution adequately describing the medium access scheme operation. This problem is closely related to MAP fitting and will also be discussed further.

3 Related Work

There is a plenty of works describing various MAP and PH fitting. These studies could be divided into three areas. The first direction is the reconstruction of MAP and PH-distributions based on the known moments and lag-k correlation coefficients [7]. The second direction is to improve distributions already constructed and to choose the parameters closest (in the sense of some criterion) to the parameters of the statistical series [16]. The third one is to find MAPs and PH distributions maximizing the likelihood function based on the statistical data. These approaches are often based on the expectation-maximization (EM) algorithms [11, 17, 19]. We refer a reader to [2, 16] for the state-of-art and open problems in this area.

Bodrog et al. [3] describe a method to find second-order matrices for MAP and phase distributions. To describe MAP with a large number of states and a specified correlation coefficient, it was suggested in [7] to build a phase-type distribution with a given number of states first, and then use it to construct MAP matrices. The inter-arrival time distribution is fitted by a PH distribution where the PH generator determines matrix $D_{0}$ of MAP and the initial probability vector $\varvec{\pi }$ determines the steady state probability vector of the MAP embedded process. On the next stage the matrix $D_{1}$ is constructed by approximating the lag-k correlation values. Note that the system for matrix $D_{1}$ contains $2n+1$ equations for $n^{2}$ unknowns leading to a linearly constrained non-linear optimization problem. The matching of order 3 and higher phase distributions was considered in [1, 8, 9].

Bobbio et al. [1] proposes a method to compose minimal order phase type distribution with first three moments and present a simple transformation from APH(n-1) (acyclic phase type distribution of order $n-1$) to APH(n) with an additional phase. The authors also evaluate the bounds for the first three moments of APH(n).

Telek and Horvath [18] present the minimal representations of PH and MAP (Markovian, Jordan, Laplace, moments and MRP representations) and transformations between them. They construct an algorithm to optimize $D_{0}$ and $D_{1}$ matrices of MAP by means of a transformation matrix B such that matrices $B^{-1}D_{0}B$ and $B^{-1}D_{1}B$ minimize a goal function (or improve its value). The method allows improving any MAP fitted by other methods.

Casale et al. [4] propose a MAP fitting algorithm based on the first three moments and high order autocorrelations. They define a process composition method called a Kronecker Product Composition (KPC). Given J MAPs with matrices $D_{0}^{(j)}$ and $D_{1}^{(j)}$, $j=\overline{1,J}$, the composed MAP is defined as

$$\begin{aligned} D_{0}=(-1)^{J-1}D_{0}^{(1)}\otimes \cdots \otimes D_{0}^{(J)},\quad D_{1}=D_{1}^{(1)}\otimes \cdots \otimes D_{1}^{(J)} \end{aligned}$$

(4)

and can be constructed of any order to fit data traces or reduce a state space of an arbitrary MAP. The algorithm consists of three steps. The first step fits the sample squared coefficient of variation and correlation coefficient to minimize the distance between sample lag-k correlations and numerical ones. On the second step, the first and third moments for each MAP $D_{0}^{(j)}$ and $D_{1}^{(j)}$, $j=\overline{1,J}$, are determined from an acceptable region and further optimized to minimize the distance between the sample joint moments and their estimated values. Based on the optimal values of the first three moments and the correlation coefficients, we can construct J MAPs $D_{0}^{(j)}$ and $D_{1}^{(j)}$, $j=\overline{1,J}$ (e.g., of the second order) and compose the final form of matrices (4).

In this paper we use three different approaches to reduce the tandem departure processes state spaces: MAP fitting as a solution of nonlinear optimization problem, EM-based approach [1, 8] and a method of building a phase-type distribution with a given number of states and construction of a $D_1$ matrix for fitting lag-k correlation coefficients [7]. We also use G-FIT approach based on EM procedure [19] to fit the PH distributions. These methods will be described in more details in the following sections.

4 MAP and PH Fitting

The fitting methods allow to construct a markovian arrival process or a phase-type distribution using a given trace (a set of samples) or a set of estimated metrics including moments and lag-k autocorrelation coefficients. In the tandem queueing system described above the fitting methods allow to approximate an operation of a specific communication protocol as well as to reduce the size of the departure processes (the latter case will be discussed in more details in the following section). Here we describe several fitting methods as they are; we suppose the data trace or estimated moments and lag-k autocorrelation coefficients values to be given as an input. The described methods include the expectation maximization (EM) algorithm [11, 17, 19], search for the MAP or PH as a solution of the nonlinear optimization problem constrained by the given moments and lag-k values, and a sequential independent fitting of the PH distribution using the trace or estimated moments values and MAP matrix $D_1$ using lag-k values constraints [7].

4.1 Fitting by Trace

The paper [19] describes a PH distribution fitting technique based on the EM algorithm (the authors call this algorithm G-FIT). MAP fitting using the EM algorithm is described in the papers [11, 17]. While both algorithms will be used in numerical experiments, we describe briefly only G-FIT algorithm here due to the paper space limitations. The details of the algorithms could be found in the papers cited above.

G-FIT algorithm attempts to find a PH distribution fitting the given trace as a Hyper-Erlang distribution. Let X be a Hyper-Erlang random variable with M mutually independent Erlang distributions weighted with probabilities $\varvec{\alpha } = (\alpha _1,\ldots ,\alpha _M)$, m-th chain containing $r_m$ phases jointly forms a vector $\varvec{r} = (r_1, \ldots , r_M)$ and its intensities describe a vector $\varvec{\lambda } = (\lambda _1, \ldots , \lambda _M)$. Then the pdf of X is $f_X(x) = \sum _{m=1}^M \alpha _m \frac{(\lambda _m x)^{r_m -1}}{(r_m-1)!} \lambda _m e^{-\lambda _m x}$.

The parameters $(\varvec{r}, \varvec{\alpha }, \varvec{\lambda })$ are chosen while fitting. Consider EM algorithm to maximize a log-likelihood expression. The authors first apply it for a general set of independents distributions with density functions $p_m$ such that $p(x|\varvec{\varTheta }) = \sum _{m=1}^M \alpha _m p_m(x|\theta _m)$ where $\varvec{\varTheta } = (\varvec{\alpha }, \varvec{\theta })$ and $\theta _i$ is a parameter (or vector) of $p_m$.

Then the authors suggest considering an unobserved random variable Y having values in $\{1, \ldots , M\}$ and specifying which component is used to generate a specific item $x_k$ of the trace in order to simplify the a log-likelihood calculation. Applying this idea the expected value of complete log-likelihood is

$$\begin{aligned} \begin{array}{ll} Q(\varvec{\varTheta }, \hat{\varvec{\varTheta }}) &{} = \sum \limits _{m=1}^M \sum \limits _{k=1}^K \log (\alpha _m) q(m|x_k, \hat{\varvec{\varTheta }}) \\ &{} + \sum \limits _{m=1}^M \sum \limits _{k=1}^K \log (p_m(x_k|\theta _m)) q(m|x_k, \hat{\varvec{\varTheta }}) \end{array} \end{aligned}$$

(5)

where $\varvec{\hat{\varTheta }}$ is an initially chosen parameter set, required to compute a conditional pdf of Y:

$$\begin{aligned} q(y_k|x_k, \hat{\varvec{\varTheta }}) = \frac{\hat{\alpha }_{y_k} p_{y_k}(x_k|\hat{\theta }_{y_k})}{\sum \limits _{m=1}^M \hat{\alpha }_m p_m (x_k|\hat{\theta }_m)}. \end{aligned}$$

(6)

Computing expression (5) for some vector $\varvec{\hat{\varTheta }}$ is a E-step of EM algorithm. For performing M-step (maximization), parameters $\varvec{\varTheta } = (\varvec{\alpha }, \varvec{\theta })$ maximizing $Q(\varvec{\varTheta }, \hat{\varvec{\varTheta }})$ should be found. $\varvec{\alpha }$ can be found by applying Lagrange multipliers to (5); to find $\varvec{\theta }$ a specific pdf required, so let $\varvec{\theta } = \varvec{\lambda }$ for Hyper-Erlang. Then

$$\begin{aligned} \alpha _m = \frac{1}{K} \sum \limits _{k=1}^K q(m|x_k, \varvec{\hat{\varTheta }}), \qquad \lambda _m = \frac{r_m \cdot q(m|x_k, \hat{\varvec{\varTheta }}) }{\sum \limits _{k=1}^K q(m|x_k, \hat{\varvec{\varTheta }}) \cdot x_k }. \end{aligned}$$

(7)

4.2 Fitting as Optimization

The MAP or PH distribution fitting may be described as a solution of the optimization problem constrained by the values of the moments and lag-k autocorrelation coefficient values. Let $\mathbf {m}_{K_m}$ be the vector of the first $K_m$ moments of MAP, $\mathbf {l}_{K_l}$ be the vector of the first $K_l$ lags given in (1) and (2) correspondingly; $\varvec{\mu }$ and $\varvec{\nu }$ be the vectors of moments and lags of a random process to fit correspondingly. Using this notation the problem of MAP fitting can be formulated via solution of a nonlinear algebraic system

$$\begin{aligned} \left\{ \begin{array}{ll} \mathbf {m}_{K_m}(D_0, D_1) = \varvec{\mu }, \\ \mathbf {l}_{K_l}(D_0, D_1) = \varvec{\nu }. \end{array} \right. \end{aligned}$$

(8)

System (8) should be solved for $D_0$ and $D_1$ such that $D = D_0 + D_1$ is an infinitesimal generator and $D_0$ is a subgenerator. By these restrictions, the system may have no solution for some pairs $(\varvec{\mu }, \varvec{\nu })$ and the order N thus a MAP with such lags and moments does not exist. It should be noticed that there are no known closed form margins for the moments and lags values for MAPs and PH distributions of an arbitrary order making the problem much harder.

We suggest that approximate solution of the system can be brought to an optimization problem as follows. Define a loss function $\mathscr {L}(\cdot ) = (|\cdot |)^2$ and a loss functional

$$\begin{aligned} Q(D_0, D_1) = \mathscr {L}(\mathbf {m}_{K_m}(D_0, D_1) - \varvec{\mu }) +\mathscr {L}(\mathbf {l}_{K_l}(D_0, D_1) - \varvec{\nu }). \end{aligned}$$

(9)

Then a proper MAP is found as a solution of $(D_0, D_1) = \mathop {\hbox {arg min}}\limits _{D_0, D_1} Q(D_0, D_1)$. The fitting procedure is iterative and start with the lower possible N. The tolerance $\epsilon$ should be chosen such that $\min Q(D_0, D_1) < \epsilon$ holds. If for given N there is no solution $(D_0, D_1)$ the order N should be incremented and the new fitting procedure starts until the criterion is satisfied or the maximum number of iteration is exhausted. Otherwise, the pair $(D_0, D_1)$ with the lower error $\min Q$ is supposed to be a solution. Also another loss function $\mathscr {L}$ can be considered.

For PH distribution the optimization problem can be simplified as it has zero lags and less difficulty in moments computation. The loss functional for PH fitting is as follows:

$$\begin{aligned} Q(\varvec{\tau }, S) = \mathscr {L}(\mathbf {m}_{K_m}(\varvec{\tau }, S) - \varvec{\mu }). \end{aligned}$$

The problem described is generally nonconvex which leads to local optima solutions and require additional effort to randomize the initial vectors and look for the best solution.

4.3 MAP Fitting by Given PH

The MAP moments depend on the matrix $D_0$ and a steady state probability distribution of the embedded discrete process which allows to fit them independently of the lag-k autocorrelation values; the lag-k values could be used to find the appropriate matrix $D_1$ [10]. Suppose we have a PH($\varvec{\tau }, S$) distribution. It is assumed that the MAP($D_0, D_1$) has $D_0 = S$ and $\varvec{\pi } = \varvec{\tau }$ where $\varvec{\pi }$ is a steady state probability distribution of the embedded Markov chain with the transition matrix $P = (-D_0)^{-1}{D_1}$. Combining the restrictions for $D_1$ to be held and considering the autocorrelation $c_{corr}$ the authors [10] obtained a linear system:

$$\begin{aligned} D_1 \mathbf {1} = -D_0 \mathbf {1}, \quad \varvec{\pi } (-D_0)^{-1}D_1 = \varvec{\pi }, \quad \varvec{\delta } D_1 \mathbf {f} = \upsilon \end{aligned}$$

where the values $\varvec{\delta }$, $\mathbf {f}$ and $\upsilon$ can be derived from the lag-1 expression (2). Considering a vector $\mathbf {x} = [\mathbf {d}_1, \mathbf {d}_2, \ldots , \mathbf {d}_M ]^T$ where $\mathbf {d}_i$ is the i-th column vector of $D_1$, the authors has transformed these three matrix equations into one that have the following form:

(10)

This linear equations should be solved for non-zero elements of $\mathbf {x}$. To find the higher-order lags the authors suggest to use an optimization procedure.

5 State Reduction

While the process fitting is the only approach for obtaining PH distributions of the service time when only the trace is known, the departure MAP processes state space could be reduce by other methods. Generally any reduction method supposes the given matrices $D_0$ and $D_1$ of a MAP to decrease the order. For PH-distribution the problem is set in the same way taking into account a vector $\varvec{\pi }$ and a matrix S instead of $D_0$ and $D_1$.

To apply the fitting methods described in the previous section to MAP state space reduction, the moments and lags of the source MAP should be calculated. If the fitting method requires a trace (e.g. EM algorithm), the source MAP should be randomized to get a trace. It should be noticed that for the MAPs with a huge number of states the consistent trace may contain over a million samples. To simplify the problem and avoid the randomization, two additional techniques of state space reduction are described below including the nonlinear optimization problem solving constrained by the distance between the cumulative distribution functions and cutting the tail states of the QBD (quasi-death-and-birth) process.

5.1 Reduction as Optimization

The state reduction can be performed by solving an optimization problem. For that aim let us consider the difference of the stationary cumulative distribution function of the given MAP and some lower order MAP

$$\begin{aligned} \Delta F(t) = F(t) - F'(t) = \varvec{\pi }' e^{D_0't}\mathbf {1}' - \varvec{\pi } e^{D_0t}\mathbf {1}. \end{aligned}$$

Taking into account that $e^{D_0t} \approx I + \sum _{k=1}^K \frac{1}{k!} D_0^k t^k$ for some K and $\varvec{\pi }\mathbf {1} = \varvec{\pi }'\mathbf {1}' = 1$ this difference takes a form:

$$\begin{aligned} \Delta F(t) = \sum \limits _{k=1}^K \frac{t^k}{k!} \left( \varvec{\pi }' (D_0')^k \mathbf {1}' - \varvec{\pi } D_0^k \mathbf {1} \right) = \sum \limits _{k=1}^K w(k, t) \left( \varvec{\pi }' (D_0')^k \mathbf {1}' - \varvec{\pi } D_0^k \mathbf {1} \right) , \end{aligned}$$

(11)

where $w(k, a) = a^k / k!$ is a weight for the k-th power of $D_0$. Multiple ways to define the weights exist; here we define the weights as $\frac{T^{k+1}}{(k+1)!}$ applying $a=T$ that arises out of integrating (11) in a range [0, T]

$$\begin{aligned} \Delta F = \int \limits _0^T \Delta F(t) dt =&\sum \limits _{k=1}^K \left[ \int \limits _0^T \frac{t^k}{k!} dt \right] \left( \varvec{\pi }' (D_0')^k \mathbf {1}' - \varvec{\pi } D_0^k \mathbf {1} \right) \end{aligned}$$

Taking $D_0' = S, D_1' = \tau$ in case of PH and $D_0, D_1$ in case of MAP reduction, the loss functional can be expressed as

$$\begin{aligned} Q(D_0', D_1') = \mathscr {L}(\Delta F(D_0', D_1')). \end{aligned}$$

(12)

5.2 State Truncation

This method is applied to servers without the memory, i.e. MAP/PH/1 systems when the utilization coefficient is sufficiently small. A system with a limited memory could be approximated if it has a very large capacity. The authors of [6] consider the departure MAP as a pair of block matrices and suggest to trunk the tail blocks stating with some level $N + 1$ by merging the stationary probabilities into N-th state: $\varvec{\pi }_N^+ = \sum _{i=N+1}^\infty \varvec{\pi }_i$ and considering matrices:

$$\begin{aligned} \begin{array}{ll} \hat{A}_0 = &{} A_0 + A_1, \\ \hat{A}_2 = &{} \text {diag}(\varvec{\pi }_N)\text {diag}^{-1}(\varvec{\pi }_N + \varvec{\pi }_N^+) A_2, \\ \check{A}_2 = &{} \text {diag}(\varvec{\pi }_N^+)\text {diag}^{-1}(\varvec{\pi }_N + \varvec{\pi }_N^+) A_2 \end{array} \end{aligned}$$

to describe the reduced matrices of the departure MAP

(13)

The matrices $A_i, B_i$ for $i=0,1,2$ describing the blocks of the initial departure MAP and their definition are provided in [6]. This method allows to restrict the state space growth by decreasing the effective queue length. Unfortunately, the state space continues exponential increasing along with the number of queues in the tandem since the size of the service time PH-distribution is greater than 1 which makes the method not applicable to analyse a tandem queuing systems with an arbitrary number of queues.

6 Experimental Results

In the numerical experiments we used three different methods of MAP fitting:

• 1. Searching for a MAP (defined by the matrices $D_0$ and $D_1$) as a solution of an optimization problem constrained by the values of the first moments and lags (this method is referred to as OPT below).

• 2. MAP fitting using the EM algorithm [11];

• 3. Successive independent fitting of $D_0$ matrix as a PH distribution using the moments or a trace provided and looking for $D_1$ as a solution of the optimization problem constrained by the lag-k correlation coefficients (INDI in the following text). The algorithm was described in [7].

Queueing system analysis framework [14] was developed in the Python 3 language using NumPy/SciPy packages. We used EM algorithms implementations from a BuTools [12] package. Simulation models were developed using OMNeT++ network simulator. All the experiments ran on a generic laptop with i7 processor and 16 GB of RAM.

While the OPT method shown good results, it often fell into a local optima and required initial solutions randomization to converge good. The key problem is a lack of easy checkable conditions on the solution existence and moments and lags values, so it was often hard or impossible to find a solution of a given order under the given constraints while the attempt to find it takes significant time. It should be noted that algorithm converged rapidly for small MAPs and PHs with up to 8 states but required lots of time when called for bigger orders (5 min and more). It was also noticed that order increasing didn’t provide better results in many cases so we decided to use the algorithm with small orders. The solution error was also reduced by normalizing the moments and the $D_0$ and $D_1$ matrices consequently.

The EM algorithm provided good results but required too much time to converge. Typically, it takes up to 20 min to fit a given trace with 40000 samples using a MAP with 12 states. While it is possible to speed up the algorithm as described in [19], it didn’t completely solve the problem and the algorithm still required lots of processor resources. Since the algorithm had to be applied several times, we decided to limit the search with MAPs containing up to four states. The similar problem arose during G-FIT execution while it still allowed to fit PH distributions with up to 10 states in a reasonable time. Due to the order limitation, the EM algorithm for MAP fitting provided the worst results considering moments and lags matching.

The third (INDI) approach was implemented as described in the paper [7]. We tried both nonlinear optimization and G-FIT [19] algorithm for fitting the PH distribution for $D_0$ matrix construction, and G-FIT provided much better overall results. To keep the problem of $D_1$ construction linear, we limited the constraints with lag-1 correlation. In this case the problem could be solved as a linear minimization problem $||Ax - b ||_2 \rightarrow \min$. The key problem was that the existence of $D_1$ matrix was dependent on the particular $D_0$ and it sometimes required several $D_0$ fitting iterations to find an appropriate matrix to make the $D_1$ construction with a reasonable error possible.

First of all, the fitting algorithms were applied to fit the PH-distribution approximating data transmission intervals. To simplify the analysis, a tandem consisting of two stations was considered. The wireless channel bitrate was 5 mbps (e.g. a slow sensor network link) and an arrival traffic bitrate was 2.8 mbps. The arrival traffic was described with a MAP approximating a real network trace LBL-TCP-3 described in [10]:

$$ D_0 = \begin{bmatrix} -508.11&0&0&0 \\ 0&-526.82&0&0 \\ 0&0&-112.88&0 \\ 0&0&0&-292.87 \end{bmatrix} $$

$$ D_1 = \begin{bmatrix} 281.9&226.06&0&0.15872 \\ 526.66&0.024505&0.13422 \\ 0&0&82.094&30.79 \\ 0.056728&0&38.799&254.01 \end{bmatrix} $$

The packets sizes were assumed to have a normal distribution truncated to positive values with an average value 12 kbit and standard deviation 3 kbit. We applied G-FIT algorithm [19] and nonlinear optimization approach with a number of moments equations equal to 3 for PH orders 4, 6 and 8. The results are shown on Fig. 2 (while more lags could allow to fit the service time distribution better, it was crucial to use a small distribution due to the state space growth appearing on the next stations). It should be also noticed that applying G-FIT for a greater number of states takes a rather long time due to combinatorial complexity of inspecting various structures of the Hyper-Erlang distributions.

Fig. 2.

Service time fitting. Lines labeled as ‘opt-n’ show solutions of a nonlinear optimization problem and ‘gfit-n’ show G-FIT [19] where ‘n’ is the order of PH

Table 1. Moments and lags of the approximated departure processes from the first station.

The PH distribution obtained with G-FIT containing 8 states was used for the later computations. This distribution matched the mean value and had a 32% error in standard deviation. It was used to build the departure process of the first station having capacity 5, which was approximated with the EM-algorithm [11], nonlinear optimization with moments and lags constraints and the approach of independent construction of a $D_0$ matrix as a PH-distribution and $D_1$ matrix with linear constraints [7]. In the latter approach only the lag-1 correlation coefficient was constrained. The results are shown in Table 1. The last row describes a separate $D_0$ fitting with G-FIT and $D_1$ as a solution of linear minimization problem [7]. It should be noticed that EM-algorithm was used for a small MAP order equal to 3, its stop condition was reduced to $10^{-3}$ and the maximum number of iterations was 100. This could be the reason of the worst results shown.

Fig. 3.

Number of packets probability distributions of the second station with and without the cross-traffic and various fitting algorithms.eps

Fig. 4.

End-to-end delays and busy ratios computed for a wireless network tandem model.

The system size distribution of the second station was also investigated. Since the arrival traffic required more than a half of the modeled channel bandwidth, adding the cross-traffic caused a system overflow. All the described algorithms allowed to get sufficient approximation of the system states distributions as shown on Fig. 3.

Finally, the OPT approach was applied to fit the departure MAP processes in the model of a real wireless network containing 10 nodes and operating under the IEEE 802.11 standard. To simplify the simulation a simple DCF channel access scheme was considered and the wireless channels provided 54 mbps bitrate. Each arrival process was described with the same MAP as above. The cross-traffic arrived at each wireless station.

The measured transmission time was fitted by the first three moments with 0.05 relative error with a PH-distribution $PH(S, \tau )$:

$$ S = \begin{bmatrix} -6267.56&1412.75&0.001814&943.60 \\ 1008.28&-3337.85&0.000100&258.21 \\ 0.002726&0.0000027&-107.766&2.744 \\ 1565.226&1563.65&3.9327&-6778.49 \end{bmatrix} $$

$$ \tau = \begin{bmatrix} 0.038351&0.961517&0&0.000132 \end{bmatrix} $$

The measured end-to-end delay and busy ratios are shown on Fig. 4. The busy ratios were approximated well but end-to-end delays approximated values were not precise. This problem could be solved with other approximation methods or fitting PH distributions and MAP arrivals with higher order processes.

7 Conclusion and Future Work

It was shown that departure MAP state space reduction provided sufficient precision while allowing to analyze the tandem queueing systems of an arbitrary length. However the fitting algorithms performance along with time limitations may lead to accuracy degradation. The nonconvex nature of the problems arising leads to local optima convergence and impossibility to find the optimal solution in many cases. To face these issues, a randomization of initial parameters should be applied to find multiple optima and more efficient algorithms along with the existing algorithms optimization should be explored. These investigations are the focus of our future work.

The combined PH fitting using G-FIT algorithm with $D_1$ construction using autocorrelation coefficient constraint provided a good accuracy with sufficient performance and looks promising. The best results were retrieved with the solution of the nonlinear optimization problem constrained by the moments and lag-k autocorrelation coefficient constraints while the EM algorithm application to MAP fitting was limited by the performance issues. While several approaches were studied in this paper, there is still a plenty of methods to be examined, including the KPC approach. These methods would be applied and optimized in the future works.

Finally, it should be noticed that the lag-k autocorrelation coefficients of the departure processes grow along with the number of stations in the tandem network. While the typical moments values allowed to fit the service time distribution with a good precision, it was often a problem to find a valid MAP process with the precise autocorrelation coefficients values. The solution may be found using the processes with the greater number of states, but this requires more intelligent methods of predicting the structure of the approximating MAPs due to performance limitations. These methods will also be studied in the future works.